Функции нескольких переменных. Ряды. Обыкновенные дифференциальные и разностные уравнения
Контрольная работа №3 (3 семестр)
Темы: Функции нескольких переменных.
Ряды Обыкновенные дифференциальные и разностные уравнения
Задача 1.
Задана
функция 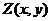 . Найти:
. Найти:
а)
наименьшее и наибольшее значение функции 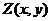 в
ограниченной области Д,
в
ограниченной области Д,
б)
вектор 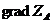 - градиент функции
- градиент функции 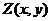 в точке
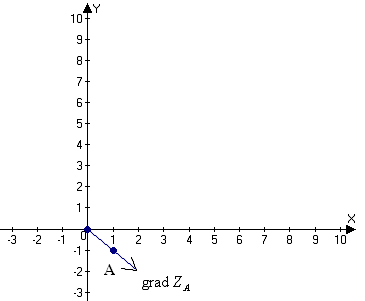
А. Область Д и вектор
в точке
А. Область Д и вектор 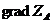 изобразить на чертеже.
изобразить на чертеже.
.10.
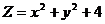 ; а) Д:
; а) Д: 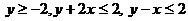 ; б)
; б) 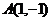 .
.
Решение
а)
наименьшее и наибольшее значение функции 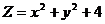 в
ограниченной области Д
в
ограниченной области Д 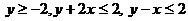 .
.
Построим
область Д.
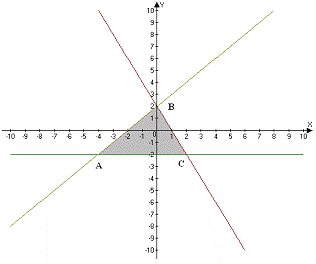
Найдем стационарные точки:
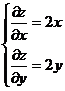
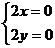
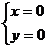
функция ряд интеграл дифференциальный
М(0; 0) - стационарная точка
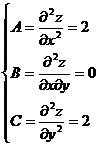
∆
= АС - В2 = 2∙2 - 02 = 4 > 0
В
т. М(0; 0) минимум функции Z. Zmin = 02 + 02 + 4 = 4
Рассмотрим
по отдельности три отрезка:
1) АВ: y = 2 + x, -4 ≤ x ≤ 0. = x2 +
(2 + x)2 + 4 = 2x2 + 4x + 8
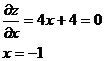
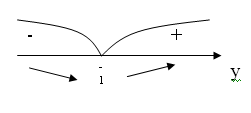
В
т.x = -1 - min функции
z(-1) = 2∙(-1)2 + 4(-1) + 8 = 6
2) ВС: y = 2 - 2x, 0 ≤ x ≤ 2. = x2 +
(2 - 2x)2 + 4 = 5x2 - 8x + 8
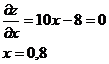
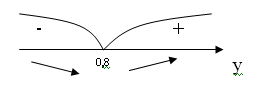
В
т.x = 0,8 - min функции
z(0,8) = 5∙0,82
- 8∙0,8 + 8 = 4,8
3) AC: y = -2, -4 ≤ x ≤ 2.
z = x2 + (-2)2 + 4 = x2
+ 8
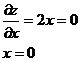
Данная
точка уже исследовалась.
Найдем
значения функции в граничных точках:
z(A) = z(-2;
-4) = (-2)2 + (-4)2 + 4 = 24
z(B) = z(0;
2) = 0 + 22 + 4 = 8
z(C) = z(2;
-2) = 22 + (-2)2 + 4 = 12
Таким
образом, получим, что наименьшее значение функции z достигается в
точке (0; 0) zнаим = 4,
а наибольшее значения функции в точке А(-2; -4) zнаиб = 24.
б)
вектор 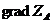 - градиент функции
- градиент функции 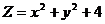 в
точке А(1; -1).
в
точке А(1; -1).
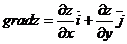
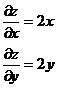
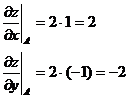
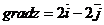
Задача 2
Исследовать на сходимость данный ряд:
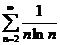 .
.
Решение
Воспользуемся интегральным признаком Коши:
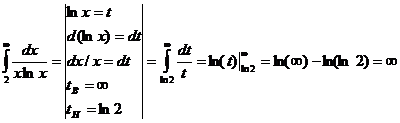
Так
как интеграл 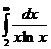 расходится, то и ряд
расходится, то и ряд 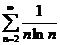 тоже расходится.
тоже расходится.
Задача 3
Найти область сходимости данного ряда.
.10. 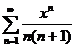 .
.
Решение
Общий
член ряда 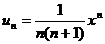
Для
исследования ряда на абсолютную сходимость применим признак Даламбера.
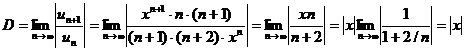
Таким
образом, при 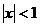 , то есть при -1 < x < 1
исходный ряд сходится абсолютно.
, то есть при -1 < x < 1
исходный ряд сходится абсолютно.
Выясним
вопрос о сходимости ряда на концах интервала.
При
х = -1 заданный ряд принимает вид:
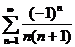
Это
числовой знакочередующийся ряд. Его общий член по абсолютной величине монотонно
убывает и стремится к нулю при 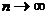 . Таким
образом, оба условия признака Лейбница выполнены и ряд сходится.
. Таким
образом, оба условия признака Лейбница выполнены и ряд сходится.
При
х = 1 заданный ряд принимает вид:
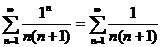
Ряд
расходится как гармонический.
Область
сходимости исходного степенного ряда: 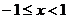 . Вне
этого интервала ряд расходится.
. Вне
этого интервала ряд расходится.
Задача 4
Найти общее решение или общий интеграл дифференциального уравнения:
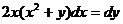 .
.
Решение
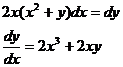
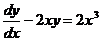
Подставим
в исходное уравнение
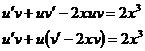
Подберем
функцию v = v(x) так, чтобы выражение, содержащееся в скобке было
равно нулю.
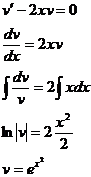
Для
определения функции u(x) имеем
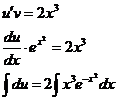
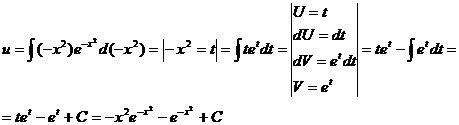
Таким
образом, общее решение исходного дифференциального уравнения имеет вид:
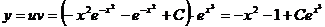
Задача 5.
Найти частное решение дифференциального уравнения, удовлетворяющее
заданным начальным условиям.
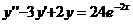 ,
,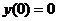 ,
,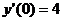 .
.
Решение
Находим общее решение Y
однородного уравнения с теми же коэффициентами, что и в левой части заданного
уравнения.
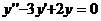
Составим
характеристическое уравнение
k2 - 3k + 2 = 0
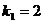
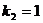
Общее
решение однородного уравнения имеет вид:
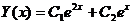
Подбираем
частное решение исходного неоднородного уравнения.
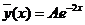
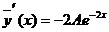
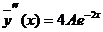
Подставим
в исходное уравнение.
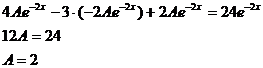
Общее
решение заданного неоднородного дифференциального уравнения имеет вид
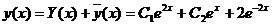
Найдем частное решение дифференциального уравнения.
Подставляя начальные условия в общее решение и его производную, получим
систему уравнений относительно С1 и С2.
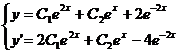
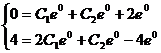
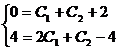
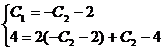
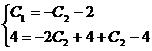
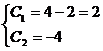
Частное
решение линейного неоднородного дифференциального уравнения имеет вид: