Точка экстремума и точка перегиба. Расчет области функции
ГОУ ВПО
«ВСГАО»
Кафедра
математики и методики обучения математике
Контрольная
работа по дисциплине
«МАТЕМАТИКА»
Выполнила:
Шепчугова
Наталья Викторовна
Курс:
1 (2010-2011 уч.годы)
Проверил:
ст. пр. Курьякова Т.С.
Иркутск -
2010
Задание 1.
Исследование функции
Элементарное исследование:
Область определения функции
очки пересечения с осями координат, промежутки
знакопостоянства.
Пересечение с осью ОХ: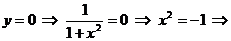 
График не
пересекает ось ОХ
Пересечение с осью ОУ: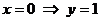 
. В точке 
.
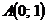При любых значениях x,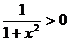 
следовательно,
график функции располагается выше оси ОХ на всей числовой прямой.
Исследование функции на непрерывность:
Следуя из области определения -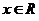
, график 
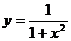не имеет
точек разрыва, т.е. является непрерывным
Асимптоты
Наклонные асимптоты:
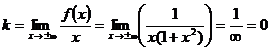
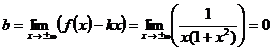
Наклонная асимптота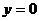 
или ось ОХ.
Исследование функции на
четность-нечетность и периодичность:
;
;
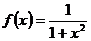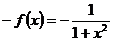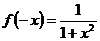
Функция является четной, так как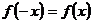 
,
следовательно, ее грфик симметричен относительно оси ОХ.
Функция не является периодической,
так как равенство
будет верно только в случае, если T=0
Исследование функции по первой
производной (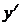
)
Определить точки экстремума
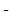
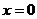- точка максимума
Экстремум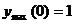 
. 
.
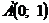Определить промежутки монотонности
Функция возрастает при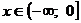 
.
Функция убывает при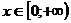 
.
Исследование функции по второй
производной (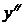
)
Найдем вторую производную:
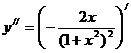
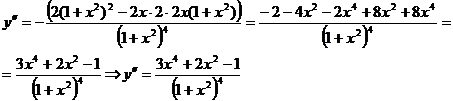
точки перегиба.
Получаем точки:
Определим характер выпуклости
Функция выпукла вниз при
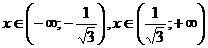
Функция выпукла вверх при
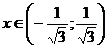
Дополнительные точки:
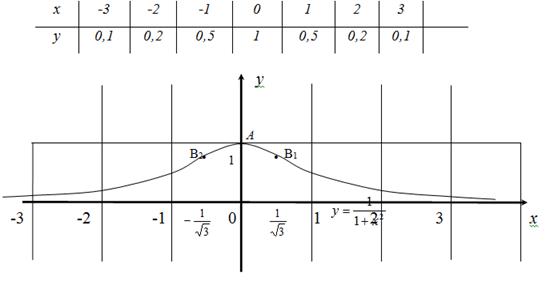
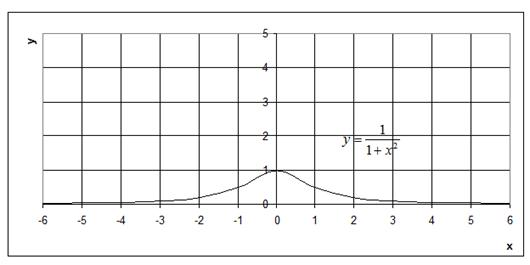
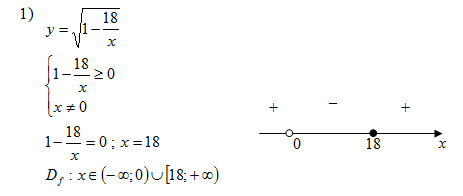
Задание 2. Найти область определения
функций, заданных аналитически
координата экстремум функция
непрерывность
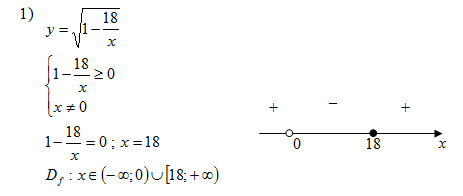
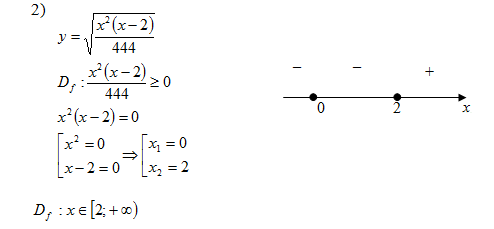
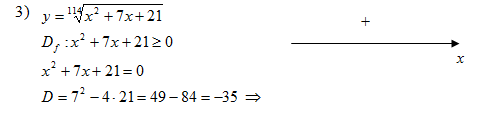
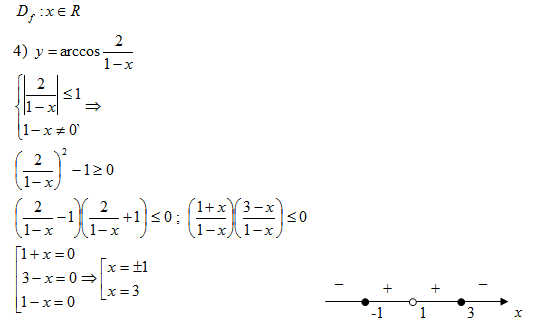
Уравнение не имеет корней
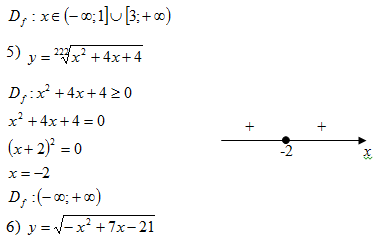
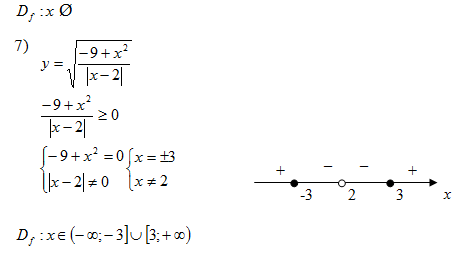
Найдём вершину параболы:
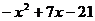
Вершина параболы -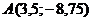
, ветви
направлены вниз, т.е. парабола расположена ниже оси OX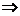 
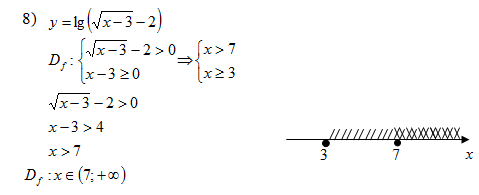
Задание 3
m)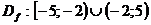
n) Функция
возрастает:
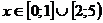
o) Функция
убывает:
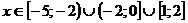
p)
Экстремумы: т. максимума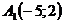 
т. минимума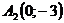 
r)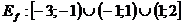 
s) Точка
минимума x=0
t) Функция ни
четная, ни нечетная (общего вида), т.к. её график не симметричен ни
относительно оси OX, ни начала координат.)
Нули
функции: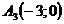
, 
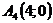
v)
)
)
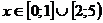
Задание 4
Так как функция имеет период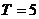 
, то
отсчитывая от начала координат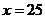 
через 5 периодов будет
соответствовать 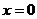, и иметь
значение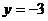 
График функции расположен ниже оси OX на
промежутке 
,
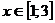следовательно, на этом промежутке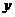 
принимает отрицательные значения,
точка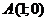 
является
нулём графика функции и точкой экстремума исходной функции.
Следовательно, функция убывает на
промежутке 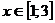. Длина
промежутка убывания равна: 