|
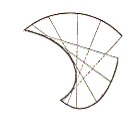
|
|
|
|
Рисунок 6.
|
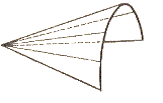
Рисунок 7.
|
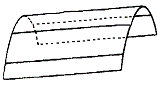
Рисунок 8.
|
К числу развертывающихся поверхностей следует причислить и плоскость,
которая очевидно может рассматриваться и как поверхность касательных плоскостей
кривой, и как коническая, и как цилиндрическая поверхность с прямолинейной
направляющей.
1.5 Огибающая касательных плоскостей
Если в каждой точке кривой
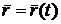
задана
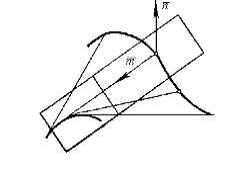
определенная касательная плоскость с единичным нормальным вектором 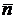 (рисунок 9), то уравнение семейства этих плоскостей
будет иметь вид
(рисунок 9), то уравнение семейства этих плоскостей
будет иметь вид
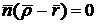 . (21)
. (21)
|
|
|
Рисунок 9.
|
Дифференцируя
это уравнение по параметру 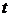 , от
которого зависит
, от
которого зависит 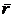 и
и 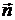 , и
принимая во внимание, что
, и
принимая во внимание, что 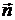 перпендикулярен касательному вектору кривой, получим
перпендикулярен касательному вектору кривой, получим
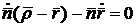
или
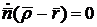 . (22)
. (22)
Уравнения
(21) и (22) определяют характеристику семейства и, очевидно, удовлетворяются
при
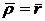 .
.
Отсюда
следует, что характеристика семейства плоскостей, касающихся данной кривой,
проходит через точку прикосновения этой кривой, соответствующей плоскости
семейства.
Этот
же результат, очевидно, можно выразить следующим образом: кривая, касающаяся
каждой плоскости семейства, лежит на огибающей этого семейства.
Зная
точку, через которую проходит характеристика, для полного ее определения
достаточно вычислить ее направляющий вектор 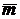 . Для
этого примем во внимание, что
. Для
этого примем во внимание, что 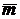 перпендикулярен
нормальным векторам плоскостей (21) и (22) и может быть определен условиями
перпендикулярен
нормальным векторам плоскостей (21) и (22) и может быть определен условиями
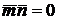 ;
; 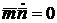 . (23)
. (23)
Уравнение
характеристики может быть получено и в явном виде
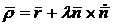 . (24)
. (24)
1.6 Развертывающаяся поверхность, составленная из нормалей
Предположим, что в каждой точке кривой
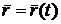
выбрана
нормаль с направляющим единичным вектором
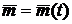 .
.
Найдем
условие, которому должен удовлетворять этот вектор, для того, чтобы выбранные
нормали были образующими развертывающейся поверхности.
Так
как данная кривая лежит на этой поверхности, то последняя есть огибающая
касательных плоскостей этой кривой и вектор 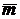 должен
удовлетворять условию (23)
должен
удовлетворять условию (23)
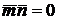 ;
; 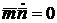 .
.
Дифференцируя
первое из них, получим
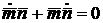 .
.
Очевидно,
что для выполнения второго из них необходимо и достаточно, чтобы
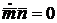 . (25)
. (25)
С
другой стороны, так как вектор 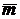 единичный,
то
единичный,
то
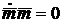 . (26)
. (26)
Векторы
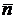 и
и 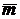 лежат в
нормальной плоскости данной кривой, а вектор
лежат в
нормальной плоскости данной кривой, а вектор 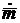 перпендикулярен
им вследствие (25) и (26) и, следовательно, направлен по касательной, так что
перпендикулярен
им вследствие (25) и (26) и, следовательно, направлен по касательной, так что
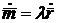 . (27)
. (27)
Обратно,
из (27) следует (25) и (26), и если вектор направлен по нормали, то для него
выполняются условия (23).
Итак:
для того, чтобы семейство нормалей данной кривой образовало развертывающуюся
поверхность, необходимо и достаточно, чтобы производная единичного вектора этих
нормалей была коллинеарна касательной этой кривой.
Чтобы
найти направление вектора 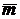 , представим его в виде
, представим его в виде

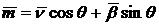 ,
,
обозначая
через 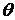 угол, который он образует с главной нормалью данной
линии.
угол, который он образует с главной нормалью данной
линии.
Дифференцируя
последнее равенство и пользуясь формулами Сере-Френе, получим после простых
преобразований
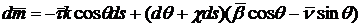 .
.
Для
того, чтобы 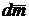 и
и 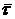 были
коллинеарны должно выполнятся условие
были
коллинеарны должно выполнятся условие
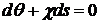 , (28)
, (28)
которое
и позволяет определить искомый угол 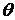 в виде
интеграла
в виде
интеграла
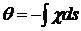 . (29)
. (29)
Таким
образом, мы видим, что из нормалей всякой кривой можно составить
развертывающуюся поверхность и при том с известным произволом, соответствующим
произволу в выборе постоянного интегрирования.
Этому
произволу можно дать простое геометрическое истолкование. Предположим, что из
нормалей данной кривой построены две различные развертывающиеся поверхности,
причем их характеристики образуют углы 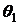 и
и 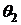 с главными нормалями данной кривой.
с главными нормалями данной кривой.
Оба
эти угла должны удовлетворять условию (23). Поэтому, обозначив через 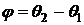 , получим
, получим
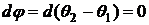
или
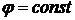 .
.
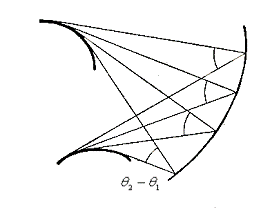
Отсюда следует, что если нормали, образующие развертывающуюся
поверхность, повернуть в нормальных плоскостях на постоянный угол, то они и
после поворота будут образовывать развертывающуюся поверхность (рисунок 10).
|
|
|
Рисунок 10.
|
Формула
(28) позволяе6т решить вопрос о виде кривых, у которых главные нормали или
бинормали образуют развертывающуюся поверхность. В этих случаях 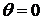 или
или 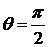 ;
;
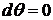 ,
,
и
следовательно, 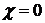 , так что это возможно только для плоской кривой.
, так что это возможно только для плоской кривой.
2. КРИВОЛИНЕЙНЫЕ КООРДИНАТЫ
2.1 Криволинейные координаты
Пусть на поверхности задано некоторое семейство линий, зависящих от
одного параметра. Будем называть это семейство «правильным» в некоторой области
точек поверхности, если через каждую точку этой области проходит одна и только
одна линия семейства.
Если на поверхности заданы два семейства линий, то будем говорить, что
они правильны, причем будем предполагать, что в этой области линии различных
семейств не совпадают между собою и не касаются друг друга и пересекаются
только в одной точке.
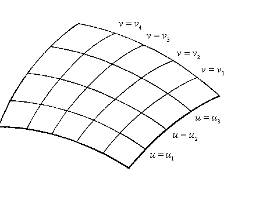
Предположим,
что на поверхности задана сеть, удовлетворяющая всем этим условиям. Пусть линия
одного семейства этой сети определяется значением параметра 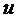 , а линия другого семейства значением параметра
, а линия другого семейства значением параметра  (рисунок 11).
(рисунок 11).
|
|
|
Рисунок 11.
|
Так
как через каждую точку области проходит вполне определенные линии каждого
семейства, то всякой такой точке соответствуют вполне определенные значения
параметров  и
и  . С
другой стороны, задание этих параметров, соответствующих кривым, пересекающимся
в точке области, определит положение этой точки.
. С
другой стороны, задание этих параметров, соответствующих кривым, пересекающимся
в точке области, определит положение этой точки.
Вследствие
этого значения параметров 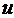 и
и 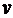 ,
определяющих кривые сети, пересекающиеся в данной точке поверхности, называются
криволинейными координатами этой точки.
,
определяющих кривые сети, пересекающиеся в данной точке поверхности, называются
криволинейными координатами этой точки.
Сами
эти линии и образованная ими сеть называются координатными.
Вдоль
координатной линии изменяется только одна криволинейная координата, другая же
остается постоянной.
Рассмотрим
некоторые примеры.
.
Семейство прямых, параллельных между собою, очевидно, будет правильным во всей
плоскости. Два таких семейства, образованных прямыми различных направлений
(например, ортогональных между собою), образуют сеть. Параметризируя эти
семейства так, чтобы каждой прямой соответствовало, например, значение
расстояния этой прямой от некоторой, принятой за начальную, и приписывая этому
расстоянию знак, зависящий от того, на какую сторону от начальной прямой взята
данная, мы и получим обычную декартову систему координат (рисунок 12).
|

|
|
Рисунок 12.
|
. Рассмотрим сеть, образованную прямыми некоторого собственного пучка и
семейством концентрических окружностей с центрами в вершине этого пучка. Оба
семейства будут правильными во всей плоскости за исключением вершины пучка.
Такую исключительную точку мы будем в дальнейшем называть особой точкой
координатной сети. Параметризируем семейство прямых, принимая за начальную, и
данной прямой пучка, а семейство окружностей параметризируем, относя каждой из
них значение ее радиуса. Система криволинейных координат, которую мы получим,
таким образом, совпадает с полярной (рисунок 13).
|

|
|
Рисунок 13.
|
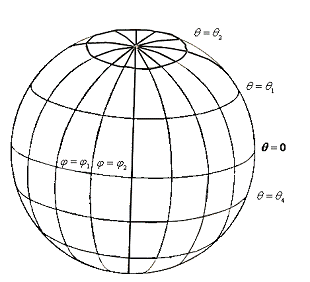
. В качестве третьего примера рассмотрим так называемые «географические»
координаты на сфере. Зафиксировав «полярную ось» - один из диаметров это сферы
- рассмотрим семейство «меридианов», т.е. больших кругов, полученных от
пересечения поверхности сферы плоскостями, содержащими этот диаметр.
Параметризируем его, приняв за параметр «долготу», т.е. угол между плоскостью
меридиана, принятого за начальный, и плоскостью данного меридиана. Второе
семейство «параллелей» получим, пересекая поверхность сферы плоскостями,
перпендикулярными избранному вначале диаметру. Это семейство будет содержать
один большой круг - «экватор». За параметр второго семейства примем «широту» -
угловую меру дуги меридиана, заключенной между плоскостью экватора и плоскостью
данной параллели, приписав ему знак в зависимости от того, на каком полушарии
«северном» или «южном» расположена параллель. Оба семейства будут правильными
на всей поверхности сферы за исключением «полюсов», т.е. точек пересечения
поверхности сферы с полярной осью (рисунок 14).
|
|
|
Рисунок 14.
|
2.2 Параметрическое уравнение поверхности
Если
на поверхности введены криволинейные координаты, то говорят также, что
поверхность параметризована. В таком случае, всякой паре значений параметров 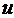 и
и 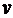 соответствует
определенная точка поверхности. Значение радиус-вектора этой точки вполне
определяется заданием значений независимых переменных
соответствует
определенная точка поверхности. Значение радиус-вектора этой точки вполне
определяется заданием значений независимых переменных 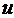 и
и 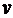 , и мы
можем сказать, что векторная переменная
, и мы
можем сказать, что векторная переменная 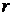 является
функцией двух скалярных аргументов
является
функцией двух скалярных аргументов 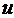 и
и 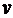 , и записать это так
, и записать это так
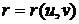 . (30)
. (30)
Зависимость
радиус-вектора точки параметризованной поверхности от криволинейных координат
этой точки называется параметрическим уравнением поверхности. Найдем
параметрические уравнения поверхности, соответствующие трем примерам
предыдущего пункта.
.
Пусть 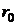 есть радиус-вектор начала, а
есть радиус-вектор начала, а 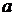 и
и 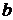 координатные
векторы декартовой системы координат плоскости. Обозначая через
координатные
векторы декартовой системы координат плоскости. Обозначая через 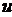 и
и 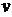 декартовы
координаты, соответствующие этой системе, получим параметрическое уравнение
плоскости
декартовы
координаты, соответствующие этой системе, получим параметрическое уравнение
плоскости
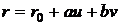 . (31)
. (31)
.
Предположим теперь, что 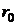 есть радиус-вектор полюса,
есть радиус-вектор полюса, 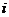 есть единичный вектор, направленный по полярной оси,
а
есть единичный вектор, направленный по полярной оси,
а 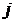 единичный вектор, перпендикулярный этой оси.
Обозначив как обычно через
единичный вектор, перпендикулярный этой оси.
Обозначив как обычно через 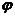 и
и  полярные координаты точки на плоскости, получим ее
параметрическое уравнение в этих координатах
полярные координаты точки на плоскости, получим ее
параметрическое уравнение в этих координатах
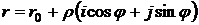 или
или 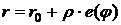 . (32)
. (32)
.
Предположим для простоты, что центр сферы радиуса 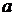 совпадает с началом прямоугольной системы координат,
координатные векторы которых есть
совпадает с началом прямоугольной системы координат,
координатные векторы которых есть 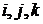 .
Начальный меридиан поместим в плоскости,
.
Начальный меридиан поместим в плоскости, 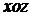 и будем
отсчитывать долготу
и будем
отсчитывать долготу 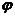 от положительного направления оси
от положительного направления оси 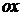 к положительному направлению оси
к положительному направлению оси 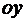 . Экваториальную плоскость будем считать совмещенной с
плоскостью
. Экваториальную плоскость будем считать совмещенной с
плоскостью 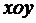 , а широту
, а широту 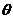 примем
положительной для точек с положительными аппликатами
примем
положительной для точек с положительными аппликатами 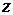 и отрицательной в противоположном случае (рисунок
15).
и отрицательной в противоположном случае (рисунок
15).
|

|
|
Рисунок 15.
|
Проекция
радиус-вектора точки 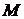 сферы на ось
сферы на ось 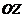 и
плоскость
и
плоскость 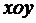 будут соответственно равны
будут соответственно равны 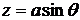 ,
, 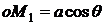 ,
проекции же вектора
,
проекции же вектора 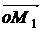 на оси
на оси 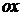 и
и 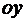 будут
будут 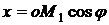 ,
, 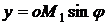 . Таким образом, параметрическое уравнение сферы в
географических координатах имеет вид
. Таким образом, параметрическое уравнение сферы в
географических координатах имеет вид
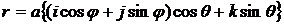 или
или 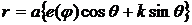 . (33)
. (33)
В
анализе и при изложении элементов теории поверхностей часто задают поверхность
уравнением
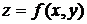 . (34)
. (34)
Легко
видеть, что это уравнение следует считать частным случаем параметрического.
Действительно, принимая за параметры абсциссу и ординату точки поверхности,
можем написать ее параметрическое уравнение в следующем виде 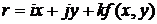 . Такое параметрическое задание будем называть
элементарным. Следует оговориться, что при элементарном задании однозначность
соответствия между значением параметров и точками поверхности имеет место
только при однозначности функции
. Такое параметрическое задание будем называть
элементарным. Следует оговориться, что при элементарном задании однозначность
соответствия между значением параметров и точками поверхности имеет место
только при однозначности функции 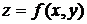 и там,
где эта однозначность существенна, приходится рассматривать поверхность как бы
составленной из отдельных частей, отвечающих отдельным однозначным ветвям
функции. Так, например, в уравнении сферы
и там,
где эта однозначность существенна, приходится рассматривать поверхность как бы
составленной из отдельных частей, отвечающих отдельным однозначным ветвям
функции. Так, например, в уравнении сферы 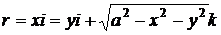 два
значения радикала соответствуют двум полушариям, расположенным по разные
стороны плоскости
два
значения радикала соответствуют двум полушариям, расположенным по разные
стороны плоскости 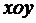 .
.
2.3 Специальные параметризации поверхности
Регулярная поверхность в окрестности каждой своей точки
допускает бесчисленное множество параметризаций.
Действительно, пусть
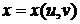 ,
, 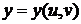 ,
, 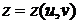
какая-нибудь
параметризация поверхности в окрестности точки 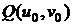 .
.
Если
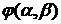 и
и 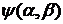 - любые
регулярные функции, удовлетворяющие в точке
- любые
регулярные функции, удовлетворяющие в точке 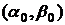 условиям
условиям
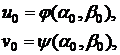
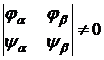 ,
,
то
уравнения
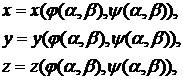
дают
также регулярную параметризацию поверхности. Это очевидным образом вытекает из
того, что формулами
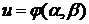 ,
, 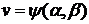
задается
топологическое отображение достаточно малой окрестности точки 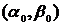 плоскости
плоскости 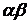 на
некоторую окрестность точки
на
некоторую окрестность точки 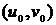 плоскости
плоскости
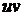 .
.
При
исследовании регулярных поверхностей бывает полезно пользоваться специальными
параметризациями. Рассмотрим наиболее употребительные из них.
Теорема.
Пусть 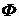 - регулярная поверхность и
- регулярная поверхность и
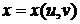 ,
, 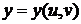 ,
, 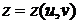
какая-нибудь
ее регулярная параметризация в окрестности точки 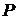 . Пусть в точке
. Пусть в точке 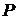
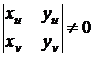
Тогда
в окрестности точки 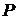 поверхность
поверхность 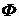 допускает
задание уравнением
допускает
задание уравнением
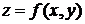 ,
,
где
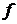 - регулярная функция.
- регулярная функция.
Доказательство.
По теореме о неявных функциях существуют регулярные функции 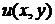 ,
, 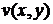 , которые
при подстановке их в уравнения
, которые
при подстановке их в уравнения 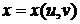 и
и 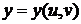 обращают последние в тождества.
обращают последние в тождества.
Так
как
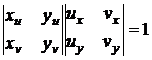 ,
,
то
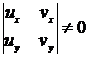
Вводя
новые параметры 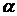 и
и 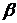 согласно
формулам
согласно
формулам
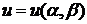 ,
, 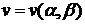
получаем:
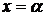 ,
, 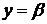 ,
, 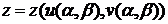
или,
что то же самое,
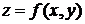
Теорема
доказана.
Теорема.
Пусть 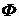 регулярная поверхность,
регулярная поверхность, 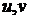 - ее регулярная параметризация. Пусть в окрестности
точки
- ее регулярная параметризация. Пусть в окрестности
точки 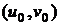 заданы два дифференциальных уравнения
заданы два дифференциальных уравнения
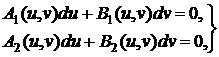 (35)
(35)
коэффициенты
которых в точке 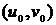 удовлетворяют условию
удовлетворяют условию
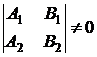 .
.
Тогда
в окрестности этой точки поверхность 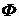 можно
параметризовать так, что координатные линии будут интегральными кривыми
уравнений (35).
можно
параметризовать так, что координатные линии будут интегральными кривыми
уравнений (35).
Доказательство.
Не ограничивая общности, можно считать 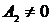 и
и 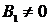 . Пусть
. Пусть 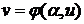 -
решение первого из уравнений (35), которое при
-
решение первого из уравнений (35), которое при 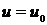 обращается
в
обращается
в 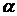 , а -
, а - 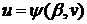 решение
второго уравнения, которое при
решение
второго уравнения, которое при 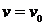 обращается
в
обращается
в 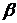 . Уравнения
. Уравнения 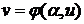 и
и 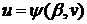 разрешимы относительно
разрешимы относительно 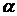 и
и 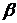 соответственно в окрестности точки
соответственно в окрестности точки 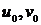 , так как
, так как
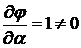 при
при 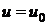 ,
,
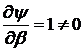 при
при 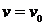 .
.
Пусть
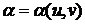 и
и 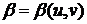 - эти
решения. Покажем, что
- эти
решения. Покажем, что
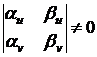 .
.
Так
как 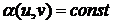 есть интеграл первого из уравнений (35), то уравнения
есть интеграл первого из уравнений (35), то уравнения
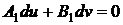 и
и 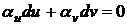
Совместны.
Отсюда
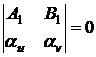 .
.
Аналогично,
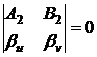 .
.
Если
предположить, что
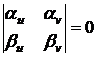 ,
,
то
немедленно получается
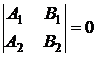 ,
,
а
это невозможно. Итак,
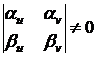 .
.
Отсюда
следует, что 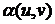 и
и 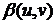 можно
ввести в качестве новых параметров на поверхности. Если это сделать, то
координатные линии (
можно
ввести в качестве новых параметров на поверхности. Если это сделать, то
координатные линии (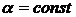 и
и 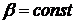 ) будут
интегральными кривыми уравнений (35).
) будут
интегральными кривыми уравнений (35).
Теорема
доказана.
Замечание.
Система уравнений (35), которая фигурирует в формулировке теоремы, часто бывает
задана одним уравнением второй степени
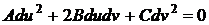 .
.
Соответствующее
условие на коэффициенты сводится к неравенству
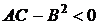 .
.
2.4 Касательная прямая
Чтобы
иметь возможность применить метод дифференциальной геометрии, нужно ограничить
класс поверхностей, подлежащих рассмотрению. В дальнейшем будут рассмотрены
только такие поверхности в параметрическом уравнении, которых функция 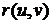 имеет частные производные, по крайней мере, первых
двух порядков.
имеет частные производные, по крайней мере, первых
двух порядков.
Прямая
касается поверхности, если она касается некоторой кривой, принадлежащей
поверхности. Допустим, что поверхность задана параметрическим уравнением
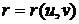 , (30)
, (30)
а
принадлежащая ей кривая в свою очередь параметризована с помощью параметра 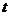 . В таком случае каждому значению этого параметра
соответствует некоторая точка кривой, а ее положению на поверхности
соответствует в свою очередь определенные значения криволинейных координат
. В таком случае каждому значению этого параметра
соответствует некоторая точка кривой, а ее положению на поверхности
соответствует в свою очередь определенные значения криволинейных координат 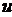 и
и 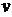 .
.
Таким
образом, криволинейные координаты точек кривой, расположенной на поверхности,
являются функциями параметра 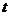 .
.
Соответствующую
систему соотношений
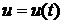 ;
; 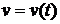 (36)
(36)
будем
называть внутренними уравнениями кривой на поверхности.
Внутренние
уравнение вполне характеризуют кривую, если задано параметрическое уравнение
поверхности, так как подстановка (36) в (30) приводит нас к уравнению
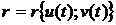 , (37)
, (37)
являющемуся
параметрическим уравнением данной линии.
Касательный
вектор этой кривой, а, следовательно, и направляющий вектор прямой, касающейся
поверхности, получим обычным приемом, дифференцируя радиус-вектор 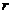 по параметру
по параметру 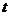 . Однако,
при этом примем во внимание, что в силу (37)
. Однако,
при этом примем во внимание, что в силу (37) 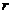 зависит
от
зависит
от 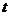 , через посредство аргументов
, через посредство аргументов 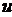 и
и 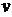 получим
получим
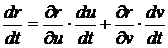 . (38)
. (38)
Правая
часть этого выражения представляет собою линейную комбинацию двух векторов,
которые для краткости обозначают так
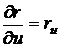 ;
; 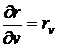 (39)
(39)
и
называются координатными векторами, соответствующими той точке, криволинейные
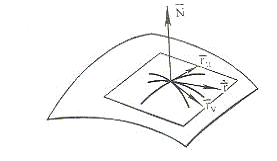
координаты которой подставляются при их вычислении. Легко видеть, что
координатные векторы есть векторы касательных к координатными линиям (рисунок
16). Действительно, рассмотрим одну из координатных линий. Ее параметрические
уравнения, очевидно, можно представить в виде
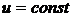 ;
; 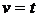 .
.
|
|
|
Рисунок 16.
|
Таким
образом, формула (39) показывает, что направляющий вектор всякой прямой,
касающейся поверхности в данной точке, является линейной комбинацией
координатных векторов, соответствующих этой точке, а его направление
определяется отношением 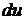 и
и 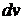 , т.е.
дифференциалов криволинейных координат, соответствующих направлению кривой,
которой касается данная прямая.
, т.е.
дифференциалов криволинейных координат, соответствующих направлению кривой,
которой касается данная прямая.
2.5 Касательная плоскость
Так как все касательные векторы, соответствующие данной точке
поверхности, выражаются линейно через координатные, то все они компланарны.
Откуда снова приходим к тому результату, что все прямые, касающиеся поверхности
в данной точке, располагаются в одной плоскости - касательной плоскости
поверхности.
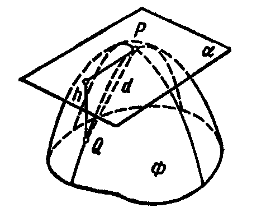
Пусть
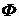 - поверхность,
- поверхность, 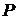 - точка
на ней и
- точка
на ней и 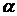 - плоскость, проходящая через точку
- плоскость, проходящая через точку 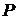 . Возьмем на поверхности точку
. Возьмем на поверхности точку 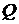 и обозначим ее расстояния от точки
и обозначим ее расстояния от точки 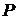 и плоскости
и плоскости 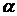 через
через 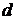 и
и 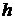 соответственно.
соответственно.
|
|
|
Рисунок 17.
|
Теорема.
Гладкая поверхность 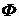 имеет в каждой точке касательную плоскость и притом
единственную.
имеет в каждой точке касательную плоскость и притом
единственную.
Если
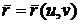 какая-нибудь гладкая параметризация поверхности, то
касательная плоскость в точке
какая-нибудь гладкая параметризация поверхности, то
касательная плоскость в точке 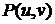 параллельна
векторам
параллельна
векторам 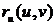 и
и 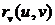 .
.
Доказательство.
Допустим, что поверхность 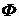 в точке
в точке 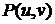 имеет
касательную плоскость
имеет
касательную плоскость 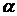 . Пусть
. Пусть 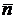 -
единичный вектор, перпендикулярный плоскости
-
единичный вектор, перпендикулярный плоскости 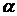 .
Расстояние
.
Расстояние 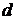 точки
точки 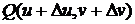 от точки
от точки 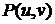 равно
равно 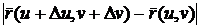 .
Расстояние точки Q от плоскости
.
Расстояние точки Q от плоскости 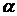 равно
равно
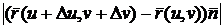 ,
,
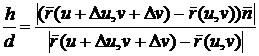 .
.
Согласно
определению 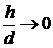 , когда
, когда 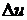 и
и 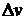 независимо стремятся к нулю. В частности,
независимо стремятся к нулю. В частности,
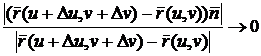 при
при 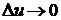 .
.
Но
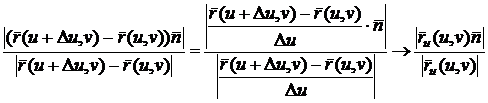 .
.
Таким
образом,
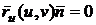
Так
как 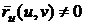
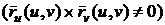 , то равенство
, то равенство 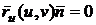 возможно
только в том случае, если вектор
возможно
только в том случае, если вектор 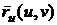 параллелен
плоскости
параллелен
плоскости 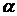 .
.
Аналогично
показывается, что и вектор 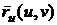 тоже
параллелен плоскости
тоже
параллелен плоскости 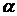 , и так как векторы
, и так как векторы 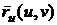 и
и 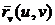 отличны от нуля и непараллельны (
отличны от нуля и непараллельны (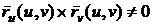 ), то касательная плоскость, если она существует,
единственная.
), то касательная плоскость, если она существует,
единственная.
Докажем
теперь существование касательной плоскости. Пусть плоскость 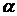 параллельна векторам
параллельна векторам 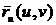 и
и 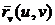 . Покажем, что она является касательной плоскостью
поверхности в точке
. Покажем, что она является касательной плоскостью
поверхности в точке 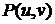 .
.
Имеем
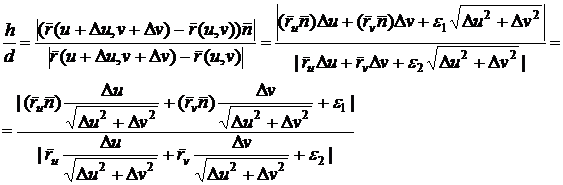 ,
,
где
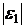 и
и 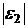 стремятся
к нулю, когда
стремятся
к нулю, когда 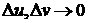 .
.
Допустим,
что существует последовательность пар 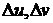 ,
сходящихся к нулю и таких, что соответствующее им
,
сходящихся к нулю и таких, что соответствующее им 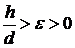 . Из последовательности пар
. Из последовательности пар 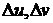 можно выделить такую подпоследовательность, для
которой отношения
можно выделить такую подпоследовательность, для
которой отношения
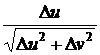 и
и 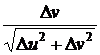
будут
сходиться. Пусть 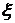 и
и 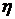 -
предельные значения этих выражений. Очевидно,
-
предельные значения этих выражений. Очевидно, 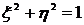 .
Переходя к пределу отношения
.
Переходя к пределу отношения 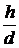 по
выделенной подпоследовательности пар
по
выделенной подпоследовательности пар 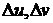 ,
получим:
,
получим:
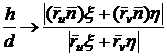 .
.
Так
как 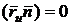 ,
, 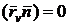 , а
, а 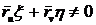 (
(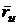 и
и 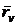 непараллельны), то
непараллельны), то 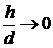 . Но это
противоречит тому, что все допредельные значения
. Но это
противоречит тому, что все допредельные значения 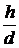 по
предположению больше
по
предположению больше 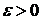 .
.
Теорема
доказана полностью.
Зная
направление касательной плоскости, нетрудно написать ее уравнение.
Пусть
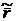 - вектор произвольной точки касательной плоскости
поверхности в точке
- вектор произвольной точки касательной плоскости
поверхности в точке 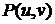 . Тогда векторы
. Тогда векторы 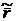 -
- 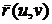 ,
, 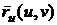 ,
, 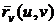 параллельны касательной плоскости, следовательно, их
смешанное произведение равно нулю. Отсюда уравнение касательной плоскости
параллельны касательной плоскости, следовательно, их
смешанное произведение равно нулю. Отсюда уравнение касательной плоскости
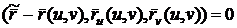 .
.
Пусть
поверхность задана уравнениями
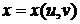 ,
, 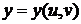 ,
, 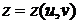 .
.
Из
векторного уравнения касательной плоскости следует, что уравнение касательной
плоскости, соответствующее такой форме задания поверхности, будет
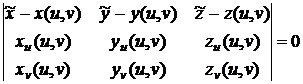 .
.
Уравнение
касательной плоскости поверхности, заданной уравнением 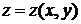 , получается из найденного только что. Достаточно
заметить, что задание поверхности уравнением
, получается из найденного только что. Достаточно
заметить, что задание поверхности уравнением 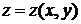 есть
лишь краткая запись параметрического задания
есть
лишь краткая запись параметрического задания
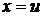 ,
, 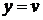 ,
, 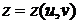 .
.
Поэтому
уравнение касательной плоскости в случае задания поверхности уравнением 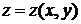 будет
будет
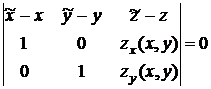 ,
,
или
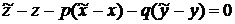 ,
,
где
через 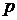 и
и 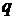 обозначены
первые производные функции
обозначены
первые производные функции 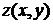 .
.
Найдем,
наконец, уравнение касательной плоскости для случая задания поверхности
уравнением 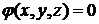 . Пусть
. Пусть 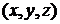 - точка
поверхности, в которой
- точка
поверхности, в которой 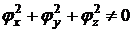 и
и 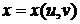 ,
, 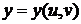 ,
, 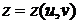 -
какая-нибудь гладкая параметризация поверхности в окрестности этой точки. Если
подставить вместо
-
какая-нибудь гладкая параметризация поверхности в окрестности этой точки. Если
подставить вместо 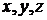 в уравнение поверхности
в уравнение поверхности 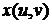 ,
, 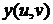 ,
, 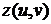 , то получим тождество относительно
, то получим тождество относительно 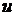 и
и 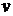 .
Дифференцируя это тождество, в точке
.
Дифференцируя это тождество, в точке 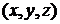 получим:
получим:
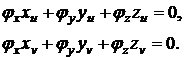
Рассматривая
эти равенства как систему уравнений для 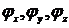 и решая
ее, получим:
и решая
ее, получим:
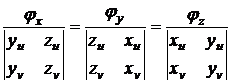 .
.
Для
случая параметрического задания поверхности уравнение касательной плоскости
будет
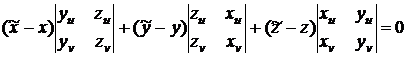
Принимая
во внимание полученную выше пропорцию, получаем уравнение касательной плоскости
поверхности 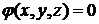 в точке
в точке 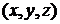
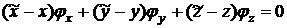 .
.
Чтобы
получить уравнение касательной плоскости, примем во внимание, что она содержит
векторы 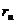 и
и 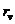 и ее
нормальный вектор им перпендикулярен. Поэтому этот вектор может быть положен
равным
и ее
нормальный вектор им перпендикулярен. Поэтому этот вектор может быть положен
равным
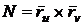 . (40)
. (40)
Правая
часть не может быть равна нулю там, где существует правильная координатная
сеть, так как по условию ее определения координатные линии не могут касаться
друг друга, и векторы 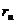 ,
, 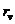 неколлинеарны.
неколлинеарны.
Исключим
из рассмотрения и точки, в которых векторы 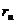 или
или 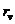 обращаются в нуль, так как эти точки будут особыми
для параметризации координатных линий. Вообще мы будем называть особой точкой
параметризованной поверхности точку, в которой
обращаются в нуль, так как эти точки будут особыми
для параметризации координатных линий. Вообще мы будем называть особой точкой
параметризованной поверхности точку, в которой 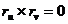 и
исключим в дальнейшем эти точки из нашего рассмотрения. Обозначив радиус-вектор
текущей точки касательной плоскости через
и
исключим в дальнейшем эти точки из нашего рассмотрения. Обозначив радиус-вектор
текущей точки касательной плоскости через 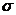 , а
радиус-вектор точки прикосновения через
, а
радиус-вектор точки прикосновения через 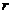 , получим
уравнение касательной плоскости в виде равенства нулю смешанного произведения
, получим
уравнение касательной плоскости в виде равенства нулю смешанного произведения
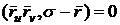 . (41)
. (41)
Прямая,
перпендикулярная касательной плоскости и проходящая через точку прикосновения,
называется нормалью, а ее направляющий вектор (40) - нормальным вектором
поверхности. Составить уравнение нормали после того, как известно уравнение
касательной плоскости для различных случаев задания поверхности, не составляет
труда.
3. ПЕРВАЯ КВАДРАТИЧНАЯ ФОРМА ПОВЕРХНОСТИ
Пусть
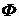 - регулярная поверхность,
- регулярная поверхность, 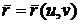 - какая-нибудь ее регулярная параметризация и
- какая-нибудь ее регулярная параметризация и 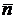 - единичный вектор нормали к поверхности в точке
- единичный вектор нормали к поверхности в точке 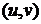 .
.
В
теории поверхностей важную роль играют квадратичные формы, связанные с
поверхностью:
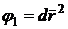 ,
, 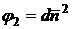 .
.
Первой
квадратичной формой поверхности называют выражение
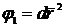 .
.
Запишем
это выражение подробнее. Имеем
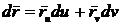 ,
, 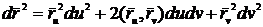 , (42)
, (42)
или
вводя обозначения
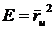 ,
, 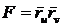 ,
, 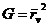 , (43)
, (43)
получим
уравнение первой квадратичной формы
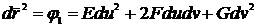 . (44)
. (44)
Первая
квадратичная форма играет основную роль во всей теории поверхностей. В правой
его части представлены коэффициенты, являющиеся функциями точки поверхности и
переменными 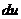 и
и 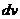 -
дифференциалами криволинейных координат, которые зависят от направления кривой,
проходящей через данную точку. Форма
-
дифференциалами криволинейных координат, которые зависят от направления кривой,
проходящей через данную точку. Форма 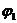 называется
первой основной квадратичной формой поверхности. Кроме того, ее называют еще
для краткости просто линейным элементом поверхности, подчеркивая этим, что
знание ее является основой для вычисления длин дуг. Действительно, если
линейный элемент задан, т.е. заданы его коэффициенты
называется
первой основной квадратичной формой поверхности. Кроме того, ее называют еще
для краткости просто линейным элементом поверхности, подчеркивая этим, что
знание ее является основой для вычисления длин дуг. Действительно, если
линейный элемент задан, т.е. заданы его коэффициенты 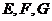 в функции
в функции 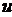 и
и 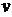 и известно внутреннее уравнение кривой, то ее дугу
можно вычислить даже в том случае, если параметрическое уравнение поверхности
неизвестно. Отметим некоторые важные неравенства, которым удовлетворяют
коэффициенты линейного элемента.
и известно внутреннее уравнение кривой, то ее дугу
можно вычислить даже в том случае, если параметрическое уравнение поверхности
неизвестно. Отметим некоторые важные неравенства, которым удовлетворяют
коэффициенты линейного элемента.
Из
равенств 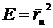 ;
; 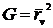 следует,
что для всякой неособенной точки поверхности
следует,
что для всякой неособенной точки поверхности
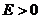 ;
; 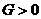 . (45)
. (45)
Применяя
тождество Лагранжа, получим
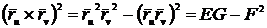 .
.
Выражение
в правой части есть дискриминант линейного элемента. Во всякой неособенной
точке 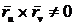 .
.
Поэтому
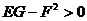 . (46)
. (46)
Неравенства
(45) и (46) соответствуют тому факту, что основная квадратичная форма
положительна и не может обратиться в нуль при значении переменных 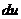 и
и 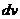 , не
равных нулю одновременно. Квадратичные формы, обладающие этим свойством,
называются положительно-определенными.
, не
равных нулю одновременно. Квадратичные формы, обладающие этим свойством,
называются положительно-определенными.
4. ПРИМЕНЕНИЕ ПЕРВОЙ КВАДРАТИЧНОЙ ФОРМЫ
4.1 Вычисление длины дуги кривой на поверхности
Вычислим длину дуги линии, расположенной на поверхности. Для этого
воспользуемся внутренним уравнением кривой (36) и подстановкой (37). Найдем
дифференциал дуги.
Так как
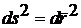 ,
, 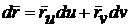 , то
, то 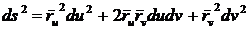 .
.
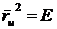 ;
; 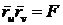 ;
; 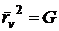 ,
,
получим
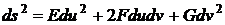 . (47)
. (47)
Если
мы хотим вычислить длину дуги, ограниченную точками кривой, соответствующими
значениям параметра 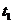 и
и 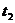 , то она
выразится интегралом
, то она
выразится интегралом
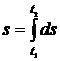 .
.
Подставляя
вместо 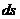 его выражение из (47) и вводя явно переменное
интегрирование
его выражение из (47) и вводя явно переменное
интегрирование 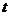 , получим окончательно
, получим окончательно
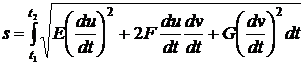 . (48)
. (48)
Зная
внутреннее уравнение кривой, мы должны выразить 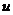 и
и 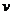 через
через 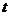 в
выражениях
в
выражениях 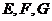 , найти производные
, найти производные 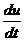 и
и 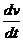 , подставить все это в подынтегральную функцию (48) и
задача сведется к вычислению интеграла, вида
, подставить все это в подынтегральную функцию (48) и
задача сведется к вычислению интеграла, вида
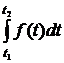 .
.
4.2 Угол между двумя линиями на поверхности
Если две кривые пересекаются, то угол между ними называют угол между их
касательными в точке пересечения. Предположим, что кривые лежат на одной
поверхности и пересекаются в некоторой точке. Касательные векторы этих кривых
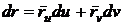 ;
; 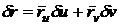
будем
различать, употребляя различные обозначения для дифференциалов криволинейных
координат, соответствующих изменениям последних вдоль рассматриваемых линий
(рисунок 18). Искомый угол 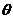 определится
по формуле
определится
по формуле
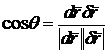 ,
,
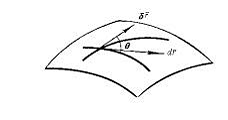
в
которой следует положить
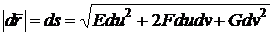
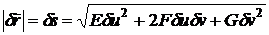
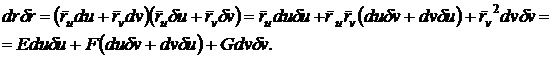
|
|
|
Рисунок 18.
|
Таким образом,
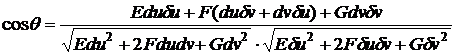 . (49)
. (49)
Полученная
формула показывает, что на данной поверхности угол двух кривых зависит только
от отношения дифференциалов криволинейных координат, взятых вдоль кривых в
точке их пересечения. Кроме того, следует заметить, что для определения угла,
так же как и в случае вычисления дуги, не нужно знать параметрического
уравнения поверхности, а достаточно считать известным выражение ее линейного
элемента.
Из
формулы (49) легко получить выражение координатного угла, т.е. угла между
линиями координатной сети. Действительно, для этих линий можно считать
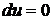 ;
; 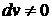
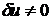 ;
; 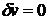 ,
,
откуда
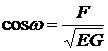 . (50)
. (50)
В
частности, для того, чтобы координатные линии пересекались под прямым углом,
т.е. чтобы они образовали ортогональную сеть, необходимо и достаточно, чтобы
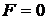
и
линейный элемент имел вид
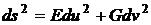 . (51)
. (51)
Такой
вид имеют линейные элементы плоскости в прямоугольных и полярных координатах и
сферы в координатах географических, так как во всех этих случаях условие
ортогональности выполнено.
4.3 Вычисление площади поверхности
Определение длины дуги кривой линии сводится к вычислению суммы длин
прямоугольных отрезков с последующим переходом к пределу.
Аналогичным образом и определение площади частей криволинейной
поверхности сводится к измерению площадей плоских фигур.
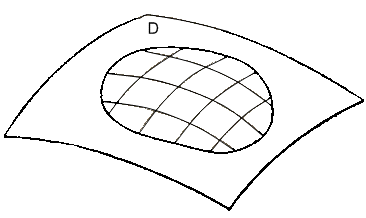
Предположим,
что на поверхности задана некоторая замкнутая область 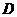 (рисунок 19). Разобьем эту область на частичные
области
(рисунок 19). Разобьем эту область на частичные
области 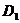 ,
, 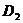 , …,
, …, 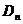 .
.
|
|
|
Рисунок 19.
|
Во
внутренней точке каждой из этих областей построим касательную плоскость и
спроектируем на нее соответствующую частичную область. Пусть площадь плоской
области, получившейся проектированием области 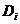 , есть
, есть 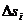 . Составим сумму всех этих площадей
. Составим сумму всех этих площадей
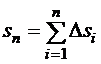 .
.
Предел
этой сумму при неограниченном возрастании числа частичных областей и при
стягивании каждой области к точке называется площадью области 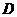 на поверхности.
на поверхности.
Наметим
теперь в общих чертах ход рассуждений, сводящих вычисление площади 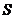 к интегралу.
к интегралу.
Параметризируем
поверхность в области 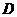 и выберем границы частичных областей так, чтобы они
совпадали с координатными линиями. Рассмотрим одну из этих областей,
предположив, что ограничивающие ее линии пересекаются в точках
и выберем границы частичных областей так, чтобы они
совпадали с координатными линиями. Рассмотрим одну из этих областей,
предположив, что ограничивающие ее линии пересекаются в точках 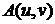 ;
; 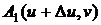 ;
; 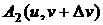 ;
; 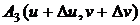 .
.
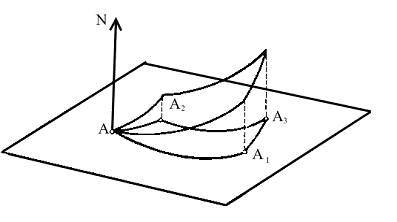
Будем
проектировать ее на касательную плоскость в точке 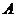 (рисунок 20).
(рисунок 20).
|
|
|
Рисунок 20.
|
Радиус-векторы
угловых точек 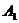 и
и 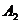 равны
равны
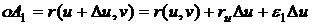
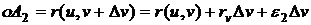 ,
,
(рисунок
21), где 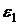 и
и 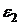 стремятся
к нулю вместе с
стремятся
к нулю вместе с 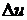 и
и 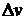 .
.
|
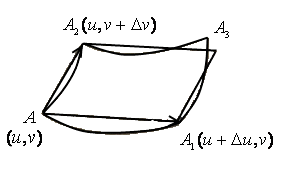
|
|
Рисунок 21.
|
Отсюда
следует, что, пренебрегая малым более высокого порядка, мы можем принять
проекции векторов 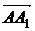 и
и 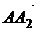 на
касательную плоскость, равными векторам
на
касательную плоскость, равными векторам
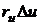 и
и 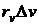 .
.
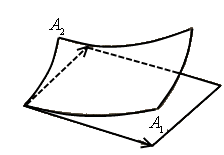
Наконец,
снова отбросив малые высшего порядка, заменим площадь проекции площадью
параллелограмма, построенного на векторах 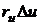 и
и 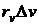 как на сторонах (рисунок 22), и получим
как на сторонах (рисунок 22), и получим
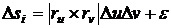 .
.
|
|
|
Рисунок 22.
|
Имея
в виду, что 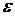 есть бесконечно малая более высокого порядка, чем
площадь проекции частичной области, получим, наконец,
есть бесконечно малая более высокого порядка, чем
площадь проекции частичной области, получим, наконец,
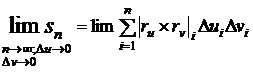 .
.
Таким
образом, площадь области 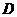 поверхности выражается двойным интегралом
поверхности выражается двойным интегралом
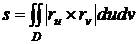 (52)
(52)
или
так как
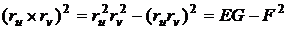 ,
,
то
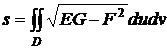 . (53)
. (53)
Последнее
выражение площади показывает, что для ее вычисления достаточно знание линейного
элемента поверхности.
Покажем,
что интеграл (52) не зависит от выбора параметризации.
Допустим,
что на поверхности введена новая система криволинейных координат 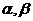 , связанных со старыми координатами зависимостями
, связанных со старыми координатами зависимостями
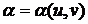 ;
; 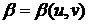 .
.
Новые
координатные векторы выразятся через старые так:
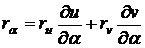 ;
; 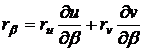 ,
,
а
их векторные произведения будут связаны зависимостью
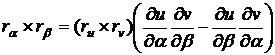 .
.
Вычисляя
интеграл (23) в новых координатах, получим
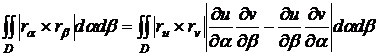 .
.
Однако,
из интегрального исчисления известно, что переменные под знаком кратного
интеграла можно преобразовать так, что при этом подынтегральные дифференциалы
умножаются на якобиан или определитель преобразования, который как раз и
появился в правой части последнего равенства.
Таким
образом,
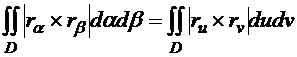 ,
,
и
интеграл не зависит от того, в каких параметрах он вычисляется.
5. ВТОРАЯ КВАДРАТИЧНАЯ ФОРМА ПОВЕРХНОСТИ
Пусть
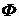 - регулярная поверхность,
- регулярная поверхность, 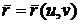 - какая-нибудь ее регулярная параметризация,
- какая-нибудь ее регулярная параметризация,  - единичный вектор нормали поверхности в точке
- единичный вектор нормали поверхности в точке 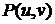 .
.
Второй
квадратичной формой - поверхности называется квадратичная форма
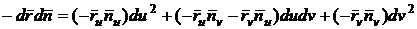 .
.
Для
коэффициентов этой формы мы будем употреблять следующие обозначения:
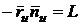 ,
, 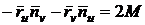 ,
, 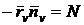 .
.
Так
как 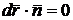 и, следовательно,
и, следовательно, 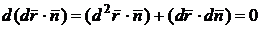 ,
,
То
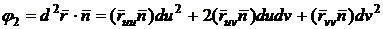 .
.
Отсюда
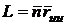 ;
; 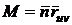 ;
; 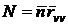 .
.
Единичный
вектор нормали выражается так
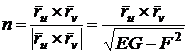 ,
,
вследствие
этого
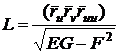 ;
; 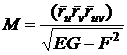 ;
; 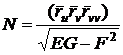 . (54)
. (54)
Полезно
отметить еще следующие выражение тех же коэффициентов
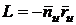 ;
; 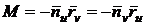 ;
; 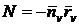 . (55)
. (55)
Эти
выражения легко получаются при дифференцировании тождеств
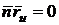 ;
; 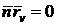 ,
,
которое
дает
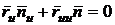 ;
;  ,
,
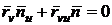 ;
; 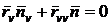 .
.
6. ПРИМЕНЕНИЕ ВТОРОЙ КВАДРАТИЧНОЙ ФОРМЫ
6.1 Нормальная кривизна линий, расположенных на поверхности
Кривизны
линий, расположенных на поверхности, связаны рядом замечательных соотношений.
Для того, чтобы получить эти соотношения, следует изучить расположение
сопровождающего трехгранника кривой по отношению к поверхности. При этом
касательный вектор кривой 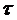 всегда расположен в касательной плоскости
поверхности, а векторы главной нормали и бинормали наклонены под некоторыми
углами к этой плоскости. Рассмотрим вектор кривизны
всегда расположен в касательной плоскости
поверхности, а векторы главной нормали и бинормали наклонены под некоторыми
углами к этой плоскости. Рассмотрим вектор кривизны
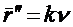
кривой,
расположенной на поверхности. Проекция вектора кривизны линии на нормаль
поверхности в точке, через которую проходит эта кривая, называется нормальной
кривизной этой кривой.
При
этом нормаль считается ориентированной с помощью заранее выбранного единичного
вектора нормали 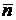 . Нормальная кривизна обозначается через
. Нормальная кривизна обозначается через 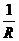 , а обратная ей величина
, а обратная ей величина 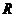 называется радиусом нормальной кривизны. Так как
нормаль считается ориентированной, то проекция
называется радиусом нормальной кривизны. Так как
нормаль считается ориентированной, то проекция 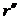 на нее
может быть положительной или отрицательной, так что радиус нормальной кривизны
выражается относительным числом в противоположность существенно положительному
радиусу кривизны кривой, рассматриваемой независимо от поверхности.
на нее
может быть положительной или отрицательной, так что радиус нормальной кривизны
выражается относительным числом в противоположность существенно положительному
радиусу кривизны кривой, рассматриваемой независимо от поверхности.
Для
вычисления нормальной кривизны будем дифференцировать выражение
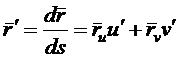
единичного
касательного вектора кривой, расположенной на поверхности. Пользуясь правилами
дифференцирования сложной функции и вводя обозначения
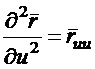 ;
; 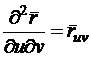 ;
; 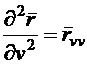 , (56)
, (56)
получим
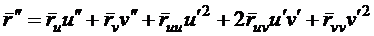 . (57)
. (57)
Чтобы
найти проекцию вектора кривизны на нормаль, достаточно умножить 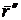 скалярно на
скалярно на 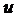 . При
этом следует принять во внимание, что векторы,
. При
этом следует принять во внимание, что векторы, 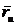 и
и 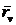 расположены в касательной плоскости и, следовательно,
перпендикулярны
расположены в касательной плоскости и, следовательно,
перпендикулярны 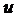 . Таким образом,
. Таким образом,
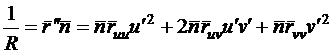 . (58)
. (58)
Скалярные
произведения единичного вектора нормали 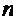 вторых
частных производных радиус-вектора точки поверхности являются функциями точки.
Введем для них особые обозначения, полагая
вторых
частных производных радиус-вектора точки поверхности являются функциями точки.
Введем для них особые обозначения, полагая
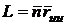 ;
; 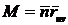 ;
; 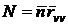 .
.
После
этого нормальная кривизна примет вид
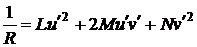 . (59)
. (59)
Так
как выражение (59), очевидно, можно переписать в следующем виде
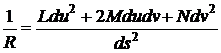 ,
,
а
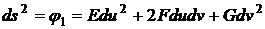 ,
,
то
нормальная кривизна
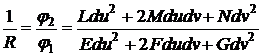 (60)
(60)
равна
отношению второй и первой квадратичной форм, определенных для отношения
дифференциалов криволинейных координат, соответствующих направлению кривой,
проходящей через ту точку поверхности, для которой подсчитаны коэффициенты
обеих форм.
№1.
Найти линейный элемент плоскости в полярных координатах.
Решение.
Предположим, что 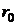 есть радиус-вектор полюса,
есть радиус-вектор полюса, 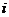 есть единичный вектор, направленный по полярной оси,
а
есть единичный вектор, направленный по полярной оси,
а 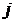 единичный вектор, перпендикулярный этой оси.
Обозначим через
единичный вектор, перпендикулярный этой оси.
Обозначим через 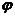 и
и 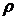 полярные
координаты точки на плоскости:
полярные
координаты точки на плоскости:
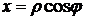 ,
, 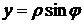 ,
, 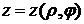 .
.
Найдем
частные производные по 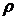 и по
и по 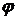 :
:
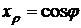 ,
, 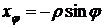 ,
,
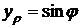 ,
, 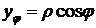 ,
,
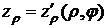 ,
, 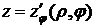 .
.
Далее
вычислим коэффициенты первой квадратичной формы:
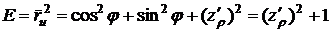 ,
,
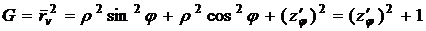 ,
,
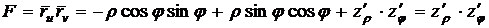 .
.
Теперь
можем вычислить первую квадратичную форму:
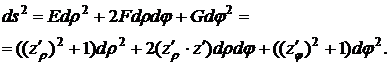
Ответ.

№2.
Найти длину дуги кривой, заданной внутренним уравнением 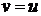 на поверхности с линейным элементом
на поверхности с линейным элементом 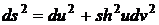 .
.
Решение.
Для того, чтобы вычислить дину дуги кривой, нужно извлечь корень из линейного
элемента поверхности, т.е.
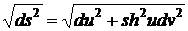
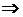
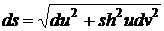 . Так как кривая задана внутренним уравнением
. Так как кривая задана внутренним уравнением
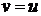 (1),
(1),
то
отсюда следует, что
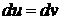 (2).
(2).
Теперь
учитывая (1) и (2) можем сделать замену в уравнении 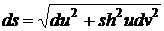 и получим следующие:
и получим следующие:
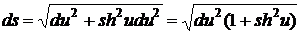
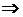
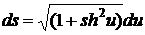 .
.
Теперь
можно вычислить длину дуги.
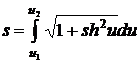 , (3)
представим синус гиперболический в следующем виде:
, (3)
представим синус гиперболический в следующем виде:
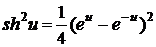 ,
подставим данное выражение в (3), получим
,
подставим данное выражение в (3), получим 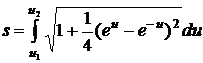 . Теперь
раскроем квадрат и проведем элементарные преобразования:
. Теперь
раскроем квадрат и проведем элементарные преобразования: 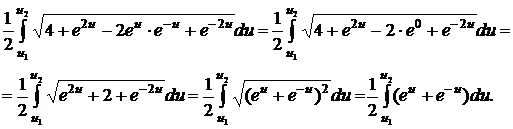
Внесем
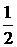 под знак интеграла и получим
под знак интеграла и получим 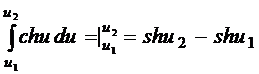 .
.
Ответ
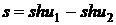
№3.
Найти линейный элемент сферы в географических координатах.
Решение.
Предположим
для простоты, что центр сферы радиуса 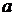 совпадает
с началом прямоугольной системы координат, координатные векторы которых есть
совпадает
с началом прямоугольной системы координат, координатные векторы которых есть 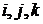 . Начальный меридиан поместим в плоскости,
. Начальный меридиан поместим в плоскости, 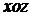 и будем отсчитывать долготу
и будем отсчитывать долготу 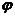 от положительного направления оси
от положительного направления оси 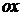 к положительному направлению оси
к положительному направлению оси 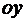 . Экваториальную плоскость будем считать совмещенной с
плоскостью
. Экваториальную плоскость будем считать совмещенной с
плоскостью 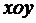 , а широту
, а широту 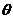 примем
положительной для точек с положительными аппликатами
примем
положительной для точек с положительными аппликатами 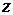 и отрицательной в противоположном случае.
и отрицательной в противоположном случае.
Проекция
радиус-вектора точки 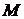 сферы на ось
сферы на ось 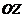 и
плоскость
и
плоскость 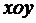 будут соответственно равны
будут соответственно равны
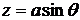 ,
, 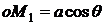 (1),
(1),
проекции
же вектора 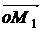 на оси
на оси 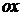 и
и 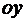 будут
будут
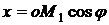 ,
, 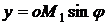 (2).
(2).
Таким
образом, параметрическое уравнение сферы в географических координатах имеет вид
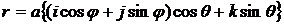 .
.
Из
(1) и (2) следует:
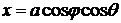 ,
,
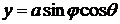 ,
,
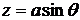 .
.
Найдем
частные производные по 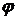 и по
и по 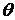 .
.
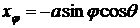 ,
, 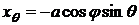 ,
,
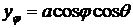 ,
, 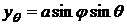 ,
,
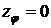 .
. 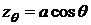 .
.
Далее
вычислим коэффициенты первой квадратичной формы.
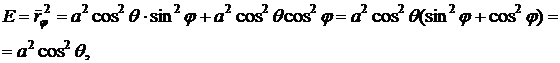
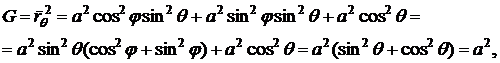
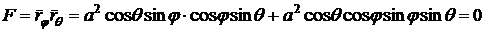 .
.
Теперь
вычислим линейный элемент сферы в географических координатах.
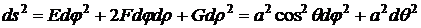 .
.
Ответ.
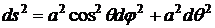
№4.
Составить выражение второй квадратичной формы сферы заданной через
географические координаты.

Из
задачи №3 мы знаем географические координаты сферы:
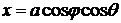 ,
,
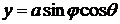 ,
,
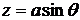 .
.
Найдем
их производные.
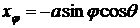 ,
, 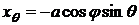 ,
,
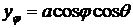 ,
, 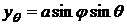 ,
,
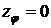 .
. 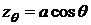 .
.
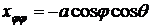 ,
, 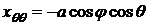 ,
, 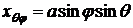 ,
,
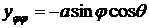 ,
, 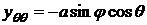 ,
, 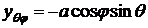 ,
,
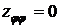 .
. 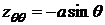 .
. 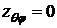 .
.
Теперь
необходимо вычислим коэффициенты 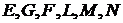 .
.
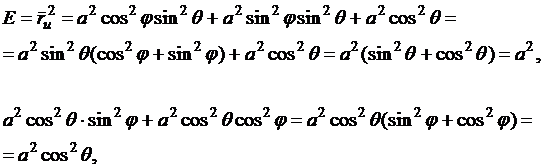
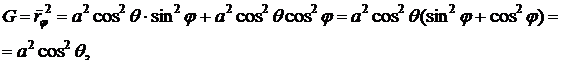
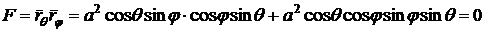 .
.
Чтобы
вычислить коэффициенты 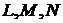 необходимо знать, чему равны следующие выражения:
необходимо знать, чему равны следующие выражения: 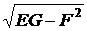 ,
, 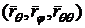 ,
, 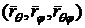 ,
, 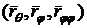 .
.
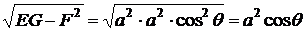

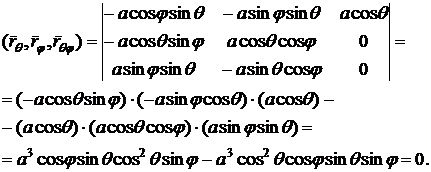
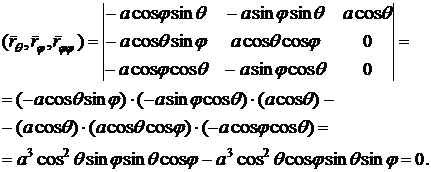
Теперь
подставим вычисленные коэффициенты в формулу второй квадратичной формы и
получим:
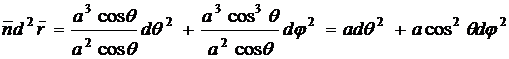
Ответ.
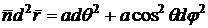
№5.
Найти периметр и внутренний угол 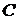 криволинейного
треугольника
криволинейного
треугольника  ,
, 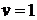 ,
расположенного на поверхности, у которой
,
расположенного на поверхности, у которой 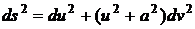 .
.
Решение.
Так
как  , то отсюда следует, что
, то отсюда следует, что 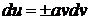 .
. 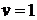
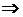
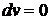 .
.
Найдем
координаты точек 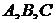 .
.
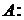
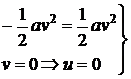
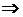
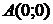 ,
,
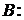
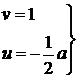
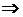
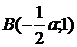 ,
,
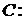
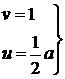
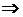
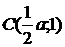 .
.
Теперь
найдем длину дуг 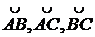 .
.
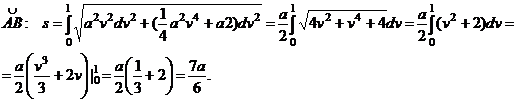
Аналогично
вычисляется длина дуги 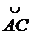 .
.
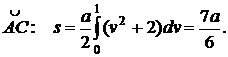
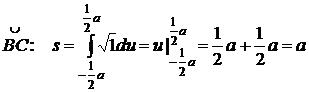 .
.
Теперь
можем вычислить периметр криволинейного треугольника:
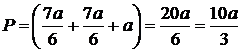 .
.
Теперь
приступим к вычислению угла 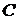 .
.
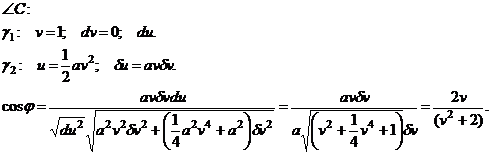
Ответ:
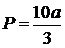 ,
, 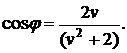
№6.
На псевдосфере
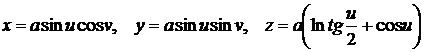
Заданы
два семейства линий: 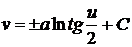 . Вычислить длину дуги линии каждого семейства между
двумя точками
. Вычислить длину дуги линии каждого семейства между
двумя точками 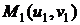 и
и 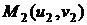 .
Доказать, что длины дуг всех линий одного семейства между двумя фиксированными
линиями второго семейства одинаковы.
.
Доказать, что длины дуг всех линий одного семейства между двумя фиксированными
линиями второго семейства одинаковы.
Решение.
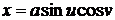 ,
,
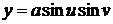 ,
,
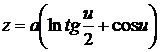 .
.
Чтобы
найти длину дуги, необходимо найти линейный элемент псевдосферы. Для вычисления
первой квадратичной формы найдем частные производные.
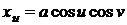 ,
, 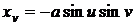
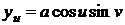 ,
, 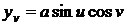
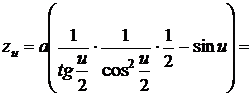
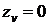
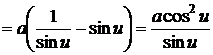 .
.
Так
как 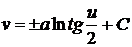 , то
, то 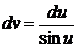 .
.
Теперь
вычислим коэффициенты первой квадратичной формы.
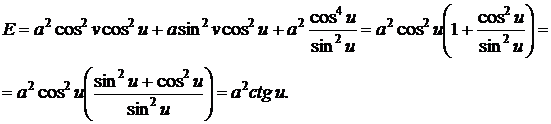
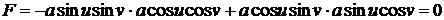 .
.
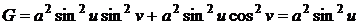 .
.
Вычисли
первую квадратичную форму поверхности:
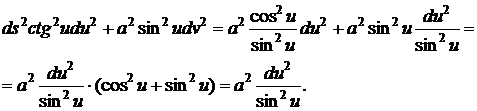
Теперь
можем вычислить длину дуги.
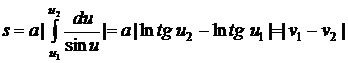 .
.
Теперь
рассмотрим семейство 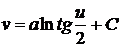 . Точка
. Точка 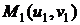 лежит на
линии
лежит на
линии 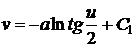 , а точка
, а точка 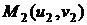 лежит на
линии
лежит на
линии 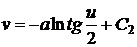 , т.е.
, т.е.
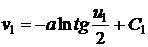 ,
, 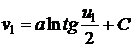 ,
,
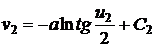 ,
, 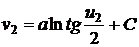 ,
,
значит,
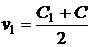 ,
, 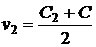 ,
,
поэтому
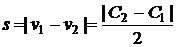 ,
,
т.е.
не зависит от 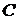 .
.
Ответ.
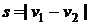
№7.
На поверхности сферы задан прямоугольный треугольник, сторонами которого
являются дуги больших кругов сферы. Найти а) соотношение между сторонами
треугольника; б) его площадь.
Решение.
а) Возьмем уравнение сферы в виде
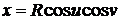 ,
,
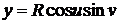 ,
,
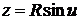 .
.
Расположим
один из катетов на линии 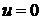 , второй - на линии
, второй - на линии 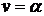 , одну из
вершин в точке
, одну из
вершин в точке 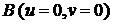 , вторую - в точке
, вторую - в точке 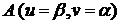 . Тогда
длины катетов равны соответственно
. Тогда
длины катетов равны соответственно 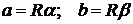 . Для
вычисления
. Для
вычисления 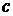 надо найти длину дуги линии
надо найти длину дуги линии 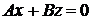 (не поверхности сферы) между указанными точками.
Уравнение гипотенузы в криволинейны координатах
(не поверхности сферы) между указанными точками.
Уравнение гипотенузы в криволинейны координатах 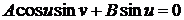 .
Так как она проходит через точку
.
Так как она проходит через точку 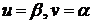 , то
, то 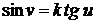 , где
, где 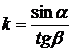 .
.
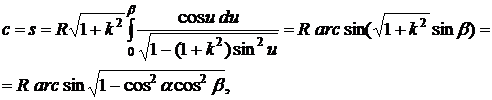
отсюда
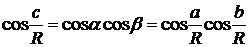 .
.
б)
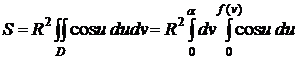 ,
,
где
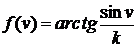 .
.
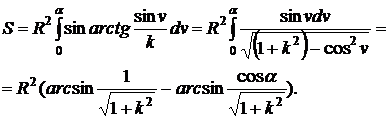
Отсюда
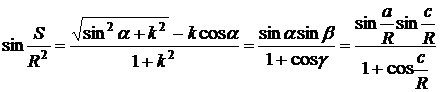 .
.
Пользуясь
соотношением
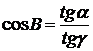 , получим
, получим
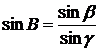 ,
, 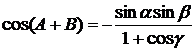 ,
,
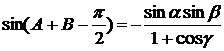 .
.
Сравнивая
с предыдущим, находим
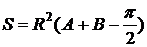 .
.
Ответ.
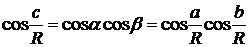 ,
, 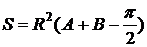 .
.
ЗАКЛЮЧЕНИЕ
Свойство поверхности и ее частей принять разделять на две группы.
Совокупность этих свойств, сохраняется при изгибании поверхности, образует ее
внутреннюю геометрию, а все остальные свойства, которые существенно зависят от
формы, принимаемой поверхностью во внешнем пространстве, называются внешними.
К внутренней геометрии относятся такие свойства: длина дуги линии,
расположенной на поверхности, угол между двумя линиями, площадь части
поверхности.
Также отметим общий прием, с помощью которого доказывается, что некоторое
свойство принадлежит внутренней геометрии. Этот прием состоит в указании на то,
что это свойство выражается соотношением между коэффициентами первой
квадратичной формы (и их производными). Так как это соотношение не может
изменится при изгибании, то сохраняется и рассматриваемое свойство.