Система линейных уравнений
Лекция 1. Определители
1. Система линейных уравнений. Решение СЛУ. Виды СЛУ
2. Определители второго и третьего порядка
. Свойства определителей
Система m линейных уравнений с n переменными имеет вид
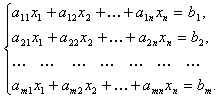
Каждый из коэффициентов при переменных aij имеет два индекса: i −
номер уравнения, j − номер переменной. Числа bi называются свободными
членами уравнений.
Прямоугольная таблица чисел, составленная из коэффициентов при переменных,
называется матрицей, состоящей из m строк и n столбцов:
Числа aij являются элементами матрицы. Если число строк матрицы равно
числу ее столбцов (m=n), то матрица называется квадратной матрицей n-го
порядка.
Решением системы уравнений называется упорядоченная совокупность n чисел 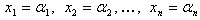 , при подстановке которых каждое
уравнение системы обращается в верное равенство.
, при подстановке которых каждое
уравнение системы обращается в верное равенство.
Система уравнений называется совместной, если она имеет хотя бы одно
решение. Система уравнений называется несовместной, если она не имеет решений.
Совместная система уравнений называется определенной, если она имеет
единственное решение. Совместная система уравнений называется неопределенной,
если она имеет более одного решения.
Для квадратных матриц вводится понятие определителя.
Определителем матрицы второго порядка, или определителем второго порядка,
называется число, вычисляемое по формуле:
Определителем матрицы третьего порядка, или определителем третьего
порядка, называется число, вычисляемое по формуле:
Свойства определителей
1. При замене всех строк соответствующими по номеру столбцами величина
определителя не изменится. Эта операция называется транспонированием.
2. При перестановке двух строк определитель изменяет свой знак на
противоположный.
. Если какая-либо строка состоит из нулей, то определитель равен
нулю.
. Если определитель содержит две одинаковые или пропорциональные
строки, то он равен нулю.
. Общий множитель элементов какой-либо строки можно вынести за
знак определителя.
. Основное свойство определителя. Определитель не изменится, если
к элементам любой строки прибавить соответствующие элементы другой строки,
умноженные на одно и то же число.
Из свойства 1 следует равноправие строк и столбцов определителя. Поэтому
все свойства 2-6 справедливы и для столбцов.
Лекция 2. Определитель n-го порядка. Правило Крамера
1. Минор и алгебраическое дополнение
2. Определитель n-го порядка
. Правило Крамера
Пусть дана квадратная матрица n-го порядка
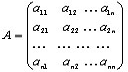 .
.
Для записи определителя, соответствующего матрице A, будем применять
обозначении
 .
.
Определение 1
Минором Mij элемента aij определителя Δ называется определитель (n−1)-го
порядка, полученный из определителя Δ вычеркиванием i-ой строки и j-го
столбца.
Определение 2 Алгебраическим дополнением Aij элемента aij определителя Δ называется произведение его минора
Mij на число (-1)i-j
Определение 3 Определителем n-го порядка называется сумма произведений
элементов первой строки определителя на их алгебраические дополнения, т.е.
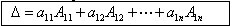
Эта сумма называется разложением определителя по элементам первой строки.
Замечание. Вместо первой строки можно взять любую другую строку
(столбец).
Правило Крамера
Пусть дана система n линейных уравнений с n переменными
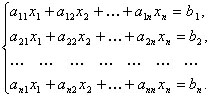
Определитель Δ, составленный из коэффициентов при переменных,
называется определителем системы, или главным определителем.
Теорема Если определитель Δ системы n×n отличен от нуля, то система имеет
единственное решение, определяемое по формулам
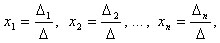
где - определитель, полученный из определителя Δ заменой его i-го столбца столбцом
свободных членов.
Если 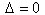 , а хотя бы один из определителей
, а хотя бы один из определителей  отличен от нуля, то система уравнений
несовместна (т.е. не имеет решений).
отличен от нуля, то система уравнений
несовместна (т.е. не имеет решений).
Если 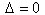 и все
и все 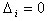 , то система уравнений неопределенна (т.е. имеет бесконечное
множество решений).
, то система уравнений неопределенна (т.е. имеет бесконечное
множество решений).
матрица
скалярный вектор плоскость
Лекция 3. Матрицы
1. Виды матриц
2. Операции над матрицами
Виды матриц
В общем случае матрица представляет собой прямоугольную таблицу чисел
размера m×n. Матрица может состоять только из одной строки или одного
столбца. В этом случае она называется соответственно матрицей-строкой или
матрицей-столбцом.
Например (2 5 1 3)−матрица-строка, 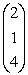 −матрица-столбец. Числа можно
рассматривать как матрицы размеров 1×1, т.е. матрицы первого порядка.
−матрица-столбец. Числа можно
рассматривать как матрицы размеров 1×1, т.е. матрицы первого порядка.
Элементы квадратной матрицы, у которых номер столбца равен номеру строки 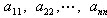 , называются диагональными и образуют
главную диагональ матрицы. Например, у приведенной ниже матрицы главную
диагональ образуют элементы 2, 1, 3.
, называются диагональными и образуют
главную диагональ матрицы. Например, у приведенной ниже матрицы главную
диагональ образуют элементы 2, 1, 3.
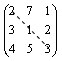
Квадратная матрица называется треугольной, если все ее элементы,
расположенные ниже (или выше) главной диагонали, равны нулю.
Квадратная матрица называется диагональной, если все ее элементы, расположенные
вне главной диагонали, равны нулю. Например, матрица A является треугольной, а
матрица B- диагональной:
Если в диагональной матрице все диагональные элементы равны единице, то
такая матрица называется единичной.
Операции над матрицами
Для матриц определяются три основные операции: умножение на число,
сложение и умножение.
. Умножение матрицы на число
Произведением матрицы A на число k называется матрица B=kA, получаемая
умножением всех элементов матрицы A, на это число: т.е.
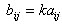
. Сложение матриц
Суммой двух матриц A и B одинакового размера называется матрица C= A+B,
каждый элемент которой равен сумме соответствующих элементов матриц A и B
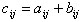
Сложение обладает обратной операцией − вычитанием.
Разность матриц определяется через две предыдущие операции:
=A-B=A + (-1)B; таким образом, 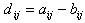 .
.
. Умножение матриц
Умножение матрицы A на матрицу B выполнимо, когда число столбцов первой
матрицы равно числу строк второй матрицы.
. Возведение в степень.
Целой положительной степенью Am(m>1) квадратной матрицы A называется
произведение m матриц, равных A.
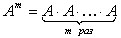 .
.
Лекция 4. Матричный метод для системы уравнений размера n×n
1. Обратная матрица
2. Теорема о существовании обратной матрицы
Обратная матрица
Определение. Матрица A-1 называется обратной для квадратной матрицы A,
если выполняется равенство 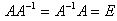 , где E - единичная матрица.
, где E - единичная матрица.
Теорема. Каждая квадратная матрица, определитель которой отличен от нуля,
имеет единственную обратную матрицу. Если определитель матрицы равен нулю, то
обратная матрица не существует
Обратную матрицу находят по формуле
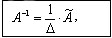 .
.
где Δ -определитель матрицы A, 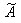 - присоединенная матрица.
- присоединенная матрица.
Присоединенной называется матрица, элементами которой являются алгебраические
дополнения Aij элементов aij матрицы A, причем алгебраические дополнения
элементов i-ой строки матрицы A образуют i-й столбец матрицы 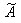
Например, 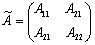 - присоединенная матрица для матрицы.
- присоединенная матрица для матрицы.
Найдем обратную матрицу для матрицы A, предполагая, что 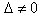 .
.
Вычислим алгебраические дополнения элементов матрицы A: Таким образом
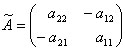
Значит, обратную матрицу для квадратной матрицы второго порядка можно находить
по формуле
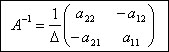
Матричный метод для системы уравнений размера n× n.
Рассмотрим систему n линейных уравнений с n переменными:
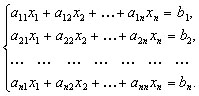
Введем следующие обозначения:- матрица коэффициентов при переменных,-
матрица-столбец переменных,- матрица-столбец свободных членов.
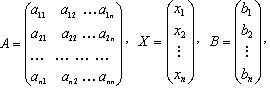
Систему уравнений можно записать в матричной форме AX=B.
Если 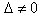 , то система имеет единственное
решение, определяемое по формуле
, то система имеет единственное
решение, определяемое по формуле
 .
.
Лекция 5. Критерий совместности системы уравнений
1. Понятие ранга матрицы
2. Элементарные преобразования матрицы
. Критерий совместности системы уравнений
Ранг матрицы
Определение 1 Минором порядка k матрицы A размера m×n называется определитель квадратной
матрицы порядка k, получаемой из матрицы A вычеркиванием каких-либо ее строк и
столбцов.
Определение 2 Рангом матрицы называется наибольший порядок отличных от
нуля миноров этой матрицы. Из определения ранга матрицы следует, что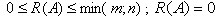 только в том случае, если все
элементы матрицы равны 0. При нахождении ранга матрицы используются матрицы
специального вида − ступенчатые.
только в том случае, если все
элементы матрицы равны 0. При нахождении ранга матрицы используются матрицы
специального вида − ступенчатые.
Примерами таких матриц являются матрицы:
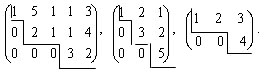
Ступенчатые матрицы отличаются следующими особенностями:
1. ступенчатая матрица не содержит нулевых строк;
2. все ступеньки матрицы имеют в высоту одну строку;
. элементы матрицы, стоящие под ступеньками, равны нулю;
. число ступенек равно числу строк матрицы.
. Ранг ступенчатой матрицы равен числу ее строк (ступенек).
Любую матрицу с помощью элементарных преобразований можно превратить в
ступенчатую.
Элементарными преобразованиями строк матрицы называются следующие
преобразования:
1. отбрасывание нулевой строки;
2. умножение всех элементов строки на ненулевое число;
. перестановка строк;
. прибавление к каждому элементу одной строки соответствующих
элементов другой строки, умноженных на некоторое число.
Матрица, полученная из данной матрицы элементарными преобразованиями
строк, называется эквивалентной данной. Ранг матрицы равен рангу эквивалентной
ей ступенчатой матрицы. Критерий совместности системы уравнений. Пусть дана
система m линейных уравнений с n переменными.
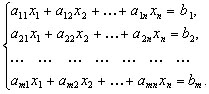
Обозначим через A матрицу из коэффициентов при переменных. Дополним
матрицу A столбцом свободных членов; полученная матрица A1 называется
расширенной.
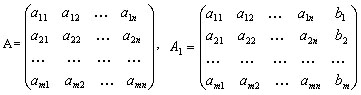
Теорема. Критерий совместности системы уравнений. Система уравнений
совместна тогда и только тогда, когда ранг матрицы системы равен рангу
расширенной матрицы этой системы
Лекция 6.
Метод Жордана- Гаусса
Метод Жордана-Гаусса опирается на следующее свойство систем уравнений:
если к какому-либо уравнению системы прибавить любое другое уравнение системы,
умноженное на некоторое число, то получится система, равносильная исходной
системе уравнений. Если такое преобразование применить к системе несколько раз,
то вновь полученная система уравнений также будет равносильна исходной системе.
С помощью элементарных преобразований исключим переменную x1 из всех уравнений,
начиная со второго; затем исключим переменную x2 из всех уравнений, начиная с
третьего, и т.д. Этот процесс называется прямым ходом и продолжается до тех
пор, пока система уравнений не приобретет ступенчатого или треугольного вида.
Если система совместна, то выполняется обратный ход − нахождение решений.
Метод Жордана-Гаусса применим для решения системы уравнений при любых m и n.
Процесс решения системы идет одновременно с процессом исследования совместности
системы уравнений.
Выполнив прямой ход, сравниваем ранги матрицы системы и расширенной
матрицы: если 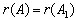 , то система уравнений совместна; если
, то система уравнений совместна; если 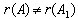 , то система уравнений несовместна.
, то система уравнений несовместна.
Для совместной системы уравнений возможны следующие случаи:
1. если 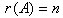 , то система уравнений имеет единственное решение;
, то система уравнений имеет единственное решение;
. если 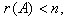 то система уравнений имеет бесконечное множество решений. В
этом случае r переменных
то система уравнений имеет бесконечное множество решений. В
этом случае r переменных 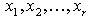 называются основными, если определитель матрицы из
коэффициентов при них отличен от нуля. Остальные n - r переменных называются
свободными.
называются основными, если определитель матрицы из
коэффициентов при них отличен от нуля. Остальные n - r переменных называются
свободными.
Пример. Решить систему уравнений
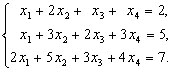
Решение. Запишем расширенную матрицу системы и выполним элементарные
преобразования строк.
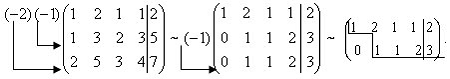
Система уравнений совместна, так как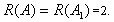 Так как число уравнений меньше числа
переменных, то система неопределенная. Определитель, составленный из
коэффициентов при переменных x1 и x2, отличен от нуля
Так как число уравнений меньше числа
переменных, то система неопределенная. Определитель, составленный из
коэффициентов при переменных x1 и x2, отличен от нуля
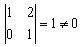
Поэтому переменные х1 и х2 будем считать основными, а х3 и х4 свободными.
Выполним обратный ход
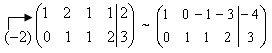
Запишем систему уравнений, соответствующую последней матрице:
Выражение основных переменных через свободные называется общим решением
системы уравнений. Придавая свободным переменным произвольные числовые
значения, получим частное решение системы уравнений. Система имеет бесконечное
множество решений
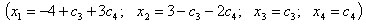 .
.
Лекция 7.
Модель Леонтьева многоотраслевой экономики
Различные отрасли материального производства тесно связаны друг с другом,
так как продукция одних отраслей необходима для выпуска продукции в других
отраслях и наоборот.
Например, для выработки электроэнергии на тепловых электростанциях
требуется уголь, а добыча угля в свою очередь невозможна без затрат
электроэнергии.
Предположим, что рассматриваются n отраслей материального производства,
каждая из которых производит свою продукцию.
Введем следующие обозначения:- общий (валовой) объем продукции - объем
продукции;- объем продукции i − ой отрасли, потребляемой j − ой
отраслью производства;- конечный продукт i − ой отрасли, т.е. ее
продукция, идущая на непроизводственное потребление, накопление, экспорт и т.д.
(все перечисленные величины имеют стоимостное выражение).
Так как валовой объем продукции любой i − ой отрасли равен
суммарному объему продукции, потребляемой n отраслями, и конечного продукта.
Обозначим через aij (i, j=1, 2, ...,n) количество продукции i − ой
отрасли, идущей на производство единицы продукции j − ой отрасли, т.е.
Числа aij в экономике называются коэффициентами прямых затрат, некоторые
из них могут быть равны нулю. Из равенства (2) следует, что
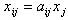
Соотношения баланса примут вид
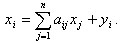
Введем обозначения:
где X - вектор валового выпуска, A - матрица прямых затрат, Y - вектор
конечного продукта. Используя введенные обозначения, запишем систему уравнений
в матричном виде:
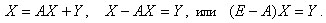
Так как определитель матрицы (E - A) отличен от нуля, то систему
уравнений можно решить матричным методом
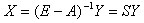
Матрица 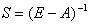 называется матрицей полных затрат.
называется матрицей полных затрат.
Выясним экономический смысл элементов матрицы S.
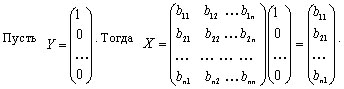
Значит, элементы первого столбца матрицы S выражают количество продукции,
которое должна произвести каждая из отраслей, чтобы получить единицу готовой
продукции первой отрасли. Таким образом, каждый элемент Sij есть величина
валового выпуска продукции i − ой отрасли, необходимого для обеспечения
выпуска единицы конечного продукта j − ой отрасли (i, j=1, 2, ...,n).
Поэтому числа Sij называют коэффициентами полных материальных затрат.
Лекция 8. Векторы
1. Понятие вектора
2. Разложение вектора по координатным осям
. Операции над векторами в координатной форме
. Условие коллинеарности векторов
1. Вектор − направленный отрезок прямой линии, т.е. отрезок у
которого различают начало и конец. Обозначение: 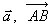 .
.
2. Длина (модуль) вектора 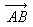 − длина отрезка АВ. Если
− длина отрезка АВ. Если 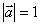 , то вектор
, то вектор 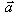 называется единичным.
называется единичным.
. Векторы, лежащие на одной или на параллельных прямых, называются
коллинеарными.
. Условие коллинеарности векторов: 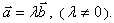
. Разложение вектора по координатным осям.
Обозначим через 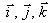 соответственно единичные векторы осей Ох, Оу, Оz. Любой
вектор в пространстве всегда можно представить в виде
соответственно единичные векторы осей Ох, Оу, Оz. Любой
вектор в пространстве всегда можно представить в виде
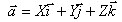
Это равенство называется разложением вектора 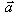 по координатным осям. Коэффициенты
этого разложения X, Y, Z − координаты вектора
по координатным осям. Коэффициенты
этого разложения X, Y, Z − координаты вектора 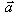 .
.
Вектор может быть записан в форме
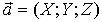
Пусть 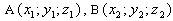 − координаты начала и конца вектора
− координаты начала и конца вектора 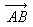 .
.
Тогда − проекции вектора 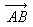 на оси координат.
на оси координат.
Координаты вектора равны разностям одноименных координат конца и начала
вектора.
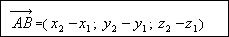
Равные векторы имеют равные координаты.
. Операции над векторами в координатной форме.
Пусть даны два вектора 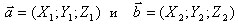 .
.
Тогда
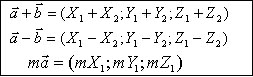 .
.
. Условие коллинеарности векторов. Условием коллинеарности двух векторов
является пропорциональность их соответствующих координат.
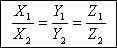
Лекция 9. Скалярное произведение векторов
1. Понятие скалярного произведения
2. Свойства скалярного произведения
. Условие перпендикулярности векторов
. Модуль вектора
Определение.
Скалярным произведением двух ненулевых векторов называется число, равное
произведению модулей этих векторов на косинус угла между ними

Углом между векторами называется наименьший угол, на который нужно
повернуть один из векторов, чтобы его направление совпало с направлением
другого вектора.
По определению, 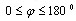 .
.
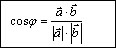
Скалярное произведение 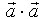 вектора
вектора 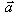 на себя называется скалярным квадратом вектора
на себя называется скалярным квадратом вектора 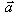 и обозначается
и обозначается 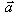 2.
2.
Так как в этом случае
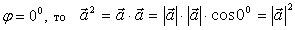 .
.
Значит, скалярный квадрат вектора равен квадрату его модуля.
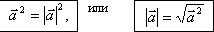
Свойства скалярного произведения
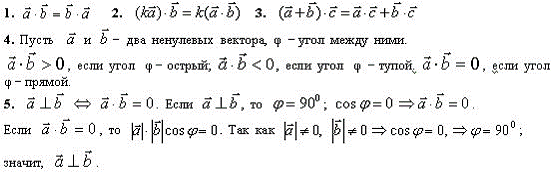
Условие перпендикулярности двух векторов
Скалярное произведение векторов в координатной форме.
Скалярное произведение двух векторов равно сумме произведений одноименных
координат этих векторов.
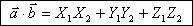
Модуль вектора. Пусть вектор a задан своими координатами: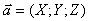 . Найдем его скалярный квадрат:
. Найдем его скалярный квадрат:
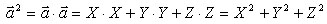 .
. 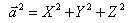 .
.
Найдем модуль вектора
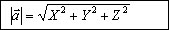
Если вектор 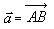 задан координатами точек
задан координатами точек 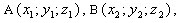 то
то
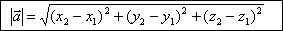 .
.
2. Способы задания прямой линии на плоскости
Определение. Уравнением линии (кривой) на плоскости Оху называется
уравнение F(x;y)=0, которому удовлетворяют координаты х и у любой точки,
принадлежащей этой линии, и не удовлетворяют координаты любой точки, не
принадлежащей этой линии.
Переменную точку M(х; у), движущуюся вдоль линии, называют текущей
точкой, а ее координаты х и у − текущими координатами.
. Общее уравнение прямой
Общее уравнение прямой имеет вид
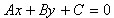
где A и B одновременно не обращаются в ноль: A2+B2≠0. Справедливы
следующие утверждения:
1. каждая прямая задается уравнением первой степени Ax+By+C=0, где
хотя бы один из коэффициентов A или B отличен от нуля;
2. каждое уравнение вида Ax+By+C=0, где хотя бы один из
коэффициентов A или B отличен от нуля, определяет прямую линию на плоскости.
. Уравнение прямой с нормальным вектором
Дана точка 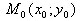 и ненулевой вектор. Любой ненулевой вектор, перпендикулярный
данной прямой, называется нормальным вектором прямой. Пусть М(x;y) −
произвольная точка прямой. Уравнение прямой имеет вид:
и ненулевой вектор. Любой ненулевой вектор, перпендикулярный
данной прямой, называется нормальным вектором прямой. Пусть М(x;y) −
произвольная точка прямой. Уравнение прямой имеет вид: 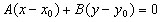 Коэффициенты A и B в общем уравнении
прямой Ax+By+C=0 являются координатами нормального вектора этой прямой.
Коэффициенты A и B в общем уравнении
прямой Ax+By+C=0 являются координатами нормального вектора этой прямой.
. Уравнение прямой с угловым коэффициентом
Пусть прямая l пересекает ось Оу в точке В(0;b) и образует с осью Ox угол
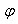 ,
, 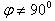 . Угол
. Угол 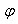 называется углом наклона прямой к оси
Ox. Тангенс угла наклона называется угловым коэффициентом прямой и обозначается
называется углом наклона прямой к оси
Ox. Тангенс угла наклона называется угловым коэффициентом прямой и обозначается
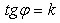 . Уравнение прямой имеет вид
. Уравнение прямой имеет вид
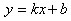
Если прямая проходит через начало координат, то ее уравнение 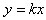 .
.
Если в общем уравнении прямой 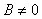 , то его можно записать в виде
уравнения с угловым коэффициентом
, то его можно записать в виде
уравнения с угловым коэффициентом
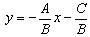
Значит, угловой коэффициент прямой равен 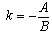 .
.
. Уравнение пучка прямых
Пусть прямая проходит через точку 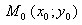 и образует с осью Ох угол
и образует с осью Ох угол 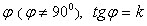 . Уравнение этой прямой имеет вид.
. Уравнение этой прямой имеет вид.
. Уравнение прямой, проходящей через две данные точки
Пусть прямая проходит через две данные точки 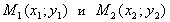 , причем
, причем 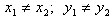 . M(x; y) − произвольная точка
прямой.
. M(x; y) − произвольная точка
прямой.
Уравнение прямой имеет вид
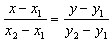
В случае прямая параллельна оси Оу и 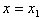 − ее уравнение;
− ее уравнение;
В случае 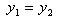 прямая параллельна оси Ox и − ее уравнение.
прямая параллельна оси Ox и − ее уравнение.
. Уравнение прямой в отрезках.
Пусть прямая проходит через точки: A(а; 0) на оси Ox и точку B(0; b) на
оси Oy  .
.
Уравнение прямой имеет вид и называется уравнением прямой в отрезках.
Лекция 11. Взаимное расположение прямых на плоскости
1. Угол между прямыми
2. Условие параллельности и перпендикулярности двух прямых
. Взаимное расположение прямых на плоскости
. Расстояние от точки до прямой
Пусть на плоскости заданы две прямые и 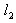 . Углом между прямыми и называется
меньший из двух смежных углов, образованных этими прямыми,
. Углом между прямыми и называется
меньший из двух смежных углов, образованных этими прямыми,  . Угол между двумя прямыми на
плоскости определяется по формуле
. Угол между двумя прямыми на
плоскости определяется по формуле
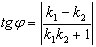
где и 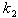 − угловые коэффициенты данных прямых.
− угловые коэффициенты данных прямых.
Если прямые параллельны, то 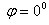 , поэтому
, поэтому . Из равенства дроби нулю следует
равенство нулю ее числителя:
. Из равенства дроби нулю следует
равенство нулю ее числителя: 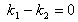 , откуда получаем условие параллельности двух прямых:
, откуда получаем условие параллельности двух прямых:
Если прямые перпендикулярны, то 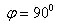 . В этом случае
. В этом случае 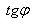 не существует, а
не существует, а 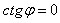 . Из формулы (1) получим
. Из формулы (1) получим
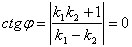
откуда 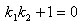 − условие перпендикулярности двух прямых.
− условие перпендикулярности двух прямых.
Взаимное расположение двух прямых на плоскости
Пусть на плоскости заданы две прямые 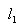 и
и 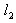 .
.
Прямая 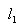 имеет уравнение
имеет уравнение 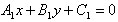 , прямая
, прямая 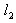 − уравнение
− уравнение 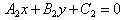 ; − нормальные векторы этих
прямых. По заданным уравнениям прямых
; − нормальные векторы этих
прямых. По заданным уравнениям прямых 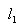 и
и 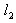 можно судить об их взаимном
расположении. Рассмотрим возможные случаи.
можно судить об их взаимном
расположении. Рассмотрим возможные случаи.
Прямые параллельны или совпадают.
Если прямые параллельны или совпадают, то их нормальные векторы
коллинеарны
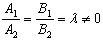
Значит, A1=λA2, B1=λB2. Перепишем уравнения прямых: 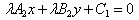 (уравнение
(уравнение 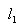 ), (уравнение
), (уравнение 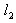 ).
).
Вычитаем из первого уравнения второе, умноженное на число λ:
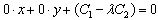
Полученное уравнение имеет решение лишь в том случае, когда его свободный
член равен нулю, т.е. C1=λC2. В этом случае прямые совпадают. Если же C1≠λC2, то уравнение решения не имеет,
значит, прямые параллельны.
Условие параллельности
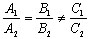
Условие совпадения
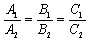
Точку пересечения прямых находим, решая систему уравнений
Система линейных уравнений имеет единственное решение, если ее
определитель отличен от нуля
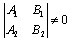
Расстояние от точки до прямой
Пусть дана точка M(x0;y0) и прямая 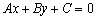 . Под расстоянием от точки M до
прямой понимается длина перпендикуляра, опущенного из точки M на прямую.
Расстояние от точки до прямой определяется по формуле
. Под расстоянием от точки M до
прямой понимается длина перпендикуляра, опущенного из точки M на прямую.
Расстояние от точки до прямой определяется по формуле
Лекция 12.
Плоскость и прямая в пространстве
1. Уравнение плоскости в пространстве
2. Уравнение плоскости в отрезках
. Условие параллельности и перпендикулярности плоскостей
Пусть плоскость a проходит через точку М0(x0;y0;z0) перпендикулярно
вектору 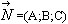 . Вектор
. Вектор  называется нормальным вектором
плоскости. Составим уравнение плоскости a. Пусть М(x;y;z) − произвольная
точка плоскости. Вектор
называется нормальным вектором
плоскости. Составим уравнение плоскости a. Пусть М(x;y;z) − произвольная
точка плоскости. Вектор 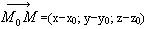 принадлежит плоскости a. Так как вектор
принадлежит плоскости a. Так как вектор 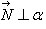 , то
, то 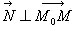 . Значит, скалярное произведение
векторов
. Значит, скалярное произведение
векторов  и равно нулю:
и равно нулю: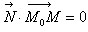 , или в координатной форме:
, или в координатной форме:
(x−x0)+B(y−y0)+C(z−z0)=0.
Раскрыв скобки в полученном уравнении, получим
+By+Cz+D=0
Полученное уравнение называется общим уравнением плоскости.
Всякое уравнение первой степени Ax+By+Cz+D=0, в котором хотя бы один из
коэффициентов A, B, C не равен нулю, является уравнением плоскости в
пространстве. Коэффициенты A, B, C являются координатами нормального вектора
плоскости.
Рассмотрим взаимное расположение двух плоскостей a1 и a2, заданных общими
уравнениями
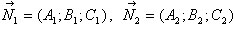 − нормальные векторы этих плоскостей.
− нормальные векторы этих плоскостей.
Если плоскости параллельны, то их нормальные векторы коллинеарны:
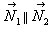
Из условия коллинеарности векторов следует, что значит, условием
параллельности плоскостей является пропорциональность коэффициентов при
одноименных переменных.
Если плоскости перпендикулярны, то их нормальные векторы также
перпендикулярны
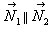
Значит, 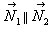 =0, или
=0, или 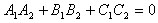
Таким образом, условием перпендикулярности плоскостей является равенство
нулю скалярного произведения их нормальных векторов.
Угол между лоскостями, заданными общими уравнениями
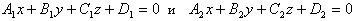
определяется как угол φ между их нормальными векторами
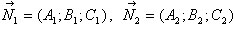
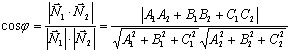
Расстояние от точки до плоскости. Пусть дана точка M(x0;y0;z0) и
плоскость Ax+By+Cz+D=0.
Под расстоянием от точки M до плоскости понимается длина перпендикуляра
d=MN, опущенного из точки M на плоскость.
Прямая в пространстве. Пусть прямая l проходит через точку М0(x0;y0;z0).
Ненулевой вектор 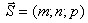 , параллельный прямой l, называется направляющим вектором
этой прямой. Пусть М(x;y;z) − произвольная точка прямой l.
, параллельный прямой l, называется направляющим вектором
этой прямой. Пусть М(x;y;z) − произвольная точка прямой l.
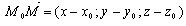
Векторы коллинеарны. Применив условие коллинеарности векторов, получим
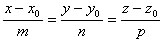
Лекция 13. Введение в анализ
1. Понятие функции одной переменной
2. Основные свойства функции
. Предел функции
. Основные свойства пределов
Определение. Если каждому числу x из множества X поставлено в
соответствие число y из множества Y, то говорят, что на множестве X задана
функция
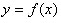
Основные свойства функции
. Четность и нечетность
Определение 1 Функция 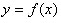 называется четной, если для любых значений x из области
определения
называется четной, если для любых значений x из области
определения
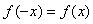
График четной функции симметричен относительно оси Oy.
Определение 2 Функция 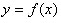 называется нечетной, если для любых значений x из области
определения
называется нечетной, если для любых значений x из области
определения
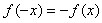
График нечетной функции симметричен относительно начала координат.
. Монотонность
Определение 1 Функция называется возрастающей на промежутке X, если
большему значению аргумента из этого промежутка соответствует большее значение
функции, т.е.
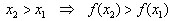 .
.
Определение 2 Функция называется убывающей на промежутке X, если большему
значению аргумента из этого промежутка соответствует меньшее значение функции,
т.е.
Предел функции
Пусть функция 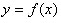 определена в некоторой окрестности точки a кроме, быть может,
самой точки a.
определена в некоторой окрестности точки a кроме, быть может,
самой точки a.
Определение 1 Число A называется пределом функции  при x, стремящемся к a (или в точке
a), если для всех значений x достаточно близких к a и отличных от a, значения
функции
при x, стремящемся к a (или в точке
a), если для всех значений x достаточно близких к a и отличных от a, значения
функции  сколь угодно мало отличаются от числа
A.
сколь угодно мало отличаются от числа
A.
Обозначение
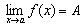
Если при стремлении x к a переменная x принимает только значения, меньшие
a, то такой предел называется левым и обозначается
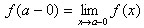
Если же переменная x принимает только значения, большие a, то такой
предел называется правым и обозначаетс
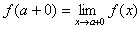
Левый и правый пределы называются односторонними пределами
Для существования предела функции  при x→a необходимо и достаточно
существование и равенство односторонних пределов:
при x→a необходимо и достаточно
существование и равенство односторонних пределов:
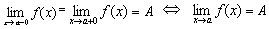
Определение 2 Число A называется пределом функции  при x, стремящемся к∞, если для
всех достаточно больших по модулю значений x соответствующие значения функции
при x, стремящемся к∞, если для
всех достаточно больших по модулю значений x соответствующие значения функции  сколь угодно мало отличаются от числа
A. Обозначение
сколь угодно мало отличаются от числа
A. Обозначение
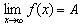
Основные свойства пределов
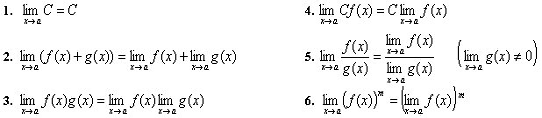
Все правила имеют смысл, если существуют конечные пределы функций  и
и 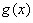 при x→a (a − число или ± ∞).
при x→a (a − число или ± ∞).
Лекция 14. Бесконечно малая и бесконечно большая функции
1. Бесконечно малая и бесконечно большая функции
2. Неопределенности 0/0, ∞/∞, 1∞. Замечательные
пределы
Определение 1 Функция  называется бесконечно малой при x→a, если
называется бесконечно малой при x→a, если
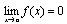
Определение 2 Функция  называется бесконечно большой при
называется бесконечно большой при
→a, если 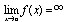
Теорема 1 Если функция  − бесконечно малая при x→a, то функция 1/f(x) −
бесконечно большая при x→a. Если функция
− бесконечно малая при x→a, то функция 1/f(x) −
бесконечно большая при x→a. Если функция  − бесконечно большая при x→a,
то функция 1/f(x) − бесконечно малая при x→a.
− бесконечно большая при x→a,
то функция 1/f(x) − бесконечно малая при x→a.
Определение 3 Функции  и
и 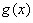 называются эквивалентными при x→a, если предел их
отношения равен единице.
называются эквивалентными при x→a, если предел их
отношения равен единице.
Это записывают так
если 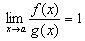 , то
, то 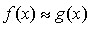 при x→a
при x→a
При x→∞ многочлен эквивалентен своему старшему члену.
Теорема 2 Предел отношения двух бесконечно малых (бесконечно больших)
функций при x→a равен пределу отношения эквивалентных им функций при x→a.
Неопределенности вида
Рассмотрим частное двух функций
Если 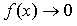 и
и 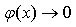 при
при 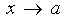 , то говорят: «имеем неопределенность вида
, то говорят: «имеем неопределенность вида 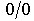 ».
».
Если же  и
и  при
при 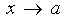 , то говорят о неопределенности вида
, то говорят о неопределенности вида 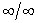
Если  и
и 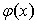 ногочлены, то для раскрытия неопределенности 0/0 применяют
сокращение дроби на множитель
ногочлены, то для раскрытия неопределенности 0/0 применяют
сокращение дроби на множитель 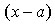 .
.
В случае неопределенности ∞/∞ пользуются теоремой 2 - находят
предел отношения старших членов многочленов.
Замечательные пределы
Первый замечательный предел
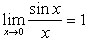
Это означает, что 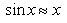 при
при 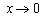 .
.
Второй замечательный предел
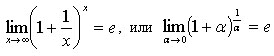 .
.
Неопределенность вида 1∞. Пусть функция имеет вид
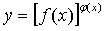
Если при 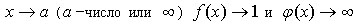 , то говорят о неопределенности 1∞.
, то говорят о неопределенности 1∞.
Пусть требуется вычислить предел
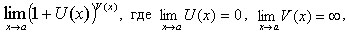
а − число или 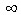 . Это неопределенность 1∞.
. Это неопределенность 1∞.
Применяя формулу второго замечательного предела, получим формулу для
вычисления этого предела
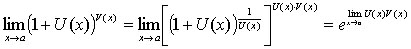 .
.
Таким образом, 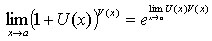 .
.
Лекция 15. Непрерывность функции
1. Понятие непрерывной функции
2. Виды точек разрыва
. Свойства непрерывных функций
Пусть функция определена в точке a и некоторой ее окрестности.
Определение 1 Функция  называется непрерывной в точке a, если предел функции и ее
значение в этой точке равны
называется непрерывной в точке a, если предел функции и ее
значение в этой точке равны
т.е. 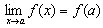
Для непрерывности функции  в точке a должны выполняться следующие условия:
в точке a должны выполняться следующие условия:
1. функция  определена в точке a, т.е. существует
определена в точке a, т.е. существует 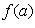 ;
;
2. функция  имеет конечный предел при
имеет конечный предел при 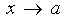 , это означает существование конечных
пределов
, это означает существование конечных
пределов
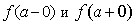
3. этот предел равен значению функции в точке a, т.е.
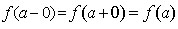
Определение 2 Функция называется непрерывной на промежутке Х, если она
непрерывна в каждой точке этого промежутка. Все элементарные функции непрерывны
в области определения.
Определение 3 Если функция  не является непрерывной в точке a
(т.е. не выполняется хотя бы одно из условий 1-3), то точка a называется точкой
разрыва.
не является непрерывной в точке a
(т.е. не выполняется хотя бы одно из условий 1-3), то точка a называется точкой
разрыва.
Виды точек разрыва
Определение 3 Если функция  в точке a имеет конечный предел, но
этот предел отличен от значения функции в этой точке (или точка не входит в
область определения функции), то точка a называется точкой устранимого разрыва
(рис.1).
в точке a имеет конечный предел, но
этот предел отличен от значения функции в этой точке (или точка не входит в
область определения функции), то точка a называется точкой устранимого разрыва
(рис.1).
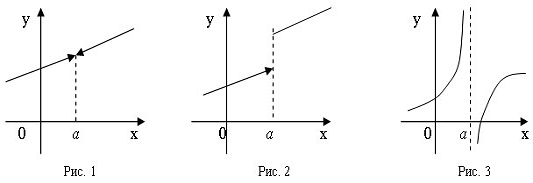
Определение 4 Если функция  в точке a имеет конечные, но не
равные друг другу односторонние пределы, то точка a называется точкой разрыва
первого рода (рис.2).
в точке a имеет конечные, но не
равные друг другу односторонние пределы, то точка a называется точкой разрыва
первого рода (рис.2).
Определение 5 Если в точке a хотя бы один из односторонних пределов равен
бесконечности, то точка a называется точкой разрыва торого рода (рис.3).
Свойства непрерывных функций
1. Если функции  и
и 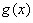 непрерывны в точке a, то их сумма
непрерывны в точке a, то их сумма 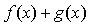 , произведение
, произведение 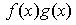 и частное (при условии
и частное (при условии 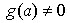 ) являются функциями, непрерывными в
точке a.
) являются функциями, непрерывными в
точке a.
2. Если функция  непрерывна на отрезке
непрерывна на отрезке 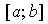 , то она достигает на этом отрезке
наибольшего и наименьшего значения.
, то она достигает на этом отрезке
наибольшего и наименьшего значения.
. Если функция  непрерывна на отрезке
непрерывна на отрезке 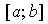 и значения ее на концах отрезка
и значения ее на концах отрезка 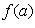 и
и 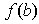 имеют противоположные знаки, то
внутри отрезка найдется точка c такая, что
имеют противоположные знаки, то
внутри отрезка найдется точка c такая, что 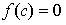 .
.
Лекция 16. Производная и дифференциал
1. Понятие производной функции
2. Дифференциал функции
. Правила вычисления производной. Производная сложной функции
Функция 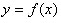 определена на промежутке X. Пусть
определена на промежутке X. Пусть 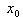 − некоторое исходное значение
аргумента,
− некоторое исходное значение
аргумента, 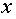 − последующее значение аргумента.
− последующее значение аргумента.
Определение 1Приращением аргумента в точке 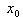 называется разность между новым
значением аргумента
называется разность между новым
значением аргумента 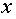 и его прежним значением
и его прежним значением
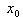 :
: 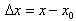 , или
, или 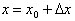
Определение 2. Приращением функции  в точке
в точке 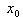 , соответствующим приращению
аргумента
, соответствующим приращению
аргумента  , называется разность
, называется разность
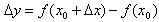
Пусть функция  определена на промежутке X. Возьмем точку
определена на промежутке X. Возьмем точку 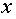 , принадлежащую этому промежутку.
Дадим значению
, принадлежащую этому промежутку.
Дадим значению 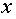 приращение
приращение  . Тогда функция получит приращение
. Тогда функция получит приращение 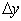 .
.
Определение 3. Производной функции 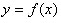 называется предел отношения
приращения функции к приращению аргумента при стремлении приращения аргумента к
нулю (если этот предел существует):
называется предел отношения
приращения функции к приращению аргумента при стремлении приращения аргумента к
нулю (если этот предел существует):
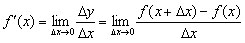 .
.
Дифференциал функции
Пусть дана дифференцируемая функция 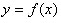 . Из определения производной следует,
что при
. Из определения производной следует,
что при 
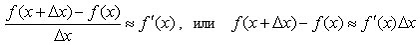 .
.
Левая часть этого выражения есть приращение функции 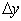 , поэтому
, поэтому 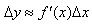 , а правая часть называется
дифференциалом функции.
, а правая часть называется
дифференциалом функции.
Определение Дифференциалом функции называется произведение ее производной
на приращение аргумента:
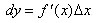 , или
, или 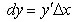
Найдем дифференциал для функции 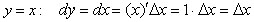 , т.е. дифференциал независимой
переменной равен приращению этой переменной. Поэтому дифференциал функции
принято записывать в виде
, т.е. дифференциал независимой
переменной равен приращению этой переменной. Поэтому дифференциал функции
принято записывать в виде
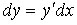
Из этого равенства следует, что
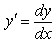
Правила вычисления производной
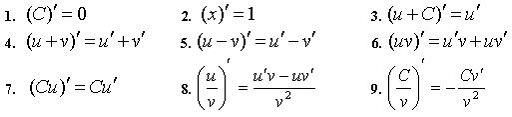
Производная сложной функции
Производная сложной функции равна произведению производной этой функции
по промежуточному аргументу на производную промежуточного аргумента по
переменной 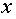 .
.
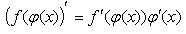 .
.
1. Геометрический смысл производной
2. Возрастание и убывание функции
. Экстремум функции. Необходимое и достаточное условие экстремума
Геометрический смысл производной
Производная функции 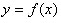 в точке
в точке 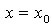 равна угловому коэффициенту касательной, проведенной к
графику функции в точке
равна угловому коэффициенту касательной, проведенной к
графику функции в точке
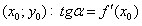 , − уравнение касательной.
, − уравнение касательной.
Возрастание и убывание функции
Достаточное условие монотонности функции
1. Если производная дифференцируемой функции положительна внутри
некоторого промежутка, то функция возрастает на этом промежутке.
2. Если производная дифференцируемой функции отрицательна внутри
некоторого промежутка, то функция убывает на этом промежутке.
Экстремум функции
Определение 1 Точка 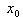 называется точкой максимума функции
называется точкой максимума функции  , если для всех
, если для всех 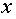 из некоторой окрестности
из некоторой окрестности 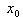 выполняется неравенство
выполняется неравенство
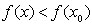
Определение 2 Точка 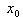 называется точкой минимума функции
называется точкой минимума функции  , если для всех
, если для всех 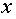 из некоторой окрестности
из некоторой окрестности 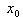 выполняется неравенство
выполняется неравенство
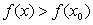
Точки максимума и минимума называются точками экстремума функции, а
значения функции в этих точках называются экстремумами функции.
Необходимое условие экстремума
Если в точке 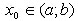 дифференцируемая функция имеет экстремум, то производная в
этой точке равна нулю.
дифференцируемая функция имеет экстремум, то производная в
этой точке равна нулю.
Определение 3 Точки, в которых производная функции равна нулю, называются
критическими. Если функция имеет экстремум, то он может быть только в
критических точках.
Первое достаточное условие экстремума
Пусть  − дифференцируемая функция,
− дифференцируемая функция, 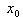 − критическая точка. Если при
переходе через точку
− критическая точка. Если при
переходе через точку 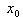 производная функции меняет свой знак с плюса на минус, то
производная функции меняет свой знак с плюса на минус, то 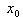 есть точка максимума функции
есть точка максимума функции  , а если с минуса на плюс, то −
точка минимума.
, а если с минуса на плюс, то −
точка минимума.
Второе достаточное условие экстремума
Пусть функция  дважды дифференцируема в точке
дважды дифференцируема в точке 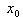 и
и
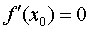
Если 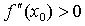 , то
, то 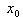 − точка минимума функции
− точка минимума функции  ;
;
если 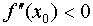 , то
, то 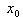 − точка максимума функции
− точка максимума функции  .
.
Если 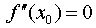 , следует применять первое правило
, следует применять первое правило