Расчет доверительных интервалов для различных числовых характеристик

Расчет доверительных интервалов для различных числовых характеристик

МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РФ

Федеральное государственное бюджетное образовательное учреждение высшего профессионального образования

ТОМСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ

СИСТЕМ УПРАВЛЕНИЯ И РАДИОЭЛЕКТРОНИКИ (ТУСУР)

Кафедра Радиоэлектроники и защиты информации (РЗИ)

Пояснительная записка к курсовой работе

по дисциплине

«Теория вероятностей и математическая статистика»

Студент гр.181

А.Д. Андрецова

Руководитель

доцент кафедры РЗИ

Н.Глазов

РЕФЕРАТ

Курсовая работа с.25, рис.1, источников 9,

ИНТЕРВАЛЬНОЕ ОЦЕНИВАНИЕ, ПРОВЕРКА ГИПОТЕЗ, РЕГРЕССИОННЫЙ АНАЛИЗ, МЕТОД МНК, ПАКЕТ Mathcad 14, СИСТЕМА КОМПЬЮТЕРНОЙ АЛГЕБРЫ.

Целью курсовой работы является закрепление теоретических знаний и получение практических навыков расчета доверительных интервалов и критериев согласия для различных числовых характеристик, а также восстановление сигнала из смеси - сигнал + шум, используя метод наименьших квадратов.

В результате были решены 2 задачи по расчету доверительных интервалов для различных числовых характеристик, а также получена универсальная программа для извлечения сигнала из смеси с помощью полинома 3 степени.

Разработанный программный продукт может быть использован для проведения регрессионного анализа.

Пояснительная записка выполнена в текстовом редакторе Microsoft Word 2007. В качестве рабочей среды был использован пакет Mathcad 14.

ВВЕДЕНИЕ

Целью данной курсовой работы является получение практических знаний в сфере точечного и интервального оценивания математического ожидания и дисперсии, проверки гипотез, а также освоение метода наименьших квадратов в регрессионном анализе.

Каждая из частей содержит теоретический обзор, математические расчеты и выводы о проделанной работе.

1. ПОСТАНОВКА ЗАДАЧИ

В первой части данной работы нужно разъяснить, что такое точечное и интервальное оценивание, а так же закрепить полученные знания на примере оценивания таких параметров, как дисперсия, математическое ожидание и вероятность.

Во второй части необходимо рассмотреть такое понятие, как регрессионный анализ, а именно метод наименьших квадратов (МНК). Также, во второй части нужно закрепить полученные знания на практике. Задача состоит в извлечении истинного тренда.

Дана выборка из N =100 значений.

Требуется:

а) найти статистический ряд;

б) построить гистограмму и полигон частот;

в) найти оценки для математического ожидания и дисперсии;

г) считая распределение генеральной совокупности нормальным,

найти границы доверительного интервала для математического ожидания и дисперсии при надёжности а= 0,95;

д) проверить с помощью критерия Х² гипотезу о том, что выборка извлечена из нормальной генеральной совокупности с математическим ожиданием и средним квадратическим отклонением равными соответственно статистическому среднему и статистическому среднему квадратичному отклонению. Уровень значимости принять равным а = 0,05.

В MathCAD с помощью датчика (генераторы) случайных чисел с нормальным законом распределения rnorm(m,μ,σ) зададим шум. Он возвращает вектор m случайных чисел, имеющих нормальное распределение с математическим ожиданием μ и среднеквадратическим отклонением σ. Математическое ожидание примем равным нулю, а дисперсию равной единице.

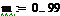
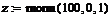
Истинный тренд имеет вид:

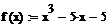
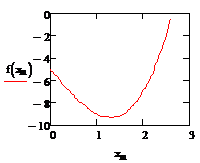
Функция сигнал + шум имеет вид: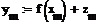

1.1 Теоретический обзор

Теория оценок.

Параметры законов распределения обычно оцениваются по выборке, т.е строится функция выборочных данных, которая мало отличается от истинного значения параметра. Существуют разные способы оценивания. Основными являются точечные и интервальные оценки параметров закона распределения.

1. Точечное оценивание - это вид статистического оценивания, при котором значение неизвестного параметра приближается отдельным числом.

Способы точечного оценивания:

.        Метод моментов.

.        Метод максимального правдоподобия

Точечные оценки характеризуются следующими свойствами:

.        Смещение. Оценка параметра называется несмещенной, если ее математическое ожидание равно истинному значению оцениваемого параметра.

2.  Состоятельность. При достаточно больших объемах выборки оценка параметра стремится к истинному значению.

3.      Эффективность. Та оценка, у которой дисперсия минимальна, называется эффективной оценкой.

Для точечных оценок математического ожидания и дисперсии были найдены следующие формулы:

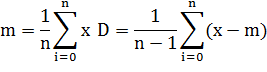
Где n - объем выборки

. Интервальное оценивание - оценка, представляемая интервалом значений, внутри которого, с задаваемой исследователем вероятностью, находится истинное значение оцениваемого параметра.

Главную роль в таком оценивании играет доверительный интервал.

Доверительный интервал - интервал, в котором находится истинное значение параметра с заданной вероятностью.

Вероятность того, что истинное значение лежит в интервале называется доверительной вероятностью (коэффициентом доверия) или надежностью, соответствующей данному доверительному интервалу.

Для построения доверительного интервала требуется знать:

. Закон распределения статистики.

. Точечная оценка параметров.

. Уровень значимости

. Квантиль P - значение случайной величины, при котором функция распределения равна P.

Формулы для расчета доверительного интервала для математического ожидания и дисперсии:

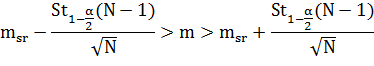
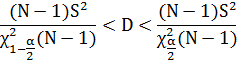
Где N объем выборки, msr - точечная оценка математического ожидания, St1-a/2(N-1) - квантиль распределения Стьюдента уровня 1-a/2 и степенью свободы N-1, S2 - точечная оценка дисперсии,

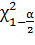(N-1)- квантиль распределения Х2 Пирсона уровня 1-а.2, и степенью свободы N-1.

Квантили этих распределений табулированы.

Критерий согласия 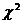Пирсона

Он основан на сравнении эмпирических частот интервалов группировки с теоретическими (ожидаемыми) частотами, рассчитываемыми по формулам теоретического распределения.

Условия применения: объем выборки 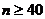, выборочные данные сгруппированы в интервальный вариационный ряд с числом интервалов не менее 7, ожидаемые (теоретические) частоты интервалов не должны быть меньше 5.

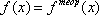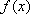Гипотеза Н0:  - плотность распределения  генеральной совокупности, из которой взята выборка, соответствует теоретической модели нормального распределения.

Альтернатива Н1:

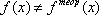
Уровень значимости: .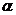

Порядок, применения:

. Формулируется гипотеза, выбирается уровень значимости .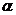

. Получается выборка объема 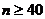 независимых наблюдений и представляется эмпирическое распределение в виде интервального вариационного ряда.

. Рассчитываются выборочные характеристики 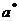и S. Их используют в качестве генеральных параметров и нормального распределения, с которым предстоит сравнить эмпирическое распределение.

. Вычисляются значения теоретических частот попадания в i-й интервал группировки. Для этого необходимо вычислить:

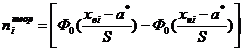
где Ф0(u) - функции Лапласа, xвi и хнi - верхняя и нижняя границы i-го интервала группировки.

Если окажется, что вычисленные ожидаемые частоты 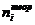 некоторых интервалов группировки меньше 5, то соседние интервалы объединяются так, чтобы сумма их ожидаемых частот была больше или равна 5. Соответственно складываются и эмпирические частоты объединяемых интервалов.

. Значени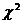е -критерия рассчитывается по формуле:

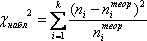
где ni - эмпирические частоты; 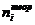- ожидаемые (теоретические) частоты; k - число интервалов группировки после объединения.

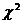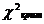. Из таблиц распределения находится критическое значение  критерия для уровня значимости 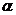и числа степеней свободы r = k-3

. Вывод: если 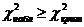 то эмпирическое распределение не соответствует нормальному распределению на уровне значимости 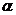, в противном случае нет оснований отрицать это соответствие.

Распределение Стьюдента

Распределение Стьюдента (t- распределение) имеет важное значение при статических вычислениях, связанных с нормальным законом, а именно тогда, когда среднеквадратичное отклонение 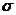 не известно и еще подлежит определению по опытным данным.

Пусть X и X1, X2, …Xn - независимые случайные величины, имеющие нормальное распределение с параметрами:

[X] = M[X1] = M [X2] = … = M[Xn] = 0

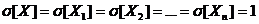
Случайная величина:

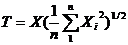
являющаяся функцией нормально распределенных случайных величин, называется безразмерной дробью Стьюдента. Распределения случайной величины T не зависит от параметров распределения независимых случайных величин X и X1, X2, …Xn, а зависит только от одного параметра - числа степеней свободы r.

Математическое ожидание и дисперсия случайной величины T соответственно равны:

M[T] = 0D[T] = 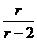r > 2

При неограниченном увеличении числа степеней свободы распределения Стьюдента асимптотически переходит в нормальное распределение Гаусса с параметрами

M[T] = 0 и D[T] = 1.

В математической статистике часто используется квантил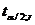и  распределения Стьюдента в зависимости от числа степеней свободы r и заданного уровня вероятности .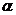

С геометрической точки зрения нахождение квантилей распределения Стьюдента 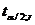, заключается в таком выборе значения 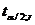, при котором суммарная площадь под кривой плотности 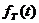 на участках  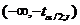и 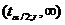была бы равно .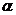

1.2 Расчеты

Дана выборка:

Количество интервалов Nint=6

Минимальное и максимальное значение выборки:

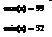
Ширина подынтервала:

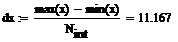
Граничные точки подынтервалов

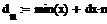
Чтобы найти полигон частот отсортируем выборку с помощью функции sort() и запустим цикл для данной выборки.

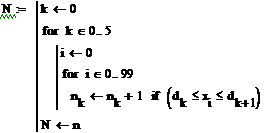
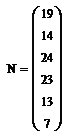
Проверим данные частоты с помощью функции hist()

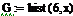
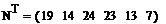
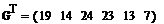
Значения верны. Построим гистограмму:

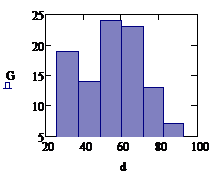
Найдем оценки для математического ожидания и дисперсии:

Для этого найдем середины отрезков данных интервалов

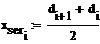
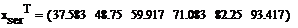
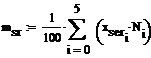
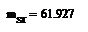
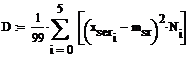
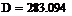
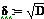
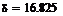
Доверительный интервал для мат.ожидания:

Надёжность равна 0.95

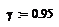
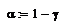
Квантили распределения Стьюдента найденные по таблице:

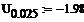
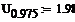
Левая и правая границы доверительного интервала:

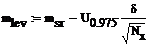
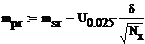
Доверительный интервал для дисперсии при той же надежности:

Квантили распределения Пирсона найденные по таблице:

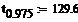
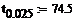
Левая и правая границы доверительного интервала:

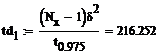
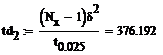
Для того чтобы проверить гипотезу о том, что наша выборка извлечена из нормальной генеральной совокупности, найдем теоретические частоты.

Функция распределения Лапласа

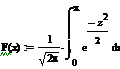
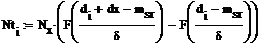
Найденные частоты:

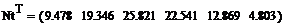
Проверим данную гипотезу с помощью критерия Х2 Пирсона:

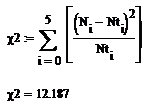
По таблице найдем критическую точку для данной выборки при уровне значимости равным 0.05 и степенями свободы равным k:

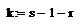
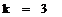
Где S -количество интервалов, т.е равно 6 и r- количество параметров, для нормального распределения их 2.

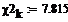
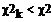
1.3 Выводы

В ходе работы над первой частью курсовой работы был написан теоретический обзор по точечному и интервальному оцениванию. В работе выполнены расчеты, связанные с нахождение доверительных интервалов для математического ожидания, дисперсии и вероятности. Для заданной генеральной совокупности построены гистограмма и полигон, найдены оценки математического ожидания и дисперсии, а также доверительные интервалы для математического ожидания и дисперсии. С помощью критерия согласия 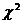Пирсона проверена гипотеза о том, что выборка извлечена из нормальной генеральной совокупности. В результате анализа, гипотеза не подтвердилась, т.к. получилось, что 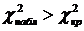. Отсюда следует вывод, что гипотеза о нормальном законе распределения генеральной совокупности должна быть отвергнута.

доверительный интервал наименьший квадрат

1.4 Регрессионный анализ. Метод наименьших квадратов. Классическая линейная модель регрессионного анализа

Линейная модель связывает значения зависимой переменной y(x) со значениями независимых показателей Xk (факторов) формулой:

y(x)=B₀+B₁X¹+:+B_pX^p+e

где e - случайная ошибка. Здесь X^k означает не "икс в степени k", а переменная X с индексом k. Величина e называется ошибкой регрессии. Первые математические результаты, связанные с регрессионным анализом, сделаны в предположении, что регрессионная ошибка распределена нормально с параметрами N(0,1), ошибка для различных объектов считаются независимыми. Кроме того, в данной модели мы рассматриваем переменные X как неслучайные значения, Такое, на практике, получается, когда идет активный эксперимент, в котором задают значения X (например, назначили зарплату работнику), а затем измеряют y(x) (оценили, какой стала производительность труда). За это иногда зависимую переменную называют откликом. Теория регрессионных уравнений со случайными независимыми переменными сложнее, но известно, что, при большом числе наблюдений, использование метода разработанного для неслучайных X корректно.

Для получения оценок 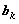 коэффициентов 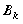 регрессии минимизируется сумма квадратов ошибок регрессии:

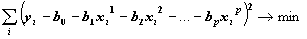
Решение задачи сводится к решению системы линейных уравнений относительно .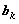

На основании оценок регрессионных коэффициентов рассчитываются значения Y:

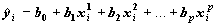
О качестве полученного уравнения регрессии можно судить, исследовав 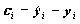 - оценки случайных ошибок уравнения.

Так как мы ищем оценки 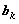, используя случайные данные, то они, в свою очередь, будут представлять случайные величины.

Запишем систему линейных уравнений в матричном виде

Искомые параметры будут находиться по формуле:

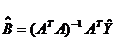
Оценка дисперсии случайной ошибки получается по формуле

,

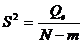где m - число параметров тренда

N - объём выборки

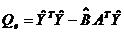
Величина S называется стандартной ошибкой регрессии. Чем меньше величина S, тем лучше уравнение регрессии описывает независимую переменную Y.

Доверительный интервал для каждого из коэффициентов тренда имеет вид:

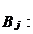
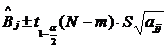
Где 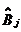 - точечная оценка параметра 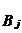- дисперсия для ошибок наблюдения

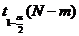 - квантиль уровня  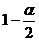от (N-m) для распределения Стьюдента

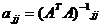
1.5 Расчеты

Дан истинный тренд функции с параметрами, и смесь сигнал+шум:

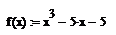
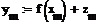
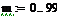
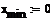
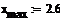
где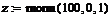

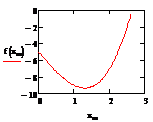
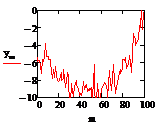
Находим коэффициенты полинома по МНК:

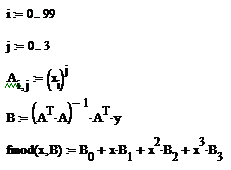
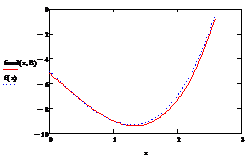
График найденной функции и тренда:

Найденные коэффициенты

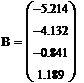
Найдем доверительный интервал для заданных коэффициентов полинома:

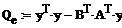
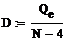
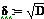
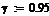
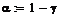
Квантили распределения Стьюдента, найденные в таблице:

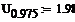
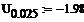
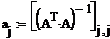
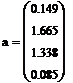
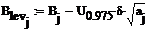
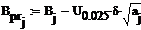
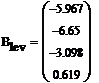
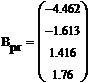
График разности тренда от найденной функции:

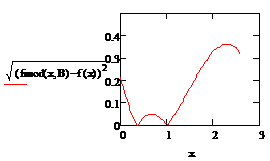
Максимальное отклонение от тренда:

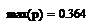
1.6 Вывод

С помощью регрессионного анализа (метода МНК) был выделен тренд в рамках модели кубической параболы, т.е. оценены значения коэффициентов модели и рассчитаны доверительные интервалы для них. График эмпирического тренда, найденный с помощью регрессионного анализа, несколько отличается от истинного тренда. Выявлены зоны, где отклонения эмпирического тренда от теоретического наибольшие.

ЗАКЛЮЧЕНИЕ

В результате проведенной работы были закреплены теоретические знания и приобретены практические навыки работы со статистиками, умение находить точечные и интервальные оценки математического ожидания и дисперсии, строить гистограммы и полигоны. Был изучен метод МНК (регрессионного анализа), при помощи которого удаётся выделить тренд из смеси сигнал + шум.

ЛИТЕРАТУРА

1. Лекции по математической статистике. Чернова Н.И.2007

. Математическая статистика. Мазманишвили А.С.2003

. Математическая статистика (учебное пособие). Ю.И.Галанов.2010

. Проверка статистических гипотез. А.Симонов, Н. Выск.1985

. Руководство к решению задач по ТВ и М.С. Гмурман В.2003