Расчёт показателей теоретического распределения
Министерство
образования и науки Российской Федерации
Федеральное
государственное бюджетное образовательное учреждение высшего профессионального
образования
«Алтайский
государственный технический университет им. И.И. Ползунова»
Факультет
«Вечерний»
Кафедра
«Организация и безопасность движения»
Отчет
по лабораторной работе №2
Расчёт
показателей теоретического распределения
по
дисциплине «Надёжность работы автомобильных дорог»
Студент Ламова А.Ю.
Руководитель проекта к.т.н.,
доцент И.В.Огнев
БАРНАУЛ
2012
Цель работы:освоить
методы статистической обработки информации оботказах и определить основные
характеристик надежности.
Немного теории
(повторение пройденного)
Среднее арифметическое значение
характеризует центр группирования случайных величин;
Дисперсия, среднее квадратическое
отклонение и коэффициент вариации характеризуют
степень разброса случайных величин около центра;
Асимметрия и эксцесс
характеризуют соответственно степень не симметрии и тупости кривой
распределения.
Законы распределения случайных
величин отражают физическую сущность рассматриваемых
явлений. Совокупность факторов или условий, приводящих к возникновению того или
другого вероятностного закона, называют математической моделью явления.
Применительно к нормальному закону математической моделью служат следующие
условия:
- исследуемое
явление является следствием или суммой воздействий достаточно большого
количества различных случайных, независимых между собой или слабо зависимых
источников;
- дисперсии и
математические ожидания складываемых источников мало отличаются друг от друга,
и от математического ожидания и дисперсии складываемой суммы.
При наличии указанных условий возникает
нормальный закон, который находит широкое применение при решении различных
инженерных и экономических задач.Применительно к математической теории
надежности нормальный закон хорошо описывает постепенные отказы изделий,
вызываемые выходом из строя их отдельных элементов.
Критерий согласия Пирсона
применяется для проверки согласованности эмпирического и теоретического
распределений.
Точечной
называют опенку, которая определяется одним числом.
Интервальной
называют оценку, которая определяется двумя числами - концами интервала.
Доверительным
называют интервал, который покрывает неизвестный параметр с заданной
надежностью  .
.
Расчет
статистический аккумулятор надежность математический
Дано:
имеется статистика отказов аккумуляторов. Было обследовано 20 аккумуляторов.
Величина выработки аккумуляторов колеблется в пределах от 6100 км до 14700 км.
Определить
параметры теоретического распределения и величину границ нижнего и верхнего
интервала оценки математического ожидания выработки аккумляторов с
доверительной вероятностью 0,95.
Решение: требуется решить следующие задачи:
- построить
гистограмму опытных частот по пробегу и по ее виду решить в первом приближении
вопрос о законе распределения (было в первой работе);
- для
предполагаемого закона распределения построить теоретическую кривую частоты
отказов по пробегу, найти основные параметры закона распределения, построить
интегральную кривую;
- дать интервальную оценку
математического ожидания.
Для удобства обработки весь объем выборки п
обычно группируется в К разрядов (интервалов).
В нашем примере нижний пробег округлен до 6 тыс.
км, верхний до 15 тыс. км. Их разность составила 6 тыс. км, что позволяет нам
все измерения сгруппировать в 9 разрядов с величиной интервала в 6 тыс. км.
Определяем числовые характеристики
статистического распределения.
Находим среднее арифметическое:
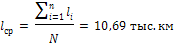
Определяем оценку дисперсии:
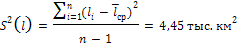
Находим оценку среднего квадратического
отклонения:
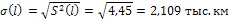
Определяем оценку величины коэффициента
вариации:
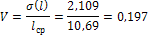
Расчёт показателей теоретического
распределения
За нулевую гипотезу принимаем, что теоретическое
распределение является нормальным (исходя из вида гистограммы).
Нормальный закон распределения характеризуется
плотностью вероятности:

где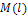 и
и
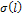 -
соответственно математическое ожидание и среднееквадратическое отклонение
случайной величины
-
соответственно математическое ожидание и среднееквадратическое отклонение
случайной величины
Определяем показатели теоретического
распределения и строим графики. Определение точек теоретических кривых удобнее
проводить в табличной форме, см. таблицу №1.
Таблица 1 - Расчёт теоритических
кривых.
|
№
|
Середина
интервалов тыс. км.
|
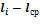 ,
тыс. км. ,
тыс. км.
|
z
|
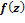
|
Теоретические
частоты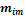
|
Накопленная
частость
|
|
|
|
|
|
|
F(z)
|
в%
|
|
1
|
6,5
|
-4,19
|
-1,99
|
0,06
|
0,53
|
0,02
|
2,35
|
|
2
|
7,5
|
-3,19
|
0,13
|
1,21
|
0,07
|
6,52
|
|
3
|
8,5
|
-2,19
|
-1,04
|
0,23
|
2,21
|
0,15
|
14,96
|
|
4
|
9,5
|
-1,19
|
-0,56
|
0,34
|
3,23
|
0,29
|
28,63
|
|
5
|
10,5
|
-0,19
|
-0,09
|
0,40
|
3,77
|
0,46
|
46,41
|
|
6
|
11,5
|
0,81
|
0,38
|
0,37
|
3,51
|
0,65
|
64,95
|
|
7
|
12,5
|
1,81
|
0,86
|
0,28
|
2,62
|
0,80
|
80,46
|
|
8
|
13,5
|
2,81
|
1,33
|
0,16
|
1,56
|
0,91
|
90,86
|
|
9
|
14,5
|
3,81
|
1,81
|
0,08
|
0,74
|
0,96
|
96,46
|
|
|
|
|
|
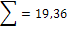
|
|
|
При этом теоретические частости подсчитываются
через так называемую табличную плотность вероятности:
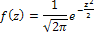
где 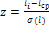
Значения этой функции подсчитаны и приводятся в
таблицах, содержащихся в литературе по математической статистике. Эта же
таблица приведена в приложении 1 настоящего методического указания.
Теоретические частоты подсчитываются по формуле:
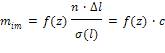
где 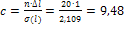 -
постоянный коэффициент.
-
постоянный коэффициент.
Умножив цифры в пятой колонке на этот
коэффициент мы получаем соответствующие им теоретические частоты, которые
заносим в шестую колонку таблицы.
Для контроля правильности ваших действий необходимо
на этом этапе в обязательном порядке подсчитать сумму теоретических частот. Она
должна получиться чуть меньше объема выборки. В нашем примере она равна 19,36
что на 0,64 меньше 20. Это очень хороший результат указывает на правильность
наших вычислений.
Рассчитываем интегральную функцию нормального
распределения:
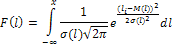
Для ее вычисления удобнее провести центрирование
и нормирование данной функций, для чего положим:
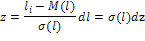
Центрированная и нормированная, т.е. табличная
функция нормального закона запишется так:
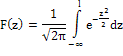
Для табличной интегральной функции составлена
таблица, см. приложение 2. По величинеZ находим значения функции. Используя
ее,занесем в гр. 7 таблицы №1 накопленные частости для каждого интервала, а в
гр. 8 ее значение в процентах.
В отчете по лабораторно-практической работе
выполняются два рисунка, на одном из которых изображается теоретическая кривая
частот распределения отказов, а на другом - интегральная кривая частот отказов,
см. рис. 1 и 2. При их выполнении необходимо соблюдать в установленном порядке
существующие на данный момент стандарты.
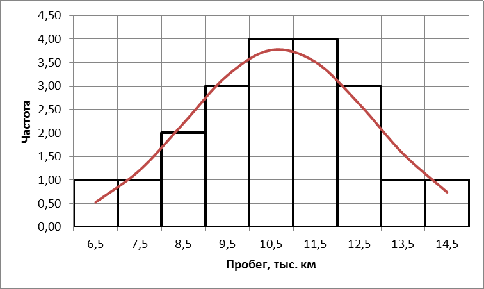
Рисунок 1 - Гистограмма и
теоритическая кривая
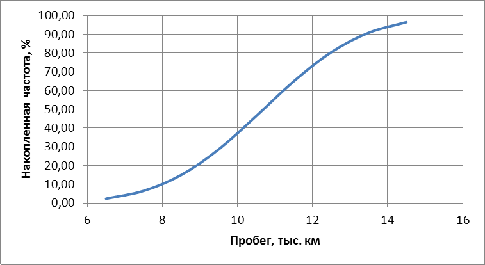
Рисунок 2 - Интегральная кривая
Проверка правильности выбора закона
распределения
Для проверки согласованности эмпирического и
теоретического распределений вычисляют наиболее распространенный критерий
согласия Пирсона по формуле:
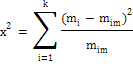
Расчет критерия согласия также удобно выполнять
табличным способом, см. таблицу 2.
Таблица 2 - Расчёт критерия согласия
Пирсона.
|
№
интервала
|
Эмпирическая
частота, 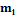
|
Округленное
значение теоретической частоты 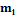
|
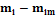
|
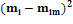
|
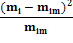
|
|
1
|
1
|
1
|
0
|
0
|
0
|
|
2
|
1
|
1
|
0
|
0
|
0
|
|
3
|
2
|
2
|
0
|
0
|
0
|
|
4
|
3
|
3
|
0
|
0
|
0
|
|
5
|
4
|
4
|
0
|
0
|
0
|
|
6
|
4
|
4
|
0
|
0
|
0
|
|
7
|
3
|
3
|
0
|
0
|
0
|
|
8
|
1
|
2
|
-1
|
1
|
|
9
|
1
|
1
|
0
|
0
|
0
|
|
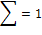
|
Далее определяется число степеней свободы г как
разность между числом интервалов К и наложенными связями (условиями) S* :
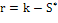
Поскольку при построении законов распределения
всегда накладывается требование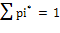 , т.е. всегда
имеется одна связь (условие), то введя замену S= S*-1, получим:
, т.е. всегда
имеется одна связь (условие), то введя замену S= S*-1, получим:
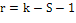
где S - количество числовых характеристик
(параметров) закона распределения.
Например, нормальный закон является
двухпараметрическим и определяется математическим ожиданием M(x) и средним
квадратическим отклонением 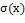 , т.е.S=2.
, т.е.S=2.
Для рассматриваемого примера число степеней
свободыr= 9-2-1 = 6.
Поrи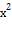 с
помощью приложения 4 определяют вероятность согласия р теоретического и
эмпирического распределений, или, иначе говоря, уровень значимости. Численное
значение уровня значимостихарактеризует вероятность допустить ошибку первого
рода, т.е. отвергнуть правильную гипотезу. Наиболее употребительными значениями
уровня значимости является: р = 0,1 и р = 0,05 (строгие условия); р = 0,01 и р
= 0,001 (менее строгие условия).
с
помощью приложения 4 определяют вероятность согласия р теоретического и
эмпирического распределений, или, иначе говоря, уровень значимости. Численное
значение уровня значимостихарактеризует вероятность допустить ошибку первого
рода, т.е. отвергнуть правильную гипотезу. Наиболее употребительными значениями
уровня значимости является: р = 0,1 и р = 0,05 (строгие условия); р = 0,01 и р
= 0,001 (менее строгие условия).
При статистическом контроле качества продукции
чаще всего используется величина р = 0,0027, равная вероятности отклонения
случайной величины, распределенной по нормальному закону за пределы ±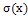 .
.
Таким образом, при проверке правдоподобности
сделанной нулевой гипотезы с помощью уровня значимости происходит сравнение
опытного значения с данным теоретическим значением вероятностир, т. е.:
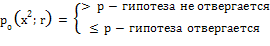
Для рассматриваемого примера приr = 6 и 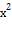 =
1
из
таблицы приложения 4 находим, что уровень значимости лежит в пределах
0,90<р< 0,99, что вполне допустимо и мы можем сделать допущение, что
принятая гипотеза о нормальном распределении не отвергается.
=
1
из
таблицы приложения 4 находим, что уровень значимости лежит в пределах
0,90<р< 0,99, что вполне допустимо и мы можем сделать допущение, что
принятая гипотеза о нормальном распределении не отвергается.
Вторая методика проверки
правильности выбора закона распределения
Можно быстро произвести проверку принятой
гипотезы с помощью критерия Романовского:
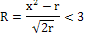
В нашем случае:
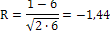
Определение доверительного интервала
для оценки среднего значения наработки на отказ
Существует точечная и интервальная оценка.Точечной
называют оценку, которая определяется одним числом. Все оценки, рассмотренные
выше - точечные. При выборе малого объема точечная оценка может значительно
отличаться от оцениваемого параметра, т.е. приводить к грубым ошибкам. По этой
причине при небольшом объеме выборки следует пользоваться интервальными
оценками.
Интервальной
называют оценку, которая определяется двумя числами - концами интервала.
Интервальная оценка позволяет установить точность и надежность оценки.
Доверительным
называют интервал(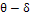 ;
; 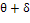 ;),
который покрывает неизвестный параметр с заданной надежностью
;),
который покрывает неизвестный параметр с заданной надежностью 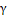 .
.
Доверительные интервалы для оценки
математического ожидания нормального распределения при неизвестном среднем
квадратичном отклонении (стандарте)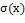 находятся
из выражения:
находятся
из выражения:
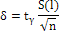
Таким образом имеем:
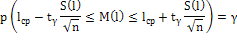
где 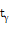 -
коэффициент Стьюдента, определяется поnи
-
коэффициент Стьюдента, определяется поnи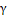 .
.
Применительно к примеру, задаваясь доверительной
вероятностью (надежностью) у= 0,95 из таблицы приложения находим 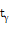 =
2,093.
=
2,093.
Тогда:
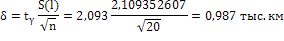
т.е. с доверительной вероятностью равной 0,95
можно утверждать, что математическое ожидание лежит в пределах от 9,70 тыс. км
до 11,68 тыс. км