Разложение в ряд функций cos x и sin x

Разложение в ряд функций cos x и sin x

Министерство образования и науки российской федерации

государственное бюджетное образовательное учреждение

высшего профессионального образования

“Тверской государственный университет”

Факультет прикладной математики и кибернетики

Курсовая работа по предмету

«Кратные интегралы и ряды»

Тема: Используя разложения в ряд функци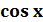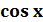й  и 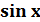 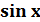доказать, что

.

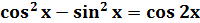
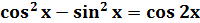Выполнил: студент 26группы

Гаврилин Евгений Константинович

Научный руководитель:

Зав. кафедрой вычислительной математики

Климок Виктор Иванович

Тверь - 2012

Тема

Используя разложения в ряд функци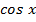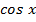й  и 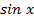 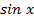доказать, что

.

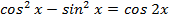
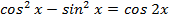Показать, применяя ЭВМ, что чем больше членов разложения, тем точнее выполняется равенство. Проиллюстрировать это графически.

Учесть, что функци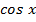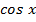и  и 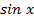 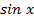могут быть представлены рядами

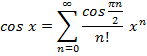
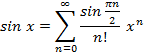
И воспользоваться правилом (Коши) перемножения рядов.

Решение

Для того, чтобы доказать, что 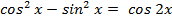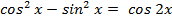, возведём ряды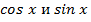 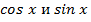в квадрат, используя правило Коши.

Теорема (для числовых рядов):

Пусть даны два сходящихся ряда: (а)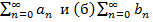

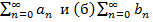
Если (а) и (б) сходятся абсолютно и их суммы соответственно равны A и B, то и ряд, являющийся произведением (а) и (б) сходится абсолютно.

Доказательство

Расположим все произведения в бесконечную матрицу:

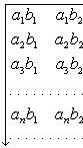
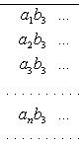
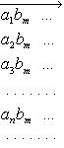 (1)

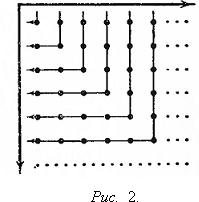
Элементы этой матрицы можно различными способами записать в форме последовательности. Для нас особенно важны способы, изображенные на рис. 1 и рис. 2.

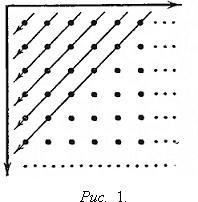
Первый из этих способов приводит к ряду

₁b₁ + a₁b₂ + a₂b₁ + a₁b₃ + a₂b₂ + a₃b₁ + a₁b₄ + a₂b₅ +... (2)

Рис. 2. приводит к ряду

₁b₁ + a₁b₂ + a₂b₂ + a₂b₁ + a₁b₃ + a₂b₃ + a₃b₃ + a₃b₂ +... (3)

Все ряды, получаемые расположением элементов матрицы (1) в форме последовательности, получаются друг из друга перестановками членов. Покажем, что все эти ряды сходятся абсолютно. Возьмем какой-нибудь из этих рядов, составим ряд абсолютных величин членов взятого ряда и обозначим через 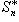 частичную сумму этого ряда абсолютных величин. Если n закреплено, а m достаточно велико, то все слагаемые суммы 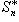 будут содержаться среди чисел, заполняющих квадрат

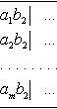
Поэтому сумма 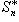 будет не больше, чем сумма всех чисел, входящих в указанный квадрат, т. е. не больше, чем

(|a₁| + |a₂| +... + |a_m|)(|b₁| + |b₂| +... + |b_m|).

Если обозначить через A* и B* суммы рядов, составленных из абсолютных величин членов рядов (а) и (б), то из сказанного ясно, что

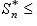
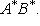
Отсюда и следует наше утверждение об абсолютной сходимости рядов, порождаемых матрицей

Произведение рядов будет находиться по формуле:

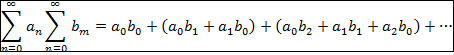
Для степенных рядов, исходя из доказательства, формула будет выглядеть аналогично.

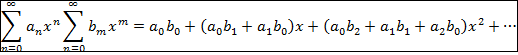
Но есть и более удобная запись этой формулы, ей и воспользуемся:

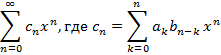
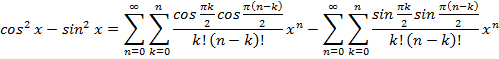
Воспользуемся следующими формулами тригонометрии:

()))    

()))     

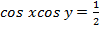
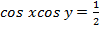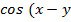
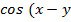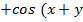
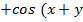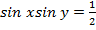
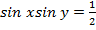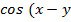
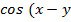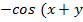
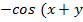Получим:

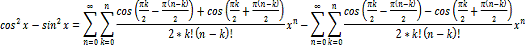
разложение функция бесконечная матрица

Запишем полученное выражение под одним знаком суммы, т.к пределы суммирования у первого и второго слагаемого совпадают. Так же вынесем 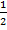 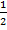перед знаком суммы.

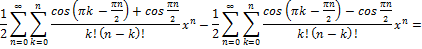
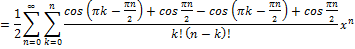
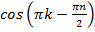
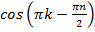 взаимно уничтожаются:

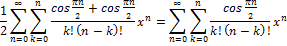
Так как 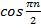 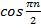не зависит от k, то его можно вынести из-под знака суммы:

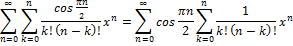
Представим 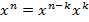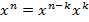, дополнительно домножив числитель и знаменатель на n!

 .

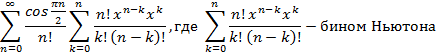
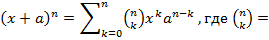
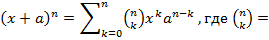
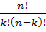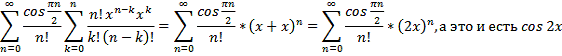
Графическая иллюстрация доказанного равенства

Число слагаемых: 1

Число слагаемых: 2

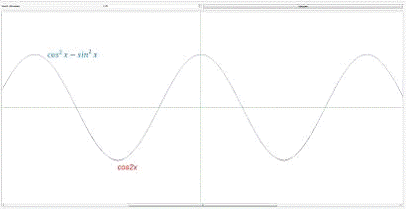
Число слагаемых: 6

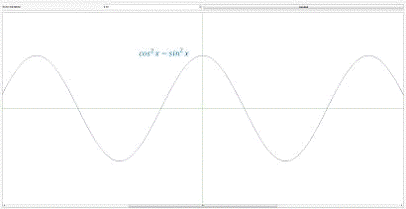
Ввод: уже приколичестве слагаемых, больших 7-8 график функции 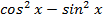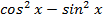, построенный через разложение рядов, практически полностью совпадает с графиком функции cos2x, взятый из библиотеки math.h.

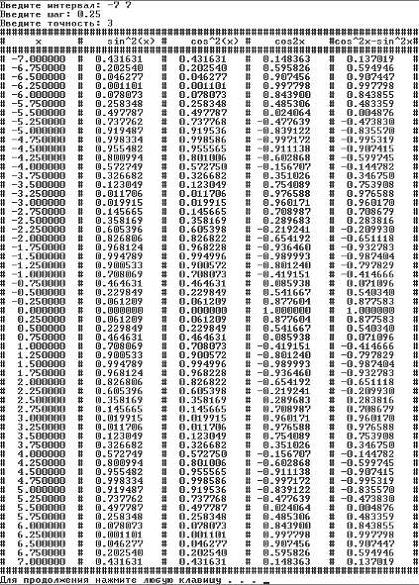
Ниже приведена таблица значений на [-7,7]. При разложении ряда использовались первые три слагаемых.

Предпоследний столбец: cos2x: функция из библиотеки math.h.

Последний столбец: разность двух рядов, в каждом из которых-3 слагаемых.

Код программы

#include "mainwindow.h"

#include "ui_mainwindow.h"

#include <math.h>int iCoff = 10;int scale = 250;//увеличение, чтобы график маленьким не казался::MainWindow(QWidget *parent)

: QMainWindow(parent), ui(new Ui::MainWindow)

{>setupUi(this);

}::~MainWindow()

{ui;

}

//cos2x - <math.h>MainWindow::cosY(double x)

{cos(2*x);

}

//cosx -собственная версияMainWindow::kv_cos(double x, int N)

{j=0;i=3;(x<0) x=-x;x1=x;(x1>M_PI_2)

{=x1-M_PI;++;

}a1, y=1, a2=-x1*x1/2;(N==0) return 1;(int steps=0; steps<N; steps++, i++)

{=a2;=-a1*x1*x1/(i*(i+1));++; y+=a1;

}(j%2)-y;y;

}

//sinx-собственная версияMainWindow::kv_sin(double x, int N){j=0;i=4;(x<0) x=-x;x1=x;(x1>M_PI_2)

{=x1-M_PI;++;

}(N==0) return 0;a1, y=x1, a2=-x1*x1*x1/6;(int steps=0; steps<N; steps++, i++)

{=a2;=-a1*x1*x1/(i*(i+1));++; y+=a1;

}(!j%2)y;-y;

}MainWindow::changeEvent(QEvent *e)

{::changeEvent(e);(e->type()) {QEvent::LanguageChange:>retranslateUi(this);;:;

}

}

//обработка события при нажатии на кнопкуMainWindow::on_doBtn_clicked()

{= ui->Num->value();Step = 0.01;yCurr;yNext;*scene = new QGraphicsScene(ui->graphGV);

// Ox and Oy axispen(Qt::green);pen1(Qt::blue);

//прорисовка осей>addLine(-iCoff*100, 0, iCoff*100, 0, pen);>addLine(0, -iCoff*100, 0, iCoff*100, pen);.setColor(Qt::red);

//рисуем график(double i=-iCoff; i<iCoff; i+=Step)

{= cosY(i);= cosY(i+Step);>addLine(i*scale, -yCurr*scale, (i+Step)*scale, -yNext*scale, pen);= kv_cos(i, N)*kv_cos(i,N)-kv_sin(i,N)*kv_sin(i,N);= kv_cos(i+Step,N)*kv_cos(i+Step,N)-kv_sin(i+Step,N)*kv_sin(i+Step,N);>addLine(i*scale, -yCurr*scale, (i+Step)*scale, -yNext*scale, pen1);

}>graphGV->setScene(scene);

}

Список литературы

1. Курант Р. Курс дифференциального и интегрального исчисления (том 1)

. Фихтенгольц Г.М. Курс дифференциального и интегрального исчисления (том 2)