Основы математического анализа
Контрольная работа №2 (мат. анализ)
Задание 1(8). Найти частные производные:
а)
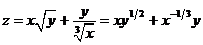
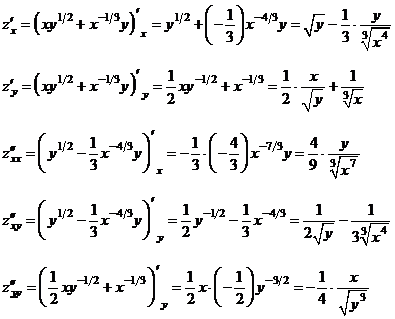
б)

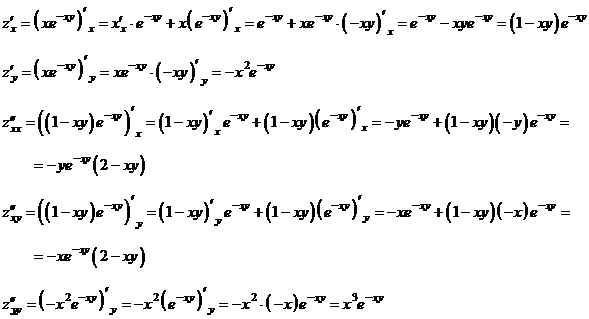
Задание
2(16). Найти градиент функции 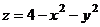 в точке
в точке 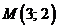
Градиент
- вектор, указывающий направление наискорейшего возрастания функции и состоящий
из ее частных производных:
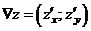
Найдем
частные производные:
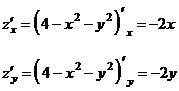
Таким
образом, градиент функции  в любой ее точке имеет вид:
в любой ее точке имеет вид:
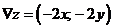 ,
,
а
в точке 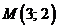 :
:

Задание
3 (24). Вычислить интеграл 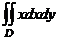 по
области
по
области 
Построим
чертеж области 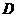
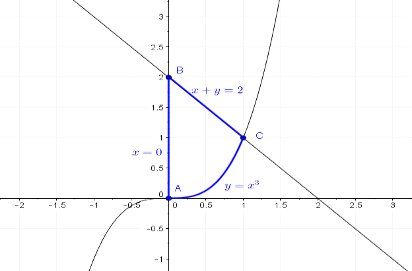
Координаты
точки 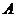 :
:

Координаты
точки  :
:

Координаты
точки 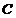
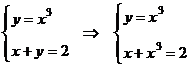
Решая
уравнение третьей степени, получим решение с радикалами или тригонометрическими
функциями, но судя по чертежу, обе функции проходят через точку 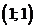 . Действительно:
. Действительно:

Т.е.
область 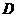 словесно можно описать следующим образом: «В то время
как
словесно можно описать следующим образом: «В то время
как 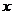 пробегает значения от
пробегает значения от 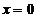 до
до 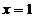 ,
, 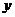 пробегает
значения от
пробегает
значения от 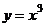 до
до 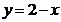 ». Это и
есть пределы интегрирования при переходе от двойного интеграла к
последовательному:
». Это и
есть пределы интегрирования при переходе от двойного интеграла к
последовательному:
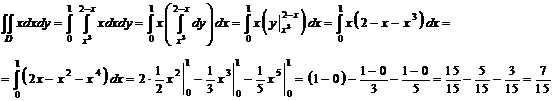
Задание
4(32). Найти общее решение дифференциального уравнения 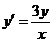 и построить графики двух различных частных решений
этого уравнения.
и построить графики двух различных частных решений
этого уравнения.
Решим
уравнение
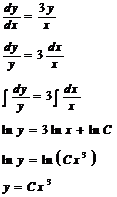
Проверим
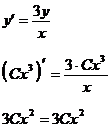
Таким
образом, общее решение уравнения:
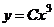
Положив
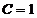 , получим частное решение
, получим частное решение
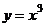
Положив
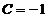 , получим частное решение
, получим частное решение
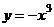
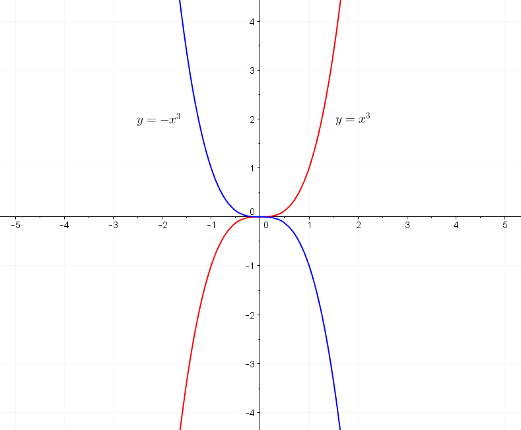
Отобразим
графики этих функций
Задание
5(50). Найти общее дифференциального уравнения 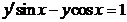 и
частное решение, удовлетворяющее условию
и
частное решение, удовлетворяющее условию 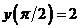 .
.
Будем
искать решение в виде

Тогда

Потребуем,
чтобы функция 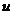 была такова, что выражение в скобках будет равно
нулю. Тогда получим систему уравнений:
была такова, что выражение в скобках будет равно
нулю. Тогда получим систему уравнений:
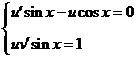
Решим
первое ее уравнение:
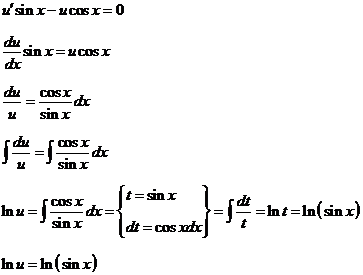
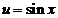 (в
выражении для функции
(в
выражении для функции  константу не добавляем, а добавляем далее, в
константу не добавляем, а добавляем далее, в 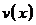 )
)
Решим
второе уравнение системы, подставив в него найденную  :
:
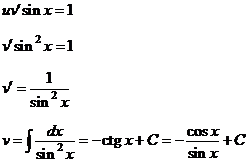
Тогда
общее решение исходного уравнения 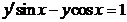 :
:
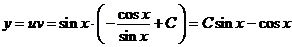
Проверим:
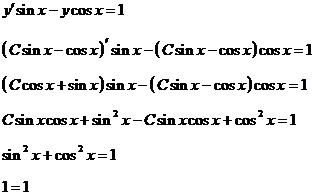
Таким
образом, общее решение:
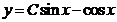
Найдем
значение константы 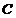 , соответствующее условию
, соответствующее условию 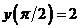 :
:

Т.е.
частное решение, соответствующее заданному условию:
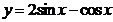
производная
функция интегрирование уравнение
Задание 6 (58). Найти общее и частное решение дифференциального уравнения
второго порядка, удовлетворяющее данным условиям:
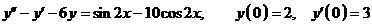
Это
уравнение с правой частью специального вида. Его общее решение следует искать в
виде суммы общего решения однородного уравнения и частного решения:
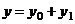
Найдем
решение однородного уравнения:

Характеристические
корни этого уравнения:
Т.к.
корни действительные и не равны друг другу, то решение однородного уравнения:
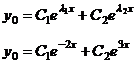
Найдем
частное решение 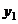 исходного уравнения. Для правой части вида
исходного уравнения. Для правой части вида 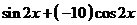 его следует искать в таком же виде:
его следует искать в таком же виде:
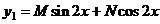
Чтобы
найти константы 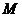 и
и 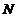 ,
подставим это решение в исходное уравнение:
,
подставим это решение в исходное уравнение:
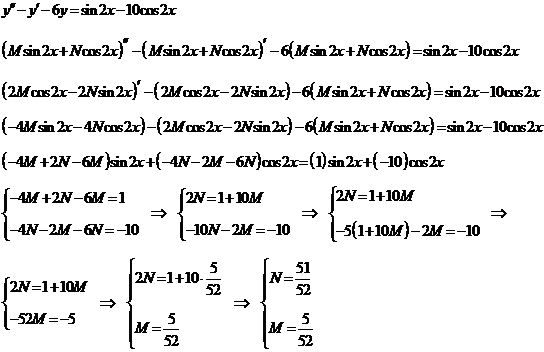
Следовательно,
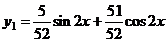
Таким
образом, общее решение исходного уравнения:
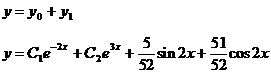
Найдем
значения констант 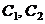 , соответствующие условиям
, соответствующие условиям 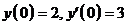 . Для этого необходимо вычислить
. Для этого необходимо вычислить  :
:
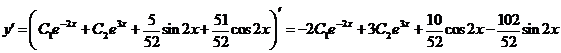
Тогда,
исходя из условий:
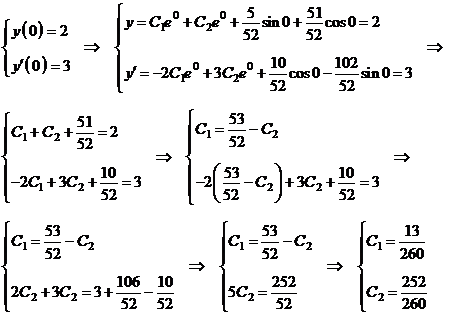
Итак,
частное решение, соответствующее заданным условиям:
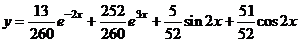
Ответ:
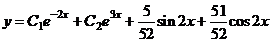 (общее)
(общее)
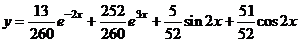 (при
заданных условиях)
(при
заданных условиях)
Задание
7 (66). Исследовать на сходимость ряд
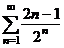
Прежде
всего, проверим необходимый признак сходимости:
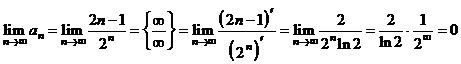
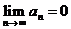 -
необходимое условие выполняется
-
необходимое условие выполняется
Далее
применим признак Даламбера:

Т.к.
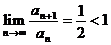 , то согласно признаку Даламбера, ряд сходится.
, то согласно признаку Даламбера, ряд сходится.
Задание
8(74). Найти радиус и интервал сходимости степенного ряда и исследовать его
сходимость на концах интервала:
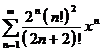
) Радиус
сходимости найдем по признаку Даламбера - ряд сходится при
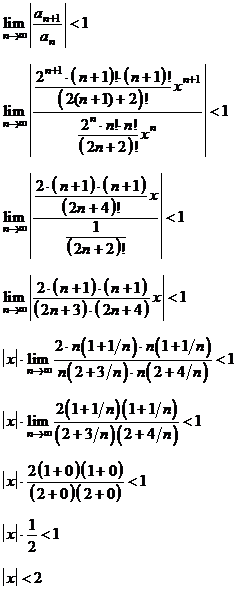
Таким
образом,
при
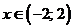 ряд сходится;
ряд сходится;
при
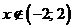 ряд расходится.
ряд расходится.
) При
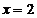 получим ряд
получим ряд
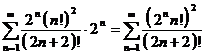
Проверим
необходимый признак сходимости. При этом воспользуемся формулой Стирлинга,
позволяющей при предельном переходе при 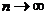 заменять
заменять
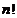 на
на 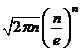
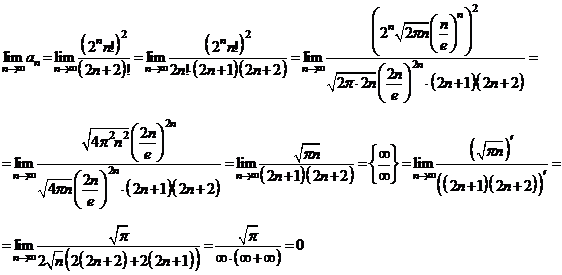
 -
условие выполняется
-
условие выполняется
Проверим
сходимость ряда с помощью интегрального признака (как и прежде предварительно
заменив член ряда 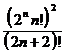 на преобразованный по формуле Стирлинга
на преобразованный по формуле Стирлинга 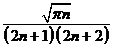 ):
):
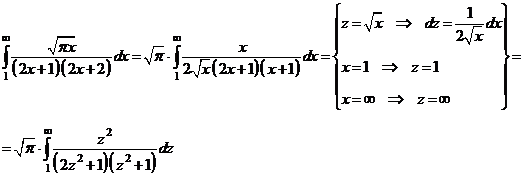
Разложим
дробь на простейшие
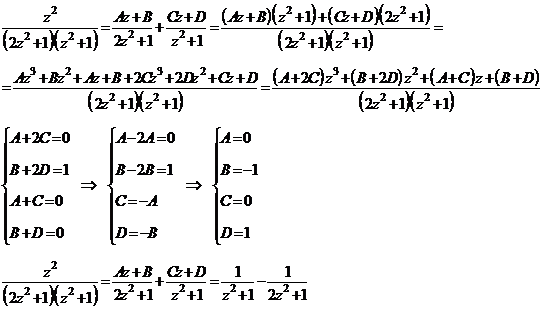
Следовательно
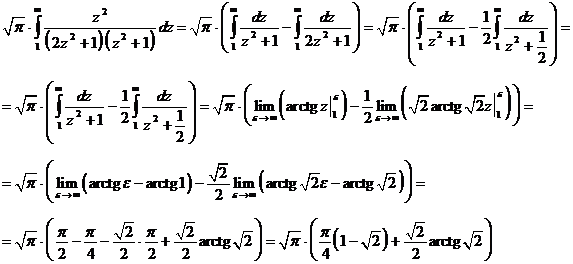
Т.е.
несобственный интеграл сходится к конечному числу.
А
значит и ряд 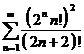 тоже сходится.
тоже сходится.
)
При 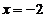 получим ряд
получим ряд
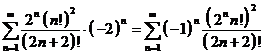
Члены
данного ряда, взятые по модулю, образуют ранее рассмотренный ряд 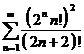 , который сходится. Следовательно, и этот
знакочередующийся ряд тоже сходится.
, который сходится. Следовательно, и этот
знакочередующийся ряд тоже сходится.
Ответ:
ряд
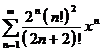 сходится при
сходится при 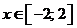 .
.