Определение вероятностей различных событий

Определение вероятностей различных событий

МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РОССИЙСКОЙ ФЕДЕРАЦИИ

ФГБОУ ВПО «Уральский государственный экономический университет»

Центр дистанционного образования

Контрольная работа

по дисциплине: Теория вероятностей

по теме: вариант № 1

Екатеринбург 2013г

Контрольная работа № 1

. Какова вероятность выиграть главный приз в спортлото, угадав 6 номеров из 49?

Решение

Так как угадано 6 номеров, то число элементарных событий, благоприятных событию А, равно 6, т. е. m = 6 и общее число номеров n = 49, то вероятность выиграть главный приз в спортлото равна

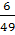
Р(А) =  =  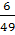= 0,122

. Рабочий обслуживает 3 станка. Вероятность того, что в течение часа станок не потребует к себе внимания рабочего для 1 станка равна 0.9, для 2-го равна 0.8, для 3-го - 0.85. Найти вероятность того, что в течении часа 1) ни один станок не потребует внимания рабочего, 2) по крайней мере 1 станок не потребует внимания рабочего

Решение

Имеем Р(А) = 0,9; Р(В) = 0,8; Р(С) = 0,85

) Р(АВС) = Р(А)∙ Р(В)∙ Р(С) = 0,9∙ 0,8∙0,85 = 0,612.

) Р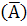 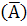= 1 - 0,9 = 0,1 (вероятность того, что первый станок потребует внимания рабочего в течение часа);

Р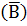 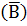= 1 - 0,8 = 0,2 (вероятность того, что второй станок потребует внимания рабочего в течение часа);

Р = 1 - 0,85 = 0,15 (вероятность того, что третий станок потребует внимания рабочего в течение часа).

Тогда Р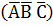 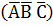- вероятность того, что одновременно внимания рабочего в течение часа потребуют все 3 станка - определится следующим образом:

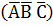
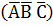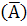
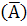Р = Р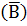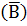∙ Р∙ Р = 0,1∙ 0,2∙0,15 = 0,003.

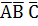
Но событием, противоположным событию 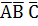, является событие, что по крайней мере 1 станок не потребует внимания рабочего в течение часа. Следовательно, искомая вероятность найдется по формуле:

Р = 1 - Р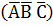 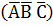= 1 - 0,003 = 0,997.

Ответ: 1) 0,612; 2) 0,997.

. Достигшему 60-летнего возраста человеку вероятность умереть на 61 году жизни равна при определенных условиях 0.09. Какова в этих условиях вероятность, что из 3-х человек в возрасте 60 лет 1) все трое будут живы через год, 2) по крайней мере, один из них будет жив

Решение

Имеем схему Бернулли с параметрами р = 0,009 (вероятность того, что человек умрет), n = 3 (количество человек), k (число «успехов», живых людей). Будем использовать формулу Бернулли:

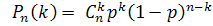
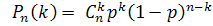
Получаем:

)  = 0,000729 - вероятность того, что из 3-х человек все трое будут живы через год.

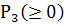
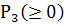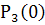
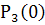)  = 1 - 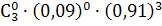 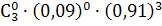= 1 -  = 1 - 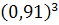 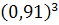= 0,246429 - вероятность того, что по крайней мере один человек будет жить (нашли через вероятность противоположного события).

Ответ: 1) 0,000729; 2) 0,246429.

. Посев производится семенами пшеницы 4 сортов, перемешанных между собой. При этом зерна первого сорта составляют 12% от общего количества, зерна второго сорта - 9%, третьего сорта - 14%, четвертого сорта - 65%. Вероятность того, что из зерна вырастет колос, содержащий не менее 50 зерен для пшеницы первого сорта составляет 0,25, для пшеницы второго сорта - 0,08, для пшеницы третьего сорта - 0,04, для четвертого сорта - 0. Найти вероятность того, что из взятого наугад зерна вырастет колос, содержащий не менее 50 зерен

Решение

Пусть событие А состоит в том, что из взятого наугад зерна вырастет колос, содержащий не менее 50 зерен. Возможны четыре гипотезы:

Н₁ - колос вырастет из зерна первого сорта;

Н₂ - колос вырастет из зерна второго сорта;

Н₃ - колос вырастет из зерна третьего сорта;

Н₄ - колос вырастет из зерна четвертого сорта;

Вероятности:

Р(Н₁) = 12% = 0,12; Р(Н₂) = 9% = 0,09; Р(Н₃) = 14% = 0,14;

Р(Н₄) = 65% = 0,65.

Условные вероятности:

Р(А\Н₁) = 0,25; Р(А\Н₂) = 0,08; Р(А\Н₃) = 0,04; Р(А\Н₁) = 0.

Тогда вероятность события А найдем по формуле полной вероятности:

Р(А) = (А\Н₁) ∙ Р(Н₁) + (А\Н₂) ∙ Р(Н₂) + (А\Н₃) ∙ Р(Н₃) + (А\Н₄) ∙ Р(Н₄) =

= 0,25∙0,12+ 0,08∙0,09 + 0,04∙0,14 + 0∙0,65 = 0,0428

Ответ: 0,0428.

. Успешно написали контрольную работу 30% студентов. Вероятность правильно решить задачу на экзамене для студента, успешно написавшего контрольную, равна 0.8, для остальных - 0.4. Студент не решил задачу на экзамене. Какова вероятность, что он не написал контрольную работу?

Решение

Пусть событие А состоит в том, что студент не решил задачу на экзамены.

Возможны две гипотезы:

Н₁ - студент успешно написал контрольную работу;

Н₂ - студент не написал контрольную работу.

Вероятности:

Р(Н₁) = 30% = 0,3; Р(Н₂) = 1 - Р(Н₁) = 1-0,3 = 0,7.

Условные вероятности:

Р(А\Н₁) = 0,8; Р(А\Н₂) = 0,4.

Найдем сначала вероятность события А по формуле полной вероятности:

Р(А) = (А\Н₁) ∙ Р(Н₁) + (А\Н₂) ∙ Р(Н₂) = 0,8∙0,3 + 0,4∙0,7 = 0,52.

Теперь найдем апостериорные вероятности того, что если студент не решил задачу на экзамене, то он не написал контрольную, по формуле Байеса:

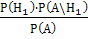
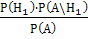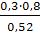
Р(Н₁\А) =  =  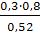= 0,4615;

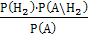
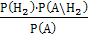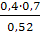
Р(Н₂\А) =  =  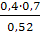= 0,5385.

Таким образом, вероятность того, что студент не написал контрольную работу, равна 0,5385.

Ответ: 0,5385

вероятность дискретный дисперсия случайный

Контрольная работа № 2

Задание 1. Составить закон распределения дискретной случайной величины Х, вычислить математическое ожидание, дисперсию и среднеквадратическое отклонение случайной величины.

ОТК проверяет изделия на стандартность. Вероятность того, что изделие стандартно, равно 0,7. Проверено 20 изделий. Найти закон распределения случайной величины Х - числа стандартных изделий среди проверенных. Вычислить математическое ожидание, дисперсию и среднеквадратическое отклонение случайной величины.

Решение

P(X=k) = P_n(k) =  =  =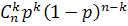

= ,

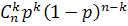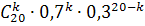
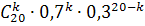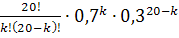
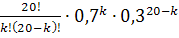где k = 0, 1, 2, ……., 20.

Получим ряд распределения

Расчеты произведены правильно, так как сумма 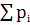 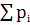= 1

Математическое ожидание:

m_x = n∙p = 20∙0,7 = 14.

Дисперсия:

D_x = n∙p∙(1-p) = 20∙0,7∙0,3 = 4,2

Среднеквадратическое отклонение:

 =  .

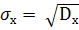
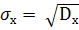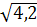
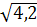
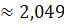
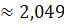Задание 2. Случайная величина Х задана функцией распределения F(X). Найти плотность распределения, математическое ожидание, дисперсию, а также вероятность попадания случайной величины в интервал (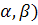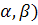. Построить графики функций F(X) и f(X).

F(x) =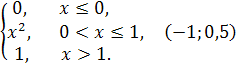

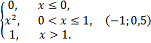
Решение

. Найдем плотность вероятности, как производную от функции распределения:

f(x) = F^′(x) =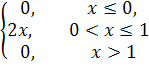

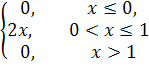
. Найдем математическое ожидание:

М =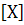

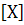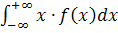
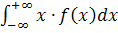
М =  =  =  =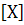

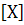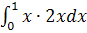
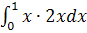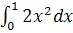
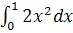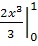
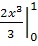. Находим дисперсию:

D = ∙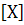

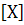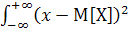
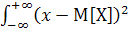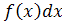
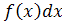
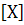
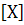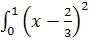
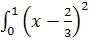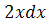
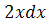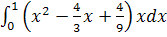
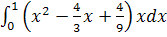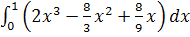
D=∙= =  = 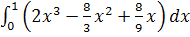2∙- + =  =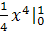

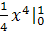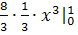
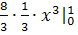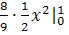
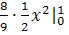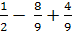
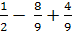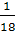
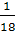
. Найдем вероятность попадания случайной величины в интервал (: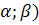

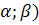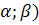
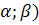( = (-1; 0,5)

р(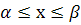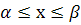) = F(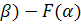

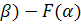
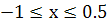
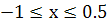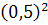
р() = F( =  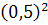- 0 = 0,25

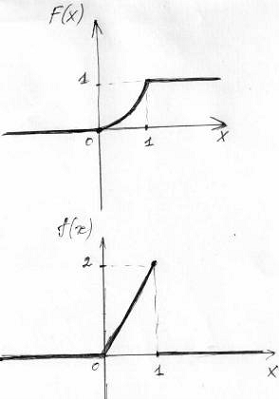
Список литературы

1. Вентцель Е.С.. Теория вероятностей, М., Наука, 1969

2. Гмурман В.Е. Руководство к решению задач по теории вероятностей и математической статистике. М., Высшая школа, 1975

. Гмурман В.Е.. Теория вероятностей и математическая статистика, М., Высшая школа, 1972