Нахождения оптимального решения игры двух лиц с нулевой суммой

КУРСОВАЯ РАБОТА

по дисциплине "Математические методы"

по теме "Нахождения оптимального решения игры двух лиц с нулевой суммой".

Аннотация

Курсовой проект по дисциплине "Математические методы" по теме "Нахождения оптимального решения игры двух лиц с нулевой суммой".

Основными разделами являются:

1.   Введение, в котором отражены поставленные цели.

2.   Расчетная часть, раскрывающая предметную область задачи, содержащая:

·   Постановку задачи;

·   Построение математической модели;

·   Описание метода решения задачи;

·   Информационное обеспечение задачи, которое в свою очередь содержит описание входной и выходной информации;

3. Описательная часть, содержащая:

·   Алгоритм решения задачи;

·   Описание программы;

·   Контрольный пример;

·   Руководство по эксплуатации и сопровождению;

3.   Заключение, которое отражает достигнутые результаты.

4.   Список используемой литературы.

Пояснительная записка также включает в себя раздел "заключение", который отражает результаты, достигнутые в результате разработки задачи, список используемой литературы.

Данная пояснительная записка состоит из 2х таблиц и 3х рисунков.

Разработка программного средства осуществляется на персональном компьютере под управлением операционной системы Microsoft Windows XP, в среде программирования Borland C++ Builder 6.0.

Содержание

Аннотация

Введение

1. Расчетная часть

1.1 Постановка задачи

1.2 Математическая модель

1.3 Описание метода решения задачи

1.4 Информационное обеспечение

2. Описательная часть

2.1 Алгоритм решения задачи

2.2 Описание программы

2.3 Контрольный пример

2.4 Руководство пользователя

Заключение

Список литературы

Введение

Проблема выполнения различных вычислений была актуальна во все времена. По мере развития общественно-экономических отношений усложнялись постановленные задачи, которые для своего решения требовали разработки новых методов вычислений. На смену простейшим арифметическим и геометрическим вычислениям пришли алгебраические и тригонометрические вычисления.

Организация современного производства требует не только наличия современных станков и оборудования, но и разработки новых технологических процессов и современных методов управлением производством. Для решения каждой из поставленных задач разрабатываются математические модели, анализируя которые удается найти наилучшее решение поставленной задачи. Создание математической модели - сложная кропотливая работа, которая в современных условиях под силу коллективам разработчиков. Для создания математической модели одного и того же объекта различные коллективы могут использовать различный математический аппарат. В коллектив разработчиков математических моделей привлекаются высококвалифицированные специалисты, которые, с одной стороны, хорошо знают физические процессы, протекающие при работе объекта, и, с другой стороны, глубоко и всесторонне владеют соответствующим математическим аппаратом. После создания математической модели специалистами-аналитиками за дело принимаются специалисты-программисты, которые реализуют созданную модель в виде программных кодов. Далее с математической моделью работают специалисты-практики, целенаправленно воздействуя на модель, они изучают её поведение и подбирают оптимальный режим работы для реального объекта.

Наиболее полно разработан математический аппарат игр с нулевой суммой, когда выигрыш одного игрока равен выигрышу другого игрока, т.е. общая сумма выигрыша всех игроков равна нулю. При построении игровых моделей предполагается, что каждый из игроков будет выбирать только лучшую (для себя) стратегию. Результатом исследования игровой модели является определение наиболее осторожной стратегии поведения игрока либо обеспечение гарантированного выигрыша. Риски при получении большего выигрыша не учитываются и не оцениваются.

Таким образом, результат исследования игровых моделей указывает на оптимальную стратегию поведения (гарантированный выигрыш), а какой стратегией воспользуется игрок в реальной жизни - дело самого игрока.

В данном курсовом проекте для реализации решения задачи используется метод Брауна-Робинсона решения игровых задач с нулевой суммой. Суть данного метода заключается в многократном фиктивном разыгрывании игры с заданной матрицей выигрыша.

Целью данного курсового проекта является: научиться от словесного описания задачи перейти к абстрактной математической модели, реализовать математическую модель в виде программных кодов, провести исследование математической модели и получить вектор входных воздействий, доставляющих оптимальное решение. Речь идет о простых математических моделях, позволяющих решить элементарные задачи.

1. Расчетная часть

1.1 Постановка задачи

Теория игр - математическая теория конфликтных ситуаций. Экономические соревнования, спортивные встречи, боевые операции - примеры конфликтных ситуаций. Простейшие модели конфликтных ситуаций - это салонные и спортивные игры.

В игре могут сталкиваться интересы двух противников (игра парная или игра двух лиц), интересы n (n > 2) противников (игра множественная или игра n лиц). Существуют игры с бесконечным множеством игроков.

Игра называется парной, если в ней сталкиваются интересы двух противников. Игра называется с нулевой суммой, если один игрок выигрывает столько, сколько второй проигрывает в той же партии.

Задача первого игрока - максимизировать свой выигрыш.

Задача второго игрока - максимизировать свой выигрыш - сводится к минимизации проигрыша второго, что эквивалентно задаче минимизации выигрыша первого игрока.

Необходимо создать программу для автоматизированного решения данной задачи с использованием ЭВМ.

1.2 Математическая модель

Матричной называют парную игру с нулевой суммой при условии, что каждый игрок имеет конечное число чистых стратегий. Матричные игры относятся к разряду так называемых антагонистических игр, т.е. игр, в которых интересы игроков прямо противоположны.

Стратегией игрока называется система правил, однозначно определяющих выбор поведения игрока на каждом ходе в зависимости от ситуации, сложившейся в процессе игры. В зависимости от числа возможных стратегий игры делятся на конечные и бесконечные.

Каждая фиксированная стратегия, которую может выбрать игрок, называется его чистой стратегией.

Процесс игры состоит в выборе каждым игроком i одной своей стратегии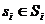. В результате сложившейся ситуации s игрок i получает выигрыш.

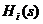Процесс игры состоит в выборе каждым игроком i одной своей стратегии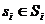. В результате сложившейся ситуации s игрок i получает выигрыш.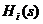

Игры, в которых целью каждого участника является получение по возможности большего индивидуального выигрыша, называются бескоалиционными в отличие от коалиционных, в которых действия игроков направлены на максимизацию выигрышей коллективов (коалиции) без дальнейшего разделения выигрыша между участниками.

Ситуация s в игре называется приемлемой для игрока i, если этот игрок, изменяя в ситуации s свою стратегию si на какую-либо другую si', не может увеличить своего выигрыша.

Ситуация s, приемлемая для всех игроков, называется ситуацией равновесия.

Процесс нахождения ситуации равновесия в бескоалиционной игре есть процесс решения игры.

Рассмотрим игру, в которой участвуют два игрока, причем каждый их них имеет конечное число стратегий. Обозначим для удобства одного из игроков через А, а другого через В.

Предположим, что игрок А имеет m стратегий: А₁, А₂, …, А_m а игрок В - n стратегий: B₁, B₂, …, B_m

Пусть игрок А выбрал стратегию А_i, а игрок В - стратегию B_j. Будем считать, что выбор игроками стратеги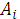й  А_i  и 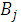 B_j.  однозначно определяет исход игры - выигрыш a_ij игрока А и выигрыш b_ij игрока В, причем эти выигрыши связаны равенством bij = a_ij.

Последнее условие показывает, что в рассматриваемых обстоятельствах выигрыш одного из игроков равен выигрышу другого, взятому с противоположным знаком. Поэтому при анализе такой игры можно рассматривать выигрыши только одного из игроков. Пусть это будет, например, выигрыши игрока А.

Если нам известны значения 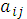 a_ij выигрыша при каждой паре стратегий 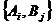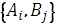, i = 1,2,…,m, j = 1,2,…,n, то их удобно записывать или в виде матрицы, строки которой соответствуют стратегиям игрока А, а столбцы - стратегиям игрока В (табл.1),

Таблица 1. Общий вид платёжной матрицы матричной игры

Полученная матрица имеет размер m 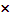 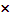n и называется матрицей игры или платежной матрицей.

1.3 Описание метода решения задачи

Решение данной задачи будет искать, используя метод Брауна-Робинсона (метод фиктивного разыгрывания).

Часто в практических задачах нет необходимости находить точное решение матричной игры. Достаточно найти приближённое решение, которое даёт средний выигрыш, близкий к цене игры и приближённые оптимальные стратегии игроков.

программа математическая модель игра

Ориентировочное значение цены игры может дать уже простой анализ матрицы выигрышей и определение нижней и верхней цен игры. Если они близки, то поисками точного решения заниматься не обязательно, так как достаточно выбрать чистые минимаксные стратегии. Если же они не близки, можно получить приемлемое для практики решение с помощью численных методов решения игр, из которых рассмотрим метод итераций.

Пусть разыгрывается матричная игра ГА с матрицей А={a_ij} размера (m´n). Идея метода - многократное фиктивное разыгрывание игры с заданной матрицей. Одно разыгрывание игры будем называть партией, число которых неограниченно.

В 1-ой партии оба игрока выбирают совершенно произвольные чистые стратегии. Пусть игрок 1 выбрал i-ю стратегию, а игрок 2 - j-ю стратегию. Во второй партии игрок 1 отвечает на ход игрока 2 той своей стратегией, которая даёт ему максимальный выигрыш. В свою очередь, игрок 2, отвечает на этот ход игрока 1 своей стратегией, которая обращает его проигрыш в минимум. Далее третья партия.

С ростом числа шагов процесса смешанные стратегии, которые приписываются игрокам, приближаются к их оптимальным стратегиям. Этот процесс приближённого нахождения оптимальных стратегий игроков называется итеративным, а его шаги - итерациями.

Итак, предположим, что за первые k разыгрываний игрок 1 использовал i-ю чистую стратегию 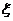ik раз (i=1,…,m), а игрок 2 j-ю чистую стратегию  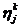раз (j=1,…,n). Тогда их смешанными стратегиями будут векторы

.

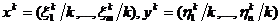Игрок 1 следит за действиями игрока 2 и с каждым своим ходом желает получить как можно больший выигрыш. Поэтому в ответ на применение игроком 2 своей смешанной стратегии yk, он будет использовать чистую стратегию ik+1, которая обеспечит ему лучший результат при разыгрывании (k+1) - ой партии. Игрок 2 поступает аналогично. В худшем случае каждый из них может получить:

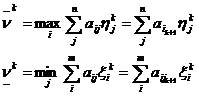
Где

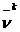 - наибольшее значение проигрыша игрока 2 и  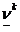- наименьшее значение выигрыша игрока 1.

Рассмотрим отношения, которые определяют средние значения проигрыша игрока 2 и выигрыша игрока 1:

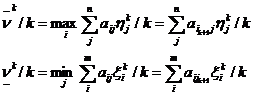
Пусть ν - цена матричной игры ГА. Её значение будет больше выигрыша игрока 1, но меньше проигрыша игрока 2, т.е.

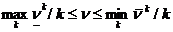. (1)

Таким образом, получен итеративный процесс, позволяющий находить приближённое решение матричной игры, при этом степень близости приближения к истинному значению игры определяется длиной интервала:

.

Сходимость алгоритма гарантируется следующей теоремой.

Теорема. .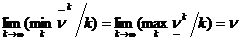

Схема доказательства.

Лемма. Для всякой матрицы А и "e>0 существует такое k0, что

.

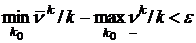При предельном переходе в неравенстве (1) при k®¥ имеем:

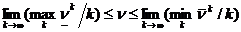. (2)

Отсюда получаем оценку разности пределов:

.

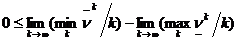Из леммы следует, что

.

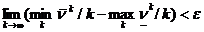На основании неравенства (1) имеем:

.

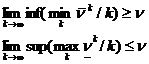Следовательно, в силу ограниченности пределов

.

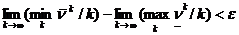Получаем оценку для разности пределов:

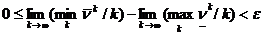 для "e>0.

Можем заключить, что 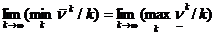. Осталось показать равенство пределов n. Это следует из неравенства (2).

Итак, .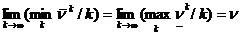

1.4 Информационное обеспечение

Входными данными для задачи является матрица игры, содержащая значения выигрыша при выбранных стратегиях для игроков 1 и 2.

Выходной информацией является значение цены игры и вероятностные показатели эффективности стратегий игры для игроков 1 и 2.

2. Описательная часть

2.1 Алгоритм решения задачи

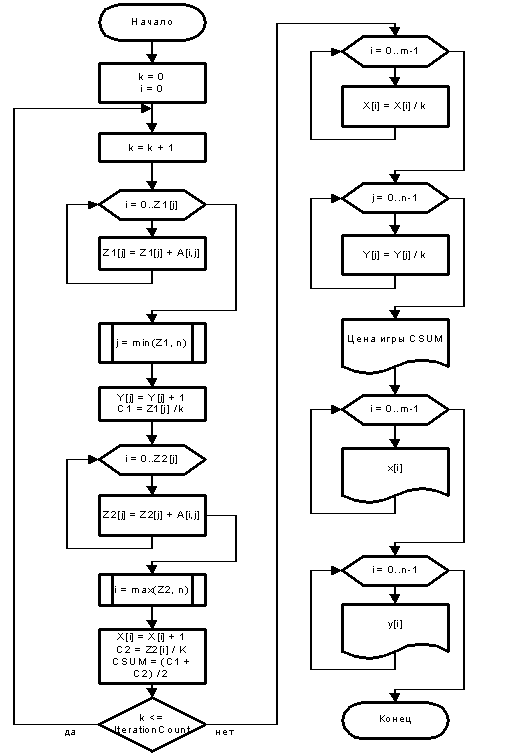
Рис. 1. Блок-схема алгоритма

2.2 Описание программы

Программа реализована на языке программирования C++ в среде программирования Borland C++ Builder 6

Программа состоит из одного модуля Unit1, включающего в себя все необходимые процедуры и функции.

Таблица 2. Процедуры и функции

2.3 Контрольный пример

Рассмотрим игру с матрицей А=.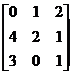

Итерация 0.1. Пусть игрок 1 выбрал свою 1-ю стратегию, т.е. А0= [0, 1, 2]. Тогда за начальные условия примем следующие: x0= (1, 0, 0) - приближение оптимальной стратегии игрока 1; c0=a1= (0, 1,2) - возможный выигрыш игрока 1.

Найдём множество индексов, на которых игрок 1 может получить, в худшем случае, наименьший выигрыш: 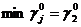, значит множество индексов J0={1}. Для этого индекса выигрыш равен 0. Это есть значение нижней оценки цены игры, т.е. .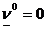

. На этом шаге определим, пользуясь начальными значениями, компоненты векторов 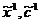. Для этого рассмотрим подигру 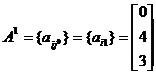. Для этой подигры оптимальной стратегией игрока 1 будет его 2-ая стратегия, так как она принесёт ему наибольший выигрыш.

Обозначим её через 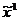: 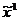= (0, 1, 0). Зная 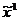, можем вычислить 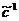=0а1+1а2+0а3=а2= (4, 2, 1).

. Найдём e1. Для этого рассмотрим подыгру (2´3) с матрицей 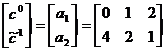. Решая матрицу графическим способом, получаем, что e1=1/2.

. Проведённые вычисления позволяют найти значения векторов x1, c1:

=1/2x0+1/2 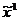=1/2 (1, 0, 0) +1/2 (0, 1, 0) = (1/2, 1/2, 0);=1/2c0+1/2 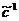=1/2 (0, 1,2) +1/2 (4, 2, 1) = (2, 3/2, 3/2).

Итерация 1. Так как e1 не равно 0, то процесс продолжается дальше. Теперь за начальные условия примем найденные значения векторов x1, c1. С их помощью вычисляем 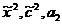, которые с большей точностью будут близки к истинным оптимальным стратегиям игрока 1.

. Итак, пусть x1= (1/2, 1/2, 0), c1= (2, 3/2, 3/2).

Найдём множество индексов 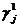, на которых игрок 1 может получить наименьший выигрыш: 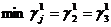, значит, J1={2,3}. Для этих индексов выигрыш равен 3/2. Это есть значение нижней оценки цены игры, т.е. 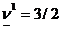. Заметим, что .

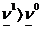. Далее найдём компоненты векторов 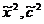. Для этого рассмотрим подигру 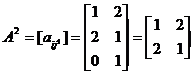. В силу симметричности матрицы ее решением будет вектор (1/2, 1/2), т.е. 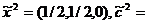1/2a1+1/2a2+0a3=

= (4/2, 3/2, 3/2).

. Вычислим коэффициент e₂. Для этого решим подигру (2´3): 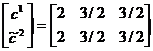. Стратегии игроков совпадают, поэтому e₂=0. В этом случае цена игры совпадает со своим нижним значением, т.е. 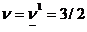. Возвращаемся к предыдущему шагу.

Итак, оптимальной стратегией игрока 1 является стратегия x*=x1= (1/2, 1/2, 0) при стоимости игры .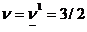

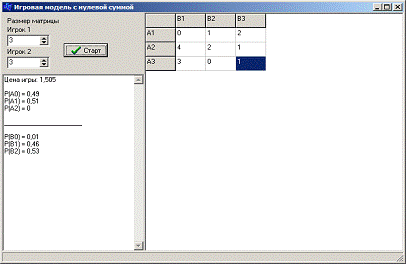
Рис 2. Результаты контрольного расчета

Как видно из полученных данных, результаты ручного расчета контрольного примера и результаты расчета практически совпадают. Это вызвано тем, что данный метод поиска решения итеративный, и полученное с его помощью решение является приближенным решением.

2.4 Руководство пользователя

Запуск программы осуществляется с помощью файла "Project1. exe".

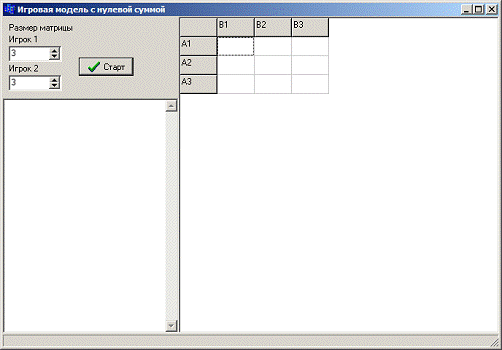
Рис 3. Окно программы

Задание размера матрицы игры осуществляется с помощью окон ввода с названиями "Игрок 1" и "Игрок 2".

Матрица игры заданного размера расположена внизу экрана. В ее ячейки вводятся значения выигрыша для данной стратегии.

Запуск поиска решения осуществляется кнопкой "Старт", после нахождения решения результаты поиска будут отображены в окне в правой части программы.

Заключение

Во время выполнения курсового проекта по дисциплине "Математические методы" были систематизированы, закреплены и расширены теоретические знания, приобретены необходимые практические умения и навыки в области программирования и обработки данных.

Были собраны различные материалы для разработки курсового проекта, освоены приемы работы в Borland C++ Builder, а так же применены полученные навыки по самостоятельной разработке технической документации и по автоматизированной обработки информации для конкретной задачи. Так же был разработан алгоритм, способный решить поставленную задачу нахождения решения игры с нулевой суммой методом Брауна-Робинсона.

В результате выполнения курсового проектирования была осуществлена подготовка к экзамену по дисциплине "Математические методы", и приобретены навыки работы с учебно-справочной литературы.

Список литературы

1. Архангельский А.Я., Тагин М.А. Программирование в C++Builder 6 и 2006 (+ CD-ROM). ООО "Бином-Пресс", 2006 г. - 1184 с.: ил.

. Агальцов, В.П. Математические методы в программировании / В.П. Агальцов, И.В. Володайская. - ИД Форум - Инфра. - М. - 2006. - 224с.

. Беленький В.З. Итеративные методы в теории игр и программировании. М. - "Наука" - 1974. - 240с.