Математичне моделювання на ЕОМ
Зміст
Вступ
Приведення
рівняння до безрозмірної форми
Знаходження
точного розв'язку рівняння
Підбирання
початкових умов
Зведення
рівняння до нормальної форми Коші
Складання
М-файлу правих частин рівняння у формі Коші
Створення
підпрограми інтегрування
Створення
керуючої програми
Проведення
експериментів з обчислення похибок
Графік
залежності амплітуди похибки від кроку інтегрування
Висновки
Список
використаної літератури
Вступ
Завданням передбачено вивчити
рівняння маси тіла m, яке з’єднане з основою пружиною жорсткістю с з
коефіцієнтом демпфірування f, під дією гармонічно змінюваної сили з амплітудою ω
і
початковою фазою ε.
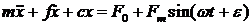
Сучасне комп'ютерне
моделювання пропонує цілий набір інтегрованих програмних систем та пакетів
програм для автоматизації математичних розрахунків: Eureka, Gauss, TK Solver!,
Derive, Mathcad, Mathematica, Maple V і ін Виникає питання: «А яке місце займає
серед них система MATLAB?»- одна з найстаріших, ретельно опрацьованих і
перевірених часом систем автоматизації математичних розрахунків, побудована на
розширеному поданні і застосуванні матричних операцій.
Це знайшло відображення в
назві системи - MATrix LABoratory - матрична лабораторія.
Однак синтаксис мови
програмування системи продуманий настільки ретельно, що ця орієнтація майже не
відчувається тими користувачами, яких не цікавлять безпосередньо матричні
обчислення.
Матриці широко застосовуються
в складних математичних розрахунках, наприклад при вирішенні задач лінійної
алгебри та математичного моделювання статичних і динамічних систем і об'єктів.
Вони є основою автоматичного складання і рішення рівнянь стану динамічних
об'єктів і систем.
Прикладом може служити
розширення MATLAB - Simulink. Це істотно підвищує інтерес до системи MATLAB, що
увібрала в себе кращі досягнення в області швидкого вирішення матричних задач.
Проте в даний час MATLAB
далеко вийшла за межі спеціалізованої матричної системи і стала однією з
найбільш потужних універсальних інтегрованих СКМ. Слово «інтегрована» вказує на
те, що в цій системі об'єднані зручна оболонка, редактор виразів і текстових
коментарів, обчислювач і графічний програмний процесор.
У новій версії
використовуються такі потужні типи даних, як багатовимірні масиви, масиви
осередків, масиви структур, масиви Java і розріджені матриці, що відкриває
можливості застосування системи при створенні та налагодженні нових алгоритмів
матричних і заснованих на них паралельних обчислень і великих баз даних.
У цілому MATLAB - це
унікальна колекція реалізацій сучасних чисельних методів комп'ютерної
математики, створених за останні три десятки років. Вона увібрала в себе і
досвід, правила і методи математичних обчислень, накопичені за тисячі років
розвитку математики.
Це поєднується з потужними
засобами графічної візуалізації і навіть анімаційної графіки.
Систему з доданою до неї
обширною документацією цілком можна розглядати як фундаментальний багатотомний
електронний довідник з математичного забезпечення ЕОМ - від масових
персональних комп'ютерів до супер -ЕОМ.
Важливими перевагами системи
є її відкритість і розширюваність. Більшість команд і функцій системи
реалізовані у вигляді текстових m-файлів (з розширенням. M) і файлів на мові
Сі, причому всі файли доступні для модифікації.
Користувачеві надана
можливість створювати не тільки окремі файли, але й бібліотеки файлів для
реалізації специфічних завдань.
Вражаюча легкість модифікації
системи та можливість її адаптації до вирішення специфічних завдань науки і
техніки призвели до створення десятків пакетів прикладних програм (toolbox),
набагато розширили сфери застосування системи.
Деякі з них, наприклад
Notebook (інтеграція з текстовим процесором Word і підготовка «живих»
електронних книг), Symbolic Math і Extended Symbolic Math (символьні обчислення
із застосуванням ядра системи Maple V R5) і Simulink (моделювання динамічних
систем і пристроїв, заданих у вигляді системи блоків), настільки органічно
інтегрувалися із системою MATLAB, що стали її складовими частинами.
Приведення рівняння до безрозмірної
форми
Вихідне рівняння має вигляд:
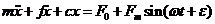 ; (1)
; (1)
Його можна значно спростити,
не зменшуючи(навіть збільшуючи) узагальненості одержуваних результатів, якщо
замість нього розглядати його безрозмірний аналог, тобто таке рівняння в якому
усі величини не мають фізичної розмірності.
Задане рівняння
двоступеневого гірокомпаса переведемо до безрозмірної форми:
Для цього усі члени рівняння
(1) поділимо на масу
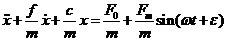 .
.
Коефіцієнт 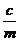 можна
позначити , як квадрат деякої величини:
можна
позначити , як квадрат деякої величини:
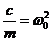
Величина

має розмірність кутової
швидкості і вимірюється у радіанах за секунду. Як в подальшому стане ясним,
вона є коловою частотою власних коливань системи, за умови, що тертя відсутнє .
Коефіцієнт при другому члені
лівої частини можна подати як добуток деякої безрозмірної величини 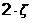 на величину
введеної частоти власних коливань
на величину
введеної частоти власних коливань 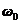 :
:

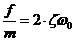
Введений у такий спосіб
безрозмірній коефіцієнт:
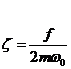
Зазвичай даний коефіцієнт
називають коефіцієнтом згасання. Він характеризує властивості коливальної
ланки.
З урахуванням цих перетворень
рівняння можна подати у вигляді:
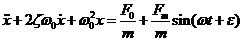 (2)
(2)
Тепер введемо поняття
безрозмірного часу 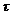 , який
пов’язаний зі звичайним часом співвідношенням:
, який
пов’язаний зі звичайним часом співвідношенням:
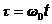 (3)
(3)
Зміст безрозмірного часу
досить простий ,- це час , який вимірюється в одиницях періоду 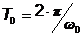 власних
коливань системи.
власних
коливань системи.
Замінимо розмірний час на
безрозмірний. Похідна за часом
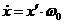
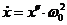
Позначено, що ’’ штрих’’
похідна по безрозмірному часу.
Зробимо ще деякі позначення:
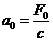 ;
; 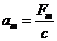 ;
; 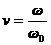 - відносна частота зовнішньої сили.
- відносна частота зовнішньої сили.
Остаточно одержимо:
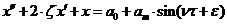 ; (1)
; (1)
Знаходження
точного розв'язку рівняння
Точний розв’язок лінійного
диференціального рівняння зі сталими коефіцієнтами можна подати у вигляді
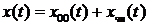 ,(2)
,(2)
де 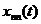 - загальний
розв'язок відповідної однорідної системи диференційних рівнянь (тобто такої, у
який відкинуті усі члени, що залежать тільки часу;
- загальний
розв'язок відповідної однорідної системи диференційних рівнянь (тобто такої, у
який відкинуті усі члени, що залежать тільки часу; 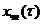 - деякий
частковий розв'язок початкової системи.
- деякий
частковий розв'язок початкової системи.
Відповідно однорідне рівняння
має вигляд:
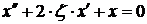 (3)
(3)
Характеристичне рівняння його буде
мати вигляд
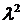 +2
+2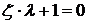
Корені цього квадратного
рівняння матимуть вигляд, враховуючи що 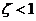 :
:
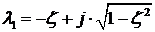 ;
; 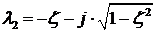
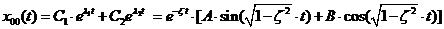 (4)
(4)
Частковий розв’язок рівняння
шукатимемо у вигляді:
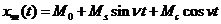 .(5)
.(5)
Продиференціюємо вираз (5)
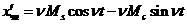 ,` (6)
,` (6)
і другий раз
 .(7)
.(7)
Коефіцієнти 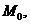
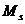 ,
,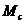 знаходяться шляхом підставляння (5)
(6) (7) у рівняння (1) і прирівнювання коефіцієнтів у лівій і правій частині
при:
знаходяться шляхом підставляння (5)
(6) (7) у рівняння (1) і прирівнювання коефіцієнтів у лівій і правій частині
при:
сталих членах;
синусах від 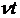 ;
;
косинусах від 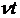 .
.
Система рівнянь:
Розв’язуючи ці алгебраїчні
рівняння, отримаємо:
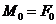 ;
;
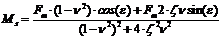 ;
; 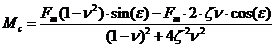 (8)
(8)
Отже загальний розв’язок (2)
рівняння набуде вигляду:
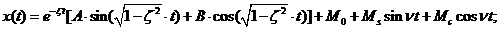 (9)
(9)
Похідна від цього розв’язку
матиме вигляд
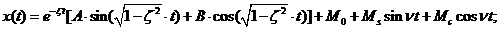 (9)
(9)
Сталі інтегрування A i B
визначаються підстановкою в (9), (10) початкових умов:
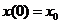
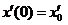 .
.
В результаті отримаємо
рівняння:
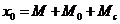
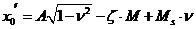
з яких виходить:
B=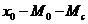 ; A=
; A=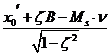 ;
;
Підбирання
початкових умов
Для утворення програми
важливо , з метою зменшення очікуваного терміну інтегрування диференційного
рівняння, підібрати такі початкові умови з умови відсутності у вихідному
процесі власних коливань .
Для відсутності коливань
системи сталі інтегрування повинні дорівнювати нулю, тоді
=0. B=0
Тому початкові умови будуть
наступними:
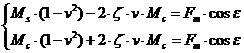
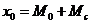 ;
;
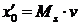 ;
;
Зведення
рівняння до нормальної форми Коші
Методи чисельного
інтегрування орієнтовані на системи диференційних рівнянь, приведених до
нормальної форми Коші - це подання системи звичайних диференційних рівнянь, у
вигляді сукупності диференційних рівнянь 1-го порядку розміщених відносно
похідних:
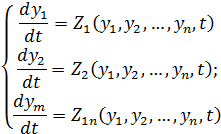
,Z2,Z3 - відомі функції змінних у і
часу t.
Змінні у1…уn, які допускають
можливість такого представлення рівнянь, називаються змінними стану системи або
фазовими змінними системи.
Тому приведемо рівняння до цієї
форми. Для цього позначимо:
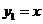 ;
; 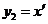 .
.
Подамо рівняння у вигляді
наступної системи диференціальних рівнянь першого порядку, за новими змінними
(змінними стану):
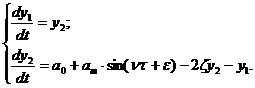
Це і є нормальна форма Коші.
кладання
М-файлу правих частин рівняння у формі Коші
Для складання програми
введемо позначення:
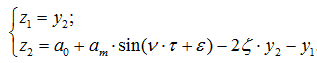
Підпрограма правих частин матиме
вигляд:
Z=KolZv(t,y);F0 Fm v Eps
Dz(1)=y(2);(2)=F0+Fm*sin(v*t+Eps)-2*Dz*y(2)-y(1);
Складання підпрограми методу
інтегрування
|
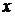 переміщення
тіла відносно основи у напрямку дії сили переміщення
тіла відносно основи у напрямку дії сили
|
|
|
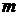 маса маса
|
|
|
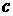 жорсткість
пружини жорсткість
пружини
|
|
|
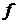 коефіцієнт
в’язкого тертя демпфера коефіцієнт
в’язкого тертя демпфера
|
|
|
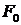 величина
сталої величина
сталої
|
|
|
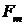 амплітуда
змінювання сили амплітуда
змінювання сили
|
|
|
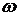 колова
частота змінювання сили колова
частота змінювання сили
|
|
Метод Рунге-Кутта четвертого порядку
настільки широко розповсюджений, що його часто називають просто методом
Рунге-Кутта.
Розглянемо задачу Коші:
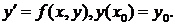
Тоді наближене значення в
наступних точках обчислюється за по ітераційній формулі :
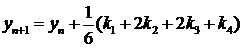
В даному випадку ми маємо
метод 4-го порядку, який є одним з найбільш вживаних на практиці, так як
забезпечує високу точність і в той же час відрізняється порівняльною простотою.
Тому в більшості випадків він згадується в літературі просто як «метод
Рунге-Кутта» без зазначення його порядку.
Цей метод має четвертий
порядок точності, тобто сумарна помилка на кінцевому інтервалі інтегрування має
порядок 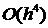 (помилка на
кожному кроці порядку
(помилка на
кожному кроці порядку 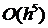 ).
).
Ще нам потрібно створити
програму метода інтегрування випадку це метод Ейлера.
Нижче подана загальна
характеристика цього методу(Таблиця 1).
Таблиця 1
|
Порядок методу
|
Формула методу
|
Допоміжні величини
|
Назва методу
|
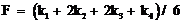 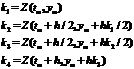 Рунге-Кутта Рунге-Кутта
|
|
|
Текст підпрограми інтегрування має
вигляд:
[yout,tout]=RK41GAI(Zpfun,t,y,h)
%Грандюк
Андрій,ПГ-11=feval(Zpfun,t,y);=feval(Zpfun,t+h/2,y+h/2*K1);=feval(Zpfun,t+h/2,y+h/2*K2);=feval(Zpfun,t+h,y+h*K3);=(K1+2*K2+2*K3+K4)/6;=y+h*F;=t+h;
Створення керуючої програми
Текст керуючої програми за допомогою
якої ми вводимо параметри диференціального рівняння та його початкові умови,
організовує процес покрокового чисельного інтегрування диференціального
рівняння за допомогою методу Ейлера 1.1, має такий вигляд:
Основна програма
Грандюк Андрій,ПГ-11all,clcF0 Fm v
Eps Dz
Введення первісних даних
=0.1; Fm=1.5;=3;=0;=0.4;
Розрахунок коефіцієнтів значеннь
=F0;=(Fm*cos(Eps)*(1-v^2)+Fm*sin(Eps)*2*Dz*v)/((1-v^2)^2+4*v^2*Dz^2);=(Fm*sin(Eps)*(1-v^2)-Fm*cos(Eps)*2*Dz*v)/((1-v^2)^2+4*v^2*Dz^2);=M0+Mc;=Ms*v;=sqrt(1-Dz^2);
Крок інтегрування
=0.01;
Підготовка початкових умов
=0;=[x0,xt0];=30;=1;(K)=t;(K)=y(1);
Цикл інтегрування
t<T
[yout,tout]=RK41GAI('KolZv',t,y,h);=yout;=tout;=K+1;(K)=t;(K)=y(1);
Розрахунок початкових значення
точного розв'язку
=M0+Mc.*cos(v*tt)+Ms.*sin(v.*tt);
Формування похибок
=X-Xt;
Виведення графіка
(2,1,1)(tt,X,tt,Xt,'.-'),grid('Рівняння:
X''''+2\zetaX''+X=F_0+F_msin(\nut+E) Рунге-Кутта');('Час t')('Похибка
інтегрування методом RK-41');('Проінтегрований процес','Точний
процес','FontName','MS Sans Serif')(2,1,2)(tt,dX),grid(gca,'FontName','MS Sans
Serif')('Грандюк Андрій','FontName','MS Sans Serif')=sprintf('Крок інтегрування
h=%g',h)([strh,' '])('Похибка')
інтегрування рівняння
кош похибка
Проведення експериментів з
обчислення похибок
Принципові похибки чисельних методів
інтегрування диференційних рівнянь мають подвійних характер:
Похибки внаслідок того, що
нескінченний ряд змінюється на скінчений, який має декілька перших членів ряду;
при цьому відкинуті члени утворюють похибку;
Похибки внаслідок неточного
обчислення похідних у попередній точці; у власну чергу, вони зазвичай також
обумовленні тим, що замість нескінченного ряду при їхньому обчисленні
використовуються лише обмежена кількість його членів.
Обидві похибки - єдиного типу. Ці
похибки чисельного метода не пов’язані з точністю здійснення математичних
операцій,- вони викликані обмеженням нескінченних рядів скінченою кількістю їх
членів. Тому вони отримали назву похибок обмежування (на відміну від похибок
округлення, які визначають точність проведення обчислення)
Характерна особливість похибок
обмежування - при зменшені кроку інтегрування вони також зменшувались. Цим вони
суттєво відрізняються від похибок округлення, які визначаються кількістю
математичних операцій. Через те, що при зменшені кроку кількість операцій, що
інтегрується, пропорційно збільшується, то похибки округлення теж збільшується
зі зменшенням кроку.
Якісна картина залежності похибки
від кроку інтегрування наведена на Рис. 1.
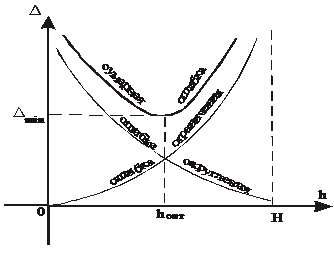
Рис. 1 - Залежність похибок
від кроку інтегрування
Таким чином змінюючи крок
інтегрування, і визначаючи похибку, з графіка похибок, маємо наступні
результати:
h=0.5; ∆=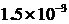
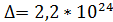 (Рис.1)
(Рис.1)
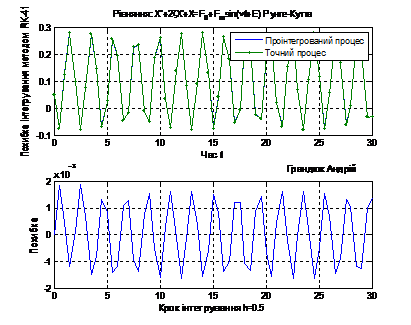
Рис. 2
=0.1; ∆=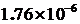
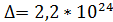 (Рис.2)
(Рис.2)
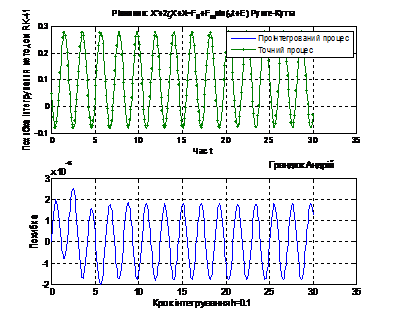
Рис. 3
h=0.05; ∆=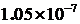
 (Рис.4)
(Рис.4)
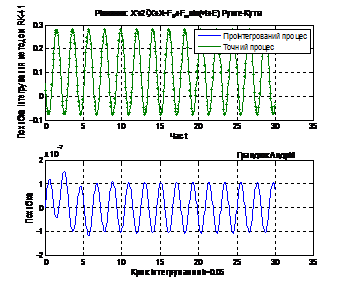
Рис. 4
=0.01; ∆=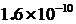
 (Рис.5)
(Рис.5)
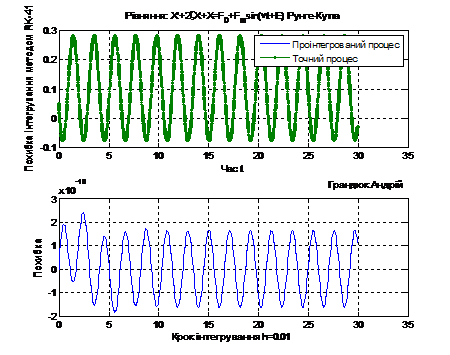
Рис. 5
h=0.005; ∆=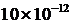
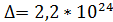 (Рис.5)
(Рис.5)
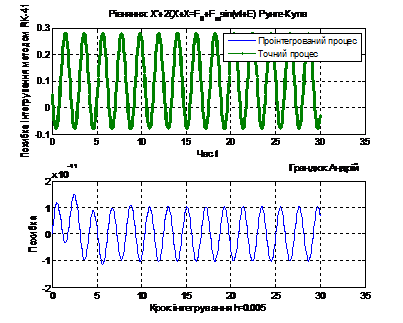
Рис. 6
=0.001; ∆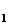 =
=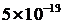 ;
;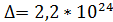 ∆
∆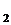 =
=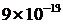 ;
;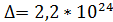 (Рис. 7)
(Рис. 7)
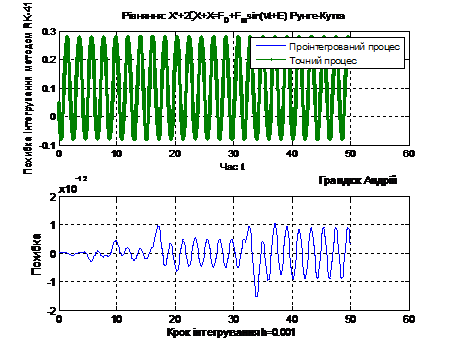
Рис. 7
h=0.0001; ∆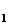 =
=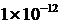 ;
;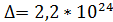 ∆
∆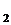 =
=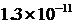 ;
;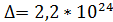 (Рис. 8)
(Рис. 8)
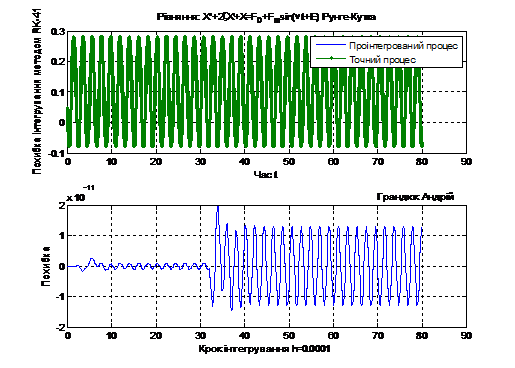
Рис. 8
Графік
залежності амплітуди похибки від кроку інтегрування
Для побудови графіку
використаємо окремий М-файл текст якого буде наступним:
all=[0.0001,0.0003,0.0005,0.001,0.002,0.003,0.01,0.03,0.05,0.07,0.1];=[1*10^(-12),3.7*10^(-12),1.85*10^(-12),5*10^(-13),7.4*10^(-13),1.33*10^(-12),1.6*10^(-10),1.35*10^(-8),1.06*10^(-7),4.15*10^(-7),1.76*10^(-6)];(h,dx,'*-');(gca,'FontName','MS
Sans Serif')('Похибка чисельного інтегрування методом Рунге-Кутта
4.1');('Амплітуда похибки');('Крок інтегрування');('Грандюк Андрій
ПГ-11','FontName','MS Sans Serif'),grid;
В результаті маємо графік
залежності амплітуди похибки від кроку інтегрування (Рис. 9).
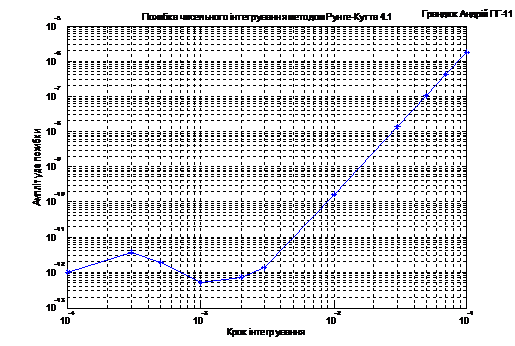
Рис. 9
Знайдемо рівняння залежності
похибки від кроку інтегрування:
На графіку ми бачимо лінійну
залежність, отже, загальним рівнянням буде:
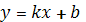
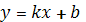
де 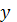
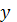 - це координата осі похибки;
- це координата осі похибки;
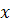
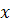 - це координата осі кроку
інтегрування;
- це координата осі кроку
інтегрування;
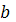
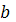 - це вільний член;
- це вільний член;
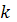
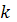 - це кутовий коефіцієнт, тангенс
нахилу прямої до осі кроку інтегрування.
- це кутовий коефіцієнт, тангенс
нахилу прямої до осі кроку інтегрування.
Перша точка має координати: 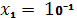
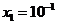 ,
, 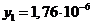 ;
;
Друга точка має координати: 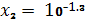
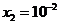 ,
, 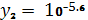
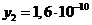 ;
;
Оскільки графік побудований у
логарифмічному масштабі, то переведемо координати в звичайному масштабі:
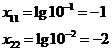 ;
;
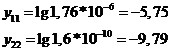
Кутовий коефіцієнт к
знаходимо відношенням різниці координат по осі похибки до різниці координат по
осі Крок інтегрування:
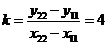 ;
;
Знайдемо вільний член 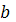
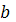 з рівняння , підставивши координати
будь-якої точки з даного графіка:
з рівняння , підставивши координати
будь-якої точки з даного графіка:
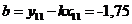 ;
;
Оскільки 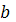
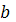 задано в логарифмічному масштабі,
то переведемо в звичайний:
задано в логарифмічному масштабі,
то переведемо в звичайний:
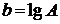 ;
;
Звідки:
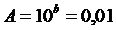 ;
;
Виводимо формулу залежності
похибки від кроку інтегрування
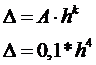
Висновки
Аналізуючи результати які ми
одержали при виконанні даної роботи, можна зробити висновки:
характер змінювання у часі похибки
чисельного інтегруванні при кількості кроків на мінімальному періоді нагадує
характер змінювання у часі самої інтегрованої величини; вона складається з
загасаючої складової, яка відповідає власним коливанням з деяким періодом і
сталих вимушених коливань з утричі більшим періодом; це є ознакою того, що у
цьому діапазоні змінювання кроку інтегрування на перший план висувається
похибки методу інтегрування, які визначаються розв’язком рівняння похибок.
похибки чисельного інтегрування у
цьому діапазоні змінювання кроку інтегрування зменшуються з його зменшенням
пропорційно до величини кроку інтегрування у степені, який збігається з
порядком методу інтегрування;
при зменшенні кроку інтегрування
менше за той, що відповідає кількості кроків на мінімальному періоді, похибка
інтегруванні вже не зменшується, а навпаки, збільшується; при цьому і характер
змінювання похибки у часі теж різко змінюється, - в ньому вже важко виділити
якість періодичні складові, змінювання похибки набуває характеру випадкового
процесу; це є ознака того, що у цьому діапазоні змінювання кроків переважає
друга складова похибки інтегрування - похибки внаслідок округлень при
здійсненні операцій чисельного інтегрування;
якщо кількість кроків на
мінімальному періоді збільшувати, процес чисельного інтегрування наближається
до межі своєї стійкості; починаючи з кроку h=0,1 похибка інтегруванні (методу)
починає збільшуватись у часі необмежено; при кроці h=2 ( рис.2) процес, що
одержується через чисельне інтегрування, вже не має нічого спільного з точним
розв’язком диференційного рівнянні, як говорять, метод «вибухає».
Список використаної літератури
1.
Лазарєв Ю.Ф. Моделювання на ЕОМ: Навчальний посібник.-К: «Корнійчук», 2007. -
290 с.
.
Лазарєв Ю.Ф. Початки програмування в середовищі MatLAB: Навчальний посібник. -
К.: "Корнійчук", 19999. - 160 с.
.
Вержбицький В.М. Чисельні методи (лінійна алгебра і нелінійні рівняння):
Навчальний посібник для вузів. - М.: «Оникс 21 век», 2005. - 432 с.
.
Вержбицький В.М. Чисельні методи (математичний аналіз і звичайні диференціальні
рівняння): Навчальний посібник для вузів. - М.: «Оникс 21 век», 2005. - 400 с.
.
Гутер Р.С. Елементи чисельного аналізу і математичної обробки результатів):
Навчальний посібник для вузів. - М.: «Наука», 1979. - 432 с.