Двойное векторное произведение
Оглавление
Введение
Глава
1.
Векторы и основные линейные операции над ними
.1
Векторные величины
.2
Единичный вектор
Глава
2. Векторное произведение и его свойства
.1
Определение векторного произведения
Глава
3. Двойное векторное произведение
Заключения
Список
используемой литературы
Введение
При изучении двойного векторного произведения
необходимо знание вектора и основные линейные операции над ними.
Вектором называется всякая величина, обладающая
направлением. Скалярной величиной, или скалярном, называется величинами, не
обладающая направлением. Над векторми производяться действия, называемые
сложением, вычитанием и умножением векторов. Эти действия имеют много общих
свойств с алгебраическими действиями сложения, вычитания и умножения. Поэтому
учение о действиях над векторами называется векторной алгеброй.
Двойным векторным произведением называеться
выражение вида:
Двойное векторное произведение есть вектор,
комплонарный с векторами b и c; оно выражаеться через векторы b и c следующим
образом:
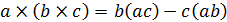
Глава 1. Векторы и основные линейные
операции над ними
.1 Векторные величины
В отличие от скалярной величины, которую можно
задать одним числом и отложить на некоторой шкале (отсюда и название -
«скалярная») - площадь, объём, температура - векторную величину, или просто
вектор, можно задать с помощью числа и некоторого направления (скорость, сила).
Итак, мы можем сказать, что вектор 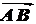 - это
величина, которая характеризуется числом, совпадающим с длиной отрезка
- это
величина, которая характеризуется числом, совпадающим с длиной отрезка 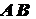 , и
направлением, совпадающим с направлением луча
, и
направлением, совпадающим с направлением луча 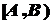 (рис. 1).
(рис. 1).
При этом длину вектора обозначают 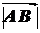 ,
, 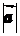 или ещё
или ещё 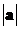 . Длину
вектора также называют модулем этого вектора. Векторы
. Длину
вектора также называют модулем этого вектора. Векторы  и
и  называют
равными, если совпадают их длины и направления.
называют
равными, если совпадают их длины и направления.
Векторы  и
и  называют
противоположными, если их длины равны, а направления противоположны. Заметим,
что при этом начало вектора можно поместить в любой точке пространстве. Такие
векторы называют свободными.
называют
противоположными, если их длины равны, а направления противоположны. Заметим,
что при этом начало вектора можно поместить в любой точке пространстве. Такие
векторы называют свободными.
Если начало и конец вектора
совпадают, то такой вектор называется нулевым (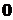 ). Направление нулевого вектора не
определено.
). Направление нулевого вектора не
определено.
Умножение вектора на скаляр
Определение 1. Произведением вектора
 на число
на число 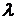 называется
такой вектор
называется
такой вектор 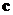 , что
, что 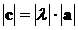 , а
направление его совпадает с направлением вектора
, а
направление его совпадает с направлением вектора  , если
, если 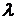 >0, и ему
противоположно, если
>0, и ему
противоположно, если 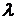 <0; если
<0; если 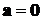 или
или 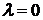 , то
, то 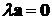 .
.
Ясно, что векторы  и
и 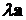 (если
(если 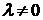 ) можно
поместить на одной прямой (рис.2). Вектор
) можно
поместить на одной прямой (рис.2). Вектор 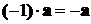 , очевидно, является противоположным
вектору
, очевидно, является противоположным
вектору  .
.
Определение 2. Два ненулевых вектора
 и
и  , лежащих на
одной прямой или на параллельных прямых, называются коллинеарными.
, лежащих на
одной прямой или на параллельных прямых, называются коллинеарными.
1.2 Единичный вектор
Определение 3. Вектор 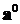 , длина
которого равна единице, называется единичным вектором, или ортом. Если задан
некоторый вектор
, длина
которого равна единице, называется единичным вектором, или ортом. Если задан
некоторый вектор  (
(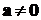 ), то всегда
можно подобрать множитель
), то всегда
можно подобрать множитель 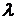 , такой,
чтобы после умножения на него длина вектора
, такой,
чтобы после умножения на него длина вектора 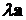 была бы равна единице. Очевидно, что
в качестве такого числа нужно взять
была бы равна единице. Очевидно, что
в качестве такого числа нужно взять 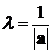 . Тогда
. Тогда 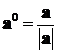 , и при этом
, и при этом
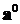 называется
единичным вектором, соответствующим вектору
называется
единичным вектором, соответствующим вектору  , или ортом вектора
, или ортом вектора  . Очевидно,
что направление единичного вектора всегда совпадает с направлением вектора
. Очевидно,
что направление единичного вектора всегда совпадает с направлением вектора  . Ясно
также, что
. Ясно
также, что 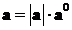 .
.
Точно так же единичный вектор 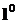 ,
направление которого совпадает с направлением оси
,
направление которого совпадает с направлением оси 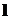 , называется
ортом оси
, называется
ортом оси 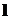 , или её единичным
вектором.
, или её единичным
вектором.
Сложение векторов
Определение 4. Суммой векторов  и
и  ,
расположенных так, что начало вектора
,
расположенных так, что начало вектора  совпадает с концом вектора
совпадает с концом вектора  , называется
вектор
, называется
вектор 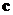 , начало
которого совпадает с началом вектора
, начало
которого совпадает с началом вектора  , а конец - с концом вектора
, а конец - с концом вектора 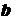 . (правило
треугольника - рис. 2 а).
. (правило
треугольника - рис. 2 а).
При этом пишут: 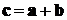 . Аналогично
определяется сумма n векторов
. Аналогично
определяется сумма n векторов
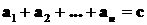 .
.
А именно: суммой называют вектор 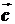 ,
проведённый из начала первого в конец последнего вектора, при условии, что
начало вектора
,
проведённый из начала первого в конец последнего вектора, при условии, что
начало вектора 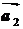 совпадает с
концом вектора
совпадает с
концом вектора 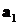 , начало
вектора
, начало
вектора 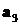 совпадает с
концом вектора
совпадает с
концом вектора 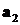 и т.д.
(правило многоугольника - рис. 3.б).
и т.д.
(правило многоугольника - рис. 3.б).
Замечание. Если на векторах  и
и  построить
параллелограмм, поместив их начало в общую точку, то сумма
построить
параллелограмм, поместив их начало в общую точку, то сумма 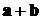 будет
лежать на диагонали параллелограмма, выходящего из общего начала векторов
будет
лежать на диагонали параллелограмма, выходящего из общего начала векторов  и
и  (правило
параллелограмма - рис. 2 , в).
(правило
параллелограмма - рис. 2 , в).
) 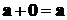 - поглощение нулевого вектора
- поглощение нулевого вектора
) 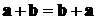 - перестановочное, или
коммутативное
- перестановочное, или
коммутативное
) 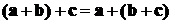 - сочетательное, или ассоциативное.
- сочетательное, или ассоциативное.
Для всякого ненулевого вектора 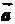 существует
противоположный вектор -
существует
противоположный вектор -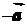 , такой, что
, такой, что
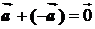 .
.
Вычитание векторов
Определение 5. Вектор 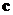 называется
разностью векторов
называется
разностью векторов  и
и  , т.е.
, т.е. 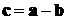 , если
, если 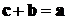 . Отсюда
следует, что
. Отсюда
следует, что 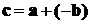 т.е.
вычитание векторов сведено к сложению (рис. 4). Нетрудно заметить, что разность
век-торов лежит на второй диагонали параллелограмма, построенного на векторах
т.е.
вычитание векторов сведено к сложению (рис. 4). Нетрудно заметить, что разность
век-торов лежит на второй диагонали параллелограмма, построенного на векторах  и
и  ,
проведённой из конца вектора -
,
проведённой из конца вектора -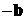 в конец вектора
в конец вектора  .
.
Глава 2. Векторное произведение и
его свойства
.1 Определение векторного
произведения
Определение. Векторным произведением
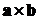 ненулевых
векторов
ненулевых
векторов  и
и  называется
такой вектор
называется
такой вектор 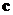 , который
удовлетворяет трём условиям:
, который
удовлетворяет трём условиям:
. 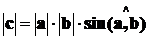 , т.е. длина вектора
, т.е. длина вектора 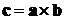 численно
равна площади параллелограмма, построенного на этих векторах.
численно
равна площади параллелограмма, построенного на этих векторах.
. Вектор 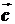 перпендикулярен
плоскости, в которой лежат векторы
перпендикулярен
плоскости, в которой лежат векторы  и
и  .
.
. Тройка  ,
,  ,
, 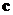 - правая
(рис.5)
- правая
(рис.5)
Если хотя бы один из векторов  и
и  нулевой, то
по определению
нулевой, то
по определению 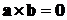 . Заметим,
что иногда векторное произведение двух векторов
. Заметим,
что иногда векторное произведение двух векторов  и
и  обозначается символом
обозначается символом 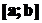 .
.
Свойства векторного произведения
. 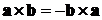 .
.
Это очевидно, так как при
перестановке векторов изменится ориентация тройки.
. Свойство сочетательности
относительно скалярного множителя:
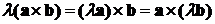 .
.
(без доказательства)
. Распределительное свойство
относительно сложения векторов :
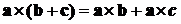 .
.
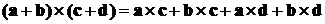 .
.
Следствие. 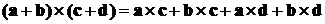 .
.
То есть скобки можно раскрывать, как
при обыкновенном умножении, не переставляя местами множители (без
доказательства).
. Необходимое и достаточное условие
коллинеарности двух ненулевых векторов
Теорема. Для того, чтобы два
ненулевых вектора  и
и  были
коллинеарны, необходимо и достаточно, чтобы их векторное произведение было бы
равно нулю.
были
коллинеарны, необходимо и достаточно, чтобы их векторное произведение было бы
равно нулю.
Доказательство. Необходимость. Пусть
векторы  и
и  коллинеарны,
тогда они лежат на одной прямой, следовательно,
коллинеарны,
тогда они лежат на одной прямой, следовательно, 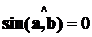 =>
=> 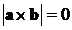 . Значит,
. Значит, 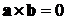
Достаточность. Пусть векторное
произведение 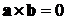 . Так как
. Так как 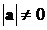 ,
, 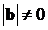 , то значит
, то значит 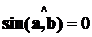 , т.е.
, т.е. 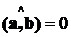 или
или 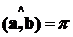 , а это
означает, что векторы
, а это
означает, что векторы  и b
коллинеарны.
и b
коллинеарны.
Замечание. Заметим, что если два
вектора 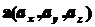 и
и 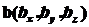 коллинеарны,
то существует такое число
коллинеарны,
то существует такое число 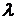 , при
котором
, при
котором 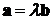 , т.е.
, т.е.
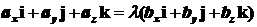 =>
=> 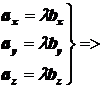
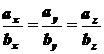 .
.
Итак, мы доказали, что если два
вектора коллинеарны, то их координаты пропорциональны.
. Векторное произведение векторов,
заданных своими координатами
Заметим, что 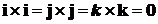 . Далее
очевидно, что
. Далее
очевидно, что
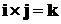 ,
, 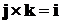 ,
, 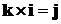 ,
, 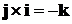 ,
, 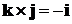 ,
, 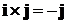 .
.
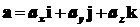 и
и 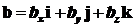
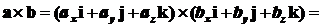
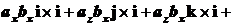
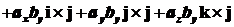
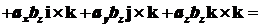
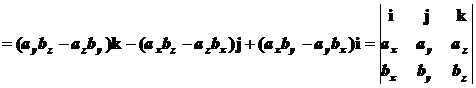 .
.
. Механический смысл векторного
произведения
Если сила 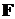 поворачивает
тело вокруг оси
поворачивает
тело вокруг оси 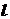 , то момент
, то момент 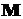 силы
силы 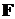 , как
известно, равен
, как
известно, равен 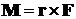 (рис.5).
(рис.5).
Пример 1.
Найти площадь треугольника с вершинами в
точках(-1,1,2), B(2,3,3) и C(1,2,-1);
. Найти единичный вектор, перпендикулярный к
плоскости, в которой лежат точки A,B и C.
Решение.
1. 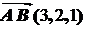 ,
, 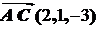
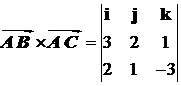 =
= 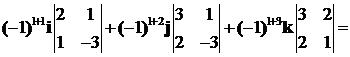
=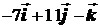
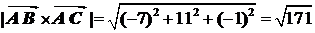 .
.
Площадь треугольника равна половине
площади параллелограмма, построенного на векторах 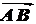 и
и 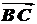 ,
следовательно
,
следовательно 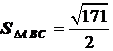 .
.
. В силу определения векторного
произведения вектора 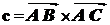 , два
вектора
, два
вектора
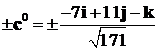
удовлетворяют поставленной задаче
(рис. 7).
Глава 3. Двойное векторное
произведение
Определение. Двойным векторным произведением
трёх ненулевых векторов 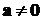 ,
, 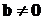 и
и 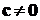 называется
называется 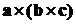 ; если хотя
бы один из векторов
; если хотя
бы один из векторов  ,
,  или
или 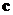 равен нулю,
то
равен нулю,
то 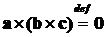 .
.
Итак, мы видим, что двойное
векторное произведение представляет собою векторную величину. Заметим, что
объекты типа 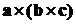 часто
встречаются в физике и механике. Выведем простую форму для вычисление двойного
векторного произведения.
часто
встречаются в физике и механике. Выведем простую форму для вычисление двойного
векторного произведения.
Итак, допустим, что нам известны
координаты векторов, т.е.
вектор скаляр
произведение тождество
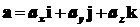 ,
, 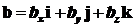 ,
, 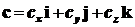 .
.
Вычислим 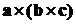 .
.
Обозначим 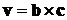 ,
, 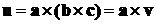 .
.
Очевидно, что нас интересует вектор 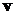 . Известно,
что вектор
. Известно,
что вектор 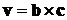 выражается
через координаты векторов
выражается
через координаты векторов  и
и 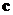 так:
так:
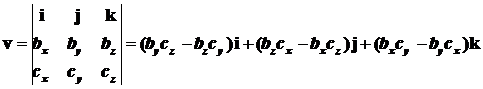 ,
,
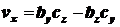 ,
, 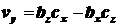 ,
, 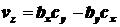 .
.
В свою очередь, аналогично
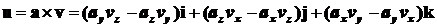 .
.
Подставим в правую часть этого
равенства полученные выражения для 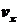 ,
, 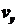 и
и 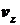 и, кроме того, выполним
искусственное преобразование, добавив и отняв к правой части выражения
и, кроме того, выполним
искусственное преобразование, добавив и отняв к правой части выражения 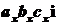 ,
, 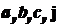 ,
, 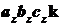 . Получим:
. Получим:
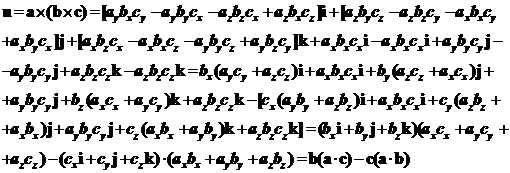
Итак, получили: 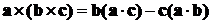 .
.
Отметим, что справа в скобках стоят
числа, равные скалярным произведениям 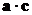 и
и 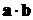 ; они являются коэффициентами
линейной комбинации векторов
; они являются коэффициентами
линейной комбинации векторов  и
и 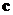 , через которые выражается двойное
векторное произведение
, через которые выражается двойное
векторное произведение 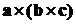 . Нетрудно
заметить, что двойное векторное произведение представляет собою вектор, который
лежит в той же плоскости, что и вектора
. Нетрудно
заметить, что двойное векторное произведение представляет собою вектор, который
лежит в той же плоскости, что и вектора  и
и 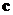 , т.е. векторы
, т.е. векторы 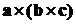 ,
,  и
и 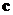 компланарны.
компланарны.
Остановимся теперь на вычислении
выражения 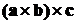 , которое,
вообще говоря, также является двойным векторным произведением. Действительно:
, которое,
вообще говоря, также является двойным векторным произведением. Действительно:
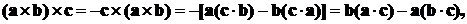
т.е. 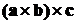 представляет собою вектор, лежащий
в одной плоскости с векторами
представляет собою вектор, лежащий
в одной плоскости с векторами  и
и  . Очевидно также, что
. Очевидно также, что 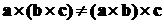 .
.
Другие свойства двойного векторного
произведения нетрудно проанализировать, принимая во внимание свойства
скалярного и векторного произведения.
Доказать тождество Лагранжа
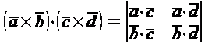 .
.
Решение
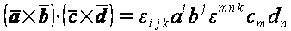 ;
;
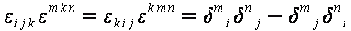 ;
;
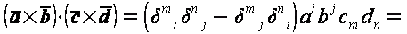
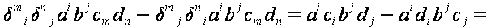
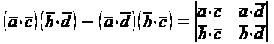
. Доказать формулу
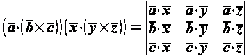
Решение
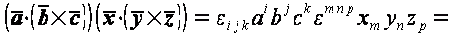
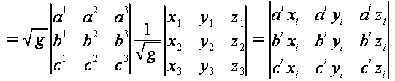
Следовательно:
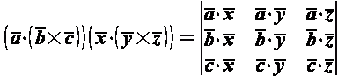 .
.
Что и требовалось доказать.
Пример 1. Доказать тождество Якоби:
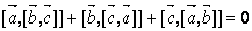 .
.
Имеем
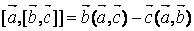 ,
,
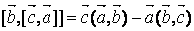 ,
,
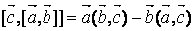 .
.
Суммируя эти равенства, получим тождество Якоби.
Пример 2. Показать, что точки А (1,2,1), В
(3,3,3), С (4,1,2) и D (5,4,5) лежат в одной плоскости.
Решение. Найдем координаты векторов 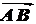 ,
, 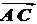 и
и 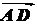 .
.
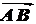 (2,1,2),
(2,1,2), 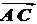 (3,-1,1),
(3,-1,1), 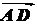 (4,2,4).
(4,2,4).
Если точки А, В, С и D лежат в одной
плоскости, то и векторы лежат в одной плоскости (рис. 2.8.1), а тогда смешанное
произведение этих векторов равно нулю.
Действительно,
(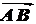 ,
, 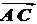 ,
,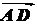 ) =
) = 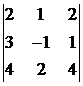 = 0,
= 0,
т.к. первая и вторая строки
определителя пропорциональны.
Пример 2. Доказать, что векторы 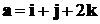 ,
, 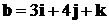 и
и 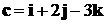 линейно
зависимы и найти эту линейную зависимость.
линейно
зависимы и найти эту линейную зависимость.
( ,
, ,
,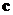 )=
)=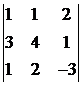 =0,
=0,
следовательно, векторы  ,
,  и
и 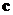 компланарны,
а значит, они линейно зависимы, т.е. существуют константы
компланарны,
а значит, они линейно зависимы, т.е. существуют константы 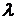 ,
, 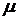 и
и 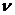 такие, что
такие, что 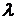
 +
+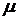
 +
+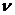
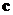 =0, т.е.
=0, т.е. 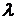 (
(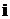 +
+ 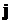 +
+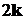 )+
)+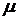 (3
(3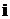 + 4
+ 4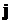 +
+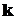 ) +
) + 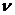 (
(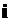 +2
+2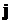 -3
-3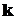 )=
)=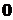 , откуда
следует: (
, откуда
следует: (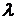 + 3
+ 3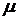 +
+ 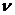 )
)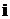 + (
+ (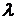 + 4
+ 4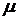 + 2
+ 2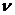 )
)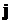 + (2
+ (2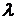 +
+ 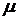 -3
-3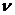 )
)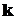 =
=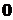 , т.к.
, т.к. 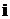 ,
, 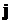 ,
, 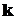 - базисные
векторы, то имеем такую систему для нахождения
- базисные
векторы, то имеем такую систему для нахождения 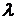 ,
, 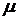 и
и 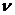 :
:
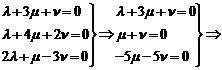
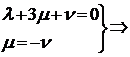
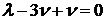
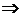
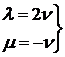
Здесь 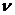 выступает в качестве параметра, и
данная система имеет бесчисленное множество решений. Подставим
выступает в качестве параметра, и
данная система имеет бесчисленное множество решений. Подставим 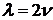 ,
, 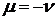 в указанную
выше линейную комбинацию:
в указанную
выше линейную комбинацию: 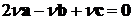 . Сократим
на
. Сократим
на 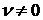 . Получим
искомую линейную зависимость
. Получим
искомую линейную зависимость 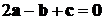 .
.
Заключение
Двойное векторное произведение играют
существенную роль и в других науках, таких, как физика, электротехника; в
действительности, они возникают везде, где есть необходимость количественного
(числового) описания явлений.
Список использованной литературы
1. Александров
П.С., Лекции по аналитической геометрии.- М.: Наука, 1968-912 с.
2. Беклемишев
Д.В., Курс аналитической геометрии и линейной алгебры. - М.: Наука, 1971 - 328
с.
. Гусак
А.А., Гусак Г.М., Бричникова Е.А. Справочник по высшей математике. - М.:
ТетраСистемс, 1999- 640 с.
. Мусхелишвили
Н.И., Курс аналитической геометрии. - М.: Высшая школа, 1967- 655 с.