Вычисление модулей гладкости
1. Вспомогательные леммы
Будем говорить, что 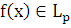
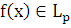 , если для
, если для 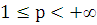
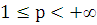 функция
функция 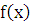
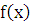 измерима на отрезке
измерима на отрезке 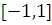
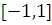 и
и 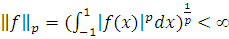
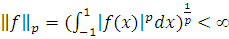 , а для
, а для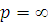
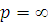 функция
функция 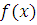
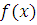 непрерывна на отрезке
непрерывна на отрезке 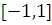
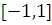 и
и 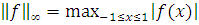
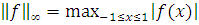 .
.
Будем также говорить,
что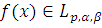
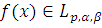 , если
, если 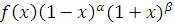
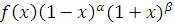 , причем
, причем 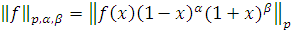
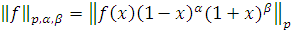 .
.
Для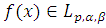
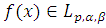 и данных чисел
и данных чисел 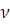
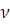 и
и 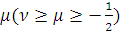
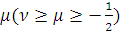 введем оператор
обобщенного сдвига
введем оператор
обобщенного сдвига 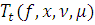
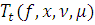 по правилу:
по правилу:
) для 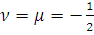
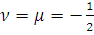 ,
, 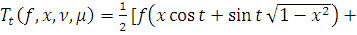
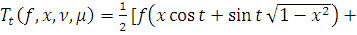
+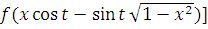
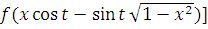
) для 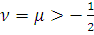
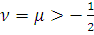 ,
, 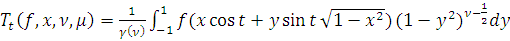
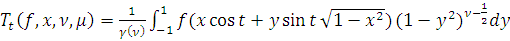
) для 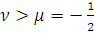
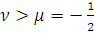 ,
, 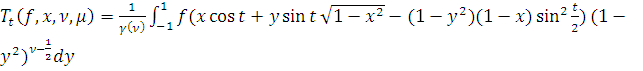
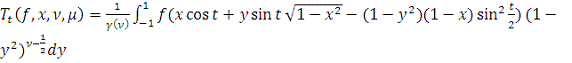
) для 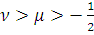
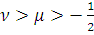 ,
, 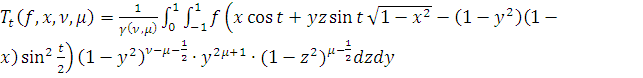
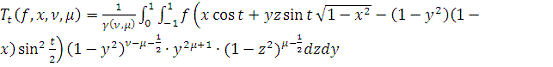 , где
, где
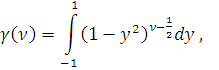
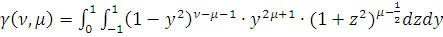
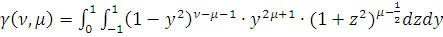 .
.
 . Пусть заданы числа
. Пусть заданы числа 
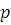 ,
, 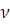
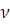 и
и 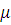
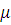 такие, что
такие, что 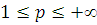
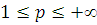 ,
, 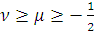
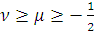 . Пусть числа
. Пусть числа 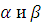
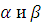 выбраны по правилу:
выбраны по правилу:
) если 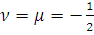
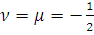 , то
, то 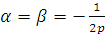
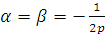 при
при 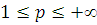
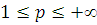
) если 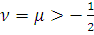
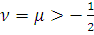 , то
, то 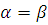
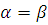 и
и 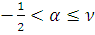
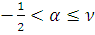 при
при 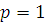
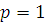 ,
, 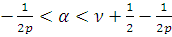
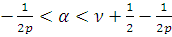 при
при 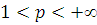
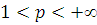 ,
, 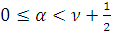
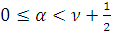 при
при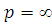
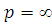
) если 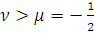
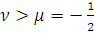 , то
, то 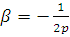
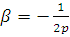 и
и 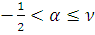
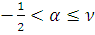 при
при 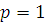
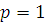 ,
, 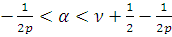
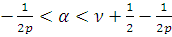 при
при 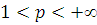
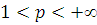 ,
, 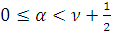
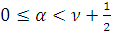 при
при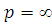
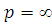
) если 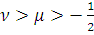
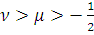 , то
, то 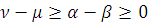
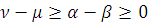 и
и 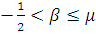
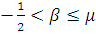 при
при 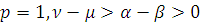
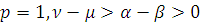 и
и 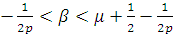
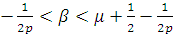 при
при 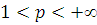
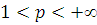 ,
, 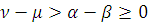
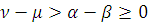 и
и 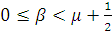
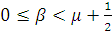 при
при 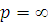
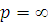 .
.
Тогда
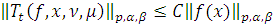
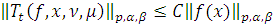 ,
,
где положительная
постоянная 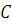
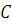 не зависит от
не зависит от 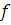
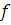 и
и 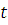
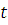 .
.
Лемма 2. Пусть 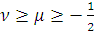
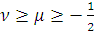 и
и 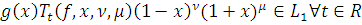
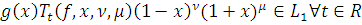 . Тогда
. Тогда 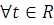
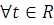
Доказательство. Пусть 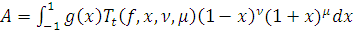
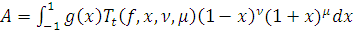
1) 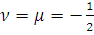
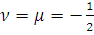
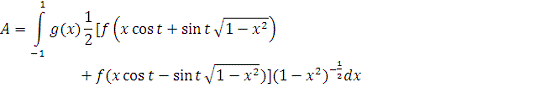
Сделаем замену
переменной 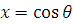
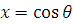 . Тогда
. Тогда
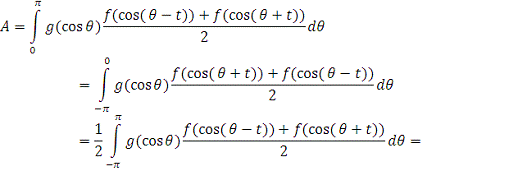
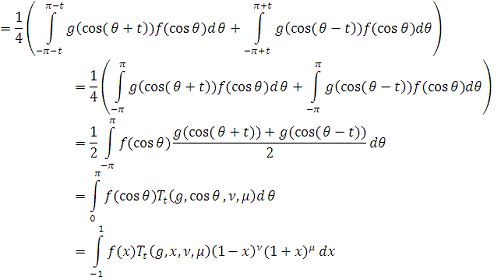
) 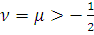
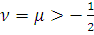 ,
,
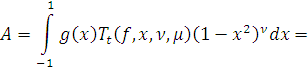
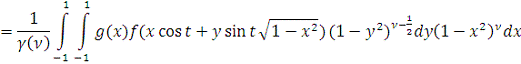
Сделаем замену переменных
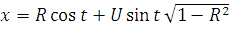
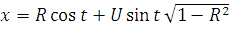 ,
, 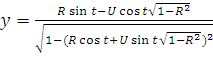
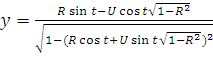
тогда 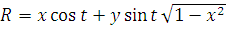
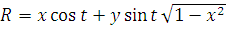
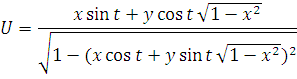
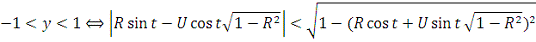
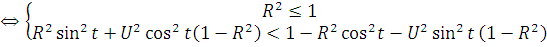
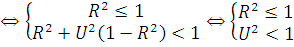
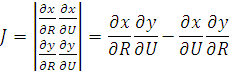
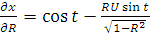
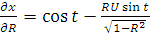 ,
, 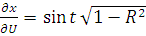
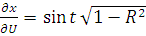
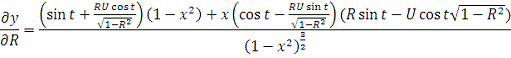
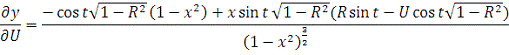
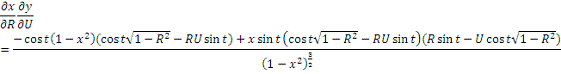
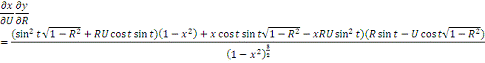
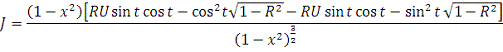
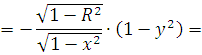
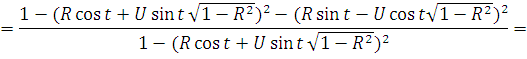
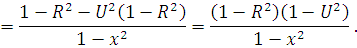
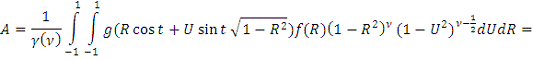
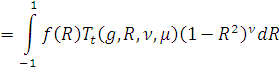
) 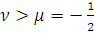
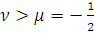 ,
,
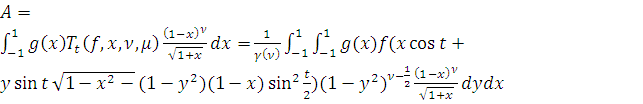
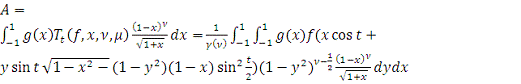
Сделаем замену
переменной 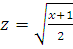
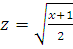
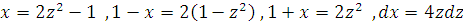
Тогда
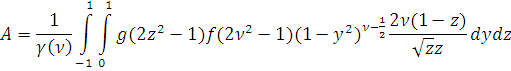
где 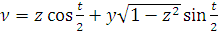
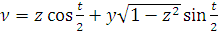
Сделаем еще замену
переменных

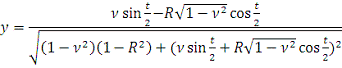
Тогда

 ,
, 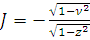
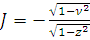
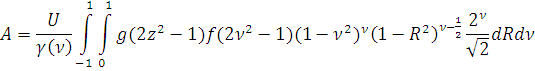
Далее замена переменной 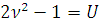
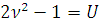
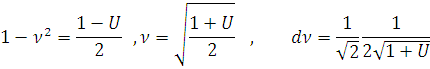
Тогда
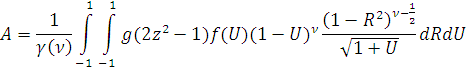
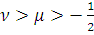
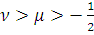 ,
, 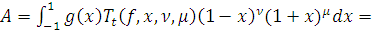
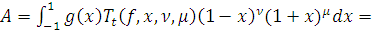
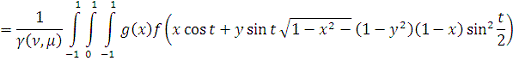
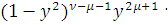
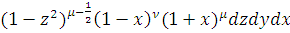
Сделав замену переменных
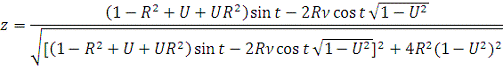
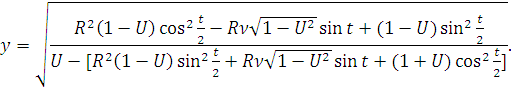
Получим
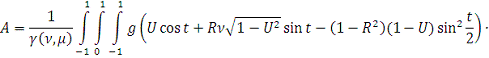
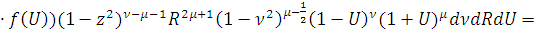
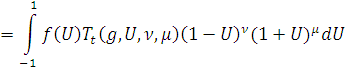
Лемма 2 доказана.
Лемма 3. Если функция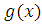
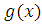 имеет абсолютно
непрерывную
имеет абсолютно
непрерывную 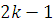
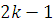 (
(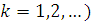
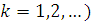 производную на каждом
отрезке
производную на каждом
отрезке 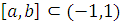
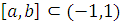 , тогда при
фиксированном
, тогда при
фиксированном 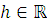
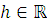 функция
функция 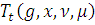
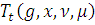 также имеет абсолютно
непрерывную
также имеет абсолютно
непрерывную 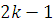
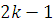 производную на каждом
отрезке
производную на каждом
отрезке 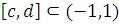
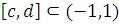
Доказательство. Пусть 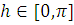
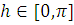 . Выберем произвольный
отрезок
. Выберем произвольный
отрезок 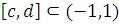
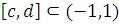 . На нем имеем:
. На нем имеем:
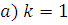
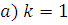 1)
1) 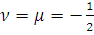
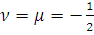
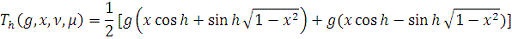
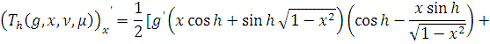
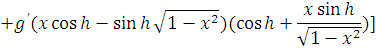
Функции 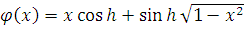
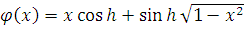 и
и 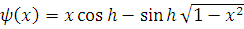
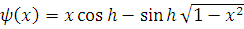 абсолютно непрерывны на
абсолютно непрерывны на
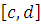
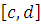 и так как
и так как 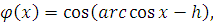
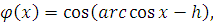 а
а 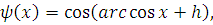
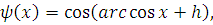 то в силу строгой
монотонности
то в силу строгой
монотонности 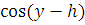
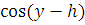 на
на 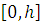
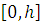 и
и 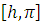
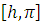 , строгой монотонности
, строгой монотонности 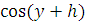
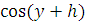 на
на 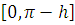
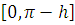 и
и 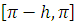
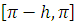 и строгой монотонности
и строгой монотонности 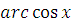
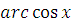 ,
, 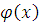
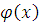 строго монотонна на
строго монотонна на 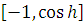
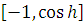 и
и 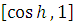
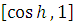 , а
, а 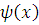
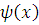 строго монотонна на
строго монотонна на 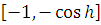
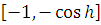 и
и 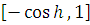
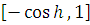 . В силу теоремы: пусть
абсолютно непрерывная функция
. В силу теоремы: пусть
абсолютно непрерывная функция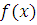
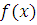 , заданная на отрезке
, заданная на отрезке 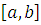
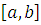 строго возрастает. Если
строго возрастает. Если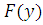
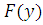 , абсолютно непрерывна
на
, абсолютно непрерывна
на 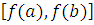
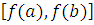 , то функция
, то функция 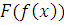
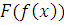 , абсолютно непрерывна
на
, абсолютно непрерывна
на 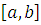
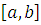 (если
(если 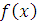
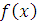 строго убывает
доказательство не меняется) функция
строго убывает
доказательство не меняется) функция
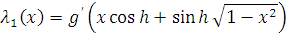
абсолютно непрерывна на
каждом из отрезков 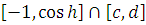
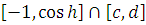 и
и 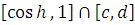
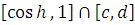 , а
, а
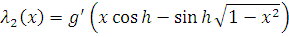
абсолютно непрерывна на 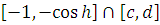
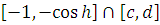 и
и 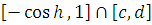
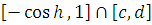 . А поскольку
. А поскольку 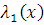
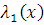 и
и 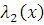
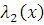 непрерывны на
непрерывны на 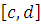
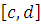 . Поскольку сумма,
разность, произведение и частное, если знаменатель не обращается в нуль,
абсолютно непрерывных функций абсолютно непрерывны, то
. Поскольку сумма,
разность, произведение и частное, если знаменатель не обращается в нуль,
абсолютно непрерывных функций абсолютно непрерывны, то 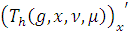
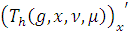 абсолютно непрерывна на
абсолютно непрерывна на
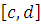
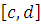 .
.
) 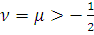
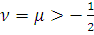
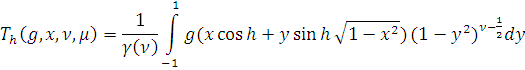
Пусть
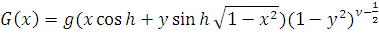
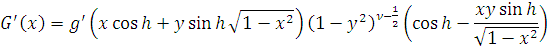
Как и в случае 1)
доказывается, что 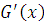
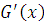 абсолютно непрерывна на
абсолютно непрерывна на
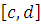
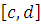 . Так как по теореме
Лагранжа о среднем
. Так как по теореме
Лагранжа о среднем
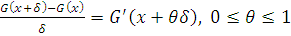
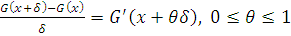 ,
,
то 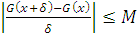
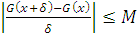 при любых
при любых 
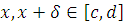 . Тогда по теореме
Лебега о предельном переходе под знаком интеграла при фиксированном
. Тогда по теореме
Лебега о предельном переходе под знаком интеграла при фиксированном 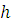
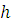 на отрезке
на отрезке 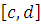
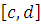 существует конечная
производная
существует конечная
производная
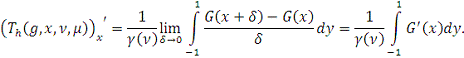
В силу абсолютной
непрерывности 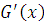
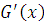 на
на 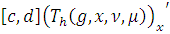
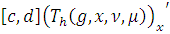 также абсолютно
непрерывна на
также абсолютно
непрерывна на 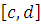
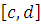 . 3) и 4) разбираются
также как и 2).
. 3) и 4) разбираются
также как и 2).
б)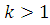
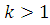 1)
1) 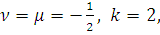
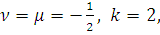
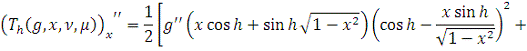
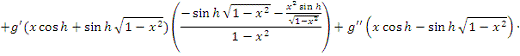
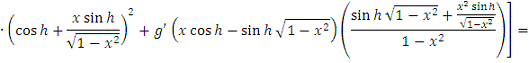
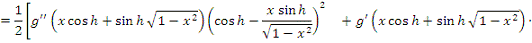
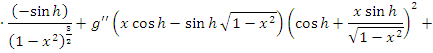
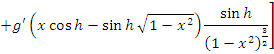
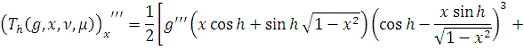
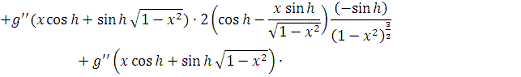
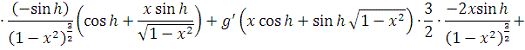
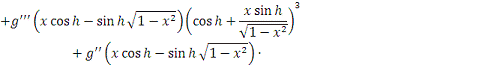
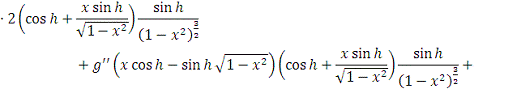
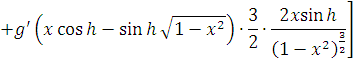
В силу абсолютной
непрерывности 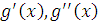
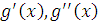 и
и 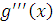
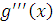 на каждом отрезке
на каждом отрезке 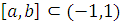
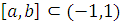 рассуждая как и в случае
а) 1) получаем, что
рассуждая как и в случае
а) 1) получаем, что 
 абсолютно непрерывна на
абсолютно непрерывна на
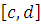
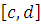
) 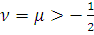
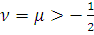 ,
, 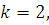
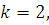
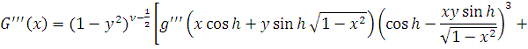
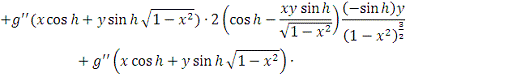

Таким образом, 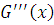
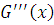 также абсолютно
непрерывна на
также абсолютно
непрерывна на 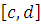
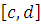 и воспользовавшись как
и в случае а) 2) теоремой Лебега о предельном переходе под знаком интеграла
получим, что
и воспользовавшись как
и в случае а) 2) теоремой Лебега о предельном переходе под знаком интеграла
получим, что 
 абсолютно непрерывна на
абсолютно непрерывна на
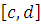
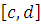 и в этом случае.
и в этом случае.
) и 4)
разбираются также как и 2). Для произвольного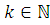
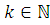 доказывается индукцией
по
доказывается индукцией
по 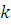
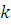 .
.
Через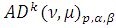
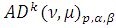 обозначим множество
таких функций
обозначим множество
таких функций 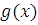
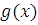 , что
, что 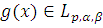
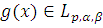 ,
, 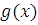
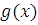 имеет абсолютно
непрерывную
имеет абсолютно
непрерывную 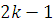
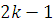 производную на каждом
отрезке
производную на каждом
отрезке 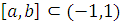
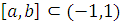 и
и 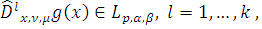
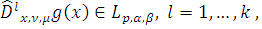 где
где
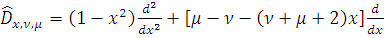
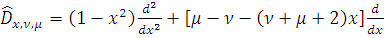
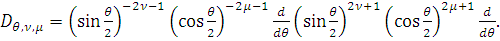
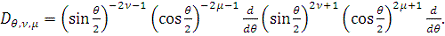
Тогда 
 . Действительно,
. Действительно,
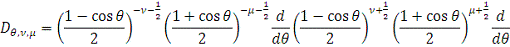
Сделав замену переменной
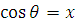
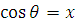 имеем
имеем
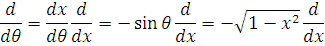

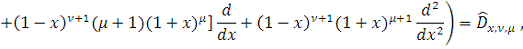
где 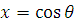
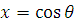 .
.
Лемма 4. Пусть 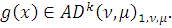
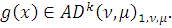 Тогда
Тогда
) для почти всех 
 и почти всех
и почти всех 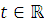
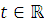 справедливы равенства:
справедливы равенства:
а) 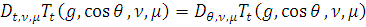
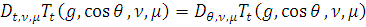
б)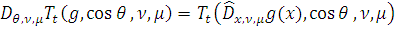
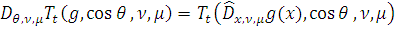
) для почти всех 
 и для любых
и для любых 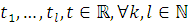
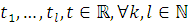
а) 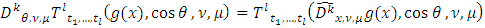
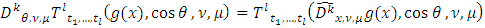 ,
,
где
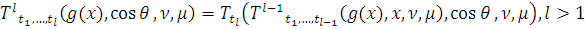
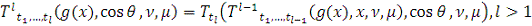
б) 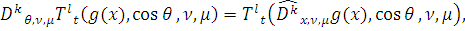
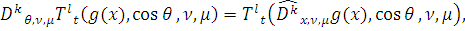
) если 
 , то для почти всех
, то для почти всех 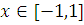
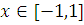 и для любых
и для любых 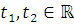
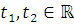
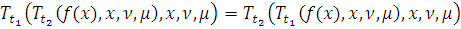
Лемма 9. 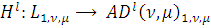
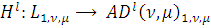 и
и
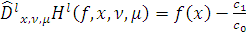
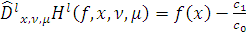 (4)
(4)
Доказательство: Из Леммы
8 следует, что 
 . Далее применим
индукцию по
. Далее применим
индукцию по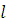
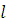 .
.
) 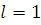
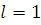 . Ясно, что функция
. Ясно, что функция
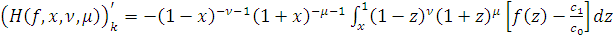
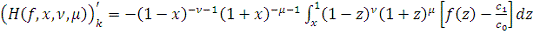
абсолютно непрерывна на
каждом отрезке 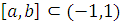
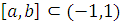 и поскольку
и поскольку
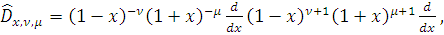
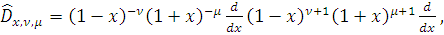 то
то
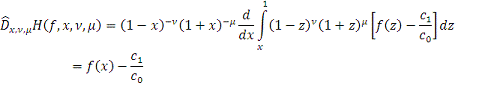
для почти всех 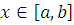
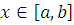 .
.
) Предположим 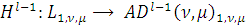
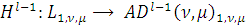 и
и

 . Тогда имеем:
. Тогда имеем:
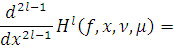
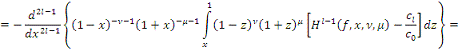
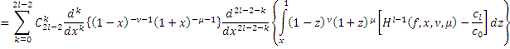
где 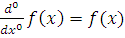
 .
.
Так как
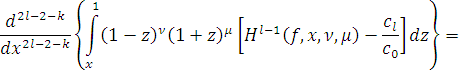
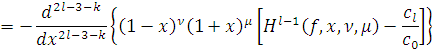
и по предположению 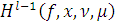
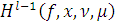 имеет
имеет 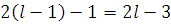
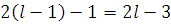 производную, абсолютно
непрерывную на каждом
производную, абсолютно
непрерывную на каждом 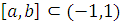
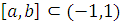 , то и
, то и 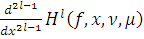
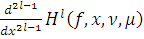 абсолютно непрерывна на
любом отрезке
абсолютно непрерывна на
любом отрезке 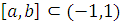
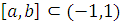 . На основании 1) и
предположения индукции имеем
. На основании 1) и
предположения индукции имеем

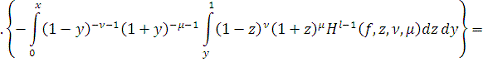
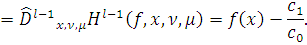
Лемма 9 доказана.
Для 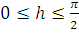
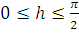 рассмотрим оператор
рассмотрим оператор
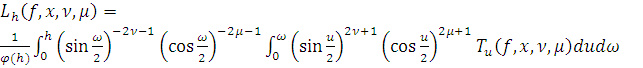
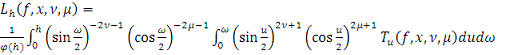 ,
,
где 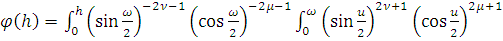
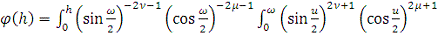
Пусть 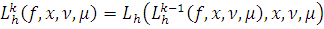
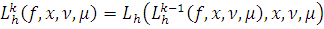 и
и
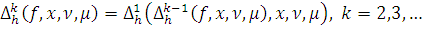
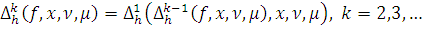
Лемма 10. Пусть 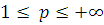
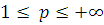 ,
, 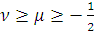
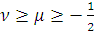 и числа
и числа 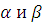
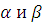 выбраны по правилу
Леммы 7. Тогда для
выбраны по правилу
Леммы 7. Тогда для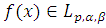
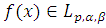 и
и 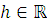
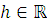 выполнено равенство:
выполнено равенство:
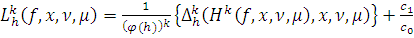
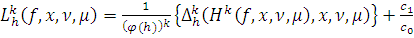 (5)
(5)
Доказательство: Применим
индукцию по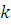
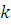
) 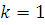
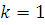 . Из равенства (4) Леммы
9 при
. Из равенства (4) Леммы
9 при 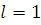
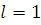 следует, что
следует, что
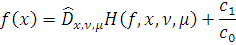
И поскольку 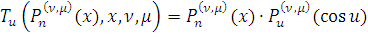
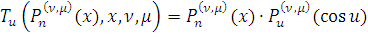 , то для
, то для 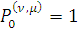
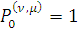 имеем
имеем 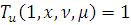
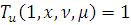 .
.
Поэтому
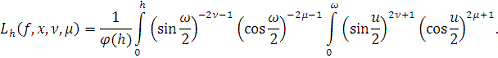
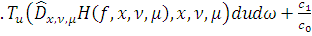
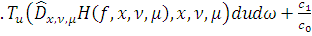 .
.
По Лемме 9 имеем, что 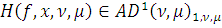
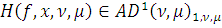 . Применив Лемму 6,
получим
. Применив Лемму 6,
получим
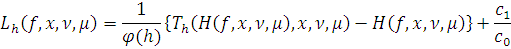
2) Предположим
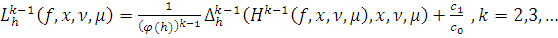
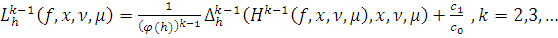
Так же как и при
доказательстве равенства (4) при 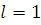
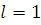 получаем, что
получаем, что
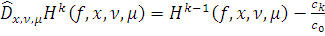
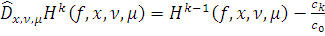 (6)
(6)
Из Лемм 1, 3 и 9
следует, что 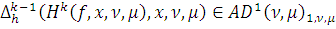
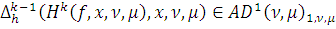 . Поэтому пользуясь
предположением индукции, Леммой 4. 2) б) и Леммой 6. 1) имеем:
. Поэтому пользуясь
предположением индукции, Леммой 4. 2) б) и Леммой 6. 1) имеем:
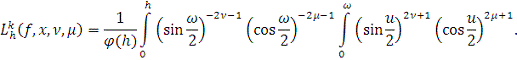
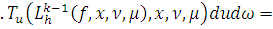
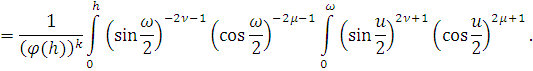
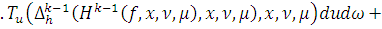
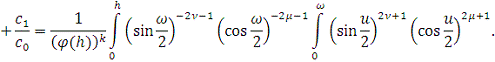
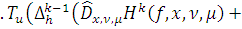
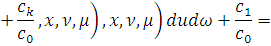
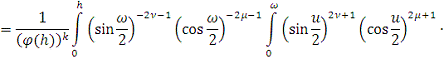
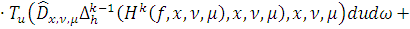
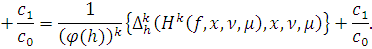
На основании индукции
Лемма 10 доказана.
Лемма 11. Пусть 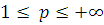
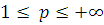 ,
, 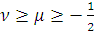
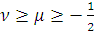 ,
, 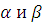
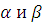 выбраны по правилу
Леммы 7. Тогда, если
выбраны по правилу
Леммы 7. Тогда, если 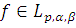
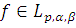 , то
, то
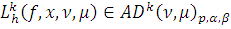
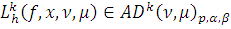 и
и
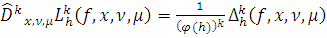
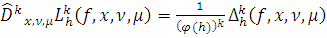 (7)
(7)
Доказательство: То, что 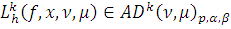
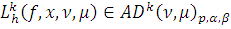 следует из Лемм 10, 9,
1 и 3. Из равенства (5), Леммы 4. 2) б) и равенства (4) следует, что
следует из Лемм 10, 9,
1 и 3. Из равенства (5), Леммы 4. 2) б) и равенства (4) следует, что
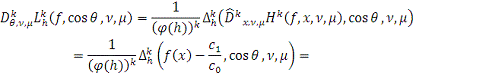
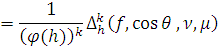
Лемма 11 доказана.
2. Теоремы Джексона для
к-го обобщенного модуля гладкости
Для 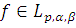
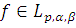 и данных чисел
и данных чисел 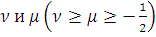
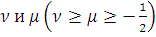 введем - функционал по
формуле:
введем - функционал по
формуле:
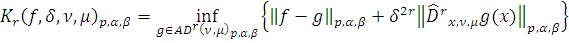
Теорема 1. Пусть заданы
числа 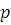
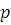 ,
, 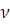
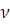 и
и 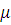
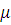 такие, что
такие, что 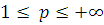
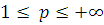 ,
, 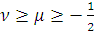
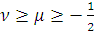 . Пусть числа
. Пусть числа 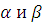
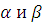 выбраны по правилу:
выбраны по правилу:
) если 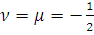
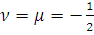 , то
, то 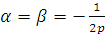
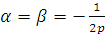 при
при 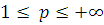
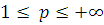
) если 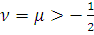
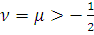 , то
, то 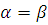
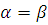 и
и 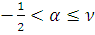
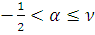 при
при 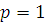
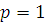 ,
, 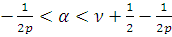
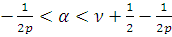 при
при 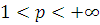
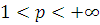 ,
, 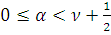
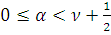 при
при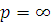
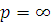
Тогда для 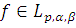
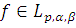 справедливы
неравенства:
справедливы
неравенства:
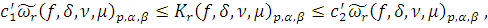
где положительные
постоянные 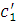
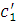 и
и 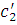
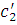 не зависят от
не зависят от 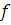
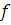 и
и 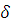
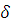 .
.
Доказательство:
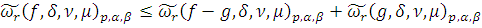
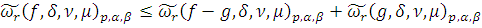
для любой функции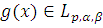
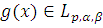 . По Лемме 1
. По Лемме 1 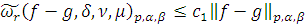
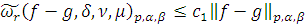 , где положительная
постоянная
, где положительная
постоянная 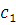
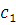 не зависит от
не зависит от 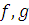
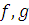 и
и 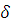
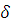 . Если
. Если 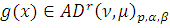
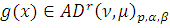 , то в силу Леммы 7
, то в силу Леммы 7
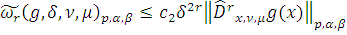
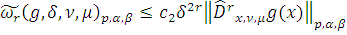 ,
,
где положительная
постоянная 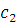
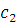 не зависит от
не зависит от 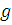
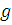 и
и 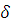
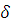 .
.
Поэтому 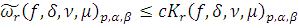
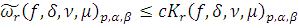 . Для доказательства
правого неравенства рассмотрим функцию
. Для доказательства
правого неравенства рассмотрим функцию

где 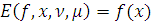
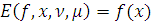 .
.
Так как 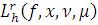
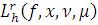 имеет
имеет 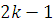
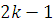 абсолютно непрерывную
производную на каждом
абсолютно непрерывную
производную на каждом 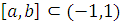
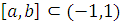 , то применяя Теорему
Лебега о предельном переходе под знаком интеграла (так же как и при
доказательстве случая 2) Леммы 3), Лемму 4. 1) б), обобщенное неравенство
Минковского и Лемму 1 имеем для
, то применяя Теорему
Лебега о предельном переходе под знаком интеграла (так же как и при
доказательстве случая 2) Леммы 3), Лемму 4. 1) б), обобщенное неравенство
Минковского и Лемму 1 имеем для 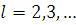
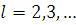 и при
и при 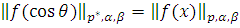
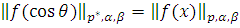
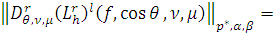
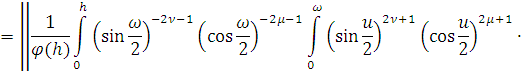

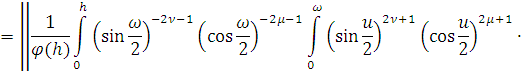
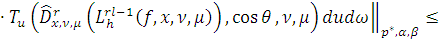
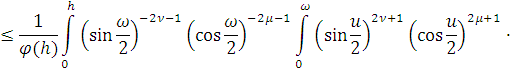
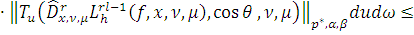
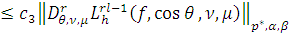
Так как 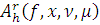
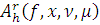 представляет собой
сумму произведений
представляет собой
сумму произведений 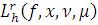
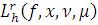 , то
, то
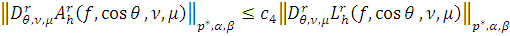
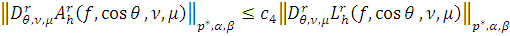
и применяя равенство (7)
Леммы 11 имеем
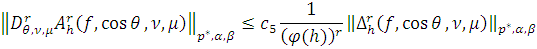
Поскольку для 
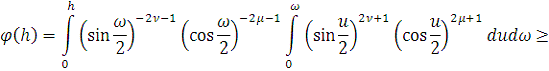
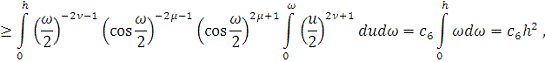
где положительные
постоянные
 и
и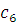
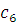 не зависят от
не зависят от 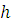
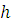 , то
, то
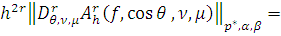
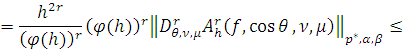
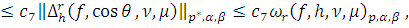
где 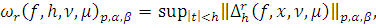
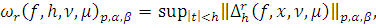
с другой стороны
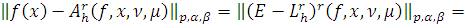

Так как
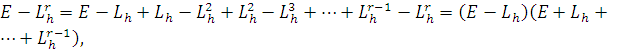

то учитывая, что
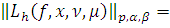
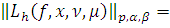
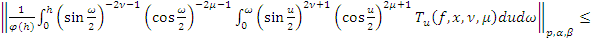
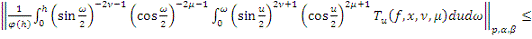
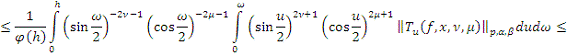
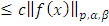
имеем:
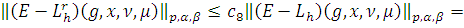
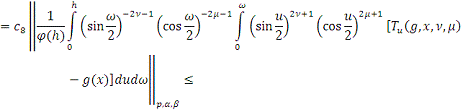
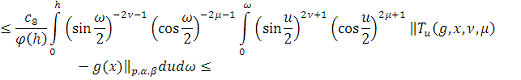
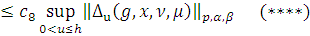
Из Леммы 4. 3) получаем
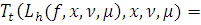
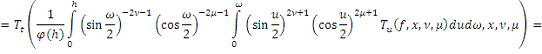
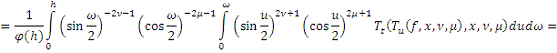
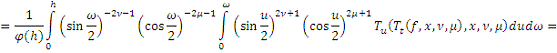
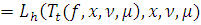
Поэтому из равенства (8)
и неравенства (****) следует, что
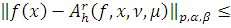
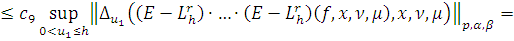
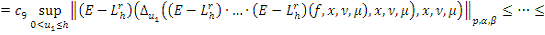
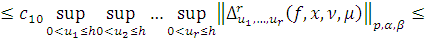
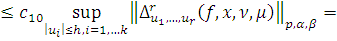
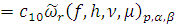
Таким образом для 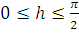
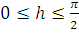
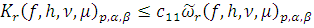
Пусть
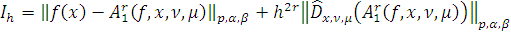
Тогда 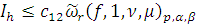
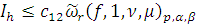 , а для
, а для 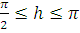
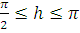 имеем:
имеем:
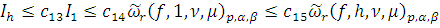
Итак для любого 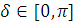
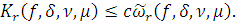
Теорема 1 доказана.
Пусть заданы натуральные
числа 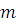
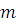 и
и 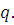
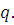 Известно, что функция
Известно, что функция 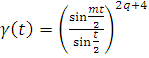
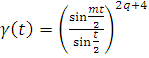 есть четный
тригонометрический полином порядка
есть четный
тригонометрический полином порядка 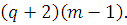
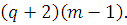 Функция
Функция 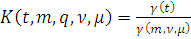
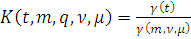 , где
, где
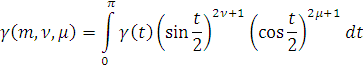
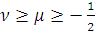
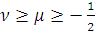 обладает для
обладает для 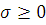
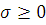 и
и 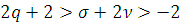
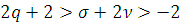 свойствами:
свойствами:
) 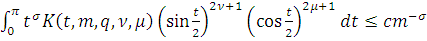
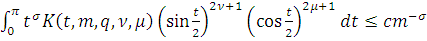 ,
,
где положительная
постоянная не зависит от 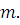
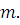
Лемма 12. Если 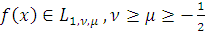
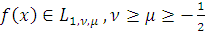 , то
, то
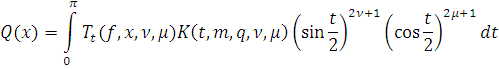
есть алгебраический
многочлен степени не выше, чем 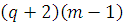
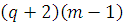 .
.
Обозначим через 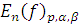
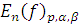 наилучшее приближение
функции
наилучшее приближение
функции 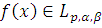
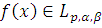 при помощи
алгебраических многочленов
при помощи
алгебраических многочленов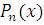
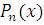 степени не выше, чем
степени не выше, чем 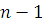
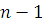 , в метрике
, в метрике 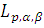
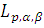 , то есть
, то есть
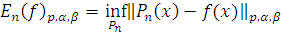
Лемма 13. Пусть 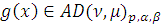
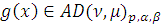 ,
, 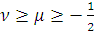
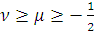 и
и 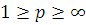
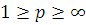 .
.
Тогда
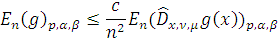
Доказательство: Пусть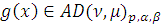
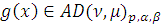 . Положим
. Положим
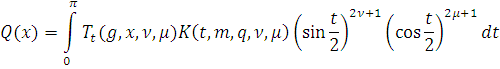
Для фиксированного 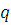
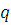 подберем
подберем 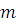
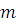 так, что
так, что 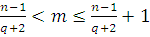
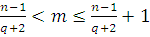 . По Лемме 12
. По Лемме 12 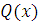
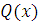 есть алгебраический
многочлен степени не выше, чем
есть алгебраический
многочлен степени не выше, чем 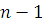
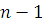 . Используя обобщенное
неравенство Минковского, неравенство (3) при
. Используя обобщенное
неравенство Минковского, неравенство (3) при 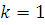
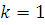 и свойство 2)
и свойство 2) 
 имеем:
имеем:
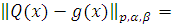
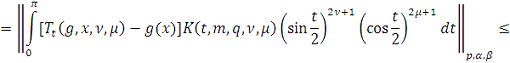
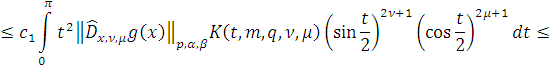
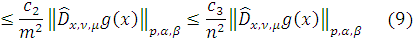
Пусть
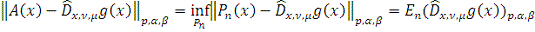
Поскольку любой
многочлен можно представить в виде линейной комбинации многочленов Якоби, то
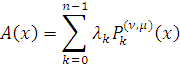
Положим

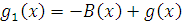
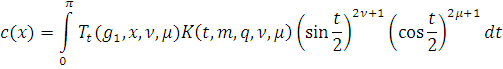
Тогда из (9) следует
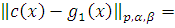
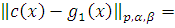
=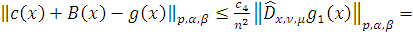
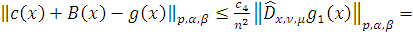
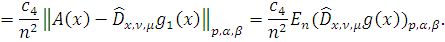
поскольку
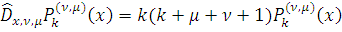
Таким образом
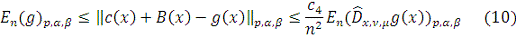
Лемма 13 доказана.
Следствие. Пусть 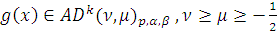
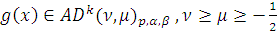 и
и 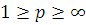
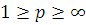 . Тогда
. Тогда
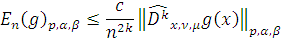
Доказательство: Применяя
неравенство (10) 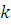
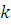 раз получаем
раз получаем
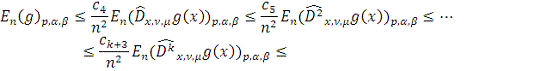
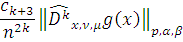
Следствие доказано.
Лемма 14. Пусть 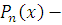
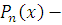 алгебраический полином
степени не выше, чем
алгебраический полином
степени не выше, чем 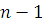
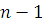 ,
, 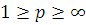
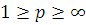 ,
, 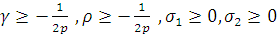
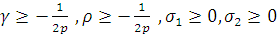 . Тогда справедливы
неравенства:
. Тогда справедливы
неравенства:
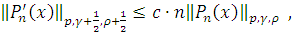
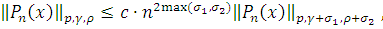
где положительная
постоянная 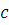
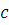 не зависит от
не зависит от 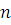
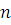 .
.
Теорема 2. Пусть даны
числа 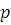
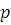 ,
, 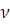
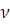 и
и 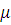
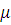 такие, что
такие, что 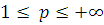
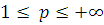 ,
, 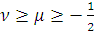
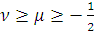 . Пусть числа
. Пусть числа 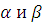
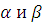 выбраны по правилу
Теоремы 1
выбраны по правилу
Теоремы 1
 Тогда для
Тогда для 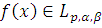
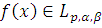 справедливы неравенства:
справедливы неравенства:

где положительные
постоянные 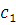
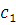 и
и 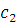
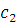 не зависят от
не зависят от 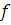
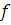 и
и 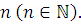
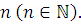
Доказательство: Пусть 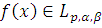
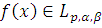 . Для любой функции
. Для любой функции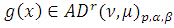
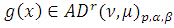 можем записать
можем записать
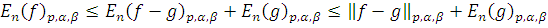
По следствию
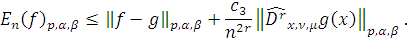
Переходя к точной нижней
грани по всем 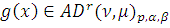
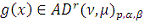 , получим
, получим

и по теореме 1 

Таким образом первое
неравенство теоремы доказано. Докажем второе.
Пусть 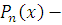
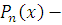 алгебраический
многочлен наилучшего приближения для
алгебраический
многочлен наилучшего приближения для 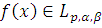
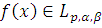 степени не выше, чем
степени не выше, чем 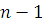
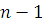 . Пусть
. Пусть 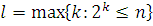
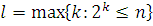 . Из теоремы 1 следует,
что
. Из теоремы 1 следует,
что
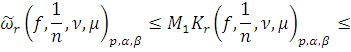
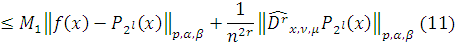
Так как 
 то используя равенство
типа Маркова
то используя равенство
типа Маркова

где 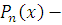
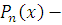 многочлен степени
многочлен степени 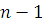
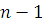 , которое сразу следует
из Леммы 14, получаем:
, которое сразу следует
из Леммы 14, получаем:
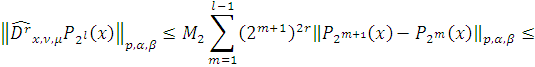
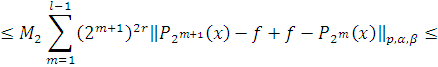
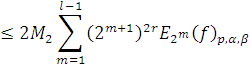
Отсюда с учетом (11)
имеем
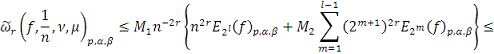
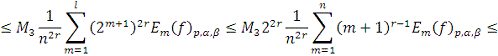
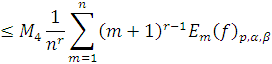
Теорема 2 доказана.
. Вычисление модулей
гладкости для некоторых функций
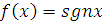
По определению
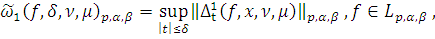
где
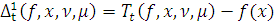
Пусть 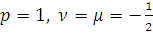
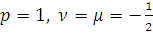 . Тогда обобщенный
оператор обобщенного сдвига
. Тогда обобщенный
оператор обобщенного сдвига 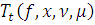
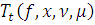 имеет вид:
имеет вид:
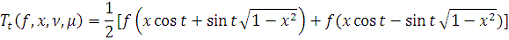
Т.к. 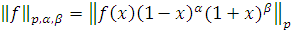
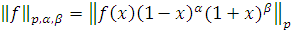 , то окончательно
получаем:
, то окончательно
получаем:
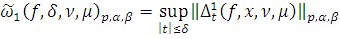
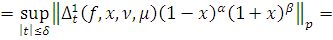

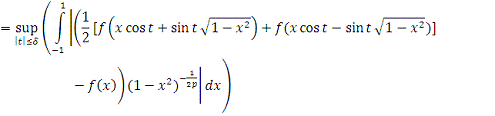
Сделаем замену
переменных 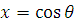
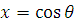 . Тогда
. Тогда
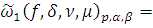
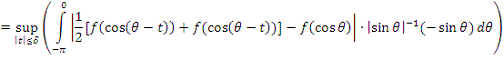
Т.к. 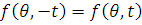
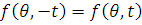 , то
, то 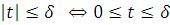
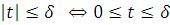 . Тогда
. Тогда
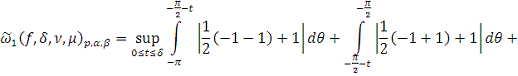
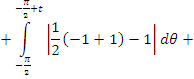
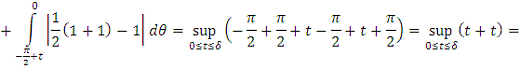
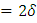
2. Найти модуль гладкости 2-го
порядка для функции
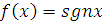
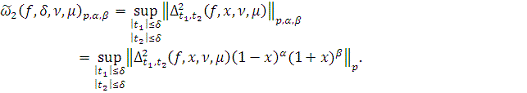
Найдем 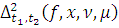
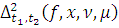
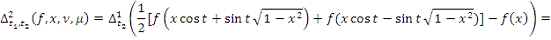
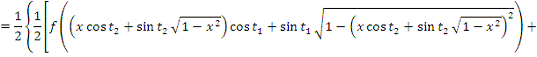
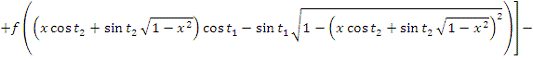
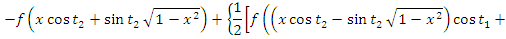
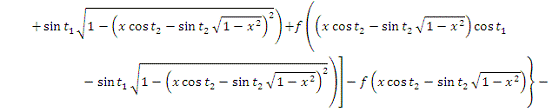
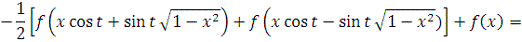
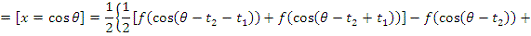
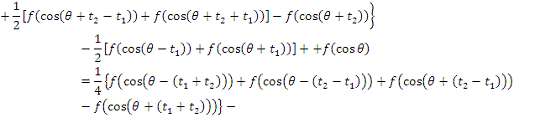
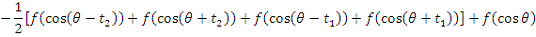
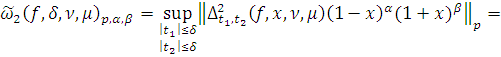
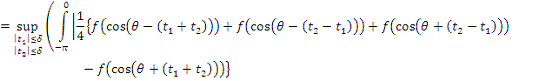
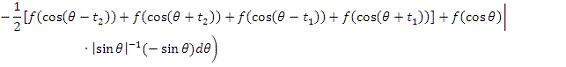
Поскольку 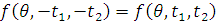
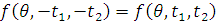 , то
, то 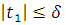
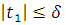 и
и 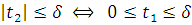
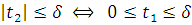 и
и 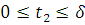
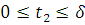 и достаточно
рассмотреть случай
и достаточно
рассмотреть случай 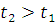
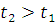 . Тогда
. Тогда
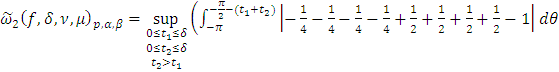
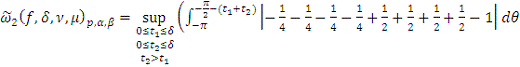 +
+
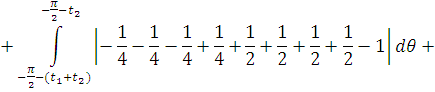
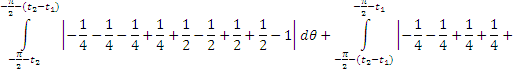
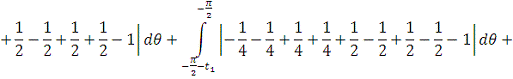
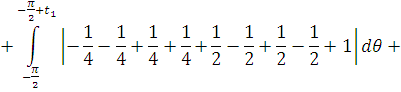
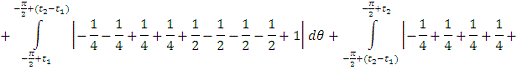
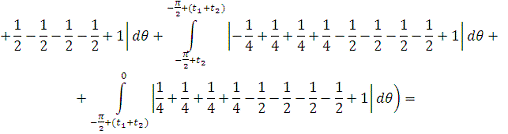
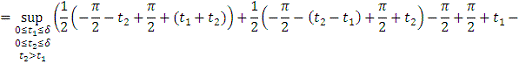
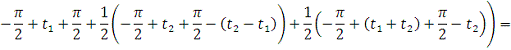
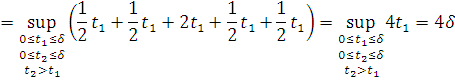
Заключение
Для 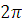
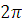 - периодических функций
хорошо известны прямая и обратная теоремы теории приближений, которые можно
записать в виде неравенств:
- периодических функций
хорошо известны прямая и обратная теоремы теории приближений, которые можно
записать в виде неравенств:
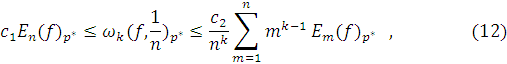
где 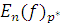
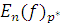 - наилучшее приближение
непрерывной
- наилучшее приближение
непрерывной 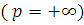
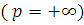 или интегрируемой в
или интегрируемой в 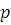
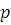 - й степени
- й степени 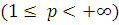
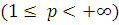 функции
функции 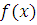
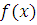 при помощи
тригонометрических полиномов порядка не выше, чем
при помощи
тригонометрических полиномов порядка не выше, чем 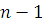
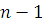 в метрике
в метрике 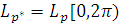
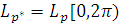 ,
, 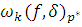
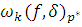 -
- 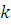
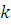 - й модуль гладкости
- й модуль гладкости 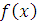
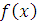 в метрике
в метрике 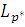
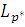 и положительные
постоянные
и положительные
постоянные 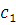
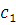 и
и 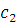
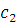 не зависят от
не зависят от 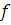
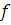 и
и 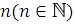
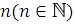 .
.
При рассмотрении
непериодических функций уже не удается получить такие же связи, как неравенства
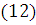
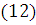 , между модулями
гладкости функции и ее наилучшими приближениями алгебраическими многочленами. В
данной дипломной работе были получены аналоги неравенств
, между модулями
гладкости функции и ее наилучшими приближениями алгебраическими многочленами. В
данной дипломной работе были получены аналоги неравенств 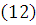
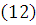 , где обычный модуль
гладкости заменен обобщенным модулем гладкости. Такие обобщенные модули
гладкости были определены при помощи операторов обобщенного сдвига. В ходе
выполнения дипломной работы были рассмотрены вспомогательные леммы и с помощью
них доказаны аналоги неравенств
, где обычный модуль
гладкости заменен обобщенным модулем гладкости. Такие обобщенные модули
гладкости были определены при помощи операторов обобщенного сдвига. В ходе
выполнения дипломной работы были рассмотрены вспомогательные леммы и с помощью
них доказаны аналоги неравенств 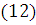
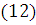 для обобщенных модулей
гладкости.
для обобщенных модулей
гладкости.
лемма гладкость полином
модуль