Проведение исследовательской работы со статистическими данными
ВВЕДЕНИЕ
Развитие статистики сходно с развитием языка и счета. Эта наука имеет
древние корни. Она зародилась как результат обобщения уже достаточно развитой
статистической практики, вызванной потребностями развития общества. Например, в
Китае более чем за две тысячи лет до нашей эры производились исчисления
населения по полу и возрасту, а также собирались сведения о состоянии
промышленности и сельского хозяйства. Упоминания о статистических обследованиях
встречаются и в библейские времена. В Древнем Риме велась статистика
численности населения и имущественного положения граждан.
Однако если собирание статистических данных началось в самой глубокой
древности, то их обработка и анализ, т.е. зарождение статистики-науки,
относятся к более позднему периоду - второй половине XVII в. В это время и было введено в научный обиход само
слово «статистика».
Не зависимо от уровня и стадии экономического развития, характера
политической системы, статистика на протяжении сотен лет своего существования
всегда выступала как необходимый и эффективный инструмент государственного
управления и одновременно, как наука, исследующая количественную сторону
массовых явлений. Выполняя самые разнообразные функции сбора, систематизации и
анализа сведений, характеризующих экономическое развитие общества, она всегда
играла главную роль поставщика фактов для управленческих,
научно-исследовательских и прикладных практических нужд различного рода
структур, организаций и населения.
Дать определение статистики как науки пытались многие философы, математики,
экономисты, социологи, государственные деятели и сами статистики. Сначала ее
определяли как - государствоведение (описание достопримечатель-ностей
государств). Но статистика постепенно отходила от описания
достопримечательностей потому, что с развитием знаний вопросами
государствоведения стали заниматься многие науки.
В настоящее время, учитывая все закономерности развития, можно
сформулировать определение статистики как науки. Статистика - общественная
наука, которая изучает количественную сторону качественно определенных массовых
социально-экономических явлений и процессов, их структуру и распределение,
размещение в пространстве, движение во времени, выявляя действующие
количественные зависимости, тенденции и закономерности, причем в конкретных
условиях места и времени.
Особенность статистики как науки состоит в том, что в ней исследуются не
отдельные факты, а массовые социально-экономические явления и процессы,
выступающие как множества отдельных фактов, обладающих как индивидуальными, так
и общими признаками.
Среди задач статистики особое внимание уделяется совершенствованию
экономического анализа и повышению качества статистической информации,
упорядочиванию отчетности и обеспечению достоверности, расширению гласности и
так далее.
Задача статистического исследования состоит в получении обобщающих
показателей и выявлении закономерностей общественной жизни в конкретных
условиях места и времени, которым проявляются лишь в большой массе явлений
через преодоление свойственной единичным элементам случайности. Общественная
жизнь столь сложна и многообразна, что почти всегда можно подобрать факты,
примеры как подтверждающие, так и опровергающие одно и то же положение. Чтобы
охарактеризовать массовое или общественное или процесс в целом, необходимо рассмотреть
всю или большую массу относящихся к ним отдельных явлений или процессов.
Целью данной курсовой работы является проведение исследовательской работы
со статистическими данными, сбор информации, систематизация и анализ сведений,
характеризующих экономическое и социальное развитие выбранного для описания
региона (Калужской области).
Задачи курсовой работы:
ознакомиться с этапами составления организационного плана наблюдения;
научиться графически отображать и анализировать получаемые данные;
освоить порядок составления интервальных и дискретных вариационных рядов,
порядок оценки однородности и характера распределения совокупности;
провести анализ и выявить взаимосвязи между признаками;
рассчитать экономические индексы.
Данная работа будет служить не только обобщением по курсу теории
статистики и практическим отчетом по изученному материалу, но и фундаментом для
дальнейшего изучения экономической статистики, социально-демографической
статистики, а так же многих отраслевых статистических дисциплин.
1.
ИСХОДНЫЕ ДАННЫЕ ДЛЯ СТАТИСТИЧЕСКИХ РАСЧЕТОВ
Статистическое исследование социально-экономического положения Калужской
области. Климат Калужской области умеренно-континентальный с резко выраженными
сезонами года: умеренно жарким и влажным Летом и умеренно холодной зимой с
устойчивым снежным покровом. Площадь территории - 29,9 тыс. км2. Калужская
область расположена в центральной полосе европейской части России, в 180 км к
западу от Москвы. Административный центр области - город Калуга. Численность
населения области - 1002,9 тыс. человек (2009), плотность населения 33,5 чел/км²
(2009), удельный вес
городского населения: 76,1 % (2007)
Экономика области в 2006 году. В структуре валового национального
продукта в 2005 г. основными видами экономической деятельности являлись: добыча
полезных ископаемых; производство и распределение электроэнергии, газа и воды;
сельское хозяйство, охота и лесное хозяйство; обрабатывающие производства.
Индекс промышленного производства по сравнению с 2005 г. составил 106,5%,
по видам деятельности «Добыча полезных ископаемых» - 116,8%, «Обрабатывающие
производства» - 113,7%, «Производство и распределение электроэнергии, газа и
воды» - 90,6%.
Оборот розничной торговли составил 48,8 млрд. руб., или 123,6% (в
сопоставимых ценах) к 2005 г.
В объеме инвестиций в основной капитал 37,0% заняли собственные средства,
63,0% - привлеченные средства.
Для исследования социально-экономических показателей по Калужской области
были взяты следующие данные.
Таблица 1.1
Демографические показатели
|
Показатели
|
Периоды
|
|
2004
|
2005
|
2006
|
2007
|
2008
|
2009
|
2010
|
2011
|
2012
|
|
Численность населения (на
конец года), тыс. человек
|
1328,9
|
1325,4
|
1266,4
|
1248,6
|
1231,1
|
1214,5
|
1199,1
|
1183,9
|
1170,7
|
|
Мужчины
|
607,9
|
609,9
|
580,9
|
571,6
|
562,3
|
553,9
|
545,9
|
537,9
|
531,1
|
|
Женщины
|
721,0
|
715,5
|
685,5
|
677,0
|
668,8
|
660,6
|
653,2
|
646,0
|
639,6
|
|
Население в трудоспособном
возрасте, тыс. человек
|
713,7
|
713,8
|
719,7
|
716,9
|
717,8
|
719,9
|
719,3
|
718,3
|
714,2
|
|
Число родившихся на 1000
человек населения
|
11,9
|
8,6
|
8,2
|
8,4
|
8,5
|
8,8
|
9,0
|
8,6
|
9,0
|
|
Число умерших на 1000 человек
населения
|
13,9
|
16,9
|
18,6
|
18,7
|
19,3
|
19,7
|
19,4
|
19,7
|
19,1
|
|
Естественный прирост,
убыль(-) на 1000 человек населения
|
-2,0
|
-8,3
|
-10,4
|
-10,3
|
-10,8
|
-10,9
|
-10,4
|
-11,1
|
-10,1
|
|
Ожидаемая продолжительность
жизни всего населения при рождении, число лет
|
69,01
|
66,04
|
65,32
|
65,51
|
64,89
|
65,01
|
64,95
|
64,99
|
66,06
|
|
Мужчины
|
63,01
|
59,85
|
58,87
|
58,90
|
58,15
|
58,53
|
58,11
|
57,98
|
59,84
|
|
Женщины
|
74,78
|
72,76
|
72,61
|
72,99
|
72,65
|
73,40
|
72,76
|
73,09
|
73,21
|
Таблица 1.2
Показатели труда
|
Показатели
|
Периоды
|
|
2004
|
2005
|
2006
|
2007
|
2008
|
2009
|
2010
|
2011
|
2012
|
|
Среднегодовая численность
занятых в экономике, тыс.человек
|
681,3
|
593,9
|
616,6
|
606,4
|
607,9
|
591,6
|
587,8
|
600.4
|
594,3
|
|
Численность работников,
занятых в органах государственной власти и местного самоуправления,
тыс.человек
|
|
11,5
|
12,8
|
12,4
|
13,7
|
14,1
|
14,3
|
15,5
|
15,9
|
|
Численность безработных,
тыс.человек
|
|
35,4
|
66,5
|
64,1
|
43,8
|
49,6
|
44,2
|
43,00
|
43,2
|
|
Уровень безработицы,
процентов
|
|
6,00
|
10,5
|
10,5
|
7,1
|
8,5
|
7,5
|
7,1
|
7,3
|
|
Численность не занятых
трудовой деятельностью граждан, зарегистрированных в органах государственной
службы занятости (на конец года), тыс.человек
|
|
9,4
|
6,8
|
7,2
|
10,1
|
10,1
|
10,9
|
9,3
|
8,2
|
|
из них признанных
безработными
|
|
9,0
|
6,6
|
7,0
|
10,1
|
10,0
|
10,9
|
9,2
|
8,2
|
Таблица 1.3
Показатели уровня жизни населения
|
Показатели
|
Периоды
|
|
2004
|
2005
|
2006
|
2007
|
2008
|
2009
|
2010
|
2011
|
2012
|
|
Среднедушевые денежные
доходы (в месяц), руб. (1990, 1995 гг. - тыс.руб.)
|
0,188
|
313,4
|
1464,9
|
1979,9
|
2698,5
|
3371,4
|
4233,0
|
5196,8
|
6706,9
|
|
Среднемесячная номинальная
начисленная заработная плата работников организаций, руб. (1990, 1995 гг. - тыс.руб.)
|
0,253
|
320,6
|
1453,6
|
2011,3
|
2866,0
|
3973,7
|
4889,1
|
5475,9
|
6924,9
|
|
Численность пенсионеров (на
конец года), тыс.человек
|
368
|
404
|
401
|
399
|
394
|
389
|
385
|
382
|
378
|
|
Удельный вес численности
населения с денежными доходами ниже величины прожиточного минимума в общей
численности населения субъекта, процентов
|
|
19,9
|
42,2
|
39,5
|
33,7
|
30,7
|
25,0
|
20,3
|
15,7
|
Таблица 1.4
Потребление продуктов питания на душу населения
|
Показатели
|
Периоды
|
|
2004
|
2005
|
2006
|
2007
|
2008
|
2009
|
2010
|
2011
|
2012
|
|
Потребление продуктов
питания на душу населения в год, кг.:
|
|
|
|
|
|
|
|
|
|
|
мясо и мясопродукты,
включая субпродукты II категории и жир-сырец
|
75
|
57
|
55
|
57
|
59
|
59
|
60
|
57
|
58
|
|
молоко и молочные продукты
|
349
|
307
|
216
|
221
|
221
|
220
|
221
|
220
|
225
|
|
картофель
|
135
|
171
|
171
|
171
|
171
|
168
|
168
|
169
|
165
|
|
овощи и продовольственные
бахчевые культуры
|
96
|
110
|
114
|
115
|
114
|
111
|
112
|
109
|
110
|
|
хлебные продукты (хлеб и
макаронные изделия в пересчете на муку, мука, крупа, бобовые)
|
146
|
158
|
149
|
153
|
153
|
148
|
146
|
147
|
147
|
Таблица 1.5
Социальные показатели
|
Показатели
|
Периоды
|
|
2004
|
2005
|
2006
|
2007
|
2008
|
2009
|
2010
|
2011
|
2012
|
|
Общая площадь жилых
помещений, приходящаяся в среднем на одного жителя (на конец года), м2
|
18,9
|
20,4
|
20,9
|
21,2
|
21,6
|
22,0
|
22,6
|
23,1
|
23,7
|
|
в городских поселениях
|
15,9
|
18,4
|
18,8
|
19,2
|
19,5
|
20,0
|
20,9
|
21,4
|
|
в сельской местности
|
23,2
|
23,4
|
24,2
|
24,3
|
24,8
|
25,4
|
26,0
|
26,7
|
27,5
|
|
Среднемесячный размер
социальной поддержки на одного пользователя, руб.
|
|
|
17
|
29
|
47
|
64
|
75
|
105
|
109
|
|
Среднемесячный размер
субсидий на одну семью, руб.
|
|
|
63
|
128
|
220
|
362
|
378
|
383
|
404
|
|
Численность дневных
общеобразовательных учреждений (на начало учебного года)
|
992
|
946
|
907
|
891
|
888
|
884
|
880
|
876
|
868
|
|
Численность учащихся
дневных общеобразовательных учреждений, тыс.человек
|
166
|
184
|
170
|
164
|
157
|
148
|
138
|
128
|
121
|
|
Число учреждений начального
профессионального образования (на конец года)
|
42
|
42
|
39
|
37
|
36
|
34
|
34
|
33
|
30
|
|
Численность учащихся
учреждений начального профессионального образования (на конец года),
тыс.человек
|
16,8
|
16,9
|
15,9
|
15,6
|
14,6
|
13,5
|
13,4
|
13,5
|
12,2
|
|
Численность студентов в
средних специальных учебных заведениях - всего, тыс.человек
|
20,4
|
17,5
|
21,8
|
21,9
|
22,9
|
21,3
|
22,8
|
23,4
|
22,8
|
|
из них в государственных и
муниципальных
|
20,4
|
17,4
|
19.4
|
19,2
|
19,8
|
19,6
|
20,1
|
20,5
|
20,1
|
|
Численность студентов в
высших учебных заведениях - всего, тыс.человек
|
20,5
|
21,1
|
31,7
|
38,0
|
46,9
|
50,7
|
52,7
|
58,2
|
59,0
|
|
из них в государственных и
муниципальных
|
20,5
|
20,9
|
25,1
|
29,1
|
35,3
|
37,2
|
39,4
|
42,4
|
43,2
|
|
Численность врачей,
человек:
|
|
|
|
|
|
|
|
|
|
|
всего, тыс.
|
5.2
|
5,7
|
5,9
|
5,9
|
5,9
|
6,0
|
5.8
|
5.9
|
5,9
|
|
на 10 000 человек населения
|
39,1
|
43,0
|
46,7
|
47,6
|
48,2
|
49,3
|
48,2
|
49,8
|
50,4
|
|
Численность среднего
медицинского персонала, человек:
|
|
|
|
|
|
|
|
|
|
|
всего, тыс.
|
15,2
|
14,3
|
13,9
|
14,0
|
13,9
|
13,6
|
13,3
|
13,6
|
13,4
|
|
на 10 000 человек населения
|
114
|
108
|
110
|
112
|
113
|
112
|
111
|
115
|
114
|
|
Число больничных учреждений
|
131
|
111
|
98
|
97
|
94
|
85
|
86
|
86
|
87
|
|
Число больничных коек:
|
|
|
|
|
|
|
|
|
|
|
всего, тыс.
|
19,5
|
16,3
|
15,0
|
14,3
|
14,3
|
14,1
|
13,7
|
13,4
|
13,3
|
|
на 10 000 человек населения
|
147
|
123
|
118
|
115
|
116
|
116
|
114
|
114
|
114
|
|
Число зарегистрированных
преступлений:
|
|
|
|
|
|
|
|
|
|
|
всего, тыс.
|
9,9
|
24,3
|
25,0
|
23,4
|
19,6
|
20,3
|
21,8
|
26,2
|
31,3
|
|
на 10 000 человек населения
|
743
|
1830
|
1962
|
1858
|
1580
|
1658
|
1804
|
2199
|
2662
|
Таблица 1.6
Показатели промышленности
|
Показатели
|
Периоды
|
|
2004
|
2005
|
2006
|
2007
|
2008
|
2009
|
2010
|
2011
|
2012
|
|
Число действующих
организаций по видам деятельности (на конец года):
|
|
|
|
|
|
|
|
|
|
|
Добыча полезных ископаемых
|
|
|
|
|
|
|
|
12
|
11
|
|
Обрабатывающие производства
|
|
|
|
|
|
|
|
1714
|
1669
|
|
Производство и
распределение электроэнергии, газа и воды
|
|
|
|
|
|
|
|
499
|
552
|
|
Индекс промышленного
производства, в процентах к предыдущему году
|
|
101,4
|
102,5
|
86,3
|
103,9
|
119,3
|
104,7
|
104,5
|
106,5
|
Таблица 1.7
Показатели сельского хозяйства
|
Показатели
|
Периоды
|
|
2004
|
2005
|
2006
|
2007
|
2008
|
2009
|
2010
|
2011
|
2012
|
|
Продукция сельского
хозяйства всех категорий (в фактически действовавших ценах), млн. руб. (1990,
1995 гг. - млрд. руб.)
|
4,1
|
2900
|
13118
|
14873
|
16498
|
19092
|
22363
|
25154
|
27477
|
|
Продукция растениеводства
|
2,0
|
1515
|
8612
|
9150
|
10492
|
12218
|
15001
|
16415
|
18134
|
|
Продукция животноводства
|
2,1
|
1385
|
4506
|
5723
|
6006
|
6874
|
7362
|
8739
|
9343
|
|
Посевная площадь всех
сельскохозяйственных культур в хозяйствах всех категорий, тыс. га
|
1855,4
|
1639,1
|
1363,4
|
1331,5
|
1340,2
|
1200,4
|
1209,0
|
1222,5
|
1184,9
|
|
Структура посевных площадей
сельскохозяйственных культур в хозяйствах всех категорий, в процентах от всей
посевной площади:
|
|
|
|
|
|
|
|
|
|
|
Зерновые культуры
|
52,1
|
56,8
|
58,8
|
61,6
|
63,0
|
58,5
|
62,4
|
65,1
|
66,4
|
|
Технические культуры
|
10,7
|
7,6
|
7,4
|
5,2
|
6,2
|
8,6
|
6,6
|
6,2
|
8,2
|
|
Картофель и овощебахчевые
культуры
|
4,7
|
5,9
|
7,4
|
7,6
|
7,6
|
8,6
|
8,2
|
8,0
|
8,2
|
|
Кормовые культуры
|
32,5
|
29,7
|
26,5
|
25,7
|
23,3
|
24,3
|
22,8
|
20,7
|
17,2
|
Таблица 1.8
Строительство
|
Показатели
|
Периоды
|
|
2004
|
2005
|
2006
|
2007
|
2008
|
2009
|
2010
|
2011
|
2012
|
|
Число действующих
строительных организаций
|
|
665
|
457
|
420
|
421
|
470
|
455
|
438
|
445
|
|
|
2202,3
|
3325,4
|
3298,8
|
4372,5
|
6041,2
|
7125,6
|
10257,2
|
|
Ввод в действие жилых
домов, тыс. м2 общей площади
|
450
|
292
|
176
|
193
|
192
|
276
|
286
|
298
|
327
|
Таблица 1.9
Транспорт и связь
|
Показатели
|
Периоды
|
|
2004
|
2005
|
2006
|
2007
|
2008
|
2009
|
2010
|
2011
|
2012
|
|
Эксплуатационная длина железнодорожных
путей общего пользования (на конец года), км
|
1110
|
1107
|
1067
|
1063
|
1063
|
1061
|
1061
|
1061
|
1061
|
|
Протяженность автомобильных
дорог общего пользования с твердым покрытием (на конец года), км
|
4934
|
5019
|
6055
|
6097
|
6144
|
6186
|
6202
|
6206
|
6898
|
|
Грузооборот автомобильного
транспорта организаций всех видов деятельности, млн. т. км
|
2987
|
1988
|
867
|
958
|
878
|
889
|
843
|
864
|
848
|
Таблица 1.10
Торговля и услуги населению
|
Показатели
|
Периоды
|
|
2004
|
2005
|
2006
|
2007
|
2008
|
2009
|
2010
|
2011
|
2012
|
|
Оборот розничной торговли
(в фактически действовавших ценах):
|
|
|
|
|
|
|
|
|
|
|
Всего, млн. руб. (1990,
1995 гг. - млрд. руб.)
|
1,9
|
2868
|
13087
|
15996
|
18700
|
23240
|
30525
|
37071
|
48814
|
|
На душу населения, руб.
(1990, 1995 гг. - тыс. руб.)
|
1,4
|
2159
|
10271
|
12720
|
15083
|
19005
|
25294
|
31113
|
41462
|
|
Оборот общественного
питания (в фактически действовавших ценах), млн. руб. (1990, 1995 гг. - млрд.
руб.)
|
0,1
|
170
|
421
|
484
|
718
|
832
|
1002
|
1265
|
1651
|
Таблица 1.11
Финансы
|
Показатели
|
Периоды
|
|
2004
|
2005
|
2006
|
2007
|
2008
|
2009
|
2010
|
2011
|
2012
|
|
Доходы консолидированного
бюджета субъекта, млн. руб. (1995 г. - млрд. руб.)
|
|
1447
|
4445
|
5373
|
7111
|
8481
|
11523
|
15163
|
16700
|
|
Из них доходы муниципальных
образований
|
|
|
|
2912
|
2534
|
2547
|
3859
|
4512
|
7730
|
|
Расходы консолидированного
бюджета субъекта, млн. руб. (1995 г. - млрд. руб.)
|
|
1472
|
4331
|
5374
|
7487
|
8600
|
11483
|
14745
|
16399
|
|
Из них доходы муниципальных
образований
|
|
|
|
2969
|
2702
|
2864
|
3928
|
4236
|
7835
|
|
Поступление налогов, сборов
и иных обязательных платежей в бюджетную систему Российской Федерации, млн.
руб. (1995 г. - млрд. руб.)
|
|
1829
|
4967
|
7630
|
7960
|
8667
|
12495
|
15814
|
17417
|
|
Задолженность по налогам и
сборам в бюджетную систему Российской Федерации, млн. руб. (1995 г. - млрд.
руб.)
|
|
389
|
4267
|
3556
|
4342
|
4291
|
4633
|
5750
|
5795
|
Таблица 1.12
Инвестиции
|
Показатели
|
Периоды
|
|
2004
|
2005
|
2006
|
2007
|
2008
|
2009
|
2010
|
2011
|
2012
|
|
Инвестиции в основной
капитал (в фактически действовавших ценах),млн. руб. (1990, 1995 гг. - млрд.
руб.)
|
2,1
|
1398
|
5452
|
6646
|
10413
|
10112
|
15198
|
17864
|
10887
|
|
Индекс физического объема
инвестиций в основной капитал, в процентах к предыдущему году
|
99,0
|
96,4
|
89,4
|
103,2
|
147,1
|
86,5
|
131,3
|
99,7
|
100,8
|
|
Удельный вес инвестиций в
основной капитал, финансируемых за счет бюджетных средств, в общем объеме
инвестиций, процентов
|
|
14,6
|
16,4
|
14,5
|
10,4
|
11,8
|
10,6
|
18,7
|
12,4
|
|
В том числе за счет
федерального бюджета
|
|
5,7
|
5,1
|
6,5
|
5,0
|
6,6
|
3,2
|
7,9
|
5,6
|
Таблица 1.13
Цены
|
Показатели
|
Периоды
|
|
2004
|
2005
|
2006
|
2007
|
2008
|
2009
|
2010
|
2011
|
2012
|
|
Индекс потребительских цен
(декабрь к декабрю предыдущего года), процентов
|
|
251,1
|
119,1
|
122,9
|
116,6
|
116,2
|
109,9
|
109,4
|
111,7
|
|
Стоимость фиксированного
набора потребительских товаров и услуг (на конец года):
|
|
|
|
|
|
|
|
|
|
|
Руб.
|
|
|
1955,0
|
2387,0
|
2805,9
|
3445,5
|
3867,2
|
4285,0
|
4587,3
|
|
В процентах к
среднероссийской стоимости
|
|
|
87
|
88
|
88
|
96
|
95
|
91
|
88
|
2. КРАТКАЯ ХАРАКТЕРИСТИКА СОЦИАЛЬНО-ЭКОНОМИЧЕСКИХ ЯВЛЕНИЙ РЕГИОНА
Калужская область расположена в центре европейской части Российской
Федерации. Граничит с Московской, Тульской, Брянской, Смоленской, Орловской
областями.
Площадь: 29,9 тыс. кв. км, что составляет 17% территории Центрально -
Черноземного региона и 0,2% территории России.
Экономика. Валовой внутренний продукт: 84,8 млрд руб. (2006) (74,5 -
2005)
ВВП на душу населения: 83,8 тыс. руб. (2006) (73,2 - 2005)
Структура экономики в целом характерна для центрального района. В
промышленности формируется около 39,4 % ВВП (2006), из них 29,0 % в
обрабатывающих производствах (прежде всего машиностроение и пищевая
промышленность), 5,8 % - в строительном комплексе, 4,1 % - в энергетике. В
агропромышленном комплексе создаётся 10,9 % ВВП (2006) (11,5 % - 2005).
Промышленность. Наибольшую долю в объёме промышленного производства на
2004 год имеют машиностроение и металлообработка (42,7 %); пищевая (22,5 % с
тенденцией к увеличению); лесная, деревообрабатывающая и целлюлозно-бумажная
промышленность (11,4 %); и энергетика (9,4 %).
Отраслью специализации региона является машиностроение: транспортное
(Людиновский тепловозостроительный завод, автоконцерн «Фольксваген»,Калужский
завод путевых машин и гидроприводов, Калужский завод транспортного
машиностроения), турбинное (Калужский турбинный завод), котельное (Киров),
авиамоторостроение (Калужский двигатель), сельскохозяйственное машиностроение
(Людиново), специальное автомобилестроение (Козельск), приборостроение
(лазерная техника в Калуге, сборка компьютеров компанией Kraftway в Обнинске) и
радиоэлектроника, технологическое оборудование (Завод металлоконструкций
«ЮВС»), а также производство стройматериалов (в том числе ОАО
Стройполимеркерамика (Воротынск) в составе трех заводов: Сантери, Воротынский
кирпич и Воротынская керамика).
Благодаря относительно высокой рентабельности особенное развитие в
последнее время получает пищевая промышленность (Ликероводочный завод Кристалл,
Калужский мясокомбинат, Калужский хлебокомбинат и др.), деревообрабатывающая и
целлюлозно-бумажная промышленность (целлюлозно-бумажный завод StoraEnso в
Балабанове и др.), строительный комплекс, имеется атомная промышленность
(Товарково и Обнинск), лёгкая промышленность (Фабрика «Художественная вышивка»
в Тарусе), чёрная и цветная металлургия (порошковая и цветная в Калуге)
Транспорт. Основные транспортные узлы региона - Калуга, Обнинск и
Сухиничи.
Основной автомобильной магистралью является М3 «Украина», с
интенсивностью движения до 13800 авт./сутки, проходящая через города
Балабаново, Обнинск, вблизи Малоярославца, Калуги, Сухиничи и города Жиздра.
Важное значение имеет и федеральная автодорога A101 Москва - Варшава («Старая
Польская», «Варшавка»), с интенсивностью движения до 11 500 авт./сутки,
проходящая через Белоусово, Обнинск, Малоярославец, Медынь, Юхнов, около
Спас-Деменска. Кроме того региональное значение имеет автодорога Р132 Вязьма -
Калуга - Тула - Рязань с интенсивностью движения до 6750 авт./сутки, и участок
А108 «МБК» проходящий через город Балабаново. Протяжённость автомобильных дорог
с твердым покрытием составляет 6564 км. Плотность автодорог общего пользования
с твердым покрытием - 165 км на 1000 км².
Основная железнодорожная магистраль - Москва - Киев, проходящая через
Балабаново, Обнинск, Малоярославец, Сухиничи. Кроме того важны однопутные
тепловозные линии Вязьма - Калуга - Тула (через Мятлево, Полотняный Завод,
Пятовский и Калугу), Сухиничи - Смоленск (через Спас-Деменск), Сухиничи -
Рославль (через Киров), Сухиничи - Тула (через Козельск), Козельск - Белёв,
Вязьма - Брянск (через Киров и Людиново) а также ветка Брянск - Дудоровский. В
Калуге размещено крупное локомотивное и моторвагонное депо. Протяжённость
железных дорог общего пользования составляет 872 км. Плотность железных дорог
общего пользования - 29 км на 1000 км².
В области размещено четыре аэродрома среди них один гражданский - вблизи
Калуги аэродром « Грабцево» (на 2008 год закрыт), военные в городе Ермолино и
крупный военный аэродром Шайковка.
В перечень внутренних водных путей России включён участок течения Оки от
Калуги, по реке осуществляются туристические поездки, организованы
экскурсионные линии Серпухов - Таруса, Серпухов - Велегож, кроме того двумя
теплоходами «Луч» организована линия Калуга - Алексин. Протяжённость судоходных
и условно судоходных внутренних водных путей составляет 101 км.
В межобластном пассажирском сообщении особое значение имеет
железнодорожный экспресс Москва - Калуга (три отправления в сутки, время в пути
2 часа 40 минут).
Городской транспорт Калуги примечателен своей троллейбусной системой.
Население. По итогам переписи населения 2002 года численность населения
1040,9 тыс. чел., из них городского населения 779,7 тыс. чел. (74,9 %),
сельского - 261,2 тыс. чел (25,1 %).
На 2007 год население области составляет 1005,6 тыс. человек, городское
население - 765,8 тыс. человек (76,1 %).
|
Народ
|
Численность
|
|
Русские
|
973589
|
|
Украинцы
|
23162
|
|
Армяне
|
7059
|
|
Белорусы
|
6609
|
|
Татары
|
4299
|
|
Цыгане
|
3187
|
|
Азербайджанцы
|
3002
|
|
Немцы
|
1548
|
|
Молдоване
|
1443
|
|
Мордва
|
1413
|
|
Чуваши
|
1108
|
|
Грузины
|
1071
|
|
Показаны народы с численностью
более 1000 человек
|
Агропромышленный комплекс. В состав агропромышленного комплекса области
входит более 900 организаций, в том числе 320 работающих сельскохозяйственных
предприятий и около 400 организаций пищевой и перерабатывающей промышленности.
По данным органов государственной статистики на территории области
осуществляют деятельность около 2 300 крестьянских (фермерских) хозяйств с
общей земельной площадью 48,5 тыс. га и 105,9 тыс. владельцев личных подсобных
хозяйств на площади 50,1 тыс.га.
В структуре земельного фонда Калужской области земли
сельскохозяйственного назначения составляют около 1 млн. 824 тыс. га, в том
числе сельскохозяйственные угодья - 1 млн. 150 тыс. га, включая 860 тыс. га
пашни.
Объем производства сельскохозяйственной продукции в хозяйствах всех
категорий в 2009 году составил 21 млрд. руб., индекс физического объема - 105
%.
Удельный вес сельскохозяйственной продукции в валовом региональном
продукте составляет около 11 процентов.
Основное направление специализации сельскохозяйственного производства -
молочно-мясное скотоводство. Наряду с основной отраслью сельскохозяйственные
товаропроизводители занимаются птицеводством, выращиванием зерновых культур,
картофеля, овощей, льна-долгунца.
По состоянию на 1 января 2010 года численность крупного рогатого скота в
хозяйствах всех категорий составила 129,5 тыс. голов, в том числе коров - 55,8
тыс. голов, поголовье свиней - 53 тыс. голов, птицы - 4,1 млн. голов.
В 2010 году хозяйствах всех категорий будет произведено скота и птицы на
убой (в живом весе) 79 тыс. тонн (108 % к уровню 2009 года), молока - 231,2
тыс. тонн (102 %), яиц куриных - 241 млн.шт. (112 %), зерна - 197 тыс. тонн
(109 %), картофеля - 352 тыс. тонн (109 %).
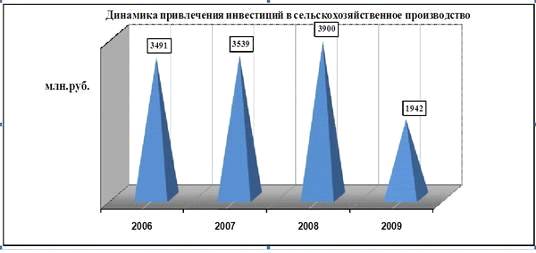
Ключевым направлением по развитию сельского хозяйства остается
привлечение частных инвестиций. В течение 2006-2009 года объем частных
инвестиций в развитие сельского хозяйства составил 8,2 млрд. руб.
В рамках льготного инвестиционного кредитования с начала реализации
НацПроекта кредитные договора с коммерческими банками по восьмилетнему
кредитованию оформила 51 сельскохозяйственная организация на сумму 3,37 млрд.
руб., пятилетние кредиты оформили 106 сельскохозяйственных организации в объеме
3,88 млрд. руб.
Всего по восьмилетним, пятилетним и трехлетним инвестиционным кредитам
сельскохозяйственными организациями области заключено кредитных договоров на
сумму более 7,3 млрд. руб.
Общий объем финансирования Государственной и областной программ развития
сельского хозяйства составил более 800 млн. руб.

Строительный комплекс. Строительный комплекс области сегодня представляют
805 подрядных организаций самого различного профиля и организационно-правовых
форм, 49 проектно-изыскательских организаций и 152 предприятия промышленности
строительных материалов, в которых занято свыше 53 тысяч человек
В строительстве утвердилось многообразие форм собственности, доля
негосударственного сектора в общем объеме работ, выполненных по договора
строительного подряда, достигла 95 процентов.
Объем строительной продукции в 2001 году составил 3,4 млрд. рублей, что
на 4% превысил уровень предыдущего года.
На 10-40 процентов обеспечили прирост объема работ строительные
организации Юхновского, Медынского, Жуковского районов и г. Обнинска. Мощный
производственный потенциал сохраняют строительные организации Кировского,
Малоярославецкого, Сухиничского, Хвастовичского районов и г. Калуги.
Строительными организациями за 2001 год получено 83 млн. рублей прибыли,
доля прибыльных предприятий и организаций отрасли “Строительство” составила
около 60 процентов.
Средняя заработная плата одного работающего на крупных и средних
предприятиях и организациях в 2001 году увеличилась по сравнению с предыдущим
годом на 47 % и составила 3,5 тыс. рублей, что на 33 % выше, чем в среднем по
области.
Строителями в прошедшем году сданы в эксплуатацию производственные
мощности и объекты социальной сферы: автоматические телефонные станции,
междугородные кабельные линии связи, трансформаторные подстанции, линии
электропередачи, торговые предприятия, автомобильные дороги и объекты
коммунального хозяйства, школы, жилые дома.
В 2001 году проведено 60 подрядных торгов, на которых заключено 76
контрактов на выполнение подрядных работ для государственных заказчиков на
сумму 120 млн. рублей.
3. ПОСТРОЕНИЕ СТАТИСТИЧЕСКИХ ГРАФИКОВ
Анализ рядов распределения сопровождается их графическим изображением.
Именно по графикам можно судить о форме распределения. Для этой цели строят полигон,
кумуляту, гистограмму и огиву распределения.
Полигон - ломаная кривая, строящаяся на основе прямоугольной системы
координат, когда по оси Х откладываются ранжированные значения варьирующего
признака, а по оси Y - частоты.
Полигон используется при изображении дискретных вариационных рядов.
Проанализируем изменение численности населения Калужской области (таблица
1.1), построив полигон (рис. 3.1).
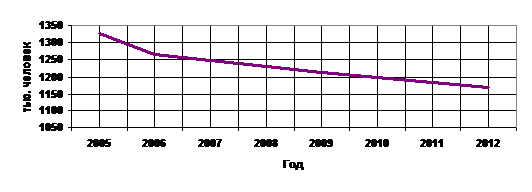
Рис.
3.1. Полигон изменения численности населения Калужской области по годам, тыс.
человек
По данным графика ясно, что с каждым годом численность населения
Калужской области уменьшается.
Гистограмма применяется для изображения интервального вариационного ряда.
При построении гистограммы на оси абсцисс откладываются величины интервалов, а
частоты изображаются прямоугольниками, построенными на соответствующих
интервалах. Высота столбиков в случае равных интервалов должна быть
пропорциональна частотам.
Построим гистограмму для группировки строительных организаций. (таблица
4.2).
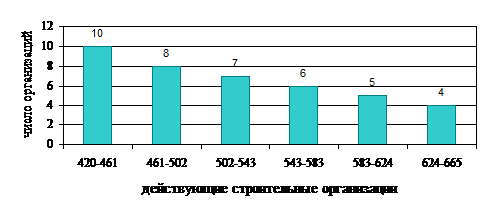
Рис. 3.2. Гистограмма распределения действующих строительных организаций.
По данной гистограмме (рис. 3.2) можем судить, что наибольшее число
строительных организаций попадают в интервал от 420 до 461.
Для графического изображения вариационных рядов может также
использоваться кумулятивная кривая. При помощи кумуляты изображается ряд
накопленных частот, которые определяются путем последовательного суммирования
частот по группам. Накопленные частоты показывают, сколько единиц совокупности
имеют значения признака не больше, чем рассматриваемое значение.
Построим кумуляту распределения транспортных организаций по грузообороту
транспорта всех видов деятельности (таблица 4.1) - рис. 3.3.
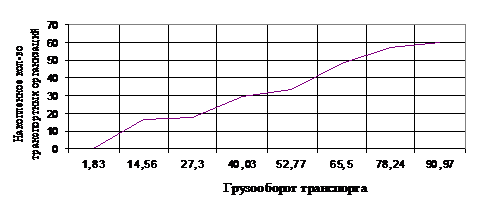
Рис.
3.3. Распределение транспортных организаций по грузообороту транспорта всех
видов деятельности, млн. т. км
Если
при графическом изображении вариационного ряда в виде кумуляты оси поменять
местами, то получим огиву.
Построим
огиву распределения для этой же таблицы (рис. 3.4).

Рис.
3.4. Распределение транспортных организаций по грузообороту транспорта всех
видов деятельности, млн. т. км
Проанализируем
другие социально-экономические показатели, предоставленные нам для
исследования. Для этого построим различные виды диаграмм.
Наиболее
распространенными диаграммами сравнения являются столбиковые диаграммы, принцип
построения которых состоит в изображении статистических показателей в виде
представленных по вертикали прямоугольников - столбиков. Правила построения
столбиковых диаграмм допускают одновременное расположение на одной
горизонтальной оси изображений нескольких показателей. В этом случае столбики
располагаются группами (рис. 3.5)
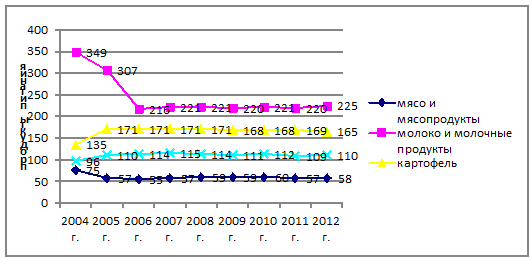
Рис. 3.5. Распределение продуктов питания на душу населения в год, кг.
По данной диаграмме можно сказать, что продукты питания в социальной
сфере с каждым годом то возрастают, то убывают.
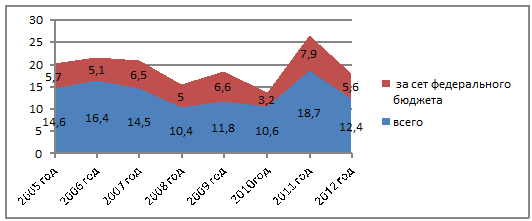
Рис. 3.6. Распределение удельного веса инвестиций в основной капитал,
финансируемых за счет бюджетных средств, %.
По представленной выше диаграмме мы можем судить, что во всех годах
наибольшие финансы приносит весь удельный вес. Год с самым большим числом
удельного веса, пользующихся всем удельным весом - 2005 год - 18,7%. Во всех
годах наименьшие финансы приносит удельный вес за счет федерального бюджета.
Основное назначение структурных диаграмм заключается в графическом
представлении состава статистических совокупностей, характеризующихся как
соотношение различных частей каждой из совокупностей. Построим секторную
диаграмму по данным об удельном весе численности населения по годам (рис. 3.7),
взятым из таблица 1.3.
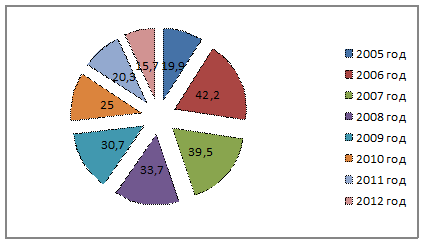
Рис. 3.7. Распределение удельного веса численности населения, в %.
Построим диаграмму распределения структур посевных площадей по таблице
1.7 и проанализируем ее (рис. 3.8).
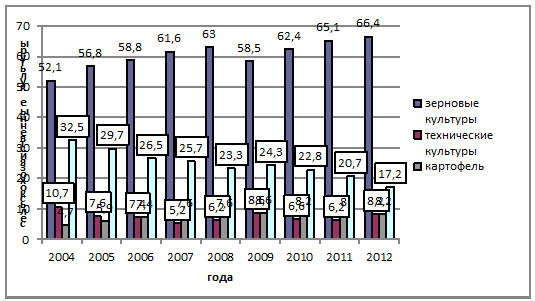
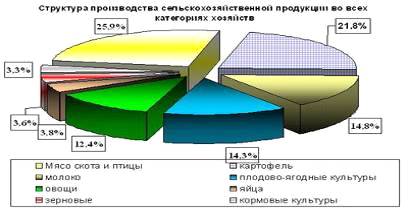
Рис. 3.8. Распределение структур посевных площадей, в %.
По данной диаграмме видно, что наибольшим спросом во всех годах
пользуется зерновая культура, самый большой показатель - 66,4 % -
зарегистрирован в 2006 году. На втором месте по популярности - кормовые
культуры; наибольшим спросом она пользуется в 1990 году - 32,5 %. Показатели
технических и картофельных культур невелики во всех годах.
4.ПОСТРОЕНИЕ РЯДОВ РАСПРЕДЕЛЕНИЯ
4.1. Построение с помощью формулы Стержесса
Для обработки статистических данных группировка единиц объекта проводится
с помощью стандартных процедур. Одна из таких процедур основана на
использовании формулы Стерджесса для определения оптимального числа групп.
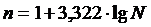 , (4.1)
, (4.1)
где
n - число групп;
N - число единиц
совокупности.
Для
исследования грузооборота автомобильного транспорта по исходным данным табл.
1.9 составим ряд чисел:
|
843
|
848
|
862
|
867
|
878
|
889
|
896
|
950
|
958
|
1010
|
|
1063
|
1116
|
1170
|
1223
|
1276
|
1329
|
1381
|
1432
|
1485
|
1538
|
|
1591
|
1642
|
1695
|
1748
|
1801
|
1854
|
1908
|
1962
|
1988
|
2015
|
|
2068
|
2121
|
2174
|
2227
|
2380
|
2486
|
2591
|
2745
|
2904
|
2987
|
Анализ полученного не сгруппированного ряда позволяет сделать вывод о
неравномерном характере распределения частот. Это позволяет применить формулу
Стерджесса:
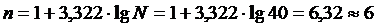 (4.1)
(4.1)
В
результате расчетов число групп примем равное 6.
После
определения числа групп следует определить интервалы группировки, то есть
значение варьирующего признака, лежащего в определенных границах (верхней и
нижней).
Так
как распределение носит более или менее равномерный характер, то построим
группировку с равными интервалами. Величина равного интервала определяется по
формуле:
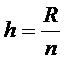 , (4.2)
, (4.2)
Размах
вариации (R) вычисляется по формуле:
R = Xmax
- Xmin , (4.3)
где
Xmax - максимальное значение признака;
Xmin -
минимальное значение признака.
В
нашем случае размах вариации R = 2987 - 843 = 2144 млн. тыс. км.
По
формуле 4.2 определим величину интервала:
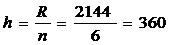
Построим
интервальный вариационный ряд (табл. 4.1).
Таблица
4.1
Группы
организаций по грузообороту автомобильного транспорта
|
№ п/п
|
Группы транспортных
организаций по грузообороту автомобильного транспорта, млн. тыс. км
|
Количество организаций
|
Накопленное число
организаций
|
|
1
|
843 - 1200
|
13
|
13
|
|
2
|
1200 - 1557
|
7
|
20
|
|
3
|
1557 - 1914
|
7
|
27
|
|
4
|
1914 - 2271
|
5
|
32
|
|
5
|
2271 - 2628
|
5
|
37
|
|
6
|
2628 - 2985
|
3
|
40
|
|
Итого
|
40
|
|
Таким образом, по полученному ряду распределения можно определить, что
наибольшее число организаций попало в интервал (843 - 1200), наименьшее
количество организаций содержится в интервале (2628 - 2985).
Для исследования числа действующих строительных организаций по исходным
данным табл. 1.8 составим ряд чисел:
|
420
|
421
|
426
|
432
|
438
|
444
|
445
|
450
|
455
|
457
|
|
463
|
469
|
470
|
476
|
482
|
488
|
494
|
500
|
506
|
512
|
|
518
|
524
|
530
|
536
|
542
|
548
|
554
|
560
|
566
|
572
|
|
578
|
584
|
590
|
596
|
602
|
618
|
631
|
642
|
656
|
665
|
Для построения вариационного ряда используем формулу Стерджесса 4.1
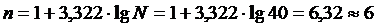
В
этом случае размах вариации (4.3) R = 665 - 420 = 245
По
формуле 4.2 определим величину интервала:
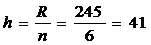
Построим
интервальный вариационный ряд (табл. 4.2).
Таблица
4.2
Группировка
действующих строительных организаций
|
№ п/п
|
Действующие строительные
организации
|
Количество строительных
организаций
|
Накопленное число
организаций
|
|
1
|
420 - 461
|
10
|
10
|
|
2
|
461 - 502
|
8
|
18
|
|
3
|
502 - 543
|
7
|
25
|
|
4
|
543 - 583
|
6
|
31
|
|
5
|
583 - 624
|
5
|
36
|
|
6
|
624 - 665
|
4
|
40
|
|
Итого
|
40
|
|
Таким образом, по полученному ряду распределения можно определить, что
наибольшее число строительных организаций попало в интервал (420 - 461),
наименьшее количество строительных организаций содержится в интервале (624 -
665).
4.2 Построение рядов распределения
с произвольными интервалами
Метод построения рядов распределения с произвольными интервалами
заключается в том, что определение интервалов происходит с помощью нахождения
коэффициента вариации для единиц совокупности, входящих в данный интервал.
Причем, интервал найден правильно, если коэффициент вариации не превышает 33%.
Для построения группировок используем формулу коэффициента вариации:
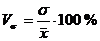 , (4.4)
, (4.4)
где
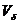 - коэффициент вариации, %;
- коэффициент вариации, %;
 - среднее
квадратичное отклонение;
- среднее
квадратичное отклонение;
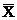 - среднее
значение.
- среднее
значение.
Найдем
среднее значение (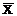 ) по формуле:
) по формуле:
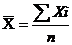 , (4.5)
, (4.5)
где
х - значение признака (вариант);
n -число
группировок.
Рассчитаем
среднее квадратичное отклонение ( ) по
формуле:
) по
формуле:
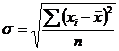 , (4.6)
, (4.6)
где
 - среднее квадратическое отклонение;
- среднее квадратическое отклонение;
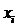 - i-ый
признак;
- i-ый
признак;
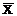 -
среднее значение;
-
среднее значение;
n - количество
признаков.
С
целью исследования общей площади жилых помещений, приходящейся в среднем на
одного жителя, по исходным данным табл. 1.5 составим ряд чисел:
|
18,9
|
19,1
|
19,3
|
19,5
|
19,7
|
19,8
|
20
|
20,2
|
20,4
|
20,6
|
|
20,8
|
20,9
|
21
|
21,2
|
21,4
|
21,6
|
21,8
|
22
|
22,1
|
22,3
|
|
22,4
|
22,6
|
22,7
|
22,9
|
23,1
|
23,2
|
23,4
|
23,5
|
23,6
|
23,7
|
Первый интервал: (18,9 - 20,9)
Определим
среднее значение (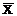 ) по формуле (4.5):
) по формуле (4.5):
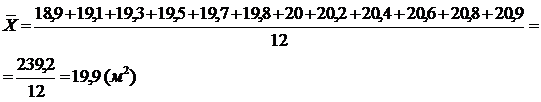
Рассчитаем
среднее квадратичное отклонение по формуле (4.6):
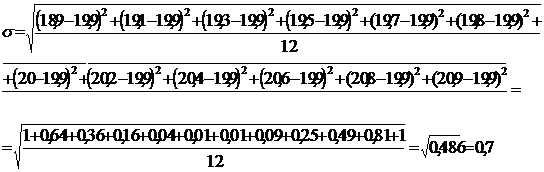
Вычислим
коэффициент вариации по формуле 4.4:
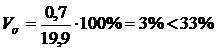
По
результатам расчетов показатель вариации, равный 3%, не превышает 33,3%,
следовательно можно построить группировку.
Второй
интервал: (21 - 22,3)
Вычислим
среднее значение для интервала (21 - 22,3) по формуле 4.5:
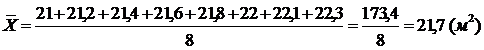
Рассчитаем
среднее квадратичное отклонение по формуле (4.6):
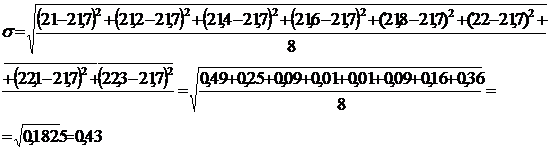
Вычислим
коэффициент вариации по формуле 4.4:
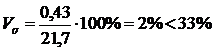
По
результатам расчетов показатель вариации, равный 2%, не превышает 33,3%,
следовательно можно построить группировку.
Третий
интервал: (22,4 - 23,7)
Вычислим
среднее значение для интервала (22,4 - 23,7) по формуле 4.5:
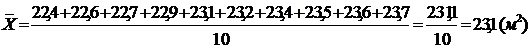
Рассчитаем
среднее квадратичное отклонение по формуле (4.6):
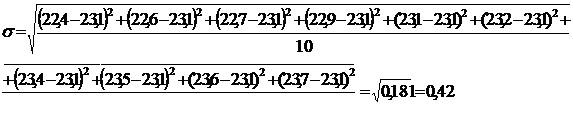
Вычислим
коэффициент вариации по формуле 4.4:
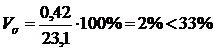
По
результатам расчетов показатель вариации, равный 2%, не превышает 33,3%,
следовательно, можно построить группировку.
Построим
интервальный вариационный ряд (табл. 4.2).
ряд распределение интервал вариация
Таблица
4.3
Группировка
площадей жилых помещений (в среднем на одного жителя)
|
Группы площадей, м2
|
Численность жилых помещений
|
Середина интервала
|
Накопленное число жилых
помещений
|
|
18,9 - 20,9
|
12
|
19,9
|
12
|
|
20,9 - 22,3
|
8
|
21,6
|
20
|
|
22,3 - 23,7
|
10
|
23
|
30
|
|
Итого
|
30
|
|
|
Середина интервала высчитывается:
1-й
равен 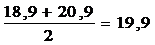 (руб.)
(руб.)
-й
равен  (руб.)
(руб.)
3-й
равен 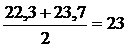 (руб.)
(руб.)
Таким
образом, в интервал (18,9 - 20,9) попадают 12 единиц совокупности, в интервал
(20,9 - 22,3) - 8 единица совокупности, а в последний интервал (22,3 - 23,7) -
10 единиц совокупности.
4.3 Построение рядов распределения
с помощью среднего квадратического отклонения
Другой
способ построения рядов распределения основан на применении показателя среднего
квадратического отклонения ( ). Если
величина интервала равна
). Если
величина интервала равна 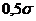 , то совокупность разбивается на 12 групп, а когда
величина интервала равна
, то совокупность разбивается на 12 групп, а когда
величина интервала равна 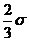 и
и  , то
совокупность делится соответственно на 9 и 6 групп.
, то
совокупность делится соответственно на 9 и 6 групп.
Если совокупность разбивается на 12 групп, то интервалы групп строятся
следующим образом:
от
 -3,0
-3,0  до
до  -2,5
-2,5 
от
 -2,5
-2,5  до
до  -2,0
-2,0 
от
 -2,0
-2,0  до
до  -1,5
-1,5 
от
 -1,5
-1,5  до
до  -1,0
-1,0 
от
 -1,0
-1,0  до
до  -0,5
-0,5 
от
 -0,5
-0,5  до
до 
от
 до
до  +0,5
+0,5 
от
 +0,5
+0,5  до
до  +1,0
+1,0 
от
 +1,0
+1,0  до
до  +1,5
+1,5 
от
 +1,5
+1,5  до
до  +2,0
+2,0 
от
 +2,0
+2,0  до
до  +2,5
+2,5 
от
 +2,5
+2,5  до
до  +3,0
+3,0  ,
,
где
 - среднее значение признака по совокупности, которое
определяется по формуле (4.5);
- среднее значение признака по совокупности, которое
определяется по формуле (4.5);
 -
среднее квадратичное отклонение, рассчитываемое формуле (4.6).
-
среднее квадратичное отклонение, рассчитываемое формуле (4.6).
Когда
число групп равно 9, получаются следующие интервалы групп:
от
 -3
-3  до
до  -7/3
-7/3 
от
 -7/3
-7/3  до
до  -5/3
-5/3 
от
 -5/3
-5/3  до
до  -
- 
от
 -
-  до
до  -1/3
-1/3 
от
 -1/3
-1/3  до
до  +1/3
+1/3 
от
 +1/3
+1/3  до
до  +
+ 
от
 +
+  до
до  +5/3
+5/3 
от
 +5/3
+5/3  до
до  +7/3
+7/3 
от
 +7/3
+7/3  до
до  +3
+3 
Когда
число групп равно 6, получаются следующие интервалы групп:
от
 -3
-3  до
до  -2
-2 
от
 -2
-2  до
до  -
- 
от
 -
-  до
до 
от
 до
до  +
+ 
от
 +
+  до
до  +2
+2 
от
 +2
+2  до
до  +3
+3 
С
целью исследования общей площади жилых помещений, приходящейся в среднем на
одного жителя, по исходным данным табл. 1.5 составим ряд чисел:
|
18,9
|
20,1
|
20,3
|
20,4
|
20,6
|
20,8
|
20,9
|
21
|
21,2
|
21,4
|
|
21,6
|
21,8
|
22
|
22,2
|
22,4
|
22,6
|
22,8
|
23,1
|
23,4
|
23,7
|
Построим вариационный интервальный ряд с помощью среднего квадратического
отклонения.
Для этого найдем среднюю арифметическую и среднее квадратическое
отклонение по формулам (3.5) и (3.6).
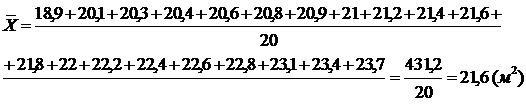
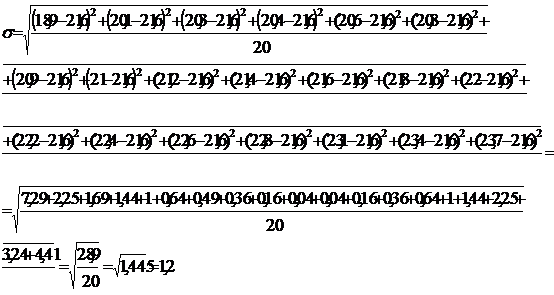
Вычислив среднюю арифметическую и среднее квадратическое отклонение,
можем найти границы интервалов.
Разделим совокупность на 12 групп и вычислим границы интервалов для нашей
группировки:
|
1
|
18
|
-
|
18,6
|
|
2
|
18,6
|
19,2
|
|
3
|
19,2
|
-
|
19,8
|
|
4
|
19,8
|
-
|
20,4
|
|
5
|
20,4
|
-
|
21
|
|
6
|
21
|
-
|
21,6
|
|
7
|
21,6
|
-
|
22,2
|
|
8
|
22,2
|
-
|
22,8
|
|
9
|
22,8
|
-
|
23,4
|
|
10
|
23,4
|
-
|
24
|
|
11
|
24
|
-
|
24,6
|
|
12
|
24,6
|
-
|
25,2
|
Составим группировку распределения площадей жилых помещений (м2):
Таблица 4.4
Группировка площадей жилых помещений (в среднем на одного жителя)
|
№ п/п
|
Группировка площадей жилых
помещений (в среднем на одного жителя), м2
|
Количество жилых помещений
|
|
1
|
18,6 - 19,8
|
1
|
|
2
|
19,8 - 20,4
|
3
|
|
3
|
20,4 - 21
|
4
|
|
4
|
21 - 21,6
|
3
|
|
5
|
21,6 - 22,2
|
3
|
|
6
|
22,2 - 22,8
|
3
|
|
7
|
22,8 - 23,4
|
2
|
|
8
|
23,4 - 25,2
|
1
|
|
Итого
|
|
20
|
4.4 Классификация рядов
распределения
Статистический ряд распределения - это упорядоченное распределение единиц
совокупности на группы по определенному варьирующему признаку.
В зависимости от признака, положенного в основу образования ряда
распределения, различают атрибутивные и вариационные ряды распределения.
Атрибутивными называют ряды распределения, построенные по качественным
признакам. Ряд распределения принято оформлять в виде таблиц.
Приведем примеры атрибутивных рядов распределения.
Таблица 4.5
Группировка продукции сельского хозяйства по категориям (млн. руб.)
|
Категории
|
1990
|
1995
|
2000
|
2001
|
2002
|
2003
|
2004
|
2005
|
2006
|
|
Продукция растениеводства
|
2000
|
1515
|
8612
|
9150
|
10492
|
12218
|
15001
|
16415
|
18134
|
|
Продукция животноводства
|
2100
|
1385
|
4506
|
5723
|
6006
|
6874
|
7362
|
8739
|
9343
|
Элементами этого ряда распределения являются значения атрибутивного
признака, представленного названиями сельскохозяйственной продукции, и
количества продукции в млн. руб. Так как данные взяты за несколько периодов (с
1990 г. по 2006 г.), то они позволят исследовать изменение структуры в сфере
сельского хозяйства.
Таблица 4.6
Группировка численности населения по половому признаку (тыс. человек)
|
Половой признак
|
1990
|
1995
|
2000
|
2001
|
2002
|
2003
|
2004
|
2005
|
2006
|
|
Мужчины
|
607,9
|
609,9
|
580,9
|
571,6
|
562,3
|
553,9
|
545,9
|
537,9
|
531,1
|
|
Женщины
|
721,0
|
715,5
|
685,5
|
677,0
|
668,8
|
660,6
|
653,2
|
646,0
|
639,6
|
Атрибутивные ряды распределения характеризуют состав совокупности по тем
или иным существенным признакам. Взятые за несколько периодов, эти данные
позволят исследовать изменение структуры.
Если группы строятся по количественному признаку, то ряд распределения
называется вариационным. Любой вариационный ряд состоит из двух элементов:
вариантов и частот. Вариантами называются отдельные возможные значения
признака. А частотами - числа, которые показывают, насколько часто встречаются
те или иные варианты в ряду распределения. Сумма всех частот определяет
численность всей совокупности, ее объем. Частоты, выраженные в долях единицы
или в процентах к итогу, называются частостями.
Вариационные ряды в зависимости от характера вариации делят на дискретные
и интервальные.
В дискретных вариационных рядах распределения группы строятся по
признаку, изменяющемуся дискретно, т.е. величина количественного признака
принимает только целые значения. Примером дискретного ряда является
распределение оборота розничной торговли Калужской области по годам,
приведенное в таблице 4.7.
Таблица 4.7
Изменение оборота розничной торговли Калужской области по годам
|
№ п/п
|
Год
|
Оборот розничной торговли,
млн. руб. (1990, 1995г. - млрд. руб.)
|
|
1
|
2004
|
1,9
|
|
2
|
2005
|
2868
|
|
3
|
2006
|
13087
|
|
4
|
2007
|
15996
|
|
5
|
2008
|
18700
|
|
6
|
2009
|
23240
|
|
7
|
2010
|
30525
|
|
8
|
2011
|
37071
|
|
9
|
2012
|
48814
|
Таблица 4.8
Изменение инвестиций в основной капитал по годам
|
№ п/п
|
Год
|
Инвестиции, млн. руб.
(1990, 1995г. - млрд. руб.)
|
|
1
|
2004
|
2,1
|
|
2
|
2005
|
1398
|
|
3
|
2006
|
5425
|
|
4
|
2007
|
6646
|
|
5
|
2008
|
10413
|
|
6
|
2009
|
10112
|
|
7
|
2010
|
15198
|
|
8
|
2011
|
17864
|
|
9
|
2012
|
20887
|
В случае непрерывной вариации величина признака у единиц совокупности
может принимать в определенных пределах любые значения, отличающиеся друг от
друга на сколько угодно малую величину. Ряд, который отражает непрерывную
вариацию признака, называется интервальным вариационным рядом. Построение интервальных
вариационных рядов целесообразно прежде всего при непрерывной вариации
признака, а также если дискретная вариация проявляется в широких пределах, т.е.
число вариантов дискретного признака достаточно велико.
5. РАСЧЕТ ОСНОВНЫХ ХАРАКТЕРИСТИК ВАРИАЦИИ
5.1 Расчет средних величин
Статистическая совокупность содержит некоторое
количество статистических величин, имеющих, как правило, разные значения и
признаки, что делает невозможным сравнение нескольких совокупностей в целом.
Для изучения закономерностей развития социально-экономических явлений в
статистике используются средние величины.
Широкое применение средних величин обусловлено их незаменимостью в
анализе явлений общественной жизни. Средняя величина всегда обобщает
количественное выражение признака и погашает индивидуальные различия
статистических величин совокупности, вызванные случайными обстоятельствами.
Итак, средняя величина - это обобщающий показатель, который дает
количественную характеристику признака в статистической совокупности в условиях
конкретного места и времени.
Средние величины делятся на две основные категории: степенные и
структурные. В данном пункте мы будем находить степенные средние величины, а
именно, среднюю арифметическую, гармоническую и хронологическую, которые
вычислим по следующим формулам:
средняя арифметическая взвешенная:
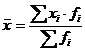 , (5.1)
, (5.1)
где
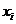 - индивидуальные значения варьирующего признака
(варианты);
- индивидуальные значения варьирующего признака
(варианты);
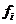 - вес
(частоты) - повторяемость вариант в исследуемой совокупности.
- вес
(частоты) - повторяемость вариант в исследуемой совокупности.
Средняя гармоническая:
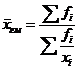 (5.2)
(5.2)
Средняя
хронологическая является разновидностью простой средней арифметической, когда
имеются моментные статистические величины на определенную одинаковую дату.
Формула средней хронологической теоретическому выводу не поддается и
записывается приближенно в виде:
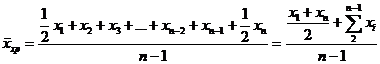 , (5.3)
, (5.3)
где
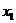 и
и 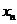 - первое
и последнее значения статистической величины;
- первое
и последнее значения статистической величины;
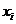 -
промежуточные значения;
-
промежуточные значения;
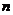 - общее
число значений.
- общее
число значений.
Для
расчета основных и структурных характеристик вариации группировки транспортных
организаций по грузообороту транспорта всех видов деятельности также дополним
таблицу 3.1 столбцами со срединными значениями интервалов (таб. 5.1):
Таблица 5.1
Группы организаций по грузообороту автомобильного транспорта
|
№ п/п
|
Группы транспортных
организаций по грузообороту автомобильного транспорта, млн. тыс. км
|
Количество организаций
|
Середина интервала
|
Накопленное число
организаций
|
|
1
|
843 - 1200
|
13
|
1021,5
|
13
|
|
2
|
1200 - 1557
|
7
|
1378,5
|
20
|
|
3
|
1557 - 1914
|
7
|
1735,5
|
27
|
|
4
|
1914 - 2271
|
5
|
2092,5
|
32
|
|
5
|
2271 - 2628
|
5
|
2449,5
|
37
|
|
6
|
2628 - 2985
|
3
|
2806,5
|
40
|
|
Итого
|
40
|
|
|
Рассчитаем средние величины по формулам (5.1) - (5.3):
Найдем среднюю арифметическую взвешенную(5.1):
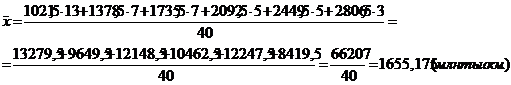
Итак, средний грузооборот автомобильного транспорта составил 1655,175
млн. т. км.
Найдем среднюю гармоническую взвешенную по формуле 5.2:
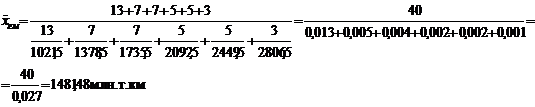
Вычислим
среднюю хронологическую по формуле 5.3:
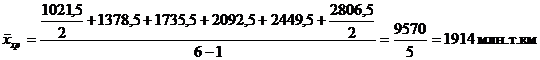
Рассчитаем средние величины на основе таблицы 4.2, а именно по
действующим строительным организациям. Дополним таблицу 4.2 столбцами со
средними значениями интервалов (таб. 5.2).
Таблица 5.2
Группировка действующих строительных организаций
|
№ п/п
|
Действующие строительные
организации
|
Количество строительных
организаций
|
Срединные значения
интервалов
|
Накопленное число
организаций
|
|
1
|
420 - 461
|
10
|
440,5
|
10
|
|
2
|
461 - 502
|
8
|
481,5
|
18
|
|
3
|
502 - 543
|
7
|
522,5
|
25
|
|
4
|
543 - 583
|
6
|
563
|
31
|
|
5
|
583 - 624
|
5
|
603,5
|
36
|
|
6
|
624 - 665
|
4
|
644,5
|
40
|
|
Итого
|
40
|
|
|
Найдем среднюю арифметическую взвешенную по формуле 5.1:
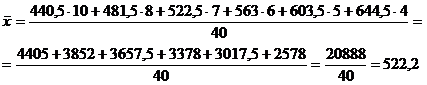
Найдем среднюю гармоническую взвешенную по формуле 5.2:
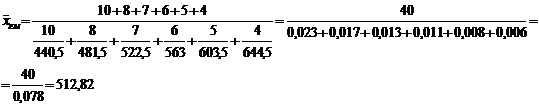
Вычислим
среднюю хронологическую по формуле 5.3:
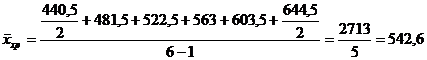
Рассчитаем средние величины на основе таблицы 5.3, а именно по площадям
жилых помещений.
Таблица 5.3
Группировка площадей жилых помещений (в среднем на одного жителя)
|
Группы площадей, м2
|
Численность жилых помещений
|
Середина интервала
|
Накопленное число жилых
помещений
|
|
18,9 - 20,9
|
12
|
19,9
|
12
|
|
20,9 - 22,3
|
8
|
21,6
|
20
|
|
22,3 - 23,7
|
10
|
23
|
30
|
|
Итого
|
30
|
|
|
Найдем среднюю арифметическую взвешенную по формуле 5.1:
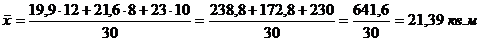
Найдем среднюю гармоническую взвешенную по формуле 5.2:
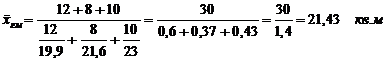
Вычислим
среднюю хронологическую по формуле 5.3:
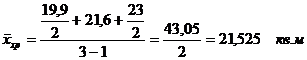
Любая статистическая совокупность состоит из единиц, значения признака
которых варьируют. Для того, чтобы судить об однородности совокупности и
типичности средней величины изучаемого признака, анализ следует дополнять
исчислением показателей вариации.
Вариация - это колеблемость, многообразие, изменяемость величины признака
у отдельных единиц совокупности.
К абсолютным показателям вариации относят: размах вариации, среднее
линейное отклонение, дисперсию и среднее квадратическое отклонение.
Размах вариации - характеристика границ вариации изучаемого признака.
Показывает, сколь велико различие между единицами совокупности, имеющими самое
маленькое и самое большое значение признака, основан на крайних значениях
варьирующего признака и не отражает отклонений всех вариант в ряду.
Определяется по формуле:
=Xmax-Xmin, (5.4)
где Xmax - максимальное значение
вариационного ряда;
Xmin -
минимальное.
Среднее линейное отклонение показывает, на какую величину отклоняется
признак в изучаемой совокупности от средней величины признака. Находится по
формуле:
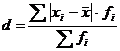 , (5.5)
, (5.5)
где
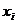 - индивидуальные значения варьирующего признака
(варианты);
- индивидуальные значения варьирующего признака
(варианты); 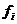 - частоты, веса;
- частоты, веса; 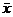 - среднее
значение варьирующего признака;
- среднее
значение варьирующего признака;
Дисперсия - средний квадрат отклонения индивидуальных значений признака
от их средней величины. Вычисляется по следующим формулам.
Первый способ определения дисперсии:
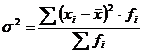 , (5.6)
, (5.6)
Второй
способ определения дисперсии (по средней арифметической):
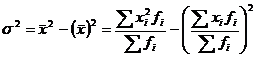 , (5.7)
, (5.7)
где
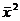 - средняя из квадратов индивидуальных значений;
- средняя из квадратов индивидуальных значений; 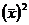 - квадрат средней величины признака.
- квадрат средней величины признака.
Среднее квадратическое отклонение - это обобщающая характеристика
размеров вариации признака в совокупности. Показывает, на какую величину в
среднем значение признака отличается от стандартного значения, определяется по
формуле:
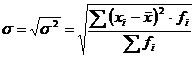 . (5.8)
. (5.8)
Чем меньше значение дисперсии и среднего квадратического отклонения, тем
однороднее (количественно) совокупность и тем более типичной будет средняя
величина.
Рассчитаем показатели вариации для группировки транспортных организаций
по грузообороту автомобильного транспорта (таблица 5.1).
Найдем размах вариации (по формуле 5.4):
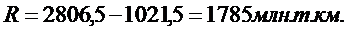
Разброс
значений грузооборота транспорта общественного пользования достаточно высок.
Вычислим
среднее линейное отклонение (по формуле 5.5):
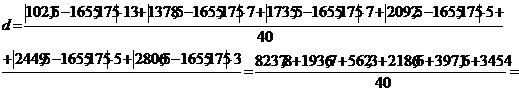
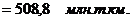
Значения
грузооборота автомобильного транспорта отличались от среднего значения на 508,8
млн. т. км.
Рассчитаем
дисперсию двумя способами (по формулам 5.6 - 5.7). Первый способ:
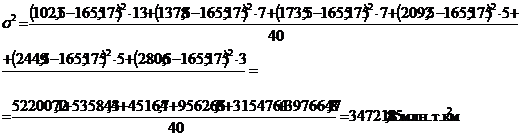
Второй
способ (по средней арифметической):
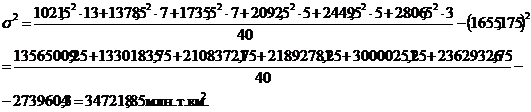
Вычислим среднее квадратическое отклонение (по формуле 5.8):
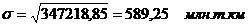 .
.
Это
значит, что грузооборот транспорта общественного пользования в среднем отличается
от стандартного значения на 23,68 млн. т. км.
Найдем
показатели вариации для группировки площадей жилых помещений (таблица 5.3),
используя формулы 5.4 - 5.8
Вычислим
размах вариации:
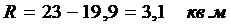
Размах
вариации в 3,1 м2 показывает нам, что разброс значений площадей жилых помещений
не очень высок.
Рассчитаем среднее линейное отклонение:
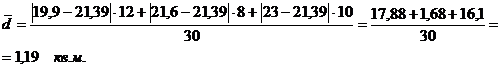
Таким
образом, значения площадей жилых помещений в изучаемой совокупности отклоняются
от средней величины на 1,19 м2.
Рассчитаем
дисперсию двумя способами.
Первый
способ:
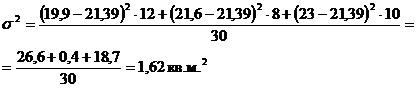
Второй
способ (по средней арифметической):
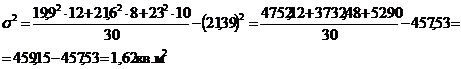
Вычислим
среднее квадратическое отклонение: 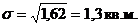
Оно
показывает, что значения площадей жилых помещений в среднем отличается от
стандартного значения на 1,3 м2 .
5.3 Коэффициенты вариации
Вариация измеряется с помощью относительных величин,
называемых коэффициентами вариации и определяемых в виде отношения среднего
отклонения к средней величине. Коэффициент вариации используют не только для
сравнительной оценки вариации единиц совокупности, но и как характеристику
однородности совокупности. Значения коэффициента вариации изменяются от 0 до
100% и чем ближе он к нулю, тем типичнее найденная средняя величина для
изучаемой статистической совокупности, а значит и качественнее подобраны
статистические данные. Совокупность считается количественно однородной, если
коэффициент вариации не превышает 33% (для распределений, близких к
нормальному). Различают следующие относительные показатели вариации:
Коэффициент вариации:
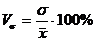 , (5.9)
, (5.9)
где
 - среднее квадратическое отклонение,
- среднее квадратическое отклонение, 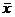 - средняя арифметическая.
- средняя арифметическая.
Линейный
коэффициент вариации:
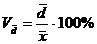 , (5.10)
, (5.10)
где
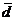 - среднее линейное отклонение.
- среднее линейное отклонение.
Коэффициент осцилляции:
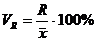 , (5.11)
, (5.11)
где
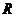 - размах вариации.
- размах вариации.
Вычислим коэффициенты вариации для группы организаций по грузообороту
автомобильного транспорта (таблица 5.1) по формулам 5.9, 5.10, 5.11
Коэффициент
вариации будет равен: 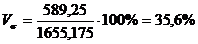 , что превышает 33%, следовательно, совокупность
неоднородна.
, что превышает 33%, следовательно, совокупность
неоднородна.
Вычислим
линейный коэффициент вариации: 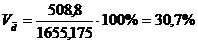 . Следовательно,
доля усредненного значения абсолютных отклонений организаций от средней
величины равна 30,7%
. Следовательно,
доля усредненного значения абсолютных отклонений организаций от средней
величины равна 30,7%
Найдем
коэффициент осцилляции: 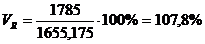 . Из этого следует, что разница между максимальным и
минимальным значениями организаций превышает среднее значение почти в 1,078
раз.
. Из этого следует, что разница между максимальным и
минимальным значениями организаций превышает среднее значение почти в 1,078
раз.
Определим коэффициенты вариации для группировки площадей жилых помещений
(в среднем на одного жителя) (таблица 5.3).
Вычислим коэффициент вариации по формуле (5.9):
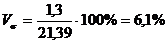 . Это значит
что коэффициент вариации не превышает 33%, следовательно, совокупность
однородна.
. Это значит
что коэффициент вариации не превышает 33%, следовательно, совокупность
однородна.
Рассчитаем
линейный коэффициент вариации по формуле (5.10):
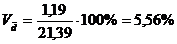 . Это
значит, что доля усредненного значения абсолютных отклонений площадей жилых
помещений от средней величины равна 5,56%.
. Это
значит, что доля усредненного значения абсолютных отклонений площадей жилых
помещений от средней величины равна 5,56%.
Найдем
коэффициент осцилляции по формуле (5.11):
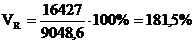 . Разница
между максимальным и минимальным значениями площадей жилых помещений не
превышает среднее значение.
. Разница
между максимальным и минимальным значениями площадей жилых помещений не
превышает среднее значение.
6. РАСЧЕТ И ПОСТРОЕНИЕ СТРУКТУРНЫХ ХАРАКТЕРИСТИК ВАРИАЦИОННОГО РЯДА
.1 Определение моды
Важным видом средних величин являются структурные (непараметрические)
средние. Их используют для изучения внутреннего строения и структуры рядов
распределения значений признака.
Мода - это величина признака (варианта), которая чаще всего встречается в
данной совокупности. В вариационном дискретном ряду модой выступает варианта,
имеющая наибольшую частоту.
В интервальных рядах с равными интервалами мода вычисляется по формуле
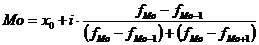 , (6.1)
, (6.1)
где
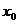 - минимальная граница модального интервала;
- минимальная граница модального интервала;  - величина модального интервала;
- величина модального интервала; 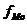 - частота модального интервала;
- частота модального интервала; 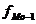 - частота интервала, предшествующего модальному;
- частота интервала, предшествующего модальному; 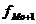 - частота интервала, следующего за модальным.
- частота интервала, следующего за модальным.
Модальный
интервал в интервальном ряду определяется по наибольшей частоте.
Определим моду для группы организаций по грузообороту автомобильного
транспорта (таблица 5.1).
Модальный
интервал - (843 - 1200).  =357;
=357; 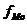 =13,
=13, 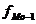 =0,
=0, 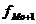 =7.
=7.
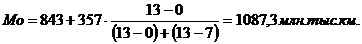 ,
,
т.е.
плотность распределения организаций достигла своего пика вокруг значения
1087,3млн.тыс.км.
Построим
моду на графике.
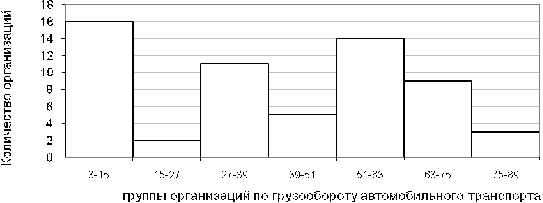
Рис.6.1.
Графическое построение моды для группы организаций по грузообороту
автомобильного транспорта, млн.тыс.км.
Определим моду для группировки действующих строительных организаций
(таблица 5.2).
Интервал
с наибольшей частотой - (420-461).  =41,
=41, 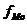 =10,
=10, 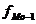 =0,
=0, 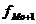 =8.
=8.
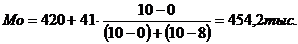 ,
,
т.е.
наиболее часто встречающееся значение организаций 454,2 тыс.
Определим
моду на графике.
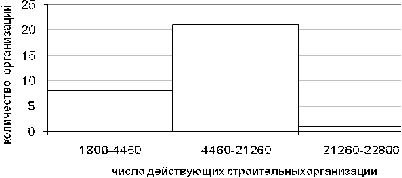
Рис.6.2.
Графическое построение моды для группировки действующих строительных
организаций, тыс.
6.2 Медиана и ее характеристика
Медиана
- это варианта, которая находится в середине вариационного ряда. Медиана делит
ряд пополам, по обе стороны от нее (вверх и вниз) находится одинаковое
количество единиц совокупности.
В
интервальном ряду с равными интервалами медиана рассчитывается по формуле
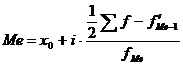 , (6.2)
, (6.2)
где
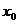 - начальное значение медианного интервала;
- начальное значение медианного интервала;  - величина медианного интервала;
- величина медианного интервала; 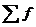 - сумма частот ряда;
- сумма частот ряда; 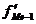 - сумма
накопленных частот в интервалах, предшествующих медианному;
- сумма
накопленных частот в интервалах, предшествующих медианному; 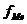 - частота медианного интервала.
- частота медианного интервала.
Для
определения медианного интервала необходимо рассчитать суммы накопленных
частот. Медианный интервал характерен тем, что его кумулятивная частота равна
полусумме всех частот ряда или превышает ее.
Вычислим
медиану для группы организаций по грузообороту автомобильного транспорта
(таблица 5.1).
Сумма
весов равна 40, полусумма - 20. Медианный интервал - (1557 - 1914). 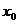 =1557,
=1557,  =357,
=357, 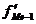 =20,
=20, 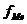 =7.
=7.
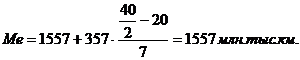 , т.е.
половина организаций имеет значение ниже 1557 млн.тыс.км., а вторая половина -
выше этого значения.
, т.е.
половина организаций имеет значение ниже 1557 млн.тыс.км., а вторая половина -
выше этого значения.
Определим
медиану по графику.
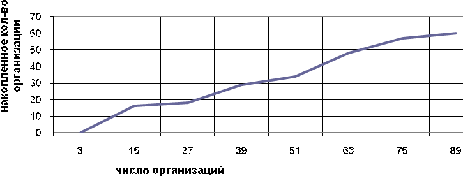
Рис.6.3.
Графическое построение медианы для группы организаций по грузообороту
автомобильного транспорта, млн.тыс.км.
Определим медиану для группировки действующих строительных организаций
(таблица 5.2).
Сумма
весов равна 40, полусумма - 20, значит, медианный интервал - (502-543). 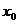 =502,
=502,  =41,
=41, 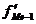 =18,
=18, 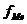 =7.
=7.
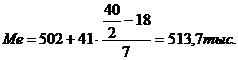
Определим
медиану графически.
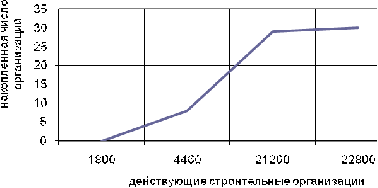
Рис.6.4.
Графическое построение медианы для группировки действующих строительных
организаций, тыс.
.3
Расчет квартилей
Квартили
- значения признака, делящие ранжированную совокупность на четыре равные части.
Нижний
квартиль (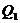 )отделяет ¼ часть совокупности с наименьшими значениями признака. Верхний квартиль
(
)отделяет ¼ часть совокупности с наименьшими значениями признака. Верхний квартиль
(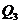 ) отсекает ¼ часть с наибольшими значениями признака. Средний квартиль (
) отсекает ¼ часть с наибольшими значениями признака. Средний квартиль (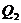 ) совпадает с медианой.
) совпадает с медианой.
Для
расчета квартилей по интервальному вариационному ряду используют формулу
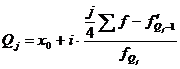 , (6.3)
, (6.3)
где
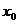 - нижняя граница интервала, содержащего квартиль;
- нижняя граница интервала, содержащего квартиль;  - величина интервала;
- величина интервала; 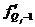 -
накопленная частота интервала, предшествующего интервалу, содержащему квартиль;
-
накопленная частота интервала, предшествующего интервалу, содержащему квартиль;
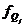 - частота интервала, содержащего квартиль.
- частота интервала, содержащего квартиль.
Рассчитаем
квартили для группы организаций по грузообороту автомобильного транспорта
(таблица 5.1).
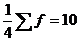 ,
следовательно, нижний квартиль находится в интервале (1200-1557),
,
следовательно, нижний квартиль находится в интервале (1200-1557),  =357,
=357, 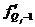 =13,
=13, 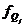 =7.
=7. 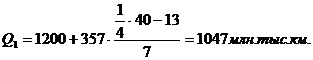 Таким
образом, у 25% организаций, грузооборот меньше 1047млн.тыс.км.
Таким
образом, у 25% организаций, грузооборот меньше 1047млн.тыс.км.
Рассчитаем
квартили для группировки действующих строительных организаций (таблица 5.2).
Вычислим
нижний квартиль. 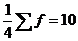 . Значит, интервал, содержащий нижний квартиль -
(461-502).
. Значит, интервал, содержащий нижний квартиль -
(461-502).  =41,
=41, 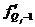 =10,
=10, 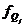 =8.
=8. 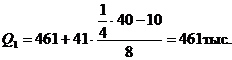 Это указывает
на то, что 25% организаций приносят убыток до 46тыс.
Это указывает
на то, что 25% организаций приносят убыток до 46тыс.
6.4 Расчет децилей
Децили
- варианты, делящие ранжированный ряд на десять равных частей. Вычисляются по
формуле
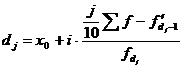 , (6.4)
, (6.4)
где
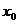 - нижняя граница интервала, содержащего дециль;
- нижняя граница интервала, содержащего дециль;  - величина интервала;
- величина интервала; 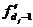 -
накопленная частота интервала, предшествующего интервалу, содержащему дециль;
-
накопленная частота интервала, предшествующего интервалу, содержащему дециль; 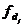 - частота интервала, содержащего дециль.
- частота интервала, содержащего дециль.
Определим
децили для группы организаций по грузообороту автомобильного транспорта
(таблица 5.1). Т.к. 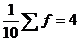 , то первый дециль находится в интервале (843-1200).
Величина интервала составляет 357.
, то первый дециль находится в интервале (843-1200).
Величина интервала составляет 357.
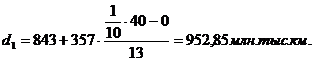 Из этого
следует, что 10% всех организаций имеют грузооборот до 952,85млн. тыс.км.
Из этого
следует, что 10% всех организаций имеют грузооборот до 952,85млн. тыс.км.
Интервал,
содержащий третий дециль также - (843 - 1200), т.к. 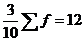 . Величина интервала равна 357.
. Величина интервала равна 357. 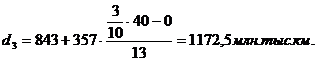 Это значит, что 30% организаций имеют грузооборот
меньше 1172,5млн.тыс.км.
Это значит, что 30% организаций имеют грузооборот
меньше 1172,5млн.тыс.км.
Найдем
пятый дециль: 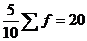 , интервал, который его содержит - (1200 - 1557).
Величина интервала составляет 357.
, интервал, который его содержит - (1200 - 1557).
Величина интервала составляет 357. 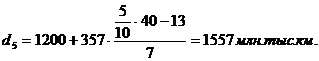 Из этого
следует, что у 50% организаций, грузооборот составляет до 1557млн.тыс.км.
Из этого
следует, что у 50% организаций, грузооборот составляет до 1557млн.тыс.км.
Определим
восьмой дециль: 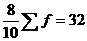 , следовательно, интервал, в который входит восьмой
дециль - (1914 -2271).
, следовательно, интервал, в который входит восьмой
дециль - (1914 -2271). 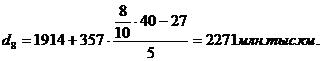 Это указывает на то, что 80% организаций имеют
грузооборот до 2271млн.тыс.км.
Это указывает на то, что 80% организаций имеют
грузооборот до 2271млн.тыс.км.
Вычислим
девятый дециль: 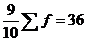 , это значит, что он попадает в интервал (1914-2271).
Величина интервала принимает значение, равное 357.
, это значит, что он попадает в интервал (1914-2271).
Величина интервала принимает значение, равное 357.
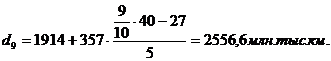 Следовательно,
у 90% организаций грузооборот не больше 2556,6млн.тыс.км.
Следовательно,
у 90% организаций грузооборот не больше 2556,6млн.тыс.км.
6.5 Расчет перцентилей
Перцентили
- значения признака, делящие ряд на 100 равных частей. Вычисляются по формуле
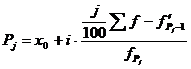 , (6.5)
, (6.5)
где
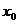 - нижняя граница интервала, содержащего перцентиль;
- нижняя граница интервала, содержащего перцентиль;  - величина интервала;
- величина интервала; 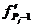 -
накопленная частота интервала, предшествующего интервалу, содержащему
перцентиль;
-
накопленная частота интервала, предшествующего интервалу, содержащему
перцентиль; 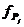 - частота интервала, содержащего перцентиль.
- частота интервала, содержащего перцентиль.
Рассчитаем перцентили для группы организаций по грузообороту
автомобильного транспорта (таблица 5.1).
 Интервал,
в котором находится шестнадцатый перцентиль - (843-1200), т.к.
Интервал,
в котором находится шестнадцатый перцентиль - (843-1200), т.к. 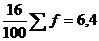 . Величина интервала принимает значение, равное 357.
. Величина интервала принимает значение, равное 357.
 Следовательно,
16% организаций имеют грузооборот не больше 1018,75млн.тыс.км.
Следовательно,
16% организаций имеют грузооборот не больше 1018,75млн.тыс.км.
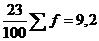 ,
следовательно, интервал, в котором находится 23-й перцентиль - (843-1200).
,
следовательно, интервал, в котором находится 23-й перцентиль - (843-1200). 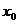 =843,
=843,  =375,
=375, 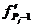 =0,
=0, 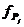 =13.
=13.
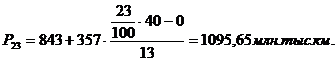 Это
значит, что 23% организаций составляет не более 1095,65млн.тыс.км.
Это
значит, что 23% организаций составляет не более 1095,65млн.тыс.км.
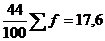 , значит,
интервал, содержащий 44-й перцентиль - (843-1200).
, значит,
интервал, содержащий 44-й перцентиль - (843-1200). 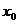 =25,4,
=25,4,  =8,5,
=8,5, 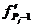 =6,
=6, 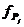 =4.
=4. 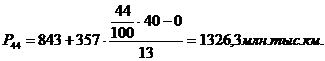 . Следовательно, 44% организаций имеют грузооборот, не
превышающий 1326,3млн.тыс.км.
. Следовательно, 44% организаций имеют грузооборот, не
превышающий 1326,3млн.тыс.км.
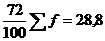 . Из
этого следует, что 72-й перцентиль находится в интервале (1557-1914).
. Из
этого следует, что 72-й перцентиль находится в интервале (1557-1914). 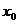 =1557,
=1557,  =357,
=357, 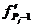 =20,
=20, 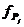 =7.
=7. 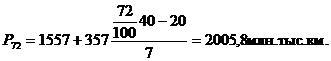 , т.е. у 72% организаций число грузооборота не
превышает 2005,8млн.тыс.км.
, т.е. у 72% организаций число грузооборота не
превышает 2005,8млн.тыс.км.
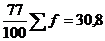 , значит
интервал, в котором находится 77-й перцентиль- (1557-1914).
, значит
интервал, в котором находится 77-й перцентиль- (1557-1914). 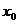 =1557,
=1557,  =357,
=357, 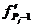 =20,
=20, 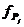 =7.
=7. 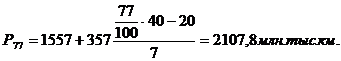 , т.е. 77% организаций имеют грузооборот не больше
2107,8млн.тыс.км.
, т.е. 77% организаций имеют грузооборот не больше
2107,8млн.тыс.км.
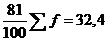 , а это
значит, что 81-й перцентиль находится в интервале (1914-2271).
, а это
значит, что 81-й перцентиль находится в интервале (1914-2271). 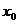 =1914,
=1914,  =357,
=357, 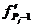 =27,
=27, 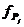 =5.
=5. 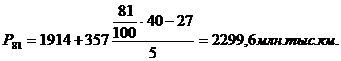 Следовательно, у 81% организаций грузооборот не
превышает 2299,6млн.тыс.км.
Следовательно, у 81% организаций грузооборот не
превышает 2299,6млн.тыс.км.
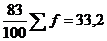 , из
этого следует, что интервал, содержащий 83-й перцентиль - (1914-2271).
, из
этого следует, что интервал, содержащий 83-й перцентиль - (1914-2271). 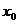 =1914,
=1914,  =357
=357 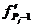 =27,
=27, 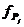 =5.
=5. 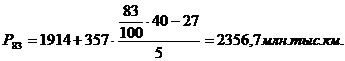 . Это значит, что у 83% организаций грузооборот
составляет не более 2356,7млн.тыс.км.
. Это значит, что у 83% организаций грузооборот
составляет не более 2356,7млн.тыс.км.
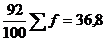 , значит,
92-й перцентиль находится в интервале (1914-2271).
, значит,
92-й перцентиль находится в интервале (1914-2271). 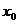 =1914,
=1914,  =357,
=357, 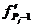 =27,
=27, 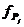 =5.
=5. 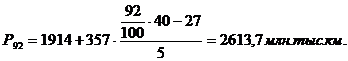 . Следовательно, 92% организаций имеют грузооборот
меньше 2613,7млн.тыс.км.
. Следовательно, 92% организаций имеют грузооборот
меньше 2613,7млн.тыс.км.
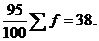 Из этого
следует, что интервал, в котором находится 95-й перцентиль,-(2271-2985).
Из этого
следует, что интервал, в котором находится 95-й перцентиль,-(2271-2985). 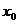 =2271,
=2271,  =357,
=357, 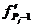 =32,
=32, 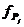 =5.
=5. 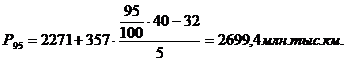 . Значит, у 95% организаций грузооборот не превышает
2699,4млн.тыс.км.
. Значит, у 95% организаций грузооборот не превышает
2699,4млн.тыс.км.
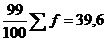 .
Следовательно, интервал, содержащий 99-й перцентиль - (2271-2985).
.
Следовательно, интервал, содержащий 99-й перцентиль - (2271-2985). 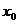 =2271,
=2271,  =357,
=357, 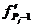 =32,
=32, 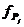 =5.
=5. 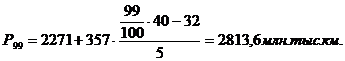 . А это значит, что 99% организаций имеют грузооборот
не более 2813,6млн.тыс.км.
. А это значит, что 99% организаций имеют грузооборот
не более 2813,6млн.тыс.км.
7.
ОБЩАЯ ХАРАКТЕРИСТИКА РАСПРЕДЕЛЕНИЯ ЕДЕНИЦ СОВОКУПНОСТИ
7.1 Расчет центральных моментов
Центральными
называются моменты распределения, при вычислении которых за исходную величину
принимаются отклонения вариантов от средней арифметической данного ряда.
Центральный
момент 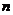 -го порядка вычисляется по формуле
-го порядка вычисляется по формуле
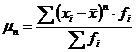 (7.1)
(7.1)
Момент
второго порядка называется дисперсией.
Рассчитаем
моменты третьего и четвертого порядка, которые нам понадобятся для нахождения
показателей асимметрии и эксцесса.
Вычислим
центральные моменты для группы организаций по грузообороту автомобильного
транспорта (таблица 5.1).
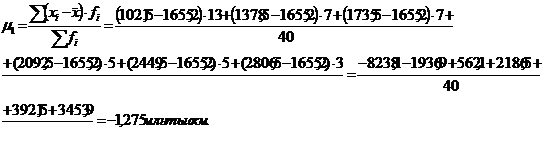
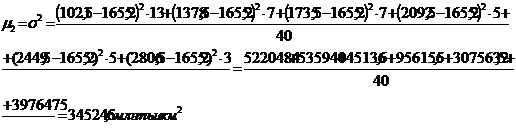
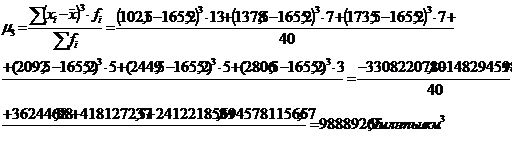
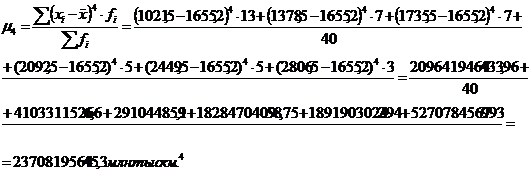
Рассчитаем
центральные моменты для группировки действующих строительных организаций
(таблица 5.2).
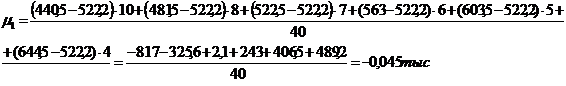
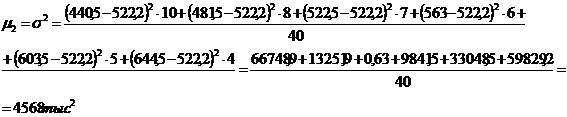
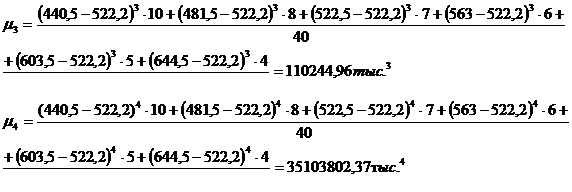
7.2 Расчет асимметрии распределения
Асимметрия распределения вычисляется по следующей формуле
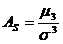 , (7.2)
, (7.2)
где
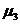 - момент 3-го порядка;
- момент 3-го порядка;  -
среднее квадратическое отклонение.
-
среднее квадратическое отклонение.
Вычислим
асимметрию для группы организаций по грузообороту автомобильного транспорта
(таблица 5.1).
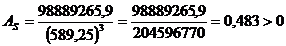 , значит,
наблюдается незначительная правосторонняя асимметрия.
, значит,
наблюдается незначительная правосторонняя асимметрия.
Определим
значение показателя асимметрии для группировки действующих строительных
организаций (таблица 5.2).
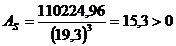 ,
следовательно, имеет место правосторонняя асимметрия распределения.
,
следовательно, имеет место правосторонняя асимметрия распределения.
7.3 Расчет эксцесса распределения
С
помощью момента 4-го порядка характеризуется эксцесс, т.е. крутизна
распределения. Эксцесс вычисляется по формуле
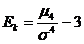 , (7.3)
, (7.3)
где
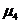 - момент 4-го порядка;
- момент 4-го порядка;  -
среднее квадратическое отклонение.
-
среднее квадратическое отклонение.
Рассчитаем
эксцесс распределения для группы организаций по грузообороту автомобильного
транспорта (таблица 5.1).
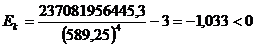 , значит,
распределение плосковершинное.
, значит,
распределение плосковершинное.
Вычислим
эксцесс для группировки действующих строительных организаций (таблица 5.2).
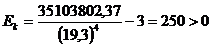 . Это
значит, что имеет место островершинное распределение.
. Это
значит, что имеет место островершинное распределение.
7.4 Оценка однородности совокупности
Во всех исследуемых группировках коэффициент вариации превысил 33%, что
уже говорит о неоднородности данных совокупностей и о том, что средняя величина
признака нетипична для нее. Предположение об отсутствии нормального закона
распределения данных группировок окончательно подтвердилось после нахождения
эксцесса и асимметрии распределения.
В группировке организаций по грузообороту автомобильного транспорта имеет
место незначительная правосторонняя асимметрия, ее показатель составил 0,483.
Эксцесс принял значение, равное -1,033, что говорит о плосковершинном
распределении.
В группировке действующих строительных организаций значение показателя
асимметрии приняло значение 15,3, что указывает на то, что асимметрия -
правосторонняя. Эксцесс составил 250. Это значит, что имеет место
островершинное распределение.
Все вышеперечисленные характеристики формы распределения представленных
нам для анализа вариационных рядов говорят об отсутствии нормального
распределения. Этот результат не явился неожиданным, т.к. в
социально-экономической статистике нормальное распределение практически вообще
не встречается. Однако, сравнение с нормальным распределением важно для
выяснения степени и характера отклонений от фактического распределения.
8. КОРРЕЛЯЦИОННО-РЕГРЕССИОННЫЙ АНАЛИЗ
Корреляция - это статистическая зависимость между случайными величинами,
не имеющими строго функционального характера, при которой изменение одной из
случайных величин приводит к изменению математического ожидания другой.
В статистике принято различать следующие варианты зависимостей.
1. Парная корреляция - связь между двумя признаками (результативными и
факторными или двумя факторными).
2. Частная корреляция - зависимость между результативным и одним
факторным признаками при фиксированном значении других факторных признаков.
. Множественная корреляция - зависимость результативного и двух
или более факторных признаков, включенных в исследование.
Корреляционно-регрессионный
анализ как общее понятие включает в себя измерение тесноты, направления связи и
установление аналитического выражения (формы) связи (регрессионный анализ).
Проанализируем зависимость между расходами консолидированного бюджета,
задолженностям по налогам и сборам в бюджет, и доходами консолидированного
бюджета на примере Калужской области. Данные для анализа представлены в таблице
1.3.
Таблица 8.1
Расчетная таблица для нахождения зависимости между расходами
консолидированного бюджета, задолженностям по налогам и сборам в бюджет, и
доходами консолидированного бюджета
|
Год
|
Расходы консолидированного
бюджета, млн. руб.
|
Задолженности по налогам и
сборам в бюджет, млн.руб.
|
Доходы консолидированного
бюджета, млн.руб.
|
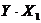
|
|
X1
|
X2
|
Y
|
|
|
1995
|
147
|
38
|
1447
|
212709
|
|
2000
|
433
|
42
|
4445
|
1924685
|
|
2001
|
537
|
43
|
5373
|
2885301
|
|
2002
|
748
|
46
|
7111
|
5319028
|
|
2003
|
860
|
57
|
8481
|
7293660
|
|
2004
|
1148
|
35
|
11523
|
13228404
|
|
ИТОГО
|
3873
|
261
|
38080
|
30863787
|
|
 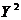 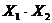 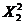 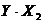
|
|
|
|
|
|
21609
|
2093809
|
5586
|
1444
|
54986
|
|
187489
|
19758025
|
18186
|
1764
|
186690
|
|
288369
|
28869129
|
23091
|
1849
|
231039
|
|
559504
|
50566321
|
34408
|
2116
|
327106
|
|
739600
|
71927361
|
49020
|
3249
|
483417
|
|
1317904
|
132779529
|
40180
|
1225
|
403305
|
|
3114475
|
305994174
|
170471
|
11647
|
1686543
|
Выясним, существует ли связь между исследуемыми признаками графическим
способом. Для этого представим данные зависимости на графике (рис. 8.1 и 8.2) и
добавим линию тренда. На графике видно, что между исследуемыми показателями
существует прямо пропорциональная связь, т.е. с увеличением числа расходов
растут и доходы Калужской области.
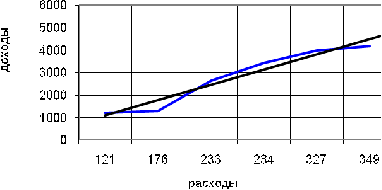
Рис. 8.1. График зависимости доходов Калужской области от расходов
Зависимость между доходами и расходами имеет линейный характер и выражена
обратной функцией.
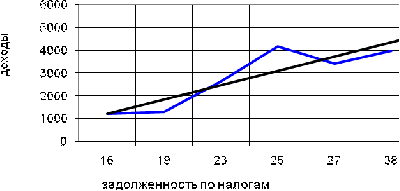
Рис. 8.2. График зависимости доходов Калужской области от задолженности
по налогам
График зависимости линейный, так как график состоит из ломаной линии.
Выясним обратная она или нет аналитически.
График
зависимости представляет собой линейную функцию вида 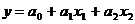 .
.
Система уравнений для данного исследования будет иметь вид:
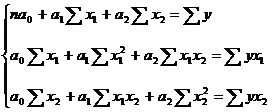
Система уравнений примет вид:
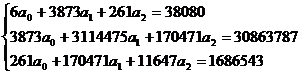
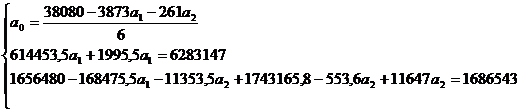
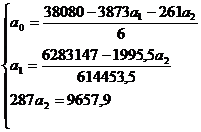
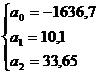
Рассчитаем частные коэффициенты эластичности, которые используются с
целью расширения возможностей экономического анализа. Они находятся по следующей
формуле:
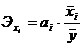 , (8.1)
, (8.1)
где
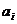 - коэффициент регрессии при соответствующем факторном
признаке;
- коэффициент регрессии при соответствующем факторном
признаке; 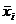 - среднее значение соответствующего факторного
признака;
- среднее значение соответствующего факторного
признака; 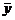 - среднее значение результативного признака, которые
находятся по формулам:
- среднее значение результативного признака, которые
находятся по формулам:
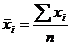 , (8.2)
, (8.2)
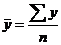 (8.3)
(8.3)
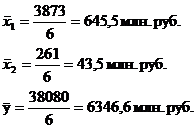
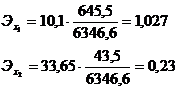
Это
значит, что при увеличении числа расходов на 1%, число доходов Калужской
области увеличится на 1,027%, а при увеличении задолженности по налогам на 1%
доходы увеличатся на 0,23%.
Рассчитаем
частные коэффициенты детерминации по формуле
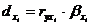 , (8.4)
, (8.4)
где
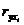 - парный коэффициент корреляции между результативным
и
- парный коэффициент корреляции между результативным
и  -м факторным признаками;
-м факторным признаками; 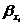 - соответствующий коэффициент уравнения множественной
регрессии в стандартизированном масштабе.
- соответствующий коэффициент уравнения множественной
регрессии в стандартизированном масштабе.
Парный
коэффициент корреляции находится по формуле:
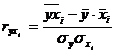 (8.5)
(8.5)
Рассчитаем
парный коэффициент корреляции между результативным и первым факторным
признаками, т.е. между доходами и расходами.
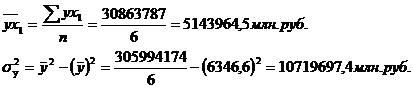
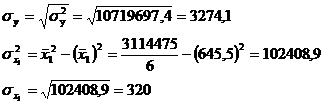
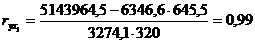 . Т.е.
связь между признаками прямая и однонаправленная.
. Т.е.
связь между признаками прямая и однонаправленная.
Рассчитаем
парный коэффициент корреляции между результативным и вторым факторным
(задолженности по налогам) признаками.
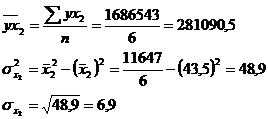
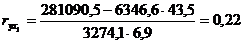 .
Значение коэффициента говорит о том, что между признаками существует прямая
связь.
.
Значение коэффициента говорит о том, что между признаками существует прямая
связь.
Найдем
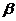 -коэффициент по формуле:
-коэффициент по формуле:
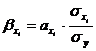 , (8.6)
, (8.6)
где
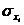 - среднее квадратическое отклонение
- среднее квадратическое отклонение  -го фактора;
-го фактора; 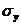 -
среднее квадратическое отклонение результативного признака.
-
среднее квадратическое отклонение результативного признака.
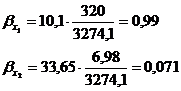
Тогда
частные коэффициенты детерминации составят:
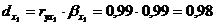
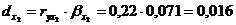
Из этого следует, что на 98% вариация доходов Калужской области
объясняется изменением числа расходов, и 1,6% вариации - изменением
задолженности по налогам в бюджет.
Найдем

 -
коэффициент по формуле:
-
коэффициент по формуле:
 =
=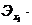
 V
V , (8.7)
, (8.7)
где
V =
= 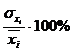 ,
следовательно
,
следовательно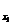 =
= 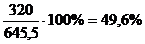

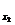 =
=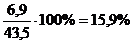


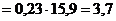
Значимость
коэффициентов регрессии определяется с помощью 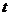 -критерия
Стьюдента:
-критерия
Стьюдента:
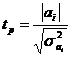 , (8.8)
, (8.8)
где
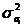 - дисперсия коэффициента регрессии.
- дисперсия коэффициента регрессии.
Наиболее
простой способ определения дисперсии заключается в том, что величина дисперсии
коэффициента регрессии может быть приближенно определена по выражению:
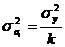 , (8.9)
, (8.9)
где
 - дисперсия результативного признака;
- дисперсия результативного признака; 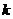 - число факторных признаков в уравнении.
- число факторных признаков в уравнении.
Определим
дисперсию коэффициента регрессии по формуле (8.9).
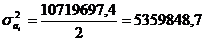 .
.
Вычислим
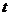 -критерий Стьюдента для
-критерий Стьюдента для 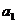 по
формуле (8.8):
по
формуле (8.8):
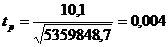 .
.
Вычислим
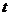 -критерий Стьюдента для
-критерий Стьюдента для 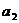 :
:
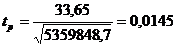 .
.
Проанализируем зависимость ВРП от числа предприятий и численности
экономически активного населения на примере Калужской области. Данные для
анализа представлены в таблице 8.2.
Таблица 8.2
Расчетная таблица для нахождения зависимости ВРП Калужской области от
числа предприятий и численности экономически активного населения
|
Год
|
ВРП, млн. руб. (1995г. -
млрд. руб.)
|
Число предприятий
|
Численность экономически
активного населения, тыс. чел.
|
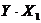
|
|
Y
|
X1
|
X2
|
|
|
1995
|
94835,1
|
53606
|
1627
|
5083730371
|
|
2000
|
69319
|
1697
|
39566605874
|
|
2001
|
753119,2
|
73598
|
1730
|
55428066882
|
|
2002
|
898722,4
|
78202
|
1759
|
70281889125
|
|
2003
|
1117514,4
|
83306
|
1788
|
93095654606
|
|
2004
|
1536733,7
|
88303
|
1815
|
135698195911,1
|
|
2005
|
2224295,7
|
95126
|
1824
|
211588352758,2
|
|
ИТОГО
|
7196010,7
|
541460
|
12240
|
610742495526,5
|
|
 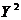 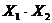 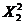 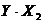
|
|
|
|
|
|
2873603236
|
8993696192,01
|
87216962
|
2647129
|
154296707,7
|
|
4805123761
|
352801452416,04
|
117634343
|
2879809
|
968630969,4
|
|
5416665604
|
567188529408,64
|
127324540
|
1992900
|
1302896216
|
|
6115552804
|
807701952261,76
|
137557318
|
3094081
|
1580852702
|
|
6939889636
|
1248838434207,36
|
148951128
|
3196944
|
1998115747
|
|
7797419809
|
2361550464715,69
|
160269945
|
3294225
|
2789171666
|
|
9048955876
|
4947491361038,49
|
173509824
|
3326976
|
405115357
|
|
42997210726
|
10267565890240
|
952464060
|
21432064
|
12851079364,2
|
Выясним, существует ли связь между исследуемыми признаками графическим
способом. Для этого представим данные зависимости на графике (рис. 8.3 и 8.4) и
добавим линию тренда. На графике видно, что между исследуемыми показателями
существует прямо пропорциональная связь, т.е. с увеличением числа предприятий и
экономически активного населения растет и ВРП Калужской области.
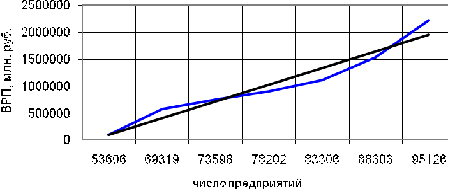
Рис. 8.3. График зависимости ВРП Калужской области от числа предприятий.
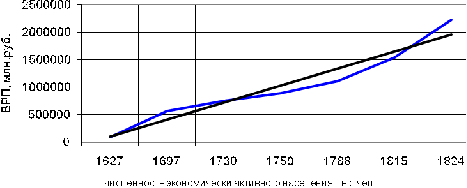
Рис. 8.4. График зависимости ВРП Калужской области от численности
экономически активного населения
График
зависимости представляет собой линейную функцию вида 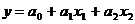 .
.
Система уравнений для данного исследования будет иметь вид:
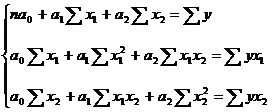
Система уравнений примет вид:
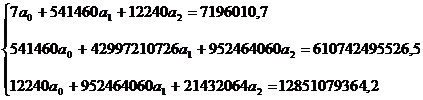
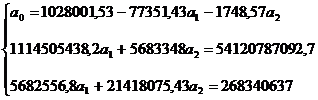
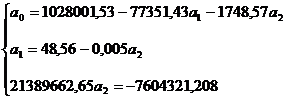
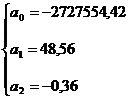
Рассчитаем частные коэффициенты эластичности, которые используются с
целью расширения возможностей экономического анализа. Они находятся по
следующей формуле:
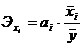 , (8.1)
, (8.1)
где
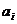 - коэффициент регрессии при соответствующем факторном
признаке;
- коэффициент регрессии при соответствующем факторном
признаке; 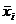 - среднее значение соответствующего факторного
признака;
- среднее значение соответствующего факторного
признака; 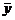 - среднее значение результативного признака, которые
находятся по формулам:
- среднее значение результативного признака, которые
находятся по формулам:
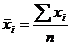 , (8.2)
, (8.2)
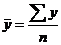 (8.3)
(8.3)
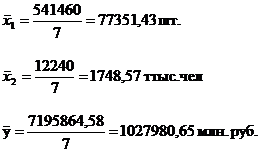
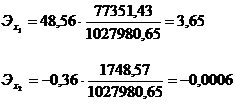
Это
значит, что при увеличении числа предприятий на 1% уровень ВРП Калужской
области увеличится на 3,65%, а при увеличении численности экономически
активного населения на 1% ВРП снизится на 0,0006%.
Рассчитаем
частные коэффициенты детерминации по формуле
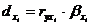 , (8.4)
, (8.4)
где
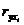 - парный коэффициент корреляции между результативным
и
- парный коэффициент корреляции между результативным
и  -м факторным признаками;
-м факторным признаками; 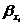 - соответствующий коэффициент уравнения множественной
регрессии в стандартизированном масштабе.
- соответствующий коэффициент уравнения множественной
регрессии в стандартизированном масштабе.
Парный
коэффициент корреляции находится по формуле:
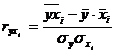 (8.5)
(8.5)
Рассчитаем
парный коэффициент корреляции между результативным и первым факторным
признаками, т.е. между ВРП и числом предприятий.
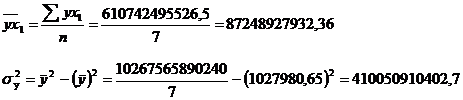
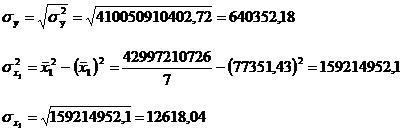
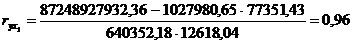 . Т.е.
связь между признаками прямая и однонаправленная.
. Т.е.
связь между признаками прямая и однонаправленная.
Рассчитаем
парный коэффициент корреляции между результативным и вторым факторным
(численность экономически активного населения) признаками.
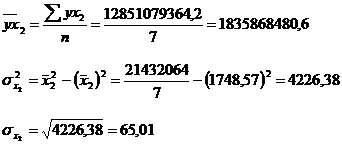
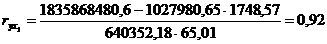 .
Значение коэффициента говорит о том, что между признаками существует прямая
связь.
.
Значение коэффициента говорит о том, что между признаками существует прямая
связь.
Найдем
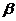 -коэффициент по формуле
-коэффициент по формуле
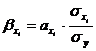 , (8.6)
, (8.6)
где
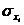 - среднее квадратическое отклонение
- среднее квадратическое отклонение  -го фактора;
-го фактора; 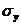 -
среднее квадратическое отклонение результативного признака.
-
среднее квадратическое отклонение результативного признака.

Тогда
частные коэффициенты детерминации составят:
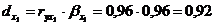
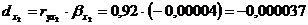
Из этого следует, что на 92% вариация ВРП Калужской области объясняется
изменением числа предприятий, и 0,0037% вариации - изменением численности
экономически активного населения.
Найдем

 Q -
коэффициент по формуле:
Q -
коэффициент по формуле:
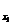 =
=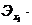
 V
V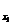

 , (8.7)
, (8.7)
Где
V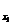
 =
= 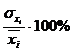 , следовательно
, следовательно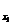
 =
= 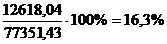
 Q
Q 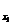
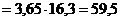
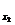 =
=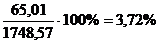
 Q
Q 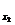
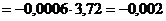
Значимость
коэффициентов регрессии определяется с помощью 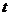 -критерия
Стьюдента:
-критерия
Стьюдента:
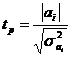 , (8.8)
, (8.8)
где
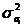 - дисперсия коэффициента регрессии.
- дисперсия коэффициента регрессии.
Наиболее
простой способ определения дисперсии заключается в том, что величина дисперсии
коэффициента регрессии может быть приближенно определена по выражению:
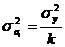 , (8.9)
, (8.9)
где
 - дисперсия результативного признака;
- дисперсия результативного признака; 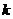 - число факторных признаков в уравнении.
- число факторных признаков в уравнении.
Определим
дисперсию коэффициента регрессии по формуле (8.9).
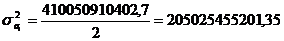 .
.
Вычислим
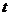 -критерий Стьюдента для
-критерий Стьюдента для 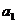 по
формуле (8.8):
по
формуле (8.8):
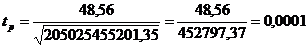 .
.
Вычислим
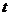 -критерий Стьюдента для
-критерий Стьюдента для 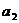 :
:
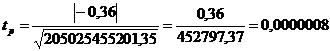 .
.
9. ИССЛЕДОВАНИЕ ДИНАМИКИ СОЦИАЛЬНО - ЭКОНОМИЧЕСКИХ ПРОЦЕССОВ РЕГИОНА
Для исследования динамики численности населения Калужской области по
исходным данным таблицы 1.1. «Демографические показатели» необходимо рассчитать
следующие показатели и построить таблицу:
абсолютный прирост
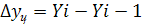
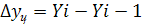 , (9.1.)
, (9.1.)
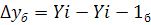
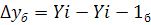 (9.2.)
(9.2.)
темп роста, %:
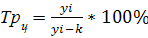
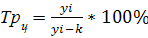 , (9.3.)
, (9.3.)
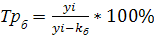
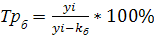 (9.4.)
(9.4.)
темп прироста:
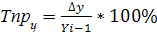
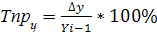 , (9.5.)
, (9.5.)
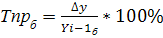
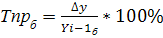 (9.6.)
(9.6.)
абсолютное значение:
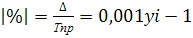
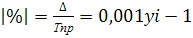 (9.7.)
(9.7.)
средний абсолютный прирост:
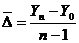 (9.8.)
(9.8.)
средний темп роста:
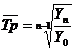 (9.9.)
(9.9.)
средний
годовой темп роста:
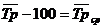 (9.10.)
(9.10.)
|
Годы
|
Численность населения,
тыс.чел.
|
Абсолютный прирост
|
Темп роста,%
|
Темп прироста
|
Абсолютное значение 1%
прироста
|
|
|
цепной
|
базис.
|
цепной
|
базис.
|
цепной
|
базис.
|
|
|
2004
|
1328,9
|
-
|
-
|
-
|
100
|
-
|
-
|
13,289
|
|
2005
|
1325,4
|
-3,5
|
-3,5
|
99,7
|
99,7
|
-0,2
|
-0,2
|
13254
|
|
2006
|
1266,4
|
-59
|
-62,5
|
95,5
|
95,2
|
-4,4
|
-4,7
|
12,664
|
|
2007
|
1248,6
|
-17,8
|
-81,3
|
98,5
|
93,8
|
-1,4
|
-6,04
|
12,486
|
|
2008
|
1231,1
|
-17,5
|
-97,8
|
98,5
|
92,6
|
-1,4
|
-7,3
|
12,311
|
|
2009
|
1214,5
|
-16,6
|
-114,4
|
99,7
|
91,3
|
-1,3
|
-8,6
|
12,145
|
|
2010
|
1199,1
|
-15,4
|
-129,8
|
98,7
|
90,2
|
-1,2
|
-9,7
|
11,991
|
|
2011
|
1183,9
|
-15,2
|
-145
|
98,7
|
89,08
|
-1,2
|
-10,9
|
11,839
|
|
2012
|
1170,7
|
-13,2
|
-158,2
|
98,8
|
88,09
|
-1,1
|
-11,9
|
11,707
|
Далее находим средний абсолютный прирост по формуле 9.8.:
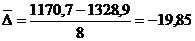 ;
;
Также
необходимо рассчитать средний темп роста по формуле 9.9. и средний годовой темп
прироста (9.10.):
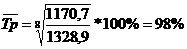
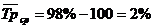
Для
исследования динамики численности действующих строительных организаций
Московского края по исходным данным таблицы 1.8. «Строительство» рассчитали
необходимые показатели и построили таблицу:
|
Годы
|
Число действующих
строительных организаций
|
Абсолютный прирост
|
Темп роста, %
|
Темп прироста
|
Абсолютное значение 1%
прироста
|
|
|
цепной
|
базис
|
цепной
|
базис
|
цепной
|
базис
|
|
|
2004
|
665
|
-
|
-
|
-
|
100
|
-
|
-
|
665
|
|
2005
|
457
|
-208
|
-208
|
119,6
|
119,6
|
-31,2
|
-31,2
|
4,57
|
|
2006
|
420
|
-37
|
-245
|
127,9
|
63,1
|
-8
|
-36,8
|
4,2
|
|
2007
|
421
|
1
|
-244
|
100,2
|
63,3
|
-0,2
|
-36,6
|
4,21
|
|
2008
|
470
|
49
|
-195
|
111,6
|
70,6
|
11,6
|
-29,3
|
4,7
|
|
2009
|
455
|
-15
|
-210
|
96,8
|
68,4
|
-3,1
|
-31,5
|
4,55
|
|
2010
|
438
|
-17
|
-227
|
96,2
|
65,8
|
-3,7
|
-34,1
|
4,38
|
|
2011
|
445
|
7
|
-220
|
101,5
|
66,9
|
1,5
|
-33
|
4,45
|
Далее находим средний абсолютный прирост по формуле 9.8.:
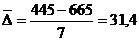 ;
;
Также
рассчитываем средний темп роста по формуле 9.9. и средний годовой темп прироста
(9.10.):
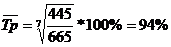
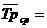 94%-100 =
-6%
94%-100 =
-6%
10. РАСЧЕТ ЭКОНОМИЧЕСКИХ ИНДЕКСОВ
Индексы относят к важнейшим обобщающим показателям статистики.
Индекс - это относительный показатель сравнения двух состояний простого
или сложного явления, состоящего из соизмеримых или несоизмеримых элементов, во
времени и пространстве.
В
теории индексного метода приняты следующие условные обозначения: 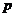 - цена за единицу товара,
- цена за единицу товара, 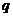 - объем продукта в натуральном выражении,
- объем продукта в натуральном выражении, 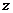 - себестоимость единицы продукции.
- себестоимость единицы продукции.
Индивидуальный
индекс характеризует динамику уровня изучаемого явления во времени за два
сравниваемых периода или выражает соотношение отдельных элементов совокупности.
Индивидуальный
индекс физического объема продукции находится по формуле
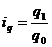 (10.1)
(10.1)
Индивидуальный
индекс цен рассчитывается следующим образом
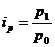 (10.2)
(10.2)
Индивидуальный
индекс себестоимости единицы продукции находят по следующей формуле
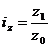 (10.3)
(10.3)
Если показатели каждого периода последовательно сравниваются с
показателями непосредственно предшествующего периода, то индексы называются
цепными.
Определим цепные и базисные индивидуальные индексы цен и физического
объема продукции по данным таблицы 9.1.
Таблица 10.1
Реализация
угля в Калужской области
|
Год
|
Цена за 1 т., руб.
|
Произведено, тыс. т
|
|
2005
|
8600
|
159732
|
|
2006
|
8200
|
98249
|
|
2007
|
9300
|
127050
|
|
2008
|
10210
|
129463
|
|
2009
|
10670
|
132592
|
|
2010
|
12400
|
145712
|
|
2011
|
12870
|
157391
|
Вычислим цепные индексы цен:
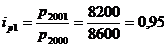 . Это
значит, что цены на уголь в 2006г. по сравнению с 2000-м годом изменились в
0,95 раз (уменьшились на 95%).
. Это
значит, что цены на уголь в 2006г. по сравнению с 2000-м годом изменились в
0,95 раз (уменьшились на 95%).
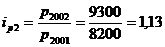 .
Следовательно, цены на уголь в 2007 г. по сравнению с 2001-м годом выросли на
13%.
.
Следовательно, цены на уголь в 2007 г. по сравнению с 2001-м годом выросли на
13%.
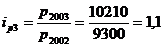 . Из
этого следует, что цены на уголь в 2008г. по сравнению с 2002 годом увеличились
на 10%.
. Из
этого следует, что цены на уголь в 2008г. по сравнению с 2002 годом увеличились
на 10%.
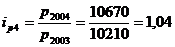 . Т.е.
цены на уголь в 2009г. выросли на 4% по сравнению с 2003 годом.
. Т.е.
цены на уголь в 2009г. выросли на 4% по сравнению с 2003 годом.
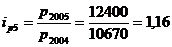 .
Следовательно, в 2010 году цены на уголь возросли на 16% по сравнению с 2004
годом.
.
Следовательно, в 2010 году цены на уголь возросли на 16% по сравнению с 2004
годом.
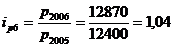 .
Значение данного индекса показывает, что по сравнению с 2011 годом цены на
уголь в 2006 году увеличились на 4%.
.
Значение данного индекса показывает, что по сравнению с 2011 годом цены на
уголь в 2006 году увеличились на 4%.
Из
этого можно сделать вывод о том, что цены на уголь в 2006 году незначительно
снизились, а затем с каждым годом начали расти. Самый большой скачок цен - на
16% - произошел в 2008 году.
Вычислим
базисные индексы цен. За базисный период примем 2006г.
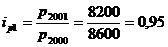 . Цены на
уголь в 2007 году уменьшились по сравнению с базисным годом на 95%.
. Цены на
уголь в 2007 году уменьшились по сравнению с базисным годом на 95%.
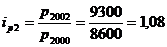 . По
сравнению с базисным периодом цены на уголь в 2008 году выросли на 8%.
. По
сравнению с базисным периодом цены на уголь в 2008 году выросли на 8%.
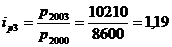 . Цены на
уголь в 2009 году по сравнению с 2006 годом выросли на 19%.
. Цены на
уголь в 2009 году по сравнению с 2006 годом выросли на 19%.
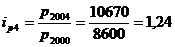 . В 2010
году цены на уголь по сравнению с 2006 годом выросли на 24%.
. В 2010
году цены на уголь по сравнению с 2006 годом выросли на 24%.
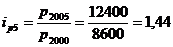 . Это
значит, что на 44% выросли цены на уголь в 2011 году по сравнению с базисным
2006 годом.
. Это
значит, что на 44% выросли цены на уголь в 2011 году по сравнению с базисным
2006 годом.
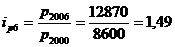 .
Следовательно, в 2012 году цены на уголь выросли на 49% по сравнению с базисным
периодом.
.
Следовательно, в 2012 году цены на уголь выросли на 49% по сравнению с базисным
периодом.
Просчитав
базисные индексы цен, можно сказать, что с 2006 года, взятого за базисный
период, цены на уголь постепенно увеличивались, и в 2012 году скачок в цене
составил 49%.
Определим
цепные индивидуальный индексы физического объема продукции.
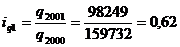 .
Следовательно, объемы производства угля в 2006 году по сравнению с 2005 годом
изменились в 0,62 раз, или уменьшились на 38%.
.
Следовательно, объемы производства угля в 2006 году по сравнению с 2005 годом
изменились в 0,62 раз, или уменьшились на 38%.
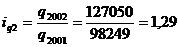 . Т.е.
объем производства угля в 2007 году вырос на 29% по сравнению с 2006 годом.
. Т.е.
объем производства угля в 2007 году вырос на 29% по сравнению с 2006 годом.
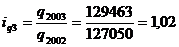 . В 2008
году угля было произведено больше на 2%, чем в предыдущий год.
. В 2008
году угля было произведено больше на 2%, чем в предыдущий год.
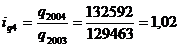 .
Следовательно, объемы производства угля в Калужской области в 2009 году
увеличились на 2% по сравнению с 2006 годом.
.
Следовательно, объемы производства угля в Калужской области в 2009 году
увеличились на 2% по сравнению с 2006 годом.
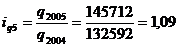 . Из
этого следует, что в 2010 году угля было произведено больше, чем в 2006 году на
9%.
. Из
этого следует, что в 2010 году угля было произведено больше, чем в 2006 году на
9%.
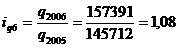 . В 2011
году объемы производства угля увеличились на 8% по сравнению с предыдущим
годом.
. В 2011
году объемы производства угля увеличились на 8% по сравнению с предыдущим
годом.
Из
всего вышеперечисленного можно сделать вывод о том, что в 2006 году произошел
спад производства угля на 38%, но затем с каждым годом объемы его производства
увеличивались. Самый большой скачок в производстве угля (на 29%) пришелся на
2007 год.
Найдем
базисные индексы физического объема продукции. За основной период примем 2007
год.
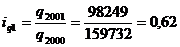 . Объемы
производства угля в 2006 году уменьшились по сравнению с базисным годом на 38%.
. Объемы
производства угля в 2006 году уменьшились по сравнению с базисным годом на 38%.
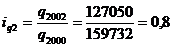 . По
сравнению с базисным периодом объемы производства угля в 2006 году снизились на
20%.
. По
сравнению с базисным периодом объемы производства угля в 2006 году снизились на
20%.
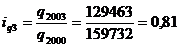 . Объемы
производства угля в 2007 году по сравнению с 2006 годом уменьшились на 19%.
. Объемы
производства угля в 2007 году по сравнению с 2006 годом уменьшились на 19%.
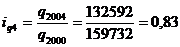 . В 2008
году объемы производства угля по сравнению с 2006 годом снизились на 17%.
. В 2008
году объемы производства угля по сравнению с 2006 годом снизились на 17%.
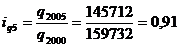 . Это
значит, что на 9% уменьшились объемы производства угля в 2009 году по сравнению
с базисным 2006 годом.
. Это
значит, что на 9% уменьшились объемы производства угля в 2009 году по сравнению
с базисным 2006 годом.
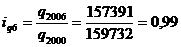 .
Следовательно, в 2010 году объемы производства угля в Калужской области
снизились на 1% по сравнению с базисным годом.
.
Следовательно, в 2010 году объемы производства угля в Калужской области
снизились на 1% по сравнению с базисным годом.
Таким
образом, в 2006 году в Калужской области произошел спад производства угля на
38%. Далее с каждым годом объемы производства угля росли, но достигнуть уровня
базисного года не смогли.
Общий
(сводный) индекс характеризует обобщающие результаты совместного изменения всех
единиц, образующих статистическую совокупность.
Общий
индекс физического объема продукции показывает, во сколько раз возросла
(уменьшилась) стоимость продукции в отчетном периоде по сравнению с базисным
периодом в результате изменения физического объема ее производства и
рассчитывается по следующей формуле
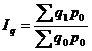 (10.4)
(10.4)
Общий
индекс стоимости продукции (товарооборота) показывает, во сколько раз возросла
(уменьшилась) стоимость продукции в отчетном периоде по сравнению с базисным
периодом за счет изменения цен на товары и объемов их производства или реализации
и находится по формуле
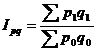 (10.5)
(10.5)
Общий
индекс цен показывает влияние цен на стоимость товаров, произведенных в
отчетном периоде, т.е. во сколько возросла (уменьшилась) стоимость продукции в
отчетном периоде по сравнению с базисным периодом в результате изменения цен.
Этот индекс рассчитывается по формуле
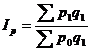 (10.6)
(10.6)
Общий
индекс себестоимости продукции показывает, во сколько раз изменились издержки
производства продукции в отчетном периоде по сравнению с базисным периодом в
результате изменения себестоимости продукции, и находится по следующей формуле
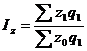 (10.7)
(10.7)
Общий
индекс физического объема продукции, взвешенный по себестоимости продукции показывает,
во сколько раз изменились издержки производства продукции в отчетном периоде по
сравнению с базисным периодом в результате роста (уменьшения) объема ее
производства. Этот индекс находится по формуле
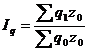 . (10.8)
. (10.8)
ЗАКЛЮЧЕНИЕ
В данной курсовой работе были представлены данные о населении, трудовой
деятельности, уровню жизни населения, социальной сфере, промышленности,
строительстве, торговле, пассажирскому транспорту и пассажирообороте, а также о
инвестициях Калужской области.
На основе вышеуказанных данных были произведены различные статистические
расчеты, всевозможные таблицы и графики, были рассчитаны показатели вариации,
были рассчитаны основные показатели динамики и экономические индексы.
Анализ группировки транспортных организаций установил, что средний
грузооборот автомобильного транспорта составляет 1788,256 млн. т. км. Признак в
данной совокупности отклоняется от средней величины примерно на 823 млн. т. км.
В целом, совокупность оказалась неоднородной, коэффициент вариации составил
38,4%. Расчет показателей асимметрии и эксцесса показал, что распределение
плосковершинное и имеет место правосторонняя асимметрия.
Исследование группировки площадей жилых помещений показало, что средний
размер площади равен 28,39 м2. Значения жилых помещений в изучаемой
совокупности отклоняются от средней величины на 7,62 м2. Коэффициент вариации
составил 6,1%, что говорит о неоднородности изучаемой совокупности. Показатели
асимметрии и эксцесса составили соответственно 15,3 и 250. Это указывает на
наличие правосторонней асимметрии и островершинного распределения.
В результате выборочного обследования жилищных условий жителей г.
Нижневартовска, проведенного на основе собственно-случайной выборки установили,
средний размер жилой площади, приходящейся на одного человека, по городу
Нижневартовску находится в пределах от 18,88 до 19,14 м2.
Был проведен 20%-ный бесповторный типический отбор рабочих с предприятий
Калужской области, в результате которого определили, что среднее число дней временной
нетрудоспособности одного рабочего лежит в пределах от 43,77 до 45,12 дней.
Установлено наличие прямо пропорциональной связи между показателем ВРП
Калужской области и числом предприятий, и незначительной обратно
пропорциональной связи между уровнем ВРП и численностью экономически активного
населения. В результате определения частных коэффициентов эластичности было
установлено, что при увеличении числа предприятий на 1% уровень ВРП Калужской
области увеличится на 3,65%, а при увеличении численности экономически
активного населения на 1% ВРП снизится на 0,0006%. С помощью показателя
частного коэффициента детерминации установили, что на 92% вариация ВРП
Тюменской области объясняется изменением числа предприятий, и 0,0037% вариации
- изменением численности экономически активного населения.
В результате вычисления индивидуальных экономических индексов по
производству и реализации угля в Калужской области было установлено, что цены
на уголь в 2001 году незначительно снизились, а затем с каждым годом начали
расти. Самый большой скачок цен - на 16% - произошел в 2005 году. В 2001 году
произошел спад производства угля на 38%, но затем с каждым годом объемы его
производства увеличивались.
Вычислив общие индексы по реализации продуктов питания в Калужской области,
можно сказать, что в результате ежегодного увеличения цен на данную продукцию
росло и значение товарооборота. Самый большой рост товарооборота был
зафиксирован в 2004 году, когда вследствие изменения цен и объемов производства
стоимость продукции возросла на 24%, или на 2070 млн. рублей.
Расчет сводных индексов по таким товарам, как ткани, трикотажные изделия
и обувь, показал, что в результате ежегодного роста себестоимости продукции
росли и издержки производства. А объемы производства на данную продукцию с 2002
года по 2004г. сокращались, что приводило к сокращению издержек производства.
Но в 2005 году произошел значительный подъем производства тканей, а в 2006 году
также имел место рост объема производства обуви, что повлияло на увеличение
издержек производства на данную продукцию на 11789,6 рублей (или на 19%) по
сравнению с предыдущим годом.
В заключении можно отметить, что выполнение данной курсовой работы
позволило приобрести навыки по обработке массивов статистических данных,
представлении их в удобном для восприятия и анализа виде и получить знания
методологических основ статистики в области анализа социально-экономических
явлений.
СПИСОК ИСПОЛЬЗОВАННОЙ ЛИТЕРАТУРЫ
1. Статистика:
учебник / под ред. И.И. Елисеевой. М.: Высшее образование, 2006
2. Теория
статистики / под ред. Проф. Р.А. Шмойловой. М.: Финансы и статистика, 2004
. Статистика
/ под ред. В.Г. Ионина. М.: ИНФРА-М, 2001
. Социально-экономическая
статистика: учебник для вузов / под ред. Б.И. Башкатова. М.: ЮНИТИ-ДАНА, 2002
. Статистика:
учебник / под ред. В.С. Мхитаряна. М.: Экономистъ, 2005
. Экономическая
статистика: учебник / под ред. Ю.Н. Иванова. М.: ИНФРА-М, 2004
. Статистика:
учебное пособие в схемах и таблицах / Н.М. Гореева, Л.Н. Демидова, Л.М.
Клигозуб, С.А. Орехов; под общей ред. Д-ра наук, проф. С.А. Орехова. - М.:
Эксмо, 2007
. Социальная
статистика / под ред. И.И. Елисеевой. М.: Финансы и статистика, 2001
. Социальная
статистика: учебник / под ред. И.И. Елисеевой. 3-е изд., перераб. И доп. М.:
Финансы и статистика, 2001.
. Регионы
России. Социально-экономические показатели. 2007: Стат. Сб. / Росстат. - М.,
2007
. Регионы
России. Основные характеристики субъектов РФ 2002.: Стат. Сб. / Госкомстат
России. - М., 2002
12. Статистика:
Учебно-методическое пособие к курсовой работе для студентов специальности
060800/ Сост. Т.Н. Плотникова; КГТУ, Красноярск, 2002. 124с.