Численные методы решения нелинейных уравнений, используемые в прикладных задачах. Нахождение корня уравнения методом простой итерации и методом хорд
Федеральное
агентство по образованию
ФГОУ СПО
«Уфимский авиационный техникум»
Курсовая
работа
Численные
методы решения нелинейных уравнений, используемые в прикладных задачах.
Нахождение корня уравнения методом простой итерации и методом хорд
по дисциплине
«Численные методы»
КР
080802.10.038.03 ПЗ
Студент А.Б.
Бобронников
Руководитель
работы Э.Р. Ахматсафина
Содержание
Введение
. Теоретическая часть
.1 Метод простой итерации
.2 Метод хорд
. Постановка и решение задачи
.1. Формулировка задачи
.2 Решение методом простых итераций
.3 Решение методом хорд
. Программная реализация
.1 Метод итераций
.1.1. Блок схема
.1.2 Программа
.1.3 Тестовый пример
.1.4 Решение задачи с помощью ЭВМ
.2 Метод хорд
.2.1 Блок схема
.2.2 Программа
.2.3 Тестовый пример
.2.4 Решение задачи с помощью ЭВМ
Заключение
Список используемой литературы
Введение
Прямые (или точные) методы, позволяют найти решение за определённое
количество шагов. Итерационные методы, основаны на использовании повторяющегося
процесса и позволяют получить решение в результате последовательных
приближений.
Метод хорд и метод простой итерации - два итерационных метода нахождения
корня уравнения.
В этой курсовой речь пойдёт о приближённом нахождении корней уравнения 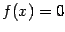 . Дело в том, что решить уравнение
"точно", то есть выразить его корни
. Дело в том, что решить уравнение
"точно", то есть выразить его корни 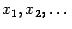 через известные постоянные (целые
числа, числа
через известные постоянные (целые
числа, числа 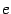 ,
, 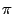 и другие им подобные) с помощью элементарных функций от этих
постоянных, удаётся далеко не всегда. Результат же всё равно получится
приближённый, поскольку вычислять дроби и корни в решении придётся приближённо.
и другие им подобные) с помощью элементарных функций от этих
постоянных, удаётся далеко не всегда. Результат же всё равно получится
приближённый, поскольку вычислять дроби и корни в решении придётся приближённо.
Цель: рассмотреть два метода нахождения приближенного корня уравнения и
применить их на практике:
метод хорд
метод простой итерации.
Состав курсовой работы:
Первая часть - Теоретическая:
В ней описывается теоретическая часть обоих методов.
Вторая часть - Практическая:
В ней реализована практическая реализация обоих методов.
Третья часть - Программная:
В ней реализованы методы с помощью программного языка ЭВМ.
1.
Теоретическая часть
.1 Метод
простой итерации
Предположим, что уравнение 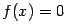 при помощи некоторых тождественных
преобразований приведено к виду
при помощи некоторых тождественных
преобразований приведено к виду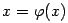 .
.
Заметим, что такое преобразование можно вести разными способами, и при
этом будут получаться разные функции 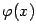 в правой части уравнения. Уравнение
в правой части уравнения. Уравнение 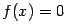 эквивалентно уравнению
эквивалентно уравнению 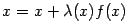 при любой функции
при любой функции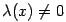 . Таким образом, можно взять
. Таким образом, можно взять 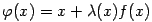 и при этом выбрать функцию (или
постоянную)
и при этом выбрать функцию (или
постоянную) 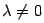 так, чтобы функция
так, чтобы функция 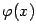 удовлетворяла тем свойствам, которые
понадобятся нам для обеспечения нахождения корня уравнения.
удовлетворяла тем свойствам, которые
понадобятся нам для обеспечения нахождения корня уравнения.
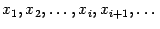
Для нахождения корня уравнения 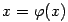 выберем какое-либо начальное
приближение
выберем какое-либо начальное
приближение 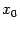 (расположенное, по возможности, близко к корню
(расположенное, по возможности, близко к корню  ). Далее будем вычислять последующие
приближения
). Далее будем вычислять последующие
приближения
по формулам
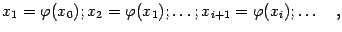
то есть используя каждое вычисленное приближение к корню в качестве
аргумента функции 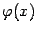 в очередном вычислении. Такие вычисления по одной и той же
формуле
в очередном вычислении. Такие вычисления по одной и той же
формуле 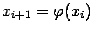 , когда полученное на предыдущем шаге
значение используется на последующем шаге, называются итерациями. Итерациями
называют часто и сами значения
, когда полученное на предыдущем шаге
значение используется на последующем шаге, называются итерациями. Итерациями
называют часто и сами значения 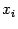 , полученные в этом процессе (то есть, в нашем случае,
последовательные приближения к корню).
, полученные в этом процессе (то есть, в нашем случае,
последовательные приближения к корню).
Заметим: тот факт, что  - корень уравнения
- корень уравнения 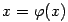 , означает, что
, означает, что  есть абсцисса точки пересечения
графика
есть абсцисса точки пересечения
графика 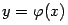 с прямой y=x. Если же при каком-либо
с прямой y=x. Если же при каком-либо 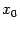 вычислено значение
вычислено значение 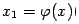 и взято в качестве нового аргумента
функции, то это означает, что через точку графика
и взято в качестве нового аргумента
функции, то это означает, что через точку графика  проводится горизонталь до прямой y=x,
а оттуда опускается перпендикуляр на ось
проводится горизонталь до прямой y=x,
а оттуда опускается перпендикуляр на ось 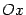 . Там и будет находиться новый
аргумент
. Там и будет находиться новый
аргумент 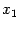 .
.
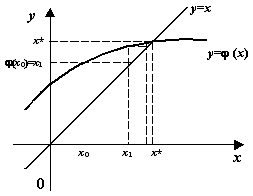
Рисунок 1. Точка  - решение уравнения
- решение уравнения 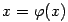 . Построение точки x1 по точке x0
. Построение точки x1 по точке x0
Проследим, как изменяются последовательные приближения xi при различных
вариантах взаимного расположения графика 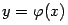 и прямой y=x.
и прямой y=x.
). График 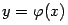 расположен, по крайней мере в некоторой окрестности корня,
включающей начальное приближение x0, в некотором угле со сторонами, имеющими
наклон менее
расположен, по крайней мере в некоторой окрестности корня,
включающей начальное приближение x0, в некотором угле со сторонами, имеющими
наклон менее 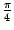 к
горизонтали (то есть стороны угла - прямые
к
горизонтали (то есть стороны угла - прямые
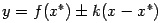
где 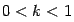 ):
):
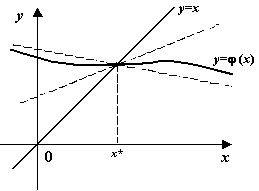
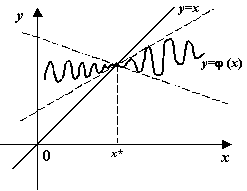
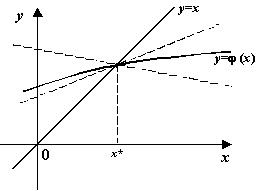
Рисунок 2. График пересекает прямую y=x под малым углом: варианты
расположения
Если предположить вдобавок, что функция 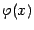 имеет производную
имеет производную 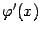 , то этот случай соответствует тому,
что выполнено неравенство
, то этот случай соответствует тому,
что выполнено неравенство 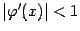 , при
, при 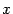 , близких к корню
, близких к корню  . Проследим в этом случае за
поведением последовательных приближений
. Проследим в этом случае за
поведением последовательных приближений 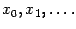
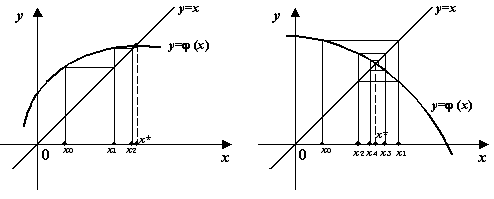
Рисунок 3. Сходящиеся к корню приближения в случае 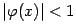 : два варианта
: два варианта
Мы видим, что каждое следующее приближение 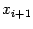 будет в этом случае расположено ближе
к корню
будет в этом случае расположено ближе
к корню  , чем предыдущее приближение
, чем предыдущее приближение 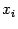 . При этом, если график при
. При этом, если график при 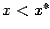 лежит ниже горизонтали
лежит ниже горизонтали 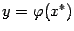 , а при
, а при 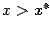 -- выше её (что, в случае наличия
производной, верно, если
-- выше её (что, в случае наличия
производной, верно, если 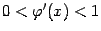 ), то приближения
), то приближения 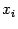 ведут себя монотонно: если
ведут себя монотонно: если 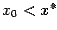 , то последовательность
, то последовательность 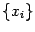 монотонно возрастает и стремится к
монотонно возрастает и стремится к  , а если
, а если 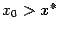 , то монотонно убывает и также
стремится к
, то монотонно убывает и также
стремится к  . Если же график функции
. Если же график функции 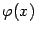 лежит выше горизонтали
лежит выше горизонтали 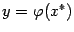 при
при 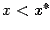 и ниже её при
и ниже её при 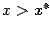 (это так, если
(это так, если 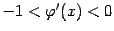 ), то последовательные приближения
), то последовательные приближения 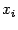 ведут себя иначе: они
"скачут" вокруг корня
ведут себя иначе: они
"скачут" вокруг корня  , с каждым скачком приближаясь к нему, но так же стремятся к
, с каждым скачком приближаясь к нему, но так же стремятся к  при
при 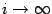 .
.
Заметим, что если функция 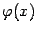 не монотонна в окрестности точки
не монотонна в окрестности точки  , то последовательные приближения
могут вести себя нерегулярно (то есть не монотонно и не оказываясь попеременно
то левее, то правее корня, а делая скачки относительно корня при произвольных
номерах (см. следующий рисунок):
, то последовательные приближения
могут вести себя нерегулярно (то есть не монотонно и не оказываясь попеременно
то левее, то правее корня, а делая скачки относительно корня при произвольных
номерах (см. следующий рисунок):
хорда
итерация приближение уравнение
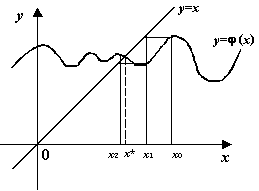
Рисунок 4. В случае немонотонной функции 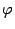 сходящиеся итерации могут вести себя
нерегулярно
сходящиеся итерации могут вести себя
нерегулярно
). График 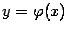 расположен, по крайней мере в некоторой окрестности корня,
вне некоторого угла со сторонами, имеющими наклон более
расположен, по крайней мере в некоторой окрестности корня,
вне некоторого угла со сторонами, имеющими наклон более 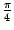 к горизонтали (то есть стороны угла -
прямые
к горизонтали (то есть стороны угла -
прямые 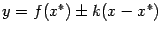 , где
, где 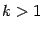 )
)
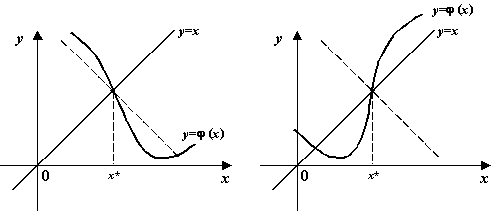
Рисунок 5. График пересекает прямую 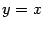 под большим углом: варианты
расположения
под большим углом: варианты
расположения
Если функция 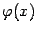 имеет производную
имеет производную 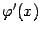 , то в этом случае при
, то в этом случае при 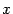 , близких к корню
, близких к корню  , выполнено неравенство
, выполнено неравенство 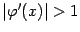 .
.
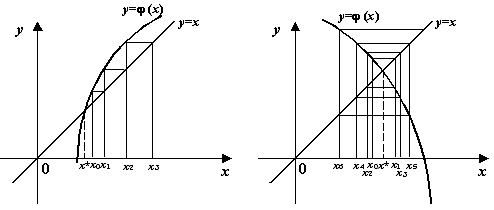
Рисунок 6. Числа 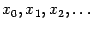 расходятся в случае
расходятся в случае 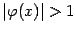 : два варианта
: два варианта
Каждая следующая итерация 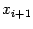 будет в этом случае расположена дальше от корня
будет в этом случае расположена дальше от корня  , чем предыдущая,
, чем предыдущая, 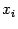 . При этом, в зависимости от того,
пересекает ли график прямую
. При этом, в зависимости от того,
пересекает ли график прямую 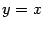 "снизу вверх" или "сверху вниз" (см.
рисунок.6 ), последовательность
"снизу вверх" или "сверху вниз" (см.
рисунок.6 ), последовательность 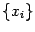 монотонно удаляется от корня
монотонно удаляется от корня  или же итерации удаляются от
или же итерации удаляются от  , оказываясь попеременно то справа,
то слева от корня.
, оказываясь попеременно то справа,
то слева от корня.
Ещё одно замечание: если не выполнено ни условие 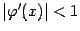 , ни условие
, ни условие 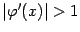 , то итерации
, то итерации 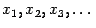 могут зацикливаться. На чертеже ниже
приведён пример зацикливания, когда уравнение имеет вид
могут зацикливаться. На чертеже ниже
приведён пример зацикливания, когда уравнение имеет вид 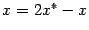 .
.
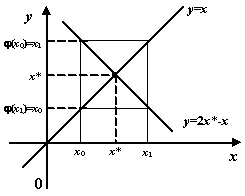
Рисунок 7. Пример зацикливания итераций
Мы видим, что для сходимости итераций к корню, вообще говоря, не
обязательно наличие производной у функции 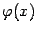 . Однако метод итераций гораздо удобнее
формулировать в терминах, связанных со значениями производной. Именно так мы и
сформулируем наши наблюдения в виде теоремы.
. Однако метод итераций гораздо удобнее
формулировать в терминах, связанных со значениями производной. Именно так мы и
сформулируем наши наблюдения в виде теоремы.
Теорема Если функция 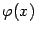 имеет производную в некоторой окрестности
имеет производную в некоторой окрестности 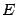 корня
корня  уравнения
уравнения 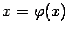 , причём
, причём 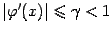 при
при 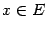 , то последовательность итераций
, то последовательность итераций 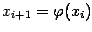 , полученных при
, полученных при 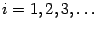 , начиная с
, начиная с 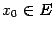 , сходится к корню
, сходится к корню  .
.
При этом скорость сходимости задаётся неравенствами
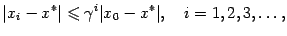
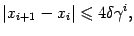
где 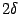 -- длина окрестности
-- длина окрестности 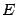 , а точность
, а точность 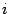 -го приближения -- оценкой
-го приближения -- оценкой
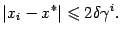
Доказательство. Пусть 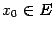 . По формуле конечных приращений, применённой к отрезку между
точками
. По формуле конечных приращений, применённой к отрезку между
точками 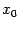 и
и  , получаем
, получаем
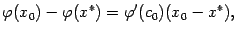
где 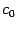 лежит между
лежит между 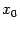 и
и  . Значит,
. Значит, 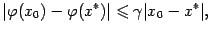 то есть
то есть 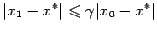 (напомним, что
(напомним, что 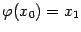 и
и 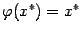 ). Повторяя рассуждения для точек
). Повторяя рассуждения для точек 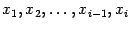 вместо
вместо 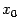 , получаем
, получаем
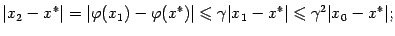
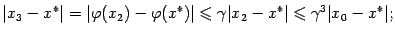

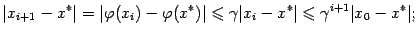

Так как 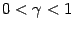 , последовательность
, последовательность 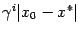 стремится к 0 при
стремится к 0 при 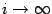 . Значит,
. Значит,  при
при 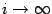 .
.
Неравенство 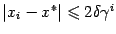 очевидно, поскольку из того, что
очевидно, поскольку из того, что 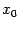 и
и  лежат в окрестности
лежат в окрестности 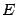 длины
длины 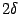 , следует, что
, следует, что 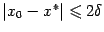 .
.
Поскольку
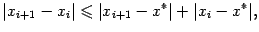
мы имеем
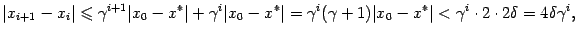
так как 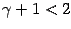 и
и 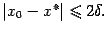
Определение Доказанные оценки показывают, что скорость сходимости
итераций к корню не меньше, чем у геометрической прогрессии со знаменателем 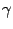 , где
, где 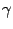 -- величина, ограничивающая сверху
абсолютную величину производной. Тем самым, чем меньше
-- величина, ограничивающая сверху
абсолютную величину производной. Тем самым, чем меньше 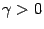 , тем быстрее сходятся итерации.
Наиболее быстро они будут сходиться, если график
, тем быстрее сходятся итерации.
Наиболее быстро они будут сходиться, если график 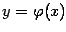 пересекает прямую
пересекает прямую 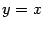 , имея горизонтальную касательную, то
есть при
, имея горизонтальную касательную, то
есть при 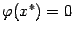 (и, разумеется, при выборе начального
приближения
(и, разумеется, при выборе начального
приближения 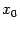 достаточно близко к корню
достаточно близко к корню  , так чтобы на отрезке между
, так чтобы на отрезке между 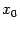 и
и  производная мало отличалась от 0).
производная мало отличалась от 0).
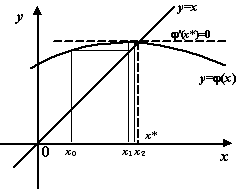
Рисунок 8. Быстрая сходимость итераций при горизонтальной касательной к
графику
Выше мы отмечали, что привести уравнение 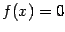 к виду
к виду  можно, выбирая
можно, выбирая 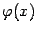 в виде
в виде
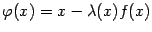
где 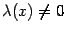 -- произвольная функция. При различных способах выбора
-- произвольная функция. При различных способах выбора 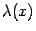 получаются разные модификации метода
итераций, которые имеют отличающиеся свойства: разную скорость сходимости (но
не меньшую той, что гарантирована теоремой) и разную потребность в вычислении
значений функции
получаются разные модификации метода
итераций, которые имеют отличающиеся свойства: разную скорость сходимости (но
не меньшую той, что гарантирована теоремой) и разную потребность в вычислении
значений функции 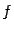 или
или 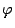 , а также их производных.
, а также их производных.
1.2 Метод
хорд
Идея метода состоит в том, что по двум точкам 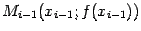 и
и 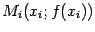 построить прямую
построить прямую 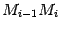 (то есть хорду, соединяющую две точки
графика
(то есть хорду, соединяющую две точки
графика 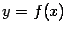 ) и взять в качестве следующего
приближения
) и взять в качестве следующего
приближения 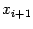 абсциссу точки пересечения этой прямой с осью
абсциссу точки пересечения этой прямой с осью 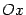 . Иными словами, приближённо заменить
на этом шаге функцию
. Иными словами, приближённо заменить
на этом шаге функцию 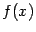 её линейной интерполяцией, найденной по двум значениям
её линейной интерполяцией, найденной по двум значениям 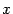 :
: 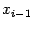 и
и 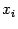 . (Линейной интерполяцией функции
. (Линейной интерполяцией функции 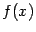 назовём такую линейную функцию
назовём такую линейную функцию 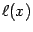 , значения которой совпадают со
значениями
, значения которой совпадают со
значениями 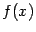 в двух фиксированных точках, в данном случае - в точках
в двух фиксированных точках, в данном случае - в точках 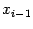 и
и 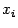 )
)
В зависимости от того, лежат ли точки 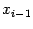 и
и 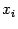 по разные стороны от корня
по разные стороны от корня  или же по одну и ту же сторону,
получаем такие чертежи
или же по одну и ту же сторону,
получаем такие чертежи
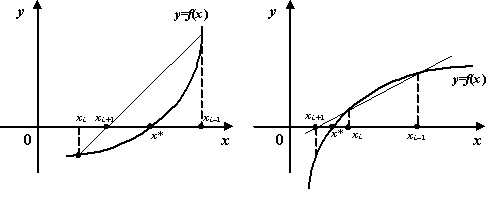
Рисунок 9. Построение последовательного приближения по методу хорд: два
случая
Итак, очередное последовательное приближение будет зависеть от двух
предыдущих:  . Найдём выражение для функции
. Найдём выражение для функции 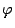 .
.
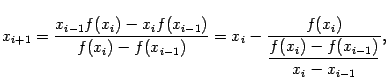
Интерполяционную линейную функцию 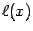 будем искать как функцию с угловым
коэффициентом, равным разностному отношению
будем искать как функцию с угловым
коэффициентом, равным разностному отношению
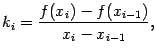
построенному для отрезка между 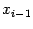 и
и 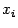 , график которой проходит через точку
, график которой проходит через точку
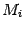
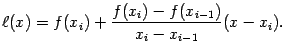
Решая уравнение 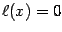 , находим
, находим
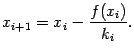
Заметим, что величина 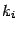 может
рассматриваться как разностное приближение для производной
может
рассматриваться как разностное приближение для производной 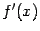 в точке
в точке 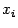 . Тем самым полученная формула (1) --
это разностный аналог итерационной формулы метода Ньютона.
. Тем самым полученная формула (1) --
это разностный аналог итерационной формулы метода Ньютона.
Вычисление по формуле (1) гораздо предпочтительнее вычисления по другой
полученной нами формуле
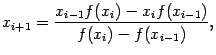
хотя эти две формулы математически тождественны, поскольку при
использовании формулы (1) в случае вычислений с округлениями (например, на
компьютере) достигается меньшая потеря значащих цифр.
Вычисления ведутся непосредственно по формуле (1) при 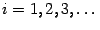 , начиная с двух приближений
, начиная с двух приближений 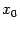 и
и 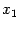 , взятых, по возможности, поближе к
корню
, взятых, по возможности, поближе к
корню  . При этом не предполагается, что
. При этом не предполагается, что  лежит между
лежит между 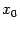 и
и 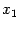 (и что значения функции f в точках
(и что значения функции f в точках 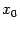 и
и 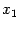 имеют разные знаки). При этом не
гарантируется, что корень попадёт на отрезок между
имеют разные знаки). При этом не
гарантируется, что корень попадёт на отрезок между 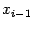 и
и 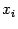 на каком-либо следующем шаге (хотя
это и не исключено). В таком случае затруднительно дать оценку погрешности, с
которой
на каком-либо следующем шаге (хотя
это и не исключено). В таком случае затруднительно дать оценку погрешности, с
которой 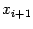 приближает истинное значение корня
приближает истинное значение корня  , и поэтому довольствуются таким
эмпирическим правилом: вычисления прекращают, когда будет выполнено неравенство
, и поэтому довольствуются таким
эмпирическим правилом: вычисления прекращают, когда будет выполнено неравенство
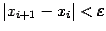 , где
, где 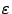 - желаемая точность нахождения
корня. При этом полагают приближённое значение корня равным
- желаемая точность нахождения
корня. При этом полагают приближённое значение корня равным 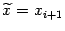 .
.
2. Постановка и решение задачи
.1
Формулировка задачи
Численные
методы решения нелинейных уравнений, используемые в прикладных задачах.
Нахождение корня уравнения методом простой итерации и методом хорд (на примере
уравнения 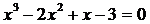 ).
).
Решение:
Разделяем
уравнение на две составляющие:
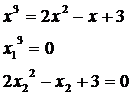
Составляем
таблицу значений для обоих уравнений:
|
Y
|
-2,00
|
-1,00
|
0,00
|
1,00
|
2,00
|
3,00
|
|
X1
|
-8
|
-1
|
0
|
1
|
8
|
27
|
|
X2
|
13
|
6
|
3
|
4
|
9
|
18
|
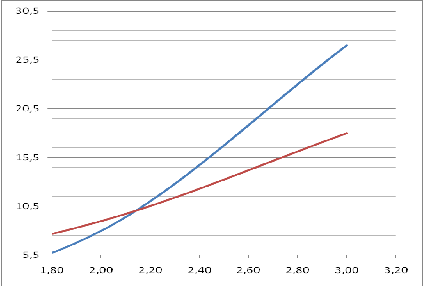
Рисунок 10. График пересечения двух функций
Ответ: Корень находится на отрезке [2;3]
2.2 Решение
методом простой итерации
Уравнение: x3-2x2+x-3=0
Заменим уравнение на x=x-1/5(x3-2x2+x-3);
Погрешность E=0,0001;
Отрезок [2;3];
Найдем корень равнения с помощью последовательности итераций:
X0=2;
X1=2-1/5(23-2*22+2-3)=
2,2 2,2-2>0,0001
X2=2,2-1/5(2,23-2*2,22+2,2-3)=
2,1664 2,1664-2,2>0,00013=2,1664-1/5(2,16643-2*2,16642+2,1664-3)=
2,17693 2,17693-2,1664>0,00014=2,17693-1/5(2,176933-2*2,176932+2,17693-3)= 2,17385 2,17385-2,17693>0,00015=2,17385-1/5(2,173853-2*2,173852+2,17385-3)= 2,17477 2,17477-2,17385>0,00016=2,17477-1/5(2,174773-2*2,174772+2,17477-3)= 2,1745 2,1745-2,17477>0,0001=2,1745-1/5(2,17453-2*2,17452+2,1745-3)= 2,17458 2,17458-2,1745<0,0001
Рисунок 11. График пересечения функции с y=x
Ответ: Корень уравнения с точностью 0,0001 равен 2,1745;
2.3 Решение
методом хорд
Уравнение: x3-2x2+x-3=0
Формула для решения:
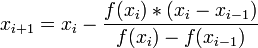
Погрешность: Е=0,00001;
X0=0;
X1=3;
Последовательность итераций:
X2=3-(f(3)*(3-0))/(f(3)-f(0))=
1,5;
|1,5-3|>0,00001 Продолжаем считать
X3=1,5-(f(1,5)*(1,5-3))/(f(1,5)-f(3))= 1,838709;
|1,838709-1,5|>0,00001 Продолжаем считать
X4=1,838709-(f(1,838709)*( 1,838709-1,5))/(f(1,838709)-f(1,5))= 2,46809;
|2,46809-1,838709|>0,00001 Продолжаем считать
X5=2,46809-(f(2,46809)*( 2,46809-1,838709))/(f(2,46809)-f(1,838709))= 2,10549;
|2,10549-2,468709|>0,00001 Продолжаем считать
X6=2,10549-(f(2,10549)*(2,10549-2,46809))/(f(2,10549)-f(2,46809))= 2,16185;
|2,16185-2,10549|>0,00001 Продолжаем считать
X7=2,16185-(f(2,16185)*( 2,16185-2,10549))/(f(2,16185)-f(2,10549))= 2,17519;
|2,17519-2,16185|>0,00001 Продолжаем считать
X8=2,17519-(f(2,17519)*( 2,17519-2,16185))/(f(2,17519)-f(2,16185))= 2,174553;
|2,174-2,175|>0,00001 Продолжаем считать
X9=2,174553-(f(2,174553)*( 2,174553-2,17519))/(f(2,174553)-f(2,17519))= 2,174559;
|2,174553-2,174559|<0,00001 Требуема точность была достигнута
Ответ: Корень уравнения, на отрезке [2;3], с точностью 0,00001, равен
2,174559.
3.
Программная реализация
.1 Метод
простой итерации
.1.1 Блок
схема
.1.2
Программа
unit Unit1;
interface
uses, Messages, SysUtils, Variants, Classes, Graphics,
Controls, Forms,, StdCtrls;= class(TForm): TEdit;: TEdit;: TButton;:
TEdit;Button1Click(Sender: TObject);
{ Private declarations }
{ Public declarations };
: TForm1;
{$R *.dfm}
TForm1.Button1Click(Sender:
TObject);x0,e,y:real;f(c:real):real;:=c*c*c-2*c*c+c-3;;:=strtofloat(edit1.text);:=strtofloat(edit2.text);:=x0-f(x0)/5;(abs(y-x0)>e)
do:=y;:=x0-f(x0)/5;;.text:=floattostrf(y,ffFixed, 20,5);;
end.
.1.3 Тестовый
пример
Для тестового примера возьмем уравнение х-3=0
Начальная точка: 0
Погрешность: Е=0,0001
Ответ: 3

3.1.4 Решение
задачи с помощью ЭВМ

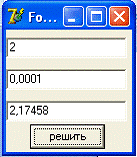
3.2
Метод хорд
.2.1
Блок схема
.2.2
Программа
Unit1;
, Messages, SysUtils, Variants, Classes, Graphics, Controls,
Forms,, StdCtrls;= class(TForm): TEdit;: TEdit;: TLabel;: TLabel;: TLabel;:
TEdit;: TButton;: TEdit;Button1Click(Sender: TObject);
{ Private declarations }
{ Public declarations };
: TForm1;
{$R *.dfm}
procedure TForm1.Button1Click(Sender: TObject);,x1,y,e:real;
k:integer;F(c:real):real;:=c*c*c-2*c*c+c-3;;:=strtofloat(edit1.Text);:=strtofloat(edit2.Text);:=strtofloat(edit3.Text);:=x1-(f(x1)*(x1-x0))/(f(x1)-f(x0));((abs(y-x1))<e)
then k:=1 else begin x0:=x1; x1:=y endk=1;.text:='Îòâåò:'+floattostrf(y,ffFixed,
20,6);
end;
3.2.3
Тестовый пример
В качестве тестового примера возьмем уравнение x-3=0
Отрезок: [0;2]
Погрешность: Е=0,00001
Ответ: 3
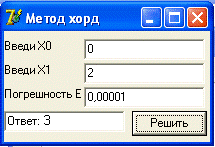
3.2.4 Решение
задачи с помощью ЭВМ
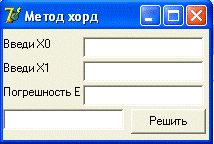
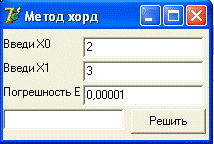
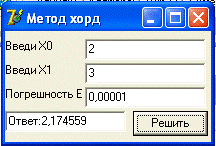
Заключение
В этой курсовой мы разобрали два итерационных метода нахождения корня
уравнения.
Мы выяснили, что в методе хорд на ось абсцисс опускаются хорды,
последовательно приближаясь к корню уравнения. А в методе простых итераций
уравнение заменяется на равносильное ему типа 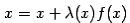 , а дальше идет поиск точки
пересечения с прямой y=x.
, а дальше идет поиск точки
пересечения с прямой y=x.
В любом методе последовательных приближений корень уравнения ищут,
учитывая определенную погрешность, тем самым увеличивая точность значения
корня.
В итоге мы выяснили что метод простых итераций является более простым в
исполнении в отличии от метода хорд, тем самым выигрывая в этом тяжелом
сравнении.
Список
литературы
1. Каханер
Д., Моулер К., Нэш С. Численные методы и программное обеспечение (пер. с
англ.). М.: Мир, 2001, 575 c.