Решение системы линейных алгебраических уравнений методом Зейделя

Министерство образования и науки Российской Федерации

Государственное образовательное учреждение

Высшего профессионального образования

"ОРЕНБУРГСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ"

Факультет экономики и управления

Кафедра математических методов и моделей в экономике

Лабораторная работа

По курсу численные методы

по теме "Решение системы линейных алгебраических уравнений методом Зейделя"

Оренбург 2011

1. Постановка задачи

Найти корни системы линейных алгебраических уравнений, используя метод Зейделя.

2. Краткие теоретические сведения

Система линейных алгебраических уравнений (СЛАУ) имеет вид Ax=b, где

, ,

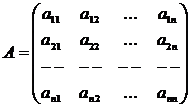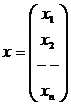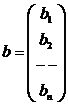
СЛАУ имеет решение, если ранг матрицы А равен n (числу переменных) и если матрица А не является вырожденной.

Метод Зейделя является модификацией метода простых итераций.

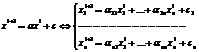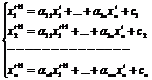Суть метода простых итераций состоит в выборе начального приближения (обычно за начальное приближение берут столбец свободных членов) и последующим нахождением элементов вектора xⁱ⁺¹ по формуле . Модификация Зейделя ускоряет сходимость за счёт того, что при расчёте элементов xⁱ⁺¹ используются уже вычисленные элементы этого вектора, т.е. . Если взять за начальное приближение вектор свободных членов, то получаем следующую итерационную последовательность:

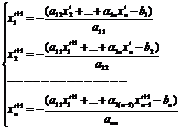
Однако, метод Зейделя сходится далеко не для любой произвольной матрицы. Для сходимости метода Зейделя необходимо либо диагональное преобладание в матрице А, либо нормальность системы Ах=b (т.е., А является симметричной и положительно определённой матрицей). В случае, если не выполняется ни одно из этих условий, а матрица А является невырожденной, то следует умножить матрицу и вектор b на матрицу А^Т слева. Тогда мы получим нормальную систему, которая может быть решена при любом начальном приближении х⁰. Перед оценкой погрешности необходимо провести некоторые преобразования. Пусть B=-D^-1(L+R), где D состоит из элементов главной диагонали матрицы А, L - из элементов, лежащих ниже и левее главной диагонали, R - из элементов, лежащих выше и правее главной диагонали. Тогда матрица B будет иметь вид 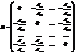, а матрица B_R будет состоять из элементов матрицы B, расположенных выше главной диагонали. Оценка погрешности производится следующим образом: 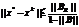. Исходя из этого, получаем  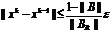- критерий останова.

. Алгоритм

) А, b, ε, х⁰=b, i:=0.

) Если 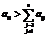, то к шагу 4. Иначе - к шагу 3.

) Если 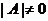, то А=А^ТА, b=A^Tb, к шагу 4). Иначе метод Зейделя не обладает сходимостью для данной матрицы.

) .

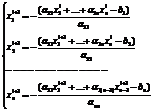) Если 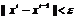, то на конец алгоритма, х^*=хⁱ. Иначе i:=i+1, к шагу 4.

4. Блок-схема

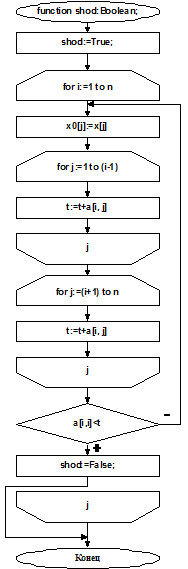
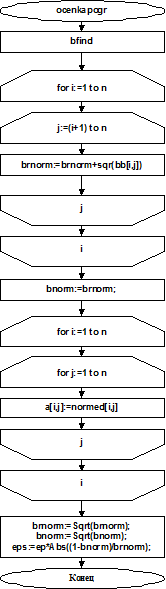
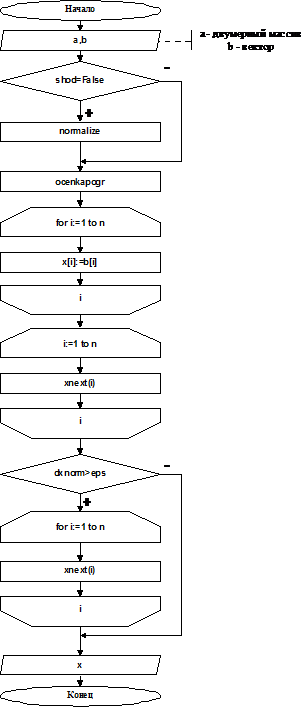
5. Код программы

Unit1;, Messages, SysUtils, Variants, Classes, Graphics, Controls, Forms,, XPMan, StdCtrls, Grids, ComCtrls;= class(TForm): TStringGrid;: TButton;: TStringGrid;: TLabel;: TXPManifest;: TEdit;: TUpDown;: TLabel;: TMemo;edt1Change(Sender: TObject);btn1Click(Sender: TObject);

{ Private declarations }

{ Public declarations };ep=0.0001;n:integer;:real;,x,b: array [1..5] of real;: array [1..5,1..5] of Real;: TForm1;

{$R *.dfm}xnext(num:integer);j:integer;:Real;j:=1 to n do x0[j]:=x[j];:=0;j:=1 to (num-1) do t:=t+a[num, j]*x[j];j:=(num+1) to n do t:=t+a[num, j]*x[j];[num]:=-(t-b[num])/a[num,num];;dxnorm:real;i:integer;:real;:=0;i:=1 to n do dx:=dx+sqr(x[i]-x0[i]);:=Sqrt(dx);;shod:Boolean;i,j:integer;:Real;:=True;i:=1 to n do begin:=0;j:=1 to (i-1) do:=t+a[i,j];j:=(i+1) to n do:=t+a[i,j];a[i,i]<t then begin:=False;;;;;normalize;i,j,k:integer;: array [1..5] of Real;: array [1..5,1..5] of Real;i:=1 to n doj:=1 to n do[i,j]:=0;i:=1 to n do begin[i]:=0;j:=1 to n do bnormed[i]:=bnormed[i]+b[j]*a[j,i];;i:=1 to n do b[i]:=bnormed[i];i:=1 to n doj:=1 to n dok:=1 to n do normed[i,j]:=normed[i,j]+a[k,i]*a[k,j];i:=1 to n doj:=1 to n do[i,j]:=normed[i,j];;ocenkapogr;i,j:integer;: array [1..5, 1..5] of real;,brnorm: Real;bfind;i,j:integer;i:=1 to n do bb[i,i]:=0;i:=1 to n doj:=1 to n doi<>j then bb[i,j]:=-a[i,j]/a[i,i];;;i:=1 to n doj:=(i+1) to n do brnorm:=brnorm+sqr(bb[i,j]);:=brnorm;i:=1 to n doj:=1 to (i-1) do bnorm:=bnorm+sqr(bb[i,j]);:=Sqrt(brnorm);:=Sqrt(bnorm);:=ep*Abs((1-bnorm)/brnorm);;TForm1.edt1Change(Sender: TObject);

begin

n:=StrToInt(Edt1.Text);.ColCount:=n;.RowCount:=n;.RowCount:=n;;TForm1.btn1Click(Sender: TObject);i,j:integer;i:=0 to (n-1) do beginj:=0 to (n-1) do[i+1,j+1]:=StrToFloat(strngrd1.Cells[j,i]);[i+1]:=StrToFloat(strngrd2.Cells[0,i]);;shod=False then normalize;;i:=1 to n do x[i]:=b[i];i:=1 to n do xnext(i);dxnorm>eps doi:=1 to n do xnext(i);.Text:='';i:=1 to n do.Text:=mmo1.Text+'x'+IntTostr(i)+'='+FloatTostr(x[i])+'; ';

end;.

6. Тестовый пример и проверка в MathCad

зейдель линейный алгебраический уравнение