Геометрия корпуса

Контрольная работа

Геометрия корпуса

Содержание

1. Теоретический чертеж

2. Главные размерения судна и коэффициенты полноты

3. Посадка судна

4. Элементы погруженного объема судна при посадке его прямо и на ровный киль

5. Элементы погруженного объема судна при посадке его прямо, но с дифферентом

Литература

1. Теоретический чертеж

Ввиду сложности формы обводы корпуса задаются графически в виде теоретического чертежа. На теоретическом чертеже изображены проекции на главные взаимно перпендикулярные плоскости линии пересечения теоретической поверхности корпуса с плоскостями, параллельными главным плоскостям. Под теоретической поверхностью понимают внутреннюю поверхность обшивки корпуса (без учета толщины обшивки и выступающих частей). Исключения составляют суда с деревянными и пластмассовыми корпусами, для которых на теоретическом чертеже изображают наружную поверхность корпуса.

В качестве главных плоскостей принимают:

диаметральную плоскость (ДП) - вертикальную продольную плоскость, делящую корпус судна на две симметричные части - правую (правый борт) и левую (левый борт);

плоскость мидель шпангоута (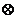) - вертикальную поперечную плоскость, проходящую по середине длины судна и делящую корпус на носовую и кормовую части;

основную плоскость (ОП) - горизонтальную плоскость, проходящую через нижнюю точку теоретической поверхности корпуса судна в плоскости мидель-шпангоута.

Линии пересечения теоретической поверхности корпуса с плоскостями параллельным ДП называют батоксами, с плоскостями параллельными ОП - теоретическими ватерлиниями (ВЛ), с плоскостями, параллельными плоскости мидель-шпангоута - теоретическими шпангоутами.

Линии пересечения ОП с ДП и ОП с плоскостью мидель-шпангоута дают продольную и поперечную основные линии.

Пересечение ДП с корпусом образуют линию киля, форштевня, ахтерштевня и верхней палубы.

корпус посадка судно киль

Совокупность проекций батоксов, теоретических ватерлиний и шпангоутов на ДП называется боком, на ОП - полуширотой, на плоскость мидель - шпангоута - корпусом. Эти три вида и составляют теоретический чертеж судна (рис. 1).

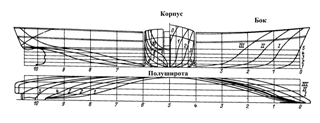
Рис. 1. Теоретический чертеж судна

Каждое сечение проектируется на одну из плоскостей в своем истинном виде, а на две другие в виде прямых линий. Например, на виде "бок" в истинном виде представлены батоксы, а теоретические шпангоуты и ватерлинии в виде прямых. Из последних выделяют конструктивную ватерлинию (КВЛ), по которую судно плавает с полной нагрузкой по проектную осадку. Любая другая ватерлиния, соответствующая конкретному случаю нагрузки называется действующей (расчетной) и обозначается (WL).

Число теоретических шпангоутов, как правило, принимается равными 11 или 21, которые образуют соответственно 10 или 20 теоретических шпаций.

Линии пересечения диаметральной плоскости с вертикальными поперечными плоскостями, проходящими через крайнюю носовую точку КВЛ и точку ее пересечения с осью баллера, называется соответственно носовым (НП) и кормовым (КП) перпендикулярами. При отсутствии баллера кормовой перпендикуляр получают, проводя вертикальную поперечную плоскость на расстоянии 97% длины судна по КВЛ от носового перпендикуляра.

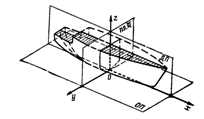
Рис. 2. Главные плоскости теоретического чертежа

Для расчета статики судна используют прямоугольную систему координат oxyz (рис. 2). Координатные плоскости системы oxyz совпадают с диаметральной плоскостью (ДП) xoz, плоскостью мидель - шпангоута yoz и основной плоскостью xoy. Начало координат располагают в точке 0, а оси направляют соответственно в нос, на правый борт и вертикально вверх.

Теоретический чертеж предназначен для наглядного изображения обводов корпуса, расчетного определения характеристик эксплуатационных качеств судна, разработки проектных чертежей.

Расчеты мореходных качеств судна в условиях его эксплуатации проводятся по документации, в которой используются данные, полученные из теоретического чертежа. Теоретический чертеж применяется при проведении ремонтных работ по корпусу, при доковании судна.

2. Главные размерения судна и коэффициенты полноты

Различают две группы главных размерений корпуса судна (рис. 3) в зависимости от того, связаны они или не связаны с положением ватерлинии:

) размеры, не связанные с положением судна относительно поверхности воды (чисто конструктивные размеры);

) размеры, связанные с этим положением и характеризующие деление корпуса судна на надводную и подводную части.

Рис. 3. Главные размерения судна

К первой группе размерений относится:

наибольшая длина судна (L_нб) - представляет собой расстояние по длине между крайними точками носовой и кормовой оконечностей корпуса;

наибольшая ширина судна (В_нб) - расстояние по ширине между крайними точками корпуса;

высота борта (D) - расстояние, измеренное в мидельном сечении от основной плоскости до линии палубы у борта.

С поправками на выступающие части величины L_нб и В_нб являются габаритными размерами судна (L_гб, В_гб).

Во вторую группу главных размерений судна входят:

длина судна по КВЛ (L_квл) - расстояние между точками пересечения КВЛ с диаметральной плоскостью судна;

длина судна (L) - расстояние между носовым и кормовым перпендикулярами;

осадка судна (d) - вертикальное расстояние в плоскости мидель-шпангоута от основной плоскости до действующей (расчетной) ватерлинии. В условиях эксплуатации судна часто используют габаритную осадку, отсчитываемую от нижней кромки киля. Габаритные осадки определяют по маркам углубления, нанесенным на бортах (рис.13);

высота надводного борта (F) - расстояние по высоте от действующей ватерлинии до линии палубы у борта;

ширина судна по КВЛ (В_квл) - наибольшая ширина конструктивной ватерлинии судна.

Для приближенной и сравнительной оценки мореходных качеств судов используются соотношения главных размерений и коэффициенты полноты. Чаще других используются соотношения:/B (относительное удлинение) - определяет ходкость судна;/d - характеризует остойчивость и ходкость судна;/d - определяет плавучесть и остойчивость судна на больших углах наклонения.

Основными безразмерными коэффициентами полноты корпуса судна являются:

α = S /LB - коэффициент полноты ватерлинии - отношение площади ватерлинии к площади прямоугольника со сторонами L и B (рис. 12, а);

b = ω /Bd - коэффициент полноты мидель-шпангоута - отношение погруженной площади мидель-шпангоута ω к площади прямоугольника со сторонами B и d (рис. 4, б);

d = V /LBd - коэффициент общей полноты - отношение объема подводной части V к объему параллелепипеда со сторонами L, B и d (рис. 12, в);

φ = V /ωL = dLBd /bBdL = d/b - коэффициент продольной полноты - отношение объема подводной части судна V к объему цилиндра, имеющего в основании погруженную площадь мидель-шпангоута ω и длину L (рис. 12, г);

χ = V /Sd = dLBd /αLBd = d/α - коэффициент вертикальной полноты - отношение объема подводной части судна к объему цилиндра, имеющего в основании площадь ватерлинии S и высоту d (рис. 4, д).

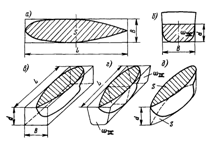
Рис. 4. Коэффициенты теоретического чертежа

Быстроходные суда имеют небольшие значения α, d и φ, характеризующие более заостренную и удобообтекаемую форму. С увеличением d ухудшается начальная остойчивость, а с увеличением α она, наоборот, увеличивается.

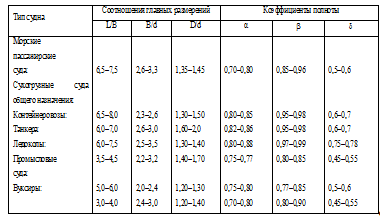
Для различных типов судов характерны определенные соотношения главных размерений и коэффициенты полноты корпуса (табл. 1.)

Таблица 1.

3. Посадка судна

Посадкой называется положение судна относительно спокойной поверхности воды. Положение действующей ватерлинии относительно корпуса, а значит, и посадку судна в общем случае определяют три параметрами:- средняя осадка (осадка на миделе);_f - дифферент (разность осадок носом и кормой);

Θ - угол крена - наклонение судна в плоскости мидель-шпангоута.

Наклонение судна в диаметральной плоскости можно выразить также и через угол дифферента Ψ.

Угол дифферента связан с дифферентом D_f

tg Ψ = = .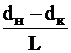

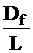При малом значении угла Ψ можно считать, что tg Ψ⁰ 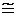 Ψ 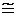Ψ⁰/57,3, тогда Ψ⁰ = 57,3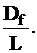

При принятой системе координат положительным считается дифферент на нос (Ψ >0), а угол крена - на правый борт (Θ >0).

Возможны следующие случаи посадки:

А. Судно плавает прямо и на ровный киль (Θ = 0, Ψ = 0). В этом случае посадка характеризуется только одним параметром - средней осадкой d.

Б. Судно плавает прямо, но с дифферентом (Θ = 0, Ψ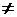0). В этом случае посадка характеризуется двумя параметрами в одном из следующих сочетаний:

средней осадкой d и углом дифферента Ψ;

осадками носом d_н и кормой d_к, измеряемые соответственно на носовом и комовом перпендикулярах.

Названные выше параметры связаны между собой следующими зависимостями:

Ψ⁰ = 57,3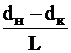; d = .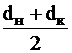

В. Судно плавает на ровный киль, но с креном (Ψ = 0, Θ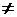0). В этом случае посадка характеризуется двумя параметрами - средней осадкой d и углом крена Θ.

Г. Общий случай посадки (судно плавает с креном и дифферентом). Посадка характеризуется тремя параметрами в одном из следующих сочетаний:, Ψ и Θ; d_н, d_к и Θ; d, D_f и Θ.

Для контроля за осадкой судна при изменении его нагрузки, а также для определения его дифферента используют марки углубления.

Марки углубления наносят на обоих бортах судна в носу и корме, а также в районе мидель-шпангоута. Высота цифр, измеренная по нормали к ОП, равна 1 дм (100 мм), расстояние между ними также 1 дм (100 мм), или соответственно 50 мм и 50 мм; при нанесении марок углублений в футах высота цифр и интервал между ними принимаются равными 0,5 футам (6 дюймам). Метрические марки наносятся арабскими цифрами, футовые - римскими (рис.5). По маркам углубления замеряют габаритную осадку т.к. нижняя кромка каждой цифры показывает расстояние по вертикали до нижней кромки горизонтального киля. Кроме того, марки углубления не обязательно располагаются на носовом и кормовом перпендикулярах судна.

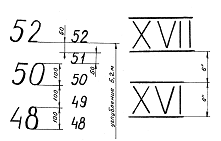
Рис. 5. Марки углублений

Судовая документация, служащая для оценки мореходных качеств судна рассчитывается и строится для осадок, отсчитываемых на перпендикулярах от основной плоскости судна. Поэтому для их получения необходимо значения осадок снятые с марок углублений исправить с помощью специальной шкалы (рис.6).

При отсутствии указанной шкалы осадки на перпендикулярах определяются по формулам:

_н = d_нм d_нм + (L /2 - l) Ψ; d_к = d_км d_км - (L /2 - l) Ψ,

где d_нм и d_км - отстояние от основной плоскости нижней кромки киля в плоскостях носовых и кормовых марок углубления (знак плюс, когда кромка проходит ниже основной плоскости, минус - выше основной плоскости), l₁ и l₂ - отстояние носовых и кормовых марок углубления от плоскости мидель-шпангоута.

На некоторых судах для определения осадок устанавливаются осадкомеры, показания от которых автоматически передаются на мостик.

Угол крена на судах замеряется кренометром. Для замера угла дифферента некоторые суда могут иметь специальные приборы - дифферентометры.

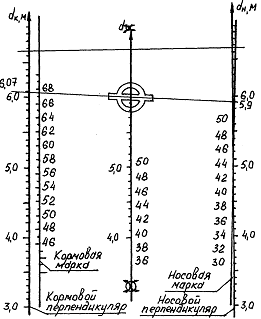
Рис. 6. Шкала, связывающая осадки на перпендикулярах с осадками на марках углубления т/х "А. Сафонцев"

4. Элементы погруженного объема судна при посадке его прямо и на ровный киль

. Общие сведения. В расчетах плавучести, остойчивости и

других эксплуатационных свойств судна используются элементы погруженного объема корпуса, а именно:

площадь ватерлинии S, координаты геометрического центра площади ватерлинии x_f, y_f, моменты инерции площади ватерлинии относительно продольной и поперечной центральных осей J_xf; J_yf;

погруженная площадь шпангоута ω и координаты геометрического центра этой площади y_ω, z_ω;

погруженный объем V и координаты геометрического центра этого объема, называемого центром величины (ЦВ) - x_с, y_с, z_c;

Центральными - называются оси, проходящие через геометрический центр.

Все эти элементы зависят от посадки судна и в общем случае являются функциями всех трех ее параметров - средней осадки d, угла крена Θ и угла дифферента Ψ. В нормальных условиях судно плавает без крена. При этом, ввиду симметрии корпуса относительно ДП y_f = 0, J_xf = J_x (здесь J_x - момент инерции площади S относительно следа ДП на данной ватерлинии), y_ω = 0 и y_с = 0, а остальные элементы погруженного объема зависят в основном от двух параметров - d и Ψ. Рассмотрим элементы погруженного объема для наиболее простого случая посадки судна прямо и на ровный киль, когда они зависят только от одного параметра - средней осадки d.

2. Элементы площади ватерлинии. Величины S, x_f, J_x и J_yf могут быть определены с помощью проекций теоретического чертежа.

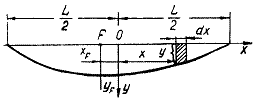
Рис. 7. К определению элементов площади ватерлинии

Для каждой теоретической ватерлинии (рис.7):

площадь ватерлинии: ;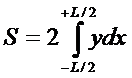

абсцисса геометрического центра тяжести площади S:

,

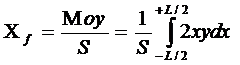где М_oy - статический момент площади S относительно следа плоскости мидель - шпангоута на плоскость данной ватерлинии;

момент инерции площади S относительно следа ДП на плоскость данной ватерлинии:

;

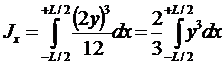момент инерции площади S относительно следа плоскости мидель - шпангоута на плоскость данной ватерлинии:

;

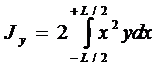·   центральные моменты инерции площади S:

J_xf = J_x,

J_yf = J_y - S x_f ².

В этих выражениях - L/2 и + L/2 измеряются в плоскости соответствующей ватерлинии.

По результатам расчетов, выполненных для всех теоретических ватерлиний, могут быть построены кривые изменения элементов площади ватерлинии с изменением осадки S (d), x_f (d), J_x (d) и J_yf (d) (рис.8).

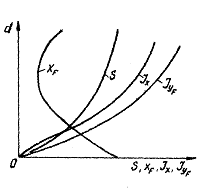
Рис. 8. Кривые изменения площади ватерлинии элементов площади ватерлинии

Элементы погруженной площади шпангоута. Величины определяются с помощью проекций "корпус" теоретического чертежа.

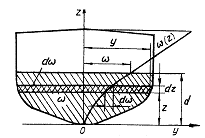
Рис. 9. К определению элементов погруженной площади

Для каждого теоретического шпангоута при плавании судна по заданную ватерлинию (рис. 9):

·   погруженная площадь шпангоута:

;

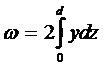аппликата геометрического центра площади ω:

_ω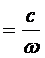

где 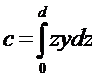 - статический момент площади ω относительно следа плоскости шпангоута на ОП.

По результатам расчетов, выполненных для каждого теоретического шпангоута при осадках, соответствующих всем теоретическим ватерлиниям, могут быть построены кривые изменения элементов погруженной площади шпангоута с изменением осадки - ω (d) и z_ω (d). На основании этих расчетов для осадок судна по каждую теоретическую ватерлинию можно построить также кривые изменения элементов погруженной площади шпангоута по длине судна ω (x) и z_ω (x). Кривая ω (x) (рис.18) называется строевой по шпангоутам. Ее ординаты в масштабе представляют площади соответствующих шпангоутов. Каждой осадке отвечает своя строевая по шпангоутам.

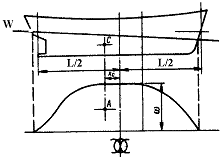
Рис. 10. Строевая по шпангоутам

Элементы погруженного объема. Величины V, х_с и z_c могут быть определены с помощью строевой по ватерлиниям S (d), или строевой по шпангоутам ω (x).

Рассмотрим использование для этой цели строевой по ватерлиниям (см. рис.16). Площадь, ограниченная строевой по ватерлиниям, осью и следом ватерлинии, определяет собой величину погруженного по эту ватерлинию объема (объемного водоизмещения):

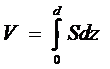
Аппликата геометрического центра объема V (аппликата ЦВ):

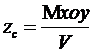
где: 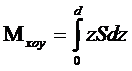 - статический момент объема V относительно плоскости x0y (ОП).

Рассмотрим использование строевой по шпангоутам (см. рис.11). Площадь ограниченная строевой по шпангоутам и осью x, определяет собой величину объема V по ватерлинию, которой соответствует эта строевая:

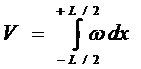
Абсцисса ЦВ:

,

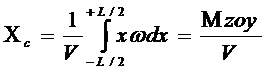где: M_zoy - статический момент объема V относительно плоскости xoy (пл. Ä).

По результатам расчета для всех теоретических ватерлиний могут быть построены кривые V (d), х_c (d), z_c (d). Кривая V (d) называется кривой объемного водоизмещения или грузовым размером (рис. 19). Наибольшая абсцисса кривой V (d) определяет собой полный непроницаемый объем корпуса судна.

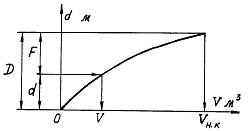
Рис. 11. Кривая объемного водоизмещения

Понятие о правилах приближенного интегрирования.

Как известно, обводы корпуса судна не воспроизводятся аналитическими зависимостями и заданы графически теоретическим чертежом. Поэтому приведенные интегралы, определяющие элементы погруженного объема судна, не удается вычислить непосредственно.

Для их вычисления используют правила приближенного интегрирования. Из них широкое применение получили три правила - правило трапеций, правило Симпсона и правило Чебышева. При выполнении ручных расчетов наибольшее практическое применение получило правило трапеций. Рассмотрим это правило.

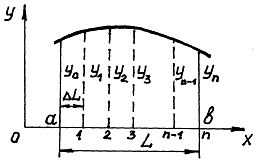
Вычисление определенного интеграла можно трактовать как вычисление площади ограниченной кривой, определяющей подынтегральную функцию, ее крайними ординатами и осью абсцисс (рис. 20.).

Для вычисления этой площади по правилу трапеций следует разделить базу кривой L на n равных промежутков и заменить саму кривую ломаной линией, опирающейся на вершины равноотстоящих ординат. При этом ординаты кривой разбивают фигуру на трапеции, суммарная площадь которых может быть приближенно принята равной площади под кривой:

А =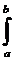у dx ≈ dL (у₀ + у₁ + у₂ + … + у_n - (у₀ + у_n) / 2)

Величина, стоящая в круглых скобках, называется исправленной суммой ординат, а вычитаемое в этих скобках - поправкой на полусумму крайних ординат.

В качестве ординат может быть принята любая подынтегральная функция: ω, S, ωx, Sz и т.д. Тогда найденная площадь кривой будет численно равна значению данного определенного интеграла. Вычисления производят в табличной форме.

Рабочие формы вычисления определенных интегралов, выражающих элементы погруженного объема судна, приводятся в специальной литературе.

Кривые элементов теоретического чертежа. В процессе эксплуатации судна часто возникает потребность в быстром определении элементов теоретического чертежа для разных значений осадок. Для этой цели кривые, определяющие зависимость от осадки судна элементов погруженного объема корпуса, представляют на общем графике, который и называют кривыми элементами теоретического чертежа (гидростатическими кривыми). Они входят в состав судовой документации и включают следующие кривые (рис.12):(d) - строевая по ватерлиниям;

х_f (d) - кривая абсциссы геометрического центра площади ватерлинии;_x (d) - кривая поперечного момента инерции площади ватерлинии;_yf (d) - кривая продольного момента инерции площади ватерлинии;(d) - кривая объемного водоизмещения;

Δ (d) - грузовой размер;_с (d) - кривая абсциссы ЦВ судна;_c (d) - кривая аппликаты ЦВ судна;_см (d) - число тонн изменяющих среднюю осадку на 1 см;

α (d) - коэффициент полноты ватерлинии;

b (d) - коэффициент полноты площади мидель-шпангоута;

d (d) - коэффициент общей полноты судна.

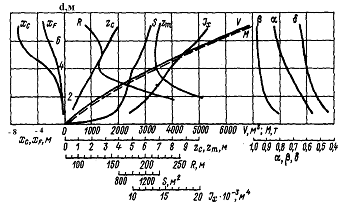
Рис. 12. Кривые элементов теоретического чертежа траулера типа "Прометей"

Вместо J_x (d) и J_yf (d) или наряду с ними, строят графики r (d), R (d) и z_m (d), характеризующие изменение с осадкой судна величин именуемых соответственно поперечными и продольными метацентрическими радиусами, аппликатой поперечного метацентра.

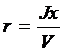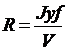; ; z_m = z_c + r,

Параметры r, R и z_m являются важными характеристиками остойчивости судна.

Характер кривых элементов теоретического чертежа определен формой обводов корпуса судна. Отсюда вытекают общие для всех судов черты и свойства этих кривых. Приведем несколько примеров.

Строевая по ватерлиниям S (d) (см. рис.16) сходна по форме с мидель-шпангоутом и обладает следующими свойствами:

площадь строевой по ватерлиниям с учетом масштаба определяет объемное водоизмещение судна V при соответствующей осадке d;

аппликата геометрического центра этой площади определяет аппликату центра величины (ЦВ) судна z_c;

отношение площади строевой по ватерлиниям к площади прямоугольника со сторонами d и S равно коэффициенту вертикальной полноты судна при соответствующей осадке;

статический момент площади строевой по ватерлиниям относительно следа ОП равен с учетом масштаба статическому моменту погруженного объема судна M_xoy.

Строевая по шпангоутам ω (x) (см. рис.18) непосредственно не входит в состав кривых элементов теоретического чертежа, представленных в судовой документации. Однако элементы ее используются при построении кривой объемного водоизмещения и кривой абсциссы ЦВ судна. Строевая по шпангоутам характеризует распределение погруженного объема по длине судна и обладает следующими свойствами:

площадь под строевой с учетом масштаба равна объемному водоизмещению судна V;

абсцисса геометрического центра площади под строевой по шпангоутам равна абсциссе ЦВ судна x_c;

отношение площади под строевой ω (x) к площади прямоугольника со сторонами L и B равна коэффициенту продольной полноты судна при соответствующей осадке;

статический момент площади под строевой по шпангоутам относительно следа пл. равен с учетом масштаба статическому моменту погруженного объема М_zoy.

Кривая объемного водоизмещения V (d) (грузовой размер Δ (d)) представлена, кривой, определяющая водоизмещение судна. Порядок определения водоизмещения по осадке судна понятен из рис. 19. По ней можно решить и обратную задачу - по водоизмещению найти осадку судна.

Свойства кривой водоизмещения:

ордината кривой с учетом масштаба равна площади под строевой по ватерлиниям соответствующей данной осадке; тангенс угла между касательной к кривой водоизмещения и осью осадок d равен соответствующей ординате строевой по ватерлиниям;

отношение отрезка АВ на оси осадок к величине осадки ОА судна (рис.22) равно коэффициенту вертикальной полноты судна по данную ватерлинию; на рис.14 точка В определяется пересечением касательной к кривой V (d) в точке D с осью осадок;

площадь под кривой водоизмещения (ОДС) равна с учетом масштаба статическому моменту объема V относительно ОП М_xoy.

Связь между водоизмещением и осадкой может быть представлена в виде номограммы (рис.13), называемой грузовой шкалой. На ее вертикальных шкалах откладываются водоизмещение в пресной и морской воде, дедвейт, осадка, число тонн на 1 см осадки (q_см), момент дифферентующий судно на 1 см (m_Д) и другие параметры. Зная одну из перечисленных величин и отметив ее на соответствующей шкале, снимают с остальных шкал искомые значения.

Необходимо помнить, что кривыми элементов теоретического чертежа и грузовой шкалой можно пользоваться только при посадке судна прямо и на ровный киль (Q=0, Y=0).

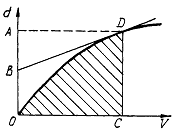
Рис. 13. Грузовой размер

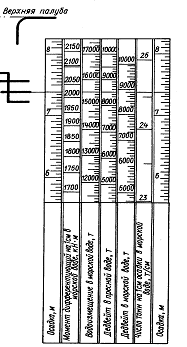
Рис. 14. Грузовая шкала

5. Элементы погруженного объема судна при посадке его прямо, но с дифферентом

Наличие дифферента заметно влияет на характеристики отдельных элементов погруженного объема корпуса судна. Определение их при наличии дифферента по кривым элементам теоретического чертежа исключено, так как приведет к большим погрешностям. Такие характеристики, как величина погруженного объема и координаты ЦВ судна в случае посадки с дифферентом требуют своих способов расчетов.

1. Масштаб Бонжана. Для определения водоизмещения и абсциссы х_с судна с дифферентом используется масштаб Бонжана (рис.24), представляющий собой совокупность интегральных кривых погруженных площадей шпангоутов (рис.17). Кривые ω_i (d) строятся при следах соответствующих шпангоутов на чертеже диаметрального сечения корпуса судна. Для удобства пользования масштаб чертежа по высоте берется в несколько раз крупнее, чем по длине, а масштаб абсцисс кривых ω_i (d) принимают соответствующим точности расчета площади ω. При использовании масштаба Бонжана вычерчивают на нем след наклонной ватерлинии по известным осадкам d_н и d_к, и отмечают точки ее пересечения с перпендикулярами, соответствующим положению шпангоутов. Площади шпангоутов ω_i снимаются по горизонтали и представляют собой расстояния от ватерлинии до соответствующей интегральной кривой.

Полученные величины подставляют в расчетные формулы, полученные по правилам приближенного интегрирования (правило трапеций):

V =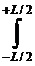ω dx @ dL [ω ₀ + ω₁ + ω₂ + … + ω_{n -} 1/2 (ω ₀ + ω_n)];

,

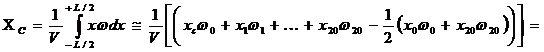
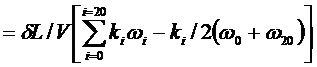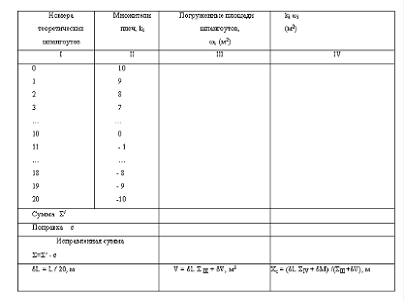
где dL = L / 20 - длина теоретической шпации; k_{i -} множители отстояния шпангоутов от плоскости миделя в теоретических шпациях. Расчет рекомендуется выполнять в табличной форме (табл.2).

Таблица 2.

Масштаб Бонжана строится, как правило, по данным теоретического чертежа и не учитывает объемы выступающих частей (рули, винты, кронштейны, гребные валы, толщина обшивки корпуса и др.). Следовательно, для определения действительных значений V и x_с в расчетные результаты следует ввести поправки на объем выступающих частей dV и их моментов относительно плоскости мидель-шпангоута dМ.

При пользовании масштабом Бонжана не следует допускать две возможные ошибки. Во-первых, в связи с различием линейных масштабов чертежа по длине и высоте нельзя наносить след ватерлинии непосредственно по заданной величине угла дифферента. Во-вторых, изменение абсцисс кривых ω_i (d) недопустимо производить по точкам пересечения следа ватерлинии с самими кривыми. Их следует отсчитывать от пересечения следа ватерлинии со следом соответствующих шпангоутов.

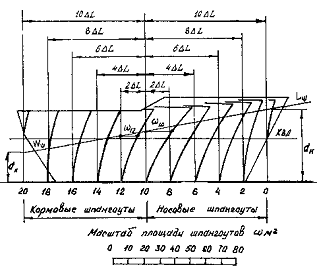
Рис. 15. Масштаб Бонжана

Дифферентные диаграммы. Для судовых условий выполнение расчетов по определению элементов погруженного объема судна с помощью масштаба Бонжана требует сравнительно много времени. С достаточной для практики точностью эти элементы могут быть непосредственно определены при помощи специальных диаграмм, получивших название дифферентных (рис.16). Широкое распространение получили диаграммы Г.А. Фирсова (рис.16, а), Петерсена, КТИРПиХ (рис.25, б) и диаграмма посадок (рис. 16, в).

На диаграмме Г.А. Фирсова в прямоугольной системе координат представлены зависимости между водоизмещением судна, абсциссами ЦВ и отвечающими им осадками носом и кормой. Цифры, стоящие на кривых, показывают, к каким значениям водоизмещения и абсциссы ЦВ относится данная кривая.

Отличаются друг от друга эти диаграммы только формой представления элементов погруженного объема и позволяют определить массу судна Δ и абсциссы ЦТ (ЦВ) x_c » x_g.

Основное достоинство дифферентных диаграмм в том, что они позволяют непосредственно определить элементы погруженного объема судна по известным параметрам посадки.

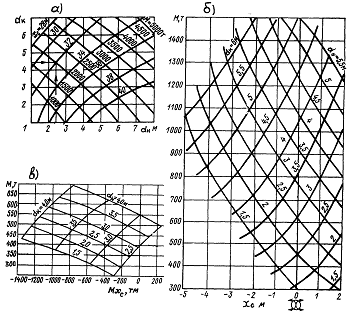
Рис. 16. Дифферентные диаграммы

Литература

1. Теория и устройство судна. Учебник под ред. д. т. н, проф. Ф.М. Кацмана. - Л.: Судостроение, 2001 г.

. Справочник по статике и динамике корабля. Под ред. д. т. н., проф Я.И. Войткунского. Тт. 1-3. Л.: Судостроение. 2006

. Правила классификации и постройки морских судов. Российский Морской Регистр судоходства, - М.: Транспорт, 2000

. Типовая информация об остойчивости и прочности грузового судна. Министерство Морского флота СССР. - М.: ЦРИА "Морфлот", 2009

. С.Н. Благовещенский, А.Н. Холодилин. Справочник по статике и динамике корабля. Тт.1-2. - Л.: Судостроение, 2006

. Л.Р. Аксютин, С.Н. Благовещенский. Аварии судов от потери остойчивости. - Л.: - Судостроение, 2005

. Л.Р. Аксютин. Борьба с авариями морских судов от потери остойчивости. - Л.: Судостроение, 2006

. Л.Р. Аксютин. Грузовой план судна. Учебное пособие. - Одесса: АО Бахва, 2006