Моделирование систем с использованием непрерывно-стохастических математических систем (моделей СМО)
РЕФЕРАТ
МОДЕЛЬ, ЗАДАЧА, МАТЕМАТИЧЕСКОЕ ОПИСАНИЕ ЗАДАЧИ,
АЛГОРИТМ, ПРОГРАММА.
В курсовой работе описана и реализована модель
задачи СМО. Основные сведения о задаче, метод ее решения. Разработана программа
по данной тематике.
ВВЕДЕНИЕ
Теория массового обслуживания опирается на
теорию вероятностей и математическую статистику.
На первичное развитие теории массового
обслуживания оказали особое влияние работы датского ученого А.К. Эрланга
(1878-1929).
Теория массового обслуживания - область
прикладной математики, занимающаяся анализом процессов в системах производства,
обслуживания, управления, в которых однородные события повторяются многократно,
например, на предприятиях бытового обслуживания; в системах приема, переработки
и передачи информации; автоматических линиях производства и др.
Предметом теории массового обслуживания является
установление зависимостей между характером потока заявок, числом каналов
обслуживан6ия, производительностью отдельного канала и эффективным
обслуживанием с целью нахождения наилучших путей управления этими процессами.
Задача теории массового обслуживания -
установить зависимость результирующих показателей работы Системы Массового
Обслуживания (СМО) (вероятности того, что заявка будет обслужена;
математического ожидания числа обслуженных заявок и т.д.) от входных
показателей (количества каналов в системе, параметров входящего потока заявок и
т.д.). Результирующими показателями или интересующими нас характеристиками СМО
являются - показатели эффективности СМО, которые описывают, способна ли данная
система справляться с потоком заявок. Примерами СМО могут служить: телефонные
станции, ремонтные мастерские, билетные кассы, стоянки такси, парикмахерские и
т.п.
Задачи теории массового обслуживания носят
оптимизационный характер и в конечном итоге включают экономический аспект по
определению такого варианта системы, при котором будет обеспечен минимум
суммарных затрат от ожидания обслуживания, потерь времени и ресурсов на
обслуживание и простоев каналов обслуживания.
Для проверки той или иной системы на
эффективность и целесообразность, производят теоретические расчеты. Часто
возникает необходимость проверки полученных теоретических результатов, для чего
лучшим средством служит модель. Не маловажный тот факт, что не всегда можно
исследовать систему на практике, в связи с ее громоздкостью или дороговизной. В
этом случае также целесообразно применять модель.
В данной работе предлагается к рассмотрению
модель системы массового обслуживания с отказами. Эта система получила широкое
распространение в телефонных сетях.
Задачу массового обслуживания, условно, можно
разделить на две задачи: задачу анализа и задачу синтеза.
Задача анализа позволяет, на основе исходных,
неизменных данных, произвести оценку эффективности заданной системы.
В то время как целью задачи синтеза служит выбор
оптимальных параметров системы, при которых будет достигаться наиболее
оптимальный результат. Для этого строиться компьютерная модель системы, в
которой производится определенное количество экспериментов с целью выявления оптимального
решения.
1. ОСНОВНЫЕ СВЕДЕНИЯ О ЗАДАЧЕ И МЕТОД ЕЕ РЕШЕНИЯ
.1 ПЕРЕЧЕНЬ СОКРАЩЕНИЙ, СИМВОЛОВ И СПЕЦИАЛЬНЫХ
ТЕРМИНОВ
n - количество
каналов обслуживания;
λ - интенсивность
входящего потока заявок;
μ - интенсивность
обслуживания канала;
ε - точность;
Р0, Р1, Р2, Р3,
Р4 - вероятности состояния системы;
tср.пост.
- среднее время поступления заявки в систему;
tср.обсл.
- среднее время обслуживания заявки в системе;
ρ - коэффициент
загрузки системы;
q - относительная
пропускная способность системы;
А - абсолютная пропускная способность системы;
k - среднее число
занятых каналов в системе;
СМО - система массового обслуживания.
1.2 ОПИСАНИЕ ЗАДАЧИ
Постановка задачи:
Пункт по ремонту радиотехники работает в режиме
отказа, состоит из 4 (n) каналов обслуживания, в него поступает простейший
(пуассоновский) поток заявок с интенсивностью 18 (l).
Интенсивность обслуживания канала - 5 (m). Необходимо
теоретически и практически рассчитать вероятности состояний системы,
вероятность отказа, среднее время между поступлением заявок, среднее время
обслуживания заявки в канале, коэффициент загрузки системы (приведенная
интенсивность), относительную пропускную способность системы, абсолютную
пропускную способность системы, среднее число занятых каналов.
Теоретический расчет подразумевает под собой
вычисление выше приведенных величин, согласно формул для случая, когда
распределение времени поступления заявок подчиняется пуассоновскому закону
распределения. Необходимые формулы будут рассмотрены ниже.
В практической части необходимо построить модель
системы, при условии, что время поступления заявок подчиняется пуассоновскому
закону распределения, и рассчитать выше описанные величины.
Следует отметить, что теоретический расчет
параметров системы для случая, когда потоки событий, переводящие систему из
состояния в состояние, распределенные по закону отличному от пуассоновского,
довольно сложен, т.к. на практике такой вариант встречается очень редко.
Поэтому аналитические формулы для характеристик СМО удается получить только для
самых простых случаев.
1.2.1 МАТЕМАТИЧЕСКОЕ ОПИСАНИЕ
ЗАДАЧИ
Параметры системы:
Тип СМО: СМО
с отказами
Входящий поток: пуассоновский
Интенсивность входящего потока заявок: λ
= 18 заявок в единицу времени
Интенсивность обслуживания канала: μ
= 5 заявок в единицу времени
Количество каналов обслуживания: n
= 4 канала
Точность: ε
= 0,01
1.2.2 МЕТОД РЕШЕНИЯ
Простейшим потоком называется поток, обладающий
следующими свойствами:
. стационарность;
. ординарность;
. отсутствие последействия.
Поток событий называется стационарным, если
вероятность попадания того или иного числа событий на участок времени длиной t
зависит только от длины участка и не зависит от того, где именно на оси времени
расположен этот участок.
Поток событий называется ординарным, если
вероятность попадания на элементарный участок Dt
двух или более событий пренебрежимо мала по сравнению с вероятностью попадания
одного события.
Ординарность означает, что поток прореженный,
т.е. между любыми двумя событиями есть временной интервал.
Поток событий называется потоком без
последействия, если для любых, не перекрывающихся участков времени число
событий, попадающих на один из них, не зависит от числа событий, попадающих на
другие.
Это означает, что заявки попадают в систему не
зависимо друг от друга. Интенсивность поступления потока заявок - l.
Простейшие потоки поступления заявок
характеризуются показательным законом распределения.
Тогда интервал времени поступления потока заявок
представляет собой случайную величину с одним и тем же распределением
вероятностей F (t).
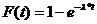 (1)
(1)
где l>0 - постоянная.
Плотность распределения
показательного закона задается формулой
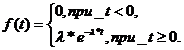
где l>0 - интенсивность поступления заявок.
Необходимо учесть, что данная
система является СМО с отказами - это означает, что в момент, когда система
занята (все каналы заняты), то пришедшая заявка получает отказ и покидает
систему.
Если в системе свободен хотя бы один
канал обслуживания, то пришедшая заявка немедленно поступает на обслуживание в
этот канал.
Длительность обслуживания потока
заявок также представляет собой случайную величину, подчиняющуюся
показательному закону распределения.
Интенсивность обслуживания потока
заявок - m. Длительность
обслуживания потока заявок представляет собой случайную величину с одним и тем
же распределением вероятностей F (t).
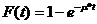
где m>0 - постоянная.
Плотность распределения
показательного закона задается формулой:
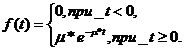
где m>0, - интенсивность обслуживания потока
заявок.
Изобразим граф состояний заданной
СМО:
Схема 1 - граф состояний заданной
СМО
λ λ
λ
λ

μ 2
μ 3
μ 4 μ
в котором: S0
- все каналы свободны (система свободна); S1
- занят один канал; S2
- занято два канала; S3
- занято три канала; S4
- все каналы заняты (система занята)
Из свободного состояния в состояние
обслуживания, систему переводит поток заявок с интенсивностью λ.
Тогда
как освобождение каналов от обслуживания происходит по такому принципу:
Из состояния Sn
в состояние Sn-1
, систему переводит интенсивность потока n*μ.
Если заявка поступает в момент времени, когда
система свободна или свободен хотя бы один канал обслуживания, то она
немедленно поступает на обслуживание. Если же все каналы заняты, то заявка
покидает систему.
1.2.3 ВЫВОД ОСНОВНЫХ ФОРМУЛ
Среднее время поступления заявок в систему:
tпост.
= 1/λ
Данный параметр является интервалом времени, из
которого генерируется появление заявки.
Среднее время (интервал) обслуживания одной
заявки одним каналом:
обс.
= 1/μ
Для того чтобы узнать какое количество заявок
поступит в систему за время обслуживания одной заявки, необходимо:
ρ = λ/μ
ρ - приведенная
интенсивность или коэффициент загрузки системы.
Составим уравнения Колмогорова для данной
системы:
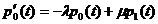 ,
,
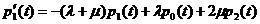 ,
,
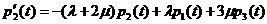
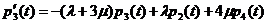
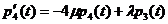
Уравнения называться уравнениями
Эрланга, в которых начальными условиями, для их решения, являются:
р0(0)=1;
р1(0)= р2(0)=
р3(0)=…= рn(0)=0,
т.е. в начальный момент времени -
система свободна.
Рассмотрим предельные вероятности
состояний P0, P1, P2,…, Pn, которые
характеризуют установившийся режим работы СМО при t - > ∞.
Р1= 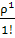 * P0;
* P0;
Р2= 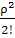 * P0;
* P0;
Р3= 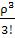 * P0;
* P0;
Р4= 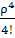 * P0;
* P0;
Р0 = 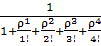
Зная все вероятности системы, можно
найти характеристики СМО:
Вероятность отказа:
Ротк = Р4 -
т.е. все каналы заняты
Относительная пропускная
способность:
q = 1 - Ротк
Абсолютная пропускная способность:
А = λ*q
Важной характеристикой СМО с отказами, является
среднее число занятых каналов (в данном случае оно совпадает со средним числом
заявок, находящихся в системе):
k = 0*Р0+1*Р1+2*Р2+3*Р3+4*Р4
,
или
k = А/μ
2. ДЕТАЛЬНОЕ ОПИСАНИЕ ПРОГРАММЫ
Данная программа написана в среде разработки Visual
C# с использованием
визуальных компонентов управления.
Результирующая программа СМО.exe
является полностью законченным программным продуктом. Для ее нормальной работы
необходимы следующие условия:
IBM совместимый
компьютер с процессором старше 386 серии;
Операционная система Windows
‘98 и выше;
Монитор класса VGA;
.1 ПРИНЦИП ОРГАНИЗАЦИИ ПРОГРАММЫ
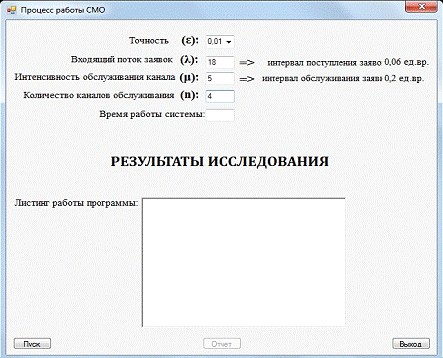
Рисунок 1- программа в рабочем состоянии
Данная программа (Рисунок 1) является
универсальной для данного типа задач.
Для удобства управления, введения данных, просмотра
результатов, присутствует графическая часть (формы, кнопки, поля ввода, поля
вывода результатов и т.п.).
Работа программы начинается с формы введения
данных.
После того как данные введены, необходимо нажать
на кнопку «Пуск», на форме программы, для запуска работы основной части
программы.
Для просмотра отчета необходимо нажать на кнопку
«Отчет», после чего появиться форма результатов работы программы с
рассчитанными характеристиками СМО.
Основные переменные в программе, являются
глобальными переменными. После того как пользователь ввел все необходимые
данные в основном окне программы, переменным присваиваются введенные
характеристики СМО.
теория массовый обслуживание канал
3. РЕЗУЛЬТАТЫ ИСПЫТАНИЯ
ПРОГРАММЫ
Входящие данные:
Интенсивность входящего потока заявок: λ
= 18 заявок в единицу времени
Интенсивность обслуживания канала: μ
= 5 заявок в единицу времени
Количество каналов обслуживания: n
= 4 канала
Точность: ε
= 0,01
.1 РЕЗУЛЬТАТ РАСЧЕТА ТЕСТОВОЙ
ЗАДАЧИ
Таблица 1 - Результат расчета
|
Аналитический
расчет
|
Программа
|
|
ρ
(коэф.
нагрузки)
|
3,6
|
4,5
|
|
Ротказа
|
27
%
|
35,96
%
|
|
q (отн. пропускная
способн.)
|
0,73
|
0,64
|
|
A (абс. пропускная
способн.)
|
13,14
|
10,89
|
|
k (ср.число
занятых каналов)
|
2,63
|
2,9
|
Полученные результаты отличаются, т.к. аналитический
расчет проводился с константными данными без имитационного процесса, тогда как
в процессе работы программы данные были динамическими, т.к. создавалась
имитация работы системы.
4. РЕЗУЛЬТАТЫ ИССЛЕДОВАНИЯ И ИХ АНАЛИЗ
После ознакомления с программой и инструкцией
пользователя, можно приступить непосредственно к проведению экспериментов и
исследований. Их целью может служить, например, сравнение параметров системы
при распределении Пуассона и равномерном распределении, можно определить при
каких значениях интенсивностей, числе каналов и мест в очереди, параметры будут
приблизительно равны. Мною замечено, что они тем меньше отличаются, чем
интенсивность обслуживания больше интенсивности поступления заявок. Также
возможно исследование загруженности каналов с целью поиска оптимального числа
каналов и мест в очереди для дальнейшего применения в сфере обслуживания.
ВЫВОДЫ
Таким образом, поставленная задача о создании
программы, позволяющей смоделировать многоканальную систему массового
обслуживания с ограниченной длиной очереди, решена. Созданная программа
позволяет произвести расчет таких параметров системы как:
· вероятности состояний Pi;
· вероятность Ps
· среднее число заявок в системе Ns
· среднее число заявок в очереди Qоч.
при заданных начальных условиях :
· число каналов обслуживания n
;
· интенсивность поступления заявок l
;
· интенсивность обслуживания m;
· параметр распределения случайного
времени ожидания
· визуально проследить работу системы
и сравнить теоретические и практические результаты расчетов.
СПИСОК ИСПОЛЬЗОВАННОЙ ЛИТЕРАТУРЫ
1. Павловская
Т.А. Программирование на языке высокого уровня С#
[электронный
ресурс] - Питер, 2008 г.
.
Либерти Д. Программирование на С#. - СПб.: Символ - Плюс, 2003.- 688 с
.
Шилдт Г. С# Учебный курс. Программирование. СПб.: Питер, 2003.
.
Жибинова И.А, С.Р. Зельцер, А.Н.Жибинов, О.В.Михайлова. Оформление учебных,
научных, проектных работ студентов. Методические указания.: Новокузнецк 2012.
.
Советов Б.Я., Яковлев С.А. Моделирование систем. Высшая школа, 2001. - 340 с.
. Статистические
методы для ЭВМ/ Под ред. К.Энслейна: Пер. с англ. Под ред. М.Б.Малютова.-
М.:Наука. Гл.ред. физ. Мат., лит. 1986.-464с.
ПРИЛОЖЕНИЕ А
ЛИСТИНГ ПРОГРАММЫ
WorkForm.cs
using
System;System.Collections.Generic;System.ComponentModel;System.Data;System.Drawing;System.Linq;System.Text;System.Windows.Forms;
CMO
{partial class WorkForm : Form
{int InOrders;int ServiceOrders;int
NumOfChannels;double Precision = 0;double OrderInterval;double
ChannelInterval;int TotalTime;double CmoTime;ulong NumOfOrders = 0;ulong
ServedOrders;int CmoPosition;int[] ChannelBusy;double[]
ServiceTimeOfChannel;Random rand = new Random();
// функция которая преобразовывает точность для
дальнейшего использования в программе и функцияхint Precition(double e)
{Tochnost = 0;
(e == 0.1)= 10;
(e == 0.01)= 100;
(e == 0.001)= 1000;
Tochnost;
}
// Число знаков для округления исходя из
точностиint ChisloZnakov(double Prec)
{a = 0;
(Prec == 0.1)= 1;(Prec == 0.01)= 2;(Prec ==
0.001)= 3;a;
}
// функция которая возвращает интервал времени
между заявками, либо интер. времени обслуж. каналаdouble OrdersInterval(int
NumOfOrders, double Tochnost)
{CelayaChast;Ostatok;
= Precition(Tochnost) / NumOfOrders;=
(Precition(Tochnost) / (double)NumOfOrders - CelayaChast) * 10;
(Ostatok >= 5)++;
(double)(CelayaChast /
(double)Precition(Tochnost));
}
// генератор моментов времениdouble
TimeGenerator(bool FirstOrder, double Interval, double Tochnost)
{NewTime;GenerationInterval = (int)(Interval *
Precition(Tochnost) + 1);
// только если это не первая заявка(!FirstOrder)
{
// исключение генерации нуля => повторяющееся
время
{= (double)(rand.Next() % GenerationInterval) /
Precition(Tochnost);
} while (NewTime == 0);
}= (double)(rand.Next() % GenerationInterval) /
Precition(Tochnost);
Math.Round(NewTime,ChisloZnakov(Tochnost));
}
// проверяет наличие новой заявкиbool
NewOrder(double TimeOfCmo, double IntervalOfOrder, ulong NumberOfOrders)
{(TimeOfCmo >= IntervalOfOrder *
(NumberOfOrders))
{true;
}return false;
}
// проверка системы в текущий момент времениvoid
CmoCheck(int TotalTime, double CmoTime, int NumOfChannels)
{i = 0;(CmoPosition != 0)
{(i < NumOfChannels)
{(ChannelBusy[i] == 1)
{(((ServiceTimeOfChannel[i] <= CmoTime)
&& (CmoTime <= TotalTime)) || ((CmoTime > TotalTime) &&
(ServiceTimeOfChannel[i] <= TotalTime)))
{[i] = 0;[i] = 0;-;.Text += (i + 1).ToString() +
"-й канал обслужил заявку" + "\n";++;
}
}++;
}
}
}
// запись заявок в каналы и генерация времени
обслуживания в канале + окончание обслуживанияvoid CmoWork(double CmoTime, int
NumOfChannels, double ChannelInterval, double e)
{ChannelWorkTime;i = 0;
// если система свободна, то запись
осуществляется в первый канал(CmoPosition == 0)
{[0] = 1;= TimeGenerator(false, ChannelInterval,
e);[0] = CmoTime + ChannelWorkTime;++;(CmoTime, 0, ChannelWorkTime);
}// иначе, идет запись в первый свободный канал
{(CmoPosition != NumOfChannels)
{(i < NumOfChannels)
{(ChannelBusy[i] == 0)
{[i] = 1;= TimeGenerator(false, ChannelInterval,
e);[i] = CmoTime + ChannelWorkTime;++;(CmoTime, i, ChannelWorkTime);;
}++;
}
}
{.Text += "Заявка не может быть принята на
обслуживание - КАНАЛЫ ЗАНЯТЫ" + "\n";.Text += "Состояние
СМО: " + CmoPosition.ToString() + "\n";(i = 0; i <
NumOfChannels; i++)
{.Text += "Состояние " + (i + 1).ToString()
+ "-го канала : " + Convert.ToString(ChannelBusy[i]) +
"\n";.Text += "Время окончания обслуживания в " + (i +
1).ToString() + " канале: " +
Convert.ToString(ServiceTimeOfChannel[i]) + "\n";
}
}
}
}
// информация о поступившей заявкеvoid
Info(double CmoTime, ulong NumOfOrders)
{.Text += "Время поступления " +
NumOfOrders.ToString() + "-й заявки: " + CmoTime.ToString() +
"\n";
}
void InfoOrder(double CmoTime, int Index, double
TimeOfChannel)
{.Text += "Заявка принята на обслуживание:
" + CmoTime.ToString() + " в " + (Index + 1).ToString() +
"-й канал" + "\n";.Text += "Время обслуживания заявки
в канале: " + TimeOfChannel.ToString() + "\n";.Text +=
"Время окончания обслуживания: " +
ServiceTimeOfChannel[Index].ToString() + "\n";
}
// конструктор формыWorkForm()
{();
}
void btnExit_Click(object sender, EventArgs e)
{.Exit();
}
// ПУСКvoid btnStart_Click(object sender,
EventArgs e)
{
// Считывание данных(TBoxOrders.Text !=
"" && TBoxOrderService.Text != "" &&
TBoxChannels.Text != "" && comboBoxPrecision.Text !=
"" && TBoxCmoWork.Text != "")
{
.Enabled = false;
= Convert.ToInt32(TBoxOrders.Text);=
Convert.ToInt32(TBoxOrderService.Text);= Convert.ToInt32(TBoxChannels.Text);=
Convert.ToDouble(comboBoxPrecision.SelectedItem.ToString());.Text =
"";i = 0;
// установление размерности массивов= new
int[NumOfChannels];= new double[NumOfChannels];
= Convert.ToInt32(TBoxCmoWork.Text);
// Перевод системы в первоначальное состояние
(обнуление всех переменных)= 0;= 0;= 0;= 0;
(i <= NumOfChannels - 1)
{[i] = 0;[i] = 0;++;
}
// Генерация поступления первой заявки=
TimeGenerator(true, OrderInterval, Precision);.Text += "\n" +
"-----------------------" + "\n";.Text += "Текущее
время СМО :" + CmoTime.ToString();.Text += "\n" + "-----------------------"
+ "\n";++;(CmoTime, NumOfOrders);(TotalTime, CmoTime,
NumOfChannels);(CmoTime, NumOfChannels, ChannelInterval, Precision);
// Последующая работа системы
{
// Генерация следующих моментов времени СМО=
Math.Round((CmoTime + TimeGenerator(false, OrderInterval,
Precision)),ChisloZnakov(Precision));
.Text += "\n" +
"-----------------------" + "\n";.Text += "Текущее
время СМО :" + CmoTime.ToString();.Text += "\n" +
"-----------------------" + "\n";
// Проверка системы в текущий момент
времени(TotalTime, CmoTime, NumOfChannels);
// Появление новой заявки((NewOrder(CmoTime,
OrderInterval, NumOfOrders)) && (CmoTime <= TotalTime))
{++;(CmoTime, NumOfOrders);(CmoTime,
NumOfChannels, ChannelInterval, Precision);
}
} while (CmoTime < TotalTime);.Text +=
"Количество поступивших заявок: " + NumOfOrders.ToString() +
"\n";.Text += "Количество обслуженных заявок: " +
ServedOrders.ToString() + "\n";
.Enabled = true;.Focus();.Enabled = true;
}MessageBox.Show("Все поля обязательны для
заполнения!");
}
// проверка вводимых значенийbool Check(string
Txt)
{
{.ToInt32(Txt);
}(Exception)
{.Show("Вводимое значение должно быть целым
числом");false;
}true;
}
// ввод входящего потокаvoid
TBoxOrders_TextChanged(object sender, EventArgs e)
{.Enabled = true;
}
// ввод интенсивности обслуживанияvoid
TBoxOrderService_TextChanged(object sender, EventArgs e)
{.Enabled = true;
}
// ввод количества каналовvoid
TBoxChannels_TextChanged(object sender, EventArgs e)
{.Enabled = true;
}
// выбор точностиvoid
comboBoxPrecision_TextChanged(object sender, EventArgs e)
{=
Convert.ToDouble(comboBoxPrecision.SelectedItem.ToString());.Enabled = true;
}
// завершение ввода входящего потокаvoid
TBoxOrders_Leave(object sender, EventArgs e)
{(TBoxOrders.Text !=
""&&(btnExit.ContainsFocus==false))
{(Check(TBoxOrders.Text))
{= Convert.ToInt32(TBoxOrders.Text);=
OrdersInterval(InOrders, Precision);.Text = OrderInterval.ToString()+"
ед.вр.";
}TBoxOrders.Focus();
}
}
// завершение ввода интенсивности обслуживанияvoid
TBoxOrderService_Leave(object sender, EventArgs e)
{(TBoxOrderService.Text != ""
&& (btnExit.ContainsFocus == false))
{(Check(TBoxOrderService.Text))
{= Convert.ToInt32(TBoxOrderService.Text);=
OrdersInterval(ServiceOrders, Precision);.Text = ChannelInterval.ToString() +
" ед.вр.";
}TBoxOrderService.Focus();
}
}
// завершение ввода количества каналовvoid
TBoxChannels_Leave(object sender, EventArgs e)
{(TBoxChannels.Text != "" &&
(btnExit.ContainsFocus == false))
{(Check(TBoxChannels.Text))
{= Convert.ToInt32(TBoxChannels.Text);
}TBoxChannels.Focus();
}
}
// ОТЧЕТvoid btnResult_Click(object sender,
EventArgs e)
{FResult = new
ResultForm(this,NumOfChannels,Precision,TotalTime,NumOfOrders,ServedOrders);.Show();
}
void WorkForm_Load(object sender, EventArgs e)
{.Enabled = false;
}
}
}.cs
using
System;System.Collections.Generic;System.ComponentModel;System.Data;System.Drawing;System.Linq;System.Text;System.Windows.Forms;
CMO
{partial class ResultForm : Form
{Form MForm;double inOrders;double
ordersInService;int numOfChannels;double precision;double ordersInterval;double
channelsInterval;int workTime;ulong totalInOrders;ulong servedOrders;
//------------------------double
koefNagruzki;double otkaz;double otnSposob;double absolSposob;double zanyatKanaly;double
Po;
//------------------------
ResultForm(Form MainF, int
NumChan,double Prec, int TotTime,ulong TotOrd,ulong ServOrd)
{.MForm = MainF;
= NumChan;= Prec;
= TotTime;= TotOrd;= ServOrd;
();
}void button1_Click(object sender,
EventArgs e)
{.Enabled =
true;.ActiveForm.Close();
}
void ResultForm_Load(object sender,
EventArgs e)
{i = 0;
[] P=new
double[numOfChannels+1];.ColumnCount=numOfChannels+1;[] row = new
string[numOfChannels + 1];
.Enabled = false;
// Расчеты
// Расчет ср. числа обслужваемых
заявок одним каналом (Мю)= (servedOrders / (double)workTime) /
(double)numOfChannels;
// Расчет ср. интервала времени
между поступл. заявок= 1 / inOrders;
// Расчет срю интервала времени
обслуживания канала= 1 / ordersInService;
// Коеффициент загрузки= inOrders /
ordersInService;
// Р0= 1 / (1 + Sum(koefNagruzki,
numOfChannels));
// Вероятность отказа=
((Stepen(koefNagruzki, numOfChannels) / Factor(numOfChannels)) * Po);
// Относительная пропускная
способность= 1 - otkaz;
// Абсолютная пропускная
способность= (totalInOrders / (double)workTime) * otnSposob;
// Число занятых каналов=
absolSposob / (double)((servedOrders / (double)workTime) / (double)numOfChannels);
// Вывод на форму.Text =
Math.Round(inOrders,ChisloZnakov(precision)).ToString()+" заявок в
ед.вр.";.Text = Math.Round(ordersInService,
ChisloZnakov(precision)).ToString() + " заявок в ед.вр.";.Text =
numOfChannels.ToString();.Text = precision.ToString();.Text =
Math.Round(ordersInterval, ChisloZnakov(precision)).ToString() + "
ед.вр.";.Text = Math.Round(channelsInterval,
ChisloZnakov(precision)).ToString() + " ед.вр.";.Text =
workTime.ToString() + " ед.вр.";.Text = totalInOrders.ToString() +
" заявок";.Text = servedOrders.ToString() + " заявок";.Text
= Math.Round(koefNagruzki, ChisloZnakov(precision)).ToString() + "
заявок";.Text = (Math.Round(otkaz * 100,
ChisloZnakov(precision))).ToString() + " %";.Text =
(Math.Round(otnSposob * 100, ChisloZnakov(precision))).ToString() + "
%";.Text = (Math.Round(absolSposob, ChisloZnakov(precision))).ToString() +
" заявок";.Text =
(Math.Round(zanyatKanaly,ChisloZnakov(precision))).ToString();
// Вероятности состояния системы
(i <= numOfChannels)
{(i == 0)
{[i] = Po;
dataGridView1.Columns[i].Name = "P" + i.ToString();[i] =
Math.Round(P[i] * 100, ChisloZnakov(precision)).ToString() + " %";
}
{[i] = (Stepen(koefNagruzki, i) /
Factor(i)) * Po;.Columns[i].Name = "P" + i.ToString();[i] =
Math.Round(P[i] * 100, ChisloZnakov(precision)).ToString() + " %";
}++;
}.Rows.Add(row);
}
// Сумма в знаменателе для расчета
Роdouble Sum(double ro, int numChan)
{summa = 0;n=1;
(n <= numChan)
{= summa + Stepen(ro,n) /
(double)Factor(n);++;
}summa;
}
// Факториалulong Factor(int num)
{factor = 1;n=0;
(n <= num)
{((n == 0) || (n == 1))1;= factor *
(ulong)n;++;
}factor;
}
// Возведение в степеньdouble
Stepen(double X, int step)
{n=1;result=X;
(X == 0)0;
(X == 1)1;(step == 1)X;
(step == 0)1;
(n <= step)
{(n>1)= result * X;++;
}result;
}
// Число знаков после запятой для
округленияint ChisloZnakov(double Prec)
{a=0;
(Prec == 0.1)= 1;(Prec == 0.01)=
2;(Prec == 0.001)= 3;a;
}
}
}
ПРИЛОЖЕНИЕ Б
ЛАБОРАТОРНАЯ РАБОТА №1
Математические схемы.
Непрерывно-детерминированные модели:
моделирование с использованием
типовых звеньев ТАР\ТАУ
Цель: Оценить реакцию модели на наборы типовых
воздействий.
Построение концептуальной модели (описание
модели, входов, выходов).
Исходные данные:
. Модель канала регулирования в виде инерционного
звена первого порядка с запаздыванием
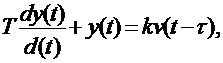 (1)
(1)
где Т = (9 ± 3) час - постоянная
времени инерции; τ
= (3±3) час
- запаздывание; k = (1,0 ± 0,2) - коэффициент
передачи. Первая цифра в скобках - базовый уровень факторов; цифра после знаков
(±) - верхний и нижний уровни факторов (+1 и -1 в нормированном пространстве
соответственно)
.Типовые входные воздействия V(t) -
ступенчатое, импульсное, синусоидальное, в виде случайного сигнала с нормальным
законом распределения.
Требуется:
. Заменив дифференциал из (1)
конечной разностью (2) вида
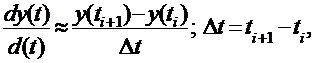 (2)
(2)
привести выражение (1) к дискретному
виду, пригодному для программирования.
В (2) обозначено: i, i+1 - моменты
отсчета времени (или, что то же самое - моменты контроля выходной величины y); ∆t = 0,1 Т -
интервал дискретизации времени.
Запаздывание приводится к
дискретному виду через очевидное соотношение: δτ = τ\Δt.
При моделировании запаздывание
учитывается сдвижкой выходной переменной относительного входного сигнала на
число отсчетов, равное δτ.
2. По матрице табл. 1 выбрать
параметры модели для «своего» варианта опытов. Номер строки табл. 1
соответствует месту исполнителя в списке группы.
. Составить алгоритм, программу и
рассчитать реакцию модели (1) при выбранных параметрах на ступенчатое,
импульсное, синусоидальное и случайное воздействие. Необходимые воздействия
генерировать из условий: диапазон изменения ± 1 (отн.); длительность
воздействия ≥ 3Т; статистические параметры случайного воздействия -
произвольные.
Таблица 1 - Поле комбинаций
настроечных параметров
|
№№
вариантов
|
Нормированные
уровни факторов
|
|
Время
инерции
|
Запаздывание
|
Коэффициент
передачи
|
ххх
|
|
6
|
+1
|
-1
|
+1
|
|

Рисунок 1 - Примеры типовых входных воздействий
Реализация:
). В данной работе используется модель в виде
дифференциального уравнения, описывающего последовательное соединение
инерционного звена первого порядка с запаздыванием. Такая модель относится к
непрерывно-детерминированным математическим схемам и хорошо подходит для
описания большинства технологических объектов управления.
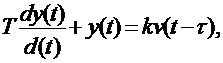
). Типовые входные сигналы
|
T=
|
12
|
|
+
|
|
тау=
|
0
|
|
-
|
|
k=
|
1,2
|
|
+
|
|
dt=
|
1,2
|
|
|
|
v=
|
1
|
|
|
где Т = (12 ± 3) час - постоянная времени
инерции; τ = (0±3) час - запаздывание;
k = (1,2 ± 0,2) -
коэффициент передачи
). Представление данных в табличной форме
|
i
|
|
ступень
|
|
v
|
импульс
|
|
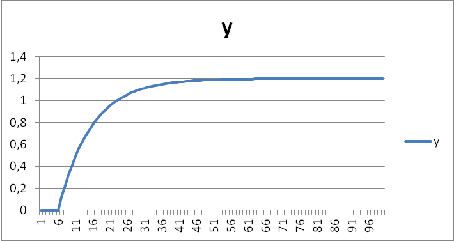
1
|
|
0
|
|
0
|
0
|
|
2
|
|
0
|
|
0
|
0
|
|
3
|
|
0
|
|
0
|
0
|
|
4
|
|
0
|
|
0
|
0
|
|
5
|
|
0
|
|
0
|
0
|
|
6
|
|
0
|
|
0
|
0
|
|
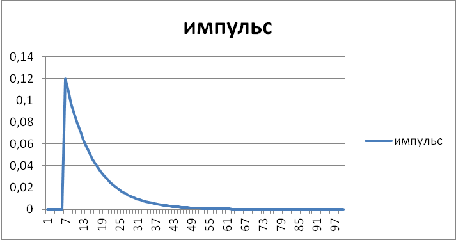
7
|
|
0,12
|
|
1
|
0,12
|
|
8
|
|
0,228
|
|
0
|
0,108
|
|
9
|
|
0,3252
|
|
0
|
0,0972
|
|
10
|
|
0,41268
|
|
0
|
0,08748
|
|
11
|
|
0,491412
|
|
0
|
0,078732
|
|
12
|
|
0,562271
|
|
0
|
0,070859
|
|
13
|
|
0,626044
|
|
0
|
0,063773
|
|
14
|
|
0,683439
|
|
0
|
0,057396
|
|
15
|
|
0,735095
|
|
0
|
0,051656
|
|
16
|
|
0,781586
|
|
0
|
0,04649
|
|
17
|
|
0,823427
|
|
0
|
0,041841
|
|
18
|
|
0,861085
|
|
0
|
0,037657
|
|
19
|
|
0,894976
|
|
0
|
0,033892
|
|
20
|
|
0,925478
|
|
0
|
0,030502
|
|
21
|
|
0,952931
|
|
0
|
0,027452
|
|
22
|
|
0,977638
|
|
0
|
0,024707
|
|
23
|
|
0,999874
|
|
0
|
0,022236
|
|
24
|
|
1,019886
|
|
0
|
0,020013
|
|
25
|
|
1,037898
|
|
0
|
0,018011
|
|
26
|
|
1,054108
|
|
0
|
0,01621
|
|
27
|
|
1,068697
|
|
0
|
0,014589
|
|
28
|
|
1,081827
|
|
0
|
0,01313
|
|
29
|
|
1,093645
|
|
0
|
0,011817
|
|
30
|
|
1,10428
|
|
0
|
0,010636
|
|
31
|
|
1,113852
|
|
0
|
0,009572
|
|
32
|
|
1,122467
|
|
0
|
0,008615
|
|
33
|
|
1,13022
|
|
0
|
0,007753
|
|
34
|
|
1,137198
|
|
0
|
0,006978
|
|
35
|
|
1,143478
|
|
0
|
0,00628
|
|
36
|
|
1,149131
|
|
0
|
0,005652
|
|
37
|
|
1,154218
|
|
0
|
0,005087
|
|
38
|
|
1,158796
|
|
0
|
0,004578
|
|
39
|
|
1,162916
|
|
0
|
0,00412
|
|
40
|
|
1,166625
|
|
0
|
0,003708
|
|
41
|
|
1,169962
|
|
0
|
0,003338
|
|
42
|
|
1,172966
|
|
0
|
0,003004
|
|
43
|
|
1,175669
|
|
0
|
0,002703
|
|
44
|
|
1,178102
|
|
0
|
0,002433
|
|
45
|
|
1,180292
|
|
0
|
0,00219
|
|
46
|
|
1,182263
|
|
0
|
0,001971
|
|
47
|
|
1,184037
|
|
0
|
0,001774
|
|
48
|
|
1,185633
|
|
0
|
0,001596
|
|
49
|
|
1,18707
|
|
0
|
0,001437
|
|
50
|
|
1,188363
|
|
0
|
0,001293
|
|
51
|
|
1,189526
|
|
0
|
0,001164
|
|
52
|
|
1,190574
|
|
0
|
0,001047
|
|
53
|
|
1,191516
|
|
0
|
0,000943
|
|
54
|
|
1,192365
|
|
0
|
0,000848
|
|
55
|
|
1,193128
|
|
0
|
0,000764
|
|
56
|
|
1,193815
|
|
0
|
0,000687
|
|
57
|
|
1,194434
|
|
0
|
0,000618
|
|
58
|
|
1,194991
|
|
0
|
0,000557
|
|
59
|
|
1,195491
|
|
0
|
0,000501
|
|
60
|
|
1,195942
|
|
0
|
0,000451
|
|
61
|
|
1,196348
|
|
0
|
0,000406
|
|
62
|
|
1,196713
|
0,000365
|
|
63
|
|
1,197042
|
|
0
|
0,000329
|
|
64
|
|
1,197338
|
|
0
|
0,000296
|
|
65
|
|
1,197604
|
|
0
|
0,000266
|
|
66
|
|
1,197844
|
|
0
|
0,00024
|
|
67
|
|
1,198059
|
|
0
|
0,000216
|
|
68
|
|
1,198253
|
|
0
|
0,000194
|
|
69
|
|
1,198428
|
|
0
|
0,000175
|
|
70
|
|
1,198585
|
|
0
|
0,000157
|
|
71
|
|
1,198727
|
|
0
|
0,000141
|
|
72
|
|
1,198854
|
|
0
|
0,000127
|
|
73
|
|
1,198969
|
|
0
|
0,000115
|
|
74
|
|
1,199072
|
|
0
|
0,000103
|
|
75
|
|
1,199165
|
|
0
|
9,28E-05
|
|
76
|
|
1,199248
|
|
0
|
8,35E-05
|
|
77
|
|
1,199323
|
|
0
|
7,52E-05
|
|
78
|
|
1,199391
|
|
0
|
6,77E-05
|
|
79
|
|
1,199452
|
|
0
|
6,09E-05
|
|
80
|
|
1,199507
|
|
0
|
5,48E-05
|
|
81
|
|
1,199556
|
|
0
|
4,93E-05
|
|
82
|
|
1,1996
|
|
0
|
4,44E-05
|
|
83
|
|
1,19964
|
|
0
|
4E-05
|
|
84
|
|
1,199676
|
|
0
|
3,6E-05
|
|
85
|
|
1,199709
|
|
0
|
3,24E-05
|
|
86
|
|
1,199738
|
|
0
|
2,91E-05
|
|
87
|
|
1,199764
|
|
0
|
2,62E-05
|
|
88
|
|
1,199788
|
|
0
|
2,36E-05
|
|
89
|
|
1,199809
|
|
0
|
2,12E-05
|
|
90
|
|
1,199828
|
|
0
|
1,91E-05
|
|
91
|
|
1,199845
|
|
0
|
1,72E-05
|
|
92
|
|
1,199861
|
|
0
|
1,55E-05
|
|
93
|
|
1,199875
|
|
0
|
1,39E-05
|
|
94
|
|
1,199887
|
|
0
|
1,25E-05
|
|
95
|
|
1,199898
|
|
0
|
1,13E-05
|
|
96
|
|
1,199909
|
|
0
|
1,02E-05
|
|
97
|
|
1,199918
|
|
0
|
9,14E-06
|
|
98
|
|
1,199926
|
|
0
|
8,23E-06
|
|
99
|
|
1,199933
|
|
0
|
7,4E-06
|
|
100
|
|
1,19994
|
|
0
|
6,66E-06
|
). Представление данных в графической форме
ПРИЛОЖЕНИЕ В
ЛАБОРАТОРНАЯ РАБОТА № 2
Технология имитационного моделирования.
Разработка комплекса алгоритмов и программ
пересчетного математического
моделирования
Моделирование доменной плавки
по каналу "влажность дутья - содержание кремния в чугуне".
Цель: Определение зависимости показателей
доменной плавки (содержание кремния в чугуне) от имитируемой влажности дутья.
Дано:
1. Реализация натурной
(реализованной на действующем агрегате) влажности дутья 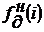 (входное
воздействие) и соответствующее ей содержание кремния в чугуне
(входное
воздействие) и соответствующее ей содержание кремния в чугуне 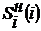 (выход),
где номер выпуска чугуна из доменной печи i =1,2,…,N
(выход),
где номер выпуска чугуна из доменной печи i =1,2,…,N
. Реализация имитируемой влажности
дутья, вырабатываемая в ходе моделирования изучаемой или проверяемой
подсистемой (например, алгоритмом регулирования): имитируемая влажность дутья
на каждом выпуске принимает значения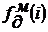 .
.
. Математическая модель (частичная)
канала “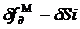 ” в
приращениях к фактическим уровням соответствующих переменных в виде
последовательного соединения инерционного звена первого порядка и звена
запаздывания со значениями динамических параметро
” в
приращениях к фактическим уровням соответствующих переменных в виде
последовательного соединения инерционного звена первого порядка и звена
запаздывания со значениями динамических параметро
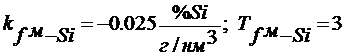 часа;
часа; 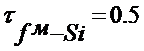 часа.
часа.
Для перехода к разностному
уравнению рассчитаем коэффициенты C1 и C2 при выбранном
интервале дискретизации Δ=1.5 час
(в соответствии с частотой поступления информации о содержании кремния в чугуне
по выпускам). Отсюда
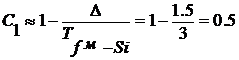 ;
; 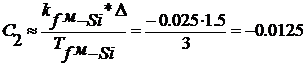
Запаздывание 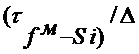 учитывается
за счет сдвига графиков - реализации
учитывается
за счет сдвига графиков - реализации 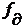 и
и 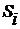 друг относительно друга на
соответствующую величину, как это сделано на рис.3.2.
друг относительно друга на
соответствующую величину, как это сделано на рис.3.2.
Требуется:
Определить содержание кремния в
чугуне (имитируемое) при заданных значениях имитируемой влажности на интервале
в N выпусков.
Таблица 1 - Исходные данные
|
|
|
T=
|
3
|
|
с1=1-dt/T
|
0,5
|
|
k=
|
-0,025
|
|
c2=k*dt/T
|
-0,0125
|
|
t=
|
0,5
|
Реализация
Таблица 2 - результаты расчета
|
№№
|
|
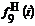
|
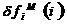 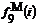
|
|
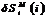 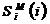
|
|
|
п/п
|
|
|
|
|
|
|
|
1
|
2
|
3
|
4
|
5
|
6
|
7
|
|
0
|
0,83
|
24
|
28
|
-4
|
0,00
|
0,83
|
|
1
|
1,02
|
24
|
29
|
-5
|
0,05
|
0,97
|
|
2
|
0,75
|
28
|
27
|
1
|
0,09
|
0,66
|
|
3
|
0,71
|
24
|
26
|
-2
|
0,03
|
0,68
|
|
4
|
0,85
|
24
|
25
|
-1
|
0,04
|
0,81
|
|
5
|
0,64
|
22
|
24
|
-2
|
0,03
|
0,61
|
|
6
|
0,60
|
22
|
23
|
-1
|
0,04
|
0,56
|
|
7
|
0,72
|
20
|
22
|
-2
|
0,03
|
0,69
|
|
8
|
0,90
|
20
|
21
|
-1
|
0,04
|
0,86
|
|
9
|
1,04
|
20
|
22
|
-2
|
0,03
|
1,01
|
|
10
|
0,98
|
-
|
-
|
-
|
0,04
|
0,94
|
Таблица 2 заполняется следующим образом.
В столбцы 2 и 3 заносятся
фактические значения переменных 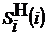 и
и 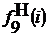 , в столбец 4 - имитируемое входное
воздействие
, в столбец 4 - имитируемое входное
воздействие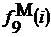 . Для
заполнения столбца 5 выполняется операция
. Для
заполнения столбца 5 выполняется операция 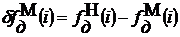 , а столбца 6 - операция
, а столбца 6 - операция 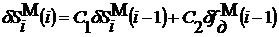
Запись 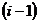 означает,
что при расчетах
означает,
что при расчетах 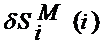 следует
взять значения переменных из предыдущей
следует
взять значения переменных из предыдущей 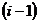 строки.
строки.
В столбец 7 заносится алгебраическая
сумма, составленная в соответствии с выражением 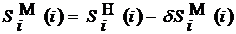
При i=0 в столбец 6 заносится 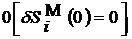 . Это
означает, что моделирование начинается с фактического значения выходной
переменной
. Это
означает, что моделирование начинается с фактического значения выходной
переменной 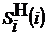 , i=0.
Искомая реализация
, i=0.
Искомая реализация 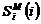 представлена
на рисунке 1.
представлена
на рисунке 1.
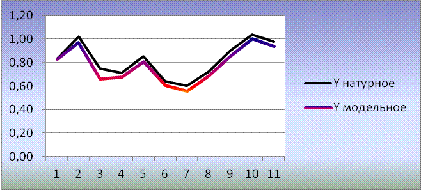
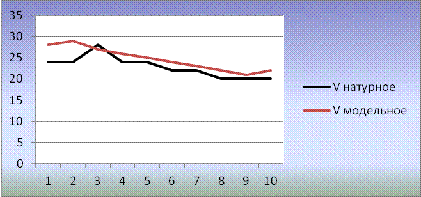
Рисунок 1 - Реализации натурных и модельных
переменных
ПРИЛОЖЕНИЕ Г
ЛАБОРАТОРНАЯ РАБОТА № 3
Моделирование случайных чисел.
Исследование алгоритмов обработки временных
рядов данных.
Цель:
. Практическое ознакомление с помехозащищенными
алгоритмами обработки временных рядов данных, методиками их настройки и
исследования качества.
. Формирование навыков оформления и
представления результатов НИР.
Постановка задачи. Исходные условия и данные:
. Задан временной ряд данных (ВРД) с моделью
следующего вида:
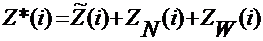 , где (1)
, где (1)
. Заданы исследуемые алгоритмы
обработки ВРД:
а). релейно-экспоненциального
сглаживания
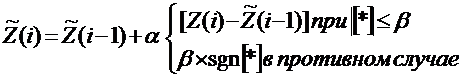 , где … (3)
, где … (3)
. Критерий оценки качества
сглаживания - среднемодульный
 , где … (4)
, где … (4)
Требуется:
1. С
помощью программы «Батенев» или самостоятельно разработанной программы
сгенерировать ВРД, соответствующий модели (1). Примечание: Ограничения на
свойства полезного сигнала, нормальных помех и выбросов определяются только
возможностями генерирующей программы и воображением исследователя (в данном
конкретном случае)
2. С
использованием схемы ПФЭ, исследовать качество оценивания полезного сигнала с
использованием РЭС II;
построить графические зависимости качества сглаживания от вариации настроек
фильтров
3. С
использованием схемы ПСМ, осуществить оптимизацию настроек РЭС II
по критерию (4);
Реализация:
. Объект исследования - сглаживающий фильтр РЭС II
(релейно-экспоненциальный 2-го порядка) с настроечными коэффициентами
(параметрами) «альфа» и «бета»
. Модель контролируемого сигнала - см. п.1
«Исходных данных»
. Критерий качества оценивания полезного сигнала
в виде средне-модульного отклонения; см. п.4 «Исходных данных», тема 1
. Модель объекта исследования в виде
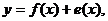 (*)
(*)
где f(х) -
функция отклика (неслучайная функция факторов); е(х) - ошибка эксперимента
(случайная величина); х - точка в факторном пространстве (определенное
сочетание уровней факторов).
. Матрица (план) полного факторного
эксперимента mn , где n - число
варьируемых факторов (принять равным 3); m - число
уровней варьирования каждого из факторов (принять равным 2)
. Варьируемые факторы: любые, из
возможных параметров шума, которыми можно управлять в программе-генераторе
сигналов
Таблица 1 - Матрица полного
факторного эксперимента
|
Номер
опыта
|
Фактор
х1
|
Фактор
х2
|
Фактор
х3
|
Функция
отклика
|
|
1
|
+1
|
+1
|
+1
|
y11,y12,y13
|
y1ср
|
|
2
|
+1
|
+1
|
-1
|
Y2
|
|
3
|
+1
|
-1
|
+1
|
Y3
|
|
4
|
+1
|
-1
|
-1
|
Y4
|
|
5
|
-1
|
+1
|
+1
|
Y5
|
|
6
|
-1
|
+1
|
-1
|
Y6
|
-1
|
-1
|
+1
|
Y7
|
|
8
|
-1
|
-1
|
-1
|
Y8
|
|
Номер
опыта
|
Фактор
х1
|
Фактор
х2
|
Фактор
х3
|
Функция
отклика
|
|
1
|
норм
|
0,5
|
2,0
|
0,179
|
0,166
|
|
|
|
|
0,168
|
|
|
|
|
|
0,151
|
|
|
2
|
норм
|
0,5
|
0,5
|
0,142
|
0,142
|
|
|
|
|
0,145
|
|
|
|
|
|
0,138
|
|
|
3
|
норм
|
0,0
|
2,0
|
0,058
|
0,056
|
|
|
|
|
0,051
|
|
|
|
|
|
0,058
|
|
|
4
|
норм
|
0,0
|
0,5
|
0,009
|
0,014
|
|
|
|
|
0,015
|
|
|
|
|
|
0,018
|
|
|
5
|
равн
|
0,5
|
2,0
|
0,186
|
0,193
|
|
|
|
|
0,205
|
|
|
|
|
|
0,188
|
|
|
6
|
равн
|
0,5
|
0,5
|
0,152
|
0,175
|
|
|
|
|
0,174
|
|
|
|
|
|
0,199
|
|
|
7
|
равн
|
0,0
|
2,0
|
0,121
|
0,117
|
|
|
|
|
0,105
|
|
|
|
|
|
0,125
|
|
|
8
|
равн
|
0,0
|
0,5
|
0,026
|
0,027
|
|
|
|
|
0,031
|
|
|
|
|
|
0,024
|
|
|
|
|
|
|
|
|