Алгебра высказываний
КУРСОВАЯ
РАБОТА
по
дисциплине «Информатика»
Введение
Алгебра высказываний является составной частью
одного из современных быстро развивающихся разделов математики - математической
логики. Математическая логика применяется в информатике, позволяет моделировать
простейшие мыслительные процессы. Одним из занимательных приложений алгебры
высказываний - решение логических задач.
В логических задачах исходными данными являются
не только и не столько числа, а сложные логические суждения, подчас весьма
запутанные. Эти суждения и связи между ними бывают иногда столь противоречивы,
что для их разрешения привлекают вычислительные машины.
Одна из главных задач логики - определить, как
прийти к выводу из предпосылок. Логика служит базовым инструментом почти любой
науки. Основателем логики считают Сократа. Позднее из логики стала выделяться
самостоятельная часть - математическая логика, изучающая основания математики и
принципы построения математических теорий.
1. Понятие высказывания. Операции над простыми
высказываниями. Таблицы истинности
Алгебру высказываний назвали в честь Джорджа
Буля (1815-1864) - английского математика. Булева алгебра (алгебра логики,
алгебра суждений) - раздел математики, в котором изучаются логические операции
над высказываниями. Буль произвел такую научную революцию, о которой сам не
подозревал. То, во что он превратил логику, было в дальнейшем положено в основу
построения электронно-вычислительных устройств. Из всей логики именно Булева
алгебра получила самое большое практическое применение в технике.
Объектами, с которыми работает алгебра
высказываний, являются повествовательные предложения, относительно которых
можно сказать, истинны они или ложны. Простым высказыванием называют
повествовательное предложение, относительно которого имеет смысл говорить,
истинно оно или ложно.
Логическими значениями высказываний является
"истина" и "ложь". Считается, что каждое высказывание либо
истинно, либо ложно и ни одно высказывание не может быть одновременно истинным
и ложным. Приведем примеры высказываний:
) Москва - столица России;
) число 27 является простым;
) Волга впадает в Каспийское море.
Высказывания 1 и 3 являются истинными.
Высказывание 2 - ложным, потому что число 27 составное 27=3*3*3.
Следующие предложения высказываниями не являются:
) давай пойдем гулять;
) 2*x>8;
) a*x2+b*x+c=0;
) который час?
Подчеркнем еще раз, что отличительным признаком
высказывания является свойство быть истинным или ложным, последние четыре
предложения этим свойством не обладают. Невозможно отнести неравенство 2 или
уравнение 3 к высказываниям пока не определено значение x. При x=3 высказывание
"2*3>8" ложно, а при x=5 "2*5>8" - истинно.
Условимся обозначать высказывания большими
буквами и, следуя Джорджу Булю, истинное (true) высказывание A обозначим так, A=1.
В том случае, когда A - ложное (false) высказывание, будем писать: A=0.
Из простых высказываний можно строить сложные,
называемые составными высказывания, соединяя простые логическими операциями.
Над простыми высказываниями определены следующие операции:
) логическое отрицание (NOT). Логическое
сложение, умножение, следование и эквивалентность являются бинарными операциями
("би" - два), потому что соединяют два операнда (два высказывания). В
отличие от них, логическое отрицание является унарной операцией, потому что
применяется лишь к одному высказыванию.
Присоединение частицы НЕ к сказуемому простого
высказывания A называется операцией логического отрицания. Для обозначения
отрицания высказывания A обычно пишут: Ā;
) логическое умножение (AND). Соединение двух
простых высказываний A и B в одно составное с помощью союза И называется
логическим умножением или конъюнкцией, а результат операции логическим
произведением.
Указание о логическом умножении двух
высказываний A и B обозначают так: AΛB. Результат
логического умножения AΛB имеет
истинное значение лишь в том случае, когда и A, и B истинны;
) логическое сложение (OR). В логическом
сложении союз ИЛИ используется в речи в двух значениях: исключающем и
неисключающем. В отличие от алгебры высказываний, где союз ИЛИ используется
только в неисключающем смысле.
Соединение двух простых высказываний A и B в
одно составное с помощью союза ИЛИ, употребляемого в неисключающем смысле,
называется логическим сложением или дизъюнкцией, а полученное составное
высказывание - логической суммой;
) логическое следование или импликация.
Соединение двух простых высказываний A и B в одно с использованием оборота речи
"ЕСЛИ :, ТО :" называется операцией логического следования или
импликацией.
Указание выполнить операцию импликации над
высказываниями A и B записывается так: A → B (читается "A
имплицирует B" или "B следует из A");
) эквивалентность. Соединение двух простых
высказываний A и B в одно с использованием оборота речи ":ТОГДА И ТОЛЬКО
ТОГДА, КОГДА" : называется операцией эквивалентности.
Выcказывания, над которыми выполняется операция
эквивалентности, помещают вместо многоточия. Указание выполнить операцию
эквивалентности над высказываниями A и B записывается так: A ~ B (читается
"A эквивалентно B").
Истинность составных высказываний, образованных
в результате выполнения каких-либо логических операций над простыми
высказываниями, зависит только от истинности исходных высказываний. Чаще всего
для установления значений сложных высказываний используют таблицы истинности.
Таблица истинности - это таблица,
устанавливающая соответствие между всеми возможными наборами логических
переменных, входящих в логическую функцию, и значениями функции.
Рассмотрим построение таблиц истинности на
примере операций, рассмотренных в предыдущем разделе. Начнем с унарной операции
отрицания Ā. Поскольку операция
выполняется над одним операндом (A), принимающим всего два значения ( 1-истина;
0-ложь), таблица будет иметь три строки и два столбца. В заголовке таблицы
укажем высказывание A и результат отрицания Ā, как
показано на рисунке.
Далее в первом столбце разместим все возможные
значения высказывания A, а во втором - значения логической функции Ā,
как
показано на рисунке.
Приведем таблицу истинности логического умножения
(конъюнкции).
|
A
|
B
|
A
Λ B
|
|
0
|
0
|
0
|
|
0
|
1
|
0
|
|
1
|
0
|
0
|
|
1
|
1
|
1
|
Заметим, что составное высказывание A Λ
B истинно
только в том случае, когда истинны ода высказывания и A, и B.
Таблица истинности логического сложения
приведена на следующем рисунке.
|
ABA
V B
|
|
|
|
0
|
0
|
0
|
|
0
|
1
|
1
|
|
1
|
0
|
1
|
|
1
|
1
|
1
|
Составное высказывание A V B ложно лишь в
случае, когда оба операнда ложны. Таблица истинности импликации, выглядит
следующим образом:
|
A
|
B
|
A
→ B
|
|
0
|
0
|
1
|
|
0
|
1
|
1
|
|
1
|
0
|
0
|
|
1
|
1
|
1
|
Составное высказывание A → B ложно лишь в
случае, когда ложь имплицируется истиной.
Таблица истинности эквивалентности представлена
на следующем рисунке.
|
A
|
B
|
A
~ B
|
|
0
|
0
|
1
|
|
0
|
1
|
0
|
|
1
|
0
|
0
|
|
1
|
1
|
1
|
Составное высказывание A ~ B истинно в том
случае, когда значения операндов совпадают. Полезно иметь под рукой сводную
таблицу истинности.
|
Сводная
таблица истинности
|
|
A
0 0 1 1 B 0 1 0 1 Коньюнкция A Λ B 0 0 0 1 Дизъюнкция A V B
0 1 1 1 Импликация A → B 1 1 0 1 Эквиваленция A ~ B 1 0 0 1
|
2. Примеры построения таблиц истинности сложных
высказываний
Рассмотрим задачу, которая решается построением
таблиц истинности сложных высказываний.
Задача. Составить таблицу истинности
высказывания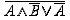 
Решение.
Данное высказывание состоит из двух операндов A
и B. Для его вычисления необходимо сначала вычислить отрицание A, то есть Ā
, затем
,
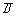далее выполнить логическое умножение 
,
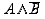затем сложение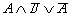 
и, наконец,
отрицание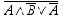 
. Таким образом, в
таблице истинности будет 7 столбцов и 5 строк.
Заполняем ячейки, соответствующие значению всем
возможным сочетаниям значений высказываний A и B.
Далее заполняем третий и четвертый столбцы
таблицы, соответственно, отрицая высказывания A и B.
|
ABĀ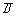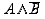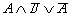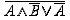
|
|
|
|
|
|
|
|
0
|
0
|
1
|
1
|
|
|
|
|
0
|
1
|
1
|
0
|
|
|
|
|
1
|
0
|
0
|
1
|
|
|
|
|
1
|
1
|
0
|
0
|
|
|
|
При заполнении пятого столбца таблицы необходимо
быть внимательным. Операндами высказывания являются A и ,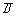
значит, при заполнении пятого столбца смотреть нужно на первый и четвертый
столбцы таблицы. Так же необходимо помнить, что результат логического умножения
имеет значение истина только в том случае, когда истинны оба операнда (единица
будет только в четвертой строке пятого столбца).
|
ABĀ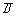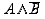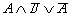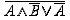
|
|
|
|
|
|
|
|
0
|
0
|
1
|
1
|
0
|
|
|
|
0
|
1
|
1
|
0
|
0
|
|
|
|
1
|
0
|
0
|
1
|
1
|
|
|
|
1
|
1
|
0
|
0
|
0
|
|
|
При заполнении шестого столбца таблицы, следует
обратить внимание на значения, стоящие в третьем и пятом столбцах, и выполнить
операцию логического сложения.
|
A
|
B
|
Ā
|
|
|
|
|
|
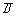
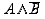
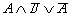
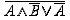
0
|
0
|
1
|
1
|
0
|
1
|
|
|
0
|
1
|
1
|
0
|
0
|
1
|
|
|
1
|
0
|
0
|
1
|
1
|
1
|
|
|
1
|
1
|
0
|
0
|
0
|
0
|
|
|
A
|
B
|
Ā
|
|
|
|
|
|
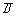
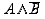
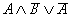
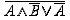
0
|
0
|
1
|
1
|
0
|
1
|
0
|
|
0
|
1
|
1
|
0
|
0
|
1
|
0
|
|
1
|
0
|
0
|
1
|
1
|
1
|
0
|
|
1
|
1
|
0
|
0
|
0
|
0
|
1
|
Для получения результата осталось заполнить
последний столбец, где отрицается высказывание, полученное в шестом столбце.
Ответ: Таблица истинности сложного высказывания
следующая:
|
A
|
B
|
|
|
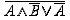
0
|
0
|
0
|
|
0
|
1
|
0
|
|
1
|
0
|
0
|
|
1
|
1
|
1
|
. Логические законы
В алгебре логики доказано, что любую логическую
функцию можно выразить только через комбинацию логических операций И, ИЛИ и НЕ.
Для приведения логических выражений к эквивалентным, но более простым в записи
используют ряд логических законов.
Закон тождества. Сформулирован древнегреческим
философом Аристотелем. Закон утверждает, что мысль, заключенная в некотором
высказывании, остается неизменной на протяжении всего рассуждения, в котором
это высказывание фигурирует:
=X
Закон противоречия говорит о том, что никакое
предложение не может быть истинно одновременно со своим отрицанием. "это
яблоко спелое" и "это яблоко неспелое".
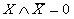
Закон исключенного третьего говорит о том, что
для каждого высказывания имеются лишь две возможности: это высказывание либо
истинно, либо ложно. Третьего не дано. "Сегодня я либо получу 5, либо не
получу". Истинно либо суждение, либо его отрицание.
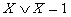
Закон двойного отрицания заключается в том, что
отрицать отрицание какого-нибудь высказывания - то же, что утверждать это
высказывание. " Неверно, что 2*2<>4".
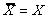
Законы Август де Моргана показывают как
отрицаются высказывания:
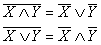
Эти законы можно выразить в следующих кратких
словесных формулировках:
отрицание логического произведения
эквивалентно логической сумме отрицаний множителей;
отрицание логической суммы эквивалентно
логическому произведению отрицаний слагаемых.
Законы идемпотентности говорят о том, что в
алгебре логики нет показателей степеней и коэффициентов. Конъюнкция одинаковых
"сомножителей" равносильна одному из них. Дизъюнкция одинаковых
"слагаемых" равносильна одному из них.
операция
таблица импликация отрицание
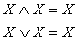
Законы коммутативности и ассоциативности говорят
о том, что конъюнкция и дизъюнкция аналогичны одноименным знакам умножения и
сложения чисел.
Законы
коммутативности: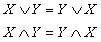 
Законы
ассоциативности: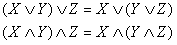 
Законы дистрибутивности говорят о том, что
логическое сложение и умножение равноправны по отношению к дистрибутивности: не
только конъюнкция дистрибутивна относительно дизъюнкции, но и дизъюнкция
дистрибутивна относительно конъюнкции.
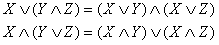
Законы поглощения показывают как упрощать
логические выражения при повторе операнда.
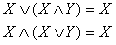
. Решение логических задач
|
Алеша:
|
"Сосуд
греческий и изготовлен в V в."
|
|
Борис:
|
"Сосуд
финикийский и изготовлен в III в."
|
|
Гриша:
|
"Сосуд
не греческий и изготовлен в IV в."
|
Рассмотрим решение логических задач на следующем
примере. Алеша, Боря и Гриша нашли в земле сосуд. Рассматривая удивительную
находку, каждый высказал по два предположения:
Учитель истории сказал ребятам, что каждый из
них прав только в одном из двух предположений. Где и в каком веке изготовлен
сосуд?
Введем следующие обозначения.
|
Обозначим
высказывание:
|
"Сосуд
греческий" буквой Г;
|
|
"Сосуд
финикийский" - Ф;
|
|
"Сосуд
изготовлен в V в." - П;
|
|
"Сосуд
изготовлен в III в." - Т;
|
|
"Сосуд
изготовлен в IV в." - Ч.
|
После того, как введены обозначения для простых
высказываний, составим сложные высказывания - предположения школьников. Алеша
сказал: "Сосуд греческий и изготовлен в V в.". Это сложное
высказывание можно записать так: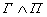 
.
Из слов учителя следует, что это высказывание ложно. Но Алеша прав в одном из
предположений, значит либо Г=1, либо П=1. Значит, истинным будет высказывание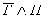 
(сосуд
не греческий, но изготовлен в V в.) или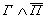 
(сосуд
греческий, но изготовлен не в V в.). Это рассуждение приводит нас к следующему
истинному высказыванию:
.
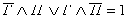Проведя аналогичные рассуждения о высказываниях
Бориса и Гриши, мы получим еще два сложных высказывания:
.
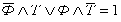
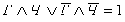Каждое из высказываний будем рассматривать как
логические уравнения, неизвестными в которых являются простые высказывания Г,
Ф, П, Т, Ч. При составлении уравнений мы учли высказывания ребят и замечание
учителя, но этого не достаточно, ведь сосуд не может быть одновременно и
греческим, и финикийским, следовательно,
;
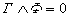Сосуд не может быть одновременно изготовлен и в
третьем и в четвертом веке
;
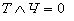Сосуд не может быть одновременно изготовлен и в
четвертом и пятом веке
;
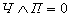Сосуд не может быть одновременно изготовлен и в
третьем и в пятом веке
.
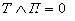Поскольку приведенные выше уравнения - это
ложные высказывания, к ним требуется применить отрицание и преобразовать их по
правилам де Моргана. В итоге получим:
;
;
;
.
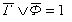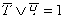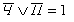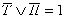Мы получили семь уравнений над пятью
высказываниями Г, Ф, П, Т, Ч. Если все эти высказывания логически перемножить,
то мы получим сложное высказывание, в котором сведено воедино все, что
говорилось о сосуде. Обозначим это высказывание S(Г, Ф, П, Т, Ч):
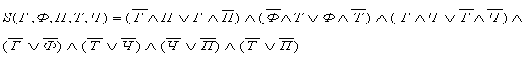.(1)
Решить задачу - значит указать, при каких
значениях высказываний Г, Ф, П, Т и Ч
(Г, Ф, П, Т, Ч) =
1.
Сделать это можно, построив таблицу истинности и
найдя единственную строку, в которой S (Г, Ф, П, Т, Ч) = 1. Поскольку таблица
истинности в данном случае очень большая, её построение можно доверить
компьютеру. ( См. Приложение 1). Можно поступить иначе: упростить выражение
(1), тогда ответ задачи будет очевиден и без построения таблицы истинности.
.Диаграммы Эйлера-Вена
Доказать законы алгебры высказываний можно:
• построив таблицу истинности для правой и левой
частей закона;
• выполнив эквивалентные преобразования над
правой и левой частями формулы для приведения их к одному виду;
• с помощью диаграмм Эйлера-Венна.
Леонард Эйлер при решении задач изображал
множества с помощью кругов, и в его честь этот метод был назван "методом
кругов Эйлера". Однако такой прием очень полезен и при решении логических
задач, когда с помощью кругов изображаются высказывания. Стоит отметить, что
этим методом математики пользовались и до Эйлера. Так, в трудах Лейбница были
обнаружены изображения таких кругов. Но, как уже говорилось, достаточно
основательно этот метод был развит Эйлером. После Эйлера метод получил развитие
в работах других ученых, однако наибольшего расцвета графические методы
достигли в сочинениях английского логика Джона Венна, подробно изложившего их в
книге "Символическая логика". Поэтому такие схемы называют
"диаграммами Эйлера-Венна".
Любое высказывание на диаграмме изображается
кругом, а его отрицание - частью плоскости, находящейся вне круга.
Если у нас есть два высказывания X и Y, то их на
диаграмме изображают двумя кругами, как правило, разного цвета.
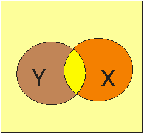
Заштрихованным на диаграмме закрашено логическое
умножение (конъюнкция) двух высказываний, а их логическое сложение (дизъюнкция)
изображено на следующем рисунке. Другими словами логическое умножение - это
пересечение кругов, а логическое сложение изображается как объединение кругов.
Практическая часть
Вариант №4
Для решения данной экономической задачи была
выбрана среда табличного процессора MS Excel.
В Microsoft
Office Excel
является средством для создания электронных таблиц, которые обладают
возможностями для проведения простых расчетов, как с использованием
арифметических действий, так и с помощью встроенных функций; для построения
разных типов диаграмм; для оформления полученных таблиц и т.д.
Общая характеристика задачи.
В бухгалтерии предприятия ООО «Гамма»
производится расчет налоговых вычетов, предоставляемых сотрудникам, и
формирование платежных ведомостей. Данные для выполнения расчета налоговых
вычетов приведены на рисунке 1. Стандартный налоговый вычет предоставляется
каждому сотруднику в размере 400 руб. до тех пор, пока совокупный доход с
начала года не превысит 50 000 руб., налоговый вычет на ребенка предоставляется
в размере 600 руб. НДФЛ - налог на доходы физических лиц (13%) рассчитывается с
начисленной суммы за минусом размера налогового вычета.
. Построить таблицы по приведенным ниже данным.
. Выполнить расчет размера налогового вычета,
предоставляемого сотрудникам в текущем месяце, результаты вычислений
представить в виде таблицы (рисунок 2).
. Сформировать и заполнить форму расчетной
ведомости по заработной плате за текущий месяц (рисунок 3).
. Результаты расчета заработной платы за текущий
месяц представить в графическом виде.
|
ФИО
сотрудника
|
Начислено
за месяц, руб.
|
Совокупный
доход с начала года, руб.
|
|
Васечкина
М.М.
|
4
890,00
|
26
000,00
|
|
Иванова
И.И.
|
6
800,00
|
|
Кузнецова
С.С.
|
5
350,00
|
42
000,00
|
|
Петрова
А.А.
|
7
500,00
|
54
000,00
|
|
Сидорова
К.К.
|
6
200,00
|
64
000,00
|
Рисунок 1: Данные для расчета налоговых вычетов.
|
ФИО
сотрудника
|
Стандартный
налоговый вычет на физ. лицо, руб.
|
Количество
детей, на которых предоставляется налоговый вычет
|
Размер
налогового вычета за текущий месяц, руб.
|
|
Васечкина
М.М.
|
400,00
|
|
|
|
Иванова
И.И.
|
400,00
|
2
|
|
|
Кузнецова
С.С.
|
400,00
|
2
|
|
|
Петрова
А.А.
|
400,00
|
1
|
|
|
Сидорова
К.К.
|
400,00
|
3
|
|
Рисунок 2: Размер налоговых вычетов,
предоставляемых сотрудникам в текущем месяце.
|
ООО
"Гамма"
|
|
|
|
|
|
|
|
|
Расчетный
период
|
|
|
|
|
с
|
по
|
|
|
|
|
|
|
|
|
|
|
|
|
|
РАСЧЕТНАЯ
ВЕДОМОСТЬ
|
|
|
|
|
|
|
|
Табельный
номер
|
ФИО
сотрудника
|
Начислено
за месяц, руб.
|
Размер
налогового вычета, руб.
|
НДФЛ,
руб.
|
К
выплате, руб.
|
|
0001
|
Иванова
И.И.
|
|
|
|
|
|
0002
|
Петрова
А.А.
|
|
|
|
|
|
0003
|
Васечкина
М.М.
|
|
|
|
|
|
0004
|
Сидорова
К.К.
|
|
|
|
|
|
0005
|
Кузнецова
С.С.
|
|
|
|
|
|
ИТОГО
ПО ВЕДОМОСТИ
|
|
|
|
|
|
|
|
Гл.бухгалтер
|
|
|
|
|
|
|
|
|
|
|
|
Рисунок 3: Расчетная ведомость
Описание алгоритма решения задач:
. Запустить табличный процессор MS
Excel.
. Создать книгу с именем «Гамма».
. Лист 1 переименовать в лист с названием
«Данные».
. На рабочем листе Данные MS
Excel создать таблицу
«Данные для расчета налогового вычета».
. Заполнить таблицу для расчета налогового
вычета исходными данными (рис. 4).
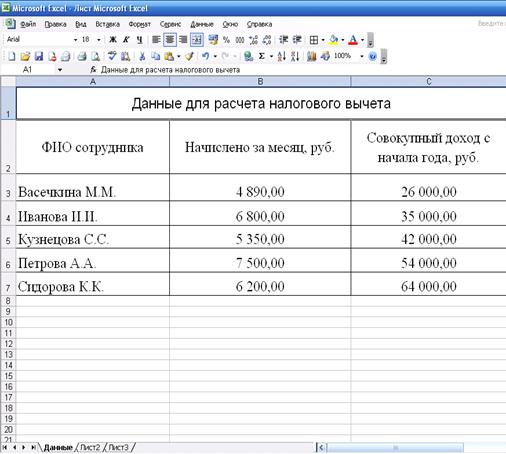
Рисунок 4: Расположение таблицы «Данные для
расчета налогового вычета» на рабочем листе Данные MS
Excel.
. Лист 2 переименовать с названием «Размер»
. На рабочем листе «Размер» MS
Excel создать таблицу
«Размер налоговых вычетов, предоставляемых сотрудникам в текущем месяце».
. Заполнить таблицу «Размер налоговых вычетов»
исходными данными. (рис. 5).
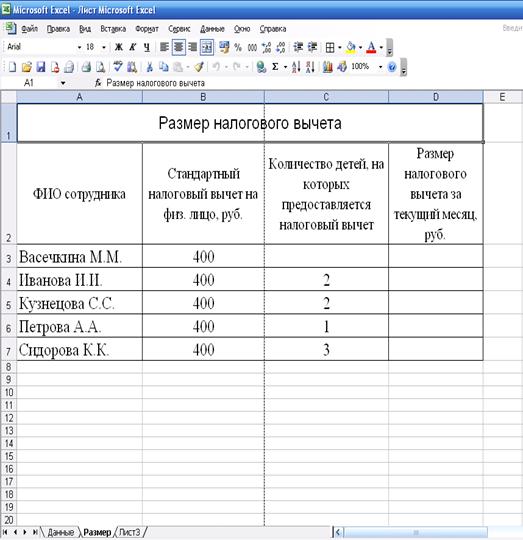
Рисунок 5: Расположение таблицы «Размер
налоговых вычетов, предоставляемых сотрудникам в текущем месяце» на рабочем
листе Размер MS
Excel
. Лист 3 переименовать с названием «Расчетная
ведомость».
. На рабочем листе «Расчетная ведомость» MS
Excel создать форму
ведомости (рис. 6) .
Рисунок 6: Расположение таблицы «Форма расчетной
ведомости фирмы ООО «Гамма»» на рабочем листе Расчетная ведомость MS
Excel
. Заполнить графу Размер налогового вычета за
текущий месяц, руб. таблицы «Размер налоговых вычетов, предоставляемых
сотрудникам в текущем месяце», находящейся на листе Размер следующим образом:
Занести в ячейку D3
формулу: =B3+(C3*600) и размножить введённую в ячейку D3
формулу до ячейки D7.
. Заполнить графу Начислено за месяц, руб. формы
«Расчетная ведомость», находящаяся на листе Расчетная ведомость следующим
образом:
В ячейку С11 занести формулу: = Данные!B3 и
размножить введенную в ячейку С12 формулу до ячейки С15.
. Заполнить графу Размер налогового вычета, руб.
следующим образом:
В ячейку D11
занести формулу: = Размер!B3 и размножить введенную в ячейку D12
формулу до ячейки D15.
. Заполнить графу НДФЛ, руб. следующим образом:
В ячейку Е11 занести формулу: =(C9-D9)*13% и
размножить введенную в ячейку Е11 формулу для остальных ячеек (с Е12 по Е15)
данной графы.
. Заполнить графу К выплате, руб. следующим
образом:
В ячейку F11
занести формулу: =C9-E9 и размножить введенную в ячейку F11
формулу для остальных ячеек (с F12
по F15) данной графы.
. Лист 4 переименовать в лист с названием
График.
. На рабочем листе График MS
Excel создать краткую
таблицу, данные взять из формы «Расчетная ведомость» (рисунок 7).
|
ФИО
сотрудника
|
К
выплате, руб.
|
|
Васечкина
М.М.
|
4
306,30
|
|
Иванова
И.И.
|
6
124,00
|
|
Кузнецова
С.С.
|
4
862,50
|
|
Петрова
А.А.
|
6
655,00
|
|
Сидорова
К.К.
|
7
420,00
|
Рисунок 7: Краткая таблица
. Результаты вычислений представить графически
(рис. 8).
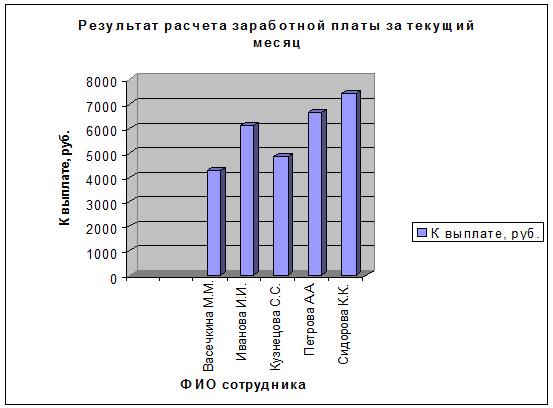
Заключение
Подведём итоги: Функция, которая может принимать
одно из двух значений 0 или 1 и зависеть от первой или нескольких переменных,
называется логическими функциями по имени создателя алгебры логики Джона Буля.
Законы Буля: Закон двойного отрицания, закон
коммутативности конъюнкции, законы ассоциации конъюнкции, закон
дистрибутивности конъюнкции, алгебра логики названная булевой алгеброй. Общий
вид булевой функции: F(Х1,Х2,…Xn),
где Хi- произвольная
величина. Функция может принимать значения либо 0, либо 1. Задача анализа
следующая: по именующейся электронной схеме составить логическую функцию путём
формальных преобразований при помощи законов алгебры; минимизировать эту
функцию и реализовать её меньшим количеством электронных элементов.
Задачи синтеза схем - по логической функции,
описывающий некоторый процесс, определить количество необходимых элементов
схемы и возможные способы их реализации. Кроме описанных двух задач анализа и
синтеза схем компьютера, математическая логика применяется при составлении
программ и при формулировании логических условий, применений пакетов прикладных
программ. Часто логическая функция задаётся не с помощью единичного выражения,
а табличным способом. Существует алгоритм, по которому таблично заданную
функцию можно преобразовать к виду логического выражения.
Приложение 1
|
Значения
простых высказываний
|
Значения
сложных высказываний
|
Значение
логической функции S
|
|
Г
|
Ф
|
П
|
Ч
|
Т
|
Алеши
|
Бориса
|
Гриши
|
о
месте изготовления сосуда
|
о
времени изготовления сосуда
|
|
|
0
|
0
|
0
|
0
|
0
|
ЛОЖЬ
|
ЛОЖЬ
|
ИСТИНА
|
ИСТИНА
|
ИСТИНА
|
ИСТИНА
|
ИСТИНА
|
ЛОЖЬ
|
|
0
|
0
|
0
|
0
|
1
|
ЛОЖЬ
|
ЛОЖЬ
|
ЛОЖЬ
|
ИСТИНА
|
ИСТИНА
|
ИСТИНА
|
ИСТИНА
|
ЛОЖЬ
|
|
0
|
0
|
0
|
1
|
0
|
ЛОЖЬ
|
ИСТИНА
|
ИСТИНА
|
ИСТИНА
|
ИСТИНА
|
ИСТИНА
|
ИСТИНА
|
ЛОЖЬ
|
|
0
|
0
|
0
|
1
|
1
|
ЛОЖЬ
|
ИСТИНА
|
ЛОЖЬ
|
ИСТИНА
|
ИСТИНА
|
ИСТИНА
|
ЛОЖЬ
|
ЛОЖЬ
|
|
0
|
0
|
1
|
0
|
0
|
ИСТИНА
|
ЛОЖЬ
|
ИСТИНА
|
ИСТИНА
|
ИСТИНА
|
ИСТИНА
|
ИСТИНА
|
ЛОЖЬ
|
|
0
|
0
|
1
|
0
|
1
|
ИСТИНА
|
ЛОЖЬ
|
ЛОЖЬ
|
ИСТИНА
|
ИСТИНА
|
ЛОЖЬ
|
ИСТИНА
|
ЛОЖЬ
|
|
0
|
0
|
1
|
1
|
0
|
ИСТИНА
|
ИСТИНА
|
ИСТИНА
|
ИСТИНА
|
ЛОЖЬ
|
ИСТИНА
|
ИСТИНА
|
ЛОЖЬ
|
|
0
|
0
|
1
|
1
|
1
|
ИСТИНА
|
ИСТИНА
|
ЛОЖЬ
|
ИСТИНА
|
ЛОЖЬ
|
ЛОЖЬ
|
ЛОЖЬ
|
ЛОЖЬ
|
|
0
|
1
|
0
|
0
|
0
|
ЛОЖЬ
|
ИСТИНА
|
ИСТИНА
|
ИСТИНА
|
ИСТИНА
|
ИСТИНА
|
ИСТИНА
|
ЛОЖЬ
|
|
0
|
1
|
0
|
0
|
1
|
ЛОЖЬ
|
ИСТИНА
|
ЛОЖЬ
|
ИСТИНА
|
ИСТИНА
|
ИСТИНА
|
ИСТИНА
|
ЛОЖЬ
|
|
0
|
1
|
0
|
1
|
0
|
ЛОЖЬ
|
ЛОЖЬ
|
ИСТИНА
|
ИСТИНА
|
ИСТИНА
|
ИСТИНА
|
ИСТИНА
|
ЛОЖЬ
|
|
0
|
1
|
0
|
1
|
1
|
ЛОЖЬ
|
ЛОЖЬ
|
ЛОЖЬ
|
ИСТИНА
|
ИСТИНА
|
ИСТИНА
|
ЛОЖЬ
|
ЛОЖЬ
|
|
0
|
1
|
1
|
0
|
0
|
ИСТИНА
|
ИСТИНА
|
ИСТИНА
|
ИСТИНА
|
ИСТИНА
|
ИСТИНА
|
ИСТИНА
|
ИСТИНА
|
|
0
|
1
|
1
|
0
|
1
|
ИСТИНА
|
ИСТИНА
|
ЛОЖЬ
|
ИСТИНА
|
ИСТИНА
|
ЛОЖЬ
|
ИСТИНА
|
ЛОЖЬ
|
|
0
|
1
|
1
|
1
|
0
|
ИСТИНА
|
ЛОЖЬ
|
ИСТИНА
|
ИСТИНА
|
ЛОЖЬ
|
ИСТИНА
|
ИСТИНА
|
ЛОЖЬ
|
|
0
|
1
|
1
|
1
|
1
|
ИСТИНА
|
ЛОЖЬ
|
ЛОЖЬ
|
ИСТИНА
|
ЛОЖЬ
|
ЛОЖЬ
|
ЛОЖЬ
|
ЛОЖЬ
|
|
1
|
0
|
0
|
0
|
0
|
ИСТИНА
|
ЛОЖЬ
|
ЛОЖЬ
|
ИСТИНА
|
ИСТИНА
|
ИСТИНА
|
ИСТИНА
|
ЛОЖЬ
|
|
1
|
0
|
0
|
0
|
1
|
ИСТИНА
|
ЛОЖЬ
|
ИСТИНА
|
ИСТИНА
|
ИСТИНА
|
ИСТИНА
|
ИСТИНА
|
ЛОЖЬ
|
|
1
|
0
|
1
|
0
|
ИСТИНА
|
ИСТИНА
|
ЛОЖЬ
|
ИСТИНА
|
ИСТИНА
|
ИСТИНА
|
ИСТИНА
|
ЛОЖЬ
|
|
1
|
0
|
0
|
1
|
1
|
ИСТИНА
|
ИСТИНА
|
ИСТИНА
|
ИСТИНА
|
ИСТИНА
|
ИСТИНА
|
ЛОЖЬ
|
ЛОЖЬ
|
|
1
|
0
|
1
|
0
|
0
|
ЛОЖЬ
|
ЛОЖЬ
|
ЛОЖЬ
|
ИСТИНА
|
ИСТИНА
|
ИСТИНА
|
ИСТИНА
|
ЛОЖЬ
|
|
1
|
0
|
1
|
0
|
1
|
ЛОЖЬ
|
ЛОЖЬ
|
ИСТИНА
|
ИСТИНА
|
ИСТИНА
|
ЛОЖЬ
|
ИСТИНА
|
ЛОЖЬ
|
|
1
|
0
|
1
|
1
|
0
|
ЛОЖЬ
|
ИСТИНА
|
ЛОЖЬ
|
ИСТИНА
|
ЛОЖЬ
|
ИСТИНА
|
ИСТИНА
|
ЛОЖЬ
|
|
1
|
0
|
1
|
1
|
1
|
ЛОЖЬ
|
ИСТИНА
|
ИСТИНА
|
ИСТИНА
|
ЛОЖЬ
|
ЛОЖЬ
|
ЛОЖЬ
|
ЛОЖЬ
|
|
1
|
1
|
0
|
0
|
0
|
ИСТИНА
|
ИСТИНА
|
ЛОЖЬ
|
ЛОЖЬ
|
ИСТИНА
|
ИСТИНА
|
ИСТИНА
|
ЛОЖЬ
|
|
1
|
1
|
0
|
0
|
1
|
ИСТИНА
|
ИСТИНА
|
ИСТИНА
|
ЛОЖЬ
|
ИСТИНА
|
ИСТИНА
|
ИСТИНА
|
ЛОЖЬ
|
|
1
|
1
|
0
|
1
|
0
|
ИСТИНА
|
ЛОЖЬ
|
ЛОЖЬ
|
ЛОЖЬ
|
ИСТИНА
|
ИСТИНА
|
ИСТИНА
|
ЛОЖЬ
|
|
1
|
1
|
0
|
1
|
1
|
ИСТИНА
|
ЛОЖЬ
|
ИСТИНА
|
ЛОЖЬ
|
ИСТИНА
|
ИСТИНА
|
ЛОЖЬ
|
ЛОЖЬ
|
|
1
|
1
|
1
|
0
|
0
|
ЛОЖЬ
|
ИСТИНА
|
ЛОЖЬ
|
ЛОЖЬ
|
ИСТИНА
|
ИСТИНА
|
ИСТИНА
|
ЛОЖЬ
|
|
1
|
1
|
1
|
0
|
1
|
ЛОЖЬ
|
ИСТИНА
|
ИСТИНА
|
ЛОЖЬ
|
ИСТИНА
|
ЛОЖЬ
|
ИСТИНА
|
ЛОЖЬ
|
|
1
|
1
|
1
|
1
|
0
|
ЛОЖЬ
|
ЛОЖЬ
|
ЛОЖЬ
|
ЛОЖЬ
|
ЛОЖЬ
|
ИСТИНА
|
ИСТИНА
|
ЛОЖЬ
|
|
1
|
1
|
1
|
1
|
1
|
ЛОЖЬ
|
ЛОЖЬ
|
ИСТИНА
|
ЛОЖЬ
|
ЛОЖЬ
|
ЛОЖЬ
|
ЛОЖЬ
|
ЛОЖЬ
|
Список литературы
1. Андреева
Е.В., Фалина И.Н. Системы счисления и компьютерная арифметика. Изд. 2-е. - М.: Лаборатория
Базовых Знаний, 2000 г. - 248 с.: ил.
2. Босова
Л.Л. Арифметические и логические основы ЭВМ. Серия "Информатика в
школе". - М.: Информатика и образование, 2000. - 208 с.: ил.
3. Логика
для всех [Электронный ресурс]: Режим доступа: http://ntl.narod.ru/logic/course/valentin.html,
свободный
. Миньков
С.Л. Информатика: Учебное пособие. - Томск: Томский межвузовский центр
дистанционного образования, 2000. - 222 с.
. Одинцов
Б.Е. Информатика в экономике: Учеб. пособие/Под ред. проф. Б.Е.Одинцова, проф.
А.Н. Романова. - М.: Вузовский учебник, 2008. - 478 с.
. Шауцукова
Л.З. "Основы информатики в вопросах и ответах", Издательский центр
"Эль-Фа", Нальчик, 1994.