Логические функции и логические уравнения
Курсовая
работа
Логические
функции и логические уравнения
Введение
Математика является наукой, в которой все истины доказываются с помощью
умозаключений.
В логических теориях описываются процессы умозаключений и законы
мышления, которые позволяют из истинности одних суждений делать заключения об
истинности или ложности других суждений.
Впервые в истории идеи о построении логики на математической основе были
высказаны Г.В.Лейбницем в конце 17 столетий. Им были заложены основы для
алгебраизации логики и построения логических исчислений. Он говорил: «Мы
употребляем знаки не только для того, чтобы передать наши мысли другим лицам,
но и для того, чтобы облегчить сам процесс нашего мышления».
С помощью математической логики решаются проблемы, выясняющие общие
свойства математических теорий (например, проблемы непротиворечивости, полноты,
разрешимости и др.).
Целью и задачей работы является рассмотрение элементов алгебры логики,
логических функций и логических уравнений, а так же их решения, построением
таблицы истинности и с помощью метода упрощения и разложения на части.
При этом предполагается, что вывод зависит только от способа связи
входящих в него утверждений и их строения, а не от их конкретного содержания.
1.
Алгебра логики
Алгебра логики - это математический аппарат, с помощью которого
записывают, вычисляют, упрощают и преобразовывают логические высказывания.
Создателем алгебры логики является живший в ХIХ веке английский математик
Джордж Буль, в честь которого эта алгебра названа булевой алгеброй
высказываний.
1.1
Логическая переменная
Логическая переменная в алгебре логики может принимать одно из двух
возможных значений: TRUE - истина, FALSE - ложь. Эти значения в цифровой
технике принято рассматривать как логическую "1" (TRUE) и логический
"0" (FALSE), или как двоичные числа 1 и 0.
1.2
Функции в алгебре логики
Логическая функция - это функция логических переменных, которая может
принимать только два значения : 0 или 1. В свою очередь, сама логическая
переменная (аргумент логической функции) тоже может принимать только два
значения : 0 или 1.
С помощью логических переменных и символов логических операций любое
высказывание можно формализовать, то есть заменить логической функцией.
1.3 Логические операции
|
|
Отрицание
|
|
|
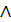
Конъюнкция
|
|
|
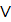
Дизъюнкция
|
|
|
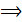
Импликация
|
|
|
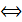
Эквивалентность
|
1.4 Законы
алгебры логики
В алгебре логики выполняются следующие основные законы, позволяющие
производить тождественные преобразования логических выражений:
|
Закон
|
ИЛИ
|
И
|
|
Переместительный
(Коммутативный)
|
 
|
|
|
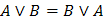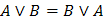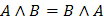
Сочетательный
(Ассоциативный)
|
  
|
  
|
|
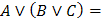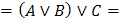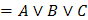
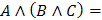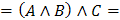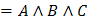
Распределительный
(Дистрибутивный)
|
 
|
 
|
|
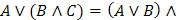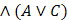
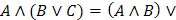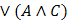
Правила де Моргана
|
|
|
|
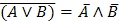
Идемпотенции
|
|
|
|
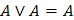
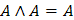
Поглощения
|
|
|
|
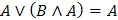
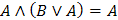
Склеивания
|
|
|
|
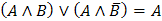
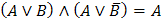
Операция переменной с ее
инверсией
|
|
|
|
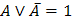
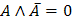
Операция с константами
|
|
|
|
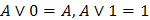
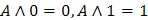
Двойного отрицания
|
|
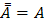
Формулы склеивания (закон исключения)
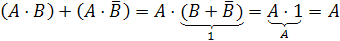
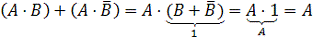
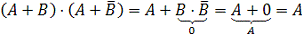
Формулы
поглощения
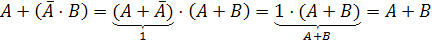
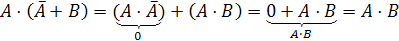
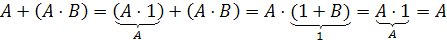
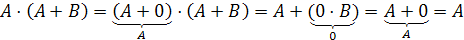
Решение
логических функций и уравнений
Разнообразие логических задач очень велико. Способов их решения тоже
немало. Но наибольшее распространение получили следующие три способа решения
логических задач:
· средствами алгебры логики;
· табличный;
· с помощью рассуждений.
В курсовой работе рассматриваются только первые два случая решения задач.
Обычно используется следующая схема решения:
1. изучается условие задачи;
2. вводится система обозначений для логических высказываний;
. конструируется логическая формула, описывающая логические связи
между всеми высказываниями условия задачи;
. определяются значения истинности этой логической формулы;
. из полученных значений истинности формулы определяются значения
истинности введённых логических высказываний, на основании которых делается
заключение о решении.
Пример 1.
Является
ли функция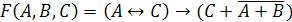 
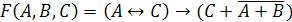тождественно
истинной?
Решение.
Решить данную задачу можно двумя способами.
Первый
способ - минимизация логической функции.
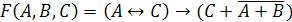
Избавимся
от операций импликации и эквивалентности, заменив эти операции на комбинацию
конъюнкции, дизъюнкции и инверсии.
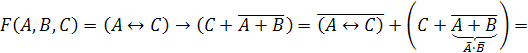
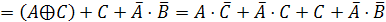
Последовательно
несколько раз применим формулы поглощения
.
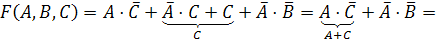
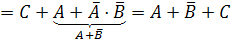
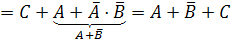Следовательно,
данная функция не является тождественно-истинной.
Второй
способ - построение таблицы истинности. У тождественно-истинной функции в
последнем столбце таблицы истинности должны стоять все единицы.
У
функции три переменные, следовательно, количество строк в таблице 23= 8.
Подсчитаем количество операций и установим порядок их выполнения.
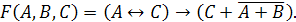
Пять
логических операций, следовательно, количество столбцов в таблице истинности -
3+5=8.
|
|
|
|
|
|
|
|
|
|
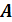
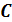
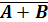
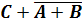
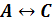
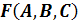
0
|
0
|
0
|
0
|
1
|
1
|
1
|
1
|
|
0
|
0
|
1
|
0
|
1
|
1
|
0
|
1
|
|
0
|
1
|
0
|
1
|
0
|
0
|
1
|
0
|
|
0
|
1
|
1
|
1
|
0
|
1
|
0
|
1
|
|
1
|
0
|
0
|
1
|
0
|
0
|
1
|
0
|
|
1
|
0
|
1
|
1
|
0
|
1
|
0
|
1
|
|
1
|
1
|
0
|
1
|
0
|
0
|
1
|
0
|
|
1
|
1
|
1
|
1
|
0
|
1
|
0
|
1
|
Анализ построенной таблицы показывает, что существует набор входных
переменных, при котором функция равна 0. Следовательно, данная функция не
является тождественно-истинной.
Пример 2.
Условие
изменения логической функции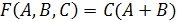 
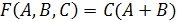при
одновременном изменении аргументов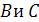 
.
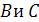Решение:
Дана логическая функция от трех переменных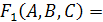 
.
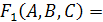
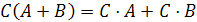
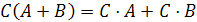Изменим
одновременно переменные :
.
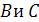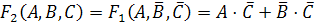
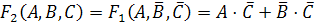Постоим
таблицу истинности для двух функций:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
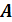
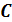
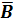
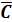
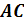
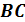
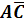
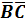
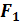
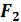
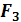
0
|
0
|
0
|
1
|
1
|
0
|
0
|
0
|
1
|
0
|
1
|
1
|
|
0
|
0
|
1
|
1
|
0
|
0
|
0
|
0
|
0
|
0
|
0
|
0
|
|
0
|
1
|
0
|
0
|
1
|
0
|
0
|
0
|
0
|
0
|
0
|
0
|
|
0
|
1
|
1
|
0
|
0
|
0
|
1
|
0
|
0
|
1
|
0
|
1
|
|
1
|
0
|
0
|
1
|
1
|
0
|
0
|
1
|
1
|
0
|
1
|
1
|
|
1
|
0
|
1
|
1
|
0
|
1
|
0
|
0
|
0
|
1
|
0
|
1
|
|
1
|
1
|
0
|
0
|
1
|
0
|
0
|
1
|
0
|
0
|
1
|
1
|
|
1
|
1
|
1
|
0
|
0
|
1
|
1
|
0
|
0
|
1
|
0
|
1
|
Анализируем
полученную таблицу. Из восьми строк таблицы лишь (2-й и 3-й) функция не
изменяет своего значения. Также в этих строках переменная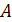 
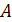не
изменяет своего значения на противоположное, а переменные -
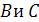
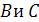изменяются.
Строим
СКНФ функции по этим строкам:
.
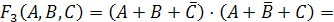
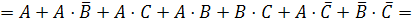
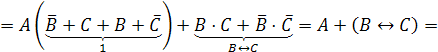
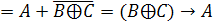
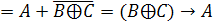Ответ:
.
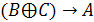
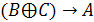Пример
3.
Условие
изменения логической функции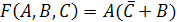 
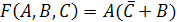при
одновременном изменении аргументов 
.
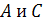
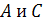Решение:
Дана логическая функция от трех переменных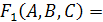
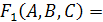
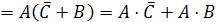
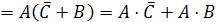. Изменим
одновременно переменные :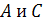 
.
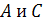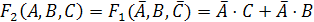
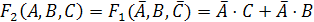Постоим
таблицу истинности для двух функций:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
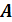
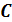
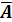
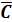
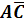
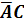
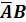
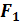
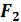
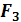
0
|
0
|
0
|
1
|
1
|
0
|
0
|
0
|
0
|
0
|
0
|
0
|
|
0
|
0
|
1
|
1
|
0
|
0
|
0
|
1
|
0
|
0
|
1
|
1
|
|
0
|
1
|
0
|
1
|
1
|
0
|
0
|
0
|
1
|
0
|
1
|
1
|
|
0
|
1
|
1
|
1
|
0
|
0
|
0
|
1
|
1
|
0
|
1
|
1
|
0
|
0
|
0
|
1
|
0
|
1
|
0
|
0
|
1
|
0
|
1
|
|
1
|
0
|
1
|
0
|
0
|
0
|
0
|
0
|
0
|
0
|
0
|
0
|
|
1
|
1
|
0
|
0
|
1
|
1
|
1
|
0
|
0
|
1
|
0
|
1
|
|
1
|
1
|
1
|
0
|
0
|
1
|
1
|
0
|
0
|
1
|
0
|
1
|
Анализируем
полученную таблицу. Из восьми строк таблицы лишь (1-й и 6-й) функция не
изменяет своего значения. Также в этих строках переменная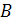 
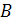не
изменяет своего значения на противоположное, а переменные -
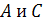
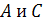изменяются.
Строим
СКНФ функции по этим строкам:
.
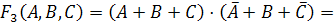
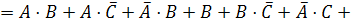
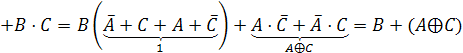
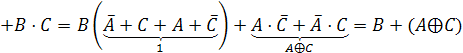Ответ:
.
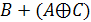
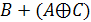Пример
4.
Условие
изменения логической функции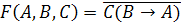 
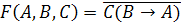при
одновременном изменении аргументов 
.
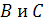
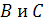Решение:
Дана логическая функция от трех переменных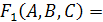
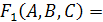
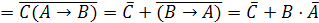
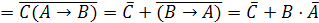. Изменим
одновременно переменные :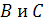 
.
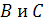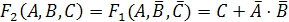
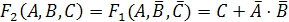Постоим
таблицу истинности для двух функций:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
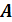
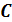
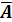
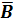
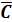
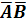
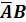
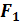
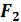
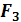
0
|
0
|
0
|
1
|
1
|
1
|
0
|
1
|
0
|
1
|
1
|
0
|
|
0
|
0
|
1
|
1
|
1
|
0
|
0
|
1
|
0
|
0
|
1
|
1
|
|
0
|
1
|
0
|
1
|
0
|
1
|
0
|
0
|
1
|
1
|
0
|
1
|
|
0
|
1
|
1
|
1
|
0
|
0
|
0
|
0
|
1
|
1
|
1
|
0
|
|
1
|
0
|
0
|
0
|
1
|
1
|
0
|
0
|
0
|
1
|
0
|
1
|
|
1
|
0
|
1
|
0
|
1
|
0
|
0
|
0
|
0
|
0
|
1
|
1
|
|
1
|
1
|
0
|
0
|
0
|
1
|
1
|
0
|
0
|
1
|
0
|
1
|
|
1
|
1
|
1
|
0
|
0
|
0
|
1
|
0
|
0
|
0
|
1
|
1
|
Анализируем
полученную таблицу. Из восьми строк таблицы лишь (1-й и 4-й) функция не
изменяет своего значения. Также в этих строках переменная 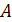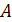не
изменяет своего значения на противоположное, а переменные -
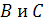
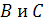изменяются.
Строим
СКНФ функции по этим строкам:
.
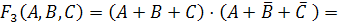
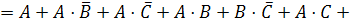
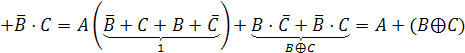
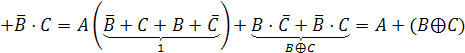Ответ:
.
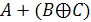
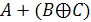Пример
5.
Условие
изменения логической функции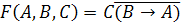 
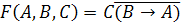при
одновременном изменении аргументов .
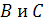
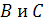Решение:
Дана логическая функция от трех переменных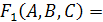
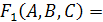
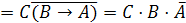
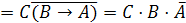. Изменим
одновременно переменные :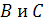 
.
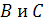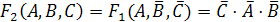
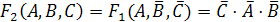Постоим
таблицу истинности для двух функций:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
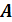
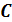
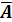
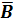
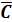
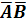
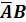
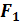
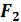
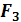
0
|
0
|
0
|
1
|
1
|
1
|
0
|
1
|
0
|
0
|
1
|
1
|
|
0
|
0
|
1
|
1
|
1
|
0
|
0
|
1
|
0
|
0
|
0
|
0
|
|
0
|
1
|
0
|
1
|
0
|
1
|
0
|
0
|
1
|
0
|
0
|
0
|
|
0
|
1
|
1
|
1
|
0
|
0
|
0
|
0
|
1
|
1
|
0
|
1
|
|
1
|
0
|
0
|
0
|
1
|
1
|
0
|
0
|
0
|
0
|
0
|
0
|
|
1
|
0
|
1
|
0
|
1
|
0
|
0
|
0
|
0
|
0
|
0
|
0
|
|
1
|
1
|
0
|
0
|
0
|
1
|
1
|
0
|
0
|
0
|
0
|
0
|
|
1
|
1
|
1
|
0
|
0
|
0
|
1
|
0
|
0
|
0
|
0
|
0
|
Анализируем
полученную таблицу. Из восьми строк таблицы лишь (1-й и 4-й) функция не
изменяет своего значения. Также в этих строках переменная 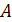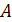не
изменяет своего значения на противоположное, а переменные -
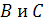
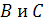изменяются.
Строим
СДНФ функции по этим строкам:
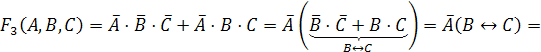
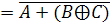
Ответ:
.
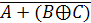
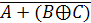Пример
6.
Найти
корень логического уравнения: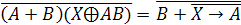 
.
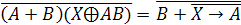Первый
способ решения - построение таблицы истинности. Построим таблицы истинности
правой и левой части уравнения и посмотрим, при каком X, значения в последних
столбцах этих таблиц совпадут.
|
|
   
|
|
|
|
|
|
|
|
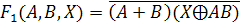
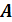
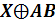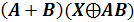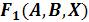
0
|
0
|
0
|
0
|
0
|
0
|
0
|
1
|
|
0
|
0
|
1
|
0
|
1
|
0
|
0
|
1
|
|
0
|
1
|
0
|
0
|
0
|
1
|
0
|
1
|
|
0
|
1
|
1
|
0
|
1
|
1
|
1
|
0
|
|
1
|
0
|
0
|
0
|
0
|
1
|
0
|
1
|
|
1
|
0
|
1
|
0
|
1
|
1
|
1
|
0
|
|
1
|
1
|
0
|
1
|
1
|
1
|
0
|
|
1
|
1
|
1
|
1
|
0
|
1
|
0
|
1
|
|
|
|
   
|
|
|
|
|
|
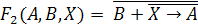
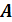
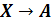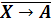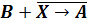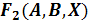
0
|
0
|
0
|
1
|
0
|
0
|
1
|
|
0
|
0
|
1
|
0
|
1
|
1
|
0
|
|
0
|
1
|
0
|
1
|
0
|
1
|
0
|
|
0
|
1
|
1
|
0
|
1
|
1
|
0
|
|
1
|
0
|
0
|
1
|
0
|
0
|
1
|
|
1
|
0
|
1
|
1
|
0
|
0
|
1
|
|
1
|
1
|
0
|
1
|
0
|
1
|
0
|
|
1
|
1
|
1
|
1
|
0
|
1
|
0
|
Сравним
полученные таблицы истинности и выберем те строки, в которых значения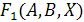 
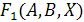и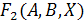 
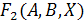совпадут.
|
|
|
|
|
|
|
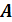
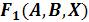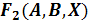
0
|
0
|
0
|
1
|
1
|
|
0
|
0
|
1
|
1
|
0
|
|
0
|
1
|
0
|
1
|
0
|
|
0
|
1
|
1
|
0
|
0
|
|
1
|
0
|
0
|
1
|
1
|
|
1
|
0
|
1
|
0
|
1
|
|
1
|
1
|
0
|
0
|
0
|
|
1
|
1
|
1
|
1
|
0
|
Перепишем только выбранные строки, оставив только столбцы аргументов.
Посмотрим на переменную Х как на функцию от A и B .
Очевидно,
что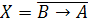 
.
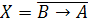Второй
способ решения - заменить знак равенства в уравнении на знак эквиваленции, а
затем упростить полученное логическое уравнение.
Для
облегчения дальнейшей работы предварительно упростим правую и левую части
логического уравнения и найдем их отрицания:
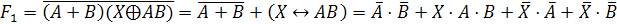
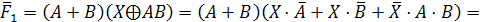
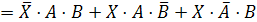
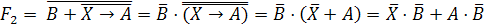
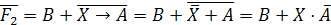
Заменим
в нашем логическом уравнении знак равенства на знак эквивалентности:
=
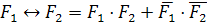
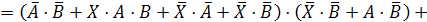
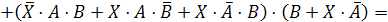
Перегруппируем
логические слагаемые данного выражения, вынеся за скобку множители X и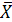 
.
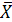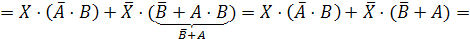
Обозначим
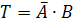
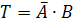, тогда
.
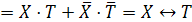
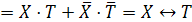Следовательно,
что логическое уравнение имеет решение:
.
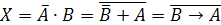
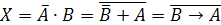Ответ:
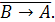
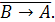
Пример
7.
Найти
корень логического уравнения: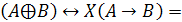 
.
|
|
  
|
|
|
|
|
|
|
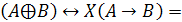
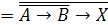
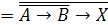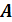
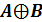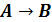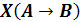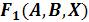
0
|
0
|
0
|
0
|
1
|
0
|
1
|
|
0
|
0
|
1
|
0
|
1
|
1
|
0
|
|
0
|
1
|
0
|
1
|
1
|
0
|
0
|
|
0
|
1
|
1
|
1
|
1
|
1
|
1
|
|
1
|
0
|
0
|
1
|
0
|
0
|
0
|
|
1
|
0
|
1
|
1
|
0
|
0
|
0
|
|
1
|
1
|
0
|
0
|
1
|
0
|
1
|
|
1
|
1
|
1
|
0
|
1
|
1
|
0
|
Первый способ решения - построение таблицы истинности. Построим таблицы
истинности правой и левой части уравнения и посмотрим, при каком X, значения в
последних столбцах этих таблиц совпадут.
.
|
|
|
 
|
|
|
|
|
|
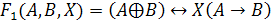
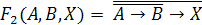
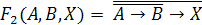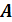
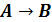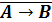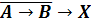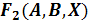
0
|
0
|
0
|
1
|
0
|
1
|
0
|
|
0
|
0
|
1
|
1
|
0
|
1
|
0
|
|
0
|
1
|
0
|
1
|
0
|
1
|
0
|
|
0
|
1
|
1
|
1
|
0
|
1
|
0
|
|
1
|
0
|
0
|
0
|
1
|
0
|
1
|
|
1
|
0
|
1
|
0
|
1
|
1
|
0
|
|
1
|
1
|
0
|
1
|
0
|
1
|
0
|
|
1
|
1
|
1
|
1
|
0
|
1
|
0
|
Сравним
полученные таблицы истинности и выберем те строки, в которых значения 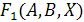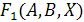и 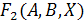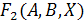совпадут.
|
|
|
|
|
|
|
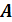
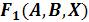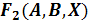
0
|
0
|
0
|
1
|
0
|
|
0
|
0
|
1
|
0
|
0
|
|
0
|
1
|
0
|
0
|
0
|
|
0
|
1
|
1
|
1
|
0
|
|
1
|
0
|
0
|
0
|
1
|
|
1
|
0
|
1
|
0
|
0
|
|
1
|
1
|
0
|
1
|
0
|
|
1
|
1
|
1
|
0
|
0
|
Перепишем только выбранные строки, оставив только столбцы аргументов.
Посмотрим на переменную Х как на функцию от A и B .
Очевидно,
что 
.
Второй
способ решения - заменить знак равенства в уравнении на знак эквиваленции, а
затем упростить полученное логическое уравнение.
Для
облегчения дальнейшей работы предварительно упростим правую и левую части
логического уравнения и найдем их отрицания:
.
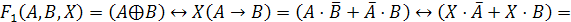
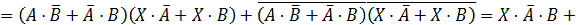
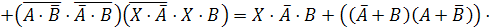
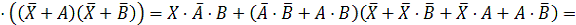
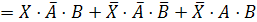
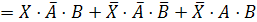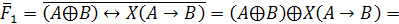
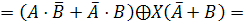
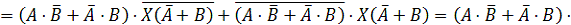
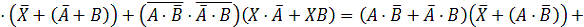
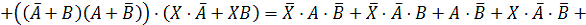
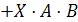
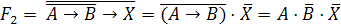
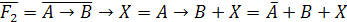
Заменим
в нашем логическом уравнении знак равенства на знак эквивалентности:
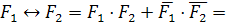
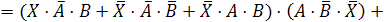
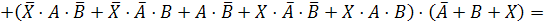
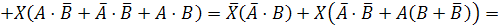
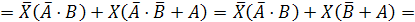
Обозначим
через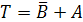 
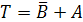, тогда
.
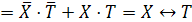
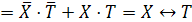Следовательно,
что логическое уравнение имеет решение:
.
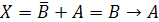
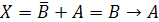Ответ:
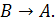
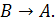
Пример
8.
Найти
корень логического уравнения: 
.
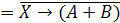
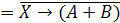Первый
способ решения - построение таблицы истинности. Построим таблицы истинности
правой и левой части уравнения и посмотрим, при каком X, значения в последних
столбцах этих таблиц совпадут.
|
|
|
|
|
|
|
|
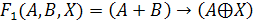
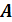
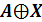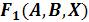
0
|
0
|
0
|
0
|
0
|
1
|
|
0
|
0
|
1
|
0
|
1
|
1
|
|
0
|
1
|
0
|
1
|
0
|
0
|
|
0
|
1
|
1
|
1
|
1
|
1
|
|
1
|
0
|
0
|
1
|
1
|
1
|
|
1
|
0
|
1
|
1
|
0
|
0
|
|
1
|
1
|
0
|
1
|
1
|
1
|
|
1
|
1
|
1
|
1
|
0
|
0
|
|
|
|
|
|
|
|
|
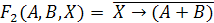
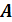
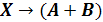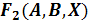
0
|
0
|
0
|
0
|
1
|
0
|
|
0
|
0
|
1
|
0
|
0
|
1
|
|
0
|
1
|
0
|
1
|
1
|
0
|
|
0
|
1
|
1
|
1
|
1
|
0
|
|
1
|
0
|
0
|
1
|
1
|
0
|
|
1
|
0
|
1
|
1
|
1
|
0
|
|
1
|
1
|
0
|
1
|
1
|
0
|
|
1
|
1
|
1
|
1
|
1
|
0
|
логика алгебра минимизация функция
Сравним
полученные таблицы истинности и выберем те строки, в которых значения 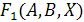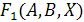и 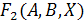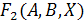совпадут.
|
|
|
|
|
|
|
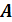
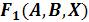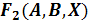
0
|
0
|
0
|
1
|
0
|
|
0
|
0
|
1
|
1
|
1
|
|
0
|
1
|
0
|
0
|
0
|
|
0
|
1
|
1
|
1
|
0
|
|
1
|
0
|
0
|
1
|
0
|
|
1
|
0
|
1
|
0
|
0
|
|
1
|
1
|
0
|
1
|
0
|
|
1
|
1
|
1
|
0
|
0
|
Перепишем только выбранные строки, оставив только столбцы аргументов.
Посмотрим на переменную Х как на функцию от A и B .
Очевидно,
что .
Второй
способ решения - заменить знак равенства в уравнении на знак эквиваленции, а
затем упростить полученное логическое уравнение.
Для
облегчения дальнейшей работы предварительно упростим правую и левую части
логического уравнения и найдем их отрицания:
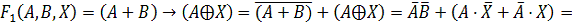
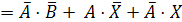
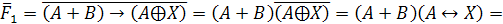
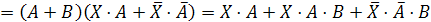
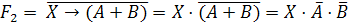
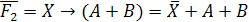
Заменим
в нашем логическом уравнении знак равенства на знак эквивалентности:
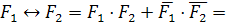
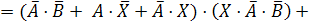
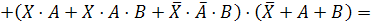
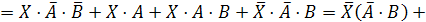
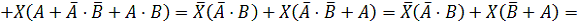
Обозначим
через 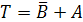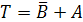, тогда
.
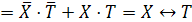
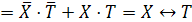Следовательно,
что логическое уравнение имеет решение:
.
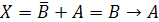
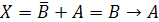Ответ:
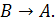
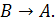
Пример
9.
Найти
корень логического уравнения: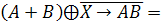 
.
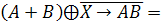
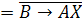
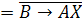Первый
способ решения - построение таблицы истинности. Построим таблицы истинности
правой и левой части уравнения и посмотрим, при каком X, значения в последних
столбцах этих таблиц совпадут.
|
|
 
|
|
|
|
|
|
|
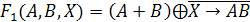
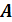
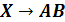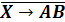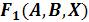
0
|
0
|
0
|
0
|
1
|
0
|
0
|
|
0
|
0
|
1
|
0
|
0
|
1
|
1
|
|
0
|
1
|
0
|
1
|
1
|
0
|
1
|
|
0
|
1
|
1
|
1
|
0
|
1
|
0
|
|
1
|
0
|
0
|
1
|
1
|
0
|
1
|
|
1
|
0
|
1
|
1
|
0
|
1
|
0
|
|
1
|
1
|
0
|
1
|
1
|
0
|
1
|
|
1
|
1
|
1
|
1
|
1
|
0
|
1
|
|
|
|
 
|
|
|
|
|
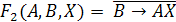
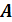
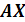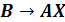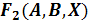
0
|
0
|
0
|
0
|
1
|
0
|
|
0
|
0
|
1
|
0
|
1
|
0
|
|
0
|
1
|
0
|
0
|
0
|
1
|
|
0
|
1
|
1
|
0
|
0
|
1
|
|
1
|
0
|
0
|
0
|
1
|
0
|
|
1
|
0
|
1
|
1
|
1
|
0
|
|
1
|
1
|
0
|
0
|
0
|
1
|
|
1
|
1
|
1
|
1
|
1
|
0
|
Сравним
полученные таблицы истинности и выберем те строки, в которых значения 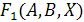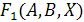и 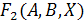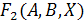совпадут.
|
|
|
|
|
|
|
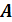
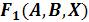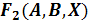
0
|
0
|
0
|
0
|
0
|
|
0
|
0
|
1
|
1
|
0
|
|
0
|
1
|
0
|
1
|
1
|
|
0
|
1
|
1
|
0
|
1
|
|
1
|
0
|
0
|
1
|
0
|
|
1
|
0
|
1
|
0
|
0
|
|
1
|
1
|
0
|
1
|
1
|
|
1
|
1
|
1
|
0
|
Перепишем только выбранные строки, оставив только столбцы аргументов.
Посмотрим на переменную Х как на функцию от A и B .
Очевидно,
что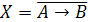 
.
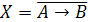Второй
способ решения - заменить знак равенства в уравнении на знак эквиваленции, а
затем упростить полученное логическое уравнение.
Для
облегчения дальнейшей работы предварительно упростим правую и левую части
логического уравнения и найдем их отрицания:
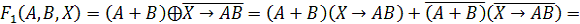
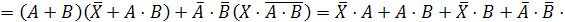
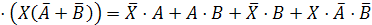
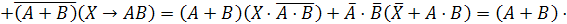
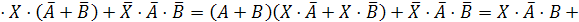
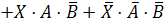
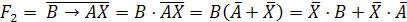
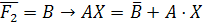
Заменим
в нашем логическом уравнении знак равенства на знак эквивалентности:
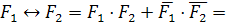
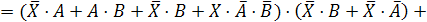
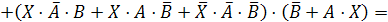
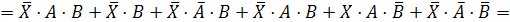
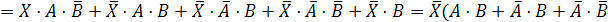
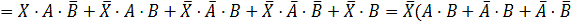
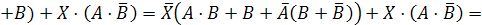
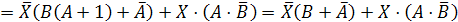
Обозначим
через 
, тогда
.
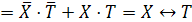
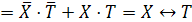Следовательно,
что логическое уравнение имеет решение:
.
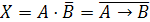
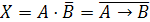Ответ:
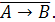
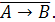
Пример
10.
Найти
корень логического уравнения: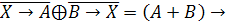 
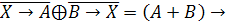
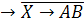
Первый
способ решения - построение таблицы истинности. Построим таблицы истинности
правой и левой части уравнения и посмотрим, при каком X, значения в последних
столбцах этих таблиц совпадут.
|
|
 
|
|
|
|
|
|
|
|
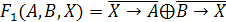
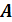
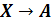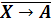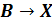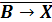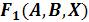
0
|
0
|
0
|
1
|
0
|
1
|
0
|
0
|
|
0
|
0
|
1
|
0
|
1
|
1
|
0
|
1
|
|
0
|
1
|
0
|
1
|
0
|
0
|
1
|
1
|
|
0
|
1
|
1
|
0
|
1
|
1
|
0
|
1
|
|
1
|
0
|
0
|
1
|
0
|
1
|
0
|
0
|
|
1
|
0
|
1
|
1
|
0
|
1
|
0
|
0
|
|
1
|
1
|
0
|
1
|
0
|
0
|
1
|
1
|
|
1
|
1
|
1
|
1
|
0
|
1
|
0
|
0
|
|
|
|
|
|
|
|
|
|
|
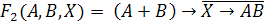
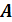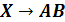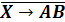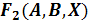
0
|
0
|
0
|
0
|
0
|
1
|
0
|
1
|
|
0
|
0
|
1
|
0
|
0
|
0
|
1
|
1
|
|
0
|
1
|
0
|
0
|
1
|
1
|
0
|
0
|
|
0
|
1
|
1
|
0
|
1
|
0
|
1
|
1
|
|
1
|
0
|
0
|
0
|
1
|
1
|
0
|
0
|
|
1
|
0
|
1
|
0
|
1
|
0
|
1
|
1
|
|
1
|
1
|
0
|
1
|
1
|
1
|
0
|
0
|
|
1
|
1
|
1
|
1
|
1
|
1
|
0
|
0
|
Сравним
полученные таблицы истинности и выберем те строки, в которых значения 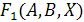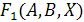и 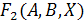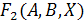совпадут.
|
|
|
|
|
|
|
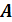
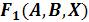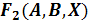
0
|
0
|
0
|
0
|
1
|
|
0
|
0
|
1
|
1
|
1
|
|
0
|
1
|
0
|
1
|
0
|
|
0
|
1
|
1
|
1
|
1
|
|
1
|
0
|
0
|
0
|
0
|
|
1
|
0
|
1
|
0
|
1
|
|
1
|
1
|
0
|
1
|
0
|
|
1
|
1
|
1
|
0
|
0
|
Перепишем только выбранные строки, оставив только столбцы аргументов.
Посмотрим на переменную Х как на функцию от A и B .
Очевидно,
что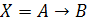 
.
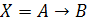Второй
способ решения - заменить знак равенства в уравнении на знак эквиваленции, а
затем упростить полученное логическое уравнение.
Для
облегчения дальнейшей работы предварительно упростим правую и левую части
логического уравнения и найдем их отрицания:
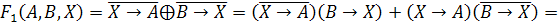
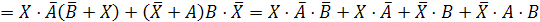
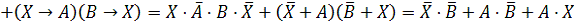
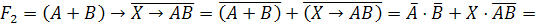
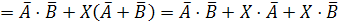
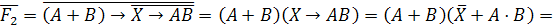
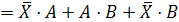
Заменим
в нашем логическом уравнении знак равенства на знак эквивалентности:
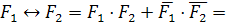
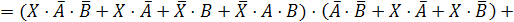
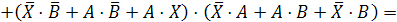
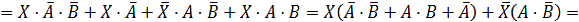
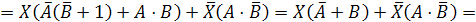
Обозначим
через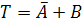 
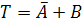, тогда
.
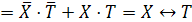
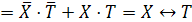Следовательно,
что логическое уравнение имеет решение:
.
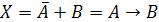
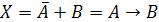Ответ:
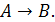
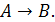
Заключение
В курсовой работе были рассмотрены решения логических функций и уравнений
с помощью двух основных методов: 1) построением таблицы истинности; 2)
упрощением и разбиением на части. В результате проделанной работы можно сделать
следующий вывод, что эти методы являются более рациональными и удобными при
решении данных задач.
Первый способ позволяет выделить из класса формул всегда истинные формулы
и всегда ложные формулы, установить отношение логического следования между
формулами, их эквивалентность.
Преимуществом второго способа является то, что при помощи простых
выражений можно упростить сложные утверждения и проверить их истинность.
Список
литературы
1. Лапшева
Е.Е. Элементы математической логики - Саратов, 2007.
2. Тесты
ЕГЭ по информатики.
3. <http://www.sgu.ru/files/nodes/14429/log.pdf>
. <http://www.examen.ru/>
. http://localhost/C:/DOCUME~1/9335~1/LOCALS~1/Temp/Rar$EX48.515/algebra.htm