Логические сети
Содержание
Введение
. Логические
сети
1.1 Определение
и реализация булевых функций
1.2 Схемы
функциональных элементов
.3 Мультиплексоры
.4 Программируемые
логические матрицы
. Практическая
часть
Заключение
Список
литературы
Введение
Логические сети - этот обобщенное название
технологий, реализующих кодовые преобразования. Например, мультиплексоры и
программируемые логические матрицы.
Мультиплексоры могут использоваться в делителях
частоты, триггерных устройствах, сдвигающих устройствах и др. Их часто используют
для преобразования параллельного двоичного кода в последовательный. Для такого
преобразования достаточно подать на информационные входы мультиплексора
параллельный двоичный код, а сигналы на адресные входы подавать в такой
последовательности, чтобы к выходу поочередно подключались входы, начиная с
первого и заканчивая последним.
В микропроцессорной технике программируемые
логические матрицы (ПЛМ) наиболее широко используются для реализации
микропрограммных устройств управления. По способу программирования различают
ПЛМ программируемые в процессе изготовления и программируемые пользователем.
В ПЛМ первого типа информация заносится в
матрицы путем подключения элементов к шинам благодаря металлизации нужных
участков схемы, что выполняется с помощью фотошаблона (маски). Никаких
изменений пользователь в этом случае в ходе эксплуатации ПЛМ сделать не может.
Подобным способом изготовляются ПЛМ, встраиваемые в МП БИС, а также автономные
ПЛМ стандартного микропрограммного обеспечения.
ПЛМ второго типа поставляются
незапрограммированными, и их функциональная ориентация производится
пользователем с помощью специального оборудования, причем существуют ПЛМ с
однократной записью информации и репрограммируемые ПЛМ, в которых записанная
информация может быть стерта ультрафиолетовым или рентгеновским лучом.
1. Логические сети
.1 Определение и реализация булевых функций
Мультиграф 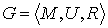 , в котором
выделено k вершин
(полюсов), называется k-полюсной сетью. Сеть G, задаваемая
неориентированным мультиграфом с k полюсами, в которой каждое ребро
помечено буквой из алфавита
, в котором
выделено k вершин
(полюсов), называется k-полюсной сетью. Сеть G, задаваемая
неориентированным мультиграфом с k полюсами, в которой каждое ребро
помечено буквой из алфавита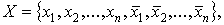 называется k-полюсной
контактной схемой.
называется k-полюсной
контактной схемой.
На рисунке 1 приведен пример
контактной схемы с двумя полюсами а1 и а6.
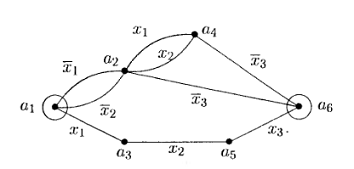
Рисунок 1
(k+1) -
полюсная схема, в которой один полюс выделен (он называется входным), а
остальные полюса (выходные) равноправны, называется (1,k)-полюсником.
Таким образом, если в приведенной на рисунке 1 двухполюсной схеме
рассматривать, например, полюс а1 как входной, а полюс а6, как выходной, то
получаем (1, 1)-полюсник.
Ребра контактной схемы называются
контактами. Контакт, соответствующий логической переменной 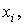 называется
замыкающим и обозначается через
называется
замыкающим и обозначается через 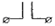 . Замыкающий контакт пропускает ток
при
. Замыкающий контакт пропускает ток
при 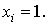 Контакт,
соответствующий литере
Контакт,
соответствующий литере 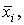 называется
размыкающим и обозначается как
называется
размыкающим и обозначается как 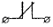 . Через него ток проходит при
. Через него ток проходит при 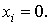 Таким
образом, значение 1 интерпретируется как состояние переключателя “ток
проходит”, а 0 - “ток не проходит”. Функции
Таким
образом, значение 1 интерпретируется как состояние переключателя “ток
проходит”, а 0 - “ток не проходит”. Функции 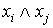 соответствует последовательное
соединение контактов
соответствует последовательное
соединение контактов 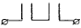 , а функции
, а функции 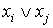 -
параллельное соединение контактов
-
параллельное соединение контактов 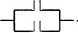
Нетрудно заметить, что схеме,
показанной на рисунке 1, соответствует электрическая схема, приведенная на
рисунке 2, а также схема контактов, изображенная на рисунке 3. На последнем
рисунке показаны контакты, зависящие от значений переменных  а также
схема соединений контактов.
а также
схема соединений контактов.
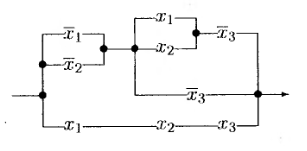
Рисунок 2
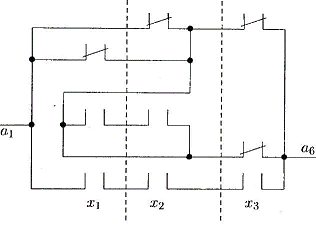
Рисунок 3
Пусть a, b - полюса контактной схемы
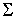 ,
, 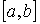 - некоторая
цепь из а в b,
- некоторая
цепь из а в b, 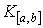 -
конъюнкция литер, приписанных ребрам цепи
-
конъюнкция литер, приписанных ребрам цепи 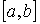 . Функция
. Функция 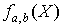 ,
определяемая формулой
,
определяемая формулой 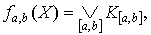 в которой
дизъюнкция берется по всем простым цепям схемы, соединяющим полюса a и b, называется
функцией проводимости между полюсами a и b схем
в которой
дизъюнкция берется по всем простым цепям схемы, соединяющим полюса a и b, называется
функцией проводимости между полюсами a и b схем  Говорят,
что функция
Говорят,
что функция 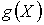 реализуется
(1, k)-полюсником,
если существует такой выходной полюс
реализуется
(1, k)-полюсником,
если существует такой выходной полюс 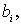 что
что  где а - входной полюс.
(1,1)-полюсники называются эквивалентными, если они реализуют одну и ту же
булеву функцию. Сложностью (1,1)-полюсника называется число контактов.
(1,1)-полюсник, имеющий наименьшую сложность среди эквивалентных ему схем,
называется минимальным. Сложность минимального (1,1)-полюсника, реализующего
функцию
где а - входной полюс.
(1,1)-полюсники называются эквивалентными, если они реализуют одну и ту же
булеву функцию. Сложностью (1,1)-полюсника называется число контактов.
(1,1)-полюсник, имеющий наименьшую сложность среди эквивалентных ему схем,
называется минимальным. Сложность минимального (1,1)-полюсника, реализующего
функцию 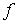 называется
сложностью функции
называется
сложностью функции 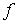 в классе
(1,1)-полюсников и обозначается через
в классе
(1,1)-полюсников и обозначается через 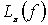 .
.
Заметим, что задача нахождения
минимального (1,1)-полюсника среди эквивалентных данному (1,1)-полюснику 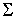 равносильна
нахождению среди функций, реализуемых схемой
равносильна
нахождению среди функций, реализуемых схемой 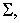 функции, имеющей наименьшее число
вхождений переменных. Действительно, функцию, реализуемую (1,1)-полюсником,
нетрудно представить в виде формулы, которая строится из литер в соответствии с
контактной схемой и имеет ровно столько вхождений переменных, сколько контактов
имеет схема. Например, изображенной на рисунке 3 схеме соответствует булева
функция:
функции, имеющей наименьшее число
вхождений переменных. Действительно, функцию, реализуемую (1,1)-полюсником,
нетрудно представить в виде формулы, которая строится из литер в соответствии с
контактной схемой и имеет ровно столько вхождений переменных, сколько контактов
имеет схема. Например, изображенной на рисунке 3 схеме соответствует булева
функция:
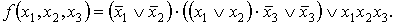 (1)
(1)
математический метод
логический матрица задача
Таким образом, задача нахождения
минимального (1,1)-полюсника сводится к минимизации соответствующей булевой
функции.
Эффективное уменьшение числа
контактов достигается с помощью нахождения минимальной ДНФ булевой функции.
Найдем минимальную ДНФ функции (1),
реализуемой схемой на рисунке 2. Придавая логическим переменным 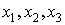 все
возможные значения, но схеме или формуле (1) получаем таблицу истинности:
все
возможные значения, но схеме или формуле (1) получаем таблицу истинности:
|
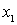 00001111 00001111
|
|
|
|
|
|
|
|
|
|
 00110011 00110011
|
|
|
|
|
|
|
|
|
|
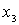 01010101 01010101
|
|
|
|
|
|
|
|
|
|
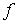 10101001 10101001
|
|
|
|
|
|
|
|
|
С помощью таблицы истинности
определим совершенную ДНФ: 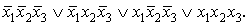
Используя один из методов нахождения
минимальной ДНФ, получаем формулу 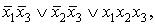 эквивалентную формуле (1) и
соответствующую схеме, состоящей из семи контактов (рисунок 4а).
эквивалентную формуле (1) и
соответствующую схеме, состоящей из семи контактов (рисунок 4а).

Рисунок 4
Отметим, что схема, изображенная на
рисунке 4а, допускает упрощение, соответствующее формуле 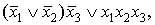 которое
приведено на рисунке 4б и является минимальной схемой. Сложность минимальной
схемы равна 6:
которое
приведено на рисунке 4б и является минимальной схемой. Сложность минимальной
схемы равна 6: 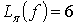 .
.
.2 Схемы из функциональных элементов
Ориентированная бесконтурная сеть, в
которой полюса делятся на входные (входы) и выходные (выходы), называется
схемой из функциональных элементов. Входные полюса помечаются символами
переменных, а каждая вершина, отличная от входного полюса, некоторым
функциональным символом. При этом должны выполняться следующие условия:
) если а входной полюс, то
полустепень захода вершины а равна нулю: 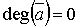 ;
;
) если вершина а не является
полюсом и помечена n-местным функциональным символом 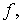 то
то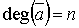 и дуги,
входящие в а, перенумерованы от 1 до n.
и дуги,
входящие в а, перенумерованы от 1 до n.
Функциональным элементом называется
всякий подмультиграф схемы, состоящий из невходного полюса а, помеченного
соответствующим символом 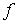 , и вершины,
из которых исходят дуги в вершину а.
, и вершины,
из которых исходят дуги в вершину а.
Пример 1. На рисунке 5а представлена
схема из функциональных элементов. Здесь входные символы помечены символами
переменных 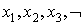 -
одноместный функциональный символ, соответствующий операции отрицания; & -
двухместный символ, соответствующий операции конъюнкции.
-
одноместный функциональный символ, соответствующий операции отрицания; & -
двухместный символ, соответствующий операции конъюнкции. 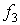 - некоторый
двухместный символ,
- некоторый
двухместный символ, 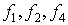 - некоторые
трехместные символы. Вершины, помеченные символами
- некоторые
трехместные символы. Вершины, помеченные символами 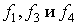 , являются
выходными полюсами. Им соответствуют термы:
, являются
выходными полюсами. Им соответствуют термы:
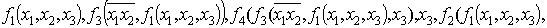
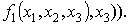 На рисунке 5б изображен
функциональный элемент, определяемый вершиной, помеченной символом
На рисунке 5б изображен
функциональный элемент, определяемый вершиной, помеченной символом 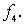 Ему
соответствует устройство, показанное на рисунке 5в.
Ему
соответствует устройство, показанное на рисунке 5в.
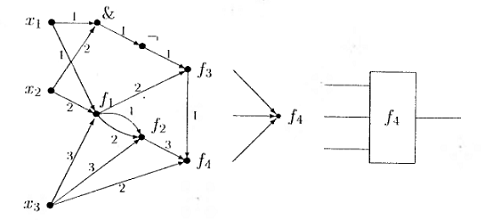
Рисунок 5
В примере 1 продемонстрировано, что каждый вывод
схемы порождает некоторый терм.
Говорят, что функция 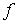 реализуется
схемой
реализуется
схемой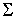 , если
существует такой выход а схемы
, если
существует такой выход а схемы 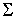 , что функция
, что функция  соответствующая
терму выхода а, эквивалента функции
соответствующая
терму выхода а, эквивалента функции 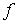 .
.
Схемы из функциональных элементов с
одним выходом, у которых входные полюса помечены символами 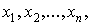 а вершины,
отличные от входных полюсов, - символами
а вершины,
отличные от входных полюсов, - символами 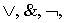 называются
называются 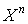 -функциональными
схемами. Сложностью схемы из функциональных элементов называется число ее
вершин, отличных от входных полюсов,
-функциональными
схемами. Сложностью схемы из функциональных элементов называется число ее
вершин, отличных от входных полюсов, 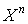 -функциональная схема
-функциональная схема 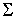 ,
реализующая функцию
,
реализующая функцию 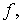 называется
минимальной, если всякая другая
называется
минимальной, если всякая другая 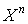 -функциональная схема, реализующая
-функциональная схема, реализующая 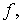 имеет
сложность, не меньшую, чем сложность схемы
имеет
сложность, не меньшую, чем сложность схемы 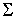 . Сложность минимальной схемы,
реализующей функцию
. Сложность минимальной схемы,
реализующей функцию 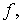 называется
сложностью функции
называется
сложностью функции 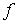 в классе
схем из функциональных элементов и обозначается через
в классе
схем из функциональных элементов и обозначается через 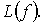
Пример 2. Сложность функции 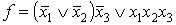 совпадает
со сложностью
совпадает
со сложностью 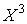 -функциональной
схемы, изображенной на рисунке 6, и равна 8:
-функциональной
схемы, изображенной на рисунке 6, и равна 8: 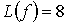 .
.
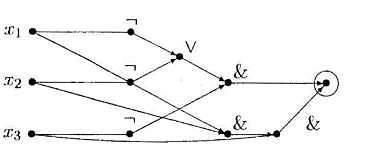
Рисунок 6
.3 Мультиплексоры
Мультиплексором 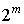 каналов
каналов 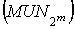 называется
схема с
называется
схема с 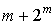 входами
входами 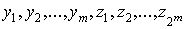 и одним
выходом
и одним
выходом 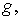 в которой
при
в которой
при 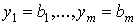 выход
выход 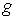 принимает
значение
принимает
значение 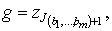 где:
где: 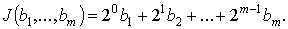
На рисунке 7 показан мультиплексор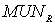 .
.
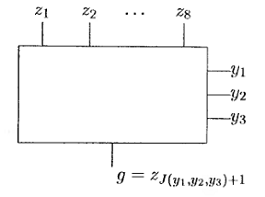
Рисунок 7
Пример 3. Если 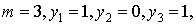 то
то 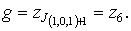
С помощью мультиплексора 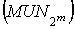 , придавая
переменным
, придавая
переменным 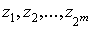 постоянные
значения, можно реализовать любую булеву функцию
постоянные
значения, можно реализовать любую булеву функцию 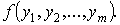
.4 Программируемые логические
матрицы
Рассмотрим схему, состоящую из 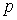 входов
входов 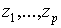 , и
, и 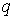 выходов
выходов 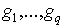 (рисунок
8), в которой значения выходов определяются матрицей соединений
(рисунок
8), в которой значения выходов определяются матрицей соединений 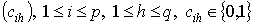 по
следующим правилам:
по
следующим правилам: 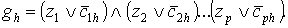
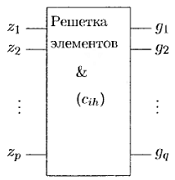
Рисунок 8
Таким образом,  где
где 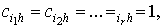 а остальные
а остальные
 равны 0.
Полученная схема называется решеткой с
равны 0.
Полученная схема называется решеткой с 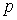 входами и
входами и 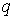 выходами
элементов &, которая определяется матрицей соединений
выходами
элементов &, которая определяется матрицей соединений 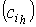 .
.
Программируемой логической матрицей
(ПЛМ) называется изображенная на рисунке 9 схема, получающаяся соединением
решетки А с 2n входами и k выходами,
определяемой матрицей соединений 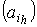 , и решетки В с k входами и m выходами,
определяемой матрицей соединений
, и решетки В с k входами и m выходами,
определяемой матрицей соединений 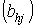 .
.
Опишем преобразования, которые
происходят при прохождении через ПЛМ значений переменных 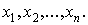 Поскольку к
каждому входу
Поскольку к
каждому входу 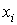 присоединен
инвертор
присоединен
инвертор 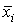 , на 2п
входов решетки А подаются значения переменных
, на 2п
входов решетки А подаются значения переменных 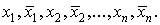 После прохождения решетки A h-й
выход принимает значение функции
После прохождения решетки A h-й
выход принимает значение функции 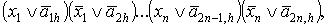 а последующей операции
инвертирования соответствует функция:
а последующей операции
инвертирования соответствует функция:
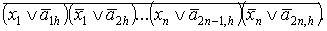
Полученные k значений 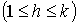 подаются на
входы решетки В, после прохождения которой на выходе j образуется значение
функции
подаются на
входы решетки В, после прохождения которой на выходе j образуется значение
функции
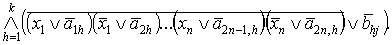
В заключение после инвертирования по
законам де Моргана на выходе j получаем значение функции:
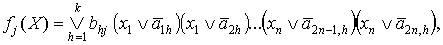
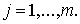
Функции 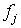 соответствует
дизъюнкция конъюнктов (определяемых формулами
соответствует
дизъюнкция конъюнктов (определяемых формулами
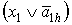
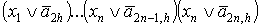 ) таких, что
) таких, что 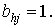
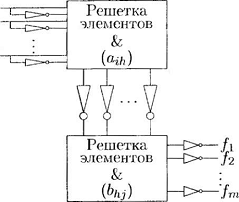
Рисунок 9
Таким образом, при соответствующем
выборе матриц 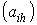 и
и 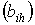 можно
одновременно реализовать m произвольных ДНФ, содержащих не
более k различных
конъюнктов переменных от
можно
одновременно реализовать m произвольных ДНФ, содержащих не
более k различных
конъюнктов переменных от 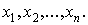
2. Практическая часть
I. Исследовать систему булевых
функций на полноту. Является ли она базисом.  .
.
|
k0
|
k1
|
kм
|
kл
|
kс
|
|
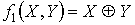 +--+- +--+-
|
|
|
|
|
|
|
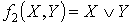 +++-- +++--
|
|
|
|
|
|
|
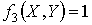 -+++- -+++-
|
|
|
|
|
|
|
X
|
Y
|
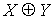 
|
|
|
0
|
0
|
0
|
0
|
|
0
|
1
|
1
|
1
|
|
1
|
0
|
1
|
1
|
|
1
|
1
|
0
|
1
|
Монотонность:
a. 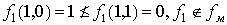 .
. 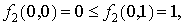
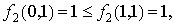
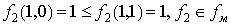
Линейность:
. 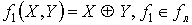 - по
определению.
- по
определению. 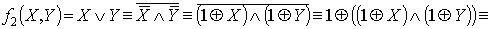
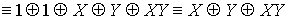
Самодвойственность:. 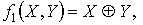
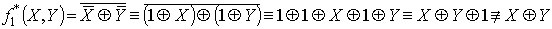
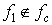 .
. 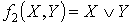
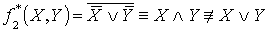
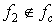 .
. 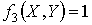
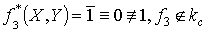
Система функций является полной.
Система функций называется базисом, если она полная, а удаление любой функции
из этой системы делает её неполной. Если удалить одну из имеющихся функций, то
система функций станет неполной. Таким образом, данная система функций является
базисом.
II. С помощью эквивалентных преобразований
привести формулу к ДНФ, КНФ; привести к СДНФ, СКНФ с помощью аналитического и
табличного способа. Проверить линейность булевой функции, заданной этой
формулой, с помощью полинома Жегалкина и методом неопределенных коэффициентов:
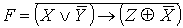 .
.
Приведение формулы к ДНФ, КНФ, СДНФ,
СКНФ аналитическим способом:
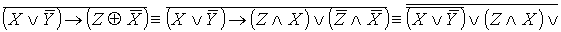
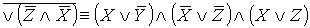 - КНФ.
- КНФ.
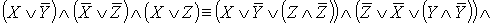
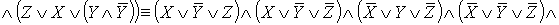
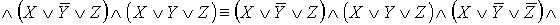
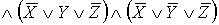 - СКНФ.
- СКНФ.
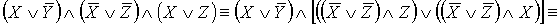
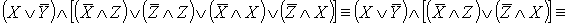
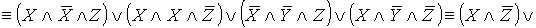
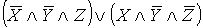 - ДНФ.
- ДНФ.
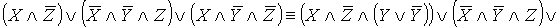
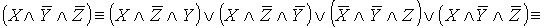
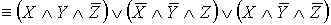 - СДНФ.
- СДНФ.
Приведение формулы к ДНФ, КНФ, СДНФ,
СКНФ табличным способом:
X Y Z 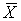
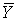
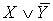
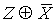

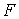 Элемент.
Элемент.
конъюнкцииЭлемент.
|
дизъюнкции
|
|
|
|
|
|
|
|
|
|
0
|
0
|
0
|
1
|
1
|
1
|
1
|
1
|
0
|
|
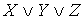
|
|
0
|
0
|
1
|
1
|
1
|
1
|
0
|
0
|
1
|
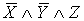
|
|
|
0
|
1
|
0
|
1
|
0
|
0
|
1
|
1
|
0
|
|
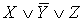
|
|
0
|
1
|
1
|
1
|
0
|
0
|
0
|
1
|
0
|
|
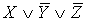
|
|
1
|
0
|
0
|
0
|
1
|
1
|
0
|
0
|
1
|
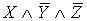
|
|
|
1
|
0
|
1
|
0
|
1
|
1
|
1
|
1
|
0
|
|
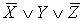
|
|
1
|
1
|
0
|
0
|
0
|
0
|
0
|
0
|
1
|
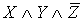
|
|
|
1
|
1
|
1
|
0
|
0
|
0
|
1
|
1
|
0
|
|
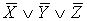
|
Пусть 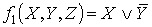 и
и 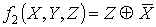 .
.
СДНФ: 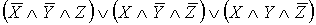
СКНФ: 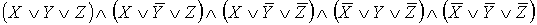
Проверка линейности булевой функции, заданной
этой формулой, с помощью полинома Жегалкина:
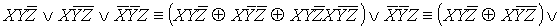

Полученный полином Жегалкина
является нелинейным, и, следовательно, функция f(X,Y,Z) также
нелинейная.
Проверка линейности булевой функции,
заданной этой формулой, с помощью метода неопределенных коэффициентов:
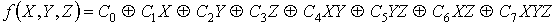
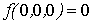
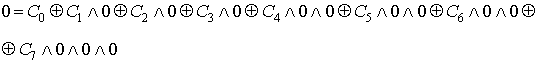
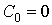
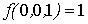
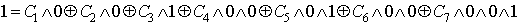
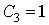
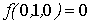
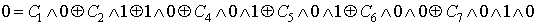
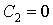
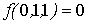
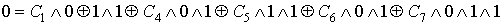
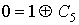
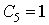
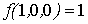
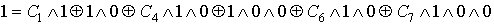
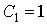
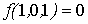
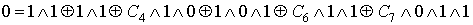
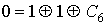
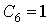
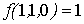
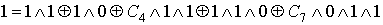
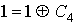
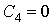
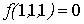
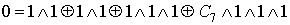
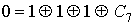
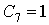
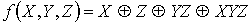
III. Минимизировать двумя способами:
a. Методом Квайна;
b. Геометрическим методом.

Методом Квайна:
1) Привести функцию к СДНФ;
2) В СДНФ произвести всевозможные
склеивания, а затем поглощения;
) Перейти от сокращенной СДНФ к
минимальной, используя импликантную матрицу.

СДНФ:
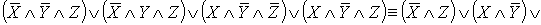
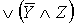 - сокращенная СДНФ
- сокращенная СДНФ
Необходимо оставить такие простые
импликанты, чтобы в каждом столбце был хотя бы один “+”, следовательно, 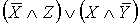 -
минимальная СДНФ.
-
минимальная СДНФ.
Геометрический метод:
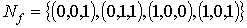 - геометрическое представление.
- геометрическое представление.

Получаем, что 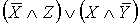 -
минимальная СДНФ.. Доопределить функции так, чтобы
-
минимальная СДНФ.. Доопределить функции так, чтобы 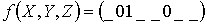 - была
монотонной;
- была
монотонной; 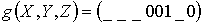 - была
линейной;
- была
линейной; 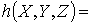
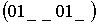 - была
самодвойственной.
- была
самодвойственной.
|
X
|
Y
|
Z
|
f
|
g
|
h
|
|
0
|
0
|
0
|
-
|
-
|
0
|
|
0
|
0
|
1
|
0
|
-
|
1
|
|
0
|
1
|
0
|
1
|
-
|
-
|
|
0
|
1
|
1
|
-
|
0
|
-
|
|
1
|
0
|
0
|
-
|
0
|
0
|
|
1
|
0
|
1
|
0
|
1
|
1
|
|
1
|
1
|
0
|
-
|
-
|
-
|
|
1
|
1
|
1
|
-
|
0
|
-
|
Функция 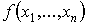 называется
монотонной, если для любых наборов нулей и единиц А=(а1,…,аn), В=(b1,…,bn) таких, что
называется
монотонной, если для любых наборов нулей и единиц А=(а1,…,аn), В=(b1,…,bn) таких, что
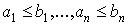 ,
выполняется условие
,
выполняется условие 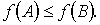
Функция называется линейной  , где
, где 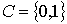 .
.
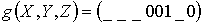

Функция 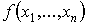 называется
самодвойственной, если она совпадает с двойственной к ней.
называется
самодвойственной, если она совпадает с двойственной к ней.
Пользуясь определениями монотонной,
линейной и самодвойственной функций, получим следующую таблицу истинности:
|
XYZfgh
|
|
|
|
|
|
|
0
|
0
|
0
|
0
|
0
|
|
0
|
0
|
1
|
0
|
1
|
1
|
|
0
|
1
|
0
|
1
|
1
|
0
|
|
0
|
1
|
1
|
1
|
0
|
1
|
|
1
|
0
|
0
|
0
|
0
|
0
|
|
1
|
0
|
1
|
0
|
1
|
1
|
|
1
|
1
|
0
|
1
|
1
|
0
|
|
1
|
1
|
1
|
1
|
0
|
1
|
V. Составить таблицу истинности. Доказать
истинность заключения дедуктивным методом. Нарисовать граф вывода заключения
дедуктивным методом. Доказать истинность заключения по методу резолюции и
нарисовать граф вывода пустой резольвенты.
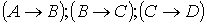 ├
├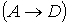
Используя дедуктивный метод, докажем
истинность заключения:
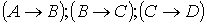 ├
├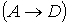
Согласно правилу цепного заключения:
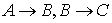 ├
├ 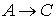
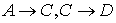 ├
├ 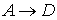
Граф вывода заключения:
Таблица истинности для данного заключения
выглядит следующим образом:
|
A
|
B
|
C
|
D
|
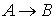 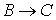 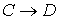 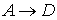 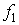 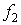 F F
|
|
|
|
|
|
|
|
0
|
0
|
0
|
0
|
1
|
1
|
1
|
1
|
1
|
1
|
1
|
|
0
|
0
|
0
|
1
|
1
|
1
|
1
|
1
|
1
|
1
|
1
|
|
0
|
0
|
1
|
0
|
1
|
1
|
0
|
1
|
1
|
0
|
1
|
|
0
|
0
|
1
|
1
|
1
|
1
|
1
|
1
|
1
|
1
|
1
|
|
0
|
1
|
0
|
0
|
1
|
0
|
1
|
1
|
0
|
1
|
1
|
|
0
|
1
|
0
|
1
|
1
|
0
|
1
|
1
|
0
|
1
|
1
|
|
0
|
1
|
1
|
0
|
1
|
1
|
0
|
1
|
1
|
0
|
1
|
|
0
|
1
|
1
|
1
|
1
|
1
|
1
|
1
|
1
|
1
|
1
|
|
1
|
0
|
0
|
0
|
0
|
1
|
1
|
0
|
0
|
0
|
1
|
|
1
|
0
|
0
|
1
|
0
|
1
|
1
|
1
|
0
|
0
|
1
|
|
1
|
0
|
1
|
0
|
0
|
1
|
0
|
0
|
0
|
0
|
1
|
|
1
|
0
|
1
|
1
|
0
|
1
|
1
|
1
|
0
|
0
|
1
|
|
1
|
1
|
0
|
0
|
1
|
0
|
1
|
0
|
0
|
0
|
1
|
|
1
|
1
|
0
|
1
|
1
|
0
|
1
|
1
|
0
|
0
|
1
|
|
1
|
1
|
1
|
0
|
1
|
1
|
0
|
0
|
1
|
0
|
1
|
|
1
|
1
|
1
|
1
|
1
|
1
|
1
|
1
|
1
|
1
|
1
|
Пусть 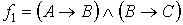 ,
, 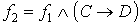 и
и 
Докажем истинность заключения по
методу резолюции:
) 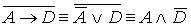 - КНФ
- КНФ
) 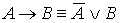
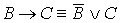
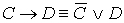
) 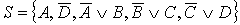
) 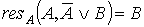
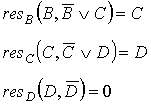
Граф вывода пустой резольвенты:
VI. Найти формулы ПНФ и ССФ, выполнить
унификацию атомов дизъюнктов.
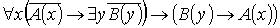
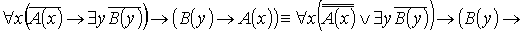
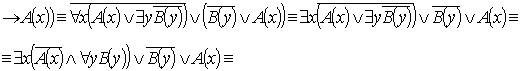
Пусть 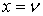 , тогда:
, тогда:
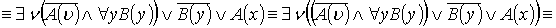
Пусть y=w, тогда:
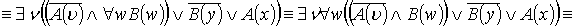
 - ПНФ.
- ПНФ.
Приведём к ССФ:
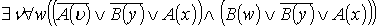
Пусть 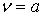 , тогда:
, тогда:
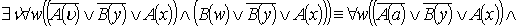
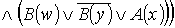 - ССФ.
- ССФ.
VII. Доказать, что функция примитивно
рекурсивна:
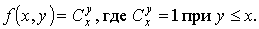
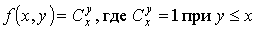
является простейшей одношаговой
рекурсивной функцией - функция константа.
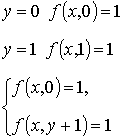
. Найти функции, получаемые
из данной числовой функции 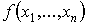 с помощью операции минимизации по
каждой её переменной:
с помощью операции минимизации по
каждой её переменной:
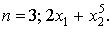
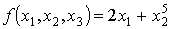
) 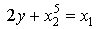
· y=0 при 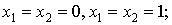
· в остальных случаях не определена.
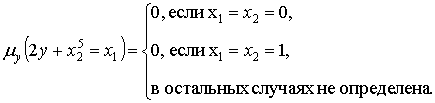
) 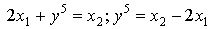
· y=0 при 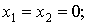
· y=1 при 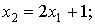
· в остальных случаях не определена.
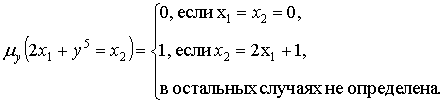
) 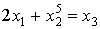
Если набор переменных таков, что левая часть
уравнения имеет смысл и уравнение выполнимо, то можно считать, что оно
выполнимо при подстановке y=0 на самом первом шаге.
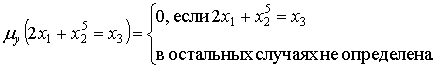
IX. Построить машину Тьюринга, которая
правильно вычисляет функцию:
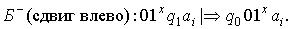
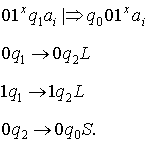
Заключение
Математическая логика изучает вопросы применения
математических методов для решения логических задач и построения логических
схем, которые лежат в основе работы любого компьютера.
Математическая логика является современной
формой, так называемой формальной логики, применяющей математические методы для
исследования своего предмета. В формальной логике и, соответственно, в
математической логике, собраны результаты законов структуры правильных выводов.
Вывод - это мыслительный процесс, в результате которого появляются новые
открытия на основании уже имеющихся без практических исследований. В
действительности, новое открытие, полученное в результате вывода, в скрытой
форме находится в предварительно имеющихся знаниях.