Законы механического движения тел
1.
Жесткая рама закреплена в точке А шарнирно, а в точке В прикреплена к
невесомому стержню с шарнирами на концах.
В точке С к раме привязан трос, перекинутый через блок и несущий на конце
груз весом Р=25 кН. На раму действует пара сил с моментом М=60 кН∙м и две
силы, модули, направления и точки приложения которых указаны.
Определить реакции связей в точках А, В, вызываемые действующими
нагрузками. При окончательных расчетах принять а=0,5 м.

Дано:
Р=25 кН
М=60 кН∙м
а=0,5 м
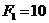 кН
кН
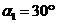
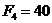 кН
кН
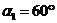
Найти:
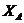 ,
, 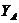 ,
, 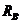
Решение:
Сила натяжения троса:
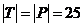 кН
кН
Составим
уравнения равновесия:
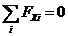
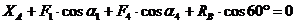 (1)
(1)
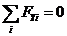
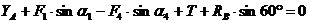 (2)
(2)
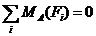
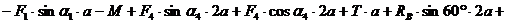
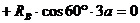 (3)
(3)
Из
уравнения (3)
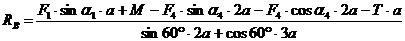
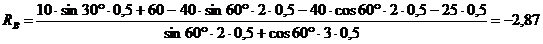 кН
кН
Из
уравнения (1):
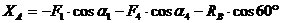
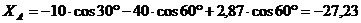 кН
кН
Из
уравнения (2):
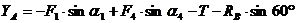
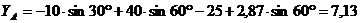 кН
кН
Ответ:
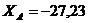 кН;
кН; 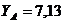 кН;
кН; 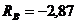 кН
кН
Знак
минус показывает, что реакции 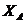 и
и 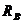 направлены в стороны, противоположно показанным на
рисунке.
направлены в стороны, противоположно показанным на
рисунке.
2. Конструкция состоит из жесткого
угольника и стержня, которые в точке С свободно опираются друг о друга. Внешними связями,
наложенными на конструкцию, являются в точке А жестка заделка; в точке В -
шарнир. На конструкцию действуют: пара сил с моментом М=60 кН∙м,
равномерно распределенная нагрузка интенсивности q=20 кН/м и еще две силы. Эти
силы, их направления и точки приложения указаны.
Определить реакции связей в точке А, В, С, вызванные заданными
нагрузками. При окончательных расчетах принять а=0,2 м.

Дано:
М=60 кН∙м
q=20
кН/м
а=0,2 м
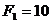 кН
кН
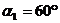
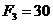 кН
кН
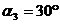
Найти:
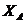 ,
, 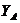 ,
, 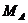 ,
, 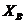 ,
, 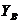 ,
, 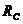
Решение:
Рассмотрим равновесие стержня BC

Составим уравнения равновесия:
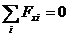
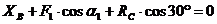 (1)
(1)
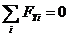
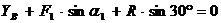 (2)
(2)
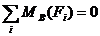
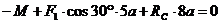 (3)
(3)
Из
уравнения (3):
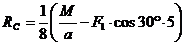
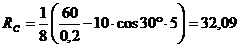 кН
кН
Из
уравнения (1):
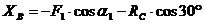
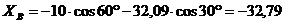 кН
кН
Из
уравнения (2):
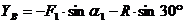
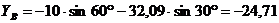 кН
кН
Рассмотрим
равновесия уголка AEL (с учетом закона о равенстве действия и
противодействия).

Составим уравнения равновесия:
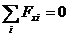
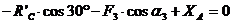 (4)
(4)
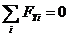
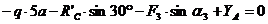 (5)
(5)
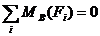
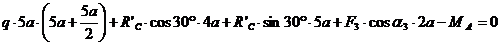 (6)
(6)
Из
уравнения (4):
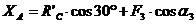
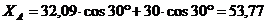 кН
кН
Из
уравнения (5):
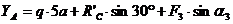
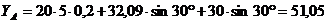 кН
кН
Из
уравнения (6):
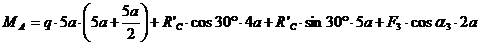
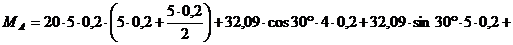
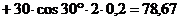 кН∙м
кН∙м
Ответ:
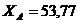 кН;
кН; 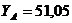 кН;
кН; 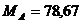 кН∙м;
кН∙м;
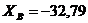 кН;
кН; 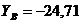
кН;
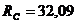 кН.
кН.
Знак
минус показывает, что реакции 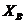 и
и 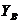 направлены в стороны, противоположно показанным на
рисунке.
направлены в стороны, противоположно показанным на
рисунке.
3.
К вершинам прямоугольного параллелепипеда со сторонами 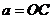 ,
, 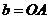 ,
, 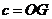 приложена система сил
приложена система сил 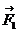 ,
, 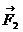 ,
, 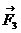 ,
, 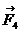 ,
, 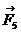 , которые
направлены по стороне, диагонали грани и диагонали параллелепипеда. Направления действия сил указаны.
Определить главный вектор и главный момент этой системы относительно начала координат.
Выяснить, к какому простейшему виду приводится эта система сил.
, которые
направлены по стороне, диагонали грани и диагонали параллелепипеда. Направления действия сил указаны.
Определить главный вектор и главный момент этой системы относительно начала координат.
Выяснить, к какому простейшему виду приводится эта система сил.

Дано:
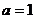 м
м
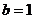 м
м
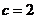 м
м
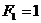 Н
Н
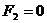 Н
Н
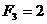 Н
Н
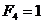 Н
Н
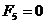 Н
Н
Найти:
F, M
Решение:
Т.к.
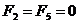 Н, то рисунок имеет вид:
Н, то рисунок имеет вид:

Главный вектор силы найдем по проекциям:
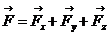
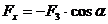
где
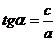
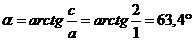
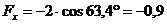 Н
Н
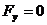
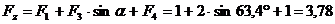 Н
Н
Получаем:
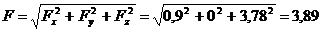 Н
Н
Аналогично
вычислим главный момент.
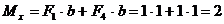 Н∙м
Н∙м
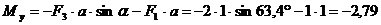 Н∙м
Н∙м
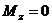 Н∙м
Н∙м
Получаем:
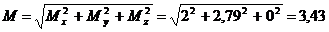 Н∙м
Н∙м
Вычислим
скалярное произведение
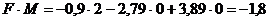
Т.к.
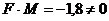 , то система сил приводится к динамическому винту.
, то система сил приводится к динамическому винту.
Ответ:
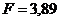 Н;
Н; 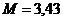 Н∙м
Н∙м
4. Две прямоугольные тонкие плиты жестко
соединены (сварены) под прямым углом друг к другу и закреплены сферическим
шарниром, в точке А, цилиндрическим шарниром (подшипником) в точке В и
невесомым стержнем; все стержни прикреплены к плитам и неподвижным опорам
шарнирами.
Размеры плит указаны на рисунке; вес большой плиты G1=5 кН, вес меньшей плиты G2=3 кН. Каждая из плит расположена параллельно одной из
координатных плоскостей.
На
плиты действует пара сил с моментом 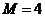 кН∙м,
лежащая в плоскости одной из плит, и две силы. Значения этих сил, их
направление и точки приложения указаны.
кН∙м,
лежащая в плоскости одной из плит, и две силы. Значения этих сил, их
направление и точки приложения указаны.
Определить
реакции связей в точках А и В и реакцию стержня. При подсчетах принять 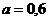 м.
м.

Дано:
G1=5 кН
G2=3 кН
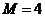 кН∙м
кН∙м
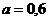 м
м
F1=6 кН
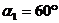
F2=8 кН
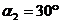
Найти:
XA, YA, ZA, YA, ZA, RC
Решение:
Составим уравнения равновесия:
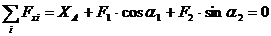 (1)
(1)
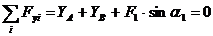 (2)
(2)
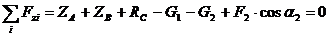 (3)
(3)
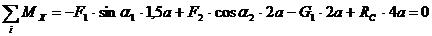 (4)
(4)
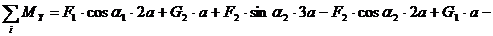
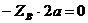 (5)
(5)
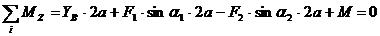 (6)
(6)
Из уравнения (1):
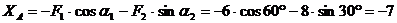 кН
кН
Из
уравнения (4)
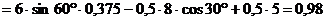 кН
кН
Из
уравнения (5):
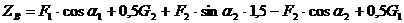
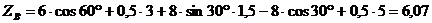 кН
кН
Из
уравнения (6):
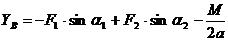
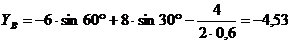 кН
кН
Из
уравнения (2):
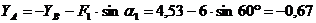 кН
кН
Из
уравнения (3):
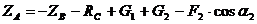
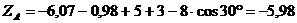 кН
кН
Ответ:
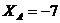 кН;
кН; 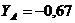 кН;
кН; 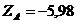 кН;
кН; 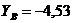 кН;
кН; 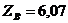 кН;
кН;
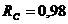 кН.
кН.
. Из однородного плоского листа
вырезана фигура, которую можно рассматривать составленной из прямоугольника,
треугольник и части (или целого) круга радиусом R=1 м. Общий вид фигуры представлен на рисунке.
Определить координаты центры тяжести плоской фигуры.

Дано:
R=1 м
Найти:
XC, YC
Решение:
Разобьем сечение на элементарные фигуры: 1 - прямоугольник, 2 -
треугольник, 3 - полукруг.
Площади элементарных фигур:
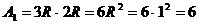 м2
м2
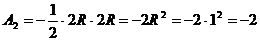 м2
м2
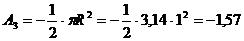 м2
м2
Координаты
центров тяжести элементарных фигур:
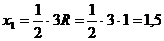 м
м
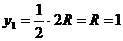 м
м
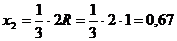 м
м
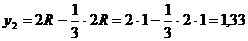 м
м
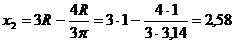 м
м
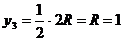 м
м
Координаты
центра тяжести сечения:
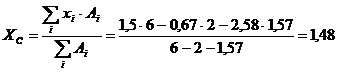 м
м
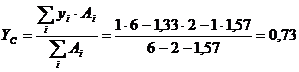 м
м
Ответ:
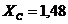 м;
м; 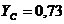 м
м
6. а) Точка движется в плоскости Оху.
Закон движения точки в координатной форме задан уравнениями:
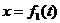 ,
, 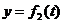 ,
,
где
х и у выражены в сантиметрах, 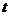 - в
секундах. Определить и
построить в масштабе траекторию точки. Найти скорость и ускорение точки,
вычислить их в указанный момент времени
- в
секундах. Определить и
построить в масштабе траекторию точки. Найти скорость и ускорение точки,
вычислить их в указанный момент времени 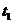 .
Для этого же момента времени вычислить радиус кривизны траектории. Построить на
рисунке в соответствующей точке траектории векторы скорости и ускорения.
.
Для этого же момента времени вычислить радиус кривизны траектории. Построить на
рисунке в соответствующей точке траектории векторы скорости и ускорения.
нагрузка
вектор момент ускорение
Дано:
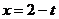 см
см
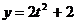 см
см
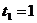 с
с
Найти:
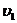 ,
, 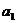 ,
, 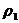
Решение:
Найдем
координаты точки в момент времени 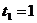 с.
с.
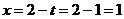 см
см
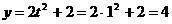 см
см
Найдем
уравнение траектории точки:
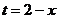
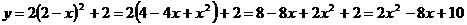
Строим
траекторию движения точки
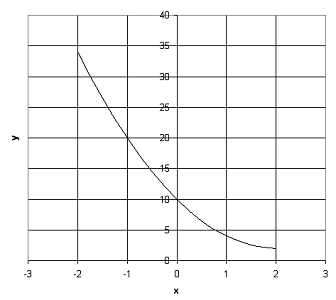
Скорость
точки найдем по ее проекциям:
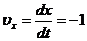 см/с
см/с
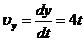 см/с
см/с
При
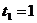 с
с
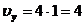 см/с
см/с
Скорость
точки:
 см/с
см/с
Аналогично
найдем ускорение точки:
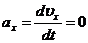 см/с2
см/с2
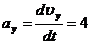 см/с2
см/с2
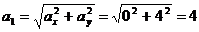 см/с2
см/с2
Для
нахождения радиуса кривизны траектории, сначала вычислим касательное ускорение:
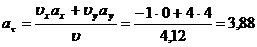 см/с2
см/с2
Нормальное
ускорение:
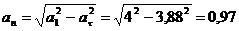 см/с2
см/с2
Радиус
кривизны траектории:
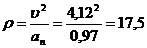 см
см
Ответ:
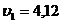 см/с;
см/с; 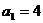 см/с2;
см/с2; 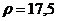 см
см
б).
Точка движется по дуге окружности
радиусом 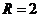 м по закону
м по закону 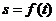 . Определить ускорение точки в момент времени
точки в момент времени
. Определить ускорение точки в момент времени
точки в момент времени 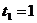 с. Изобразить на рисунке векторы
с. Изобразить на рисунке векторы 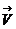 и
и 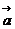 для
этого момента времени.
для
этого момента времени.
Дано:
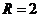 м
м
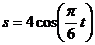
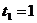 с
с
Решение:
Скорость точки:
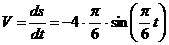
При
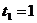 с
с
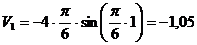 м/с
м/с
Касательное
ускорение точки:
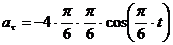
При
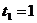 с
с
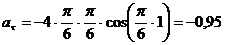 м/с2
м/с2
Нормальное
ускорение:
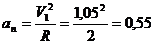 м/с2
м/с2
Полное
ускорение точки:
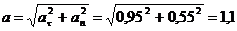 м/с2
м/с2
Строим
векторы:

Ответ:
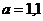 м/с2
м/с2
7.
Механизм состоит из ступенчатых колес
1-3, находящихся в зацеплении или связанных ременной передачей, зубчатой рейки
4 и груза 5, связанного к концу нити, намотанной на одно из колес. Радиусы колес у ступенчатых блоков: 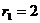 см,
см, 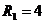 см,
см,
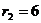 см,
см, 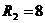 см,
см,
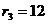 см,
см, 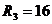 см.
Точки А, В, С находятся на ободах соответствующих колес.
см.
Точки А, В, С находятся на ободах соответствующих колес.
Определить
в момент времени 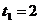 с указанные угловые скорость и ускорение тел,
линейные скорости и ускорения точек тел.
с указанные угловые скорость и ускорение тел,
линейные скорости и ускорения точек тел.

Дано:
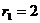 см
см
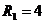 см
см
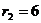 см
см
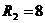 см
см
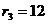 см
см
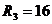 см
см
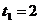 с
с
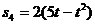 см
см
Найти:
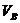 ,
, 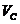 ,
, 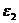 ,
, 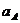 ,
, 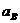
Решение:
Скорость рейки:
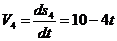
При
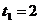 с
с
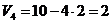 см/с
см/с
Угловая
скорость колеса 3:
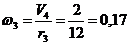 1/с
1/с
Скорость
точки С:
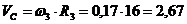 см/с
см/с
Угловая
скорость колеса 2:
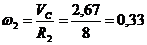 1/с
1/с
Скорость
точки В:
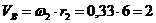 см/с
см/с
Угловая
скорость колеса 1:
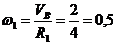 1/с
1/с
Ускорение
рейки:
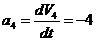 см/с2
см/с2
(Знак
минус показывает, что ускорение направлено в противоположную сторону от
скорости).
Угловое
ускорение колеса 3:
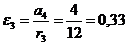 1/с2
1/с2
Угловое
ускорение колеса 2:
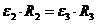
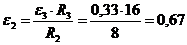 1/с2
1/с2
Касательное
ускорение точки В:
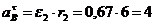 см/с2
см/с2
Нормальное
ускорение точки В:
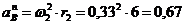 см/с2
см/с2
Полное
ускорение точки В:
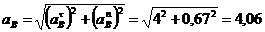 см/с2
см/с2
Угловое
ускорение колеса 2:
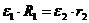
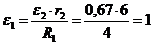 1/с2
1/с2
Касательное
ускорение точки А:
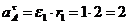 см/с2
см/с2
Нормальное
ускорение точки А:
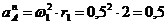 см/с2
см/с2
Полное
ускорение точки А:
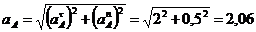 см/с2
см/с2
Ответ:
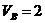 см/с;
см/с; 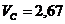 см/с;
см/с; 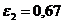 1/с2;
1/с2;
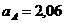 см/с2;
см/с2; 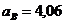 см/с2
см/с2
8.
Плоский механизм состоит из 4
стержней (1 - OA, 2 - AB, 3 - CD, 4 - BE) и ползуна D, соединенных цилиндрическими
шарнирами. В точке О стержень
ОА крепится к стойке, ползун D ограничен направляющими, направление которых по
отношению к стержню CD определяется углом j, отсчитываемым против хода часовой стрелки от стержня
CD, AC=CB. Положение механизма определяется углами a, b, g, q, j, откладываемыми против хода часовой
стрелки. Длины стержней: 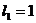 м,
м, 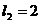 м,
м,
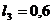 м,
м, 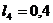 м.
Угловая скорость стержня 1 постоянная.
м.
Угловая скорость стержня 1 постоянная.
Определить указанные величины.
Дано:
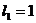 м
м
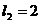 м
м
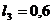 м
м
AC=CB
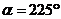
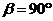
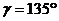
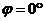
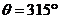
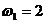 рад/с
рад/с
Найти:
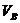 ,
, 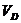 ,
, 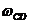 ,
, 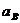 ,
, 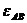
Решение:

Чтобы найти скорость точки В, найдем скорость точки А:
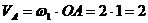 м/с
м/с
Т.к.
точки А и В принадлежат одному стержню, то
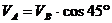
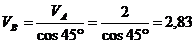 м/с
м/с
Найдем
угловую скорость звена АВ. Для этого строим мгновенный центр скоростей О2.
Треугольник О2АВ - равнобедренный (О2А=О2В).
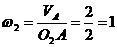 рад/с
рад/с
Скорость
точки С:
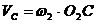
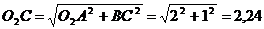 м
м
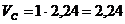 м/с
м/с
Скорость
точки D:
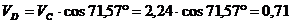 м/с
м/с
Для
нахождения угловой скорости звена СD, строим мгновенный центр
скоростей О3.
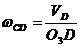
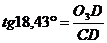
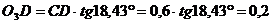 м
м
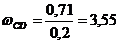 рад/с
рад/с
Чтобы
найти ускорение точки В, составим уравнение ускорений:
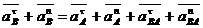
Т.к.
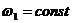 , то
, то 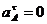
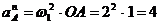 м/с2
м/с2
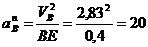 м/с2
м/с2
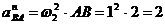 м/с2
м/с2
Спроецируем
уравнение ускорений на прямую параллельную АВ:
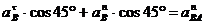
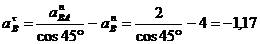 м/с2
м/с2
Полное
ускорение точки В:
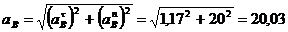 м/с2
м/с2
Спроецируем уравнение на ось, перпендикулярную прямой АВ:
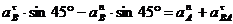
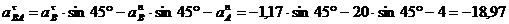 м/с2
м/с2
Угловое
ускорение звена АВ:
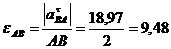 рад/с2
рад/с2
Ответ:
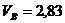 м/с;
м/с; 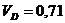 м/с;
м/с; 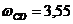 рад/с;
рад/с; 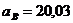 м/с2;
м/с2; 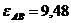
рад/с2
9.
Круглая пластина радиусом R=60
см вращается вокруг неподвижной оси по закону 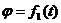 .
.
По
окружности радиуса R движется тока М; закон ее относительного движения 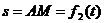 . Найти абсолютную скорость и абсолютное ускорение
точки М в момент времени
. Найти абсолютную скорость и абсолютное ускорение
точки М в момент времени 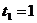 с.
с.
Дано:
R=60
см
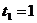 с
с
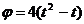
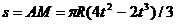
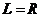
Найти:
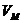 ,
, 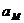
Решение:

Найдем
положение точки М в момент времени 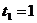 с:
с:
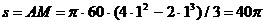
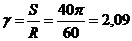 рад
рад 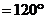
Получаем,
что треугольник ОСМ - равносторонний треугольник
Абсолютная
скорость точки М:
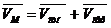
Относительная
скорость:
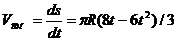
При
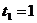 с
с
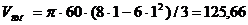 см/с
см/с
Угловая
скорость пластины:
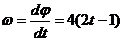
При
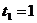 с
с
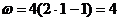 рад/с
рад/с
Переносная
скорость:
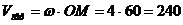 см/с
см/с
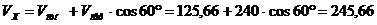 см/с
см/с
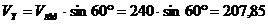 см/с
см/с
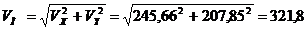 см/с
см/с
Абсолютное
ускорение точки М равно:
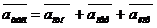
где
в свою очередь
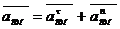
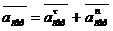
Относительные
ускорения:
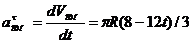
При
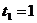 с
с
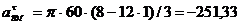 см/с2
см/с2
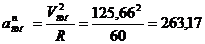 см/с2
см/с2
Переносные
ускорения:
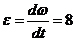 рад/с2
рад/с2
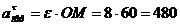 см/с2
см/с2
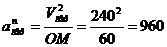 см/с2
см/с2
Кориолисово
ускорение:
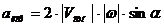 ,
,
где
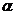 - угол между вектором
- угол между вектором 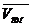 и осью
вращения. В данном случае
и осью
вращения. В данном случае 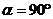
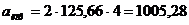 см/с2
см/с2
Полное
абсолютное ускорение найдем по проекциям:
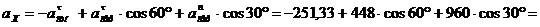
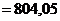 см/с2
см/с2
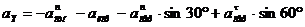
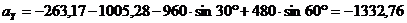 см/с2
см/с2
Полное
абсолютное ускорение точки М:
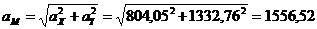 см/с2
см/с2
Ответ:
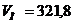 см/с
см/с
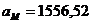 см/с2
см/с2