Динамические характеристики термопреобразователей сопротивлений

Динамические характеристики термопреобразователей сопротивлений

ДИНАМИЧЕСКИЕ ХАРАКТЕРИСТИКИ ТЕРМОПРЕОБРАЗОВАТЕЛЕЙ СОПРОТИВЛЕНИЙ

Практически все средства измерений (СИ) имеют в своем составе элементы, обладающие механической, тепловой или другой инерцией, вследствие чего величина сигнала на выходе Y(τ) зависит не только от величины входного сигнала X(τ), но и от его формы (скорости изменения) и времени. Инерционные свойства СИ определяются динамическими характеристиками, которые описываются дифференциальными уравнениями вида:

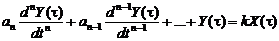                   (1)

или соответствующей передаточной функцией:

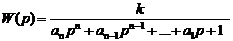,                           (2)

где a₁, a₂,…, a_n - коэффициенты, определяемые из начальных условий; k - чувствительность СИ.

инерционный измерение термометр динамический

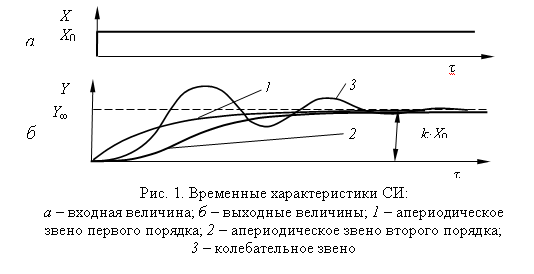
В зависимости от формы сигнала, подаваемого на вход СИ при исследовании его динамических свойств, различают временные (переходные), импульсные и частотные характеристики. Для построения временной характеристики на вход СИ подается ступенчатое воздействие, амплитуда которого принята за единицу (рис. 1, а). Форма временной характеристики определяется динамическими свойствами СИ и может иметь вид, показанный на рис. 1, б.

Динамические свойства термометра зависят от его конструкции и условий теплообмена с окружающей средой. Если пренебречь влиянием корпуса 2 (рис. 2), то временная характеристика термометра, установленного без защитного чехла, может быть описана дифференциальным уравнением первого порядка (кривая 1, рис. 1, б), решением которого является зависимость

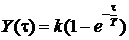,           (3)

где k - чувствительность термометра;

Т - постоянная времени, которая прямо пропорциональна теплоемкости (с) и массе (m) чувствительного элемента и обратно пропорциональна площади теплообмена (F) и коэффициенту теплоотдачи (α) от измеряемой среды к термометру:

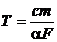.                         (4)

В ряде случаев для предотвращения механических повреждений термометры помещают в защитный чехол (рис. 2). Однако это ухудшает их динамические характеристики, что может быть частично компенсировано заполнением маслом пространства между термометром и чехлом. Динамическая характеристика такого термометра описывается дифференциальным уравнением более высокого порядка (кривая 2, рис. 1, б).

Часто получить точную динамическую характеристику аналитически невозможно из-за сложной взаимной зависимости величин, входящих в уравнение, и ее определяют экспериментально. При этом для упрощения расчетов апериодические звенья высоких порядков заменяют комбинацией двух звеньев - чистого запаздывания и апериодического первого порядка:

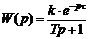                             (5)

или звеньями чистого запаздывания и апериодического второго порядка:

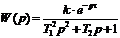.             (6)

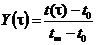,                          (7)

где t(τ), t0 и t∞ - текущее, начальное и новое установившиеся значения температуры, и сроят график зависимости: Y = f(τ) - переходный процесс.

Далее по виду кривой выбирают динамическую модель (5) или (6) и определяют ее параметры.

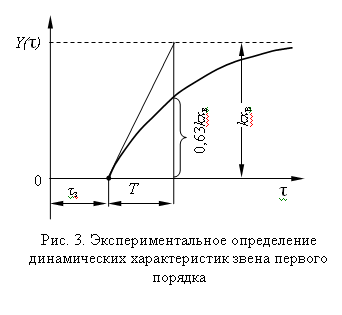
Если переходный процесс имеет вид кривой 1 (рис. 1, б), то проводят касательную в точке Y(τ)=0 до пересечения с линией Y(τ)= Yµ и находят значения времени запаздывания τз и постоянной времени T (рис. 3). Графическое построение касательной может быть выполнено со значительной погрешностью, поэтому за постоянную времени принимают время, за которое выходная величина достигла значения 0,63 Yµ.

Если переходный процесс имеет вид кривой 2 (рис. 1, б), то могут быть применены зависимости и (5), и (6). Касательную к кривой проводят в точке максимальной скорости изменения выходной величины (точка перегиба W) до пересечения с осью абсцисс и линией, соответствующей новому установившемуся значению (рис. 3).

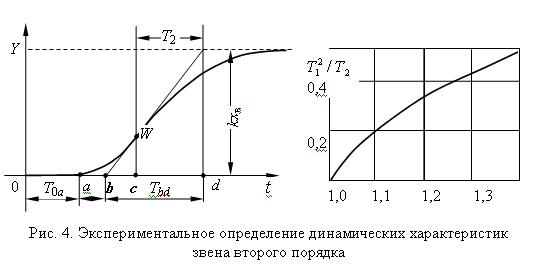
Если принимают модель (5), то время запаздывания τз = Т_0b, а постоянная времени - T = Т_bd. Если принята модель (6), то время запаздывания τ_з = Т_0а, Т₁ определяется по графику (см. рис. 4) в зависимости от отношения Т_bd/Т₂, а Т₂ = Т_cd.

Литература

1. Волынский В.А. и др. Электротехника /Б.А. Волынский, Е.Н. Зейн, В.Е. Шатерников: Учеб. пособие для вузов. - М.: Энергоатомиздат, 2007. - 528 с., ил.

. Касаткин А.С., Немцов М.В. Электротехника: Учеб. пособие для вузов. - 4-е изд., перераб. - М.: Энергоатомиздат, 2009. - 440 с., ил.

. Основы промышленной электроники: Учебник для неэлектротехн. спец. вузов /В.Г. Герасимов, О.М. Князьков, А.Е. Краснопольский, В.В. Сухоруков; под ред. В.Г. Герасимова. - 3-е изд., перераб. и доп. - М.: Высш. шк., 2006. - 336 с., ил.

. Электротехника и электроника в 3-х кн. Под ред. В.Г. Герасимова Кн.1. Электрические и магнитные цепи. - М.: Высшая шк. - 2006 г.

. Электротехника и электроника в 3-х кн. Под ред. В.Г. Герасимова Кн.2. Электромагнитные устройства и электрические машины. - М.: Высшая шк. - 2007 г.