Численное решение некоторых задач линейной алгебры
Курсовая работа
по дисциплине
«Вычислительная математика»
на тему: «Численное
решение некоторых задач линейной алгебры»
Выполнил: Пупышев В.Д.
Глазов 2012 г.
Содержание
Введение
. Теоретическая часть
1.1 Вычисление точного значения определителей
.2 Нахождение обратной матрицы методом
Гаусса
2. Практическая часть
2.1 Вычисление определителей
2.2 Пример нахождения
обратной матрицы
Заключение
Список литературы
Приложения
Введение
Линейная алгебра - часть алгебры, изучающая векторные
(линейные) пространства и их подпространства, линейные отображения (операторы),
линейные, билинейные, и квадратичные функции на векторных пространствах.
Численные методы линейной алгебры - раздел вычислительной
математики, посвященный математическому описанию и исследованию процессов
численного решения задач линейной алгебры.
Наиболее важными являются задачи линейной алгебры -
вычисление определителя, обратной матрицы, собственных значений и др.
Целями работы являются:
· изучить методы нахождения определителя и обратной
матрицы методом Гаусса;
· разработать вычислительный алгоритм в
программе Pascal ABC для вычисления определителей и для нахождения обратной матрицы.
1. Теоретическая часть
.1 Вычисление точного значения определителей
Вычисление определителей основывается на
их известных свойствах, которые относятся к определителям всех порядков. Вот
эти свойства:
. Если переставить две строки (или два
столбца) определителя, то определитель изменит знак.
. Если соответствующие элементы двух
столбцов (или двух строк) определителя равны или пропорциональны, то
определитель равен нулю.
. Значение определителя не изменится, если
поменять местами строки и столбцы, сохранив их порядок.
. Если все элементы какой-либо строки (или
столбца) имеют общий множитель, то его можно вынести за знак определителя.
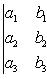
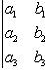
. Значение определителя не изменится, если
к элементам одной строки (или столбца) прибавить соответствующие элементы
другой строки (или столбца), умноженные на одно и то же число. Для
определителей третьего порядка это свойство может быть записано, например, так:
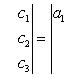
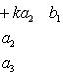
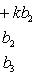
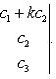
. Определитель второго порядка вычисляется
по формуле
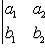
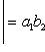
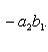
. Определитель третьего порядка
вычисляется по формуле
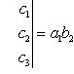
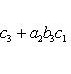
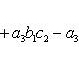
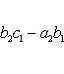
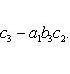
Существует удобная схема для вычисления
определителя третьего порядка (см. рис. 1 и рис. 2).
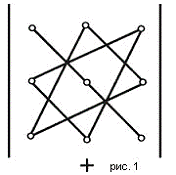
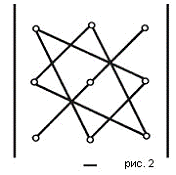
По схеме, приведенной на рис. 1,
произведения соединеных элементов берутся со своим знаком, а по схеме рис. 2 -
с обратным. Величина определителя равна алгебраической сумме полученных шести
произведений.
В определителе порядка n алгебраическим
дополнением элемента, стоящего на пересечении k-го столбца и l-й строки,
называется определитель порядка (n - 1), получаемый из данного вычеркиванием в
нем строки и столбца, на пересечении которых стоит этот элемент, причем к этому
определителю присоединяется множитель (-1)k+l, где (k + l) - сумма номеров
вычеркнутой строки и столбца. Алгебраическое дополнение элемента,
рассматриваемое без множителя (-1)k+l, называется минором этого элемента.
. Теорема Лапласа.
Определитель равен сумме произведений
каждого элемента некоторой строки (или столбца) на его алгебраическое
дополнение.
Условимся обозначать элементы определителя
маленькими буквами, а их алгебраические дополнения - соответствующими большими
буквами с теми же индексами. Так, как алгебраическое дополнение элемента a3
будем обозначать через A3, алгебраическое дополнение элемента d4 - через D4 и
т. д. На основании свойства 8 определитель (3) может быть представлен,
например, в таком виде:
D = a3A3 + b3B3 + c3C3 +
d3D3 + e3E3
Это равенство представляет собой
разложение определителя по элементам третьей строки. По свойству 8 вычисление
определителя порядка n сводится к вычислению определителей порядка (n - 1).
. Если все элементы какого-нибудь ряда
определителя, кроме одного, равны нулю, то определитель равен этому не равному
нулю элементу, умноженному на его алгебраическое дополнение.
С помощью указанных свойств можно
вычислить определитель любого порядка.
1.2 Нахождение обратной
матрицы методом Гаусса
линейный алгебра гаусс матрица
определитель
Метод Гаусса является поистине
универсальным методом в линейной алгебре, поскольку он применим и к решению
систем линейных уравнений, и к решению определителей, и к отысканию обратной
матрицы.
Теорема:
Пусть А квадратная невырожденная матрица. Если матрица (А | E) приведена с помощью
элементарных преобразований строк к виду (Е | A-1), где Е - единичная
матрица того же порядка, что и матрица А.
Из теоремы следует метод нахождения обратной матрицы методом
Гаусса:
) к матрице А приписать справа единичную матрицу Е той же
размерности;
) путем преобразований методом Гаусса над строками
расширенной матрицы (А | E) матрица А приводится к единичной матрице;
) в результате вычислительного процесса на месте приписанной
справа матрицы Е получится обратная матрица A-1.
Схематично процесс нахождения обратной матрицы выглядит
следующим образом: (А | E)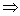
(E | A-1).
2. Практическая часть
2.1 Вычисление определителей
Пример 1: Вычислить определитель:
1) 
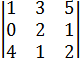
Решение:
С помощью формулы (правило треугольника):
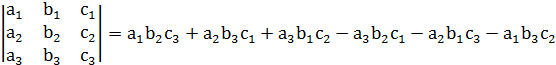
Получаем:
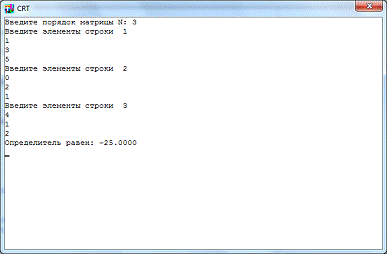
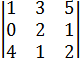= 1*2*2 + 0*5*1 + 3*1*4
- 4*2*5 - 0*3*2 - 1*1*1 = -25
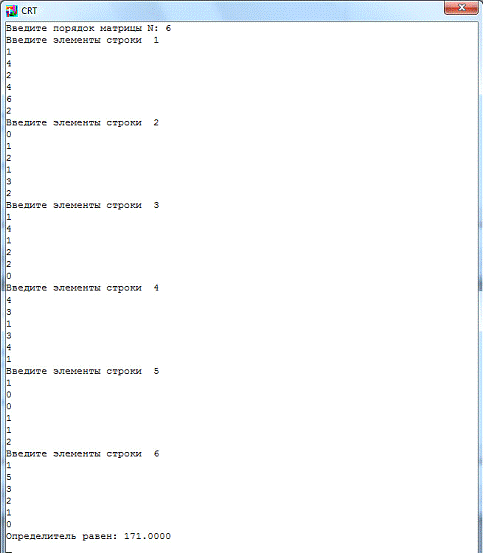
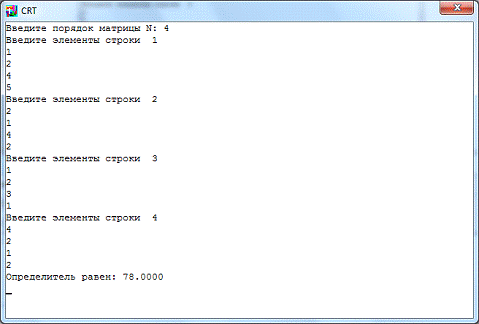
С помощью программы (см. Приложение, п.1):
. Элементы первой строки умножим на (- 3) прибавим
соответственно к элементам второй строки, получим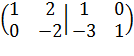 
. Затем элементы второй
строки прибавим соответственно к элементам первой строки, получим 
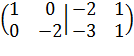. При выполнении
следующего преобразования элементы второй строки умножим на (-1/2). В
результате получим матрицу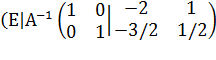 
.
. Итак, обратная матрица имеет вид A-1 =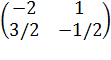 
.
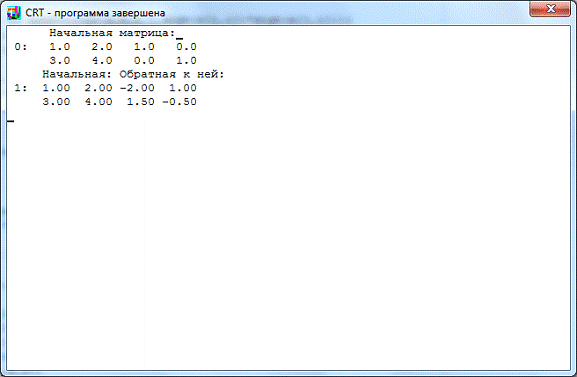
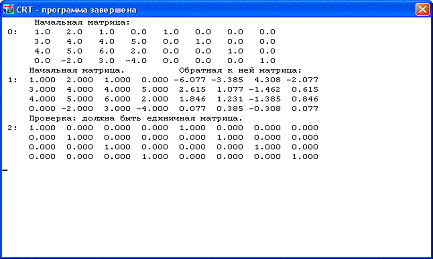
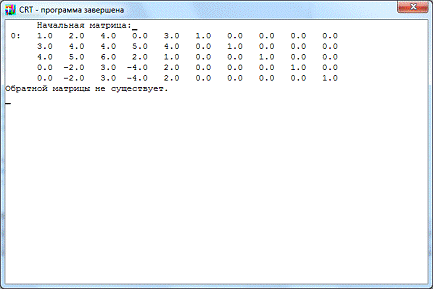
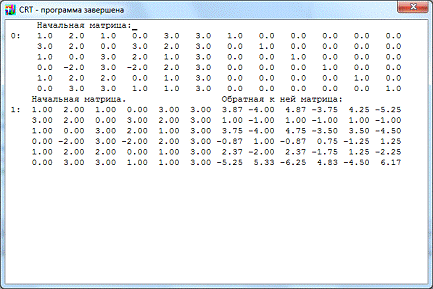
С помощью программы найдём обратную
матрицу методом Гаусса (см. Приложение, п. 1):
Заключение
В процессе создания курсовой работы было сделано следующее:
1) Изучили методы нахождения определителя и обратной матрицы
применяемых при численном решении некоторых задач линейной алгебры.
) Разработали вычислительный алгоритм в программе Pascal ABC для вычисления
определителей и для нахождения обратной матрицы.
) Решены задачи линейной алгебры и сравнили результаты.
В результате проделанной работы можно сделать следующие
выводы: легко вычисляются лишь определители невысоких порядков и некоторые
специальные типы определителей. Непосредственное нахождение определителя
требует большого объема вычислений. Можно подсчитать время вычисления
определителей на ЭВМ с заданным быстродействием. Примем для определенности
среднее быстродействие равным 100 000 операций в секунду. Тогда для вычисления
определителя 10-го порядка потребуется около 6 мин, а при n = 20 - около 1,4*1011 ч,
т.е. свыше 5*109 сут. Приведенные оценки указывают на необходимость разработки
и использования экономичных численных методов, позволяющих эффективно проводить
вычисления определителей.
Литература
1.
Пантина И.В., Синчуков. А.В. - 2-е изд., перераб. и доп. - М.: Московский
финансово-промышленный университет «Синерия», 2012. - 176 с. (Университетская
серия).
.
Турчак Л.И. Основы численных методов: Учеб. пособие. - М.: Наука. Гл. ред.
Физ.-мат. Лит., 1987. - 320 с.
.
Электронный ресурс. Определители и системы линейных алгебраических уравнений.
[http://www.pm298.ru/reshenie/opredel.php] 10.12.2012
.
Электронный ресурс. Обратная матрица. Нахождение обратной матрицы методом
алгебраических дополнений.
Приложение 1
Программый код для вычисления определителей.
program Opredelitel;crt;= 10;= array[1..N1,
1..N1] of real;: matrice;, J, N: integer;: real;Det(A: Matrice; N: integer):
real;: matrice;: integer;, Mn, S: real;Minor(var C: matrice; A: Matrice; N, I,
J: integer): real;, Jm, Ia, Ja, Nm: integer;:= N - 1; Im := 1; Ia := 1;Im <=
Nm doIa <> I then:= 1; Ja := 1;Jm <= Nm doJa <> J then[Im, Jm] :=
A[Ia, Ja];:= Ja + 1; Jm := Jm + 1;Ja := Ja + 1;:= Ia + 1; Im := Im + 1;Ia := Ia
+ 1;; {*Minor*}N = 1 then Det := A[N, N];N = 2 then Det := A[1, 1] * A[2, 2] -
A[2, 1] * A[1, 2];N > 2 then:= 0;I := 1 to N do:= Minor(B, A, N, I, 1);(I
mod 2) = 1 then begin:= Det(B, N - 1);:= S + T * A[I, 1];begin:= Det(B, N -
1);:= S - T * A[I, 1];;;:= S;;; {*Determ*}('Введите порядок матрицы N: ');
readln(N);I := 1 to N do('Введите элементы строки ', I: 2);
for J := 1 to N do readln(A[I, J]);;:= Det(A,
N);('Определитель равен: ', D: 7:
4);;
end.
Приложение 2
Программый код для нахождения обратной матрицы.
program Gayss;crt;=2;= 0.000000001; { all numbers
less than eps are equal 0 }matr=array[1..n,1..n] of
real;,b,a0:matr;,j,imx,np:integer;,s1:real;PrintMatr(m,m1:matr;n,nz,nd:integer);,j:integer;i:=1
to n do(i=1) then write(np:2,':') else write(' ');j:=1 to n do
write(m[i,j]:nz:nd);j:=1 to n do write(m1[i,j]:nz:nd);;;(np);;MultString(var
a,b:matr;i1:integer;r:real);:integer;j:=1 to n
do[i1,j]:=a[i1,j]*r;[i1,j]:=b[i1,j]*r;;;AddStrings(var
a,b:matr;i1,i2:integer;r:real);
{ процедура прибавляет к i1 строке матрицы а 2i-ю умноженную на r}
var:integer;j:=1 to n
do[i1,j]:=a[i1,j]+r*a[i2,j];[i1,j]:=b[i1,j]+r*b[i2,j];;;MultMatr(a,b:matr;var
c:matr);,j,k:byte;:real;i:=1 to n doj:=1 to n do:=0;k:=1 to n do
s:=s+a[i,k]*b[k,j];[i,j]:=s;;;sign(r:real):shortint;(r>=0) then sign:=1 else
sign:=-1;;
{MAIN};i:=1 to n doj:=1 to n
do[i,j]:=0;[i,j]:=1.0*random(8)-4;;[i,i]:=1;;
{ отладочные присвоения}[1,1]:= 1; a[1,2]:= 2; {a[1,3]:=4; a[1,4]:=
0;}[2,1]:= 3; a[2,2]:= 4; {a[2,3]:=4; a[2,4]:= 5;[3,1]:= 4; a[3,2]:= 5;
a[3,3]:=6; a[3,4]:= 2;[4,1]:= 0; a[4,2]:=-2; a[4,3]:= 3; a[4,4]:=-4;[1,1]:= 5;
a[1,2]:= 7; a[1,3]:= 7; a[1,4]:= 1;[2,1]:= 6; a[2,2]:= 6; a[2,3]:= 3; a[2,4]:=
4;[3,1]:= 5; a[3,2]:= 1; a[3,3]:= 1; a[3,4]:= 1;[4,1]:= 3; a[4,2]:= 3; a[4,3]:=
3; a[4,4]:= 3;i:=1 to n doj:=1 to n do a0[i,j]:=a[i,j];('Начальная матрица:'); np:=0;
PrintMatr(a,b,n,6,1);i:=1 to n doj:=i+1 to n do
AddStrings(a,b,i,j,sign(a[i,i])*sign(a[j,i]));
{ PrintMatr(a,b,n,6,1);}(abs(a[i,i])>eps)
then(a,b,i,1/a[i,i]);j:=i+1 to n do AddStrings(a,b,j,i,-a[j,i]);
{ PrintMatr(a,b,n,6,1);}else
writeln('Обратной матрицы не существует.');
halt;;
{writeln('Обратный ход:');}(a[n,n]>eps) theni:=n downto 1 do for
j:=1 to i-1 do(a,b,j,i,-a[j,i]);;
{ PrintMatr(a,b,n,8,4);} else writeln('Обратной матрицы не
существует.');
MultMatr(a0,b,a);('Начальная матрица. Обратная к ней матрица.:');
PrintMatr(a0,b,n,7,3);
writeln('Проверка: должна быть единичная матрица.');
PrintMatr(a,a,n,7,3);.