Теория групп и её влияние на различные области математики

Теория групп и её влияние на различные области математики

Реферат на тему

«Теория групп и её влияние на различные области математики»

Введение

В жизни современного общества очень важную роль играет математика. В настоящее время математика находит широкое применение при решении самых разнообразных проблем науки и практики.

Одной из наиболее важных и быстро развивающихся областей современной математики является абстрактная алгебра. В центре внимания современной абстрактной математики находятся различные алгебраические структуры, такие, как группы, подгруппы, полугруппы, кольца и так далее, ставшие уже классическими, а также, их далеко идущие обобщения - объекты новой природы.

Одним из фундаментальных разделов современной алгебры является теория групп. Группы, по существу, являются один из основных типов алгебраических структур.

Понадобилась работа нескольких поколений математиков, занявшая в общей сложности около ста лет, прежде чем идея группы выкристаллизировалась с ее сегодняшней ясностью.

Теория групп начала оформляться в качестве самостоятельного раздела математики в конце XVIII века. В течение первый десятилетий XIX века она развивалась медленно и практически не привлекала к себе внимания. Но затем, около 1830 года, благодаря работам Галуа и Абеля всего за несколько лет она совершила гигантский скачок, который оказал глубокое влияние на развитие всей математики. С тех пор основные понятия теории групп стали детально исследоваться.

В настоящее время теория групп является одной из самых развитых областей алгебры, имеющей многочисленные применения, как в самой математике, так и за ее пределами - в топологии, теории функций, кристаллографии, квантовой механике и других областях математики и естествознания.

Теоретико-множественные понятия и простые алгебраические структуры входят теперь, в конце XX в., в математический багаж школьника-старшеклассника и студента на самых первых порах высшего математического образования.

В свете вышесказанного, понятно, что любого, кто более или менее серьезно собирается заниматься математикой, не минует изучение теории групп. Эта много аспектная область знаний не обойдет стороной и тех, кто изучает теоретическую физику или квантовую механику.

Если открыть какой-нибудь классический учебник по теории групп, то можно увидеть уже конечный результат работы огромного количества ученых. Это конечно неплохо, но иногда для лучшего понимания предмета, полезно проследить за историей его возникновения. Это помогает лучше понять причины, по которым данная область знаний вообще появилась, зачем она была нужна и зачем она нужна сейчас. Изучение предмета в процессе его создания позволяет глубже проникнуть в суть каких-то вопросов. Мы можем следить за ходом мыслей великих ученых, увидеть сам процесс творчества. Это полезно, увлекательно и в каком-то смысле даже более интересно, чем просто чтение учебника.

Поэтому, целью данного реферата является рассказать об истории возникновения теории групп и процессе её исторического развития. История теории групп очень интересна, увлекательна, насыщенна выдающимися фактами и событиями. Более того, она не просто интересна. Изучив её подробно, можно понять суть этой теории гораздо глубже.

На данный момент имеется много книг, содержащих сведения об истории зарождения теории групп и общей алгебры. Некоторые из них содержат весьма детальную информацию, но все-таки неполную. В этом реферате, сделана попытка собрать воедино наиболее интересные факты из различных литературных источников, чтобы дать более полное представление об истории теории групп, современном положении дел в этой области и приложениях теории групп в различных областях математики, физики и др.

1. Основные понятия теории групп

Прежде чем перейти к истории, рассмотрим некоторые ключевые понятия теории групп.

Естественно, необходимо начать с самого понятия группы. Понятие группы - одна из самых важных объединяющих идей в математике. Оно собирает воедино широкий круг математических структур, для которых существует понятие комбинации или «произведения». Такие произведения включают обыкновенное арифметическое произведение чисел, но более типичный пример, - произведение или композиция функций. В частности, если f и g функции, то gf - функции, значение аргумента x которых - f(g(x)).

Определение понятия группы сформировалось не сразу. Например, Ф.Клейн и С.Ли, начавши разрабатывать теорию групп в ее приложениях к различным областям математики, дали такое определение:

Группа есть такая совокупность однозначных операций А, В, С, ..., что комбинация, двух каких-нибудь операций А, В из этой совокупности дает операцию С из той же совокупности: А*В =С.

В настоящий момент, формально определение выглядит следующим образом:

Группа G - это множество с одной бинарной операцией, подчиняющейся следующим аксиомам:

1). для 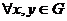 выполняется  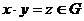(замкнутость)

). для 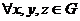 выполняется  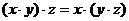(ассоциативность)

). существует единица 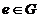 и для 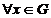 выполняется

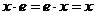
). для 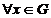 существует обратный элемент 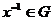, такой что выполняется тождество .

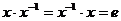Эти аксиомы развивались на протяжении более ста лет работы с особыми группами, в течение которого их основные свойства выяснялись лишь постепенно. На практике, свойства 2) и 3), как правило, очевидны, и важнее гарантировать, что операция произведения действительно определена для всех элементов G. В ответ на это желание были созданы многие математические понятия, сначала неосознанно, ради существования произведений.

Приведем пример.

Будем рассматривать перспективные и проективные преобразования. Можно убедиться, что перспективный вид перспективного вида, вообще, не является перспективным видом. Поэтому, если мы примем, что «произведение» перспективного преобразования g и перспективного преобразования f является результатом выполнения g, затем f, то gf не всегда принадлежит множеству перспективных преобразований. Множество проективных преобразований - простейшее возможное расширение множества перспективных преобразований до множества, на котором произведение всегда определено, а именно, множество конечных произведений перспективных преобразований.

Стоит отметить, что аксиомы группы никак не регламентируют зависимость операции умножения от порядка сомножителей. Поэтому, вообще говоря, изменение порядка сомножителей влияет на произведение. Группы, для которых произведение не зависит от порядка сомножителей, называют коммутативными или абелевыми группами. Абелевы группы довольно редко встречаются в физических приложениях. Чаще всего группы, имеющие физический смысл, являются неабелевыми.

Группы можно очень обобщенно разделить на конечные и бесконечные. Конечные группы содержат конечное количество элементов. Если группа имеет бесконечное число элементов, то она называется бесконечной группой.

Конечные группы небольшого размера удобно описывать при помощи т. н. «таблицы умножения».

В этой таблице каждая строка и каждый столбец соответствует одному элементу группы, а в ячейку на пересечении строки и столбца помещается результат операции умножения для соответствующих элементов.

Также группы можно классифицировать по другому критерию: дискретность или непрерывность.

Дискретная группа состоит из дискретного множества элементов. Когда элементы группы непрерывно зависят от каких-либо параметров, то группа называется непрерывной. Наиболее известным примером непрерывных групп являются группы Ли. Более точно, группа Ли - это группа, множество элементов которой образует гладкое многообразие. С помощью групп Ли как групп симметрий находятся решения дифференциальных уравнений.

Приведем еще несколько важных для дальнейшего определений:

. Группа называется циклической, если она порождена одним элементом g, то есть все её элементы являются степенями g (или, если использовать аддитивную терминологию, представимы в виде n*g, где n - целое число).

. Число элементов n = |G| конечной группы G называется ее порядком.

. Если G и G' - группы, то отображение f : G → G', для которого f(a*b) = f(a)*f(b) для всех a, b из G, называется гомоморфизмом групп. Биективный гомоморфизм называется изоморфизмом. При наличии изоморфизма f : G → G' группы G и G' называются изоморфными, обозначение: G G'. Автоморфизмом называется изоморфизм группы на саму себя.

. Говорят, что группа G действует на множестве M, если задан гомоморфизм из группы G в группу S(M) всех перестановок множества M.

. Подгруппа ― подмножество H группы G, само являющееся группой относительно операции, определяющей G.

. Подгруппа N группы G называется нормальной, если она инвариантна относительно сопряжений, то есть для любого элемента 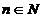и любого 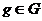, элемент .

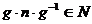. Задача классификации групп - описание групп с точностью до изоморфизма.

Как мы увидели, понятие группы очень четкое, логичное и лаконичное. Оно очень абстрактно и может быть применено во многих, порой даже неожиданных местах. Оно может быть полезно при проведении формальных доказательств. Но тем не менее и здесь есть место для критики. Например, в своей книге Феликс Клейн говорит следующее:

«Таким образом, здесь совершенно отказываются от обращения к фантазии. Взамен этого тщательно препарируется логический скелет. С этой тенденцией мы еще будем часто встречаться при продолжении наших лекций. Эта абстрактная формулировка превосходна для разработки доказательств, но совершенно не приспособлена для нахождения новых идей и методов. Она представляет собой известное завершение пройденного пути развития. Поэтому и преподавание она облегчает лишь внешне, постольку, поскольку с ее помощью можно просто и без про белов доказывать известные теоремы; с другой стороны, она внутренне очень затрудняет учащегося, так как он оказывается поставленным перед чем-то замкнутым и не знает, как пришли к такого рода определениям; к тому же он ничего не может представить себе наглядно. Вообще же этот метод имеет тот недостаток, что он не стимулирует мышления; нужно только следить за тем, чтобы не нарушить указанных четырех законов».

. Аддитивная группа (R, +) кольца R.

. Группа подстановок Sn множества из n элементов (симметрическая группа), группа An четных подстановок (знакопеременная группа).

. Группа симметрий геометрической фигуры (совокупность всех преобразований пространства, совмещающих данную фигуру с ней самой). Среди них: группа симметрий Cn правильного ориентированного n-угольника и группа Dn всех симметрий правильного n-угольника.

. Линейные группы GLn(K) обратимых (n,n)-матриц над полем K (или группы GLn(R) обратимых (n,n)-матриц над кольцом R), являющиеся группами автоморфизмов n-мерного линейного пространства над полем K (свободного R-модуля с базисом из n элементов), в частности конечные линейные группы GLn(Fq) с коэффициентами из конечного поля Fq из q элементов. Группы автоморфизмов других алгебраических систем (групп, полугрупп, колец и.т.д.) лежат в этом русле.

2. Истоки теории групп

Многие ученые склонны верить сейчас, что в действительности понятие группы является древнейшим математическим понятием, более древним, чем понятие числа, и неотделимым от самой человеческой цивилизации. Группы появляются всюду, где возникают симметрии, автоморфизмы, обратимые преобразования. Иными словами, всюду, где есть повторяющиеся и самовоспроизводящиеся узоры. А человеческая культура, подобно природе и жизни, состоит в составлении узоров. Именно на этом основана вездесущность идеи группы, универсальность этого понятия и огромное разнообразие его приложений.

Несмотря на это, термин «группа» получил повсеместное распространение не так давно. Официально теория групп возникла в начале XIX века. У теории групп три исторических корня: теория алгебраических уравнений, теория чисел и геометрия. Математики, стоящие у истоков теории групп, - это Леонард Эйлер, Карл Фридрих Гаусс, Жозеф Луи Лагранж, Нильс Хенрик Абель и Эварист Галуа. Галуа был первым математиком, связавшим теорию групп с другой ветвью абстрактной алгебры - теорией полей, разработав теорию, ныне называемую теорией Галуа.

Решение проблем теории алгебраических уравнений явилось наиболее мощным толчком к появлению групп. Поэтому остановимся на этом вопросе наиболее подробно.

3. Основные проблемы алгебры в XVIII, XIX веках

Чем была алгебра к концу XVIII века , трудно определенно сказать. Конечно, это было уже не просто искусство вычислять с числами, буквами и загадочными величинами, содержащее несколько правил, несколько формул и умение как-то правильно их толковать. Нет, комплексные числа были уже всеми почти признаны, существовала уже некоторая теория линейных уравнений, уже намечались некоторые принципы, начала теории уравнений произвольной степени от одного неизвестного, но рядом с величественным зданием анализа это было очень и очень мало. Алгебра находилась где-то на окраинах математики.

К концу XVIII в. одной из главных задач алгебры стала задача решения алгебраических уравнений в радикалах. Алгебру называли наукой о решении уравнений. Более точно ставилась задача: Найти способы выражать корни уравнений через коэффициенты уравнения с помощью четырех арифметических операций и операций извлечения арифметического корня произвольной степени. Уравнение имеет следующий вид:

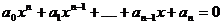
где .

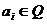К тому моменту умели решать в радикалах квадратные уравнения, кубические (метод Кардана, Тартальи) и уравнения четвертой степени (метод Феррари).

В поисках общей формулы математики перепробовали громадное количество методов. Естественно, наибольшим успехом было бы найти способы решения уравнений произвольной степени с произвольными коэффициентами, однако многочисленные поиски такого способа были безрезультатны. Постепенно начала нарастать уверенность, что в общем случае поставленная задача решения не имеет, т.е. нельзя разрешить в радикалах произвольное уравнение.

Как отмечается в книге [Колмогорова] до 1770 года не было даже известно, как решать в радикалах уравнение вида: 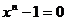 при 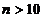. Выход в 1770 г. работы Вандермонда, где он разбирает случай 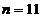, был уже существенным сдвигом. (Здесь хотелось бы отметить, что позднее это задача полностью решена Гауссом. Об этом будет подробнее далее).

Успех в выше обозначенном вопросе был достигнут только в XIX веке.

Не добившись ничего «наивной игрой» с коэффициентами многочлена в поле рациональных чисел, математики к концу XVIII века были вынуждены прибегнуть к фактическому рассмотрению полей и групп, еще не вводя этих понятий явно (Лагранж и Вандермонд в частности). Затем, уже в веке, благодаря результатам К.-Ф. Гаусса, Н.-Г. Абеля и Э. Галуа вопрос о разрешимости в радикалах был решен. Было показано, что в общем случае разрешимости в радикалах не может быть.

Решение этой задачи привело к введению в науку ряда новых понятий (в первую очередь, понятия группы). Эти понятия преобразили алгебру. Правда, вначале изменения в алгебре происходили на скрытом уровне. Этот период длился до 70-х годов XIX столетия. И как отмечается в книге [5], он наиболее труден для историка науки.

«До 70-х годов XIX в. происходил в основном скрытый период этого бурного роста алгебры. Здесь перед историком науки встает задача восстановления по черновым наброскам, работам, письмам, воспоминаниям таинственного процесса рождения, роста и взаимодействия математических идей. Эта задача трудна еще и тем, что в истории каждой крупной математической мысли имеется период неявного существования, когда она неузнаваемо.

Для современников начинает проглядывать то там, то тут в маскарадной одежде частных случаев и приложений; а потом вдруг выступает сразу во всей своей полной красе, и не сразу можно, а иногда и совсем нельзя, определить, кто помог ей сделать этот знаменательный шаг выхода на сцену.»

В итоге, преобразование алгебры оказалось настолько фундаментальным, что по сравнению с началом века, к концу его, а еще яснее к -20-м годам XX столетия, сам предмет этой науки, ее основные понятия и методы, ее место в математике неузнаваемо изменились.

3.1 Появление понятия перестановок. Достижения Лагранжа и Вандермонда

Понятие перестановок появилось еще в XIV веке. В 1321 году Леви бен Гершон на шел, что существует 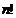 перестановок  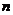предметов. Эти перестановки - обратимые функции, которые образуют группу Sn в процессе композиции. Однако поведение перестановок в процессе композиции не рассматривалось до восемнадцатого века.

В XVIII веке работы Лагранжа и Вандермонда по теории алгебраических уравнений ввели в математику первый групповой объект - подстановки. Вандермонд и Лагранж применили идею перестановки к корням полиномиальных уравнений. Тем самым и были открыты первые поистине теоретико-групповые свойства перестановок.

Особенно значителен опубликованный в 1771-1773 гг. мемуар Лагранжа «Размышления об алгебраическом решении уравнений» (Refle xions sur la resolution algebrique des equations). Кроме очень важных исследований в теории уравнений в нем доказана первая теоретико-групповая теорема:

Число значений, которые принимает функция от 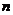 переменных при всех перестановках этих переменных, делит .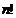

Это частный случай теоремы о том, что порядок подгруппы делит порядок группы.

Среди последователей Лагранжа и Вандермонда следует отметить Паоло Руффини. В своих исследованиях 1808-1813 гг. по теории уравнений он рассматривает не только группу подстановок, но и ее подгруппы и вводит понятия транзитивности и примитивности.

Поговорим теперь более подробно об идеях Лагранжа и Вандермонда: (основываясь на материале из книги [3]):

Вандермонд и Лагранж открыли ключ к пониманию решения уравнений в радикалах. Они начали с наблюдения, что если уравнение:

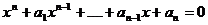имеет корни ,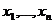

то

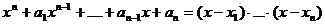
Перемножая всё в правой части и сравнивая коэффициенты, находим, что 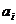 некоторые функции от 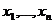. Например:

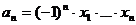 и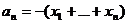

Эти функции симметричны, то есть, неизменяемы какой-либо перестановкой 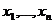, поскольку правая часть не изменяется такими перестановками. Следовательно, любая рациональная функция 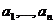 симметрична как функция 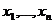. Сейчас объект решения в радикалах - применение рациональных операций и радикалов к 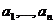, с тем чтобы получить корни, то есть, полностью асимметричные функции .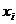

Радикалы, поэтому, должны некоторым образом уменьшать симметрию, и молено видеть, что они делают в квадратичном случае. Корни

равны

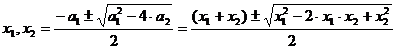
И мы замечаем, что симметричные функци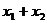и  и 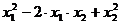 дают две две асимметричные функции 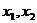, когда вводится двузначный радикал .

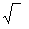Вообще, введение радикалов 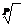 умножает число значений функции на  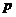и делит симметрию на  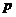в том смысле, что группа перестановок, оставляющая функцию неизменной, уменьшается до 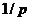 своей предыдущей величины.

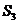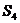Вандермонд и Лагранж нашли, что они могут объяснить предшествующие решения кубических и квадратных уравнений на основе уменьшения такой симметрии в соответствующих группах подстановок  и . Они также нашли некоторые свойства подгрупп. Однако, они не смогли добиться достаточного понимания зависимости между радикалами и подгруппами 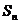, чтобы решить уравнения степени .

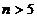3.2 Решение уравнения деления круга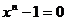

Карл-Фридрих Гаусс сделал свои первые открытия в алгебре еще совсем молодым человеком во время обучения в Геттингенском университете (1795 -1798 годы). В марте 1796 г., занимаясь задачей отыскания корней уравнения 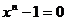 он обнаружил связь между этой задачей и делением окружности на равные части, доказав, что правильный 17-угольник можно вписать в круг с помощью циркуля и линейки. 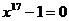Соответствующий алгебраический факт, что уравнение  разрешимо в квадратных радикалах, Гаусс обобщил вскоре, найдя критерий возможности такой разрешимости (уравнение разрешимо для простого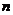 вида 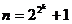) и дав его геометрическую интерпретацию.

При доказательстве этой группы предложений Гаусс развил методы, послужившие одной из исходных точек при создании теории Галуа, по собственному признанию ее автора.

Гаусс явно высказал, что цель его исследований полинома

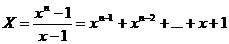
состоит в том, чтобы последовательно разлагать полином на множители вплоть до линейных, обнажая при этом структуру уравнения.

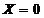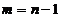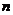Гаусс установил, что уравнение  степени , где  простое, неприводимо в поле рациональных чисел и нормально над ним, т. е. все его корни рационально выражаются через один из них. Оказалось, что эти корни имеют вид: 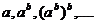, т. е. что группа автоморфизмов этого уравнения циклическая. Остается лишь один шаг для того, чтобы обнаружить, что любая подгруппа циклической группы является ее нормальным делителем. Этот шаг впоследствии сделал Галуа, учитывавший также указание Лагранжа, что подстановки корней уравнений указывают путь к построению их общей теории.

В книге [Колмогорова] по поводу метода, примененного Гауссом, говорится следующее: «Значение достижения Гаусса в теории уравнений очень велико. Неявно здесь уже играют свои роли понятия поля, группы, базиса поля над полем и, пожалуй, даже группы Галуа. Более того, вероятно, эти понятия и их значения в теории уравнений были бы гораздо трудней обнаружены, если бы у всех перед глазами не было бы столь глубоко и красиво разобранного Гауссом примера».

(Подробно метод Гаусса для решения уравнения деления круга изложен в книге [Колмогоров,с.53] ).

3.3 Вклад Нильса Генрика Абеля

Дальнейшее развитие теории алгебраических уравнений связано с именем норвежского математика Нильса Хенрика Абеля (1802-1829). Он осуществил доказательство неразрешимости в радикалах уравнений выше пятой степени.

Как было сказано ранее, поиски подходящей формы иррациональности для решения того или иного класса алгебраических уравнений сменились уверенностью, что, по-видимому, это невозможно. Задача обернулась; необходимым оказалось исследовать наиболее общие выражения, содержащие радикалы, с тем чтобы выяснить, могут ли они быть выражениями корней алгебраического уравнения пятой степени. По этому пути и повел свои исследования в самом конце XVIII в. П. Руффини. В 1799 г. он опубликовал «Общую теорию уравнений, в которой доказывается невозможность алгебраического решения общих уравнений выше четвертой степени». Но первый реальный успех выпал на долю скромного Абеля.

Еще в школе (около 1820 г.) Абель заинтересовался проблемой разрешимости уравнений в радикалах. Одно время ему казалось, что он дал доказательство разрешимости в радикалах уравнения пятой степени. Вскоре выяснилось, что это доказательство содержало ошибку. Но ошибочное доказательство сослужило свою хорошую службу. Абель получил государственную стипендию и возможность поехать в Европу для усовершенствования в математике.

Исправленное доказательство появилось в 1824 г. в «Мемуаре об алгебраических уравнениях, где доказывается невозможность разрешимости общего уравнения пятой степени». В нем Абель, по-видимому независимо от Руффини, шел тем же путем; он стремился доказать, что наиболее общие выражения, содержащие радикалы, не могут быть корнями общего алгебраического уравнения пятой степени. Интересно, что это доказательство Абеля страдало тем же недостатком, что и доказательство Руффини. Оно опиралось на предположение, что корни резольвенты должны рационально выражаться через корни данного уравнения.

Только в 1826 г. в работе Абеля «Доказательство невозможности алгебраической разрешимости уравнений, степень которых превышает четвертую» многовековая проблема получила удовлетворительное разрешение.

В своей работе Абель сделал приблизительно следующее:

1) Были построены наиболее общего вида алгебраические функции

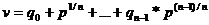
где 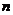- простое,  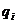- алгебраические функции того же порядка, что и 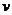, но степени не выше, чем 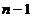. А также 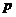- алгебраическая функция порядка на единицу ниже, чем 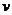, построенная так, что она не выражается рационально через 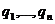. Применительно к рассмотренным конструкциям Абель доказал, что если уравнение алгебраически разрешимо, то его корню всегда можно дать такой вид, что все алгебраические функции, из которых он составляется, выражаются через рациональные функции корней данного уравнения.

2) Был рассмотрен вопрос о подстановках и о числе различных значений, которые при этом могут принимать функции нескольких переменных.

) Было показано, что никакое самое общее радикальное выражение не может быть универсальным выражением корней уравнения данной степени, большей чем четвертая.

Стоит отметить, что доказательства Абеля не дают возможности выделить классы уравнений, разрешимых в радикалах. Они не снимают также возможности такой разрешимости для уравнений с численными коэффициентами подбором подходящих иррациональностей в конкретном случае. Исследования надо было расширять. Перед Абелем, как и в свое время перед Лагранжем, встала общая проблема разрешимости - основная проблема классической теории Галуа.

Перед смертью Абель работал над задачей определения всех алгебраически разрешимых уравнений. В 1829 году Абель в «Мемуаре об одном особом классе алгебраически разрешимых уравнений» исследовал циклические уравнения, следуя в за Лагранжем, который обнаружил этот класс в свое время. Абель отыскал для них явные выражения корней через коэффициенты. Кроме того, он рассмотрел еще один класс разрешимых уравнений, которые по существу являются нормальными уравнениями с коммутативной (абелевой) группой Галуа.

Опираясь на информацию из книги [Колмогорова] расскажем подробнее о содержании мемуара Абеля 1829 г.

Первым и очень важным шагом было явное введение понятия области рациональности, аналога современного понятия поля. Абель дал следующее определение:

Область рациональности относительно величин 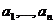 - это множество всевозможных величин, полученных из величин 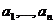 и вещественных (или рациональных) чисел с помощью четырех арифметических действий (конечно, слово множество им не употреблялось).

Введение этого понятия крайне существенно для сколько нибудь общих исследований в теории уравнений.

Вторым существенным шагом является доказательство разрешимости замечательного класса уравнений. Этот класс Абель определяет двумя условиями:

. Каждый корень 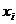 уравнения выражается в виде рациональной функции от фиксированного корня .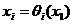

. Рациональные функции 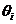 обладают свойством .

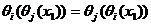Идея работы возникла у Абеля при исследовании уравнения лемнискаты, о котором упоминает Гаусс в «Арифметических исследованиях». Работа Абеля существенно дополняет и развивает идеи Гаусса и является заметным вкладом в теорию алгебраических уравнений.

Подводя итог данному разделу, хотелось бы сказать следующее.

Работы Абеля принесли большую пользу. Их появление приблизило момент, когда теория групп стала появляться везде и всюду и царствовать в математике. Абель по сути доказал теорему эквивалентную теореме Галуа:

Чтобы неприводимое уравнение было разрешимо в радикалах, необходимо и достаточно, чтобы все корни были рациональными функциями двух известных корней.

Абель исследовал структуру нескольких конкретных классов разрешимых групп. Фактически Абель исследовал структуру коммутативных групп. Он показал, что эти группы являются произведениями циклических групп. Однако понятие группы у него еще не было выделено. Кроме того, общего критерия разрешимости он не получил.

3.4 Теория Галуа

Как было сказано выше, Абель не смог дать общий критерий разрешимости уравнений с числовыми коэффициентами в радикалах. Но решение и этого вопроса не заставило себя долго ждать. Оно принадлежит Эваристу Галуа (1811 - 1832), французскому математику, скончавшемуся, как и Абель, в очень молодом возрасте. Его жизнь, короткая, но наполненная активной политической борьбой, страстный интерес к математическим занятиям представляют яркий пример того, как в деятельности одаренного человека накопленные предпосылки науки претворяются в качественно новый этап ее развития.

Галуа успел написать мало работ. В русском издании его работы, рукописи и черновые записи заняли лишь 120 страниц в книге маленького формата. Но значение этих работ огромно. Поэтому рассмотрим его замыслы и результаты подробнее.

Среди нескольких заметок и статей, опубликованных еще при жизни Галуа, наиболее замечательна статья «Из теории чисел» (Sur la theorie ¦desnombres.- Bull. sci. math., 1830). В этой статье Галуа рассматривал полиномиальные сравнения вида

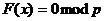
Галуа обращает в своей работе внимание на случай, когда сравнение не имеет целых корней. Он пишет, что «тогда корни этого сравнения нужно рассматривать как род воображаемых символов, так как они не удовлетворяют требованиям, предъявляемым к целым числам; роль этих символов в исчислении будет часто столь же полезной, как роль воображаемого 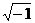 в обычном анализе». Далее он рассматривает по сути дела конструкцию присоединения к полю корня неприводимого уравнения (явно выделяя требование неприводимости) и доказывает ряд теорем о конечных полях. См [Колмогоров]

Вообще, основная проблема, рассмотренная Галуа ,- это проблема разрешимости в радикалах общих алгебраических уравнений, причем не только в случае уравнений 5-й степени, рассмотренном Абелем. Главной целью Галуа всех исследований Галуа в этой области было найти критерий разрешимости для всех алгебраических уравнений.

В связи с этим, рассмотрим более подробно содержание основной работы Галуа «Мемуар об условиях разрешимости уравнений в радикалах» (Memoiresur les conditions de resolubilite des equations par radicaux.- J. math, pures et appl., 1846).

Рассмотрим вслед за Галуа уравнение : см [Рыбников]

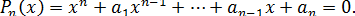
Для него определим область рациональности - совокупность рациональных функций от коэффициентов уравнения:

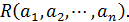
Область рациональности R является полем, т. е. совокупностью элементов, замкнутой по отношению к четырем действиям. Если 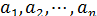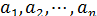- рациональны, то R - поле рациональных чисел; если же коэффициенты - произвольные величины, то R есть поле элементов вида:

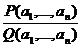
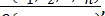Здесь числитель и знаменатель - многочлены. Область рациональности можно расширить, присоединяя к ней элементы, например корни уравнения. Если к этой области присоединить все корни уравнения, то вопрос о разрешимости уравнения делается тривиальным. Задача разрешимости уравнения в радикалах может ставиться только по отношению к определенной области рациональности. Он указывает, что можно изменять область рациональности, присоединяя как известные новые количества.

При этом Галуа пишет: «Мы увидим, сверх того, что свойства и трудности уравнения могут быть сделаны совершенно разными сообразно количествам, которые к нему присоединены».

Галуа доказал, что для всякого уравнения 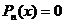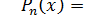,можно в той же области рациональности найти некоторое уравнение 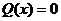, называемое нормальным. Корни данного уравнения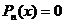 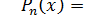 и соответствующего нормального уравнения 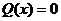выражаются друг через друга рационально.

После доказательства этого утверждения следует любопытное замечание Галуа: «Замечательно, что из этого предложения можно заключить, что всякое уравнение зависит от такого вспомогательного уравнения, что все корни этого нового уравнения являются рациональными функциями друг друга»

Анализ замечания Галуа дает нам следующее определение для нормального уравнения:

Нормальное уравнение - это уравнение, обладающее тем свойством, что все его корни рационально выражаются через один из них и элементы поля коэффициентов.

Примером нормального уравнения будет уравнение: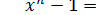 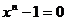 Его корни

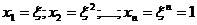
Нормальным также будет являться, например, квадратное уравнение.

Стоит ,однако, отметить, что Галуа не останавливается на специальном изучении нормальных уравнений, он отмечает только, что такое уравнение «легче решить, чем какое-нибудь другое». Галуа переходит к рассмотрению подстановок корней.

Он говорит что, все подстановки корней нормального уравнения образуют группу G. Это и есть группа Галуа уравнения Q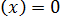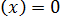, или, что то же самое, уравнения 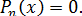 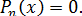Она обладает, как выяснил Галуа, замечательным свойством: любое рациональное соотношение между корнями и элементами поля R инвариантно относительно подстановок группы G. Таким образом, Галуа связал с каждым уравнением группу подстановок его корней. Он же ввел (1830) термин «группа» - адекватное современному, хотя и не столь формализованное определение.

Структура группы Галуа оказалась связанной с задачей разрешимости уравнений в радикалах. Чтобы разрешимость имела место, необходимо и достаточно, чтобы соответствующая группа Галуа была разрешима. Это значит, что в данной группе существует цепочка нормальных делителей с простыми индексами .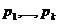

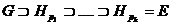
Напомним, кстати, что нормальные делители, или, что то же самое, инвариантные подгруппы 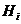 - это такие подгруппы группы G, для которых справедливо

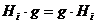
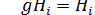где g - элемент группы G.

Общие алгебраические уравнения 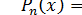 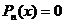 при 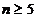 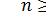, вообще говоря, такой цепочки не имеют, так как группы подстановок имеют только один нормальный делитель индекса 2 - подгруппу всех четных подстановок. Поэтому эти уравнения в радикалах, вообще говоря, неразрешимы.( И мы видим связь результата Галуа и результата Абеля.)

Галуа сформулировал следующую фундаментальную теорему :

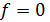
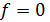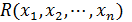
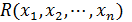Для любого наперед заданного уравнения  и любой области рациональности существует группа перестановок корней  этого уравнения, обладающая тем свойством, что любая рациональная функция - т.е. функция, построенная с помощью рациональных операций из этих корней и элементов области рациональности, - которая при перестановках этой группы сохраняет свои числовые значения, имеет рациональные (принадлежащие области рациональности) значения, и обратно: всякая функция 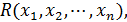 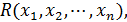принимающая рациональные значения, при перестановках данной группы сохраняет эти значения.

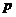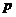Рассмотрим теперь частный пример, которым занимался еще сам Галуа. Речь идет о том, чтобы найти условия, при которых неприводимое уравнение степени , где  простое, разрешимо при помощи двучленных уравнений. Галуа обнаруживает, что условия эти заключаются в возможности так упорядочить корни уравнения, чтобы упомянутая "группа" перестановок задавалась формулами

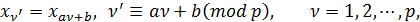
где может быть равно любому из чисел 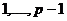, 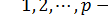а b равняется 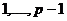.  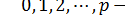Такая группа содержит самое большее p(p - 1) перестановок. В случае 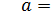 когда 𝑎=1 имеется лишь p перестановок, говорят о циклической группе; в общем случае группы называются метациклическими. Таким образом, необходимым и достаточным условием разрешимости неприводимого уравнения простой степени в радикалах является требование, чтобы его группа была метациклической - в частном случае, циклической группой.

Теперь уже можно обозначить пределы, поставленные сфере действия теории Галуа. Она дает нам некий общий критерий разрешимости уравнений с использованием резольвент, а также указывает путь к их разысканию. Но тут сразу же встает целый ряд дальнейших проблем: найти все уравнения 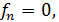 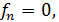имеющие при данной области рациональности определенную, наперед заданную группу перестановок; исследовать вопрос о том, сводимы ли друг к другу два уравнения такого рода, и если да, то какими средствами и т.д. Все это вместе составляет огромную совокупность проблем, не решенных еще и сегодня. Теория Галуа указывает нам на них, не давая, однако, никаких средств для их решения.

Аппарат, введенный Галуа для установления разрешимости алгебраических уравнений в радикалах, имел значение, выходящее за рамки указанной задачи. Его идея изучения структуры алгебраических полей и сопоставления с ними структуры групп конечного числа подстановок была плодотворной основой современной алгебры. Однако она не сразу получила признание.

Перед роковой дуэлью, оборвавшей его жизнь, Галуа в течение одной ночи сформулировал свои важнейшие открытия и переслал их другу О. Шевалье для публикации в случае трагического исхода. Приведем знаменитое место из письма к О. Шевалье: «Ты публично попросишь Якоби или Гаусса дать их заключение не о справедливости, но о важности этих теорем. После этого будут, я надеюсь, люди, которые найдут свою выгоду в расшифровке всей этой путаницы». При этом Галуа имеет в виду не только теорию уравнений, в этом же письме им сформулированы глубокие результаты из теории абелевых и модулярных функций.

Это письмо было опубликовано вскоре после смерти Галуа, однако идеи, содержащиеся в нем, не нашли отклика. Только через 14 лет, в 1846 г., Лиувилль разобрал и опубликовал все математические работы Галуа. В середине XIX в. в двухтомной монографии Серре, а также в работе Э. Бетти A852), впервые появились связные изложения теории Галуа. И только с 70-х годов прошлого века идеи Галуа начали получать дальнейшее развитие.

Понятие группы в теории Галуа становится мощным и гибким средством. Коши, например, тоже изучал подстановки, но он и не думал приписывать понятию группы подобную роль. Для Коши, даже в поздних его работах 1844-1846 гг. «система сопряженных подстановок» была неразложимым понятием, весьма жестким; он пользовался ее свойствами, но никогда не выявлял понятия подгруппы и нормальной подгруппы. Эта идея относительности, собственное изобретение Галуа, позднее проникла во все математические и физические теории, ведущие свое происхождение от теории групп. Эту идею в действии мы видим, например, в «Эрлангенской программе».(о ней будет рассказано позднее)

Значение работ Галуа состоит в том, что в них в полной мере были раскрыты новые глубинные математические закономерности теории уравнений. После освоения открытий Галуа вид и цели самой алгебры существенно изменились, исчезла теория уравнений - появилась теория полей, теория групп, теория Галуа. Ранняя смерть Галуа была невозместимой утратой для науки. На заполнение пробелов, понимание и улучшение работ Галуа понадобилось еще несколько десятков лет. Усилиями Кэли, Серре, Жордана и других открытия Галуа были превращены в теорию Галуа. В 1870 г. монографии Жордана «Трактат о подстановках и алгебраических уравнениях» представило эту теорию в систематическом изложении, понятном для всех. С этого момента теория Галуа стала элементом математического образования и фундаментом для новых математических исследований.

3.5 Пример применения теории Галуа

Пусть дано уравнение 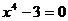; оно неприводимо над полем Q и имеет 4 различных корня

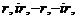
где 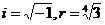. Поле разложения этого уравнения получается присоединением к Q двух величин 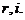Обозначим его N=Q(r,i), иначе можно записать N=Q(r+ir). Всякий элемент поля N есть линейная комбинация следующих восьми элементов: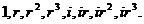

Элементы группы данного уравнения определены, если известны образы i и r; i может отображаться только в i или -i. Точно также r может отобразиться лишь в элементы r,-r,ir,-ir.

Объединяя эти условия, получаем восемь элементов группы G (восемь автоморфизмов поля N). Покажем, как они определены своим действие на порождающие элементы i, r.

Можно доказать, что эти автоморфизмы сохраняют соотношение i2=-1, r4=3.

Группа G содержит подгруппу H={I,S,S2,S3}, порожденную S, которая содержит меньшую подгруппу L={I,S2}, порожденную S2.

Каждый автоморфизм группы H оставляет i на место, следовательно он оставляет на месте каждый элемент подполя Q(i).

Меньшая группа L имеет автоморфизмы, которые оставляют на месте элементы большего поля Q(i,r2).

Таким образом, убывающей цепочке подгрупп 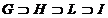 соответствует возрастающая цепочка подполей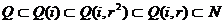

Возрастающая цепочка подполей данного уравнения дает метод решения посредством последовательного присоединения корней более простых уравнений x2=-1; y2=3; z2=31/2.

3.6 Последующее развитие оригинальной теории Галуа

Развитие идей Галуа происходило в разных направлениях. В области классической основы, наиболее близкой собственным идеям Галуа, новые задачи группировались вокруг проблемы классификации алгебраических иррациональностей и установления их арифметической природы. Сюда, например, относится теорема Кронекера - Вебера, что корни абелевых уравнений (т. е. уравнений с коммутативной группой) с рациональными коэффициентами рационально выражаются через корни из единицы. Дальнейшие обобщения этой теоремы привели к общей теории полей классов, где речь идет о классификации всех абелевых расширений данного поля алгебраических чисел. Последнее является конечным алгебраическим расширением поля рациональных чисел-. Современная теория алгебраических чисел сложилась как соединение теории этих чисел с теорией идеалов и теорией Галуа.

Постановка новых, более общих задач способствовала быстрому усложнению теории Галуа и росту общности ее результатов. Среди этих задач упомянем, например, проблему разыскания всех уравнений, которые для заданной области рациональности обладают определенной, наперед заданной группой. Проблемы такого рода привели к изучению полей общих рациональных функций (проблема Люрот-Штейница). Обобщения задачи о разрешимости уравнений в радикалах привели к проблеме общего характера о возможности сводить уравнение к цепочке вспомогательных уравнений с меньшим числом параметров. Первые общие результаты здесь были получены лишь советским математиком Н. Г. Чеботаревым в его теории резольвент. Другой советский математик - И. Р. Шафаревич в 1954 г. решил так называемую обратную задачу теории Галуа: для любой разрешимой группы любого порядка, если расширяемое поле К_0 алгебраических чисел содержит корень n-й степени из единицы, всегда существует сколько угодно его расширений К_0, имеющих над K любую наперед заданную разрешимую группу n-го порядка.

Современная теория Галуа превратилась в сложную разветвленную математическую дисциплину, включающую в себя обширный материал о связях между свойствами уравнений, алгебраических чисел и групп.

3.7 Другие предпосылки возникновения теории групп

3.7.1 Достижения Ферма и Эйлера

У Эйлера (и, может быть, у Ферма до него) встречается операция «умножения по модулю р», которая (1758) использовалась, чтобы дать, по существу, теоретико-групповое доказательство малой теоремы Ферма.

Напомним, что целые числа называются конгруэнтными по модулю р, если они отличаются по целому кратному р, что b - обратная величина а относительно умножения mod p, если ab конгруэнтно 1 по модулю р, то есть, если ab + кр = 1 для некоторого целого к. В случае простого p каждый ненулевой элемент имеет обратный по модулю p. Т.е. здесь появляется группа.

Эйлер в своем доказательстве не определил группу, но нам легко это сделать. Элементы группы - ненулевые классы вычетов mod p:

mod p={...,-p+l,l,p+l,2p+l,...},

2 mod p= {...,-p+2,2,p+2,2p + 2,...},

mod p= {...,-p+3,3,p+3,2p + 3,...},

(р - 1) mod р ={..., -1,р - 1, 2р - 1, Зр - 1,...},

с произведением, определенным (a modp) (b mod p) = (а • 6) mod р, где а • b - обычное арифметическое произведение. Групповые свойства 1) и 2) следуют из обычной арифметики; 3) следует из евклидова алгоритма (если p - простое).

Итак, мы видим, что Эйлер уже неявно оперировал с группами.

Кроме того, в процессе доказательства Эйлер впервые применил методы исследования уравнений, которые позднее были развиты Лагранжем и стали основными в его работах, посвященных вопросу решения уравнений в радикалах, а затем вошли в качестве неотъемлемой составной части в теорию Галуа.

3.7.2 Гаусс и глубокое единство математики

Одним источником теории групп была теория композиции классов квадратичных форм Гаусса из работы «Арифметические исследования». В ней операция, аналогичная сложению (или умножению) чисел, была перенесена на объекты, весьма от чисел далекие. На примере классов форм одного дискриминанта Гаусс фактически исследовал основные свойства циклических и общих абелевых групп.

Построение Гауссом теории классов бинарных квадратичных форм (заданного дискриминанта) - наиболее абстрактные примеры групп, построенные в то время. Вводя далеко не тривиальную операцию - композицию форм, Гаусс доказывает, что исходя из композиции форм можно определить композицию классов, указывает, что при композиции главного класса с любым классом К получается снова класс К, показывает, что у каждого класса существует противоположный, короче говоря, проверяет все элементарные свойства групповой операции. Ассоциативность и коммутативность композиции классов он не проверяет, но они сразу следуют из указанной им ранее ассоциативности и коммутативности композиции самих форм.

Вообще, во всех других трудах Гаусса, развиты очень мощные алгебраические методы. В этих работах обнажились многие абстрактные понятия, образующие костяк новой алгебры: отношение и класс эквивалентности, фактормножество, сравнения, кольцо и поле классов вычетов, поле расширения, абелевы группы и т. д.

В частности теорию абелевых групп Гаусс изучал не только на примере квадратичных форм. Теория конечных абелевых групп встречается в вышеупомянутых «Арифметических исследованиях» еще в трех разных контекстах: при изучении аддитивной группы целых по модулю n; при рассмотрении мультипликативной группы вычетов по модулю n; при исследовании мультипликативной группы корней n-й степени из единицы

Гаусс глубоко ощущал внутреннее единство математики, он прекрасно осветил иногда очень неожиданные восемь доказательств квадратичного закона взаимности, четыре доказательства основной теоремы алгебры, относящихся к разным ветвям математики, показал связь между комплексными числами и геометрией, между вращениями сферы и томографическими преобразованиями плоскости комплексного переменного и т. д.

Точка зрения Гаусса на многие вопросы была очень современна. Он говорил: «Математик совершает полную абстракцию от природы объектов и смысла их отношений: ему надо только перечислить эти отношения и сравнить их между собой».

Но, как ни богаты труды Гаусса новыми структурами, они находятся там в скрытом виде, как бы замаскированными.

Как говорится в книге [Колмогорова], глубокая прозорливость Гаусса не опиралась, как в XX в., на явные определения общих структур; напротив, она послужила импульсом для их выявления.

3.7.3 Гаусс и теория алгебраических чисел

В 1828 и 1832 гг. появились две части замечательной работы Гаусса «Теория биквадратичных вычетов». В этой работе не только дается геометрическая интерпретация комплексных чисел (что делалось и до него), но и, что очень важно, на комплексные числа было перенесено понятие целого числа, которое уже более 2000 лет казалось неотъемлемым свойством целых рациональных чисел. Гаусс построил арифметику целых комплексных чисел, полностью аналогичную обычной, сформулировал с помощью новых чисел биквадратичный закон взаимности.

Этим перед арифметикой были открыты новые необъятные горизонты. Вскоре Эйзенштейн и Якоби сформулировали и доказали кубический закон взаимности.

Эта работа Гаусса, содержащая глубокий результат теории алгебраических чисел, интересна и с точки зрения теории групп: в ней построен первый нетривиальный пример бесконечной абелевой группы и изучена ее структура.

3.7.4 Труды Коши

В 1815 г. О.-Л. Коши опубликовал в «Журнале Политехнической школы» два мемуара, в которых исследовал задачу, возникшую в теории уравнений : найти число значений, которые может принимать некоторая функция при всевозможных перестановках входящих в нее величин. Формулировка этой задачи и вошла в название первого мемуара. В нем Коши обрисовал контуры системы понятий, в которой развивается теория подстановок, а затем и теория групп.

Если некоторая функция зависит от n переменных, то число М различных значений, которые она может принимать при перестановке переменных, является делителем n! , а число подстановок, оставляющих эту функцию инвариантной, равно n!/ М и они образуют группу.

Этот результат уже был доказан Лагранжем, но Коши пошел значительно дальше. Он изобрел двух строчное обозначение для подстановок: образ каждого символа располагался во второй строке под этим символом. Коши изучил то, что сейчас называется циклической группой, порожденной данной подстановкой S порядка n.

Однако, как отмечет в своей книге Даальмедико, Коши еще не пользовался для обозначения подстановки одним единственным символом, как это сделал Галуа.

Впоследствии, эти мемуары Коши были прочитаны Абелем и Галуа в 1826-1832 гг., но сам Коши потерял интерес к этим вопросам почти на тридцать лет. Лишь в 1844-1846 гг., за несколько месяцев до публикации Лиувиллем наследия Галуа (см. выше), Коши вернулся к этой теме и опубликовал большой мемуар «О размещениях, которые можно составить из данных букв», а также многочисленные заметки в «Отчетах» Академии.

Эти новые работы Коши вместе составили систематическое исследование корректно определенной структуры - группы подстановок n букв; эта группа имеет порядок n! и называется ныне симметрической группой Sn. Здесь впервые изучение подстановок выходит за рамки теории уравнений. Группы подстановок - Коши называл их «системами сопряженных подстановок» - стали самостоятельным объектом

Коши в этой своей работе основал настоящее исчисление подстановок, используя при этом все направления и возможности разработанных им операторных методов.

Хотя, как отмечается в литературных источниках, это исчисление подстановок Коши не имело определенной цели, и понадобился толчок со стороны теории уравнений, чтобы проявилось все богатство теории подстановок. Этот толчок сделал Галуа.

Тем самым, Коши бесспорно внес вклад в обновление алгебры, наметившееся во второй половине XIX в.: исследование алгебраических структур как самостоятельных объектов и осознание роли операций. Хотя понятие группы он все таки четко не осознавал и идеи Галуа, когда тот представил работы на соискание награды в Академию наук, видимо не понял и не посчитал её достойной внимания.

Заключение

Итак, мы рассмотрели основные предпосылки возникновения теории групп. Многие выдающиеся ученые, такие как Лагранж, Гаусс, Коши и др., в своих работах изучали свойства групп. Но это проходило на скрытом уровне. Они действовали сообразно своей блестящей интуиции, но до конца еще не осознавали понятие группы.

Группы в работах этих ученых неявно возникали в связи с рассмотрением разных задач. Тем не менее, главной проблемой, стимулирующей появление понятия группы, был вопрос о разрешимости уравнений в радикалах. И именно исследование этого вопроса привело к наиболее радикальным последствиям.

Так что, по праву поворотным пунктом в возникновении теории групп можно опубликование в 1846 г. основных работ Галуа. Особое значение их для теории групп состоит в том, что впервые было продемонстрировано, что решение старинного, важного вопроса может быть сведено к исследованию ново го объекта - групп. Впервые группы выступают не как вспомогательный инструмент рассуждения, а как основной объект исследования.

Вскоре после работ Галуа началось уже систематическое развитие теории групп.

4. Возникновение и развитие теории групп

В первой половине XIX в. факты теории групп играли еще вспомогательную роль, главным образом в теории алгебраических уравнений. Складывающаяся теория групп была еще преимущественно теорией конечных групп - групп подстановок. К середине века выяснилось, что понятие группы имеет более широкое применение.

Артур Кэли и Огюстен Луи Коши стали одними из первых математиков, оценивших важность теории групп. Эти учёные также доказали некоторые важные теоремы из теории групп. Кэли внес огромный вклад в развитие абстрактной теории конечных групп. Им было выяснено, что наиболее важные свойства группы зависят не от характера элементов подстановки, а от групповой операции. Это произошло в 50-х годах XIX века. Тогда работы Кэли не были замечены мировым сообществом. Лишь спустя некоторое время, они обрели известность и даже использовались как учебники.

Процесс перехода к абстрактной теории групп ускорился с 1870 года. Теория групп была популяризована Серретом, который посвятил теории групп секцию из своей книги по алгебре. Он проделал большую работу и включил в свои лекции по алгебре в Сорбонне большие части теории Галуа.

Дальнейшие крупные открытия в теории групп связаны с именем воспитанника и профессора Политехнической школы, а также Коллеж де Франс, Камилла Жордана (1838-1922). В 1865 г. появляется первая работа Жордана по теории Галуа «Комментарии к мемуару Галуа» (Commentaires sur le memoire de Galois.- С. г. Acad. sci. Paris), в 1869 г. ее продолжение «Комментарии к Галуа» (Commentaires sur Galois.- Math. Ann.), Затем появились работы Жордана - «Действия над подстановками» («Traité des Substitutions et des equations algebriques»,) Эта монография стала классикой. В ней были подытожены результаты теории конечных групп в применении к теории чисел, теории функций и алгебраической геометрии. Однако, хотелось бы отметить, что у Жордана еще не было определения группы, такого, каким мы его знаем сейчас. Оно появилось не сразу. Современное определение понятия «группа» было дано только в 1882 г. Вальтером фон Дюком.

Немалую роль в популяризации теории групп сыграл Евгений Нетто (1882 г.), чей труд был в 1892 г. переведён на английский язык Коулом. Большой вклад в развитие теории групп внесли также многие другие математики XIX века: Бертран, Эрмит, Фробениус, Кронекер и Матьё.

Стоит также сказать, что до определенного момента большинство математиков рассматривало в основном конечные дискретные группы. Однако к концу XIX века на сцене появились бесконечные группы, а также непрерывные. В частности, в 1884 г. Софус Ли положил начало изучению групп преобразований . Эти группы сейчас называют группами Ли. За его трудами последовали работы Киллинга, Штуди, Шура, Маурера и Эли Картана. Теория дискретных бесконечных групп была разработана Клейном, Ли, Пуанкаре и Пикаром в связи с изучением модулярных форм и других объектов.

К концу XIX в. теория конечных групп оформилась и достигла высокого уровня. Появился ряд сводных трактатов, содержащих ее систематическую разработку. В это же время появились первые приложения теории групп. Здесь можно, например, упомянуть имена таких ученых, как: Фёдоров, Шенфлис , Клейн.

В начале XX века ощутимый вклад в теорию групп внесли и многие другие математики, такие как Артин, Эмми Нётер, Людвиг Силов и другие.

4.1 Вклад Артура Кэли

Первое определение и первые исследования абстрактных групп были опубликованы крупным английским математиком А. Кэли в 1854 г.

Он был первым, кто понял, что понятие группы независимо от объектов, к которым оно применяется. Он изложил свою концепцию в мемуаре, опубликованном в 1854 г.: «О группах, зависящих от символического уравнения 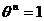». В этом мемуаре Кэли привел абстрактное определение группы в духе символической алгебры Кембриджской школы: «Множество символов 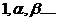 различных между собой и таких, что произведение двух из них (в произвольном порядке) либо произведение одного из них на себя принадлежит этому множеству, называется группой».

Таким образом, Кэли строго придерживался концепции конечной группы. В этом случае нет необходимости постулировать существование обратного для каждого элемента, поскольку среди всех степеней одного элемента 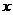 найдется по крайней мере одна, скажем 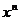 равная 1, и тогда из 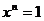следует, что .

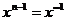Для фиксированного целого числа n Кэли рассматривал возможные таблицы умножения для групп порядка n. Кэли не делал абсолютно никаких предположений относительно символов и описывал структуру конечных групп с помощью таблиц умножения и соотношений между образующими.

Таким образом, его новаторство заключается в том, что до тех пор понятие группы, как его сформулировал Галуа, относилось к теории подстановок, и элементами или символами всегда были отображения (на современном языке - морфизмы), но элементы группы сами никогда не рассматривались как величины - несомненно, потому, что если считать их величинами, то надо было бы определять две операции и рассматривать то, что мы теперь называем структурой поля. Выделять лишь один, закон композиции было неестественно.

Пример таблицы Кэли:

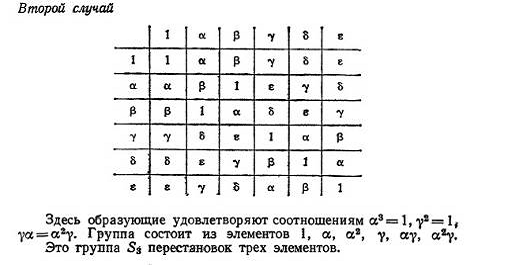
Также Кэли указал примеры групп в самых разных областях, рассмотрев с этой точки зрения теорию матриц (тогда еще совсем не формализованную), тело кватернионов, композицию квадратичных форм, а также множество корней n-й степени из единицы.

Мемуар Кэли добрых двадцать лет оставался в стороне от внимания математиков, и даже сам Кэли при изложении теории матриц не упоминал ни аддитивную, ни мультипликативную группы обратимых матриц.

4.2 Исследования К. Жордана

Рубежом в продолжающемся развитии теории групп было появление в 1870 г. капитального «Трактата о подстановках и алгебраических уравнениях» К. Жордана. Это было и первое систематическое полное изложение теории Галуа, и подробное изложение достигнутых к этому времени результатов в теории групп, включая и значительные достижения в этих областях самого Жордана. В этой книге была также введена жорданова нормальная форма матриц линейных преобразований. Появление труда Жордана стало событием во всей математике.

Камилл Жордан сделался непререкаемым авторитетом в области теории групп и теории Галуа. Можно сказать, что он предпринял научное воссоздание трудов Эвариста Галуа, дополнил его доказательства, использовал и развил все его краткие указания. Труд Жордана «Трактат о подстановках и алгебраических уравнениях» остается до наших дней непревзойденным во многих отношениях.

Работая над теорией Галуа, Жордан отказался от узких рамок теории групп перестановок и рассматривал более абстрактное понятие конечной группы. В 1868 г. он провел классификацию всех групп движений трехмерного евклидова пространства. Также он занимался изучением линейных представлений группы, действующей на векторном пространстве, т. е. поиском гомоморфизмов этой группы в группу обратимых линейных преобразований векторного пространства на себя (очевидно, тождественную группе обратимых квадратных матриц с вещественными или комплексными элементами, которая обозначается GL(n, R) или GL(n, С)).

Жордан провел систематическое изучение классических групп и их конечных подгрупп, затем он попытался определить все разрешимые конечные группы, чтобы найти все уравнения данной степени, разрешимые в радикалах.

С одной стороны, Жордан ввел основные современные понятия теории групп (факторгруппа, гомоморфизм, последовательность нормальных подгрупп некоторой группы, которую мы называем теперь последовательностью Жордана- Гёльдера, и т. д.). С другой стороны, при исследовании линейной группы он пришел к очень важным результатам о приведении матриц (так называемые жордановы формы).

Еще стоит упомянуть, что в своих сочинениях Жордан впервые рассматривает матричные группы с элементами из конечного поля, ставшие в XX в. предметом обстоятельных исследований.

При изложении теории Галуа Жордан использует уже современный способ сопоставления уравнению не некоторого множества перестановок корней, а группы подстановок, и критерий разрешимости уравнения в радикалах у него выражается в разрешимости его группы Галуа.

Ранее упоминавшийся фундаментальный трактат Жордана стал на некоторое время учебником как по теории групп, так и по теории Галуа. Выход его знаменует окончание периода рождения теории групп.

4.3 Общая характеристика дальнейшего развития теории групп

Расцвет теории конечных групп относится к концу XIX и первым десятилетиям XX столетия. В это время были получены основные результаты этой теории, намечены основные направления, созданы основные методы; вообще, теория конечных групп трудами своих крупнейших деятелей (Фробениус, Гельдер, Бернсайд, Шур, Миллер) приобрела в это время то лицо, все существенные черты которого она донесла до наших дней ).

В дальнейшем стало ясным, однако, что конечность групп является слишком сильным и не всегда естественным ограничением. Особенно важно, что это ограничение очень скоро привело к конфликту с потребностями соседних отделов математики: различные части геометрии, теория автоморфных функций, топология все чаще и чаще стали встречаться с алгебраическими образованиями, подобными группам, но бесконечными, и стали предъявлять к теории групп требования, удовлетворять которые теория конечных групп была не в состоянии. Вместе с тем с точки зрения самой алгебры, частью которой теория групп является, вряд ли можно было считать нормальным положение, при котором оставались за пределами теории такие простейшие и важнейшие группы, как, например, аддитивная группа целых чисел. Конечная группа должна была поэтому стать частью общего понятия группы, а теория конечных групп - главой в общей теории «бесконечных» (т. е. не обязательно конечных) групп.

Впервые в мировой литературе изложение основ теории групп без предположения, что рассматриваемые группы конечны, было cделано в книге О. Ю. Шмидта «Абстрактная теория групп» (Киев, 1916).Широкое развитие общей теории групп началось, однако, несколько позже и было связано с той радикальной перестройкой и тем переходом на теоретико-множественные основы, которые совершила алгебра в 20-х годах нашего века (Э. Нётер). В частности, именно отсюда пришли в теорию групп такие новые для нее понятия, как системы операторов и условия обрыва цепочек.

В дальнейшем работа в общей теории групп становилась все более бурной и разносторонней и к настоящему времени эта часть математики превратилась в широкую и богатую содержанием науку, занимающую одно из первых мест в современной алгебре. Понятно, что это развитие общей теории групп не могло игнорировать успехи, уже достигнутые в теории конечных групп. Наоборот, многое при этом развитии возникало из соответствующих частей теории конечных групп, причем руководящим было стремление заменить конечность группы теми естественными ограничениями, при которых данная теорема или данная теория еще остаются справедливыми и за пределами которых они теряют силу. Очень часто, впрочем, вопрос, простой и окончательно решенный в случае конечных групп, превращался в широко развитую и далекую от завершения теорию; такова, например, теория абелевых групп, одна из важнейших частей современной теории групп. Вместе с тем возникли и некоторые новые отделы, существенным образом связанные с рассмотрением бесконечных групп,- теория свободных групп, теория свободных произведений. Наконец, в некоторых случаях - прежде всего в вопросе о задании группы определяющими соотношениями - впервые удалось достигнуть четкости и строгости, недоступных теории групп на предшествующем этапе ее развития.

4.4 Теория представлений групп

Для начала дадим наиболее простое определение представления группы:

Представление группы (точнее, линейное представление группы) - гомоморфизм заданной группы в группу невырожденных линейных преобразований векторного пространства.

Раздел математики, который изучает представления групп, называется теорией представлений (групп). Представление можно понимать как запись группы с помощью матриц или преобразований линейного пространства. Смысл использования представлений групп заключается в том, что задачи из теории групп сводятся к более наглядным задачам из линейной алгебры. Этим объясняется большая роль теории представлений в различных вопросах алгебры и других разделов математики. Например, одномерные представления симметрической группы Sn и знакопеременной группы An играют большую роль при доказательстве невозможности разрешения в радикалах алгебраического уравнения степени выше 4.

В квантовой механике важную роль играют бесконечномерные (в которых векторное пространство - гильбертово) представления групп (в первую очередь, группы Лоренца).

Более формализовано определение представления группы выглядит так:

Пусть 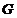 - заданная группа и 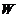- векторное пространство. Тогда представление группы 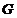 - это отображение, которое каждому 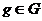ставит в соответствие невырожденное линейное преобразование 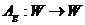, причем выполняются следующие свойства

.

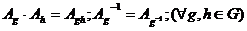Примеры представлений групп:

) Унитарная группа U(1) может быть представлена как группа вращений двумерного пространства вокруг центра.

) Представление симметрической группы 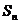 может быть получено следующим образом. Выберем в векторном пространстве 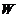 размерности  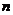базис 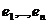. Для каждой перестановки  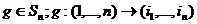определим линейное преобразование  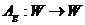переводящее базисный вектор  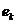в базисный вектор 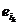, где 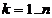. Таким образом получается n-мерное представление группы .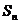

В более широком смысле, под представлением группы может пониматься гомоморфизм группы в группу всех обратимых преобразований некоторого множества X. Например: Проективное представление группы - гомоморфизм группы в группу проективных преобразований проективного пространства.

Теория представлений групп восходит к работам Эйлера, А.М. Лежандра, Гаусса, в которых появилось понятие характера коммутативной группы. В конце 18 века и в начале 19 века работами Г. Фробениуса, И. Шура (I. Schur), У. Бернсайда, Ф.Э. Молина, Р. Брауэра были заложены основы теории (конечномерных) линейных представлений (и теории характеров) конечных групп, в которой вместе с «абстрактной» группой G рассматриваются все ее гомоморфизмы в «конкретные» линейные группы GLn(K) над полями K (или, что тоже самое, модули над групповой алгеброй KG группы G над полем K). На дальнейшее развитие этого направления теории групп оказала сильное влияние монография Г. Вейля (H.Weyl, 1939), подведя итог этого периода.

Дж. фон Нейман (J. von Neumann), Г.Вейль, Э.Картан (E.J.Cartan) заложили основы теории представлений групп Ли и топологических групп. Теория двойственности Л.С.Понтрягина для характеров локально компактных абелевых групп явилась краеугольным камнем в основании топологической алгебры.

4.5 Непрерывные, бесконечные группы, группы Ли

В работах Жордана еще не появилось общее понятие группы в том виде, в котором оно существует сейчас. Рассматривая группы, он полагал их конечными. О группах преобразований и непрерывных группах речи еще не было. Хотя идея преобразования, примененного ко всему пространству, а не только к отдельным пространственным фигурам, была уже знакома геометрам благодаря развитию проективной геометрии в работах Понселе. Но связь между этой идеей и идеей «перестановки» конечного множества еще не усматривалась.

В 1870 г. Софус Ли (1842-1899) и Феликс Клейн вместе были в Париже и, ознакомившись там с работами Жордана и Галуа, начали размышлять над группами преобразований. Впервые в рамках одной концепции были поставлены рядом понятия конечного множества и некоего «пространства», наподобие пространства евклидовой геометрии. Итогом этих размышлений стала предложенная в 1872 г. «Эрлангенская программа» Клейна, в которой центральное место при изучении геометрий отводится понятию группы. Был дан толчок к изучению бесконечных групп, одним из главных творцов этой теории стал Софус Ли.

Фактически в работах Ф.Клейна с С.Ли (S.Lie) было начато исследование бесконечных дискретных и топологических групп. Трехтомный трактат С.Ли и Ф.Энгеля (F.Engel), 1883-1893, зафиксировал рождение новой области в теории групп - теории групп Ли.

Зачем же Софусу Ли вообще понадобилось рассматривать группы преобразований?

Как мы помним, первоначально конечные группы были введены Галуа в связи с вопросом о симметрии алгебраического уравнения относительно подстановок его корней. Софус Ли имел своей целью построение аналогичной теории для дифференциальных уравнений с непрерывными группами преобразований. В результате возникла специальная теория определенного класса непрерывных групп, называемых теперь группами Ли.

Дальнейшие исследования Вейля и Картана, посвященные классификации геометрических объектов относительно некоторых групп преобразований, завершили классический этап развития теории групп Ли.

В последующих исследованиях, уделялось особое внимание топологии группового пространства (Понтрягин, Брауэр, Вейль, Шевалле, Мальцев), что позволило дать законченную классификацию групп Ли и их конечномерных представлений.

С начала 50-х годов XX века в работах Гельфанда и Наймарка происходит интенсивное развитие теории бесконечномерных представлений групп Ли и некоторых других локально компактных групп. Эти вопросы в свою очередь связаны с современными вопросами симметрии квантовой теории поля.

Теория групп Ли в современном понимании в значительной степени связана с вопросом линейных представлений. Понятия представления или «обобщенной экспоненты» позволяет проследить глубокую связь, кажущихся на первый взгляд далеких друг от друга вопросов, таких как тензорный анализ и гармонический. Алгебраические основы этой теории были заложены Фробениусом на рубеже XX века. Уже тогда было ясно, что эта теория имеет тесную связь с теорией ассоциативных алгебр, которая постепенно занимает одно из главнейших мест в современной математике. Современная теория представлений может быть интерпретирована как абстрактный гармонический анализ. Если ограничиться компактными группами Ли, то получается замечательное обобщение классической теории рядов Фурье, где «обобщенные экспоненты» специального вида играют роль элементарных гармоник.

Группы Ли на данный момент имеют широкое применение в физике. Однако, несмотря на то, что с момента создания Эйнштейном теории относительности принципиальная роль теории бесконечных групп в теоретической физике стала очевидной, многие физики долгое время игнорировали использование групп Ли, ограничиваясь рассмотрением некоторых конечных групп (кристаллография). В настоящее время положение дел резко изменилось благодаря значительным успехам теоретико-группового подхода в классификации элементарных частиц.

4.6 Комбинаторная теория групп

В этом разделе будет рассказано о разделе теории групп, который развивался параллельно обычной теории групп.

В начале XX века было в некотором смысле разделение направлений исследований и развивалось два направления теории групп, ведущих свое начало от несколько разных определений самого понятия группы. Одно из этих определений - «обычное», построенное на аксиомах. Мы рассматривали его ранее. Во втором же случае, группа определяется порождающими элементами и соотношениями между ними. (С таким мы встречались у Артура Кэли. См. пример выше)

Таким образом, комбинаторную теорию групп можно охарактеризовать как теорию групп, которые описываются порождающими и определяющими соотношениями или, как теперь часто говорят, своим заданием (presentation). Конечно, это не полное определение данной области математики, но все же основную идею оно отражает.

Описание группы посредством ее задания, т. е. системы порождающих и определяющих соотношений, является на самом деле специфическим способом абстрактного описания группы.

Истоки комбинаторной теории групп, изучающей задание группы образующими и определяющими соотношениями, можно найти в работах: Ф. Клейна; А. Пуанкаре (H. Poincare) (предложившего в 1895 понятие фундаментальной группы); В. фон Дика (W. von Dyck) (доказавшего в 1882 существование свободной группы); Х. Титце (H. Tietze) (в 1908 рассмотрел вопрос об изоморфизме групп при различных заданиях); М. Дэна (M. Dehn) (рассмотревшего в 1910 проблемы равенства, сопряженности и изоморфизма). Р. Ремак (R. Remak, 1911) и О.Ю. Шмидт (1913), обобщив теорему об однозначности разложения группы в прямое произведение неразложимых сомножителей с конечных абелевых групп на класс всех конечных групп, заложили основы теории прямых разложений групп. Нильсен (J. Nielsen, 1921) и Шрайер (O. Schreier, 1927) доказали, что подгруппа свободной группы свободна. Ван Кампен (E.R. van Kampen, 1933) предложил геометрическую интерпретацию вывода следствий из определяющих соотношений групп. Теорема А.Г.Куроша (1934) дает описание строения подгрупп свободного произведения групп. И.А. Грушко (1940) и Б. Нейман (B.H.Neumann, 1943) развили метод Нильсена для свободных произведений и описали системы порождающих для таких групп.

Начало этой теории обычно связывается с работой В. Дика 1882 г., в которой впервые были введены понятия порождающих и определяющих соотношений.

Рассмотрим простой пример группы, заданной порождающими соотношениями: см [3]

Будем рассматривать правильные многогранники и их группы симметрий. Известно, что эти группы симметрий обычно являются изоморфными некоторым подгруппам группы подстановок. Т.е. можно дать аксиоматическое определение такой группы. Но можно дать определение на основе порождающих соотношений.

Например, Гамильтон (1856) показал, что группа икосаэдра может порождаться тремя элементами: 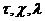 в зависимости от отношений

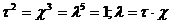
Это означает, что каждый элемент группы икосаэдра является произведением 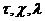 и любое соотношение между  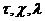следует указанных соотношений.

Дик в выше упоминавшейся работе 1882 дал похожие представления групп куба и тетраэдра.

Таким образом, мы увидели, что группы правильных многогранников были первыми, которые определили на основе порождающих элементов и соотношений. Однако, с конечными группами, такими как эти, занимаешься, главным образом, простотой и элегантностью представления; вопрос о существовании не возникает. Что касается любой конечной группы G, можно тривиально получить конечное множество порождающих элементов (а именно, всех элементов g1,..,gn группы G). и определяющих соотношений (а именно, всех уравнений gi*gj= gk, выполняющихся среди порождающих элементов). И конечно, тот же аргумент дает бесконечное множество порождающих элементов и определяющих соотношений для бесконечной группы, но это также неинтересно. Реальная проблема заключается в том, чтобы найти конечные множества порождающих элементов и определяющих соотношений для бесконечных групп, где возможно.

Впервые эта задача была решена для групп симметрии некоторых правильных мозаик студентом Клейна, Диком, и такие примеры были основой первого систематического изучения порождающих элементов и соотношений.

Обобщая идеи Дика, Пуанкаре (1882) показал, что группы симметрии всех правильных мозаик, будь то сферы, евклидовой плоскости или гиперболической плоскости, молено представить конечным числом порождающих элементов и соотношений. Эти результаты также были важны для топологии.

Впоследствии более простой подход к комбинаторному определению группы можно встретить у Дена и Магнуса (1930). Группа G у них определяется множеством {a1,..,an,…} порождающих элементов и множеством {W1=W1’; W2=W2’ ;…} определяющих соотношений. Каждый порождающий элемент ai называется буквой; ai имеет обратный элемент ai-1 и произвольные конечные последовательности («произведения») букв и обратных букв называются словами.

Слова W’, W называются эквивалентными, если W = W’ - след- ствие определяющих соотношений, то есть, если W можно обратить в W’ последовательностью замен подслов Wi на Wi’ (или наоборот) и сокращением (или вставкой) подслов ai* ai-1, ai-1* ai. Элементы G - классы эквивалентности: [W] = {W’ :W’ эквивалентно W},

Произведение элементов [U], [V] определяется :

[U][V] = [UV]

где UV обозначает результат соединения в цепь слов U, V.

4.7 Теория групп в СССР (с 1916 года по 60-е годы)

В предыдущих разделах мы рассмотрели в общем, некоторые направления развития теории групп и деятельность математиков, положивших начало фундаментальному изучению теории групп. Теперь мы поговорим о том, как происходило развитие этой области в России (точнее в СССР), какие были достигнуты результаты.

Исследования по теории групп начались в России еще до революции работами О.Шмидта. Тогда же была написана его книга «Абстрактная теория групп» (вышла в 1916 г., 2-е издание в 1933 г.). Исследования О.Ю.Шмидта продолжались и после революции; одной из самых значительных была его работа о прямых произведениях групп.

В конце 20-х годов начались исследования коллектива учеников О.Ю.Шмидта по теории конечных групп.

В 30-х годах и в первой половине 40-х годов исключительно большое развитие получили исследования советских алгебраистов по общей теории {бесконечных) групп. Из многочисленных работ в этой области наибольшее влияние на ее дальнейшее развитие оказали работы А. Г. Куроша по свободным и прямым произведениям групп, работы С. Н. Черникова по обобщенным разрешимым и нильпотентным группам и работы Л. Я. Куликова по примарным абелевым группам. В книге А. Г. Куроша «Теория групп» (вышла в 1944 г., 2-е издание в 1953 г.; вышли также немецкий перевод первого издания и венгерский и английский переводы второго издания) приведены многие из результатов, полученных советскими теоретико-групповиками за рассматриваемый период.

В топологической алгебре, развитие которой началось в СССР по инициативе А. Н. Колмогорова, был выполнен ряд исследований, среди которых исключительно важное место занимают работы Л. С. IIоитрягина по топологическим группам, в частности его теория характеров топологических абелевых групп. Также стоит отметить работы А.А. Марковао топологизации абстрактных групп. В книге Л. С. Понтрягина «Непрерывные группы» A938 г., 2-е издание в 1954 г.; вышел также английский перевод первого издания) теория топологических групп была впервые систематически изложена.

Еще в 20-х годах начались работы А. К. Сушкевича но теории полугрупп и квазигрупп, систематизированные в его книге «Теория обобщенных групп» A937 г.). К этой же области относились исследования А. И. Мальцева о вложении полугрупп в группы и ряд работ других авторов. В общем, эти работы оставались, однако, довольно разрозненными.

Наконец, к середине 30-х годов относится начало работы советских алгебраистов в теории структур. Исследования носили здесь преимущественно характер анализа теоретико-структурных основ тех или иных из крупных теорем теории групп и теории колец.

Следует особо отметить возникновение ряда новых алгебраических коллективов в различных городах СССР наряду с коллективами, уже существовавшими ранее. Продолжал развиваться руководимый А. Г. Курош е м большой коллектив московских специалистов но общей алгебре, включающий в круг своих интересов почти все разделы этой науки. В Иванове возник коллектив алгебраистов, учеников А. И. Мальцсва, со столь же широким кругом интересов. В Свердловске под руководством С. Н. Чериикова, а затем также и П. Г. Коиторович а сформировалась большая теоретико-групповая школа, развивавшаяся помимо Свердловска также в Перми. Также стоит отметить, коллектив учеников С. А. Чунихина в Томске, работающий в теории групи, преимущественно конечных, и коллектив ленинградских специалистов по теории полугрупп, учеников Е. С. Ляпина.

Теперь перейдем к обзору отдельных направлений.

Для начала хотелось бы подчеркнуть, что в первой половине XX века теория групп продолжала оставаться одним из основных разделов советской общей алгебры. Особенно много было сделано в теории обобщенных: разрешимых и нильпотентных групп. Здесь в первую очередь нужно названы работы А. II. Мальцева о разрешимых и локально нильпотентных группах, работы С. II. Черник о в а о полных нильпотентных группах и работы Б. И. Плоткина о радикальных группах. Бурное развитие этой ветви теории групп было подготовлено, в частности, обзорной статьей А. Г. Курошаи СИ. Черникова «Разрешимые и нильпотентные группы».

Существенные вклады были внесены в эти годы и в другие разделы теории групп. Так, вновь заметно оживилась теория конечных групп благодаря циклу исследований С. А. Чунихин а о силовских свойствах конечных групп. Отметим, с другой стороны, работы Д. А. Супруненко но группам подстановок и линейным группам.

Хотелось бы отметить, что советские алгебраисты занимались не только теорией групп. В теории колец и алгебр развитие в СССР в эти годы шло также бурно, и были достигнуты столь значительные результаты, что уровень этой ветви советской алгебры вполне сравним с тогдашним уровнем теории групп. Напоследок еще хотелось бы сказать, что развитие советской общей алгебры шло в самом тесном контакте с развитием алгебраических исследований в зарубежных странах.

Переплетения и взаимные влияния и связи между исследованиями советских и зарубежных алгебраистов были столь многочисленными, что советскую общую алгебру должно рассматривать как весьма значительную составную часть мировой алгебраической науки.

4.8 «Коуровская тетрадь»

В математике и в частности в теории групп всегда существовали и существуют открытые вопросы. Наиболее важные из них можно найти в так называемой «Коуровской тетради». «Коуровская тетрадь» представляет собой всемирно известный сборник нескольких тысяч нерешенных задач в области теории групп. Она издается с 1965 года с периодичностью в 2-4 года и выпускается на русском и английском языках.

Идея издания сборника нерешенных проблем теории групп была высказанаМихаилом Ивановичем Каргаполовым (1928-1976) на Дне проблем Первого Всесоюзного симпозиума по теории групп в Коуровке под Свердловском 16 февраля 1965 г. Поэтому этот сборник и получил название «Коуровская тетрадь». С техпор каждые 2-4 года появляется очередное издание, дополненное новыми вопросами и краткими комментариями к решенным задачам из предыдущих изданий.

«Коуровская тетрадь» уже более 40 лет служит своеобразным средством общения для специалистов по теории групп и смежным областям математики. Возможно, самым ярким примером успеха «Коуровской тетради» является тот факт,что около 3/4 всех задач из ее первого издания к настоящему времени уже решены. Приобретя международное признание, «Коуровская тетрадь» насчитывает свыше 300 авторов задач из многих стран мира.

Заключение

Итак, мы увидели, что теория групп прошла длинный путь прежде, чем выйти на современный уровень. Изобретение Эвариста Галуа было всего лишь первым шагом навстречу коренной перестройке алгебры и вообще математики. Потребовалось время, для того чтобы осознать оригинальные идеи Галуа, а затем вывести их на должный уровень абстракции. Не сразу математики осознали ,что при изучении математических объектов на самом деле изучаются свойства заданных в них алгебраических операций и что эти объекты следует определять аксиоматически, указывая исходные свойства операций и игнорируя природу элементов, над которыми операции производятся.

Также потребовалось немало времени, чтобы перейти от рассмотрения конечных групп к бесконечным группам.

Результаты усилий нескольких поколений математиков принесли свои плоды. Теория групп раскрылась в полной своей мере и изменила своим появлением алгебру. Она существенно повлияла на другие сферы математики благодаря, а также дала начало некоторым новым областям.

5. Влияние теории групп на другие области математики и научные сферы

Преобразование алгебры повлекло за собой преобразование всей математики. Исследование фундаментальных структур, их подструктур (например, в теории групп - конечных групп, коммутативных групп и т. д.), изучение их основных комбинаций (таких, как структуры алгебраической топологии, в которых алгебраические комбинации обладают дополнительными свойствами непрерывности, дифференцируемости и т. д») нарушили архитектуру математики, древняя схема которой (алгебра, арифметика, геометрия, анализ) устарела. Взаимопроникновение математических дисциплин стало в наши дни глубоким и всеобщим.

В первой половине XIX в. факты теории групп играли еще вспомогательную роль, главным образом в теории алгебраических уравнений. К концу же XIX в. теория конечных групп оформилась и достигла высокого уровня. Появился ряд трактатов, содержащих ее систематическую разработку. В это же время появились первые приложения теории групп.

Сейчас группы повсеместно используются в математике и естественных науках, часто для обнаружения внутренней симметрии объектов (группы автоморфизмов). Внутренняя симметрия обычно связана с инвариантными свойствами; множество преобразований, которые сохраняют это свойство, вместе с операцией композиции, образуют группу, называемую группой симметрии.

Например в оригинальной теории Галуа, которая и дала начало понятию группы, группы используются для описания симметрии уравнений, корнями которых являются корни некоторого полиномиального уравнения. Из-за важной роли, которую они играют в этой теории, получили своё название разрешимые группы.

В алгебраической топологии группы используются для описания инвариантов топологических пространств . Под инвариантами здесь имеются в виду свойства пространства, не меняющиеся при каком-то его деформировании. Примеры такого использования групп - фундаментальные группы, группы гомологий и когомологий.

Группы Ли применяются при изучении дифференциальных уравнений и многообразий; они сочетают в себе теорию групп и математический анализ. Область анализа, связанная с этими группами, называется гармоническим анализом.

В комбинаторике понятия группы подстановок и действия группы используются для упрощения подсчёта числа элементов в множестве; в частности, часто используется лемма Бёрнсайда.

Понимание теории групп также очень важно для физики и других естественных наук. В химии группы используются для классификации кристаллических решёток и симметрий молекул. В физике группы используются для описания симметрий, которым подчиняются физические законы. Особенно важны в физике представления групп, в частности, групп Ли, так как они часто указывают путь к «возможным» физическим теориям.

Рассмотрим теперь более подробно, как применяются группы в различных областях науки.

5.1 Алгебраическая топология и группы

В алгебраической топологии группы используются для описания инвариантов топологических пространств. Под инвариантами здесь имеются в виду свойства пространства, не меняющиеся при каком-то его деформировании. Примеры такого использования групп - фундаментальные группы, группы гомологий и когомологий.

В алгебраической топологии и связанных с нею областях математики фундаментальной группой называется алгебраический объект, который сопоставляется топологическому пространству и измеряет, грубо говоря, количество дырок в нем. Наличие дырки определяется невозможностью непрерывно стянуть некоторую замкнутую петлю в точку. Фундаментальная группа является первой из гомотопических групп.

Рассмотрим пример применения групп к топологии:

Допустим, что каждому топологическому пространству X сопоставлена группа F(X). Пусть кроме того каждому непрерывному отображению f:X à Y отображения одного пространства в другое сопоставлен гомоморфизм f*: F(X) à F(Y) соответствующих групп. Такое сопоставление пространствам - групп, отображениям - гомоморфизмов называется ковариантным функтором из категории топологических пространств в категорию групп, если выполняются следующие два условия: 1) Если f тождество, то f* также тождество. 2) Если суперпозиция fg определена, то (fg)* и f*g* изоморфны.

Справедлива следующая теорема: Если пространства X и Y гомеоморфные, то F(X) и F(Y) изоморфны.

На это теореме основан способ применения групп (функторов) в топологии. Допустим нам надо выяснить различны ли пространства X и Y. Возьмем какой-нибудь функтор F и сравним группы F(X) и F(Y). Если F(X) и F(Y) различны, то пространства X и Y тоже различны. Если F(X) и F(Y) изоморфны, то про пространства X и Y ничего сказать нельзя.

Таким образом, знание некоторого функтора из категории топологических пространств в категорию групп позволяет в некоторых случаях доказать различность пространств.

5.2 Теория многомерных пространств, теории алгебраических интегралов линейных дифференциальных уравнений и группы

Группы нашли своё применение в теории многомерных пространств. В частности, дискретные конечные группы (к которым принадлежат, например, Федоровские группы) получили распространение в теории многомерных пространств в связи с теорией правильных многогранников в них. В основе этих рассмотрений лежит теорема Жордана: число конечных линейных групп заданного измерения существенно конечно.

Та же теорема получила приложение на рубеже XIX-XX вв. в теории алгебраических интегралов линейных дифференциальных уравнений, римановых поверхностей и др. Например, Жордан указал на связь между линейными дифференциальными уравнениями, имеющими алгебраические интегралы, и конечными группами. Оказалось, что необходимым и достаточным условием существования алгебраических интегралов у линейного дифференциального уравнения фуксова типа является условие конечности группы линейных преобразований, претерпеваемых его интегралами при обходе независимой переменной вокруг каждой из критических точек.

5.3 Теория групп и автоморфные функции

Имеется связь между теорией групп и автоморфными функциями.

Классическая теория автоморфных функций, возникшая в трудах Клейна и Пуанкаре, была связана с изучением аналитических функций в единичном круге, инвариантных относительно дискретной группы преобразований. Поскольку сам единичный круг можно рассматривать, как плоскость Лобачевского в интерпретации Пуанкаре, то можно сказать, что классическая теория автоморфных функций связана с изучением аналитических функций на плоскости Лобачевского, инвариантных относительно некоторой дискретной группы движений этой плоскости.

Существенную роль после Клейна и Пуанкаре в развитии теории автоморфных функций сыграли Гекке, Зигель, Зельберг, Годман, Петерсон. В работах этих ученых прослеживается связь между некоторыми аспектами теории автоморфных функций и теорией групп.

Процесс развития теории автоморфных функций все более показывал важность теоретико - группового подхода. И теперь многие понятия теории автоморфных функций достаточно просто связать с некоторой произвольной группой Ли или её дискретной подгруппой.

Особенно отчетливо связь между теорией групп и автоморфными функциями проявилась в 50х, 60х годах XX века. Точнее речь идет о связи с теорией представлений групп. Стоит отметить, что все это произошло под влиянием стремительного развития теории бесконечномерных представлений групп. Построение же бесконечномерных представлений групп Ли полностью выявило все зависимости.

Одной из первых работ в этом направлении была работа Гельфанда и Фомина, в которой понятия теории представлений связывались с теорией динамических систем и теорией автоморфных функций.

Кроме бесконечномерных представлений групп Ли большую роль в формировании современной теории автоморфных функций сыграло создание алгебраических группы в работах Шевалле, Бореля, Титца.

Обобщая выше сказанное, хотелось бы сказать, что теория представлений групп позволила по-новому понять классические результаты теории автоморфных функций, шире поставить задачи этой теории и получить ряд новых важных результатов.

5.4 Алгебраические конструкции в теории автоматов

Теория автоматов оперирует с широким кругом алгебраических объектов и средств. В годы становления теории автоматов алгебраические средства активно использовались для решения её внутренней проблематики. Интересно, что со временем оказалось, методы теории автоматов можно использовать при алгебраических исследованиях.

Первой систематической работой, в которой раскрылась в полной мере связь между двумя этими областями, была работа Глушкова.

Особое место в теории автоматов занимают алгебраические конструкции, связанные с конечными полугруппами. Рассмотрим этот вопрос более подробно на простейшем примере.

Пусть есть автомат

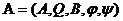
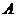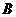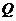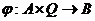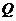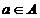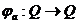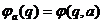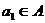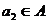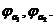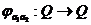Где  и , входной и выходной алфавиты соответственно, - множество состояний, функция - функция выходов. С этим конечным автоматом можно связать полугруппу подстановок на множестве . Каждая буква входного алфавита действует на Q как подстановка  , причем . Последовательное действие букв  и  соответствует произведению подстановок  Для выполняется

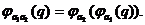
Таким образом, множество 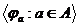 порождает конечную полугруппу 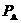, называемую внутренней полугруппой автомата  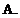Очевидно 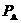является гомоморфным образом свободной полугруппы А* (А* - множество всех слов в алфавите  ).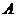

Итак, мы увидели, что полугруппы возникают фактически сразу же при определении понятия «автомат».

Методы теории полугрупп в этой области можно, вообще говоря , много где применить. Например, методы теории конечных полугрупп можно использовать для решения важной задачи декомпозиции автоматов, т.е. представления автомата в виде соединения «простых» автоматов. Оказалось, что эти методы хорошо работают в том случае, когда автомат можно разложить в суперпозицию автоматов. Среди работ в этом направлении одно из центральных мест занимает работа 60-х годов Крона и Роудза. В этой работе показано, как внутренняя полугруппа автомата суперпозиции связана с внутренними полугруппами автоматов - компонентов соединения.

Как мы увидели, с каждым автоматом можно связать полугруппу. Справедливо и обратное следствие. Каждой абстрактной полугруппе можно поставить в соответствие автомат. Правда это будет не один автомат, а бесконечное множество автоматов.

Еще отметим, что теория полугрупп применяется для решения центральной задачи теории автоматов - задачи о выразимости.

Также стоит сказать, что не только конечные полугруппы применяются при решении задач из теории автоматов. Здесь нашли своё применение и бесконечные группы.

Итак, теория автоматов активно использует классические объекты из алгебры, а также вводит в рассмотрение новые алгебраические системы и предоставляет новые «неклассические» конструкции.

5.5 Проблема интегрирования дифференциальных уравнений

Ранее мы говорили о группах Ли и непрерывных группах и проследили кратко путь их развития. Посмотрим теперь на наиболее простые и первые применения этих групп.

Напомним для начала, что группы Ли появились в конце XIX века. Около 1873 г. Норвежский математик Софус Ли ввел новый вид групп, названный им «непрерывные группы преобразований». С каждым дифференциальным уравнением он связал такую группу преобразований, которая оставляет его неизменным.

Софус Ли распространил методы теории групп на проблему интегрирования дифференциальных уравнений.

Группы Ли состояли из преобразований вида: x à f(x,a1,…,an), определяемых параметрами. Например, для вращения плоскости параметрами являются углы поворота, для пространства- так называемые эйлеровы углы. Перемножение двух преобразований, являющихся элементами группы, дает преобразование. Параметры последнего связаны с параметрами сомножителей непрерывными функциями Fi=Fi(a1,..,an; b1,..,bn).

Группы, определенные таким образом, получили название групп Ли. Структура групп Ли оказалась связанной с вопросом об интегрируемости дифференциальных уравнений в квадратурах. Соответствующие структурные свойства групп Ли получили, по аналогии с теорией Галуа, интерпретацию свойств разрешимости. С. Ли классифицировал всевозможные группы преобразований на плоскости и построил таблицу нормальных типов дифференциальных уравнений с указанием, решаются ли они в квадратурах. Вопрос, вытекает ли из непрерывности функций Fi существование таких параметров в группе, для которых функции Fi аналитичны, был включен Д. Гильбертом в число его знаменитых проблем и в настоящее время решен положительно.

5.6 Группы и геометрия

Правильные многогранники показывают, что геометрическая симметрия - фундаментально теоретико-групповое понятие. В более общем смысле, многие понятия «эквивалентности» в геометрии можно объяснить как свойства, которые сохраняются определенными группами преобразований. Однако, необходим был некоторый пересмотр классических понятий, прежде чем геометрия могла извлечь пользу из теоретико-групповых идей.

Старейшее понятие геометрической эквивалентности - это понятие конгруэнтности. Греки понимали, что фигуры F1 и F2 конгруэнтны, если имелось движение твердого тела F1, которое выносило его в F2. Недостаток этой идеи заключался в том, что движение имело значение только для отдельной фигуры. «Произведение» движений различных фигур не имело значения, и, следовательно, групп движений не имелось.

Шаг, который проложил путь к введению теории групп в геометрию, заключался в распространении Мёбиусом (1827) идеи движения на всю плоскость; он придал смысл произведению движений. Фактически, Мёбиус рассмотрел все непрерывные преобразования плоскости, которые сохраняют прямоту линий и уделил отдельное внимание нескольким подклассам этих преобразований: тем, которые сохраняют длину (конгруэнтностям), виду (подобиям) и параллелизму (аффинностям). Он показал, что самые общие непрерывные преобразования, которые сохраняют прямоту, - как раз проективные преобразования. Таким образом, одним ударом Мёбиус определил понятия конгруэнтности, подобия, аффинности и проективной эквивалентности как свойства, которые инвариантны под действием определенных классов преобразований плоскости. То, что рассматриваемыми классами были группы, стало очевидно, как только признали понятие группы. Именно признак медлительности, с которой было признано понятие группы, обусловило переформулировку идей Мёбиуса в понятиях групп только у Клейна (1872).

Формулировка Клейна получила известность как Эрлангенская программа, потому что он объявил о ней в Эрлангенском университете. Его идея заключалась в том, чтобы связать каждую геометрию с группой непрерывных преобразований, которые сохраняют ее характеристические свойства. Например, евклидова геометрия плоскости ассоциируется с группой преобразований плоскости, которые сохраняют евклидово расстояние между точками. Проективная геометрия плоскости ассоциируется с группой проективных преобразований. Гиперболическая геометрия плоскости, принимая во внимание проективную модель, может ассоциироваться с группой проективных преобразований, которые отображают единичный круг на себя. Концепция Клейна представляет собой по существу учение об инвариантах.

Важное влияние на Эрлангенскую программу, несомненно, оказал Кэли. Один из примеров группы, приведенных Кэли, позволил Клейну осознать связь геометрий и групп очень четко.

Когда геометрия была заново сформулирована таким образом, определенные геометрические вопросы стали вопросами о группах. Правильная мозаика, например, соответствует подгруппе полной группы движений, состоящей из тех движений, которые отображают мозаику на себя. В случае гиперболической геометрии, где задача классификации мозаик представляет большую сложность, взаимосвязь между геометрией и теоретико-групповыми идеями оказалась очень плодотворной. В работе Пуанкаре (1882,1883) и Клейна (1882) теория групп явилась катализатором нового синтеза геометрических, топологических и комбинаторных идей.

Отметим здесь факт, касающийся развития непрерывных групп. Ранее мы рассмотрели группы Ли и их приложения, а сейчас увидели что непрерывные группы получили многочисленные приложения в области геометрии. Открытие столь многообразных приложений теории непрерывных групп было причиной введения более общего, абстрактного определения непрерывной группы. В него входит требование задания предельного перехода, согласованного с группой операций. Вскоре удалось показать (это сделал Ван Данциг), что это определение более общее, нежели определение Ли, и что существуют непрерывные группы, не являющиеся группами Ли. (Мы вскользь упоминали этот факт в разделе, посвященном возникновению групп Ли)Так как при этом определении отвлекаются от того, что элементы группы являются преобразованиями, то приходят по существу к топологической группе и к топологическому пространству. В связи с этим создалась настоятельная необходимость объединить отдельные топологические факты в единую теорию.

Это было проделано А. Пуанкаре в его знаменитом мемуаре «Analysis situs» (1895) и в пяти прибавлениях к нему (1899 - 1911).

5.7 Группы и теория сигналов

Одним из перспективных направлений в развитии теории сигналов, является направление, основанное на теоретико-групповых представлениях. Это связано с тем, что при своем распространении сигнал подвергается различным преобразованиям, связанными со свойствами среды, а также движениями источника и приемника сигналов.

Групповой подход позволяет с единых позиций трактовать значительный круг теории сигналов - выявлять структуру, классифицировать сигналы по признаку преобразований его носителя (время, частота), что является базой для разработки единых методов их обработки, согласованных с этими преобразованиями.

На основе теоретико-групповых представлений был сильно развит понятийный аппарата теории сигналов. Также применение теории групп позволило обобщить корреляционно-спектральную теория.

5.8 Связь между распознаванием образов и теорией групп

Имеются некоторые области, в которых проявляется связь между теорией групп и распознаванием образов.

Здесь, рассматривая задачу распознавания образов, имеем в виду, что мы работаем с графическими объектами, определенными на непрерывных множествах точек плоскости.

Первая область взаимосвязи встречается при исследовании инвариантных свойств графических объектов.

Вторая же область (наиболее важная с точки зрения Ричардсона) - формирование математических моделей классов в пространстве образов. Здесь понятие группы может обеспечить нас мощными средствами для компактных описаний. Например, класс всех треугольников можно описать с помощью единого эталонного треугольника и аффинной группы.

5.9 Теория групп и криптография

Очень широкое применение нашла теория групп в области криптографии и защиты информации. Можно сказать, что это одна из основ криптографии.

Причина этого кроется в том, что современная криптография оперирует различными алгебраическими структурами. В частности, в качестве исходных пространств открытых и шифр сообщений в криптосистемах в настоящее время используются множества с одной или двумя операциями. При этом выполнение аксиом группы очень часто оказывается необходимым для правильного функционирования криптосистемы.

Примером криптосистемы, основанной именно на группах и их свойствах ( а не на кольцах или полях) может служить ассиметричная криптосистема Эль-Гамаля. В данной криптосистеме пространством открытых текстов является некая группа простого порядка. Кроме того, на свойствах используемой группы в данном случае оказывается основана безопасность данной шифр-системы. Более точно, мы знаем, что трудность взлома криптосистемы Эль-Гамаля эквивалентна трудности решения задачи о вычислении дискретного логарифма в конечной группе.

Это всего лишь один маленький пример из бесчисленного множества. Фактически любая криптосистема строится на структуре с групповыми свойствами. Структуры конечно могут быть очень разнообразны: от колец вычетов до целочисленных решеток.

Хотелось бы отметить еще, что некоторые аспекты теории групп имеют взаимосвязь с самыми новыми и востребованными областями информационной безопасности. Здесь мы имеем в виду область, которую сейчас часто называют -«облачные вычисления».

Поясним более подробно эту зависимость. Как известно, «облачные вычисления» - это некие протоколы, позволяющие осуществлять вычисления над данными в зашифрованном виде на недоверенных серверах. Т.е., облачные вычисления дают возможность что-то вычислять над данными, не раскрывая сами данные. Один из самых известных способов организовать облачные вычисления - это использовать некоторые специальные криптосистемы, которые позволяют отобразить операции над открытыми текстами в операции над шифр текстами. И здесь возникает понятия гомоморфизма, которое нам хорошо известно из теории групп. Речь идет о так называемых гомоморфных криптосистемах. Гомоморфная криптосистема имеет в своем основании две группы (пространство открытых и шифр текстов), между которыми имеется гомоморфизм. Хотя конечно здесь могут быть и не группы, а кольца и соответствующий гомоморфизм колец. Наличие криптосистемы с несколькими гомоморфизмами, образующими базис в пространстве операций, может позволить осуществлять облачные вычисления произвольного вида.

Итак, мы увидели, что теория групп, общая алгебра неразрывно связанны с современной криптографией и самыми передовыми областями защиты информации.

5.10 Применение методов теории групп к задачам управления

Методы теории групп имеют применение к задачам управления. Особое значение здесь имеют группы Ли.

Возможность применения методов теории групп Ли к решению задач управления основана на связи между задачами управления и уравнениями Рикатти

Уравнения Риккати в каком-то смысле весьма универсально и появляется во многих прикладных областях. Это уравнение с самого своего появления в 1724 году является предметом пристального внимания ученых. В настоящее время название "уравнение Риккати" обычно применяется к любым системам обыкновенных дифференциальных уравнений с квадратичной правой частью.

Каждая новая идея в исследовании дифференциальных уравнений непременно апробировалась на уравнении Риккати. Например, при работе над теорией нелинейных суперпозиций Софус Ли показал, что уравнение Риккати является наиболее общим уравнением первого порядка, которое имеет фундаментальную систему решений.

Давно замеченная связь уравнения Риккати с группой дробно-линейных преобразований, его геометрическая природа и проективные свойства определяют причины, по которым уравнения этого типа с неизбежностью возникают в различных и далеких друг от друга областях естествознания (алгебраическая геометрия, теория конформных отображений, теория вполне интегрируемых гамильтоновых систем, применение теории Бэклунда в квантовой теории поля, вариационное исчисление). Уравнение Риккати занимает особое место в теории оптимального управления.

Вообще, в теории управления имеется много математических задач, непосредственно относящихся к дифференциальным уравнениям (задачи об оптимальном управлении, задачи оценки параметров системы и ее состояния, другие задачи). Их решение для обыкновенных дифференциальных уравнений довольно часто приводит к матричным дифференциальным уравнениям Риккати . Например, при решении задач об оптимальной стабилизации и об аналитическом конструировании регуляторов для линейных систем возникает необходимость решать задачи Коши для соответствующих матричных уравнений Риккати.

Стоит также заметить, что в теории управления системами с распределенными параметрами в некоторых случаях возникает необходимость рассматривать различные обобщения уравнения Риккати в бесконечномерных пространствах. Такими обобщениями стали интегро-дифференциальные краевые задачи Риккати, которые появляются, например, при решении задач об оптимальном управлении тепловыми и диффузионными процессами.

Итак, мы увидели, что имеется связь между задачами теории управления и уравнениями Рикатти. В свою очередь для эффективного решения матричных дифференциальным уравнений Риккати имеются методы, основанные на применении методов теории групп Ли. И таким образом, мы получаем эффективные теоретико -групповые методы решения задач управления.

5.11 Теории групп и биология

Как уже стал понятно, теория групп имеет тесную связь с понятием симметрии. Это позволило ей найти свое применение в некоторых областях биологии. В частности, теория групп имеет приложение к описанию псевдосимметрий в биологических объектах. К примеру, можно применить язык теории групп при описании симметрий и псевдосимметрий актиноморфных и зигоморфных цветков. В этом аспекте язык теории групп становится очень удобным инструментом.

Также, теория групп имеет определенную связь с некоторыми проблемами терминологии биосимметрики.

Адаптация теории групп к описанию симметрий биообъектов важна не только в фундаментальном плане, но и как средство взаимопонимания между биологами, физиками, кристаллографами и другими специалистами, языком общения между которыми, может служить математика.

5.12 Применение методов теории групп в квантовохимических расчетах

Методы теории групп в настоящее время широко применяются в химии.

В частности, теория групп применяется к вопросам строения молекул. В основе применения абстрактного аппарата теории групп к конкретным вопросам строения молекул лежат свойства симметрии исследуемых объектов. Можно выделить два типа симметрии: а) симметрия относительно пространственных преобразований, б) симметрия относительно перестановок тождественных частиц. Оба эти типа симметрии вытекают из свойств уравнения Шредингера для многоэлектронных систем. Помимо симметрии относительно преобразований координат реального трехмерного пространства для ряда задач уравнение Шредингера может обладать симметрией относительно преобразования переменных в некотором фиктивном n-мерном пространстве. В таких случаях говорят о скрытой или динамической симметрии. Хорошо изученным примером такой симметрии является открытая Фоком симметрия записанного в импульсном представлении уравнения Шредингера для атома водорода в четырехмерном пространстве динамических переменных.

Многие привычные понятия, используемые в квантовой химии, основаны на теоретико-групповых свойствах многоэлектронных систем. Так, принцип Паули связан с запретом для многоэлектронных систем всех неприводимых представлений группы перестановок электронов, кроме антисимметричного. Сохранение во времени различных величин, характеризующих состояние молекулы, таких, как спин, импульс и орбитальный момент изолированной молекулы, связано с тем, что эти величины характеризуют неприводимые представления групп, операции которых оставляют инвариантным гамильтониан системы.

Привлечение аппарата теории групп дает возможность качественно выяснить ряд свойств рассматриваемых систем, не прибегая к численным расчетам: например, определить степень вырождения и симметрию разрешенных состояний, вероятность квантовых переходов (правила отбора). В то же время теория групп существенно упрощает и количественный расчет, поскольку позволяет получить эффективные расчетные формулы для матричных элементов искомых физических величин.

5.13 Группы и классификация голограмм

В настоящее время известно большое количество различных разновидностей голограмм. При этом в основу классификации обычно кладутся определенные физические характеристики, признаки и свойства голограмм, регистрирующих сред и схем записи.

В частности, в зависимости от структуры поля, записываемого на голограмме, различают голограммы сфокусированного изображения, голограммы Френеля и Фраунгофера и различные виды голограмм Фурье.

Выбор схемы голографирования (относительное расположение предметного и опорного пучков) приводит к понятию осевой голограммы с наклонным опорным пучком и голограммы во встречных пучках. При определенном положении интерференционной картины, регистрируемой на голограмме, относительно светочувствительного материала в зависимости от соотношения между толщиной материала и шагом интерференционной картины можно говорить о плоских и объемных голограммах. Использование регистрирующих сред с амплитудной и фазовой модуляцией позволяет выделить, соответственно, амплитудные и фазовые голограммы.

В зависимости от множества точек, в которых осуществляется регистрация интерференционной картины, различают непрерывные и дискретные голограммы. Последние по способу регистрации делятся на физические и математические

Приведенный достаточно большой перечень различных типов голограмм показывает, что в настоящее время отсутствует единый подход к классификации голограмм, учитывающий математическую структуру голографической записи. Последнее, естественно, затрудняет прогнозирование новых типов голограмм и схем записи. В то же время процесс регистрации голографической информации обладает резко выраженным свойством симметрии, которое можно описать с помощью принципа взаимности . Иначе говоря, при определенных условиях предметная и опорная волны могут меняться местами.

С другой стороны, при записи голограммы регистрируется интерференционная картина, которая возникает при сложении двух (или нескольких) распределений комплексной амплитуды поля (предметной и опорной волны). Идея инвариантности суммарного поля, регистрируемого на голограмме, которая лежит в основе симметрия голографической записи, наиболее полно может быть описана в рамках теории групп. Применение теоретико-группового подхода в голографии интересно тем, что при этом физические идеи не упускаются из виду.

Теоретико-групповой формализм широко используется в современной физике. Основные понятия теории групп (одного из важных разделов "неколичественной" математики) проникли во многие разделы физики и нашли применение в таких ее областях, как например, квантовая механика и кристаллография.

При этом теория групп оказывается весьма полезной при систематизации широкого круга различных физических задач, связанных с теми или иными проявлениями симметрии (выделение кристаллографических сметем, классификация уровней энергии в квантовой механике и т.п.).

В рамках скалярной теории дифракции был проведен теоретико-групповой анализ математической структуры голографической записи. Идея инвариантности интерференционного поля, обусловленной симметрией процесса голографической регистрации, оказывается полезной при систематизации имеющихся разновидностей голограмм и прогнозировании новых типов голограмм. При этом все разновидности голограмм допускают единое рассмотрение с теоретико-групповых позиций.

5.14 Применение к кристаллографии

Аппарат теории групп нашел широкое применение в кристаллографии. Здесь, как и в биологии, большую роль играет связь понятия группы и симметрии.

Свое первое применение в эт ой области теория групп нашла в конце XIX века. В 1890-1891 гг. русский кристаллограф и геометр Е. С. Федоров и немецкий математик А. Шёнфлис независимо друг от друга решили методами теории групп задачу классификации всех кристаллических пространственных решеток. Они установили наличие 230 пространственных групп симметрии, состоящих из совокупности самосовмещений кристаллических структур. Точки, получаемые друг из друга преобразованием данной группы, называются гомологичными по отношению к этой группе и образуют так называемую правильную систему.

В настоящее время исследование структуры кристаллических веществ включает в себя определение их федоровских групп.

(О первых применениях теории групп в теории кристаллов можно найти в [1].)

Напоследок хочется отметить, что сейчас в кристаллографии большую роль играют бесконечные группы и группы Ли.

5.15 Теория групп и её приложения к физике элементарных частиц

Как уже говорилось, на рубеже XIX и XX вв. теория групп приобрела необычайную разветвленность, составив ядро современной алгебры. Ее составляет ряд высокоразвитых теорий: конечных групп, бесконечных дискретных групп, непрерывных групп, в том числе групп Ли. Теоретико-групповые методы проникли в ряд математических дисциплин и их приложений. Открытия де Бройля, Шредингера, Дирака и др. в квантовой механике и в теории структуры материи показали, что современная физика должна опираться на теорию непрерывных групп, в особенности на теорию представлений групп линейными операторами, теорию характеров и др., разработанные Картаном, Г. Вейлем и другими учеными.

Теория групп в настоящий момент нашла применения во многих областях физики.

В частности теория групп имеет приложения к физике элементарных частиц. Основную роль в современной физике элементарных частиц играют унитарные групп SU(2) и SU(3). Действительно, группа SU(2) является группой спиновых и изотопических преобразований, а также составляет основу группы калибровочных преобразований электрослабых взаимодействий SU(2) x U(1) в модели Салама-Вайнберга-Глэшоу. Группа SU(3) в свою очередь, является основой модели унитарной симметрии и кварковой модели с тремя ароматами, а также группой цвета, т.е., на ней покоится все здание квантовой хромодинамики.

Также стоит отметить, что вопрос о классификации частиц тесно связан с представлениями унитарных групп.

Другими важными примерами конкретного применения формализма теории групп и их представлений служат примеры вычислений таких важнейших характеристик элементарных частиц как магнитные моменты и аксиально-векторные константы связи в модели унитарной симметрии и кварковой модели.

5.16 Применение теории групп в квантовой механике

Имеется три основных аспекта применения теории групп в квантовой механике: 1) систематизация энергетических уровней и соответствующих собственных состояний; 2) качественное исследование расщепления энергетических уровней, возникающего при добавлении поправочных членов к искомому приближенному гамильтониану; 3) для оценки произвольных матричных элементов и для установления общих правил отбора, определяющих, когда матричные элементы отличны от нуля.

Теория групп не просто является особым методом решения нескольких наиболее трудных задач квантовой теории. В квантовой механике сложных систем практически все общие утверждения, которые могут быть сделаны относительно таких систем, зависят от их свойств симметрии. Теория групп является систематическим единым методом изучения и использования этих свойств симметрии. Т.е. теория групп в квантовой механике - это инструмент, имеющий универсальное применение.

5.17 Два примера приложения теории групп в природе

. В качестве первого уникального примера группы рассмотрим стандартный (типографский) лист бумаги. Он исходно изготовлен в таких размерах, что сложение вдвое длинной стороны не меняет отношения сторон (длинной к короткой). Введём некоторое уточнение. Чтобы правило сохранения отношения сторон сохранялось, оно всегда должно равняться , и такие листы мы назовём "одинарными листами Леонардо да Винчи" (он их изобрёл). Если операцию сложения вдвое повторить, то получим "двойные листы да Винчи", у которых отношение сторон при всех последующих операциях сложения будет равно 2. После этого операцию можно продолжать и в прямом, и в обратном направлениях, всё время получая новые члены группы, обладающие тем же свойством отношения сторон.

Судя по всему, подобными групповыми свойствами обладают так называемые карликовые галактики - спутники нашего Млечного Пути. Они были обнаружены лишь недавно (2008) группой астрономов под руководством Луиса Стригари. У всех карликовых галактик - спутников Млечного Пути - гравитирующая масса одинакова, потому что она получается из "энтропии листа да Винчи", которая определяется как логарифм статистического веса, равного отношению сторон (длинной к короткой).

. Вторым уникальным примером группы является так называемая крамерсовская электродинамика, изложенная на с. 47 в книге Эдмонда Бауэра "Теория групп и её приложения к квантовой механике". В книге поясняется, что в так называемом дипольном излучении электронов, при их рассеянии на кулоновском поле иона в плазме, излучается только один единственный фотон. Этот процесс первого порядка происходит с вероятностью, пропорциональной множителю α=е2/hc=1,137 (h - постоянная Планка). Процессом второго порядка будет квадрупольное излучение, при котором излучается (или поглощается) сразу два фотона. И этот процесс пропорционален множителю α2, и так далее. В целом, разложение потенциальной энергии электрона в поле иона в ряд по мультиполям соответствует разложению в ряд по числу фотонов, участвующих в процессе; такое соответствие в теории групп называется изоморфизмом представлений процесса. Если оборвать этот ряд (например, пренебречь квадрупольным и всеми более высокими членами разложения), то получим сугубо квантовую картину излучения, весьма далёкую от классической картины с участием сразу многих фотонов.

алгебраический дифференциальный голограмма квантовый

Заключение

Итак, мы увидели, что теория групп имеет многочисленные применения в различных областях математики, физики, защиты информации, химии, биологии и других. Универсальность понятия группы позволило ему найти место везде, где требуется высокий уровень абстракции, свойства симметрии.

Теория групп оказала влияние на многие отдельные области математики. К примеру, её появление изменило теорию решений уравнений. Были найдены ответы на вековые вопросы с помощью этой теории. Проникнув в геометрию, теория групп способствовала тому, что геометрия стала более единообразной. Более того, как упоминалось, оказалось возможным переформулировать многие сложные геометрические задачи на язык теории групп и благодаря этому быстро их решить.

Теория групп принесла свои методы решения задач в некоторые математические дисциплины. Мы видели это хотя бы на примере алгебраической топологии и фундаментальных групп в ней. Можно здесь еще помимо алгебраической топологии упомянуть различные комбинаторные задачи, целочисленное программирование, математической моделирование.

Теория групп также оказала неоценимую помощь при решении задач классификации в различных областях прикладной математики, оказала влияние на развитие теории инвариантов.

Хотелось бы еще сказать, что появление теории групп способствовало появлению новых областей в математике. Например: алгебраическая теория чисел, теория колец, полей. Во многом благодаря теории групп, современная алгебра теперь такая, какой мы её знаем. Алгебра, старейшая отрасль математики, радикально перестроилась, стала теоретико-множественной и аксиоматической наукой.

И наконец, самое важное, что теория групп, как повлияла на математику в целом. Появление теории групп, теории Галуа дало толчок к полной реконструкции математики.

Взаимопроникновение математических дисциплин стало в наши дни глубоким и всеобщим.

6. Современная теория групп

В настоящее время теория групп является одной из самых развитых областей алгебры, имеющей многочисленные приложения как в самой математике, так и за ее пределами - в топологии, теории функций, кристаллографии, квантовой механике и других областях математики и естествознания.

Каждый год проходят международные конференции, посвященные теории конечных и бесконечных групп. В частности, в России это направление развивается достаточно активно. Только в 2007г. у нас прошло несколько международных конференций по теории групп. Хорошо развитые школы, занимающиеся теорией групп, имеются в Москве, Санкт-Петербурге, Екатеринбурге, Новосибирске, Омске, Томске, Иркутске, Челябинске, Красноярске и других городах России. Сотни специалистов высшей квалификации занимаются различными разделами теории групп. В России регулярно выходят журналы «Алгебра и логика», «Сибирский математический журнал», «Фундаментальная и прикладная математика», «Дискретная математика», «Доклады академии наук», которых большую долю занимают статьи по теории групп. Российскими учеными написаны десятки монографий по конечным и бесконечным группам. Достижения российских специалистов по теории групп давно и заслуженно признаны во всем мире.

Скажем несколько слов о направлениях теории групп наиболее развитых и активно используемых к настоящему моменту.

Структурная теория групп в настоящее время представляет одну из самых развитых областей алгебры и математики в целом.

Теория конечных групп - старейшая и, в то же время, наиболее активно развивающаяся ветвь теории групп. Одним из крупнейших результатов явилось завершение классификации конечных простых групп, включающей серии групп алгебраического типа, знакопеременные группы An при n³5 и 26 спорадических простых групп (среди которых наибольшая группа Большой Монстр имеет порядок

246×320×59×76×112×132×17×19×23×29×31×41×47×59×71)

Исключительная роль конечных простых групп объясняется тем, что из них может быть построена любая конечная группа. Обстоятельно исследованы конечные разрешимые группы по свойствам различных систем подгрупп (силовских, холловских, картеровских и др.) Отметим теорему У. Фейта (W.Feit) и Дж.Томпсона (J. Thompson) 1963, о том, что все конечные группы нечетного порядка разрешимы. Теория групп подстановок и теория линейных групп над конечными полями образуют крупные развитые направления теории конечных групп.

Абелевы группы - также очень сильная развитая область к настоящему моменту. Теорема Г.Фробениуса и Л. Штикельбергера (L.Stickelberg), 1878, о том, что конечная абелева группа является прямой суммой примарных циклических групп, и ее обобщение (теорема о строении конечнопорожденных абелевых групп) нашли широкое применение в математике и ее приложениях. Наиболее изучены: полные (делимые) абелевы группы; свободные абелевы группы и абелевы группы без кручения; периодические абелевы группы (в частности, их сервантные и примарные подгруппы). Развитые гомологические методы теории расширений абелевых групп позволяют в ряде случаев сводить рассмотрение общего случая к этим классам групп. Существенную роль играют функторы Hom и Ä на категории абелевых групп, изучение колец эндоморфизмов End (G) и групп автоморфизмов Aut(G) абелевых групп G.

Также хорошо развита теория нильпотентных и разрешимых групп, содержащих все абелевы группы, а также многочисленных их обобщений: локально нильпотентных групп; локально разрешимых групп; групп с нормализаторным условием; групп с субнормальными системами подгрупп различного типа.

Современная теория представлений групп и теория характеров представляет сложившуюся область, обогащенную методами теории колец и гомологической алгебры с мощным арсеналом технических средств для изучения абстрактных групп.

Теория гомологий групп занимает достойное место в современной гомологической алгебре как наиболее развитый отдел.

Как мы уже увидели, в настоящий момент теория групп является очень разветвленной областью знаний. Есть много нерешенных задач и много перспективных направлений исследований.

Сейчас, например, многими теоретико-групповиками активно изучаются производные структуры, связанные с группой G, например: группа автоморфизмов Aut(G); решетка подгрупп L(G); полугруппа эндоморфизмов End(G). Исследуются: радикалы групп, радикальные и полупростые классы; формации групп; формальные группы

Продолжается активное изучение групп с дополнительными структурами, согласованными с групповой операцией, среди них: топологические группы и группы Ли; алгебраические группы; упорядоченные группы.

Одним из наиболее перспективных и интересных направлений является изучение групп с заданными свойствами системы подгрупп. Начало таким исследованиям было положено работами У. Бернсайда, Р. Дедекинда, Г. Миллера и Г. Морено, О.Ю. Шмидта и др. Появившись сначала в области конечных групп, это направление распространилось затем на бесконечные группы и дало при этом многие новые подходы к их изучению, а также важные понятия теории групп.

В этом направлении среди наиболее значительных объектов исследований были выделены классы локально конечных групп, периодических групп, локально разрешимых и локально нильпотентных групп, локально ступенчатых групп, классы групп Куроша-Черникова. В этом направлении работали многие авторы: С.И. Адян, Р. Бэр, Б.А. Вэрфриц, X. Виланд, Дж. Вильсон, Ю.М. Горчаков, В.М. Глушков, Д. Горенстейн, Р.И. Григорчук, Д.И. Зайцев, М.И. Каргополов, О. Кегель, А.И. Кострикин, Л.Г. Курош, Л.А. Курдаченко, А.И. Мальцев, Ю.И. Мерзляков, А.Ю. Ольшанский, П.С. Новиков, Б.И. Плоткин, Д.Ю. Робинсон, А.В. Рожков, А.И. Созутов, Д. Томпсон, В. Фейт, Г. Хайнекен, Б. Хартли, Ф. Холл, B.C. Чарин, Н.С. Черников, Н. Черников, А. Чунихин, Л.А. Шеметков, В.П. Шунков и др.

Ясно, что для рассмотрения строения определенного вида групп с заданными свойствами подгрупп, необходимы существенные ограничения для подгрупп. Большое значение здесь имеет проблема исследования групп, обладающих в том или ином смысле широкой системой дополняемых подгрупп.

Здесь напомним, что подгруппа А группы G называется дополняемой в группе G, если в G существует такая подгруппа В, что G=AB и А∩В=1. При этом В называется дополнением к А в G.

Понятно, что на строение группы и ее свойства существенно влияют условия дополняемости, налагаемые на подгруппы из той или иной системы подгрупп. Так, в 1937 году Ф. Холлом была показана разрешимость конечной группы, в которой дополняемы все силовские примарные подгруппы. В связи с этим возникла потребность изучения конечных групп, в которых дополняемы все подгруппы. В этом направлении Ф. Холлом получен следующий критерий:

В конечной группе G каждая подгруппа дополняема тогда и только тогда, когда G является сверхразрешимой группой с элементарными абелевыми примарными подгруппами.

Первоначальному исследованию свойств произвольных групп с системой дополняемых подгрупп, удовлетворяющей тем или иным условиям, посвящены работы Н. В. Черниковой. Ею было получено полное конструктивное описание вполне факторизуемых групп, то есть групп, в которых дополняемы все подгруппы. Из теоремы Н.В.Черниковой следует, что в группе G каждая подгруппа дополняема тогда и только тогда, когда G=[A]B, где А разлагается в прямое произведение нормальных в G подгрупп простых порядков или А=1, а В разлагается в прямое произведение подгрупп простых порядков или В=1. Общая задача изучения групп с некоторой заданной системой дополняемых подгрупп была сформулирована Н. Черниковым. В его работах изучались группы с дополняемыми абелевыми (неабелевыми, элементарными абелевыми) подгруппами, нормальными (неинвариантными), бесконечными (бесконечными абелевыми, бесконечными неабелевыми), примарными (непримарными, нормальными непримарными) подгруппами. Впоследствии в этом направлении работали и получили многие важные результаты Ю.М. Горчаков, М.И. Каргаполов, Д.И. Зайцев, B.C. Чарин и др. (школа Н. Черникова), Н.С. Черников, Н.М. Сучков и др. (школа В.П. Шункова), К. Кристенсеном. А.С. Кондратьевым, Л.С. Казариным, В.А. Ведерниковым, B.C. Монаховым, М. Курцио, О. Бечтеллом и др.

В 70-х гг. было введено понятие сепарирующей подгруппы, и в связи с этим появился новый подход к обобщению вполне факторизуемых групп. В этом направлении были получены результаты в работах Н.С. Черникова, А. Довженко, Д. Кеппига, B.C. Чарина, А.В. Спиваковского, В.А. Крекнина и др. Одним из наиболее естественных ослаблений условия дополняемости всех подгрупп в группе является условие дополняемости подгрупп, не содержащихся в ее подгруппе Фраттини - нефраттиниевых подгрупп. Такие группы с дополняемыми нефрахтиниевыми подгруппами были полностью описаны А. Довженко в работах. Исследование групп с дальнейшими ослаблениями условия дополняемости подгрупп является актуальной и перспективной задачей. Так, нужно рассмотреть группы, в которых все недополняемые подгруппы содержатся в произведении подгруппы Фраттини Ф(0) и центра Z(G) группы G. Такое ослабление условия дополняемости приводит к существенному расширению класса рассматриваемых групп, в частности, этот класс содержит все абелевы группы.

Еще одно довольно активно развиваемое в настоящее время направление - это теория линейных групп над кольцами. По этой тематике имеется большое количество статей монографий. Помимо исследований для колец наиболее общей природы, часто возникает задача изучения линейных групп и над отдельно взятыми кольцами.

Также, в последний двадцать пять лет активно развивается теория квантовых групп (некоммутативных деформаций групп) . Общий метод построения квантовых групп, заключающийся в некоммутативной деформации алгебры функций на группе и наделении ее структурой некоммутативной алгебры Хопфа, детально разработан для всех серий простых групп . Он связан с существованием универсальных R-матриц (решений уравнения Янга-Бакстера), определяющих коммутационные соотношения образующих алгебры Хопфа. Для неполупростых групп такого общего метода не существует. В работах Громова Н.А. и его учеников с помощью метода перехода от полупростых групп к неполупростым, реализованным в виде матричных групп над алгеброй Dm, построены некоторые некоммутативные деформации групп Кэли-Клейна [а также некоторые некоммутативные деформации других видов неполупростых групп

В последнее время активно развивается также такая область математики, как суперматематика. Укажем здесь на работы Березииа Ф.А., Лейтеса Д.А. , Каца В.Г.. Наряду с коммутирующими переменными здесь рассматриваются и антикоммутирующие, а значит нильпотентные индекса 2 переменные. Одним из важных примеров супералгебр является алгебра Грассмана. Во многих физических приложениях преобразования суперпространств реализуются в виде матриц над алгеброй Грассмана. В работе [2] рассмотрены некоторые свойства алгебры Грассмана, проведена классификация ее автоморфизмов, дано определение линейных групп над алгеброй Грассмана (супераиалогов классических групп), указано на некоторые их свойства и физические приложения. Нетрудно показать, что алгебра Dm является подалгеброй алгебры Грассмана. В силу этого в суперматематике также естественным образом возникают различные алгебраические структуры над алгеброй Dm, в частности, некоторые группы преобразований суперпространств можно реализовать в виде линейных групп над алгеброй Dm.

Если линейная группа над полем действует на векторном пространстве над этим полем, то линейная группа над кольцом R является группой автоморфизмов некоторого свободного Л-модуля. Поэтому одновременно с исследованием линейных групп над алгеброй Dm естественно возникает задача исследования 1}т-модулей.

В алгебре Dm есть делители нуля, нильпотентные элементы различных индексов, и это обстоятельство относит ее к числу объектов, для которых нет полной, хорошо разработанной теории, как скажем, для полупростых алгебр. В монографии Ж.-П. Серра алгебра D2 используется для определения некоторых алгебр Ли. В монографии Шафаревича И.Р. [40] алгебра D2 используется для описания касательного пространства в точке схемы. Зайнуллиным К.В. в рассмотрены центральные расширения специальной линейной группы бесконечных матриц над алгеброй Dm.

В частном случае т = 1 мы приходим к алгебре дуальных чисел, которые были введены Клиффордом У.К. во второй половине 19-го века . Данные числа и алгебраические структуры над ними нашли применение в различных областях математики и теоретической физики. Так Котельников А.П. и Штуди Э. применяли их для построения теории винтов . Розен-фельд Б.А. и Яглом И.М. использовали их для описания неевклидовых пространств и движений в них. Дуальные числа могут быть использованы для описания структур, рассматриваемых с точностью до бесконечно малых второго порядка, на алгебраическом языке . Многообразия над алгебрами, в частности над алгеброй дуальных чисел, активно изучаются представителями казанской геометрической школы . Механику с дуальными координатами рассматривал Дуплий С.А. [15]. Определяющие соотношения классических групп над кольцом дуальных чисел рассмотрел Сатаров Ж.С. Тем не менее, нельзя сказать, что дуальные числа широко известны.

В силу вышесказанного, алгебра Dm, а также модули и линейные группы над ней представляют собой актуальные для изучения объекты, как с чисто алгебраической точки зрения, так и с точки зрения применения их в других разделах математики и теоретической физики.

По-видимому, Р.И. Пименов был первым, кто в своих работах ввел набор из нескольких взаимно коммутирующих нильпотентных именованных координат, тем самым косвенно выделив алгебру Dm и указав на ее применение в геометрии. Учитывая это, а также из соображений удобства, в дальнейшем алгебру Dm будем называть алгеброй Пименова.

Напоследок упомянем еще одну область теории групп, активно развиваемую сейчас. Речь идет о вычислительной теории групп.

Вычислительная теория групп - область науки на стыке математики и информатики, изучающая группы с помощью вычислительных машин. Она связана с проектированием, анализом алгоритмов и структур данных для вычисления различных характеристик (чаще всего - конечных) групп. Область интересна исследованием важных с различных точек зрения групп, данные о которых невозможно получить вычислениями вручную.

Основные направления исследований в этой области связаны с алгоритмами для:

·        конечно заданных групп,

·              полициклических и конечных разрешимых групп,

·              групп перестановок,

·              матричных групп,

·              теории представлений.

Важные алгоритмы в вычислительной теории групп включают:

·        алгоритм Шрайера-Симса для нахождения порядка группы перестановок,

·              алгоритм Тодда-Коксетера и алгоритм Кну́та-Бендикса для перечисления классов смежности,

·              алгоритм перемножения-замены для нахождения случайного элемента группы.

Реализации алгоритмов вычислительной теории групп доступны, в частности, в двух известных системах компьютерной алгебры, GAP и MAGMA. (о GAP мы расскажем позднее)

Некоторые достижения, непосредственно связанные с вычислительной теорией групп:

·        полное перечисление всех конечных групп порядка меньше 2000,

·              вычисление представлений всех спорадических групп.

7. Система GAP

В конце прошлого раздела мы упомянули про вычислительную теорию групп. Одной из известных реализаций алгоритмов вычислительной теории групп является система GAP. Разработка системы компьютерной алгебры GAP (название которой расшифровывается как "Groups, Algorithms and Programming", была начата в 1986 г. в г. Аахен, Германия. В 1997 г. центр координации разработки и технической поддержки пользователей переместился в Университет г. Сент-Эндрюс, Шотландия.

В настоящее время GAP является уникальным всемирным совместным научным проектом, объединяющим специалистов в области алгебры, теории чисел, математической логики, информатики и др. наук из различных стран мира. Основные центры разработки системы находятся в университетах г.Сент-Эндрюс (Шотландия), гг. Аахен, Брауншвейг (Германия) и Университете штата Колорадо (США). Текущая версия системы - GAP 4.4.10 была выпущена в октябре 2007 г.

Изначально система GAP разрабатывалась под Unix, а затем была импортирована для работы в других операционных системах. В настоящее время она работает в разнообразных версиях Unix/Linux, а также в Windows и Mac OS. Заметим, что ряд пакетов, расширяющих функциональность системы, работает только в среде Unix/Linux.является свободно распространяемой, открытой и расширяемой системой. Она распространяется в соответствии с GNU Public License. Система поставляется вместе с исходными текстами, которые написаны на двух языках: ядро системы написано на Си, а библиотека функций - на специальном языке, также называемом GAP, который по синтаксису напоминает Pascal, однако является объектно-ориентированным языком. Пользователи могут создавать свои собственные программы на этом языке, и здесь исходные тексты являются незаменимым наглядным пособием. Наконец, разработчики программ для GAP могут оформить свои разработки в виде пакета для системы GAP и представить их на рассмотрение в Совет GAP. После прохождения процедуры рецензирования и одобрения советом GAP такой пакет включается в приложение к дистрибутиву GAP и распространяется вместе с ним. Процедура рецензирования позволяет приравнивать принятые Советом GAP пакеты к научной публикации, и ссылаться на них наравне с другими источниками.

Помимо уже упомянутых пакетов, система состоит из следующих четырех основных компонент:

·        ядра системы, обеспечивающего поддержку языка GAP, работу с системой в программном и интерактивном режиме;

·              библиотеки функций, в которой реализованы разнообразные алгебраические алгоритмы (более 4000 пользовательских функций, более 140000 строк программ на языке GAP);

·              библиотеки данных, включая, например, библиотеку всех групп порядка не более 2000 (за исключением 49487365422 групп порядка 1024, точное количество которых, кстати, также было определено с помощью системы GAP), библиотеку примитивных групп подстановок, таблицы характеров конечных групп и т.д., что в совокупности составляет эффективное средство для выдвижения и тестирования научных гипотез;

·              обширной (около полутора тысяч страниц) документации, доступной в разнообразных форматах (txt, pdf, html), а также через Интернет.

Обзор возможностей GAP

Система GAP была задумана как инструмент комбинаторной теории групп - раздела алгебры, изучающего группы, заданные порождающими элементами и определяющими соотношениями. В дальнейшем, с выходом каждой новой версии системы сфера ее применения охватывала все новые и новые разделы алгебры. В разнообразии областей алгебры, охватываемых GAP сегодня, можно убедиться, даже только лишь прочитав названия разделов обширнейшей документации по системе, занимающей около 1500 страниц (которая, кстати, не только входит в состав дистрибутива, но и доступна через Интернет). Вычислительная мощь системы может быть продемонстрирована находящимся на ее сайте примером определения того, что кубик Рубик имеет 43252003274489856000 различных состояний, и сборки кубика Рубика из произвольного начального состояния в среднем за 100 ходов.дает возможность производить вычисления с гигантскими целыми и рациональными числами, допустимые значения которых ограничены только объемом доступной памяти. Далее, система работает с циклотомическими полями, конечными полями, p-адическими числами, многочленами от многих переменных, рациональными функциями, векторами и матрицами. Пользователю доступны различные комбинаторные функции, элементарные теоретико-числовые функции, разнообразные функции для работы с множествами и списками.

Группы могут быть заданы в различной форме, например, как группы подстановок, матричные группы, группы, заданные порождающими элементами и определяющими соотношениями. Более того, построив, например, групповую алгебру, можно вычислить ее мультипликативную группу, и даже задать ее подгруппу, порожденную конкретными обратимыми элементами групповой алгебры. Ряд групп может быть задан непосредственным обращением к библиотечным функциям (например, симметрическая и знакопеременная группы, группа диэдра, циклическая группа и др.).

Функции для работы с группами включают определение порядка группы, вычисление классов сопряженных элементов, центра и коммутанта группы, верхнего и нижнего центрального рядов, ряда коммутантов, Силовских подгрупп, максимальных подгрупп, нормальных подгрупп, решеток подгрупп, групп автоморфизмов, и т.д. Для ряда конечных групп доступно определение их типа изоморфизма.

Теория представлений групп также входит в область применения системы GAP. Здесь имеются инструменты для вычисления таблиц характеров конкретных групп, действий над характерами и интерактивного построения таблиц характеров, определения теоретико-групповых свойств на основании свойств таблицы характеров группы. Модулярные представления групп (т.е. представления над полем, характеристика которого делит порядок группы) также могут быть исследованы с помощью GAP.

В версии 4.3 были существенным образом расширены возможности для работы с векторными пространствами, алгебрами и модулями. В системе могут быть определены векторные пространства над всеми доступными полями и модули над всеми доступными кольцами. Имеются алгоритмы для вычисления структуры конечномерных алгебр Ли, которые могут быть, например, заданы структурными константами или порождающими элементами, вычисления различных их Лиевских подалгебр и идеалов.

Версия 4.4, заменившая версию 4.3, содержит множество новых особенностей, усовершенствованных алгоритмов и средств программирования, и поэтому мы рекомендуем ее установку всем пользователям предыдущих версий. В частности, в GAP 4.4 появились новые алгоритмы и функции для работы с базисами Гребнера, алгебраическими расширениями полей, группами Галуа, таблицами характеров, векторными пространствами; новые методы для вычисления минимальных нормальных подгрупп конечной группы и цоколя конечной группы; быстрый метод для определения, является ли заданная группа подстановок симметрической или знакопеременной группой в их естественном представлении; разнообразные функции для вычислений с целочисленными матрицами, и др. нововведения.

Кроме новых алгоритмов и функций, в GAP 4.4 усовершенствована производительность многих уже существовавших ранее алгоритмов, в т.ч. для вычисления неприводимых представлений и их характеров, вычисления нормализаторов и сопряженных подгрупп в симметрических группах подстановок, вычисления системы представителей смежных классов в группах подстановок. Разложение подстановки в произведение порождающих элементов теперь вовзращает существенно более короткие слова (например, длины около 100 для группы кубика Рубика). Усовершенствования также коснулись списков, многочленов, матриц и матричных групп, расширений конечных групп, конечномерных алгебр.

Среди других областей применения системы - теория графов и их автоморфизмов, теория кодирования, теория полугрупп, кристаллография, и многое другое. Существует графический интерфейс XGAP который работает в среде Unix/Linux и позволяет, например, графически изобразить решетку подгрупп группы.

Заключение

Итак, мы проследили в общих чертах «путь», который прошла теория Галуа и рассмотрели некоторые из её применений в современной науке.

Теория групп, порожденная впервые задачами теории уравнений, превратилась в мощную и разветвленную область знаний. Она имеет три исторические корни: теория алгебраических уравнений, теория чисел и геометрия.

Теория групп, начиная с конца XIX века, оказала огромное влияние на развитие математического анализа, геометрии, механики и, наконец, физики. Оно впоследствии проникло в другие области математики - появились группы Ли в теории дифференциальных уравнений, группы Клейна в геометрии. Возникли также группы Галилея в механике и группы Лоренца в теории относительности.

Произошло это всё благодаря универсальности этого понятия.

Ведь из каких бы «предметов» ни состояла группа: из чисел, движений или операций, - все они могут рассматриваться как абстрактные элементы, не обладающие никакими специфическими признаками. Для того чтобы определить группу, надо только сформулировать общие правила, которые должны выполняться для того, чтобы данную совокупность «предметов» можно было назвать группой. В настоящее время математики называют такие правила групповыми аксиомами. Тогда мы получаем, что теория групп состоит в перечислении всех логических следствий из этих аксиом. При этом последовательно обнаруживаются все новые и новые свойства; доказывая их, математик все более и более углубляет теорию. Существенно, что ни сами предметы, ни операции над ними никак не конкретизируются. Если после этого при изучении какой-нибудь частной задачи приходится рассмотреть некоторые специальные математические или физические объекты, образующие группу, то, исходя из общей теории, можно предвидеть их свойства. Теория групп, таким образом, дает ощутимую экономию в средствах; кроме того, она открывает новые возможности применения математики в исследовательской работе.

Введение понятия группы избавило математиков от обременительной обязанности рассматривать множество различных теорий. Оказалось, что нужно лишь выделить «основные черты» той или иной теории, и так как, по сути дела, все они совершенно аналогичны, то достаточно обозначить их одним и тем же словом, и сразу становится ясно, что бессмысленно изучать их по отдельности.

Особую полезность абстрактное понятие группы получает благодаря свойству гомоморфизм, т.е. такой связи между различными группами, при котором групповая операция сохраняется. Гомоморфизм группы различной природы имеют одинаковые свойства, и изучение одной группе можно заменить изучением другой. Например, группа поворотов трехмерного тела гомоморфную группе специальных ортогональных матриц 3×3, групповой операцией которой является умножение матриц. В большой мере именно благодаря гомоморфизмам теория групп нашла широкое применение в различных областях математики и физики, поскольку позволяет выделить общие черты в объектах очень разной природы.

В настоящий момент теория групп является важной частью более глобальной области науки - «общей алгебры». В теории групп в настоящий момент много перспективных направлений, которые активно развиваются учеными всего мира.

Теория групп все теснее проникает во все научные сферы, в том числе и самые передовые.

8. Биографии

.1 Пьер Ферма (1601-1665)

Хотя уже при жизни Пьер Ферма был признан первым математиком своего времени, а после смерти слава его еще умножилась, мы о нем самом знаем очень мало. Вот то немногое, что известно о нем: он родился на юге Франции в небольшом городке Бомон-де-Ломань, где его отец - Доминик Ферма - был «вторым консулом», т. е. чем-то вроде помощника мэра. Метрическая запись о его крещении от 20 августа 1601 года гласит: «Пьер, сын Доминика Ферма, буржуа и второго консула города Бомона». Мать Пьера, Клер де-Лонг, происходила из семьи юристов. Итак, Пьер Ферма принадлежал к третьему сословию.

Доминик Ферма дал своему сыну очень солидное образование. В колледже родного города Пьер приобрел хорошее знание языков: латинского, греческого, испанского, итальянского. Впоследствии он писал стихи на латинском, французском и испанском языках «с таким изяществом, как если бы он жил во времена Августа и провел большую часть своей жизни при дворе Франции или Мадрида».

Ферма славился как тонкий знаток античности, к нему обращались за консультацией по поводу трудных мест при изданиях греческих классиков. По общему мнению, он мог бы составить себе имя в области греческой филологии.

Но Ферма направил всю силу своего гения на математические исследования. И все же математика не стала его профессией. Ученые его времени не имели возможности посвятить себя целиком любимой науке. Виет был юристом и тайным советником французских королей, Декарт - офицером, Мерсенн и Кавальери - монахами, Ферма избирает юриспруденцию. Мы не знаем, в каком городе он изучал право. Эту честь оспаривают Тулуза и Бордо. Известно только, что степень бакалавра была ему присуждена в Орлеане. С 1630 года Ферма переселяется в Тулузу, где получает место советника в Парламенте (т. е. суде). О его юридической деятельности мы читаем в упоминавшемся уже «похвальном слове», что он выполнял ее «с большой добросовестностью и таким умением, что он славился как один из лучших юристов своего времени».

В 1631 году Ферма женился на своей дальней родственнице с материнской стороны - Луизе де-Лонг. У Пьера и Луизы было пятеро детей, из которых старший, Самюэль, стал поэтом и ученым. Ему мы обязаны первым собранием сочинений Пьера Ферма, вышедшим в 1679 году. Пьер Ферма скончался 12 января 1665 года во время одной из деловых поездок.

Вот перечень тех сухих фактов, которые мы знаем о жизни величайшего математика. К сожалению, Самюэль Ферма не оставил никаких воспоминаний об отце. Правда, жизнь ученого, как правило, бывает бедна внешними событиями. Основное ее содержание раскрывается только в творчестве, которое и составляет великий духовный подвиг ученого.

Что же осталось из произведений Ферма? Собрание сочинений, которое он неоднократно пытался написать, так и не было им создано. Да это и неудивительно при той напряженной работе в суде, которую ему пришлось выполнять. Ни одно из его сочинений не было опубликовано при жизни. Однако нескольким трактатам он придал вполне законченный вид и они стали известны в рукописи большинству современных ему ученых (это были трактаты по аналитической геометрии, о максимумах и минимумах и о квадратуре парабол и гипербол). Кроме этих трактатов осталась еще обширная и чрезвычайно интересная переписка его.

8.2 Александр Теофил Вандермонд (фр. Alexandre-Théophile Vandermonde) (28 февраля 1735; Париж - 1 января 1796; Париж)

Александр Теофил Вандермонд французский музыкант и математик, член Парижской академии наук. Известен главным образом благодаря работам по высшей алгебре, особенно по теории детерминантов.

Главным увлечением Вандермонда была музыка - он играл на скрипке, а к математике обратился лишь к 35 годам. В 1771 году Вандермонд был довольно неожиданно избран в Парижскую академию наук после написания своей первой статьи (Mémoire sur la résolution des équations), в которой он провёл исследование симметрических функций и решения круговых полиномов. Эта работа предвосхитила появившуюся позднее теорию Галуа. Как заявил Леопольд Кронекер в 1888 году, с первой работы Вандермонда началась современная алгебра. Коши также утверждал, что основные идеи теории групп принадлежит Вандермонду, а не Лагранжу.

В течение следующего года вышло ещё три статьи Вандермонта, которые явились всем его вкладом в развитие математики. Статья Remarques sur des problèmes de situation (1771 год) была посвящена задаче о ходе коня, Mémoire sur des irrationnelles de différents ordres avec une application au cercle (1772) - комбинаторике, а в работе Mémoire sur l'élimination (1772) были заложены основы теории детерминантов, причём определитель Вандермонда явно в ней не упоминался.

В честь Вандермонда был назван специальный класс матриц - матрицы Вандермонда, а также элементарное равенство в комбинаторике - свёртка Вандермонда.

В 1777 году Вандермонд опубликовал результаты экспериментов, выполненных совместно с Безу и Лавуазье, по низким температурам, в частности исследования эффектов особенно сильных морозов 1776 года. Спустя 10 лет в сотрудничестве с Гаспаром Монжом и Бертолетом Вандермонд написал две статьи по производству стали, целью которой было улучшение качество стали для штыков.

8.3 Леонард Эйлер (1707 - 1783)

Эйлер, крупнейший математик XVIII в., родился в Швейцарии. В 1727 г. по приглашению Петербургской академии наук он приехал в Россию. В Петербурге Эйлер попал в круг выдающихся ученых: математиков, физиков, астрономов, получил большие возможности для создания и издания своих трудов. Он работал с увлечением и вскоре стал, по единодушному признанию современников, первым математиком мира.

Научное наследие Эйлера поражает своим объемом и разносторонностью. В списке его трудов более 800 названий. Полное собрание сочинений ученого занимает 72 тома. Среди его работ - первые учебники по дифференциальному и интегральному исчислению.

В теории числе Эйлер продолжил деятельность французского математика П. Ферма и доказал ряд утверждений: малую теорему Ферма, великую теорему Ферма для показателей 3 и 4. Он сформулировал проблемы, которые определили горизонты теории чисел на десятилетия.

Эйлер предложил применить в теории чисел средства математического анализа и сделал первые шаги по этому пути. Он понимал, что, двигаясь дальше, можно оценить число простых чисел, не превосходящих n, и наметил утверждение, которое затем докажут в XIX в. математики П. Л. Чебышев и Ж. Адамар.

Эйлер много работает и в области математического анализа.

Ученый впервые разработал общее учение о логарифмической функции, согласно которому все комплексные числа, кроме нуля, имеют логарифмы, причем каждому числу соответствует бесчисленное множество значений логарифма.

В геометрии Эйлер положил начало совершенно новой области исследований, выросшей впоследствии в самостоятельную науку - топологию.

Имя Эйлера носит формула, связывающая число вершин (В), ребер (Р) и граней (Г) выпуклого многогранника: В - Р + Г = 2.

Даже основные результаты научной деятельности Эйлера трудно перечислить. Здесь и геометрия кривых и поверхностей, и первое изложение вариационного исчисления с многочисленными новыми конкретными результатами. У него были труды по гидравлике, кораблестроению, артиллерии, геометрической оптике и даже по теории музыки. Он впервые дает аналитическое изложение механики вместо геометрического изложения Ньютона, строит механику твердого дела, а не только материальной точки или твердой пластины.

Одно из самых замечательных достижений Эйлера связано с астрономией и небесной механикой. Он построил точную теорию движения Луны с учетом притяжения не только Земли, но и Солнца. Это пример решения очень трудной задачи.

Последние 17 лет жизни Эйлера были омрачены почти полной потерей зрения. Но он продолжал творить так же интенсивно, как в молодые годы. Только теперь он уже не писал сам, а диктовал ученикам, которые проводили за него наиболее громоздкие вычисления.

Для многих поколений математиков Эйлер был учителем. По его математическим руководствам, книгам по механике и физике училось несколько поколений. Основное содержание этих книг вошло и в современные учебники.

.4 КАРЛ ФРИДРИХ ГАУСС (1777-1855)

Дата рождения: 30 апреля 1777

Место рождения: Брауншвейг

Дата смерти: 23 февраля 1855

Место смерти: Гёттинген

Гражданство: Германия

Научная сфера: математика, физика, астрономия

Альма-матер: Гёттингенский университет

Карл Фридрих Гаусс (нем. Johann Carl Friedrich Gau.; 30 апреля 1777, Брауншвейг - 23 февраля 1855, Гёттинген) - выдающийся немецкий математик, астроном и физик, считается одним из величайших математиков всех времён.

Математический талант Гаусса проявился ещё в детстве. По легенде, школьный учитель математики, чтобы занять детей на долгое время, предложил им сосчитать сумму чисел от 1 до 100. Юный Гаусс заметил, что попарные суммы с противоположных концов одинаковы: 1+100=101, 2+99=101 и т. д., и мгновенно получил результат 50*101=5050.

С 1795 по 1798 Гаусс учился в Гёттингенском университете, где 30 марта 1796 доказал возможность построения с помощью циркуля и линейки правильного семнадцатиугольника. Кроме того, он разрешил проблему построения правильных многоугольников до конца и дал критерий возможности построения любого правильного n-угольника, показав, что если n - простое число, то оно должно быть вида (числом Ферма). Этому открытию Гаусс придавал большое значение и завещал изобразить на его могиле правильный 17-угольник, вписанный в круг.

В 1799 г. Гаусс доказал основную теорему алгебры о том, что уравнение n-й степени с одной переменной имеет ровно n решений в комплексных числах.

Первым крупным трудом Гаусса в области теории чисел стала работа 1801 года «Арифметические исследования» (нем. Disquisitiones Arithmeticae), в которой дано обстоятельное изложение теории сравнений, исследованы свойства квадратичных вычетов и доказан квадратичный закон взаимности.

С 1807 года и до самой смерти Гаусс был директором гёттингенской обсерватории и ординарным профессором Гёттингенского университета. В астрономии Гаусс, в первую очередь, интересовался небесной механикой, изучал орбиты малых планет и их возмущения. В 1809 Гаусс нашёл способ определения элементов орбиты по трём полным наблюдениям (время, прямое восхождение и склонение). Для минимизации влияния ошибок измерения Гаусс разработал метод наименьших квадратов, который сейчас повсеместно применяется в статистике, и открыл нормальный закон распределения - на это открытие, по-видимому, повлияли исследования в области теории вероятностей де Бергофского, с которым молодой Гаусс, видимо, был знаком.

В геометрии поверхностей Гаусс впервые начал изучать внутреннюю геометрию, не зависящую от вложения в пространства. Он указал некоторую характеристику поверхности (гауссову кривизну), которая не изменяется при изгибаниях, тем самым заложив основы римановой геометрии.

Гаусс был тем, кто построил неевклидову геометрию, но был вынужден держать свои исследования в секрете (вероятно, из-за того, что они шли вразрез с «обожествлением» евклидова пространства в доминирующей в то время Кантовской философии). Тем не менее, сохранилось письмо Гаусса к Лобачевскому, которое ясно даёт это понять. Чуть позже, неевклидова геометрия была переоткрыта Лобачевским, и ещё чуть позже - Бояи. Гаусс высоко оценил эту работу, в частности, он выступил за принятие Лобачевского членом-корреспондентом Гёттингенского учёного сообщества. Забавным совпадением является то, что у Гаусса и Лобачевского был один и тот же школьный учитель математики.

В физике Гаусс плодотворно сотрудничал с В. Вебером в области исследования электромагнетизма. Была создана система электромагнитных единиц измерения и сконструирован примитивный телеграф.

.5 ЖОЗЕФ ЛУИ ЛАГРАНЖ (1736 - 1813)

Жозеф Луи Лагранж; фр. Joseph Louis Lagrange (25 января 1736, Турин 10 апреля 1813, Париж) - французский математик и механик. Автор классического трактата «Аналитическая механика», расширившего основы статики и механики и установившего «общую формулу», также известную как принцип возможных перемещений. Формула конечных приращений и несколько других теорем названы его именем.

Пьер-Симон Лаплас дал такую характеристику деятельности Лагранжа: «…среди тех, кто самым эффективным образом раздвинул пределы наших знаний, Ньютон и Лагранж в самой высокой степени владели счастливым искусством открывания новых данных, представляющих собой существо знаний…»

Лагранж родился 25 января 1736 в Турине, в семье банковского чиновника. Будучи самым младшим сыном многочисленной семьи, он был вынужден рано начать самостоятельную жизнь. Сначала он интересовался филологией. Его отец хотел, чтобы сын стал адвокатом, и поэтому определил его в Туринский университет. Но в руки Лагранжа случайно попал трактат по математической оптике, и он почувствовал своё настоящее призвание. Все свои силы он посвятил изучению математики и в 19 лет (по другим источникам в 17 лет) был назначен преподавателем математики в Королевской артиллерийской школе в Турине, где пользовался, несмотря на свою молодость, славой прекрасного преподавателя.

В 1755 Лагранж послал Эйлеру свою работу об изопериметрических свойствах, ставших впоследствии основой вариационного исчисления. В 1756 по представлению Эйлера стал иностранным членом Берлинской Академии наук. Принимал участие в организации в Турине научного общества (впоследствии Туринской Академии наук). В 1764 Парижская Академия наук объявила конкурс на лучшую работу по проблеме движения Луны. Лагранж представил работу, посвященную либрации Луны (см. Точка Лагранжа), которая была удостоена первой премии. В 1766 получил вторую премию Парижской Академии за исследование, посвященное теории движения спутников Юпитера, а до 1778 был удостоен еще трёх премий.

В 1766 по приглашению Фридриха II Лагранж переехал в Берлин, где стал президентом Берлинской Академии наук. Берлинский период (1766-1787) был самым плодотворным в жизни Лагранжа. Здесь он выполнил важные работы по алгебре и теории чисел, а также по решению дифференциальных уравнений в частных производных. В Берлине был подготовлен труд «Аналитическая механика» («M.canique analytique»), опубликованный в Париже в 1788 и ставший вершиной научной деятельности Лагранжа. В основу всей статики положен т. н. принцип возможных перемещений, в основу динамики - сочетание этого принципа с принципом Д’Аламбера. Введены обобщенные координаты, разработан принцип наименьшего действия.

В 1787, после кончины Фридриха II, Лагранж переехал в Париж и стал членом Парижской Академии наук. Во время Французской революции принял участие в работе комиссии, занимавшейся разработкой метрической системы мер и весов и нового календаря. В 1797, после создания Политехнической школы, вёл преподавательскую деятельность, читал курс математического анализа. В 1795, после открытия Института Франции, стал главой его физико-математического класса.

Лагранж внёс существенный вклад во многие области математики, включая вариационное исчисление, теорию дифференциальных уравнений, решение задач на нахождение максимумов и минимумов, теорию чисел (теорема Лагранжа), алгебру и теорию вероятностей. В двух своих важных трудах - «Теория аналитических функций» («Th.orie des fonctions analytiques», 1797) и «О решении численных уравнений» («De la r.solution des .quations num.riques», 1798) - подытожил всё, что было известно по этим вопросам в его время, а содержавшиеся в них новые идеи и методы были развиты в работах математиков XIX века.

Умер Лагранж в Париже 10 апреля 1813 г.

8.6 КОШИ Огюстен Луи (Cauchi Augustin Louis 1789-1857)

Огюстен Коши родился 21 августа 1789г. в Париже в семье видного чиновника. Его отец был ревностный католик и роялист. В начале с Коши занимался его отец, прекрасный лингвист, а в 1805г. Огюстен поступил в Политехническую школу, затем в 1807г.- в Школу мостов и дорог, которую окончил в 1810г. Лагранж отметил выдающиеся математические способности юноши и предсказал ему блестящее будущее. После окончания инженерной школы Коши получил ответсвенное поручение по постройке военного порта в Шербуре. Здесь в 1811г. он написал свой первый мемуар о многогранниках, где решил некоторые вопросы, не поддававшиеся первоклассным математикам. Затем последовали еще мемуары по теории многогранников, о симметрических функциях, алгебраических уравнениях, по теории чисел. В 1816г. Коши представил на конкурс Парижской академии наук знаменитое исследование по теории волн на поверхности тяжелой жидкости и получил премию. В этом же году он был назначен правительством членом Института Франции. Тогда же началась интенсивная преподавтельская деятельность Коши: с 1816г. он профессор Политехнической школы, в 1816-1830гг.- Сорбонны, в 1848-1857гг.- Колледж де Франс.

Им написаны "Курс анализа" (1821г.), "Резюме лекций, прочитанных в Королевской политехнической школе" (1823г.), "Лекции о приложении анализа к геометрии" (1826-1828). В этих курсах Коши дал определение непрерывности функции, построил строгую теорию сходящихся рядов, ввел определенный интеграл как предел интегральных сумм. Вся система анализа построена на базе предела. Книги Коши долгое время служили образцом для курса анализа.

Революция 1830г. и изгнание Карла X резко изменили судьбу Коши: не считая возможным изменить присяге Карла X, он отказался присягнуть правительству Луи Филиппа, потерял должности и вынужден был покинуть Францию. Некоторое время он провел в Швейцарии, затем получил место в Туринском университете на кафедре математической физики. Карл X, поселившийся в Праге, пригласил Коши в 1832г. в качестве учителя и воспитателя сына. Коши несколько лет путешествовал с ним по Европе. Так было до 1838г. Коши предлагали различные должности, но он отказывался от них, руководствуясь своими католическими и роялистическими убеждениями. Во Франции и в Институт он вернулся в 1838г. Революция 1848г. отменила присягу, и Коши получил кафедру в Колледже де Франс, где и проработал до самой смерти. Умер Коши 22 мая 1857г.

Коши принадлежит определение определенного интеграла. Неопределенный интеграл Коши ввел как частный случай определенного, при переменном верхнем предел. Он доказал непрерывность такого интеграла по верхнему пределу, а также доказал справедливость формулы Ньютона-Лейбница. Кроме того, Коши исследовал несобственный интеграл.

8.7 Нильс Генрих Абель (1802-1829)

В королевском парке в Осло стоит скульптура сказочного юноши, попирающего двух поверженных чудовищ; по цоколю идет надпись "ABEL".

Что же символизируют чудовища? Первое из них, несомненно, - алгебраические уравнения 5 степени. Еще в последних классах школы Абелю показалось, что он нашел формулу для их решения, подобную тем, которые существуют для уравнений степени, не превышающей четырех. Никто в провинциальной Норвегии не смог проверить доказательство. Абель сам нашел у себя ошибку, он уже знал, что не существует выражения для корней в радикалах. Тогда Абель не знал, что итальянский математик П. Руффини опубликовал доказательство этого утверждения, содержащее, однако, пробелы.

К тому времени Абель был уже студентом университета в Осло (тогда Христиании). Он был совершенно лишен средств к существованию, и первое время стипендию ему выплачивали профессора из собственных средств. Затем он получил государственную стипендию, которая позволила ему провести два года за границей. В Норвегии были люди, которые понимали, сколь одарен Абель, но не было таких, кто мог бы понять его работы. Будучи в Германии, Абель так и не решился посетить К. Гаусса.

Во Франции Абель с интересом собирает математические новости, пользуется каждой возможностью увидеть П. Лапласа или А. Лежандра, С. Пуассона или О. Коши, но серьезных научных контактов с великими математиками установить не удалось. Представленный в академию "Мемуар об одном очень общем классе трансцендентных функций" не был рассмотрен, рукопись Абеля была обнаружена через сто лет (в скульптуре эту работу олицетворяло второе поверженное чудовище). Речь шла о рассмотрении некоторого класса замечательных функций, получивших название эллиптических и сыгравших принципиальную роль в дальнейшем развитии математического анализа. Абель не знал, что 30 лет назад в этих вопросах далеко продвинулся Гаусс, но ничего не опубликовал.

В 1827 г. Абель возвращается на родину, и там выясняется, что для него нет работы. Он получает временную работу вместо профессора, уехавшего в длительную экспедицию в Сибирь. Долги становятся его вечным уделом, но работоспособность Абеля не уменьшается. Он продолжает развивать теорию эллиптических функций, близок к пониманию того, какие уравнения решаются в радикалах. Неожиданно появляется соперник - К. Г. Якоби, который был на два года младше Абеля. Якоби публикует замечательные результаты в области, которую Абель считал своей собственностью. И Абель работает еще интенсивнее и, наконец, сообщает: "Я нокаутировал Якоби".

К работам Абеля пришло признание, математики стали проявлять заботу о его судьбе. Французские академики-математики обращаются с посланием шведскому королю, правившему Норвегией, с просьбой принять участие в судьбе Абеля. Тем временем у Абеля быстро прогрессирует туберкулез, и 6 апреля 1829 г. его не стало.

8.8 Эварист Галуа (1811-1832)

Он прожил двадцать лет, всего пять из них занимался математикой. Математические работы, обессмертившие его имя, занимают чуть более 60 страниц.

В 15 лет Галуа открыл для себя математику и с тех пор, по словам одного из преподавателей, "был одержим демоном математики". Юноша отличался страстностью, неукротимым темпераментом, что постоянно приводил его к конфликтам с окружающими, да и с самим собой.

Галуа не задержался на элементарной математике и мгновенно оказался на уровне современной науки. Ему было 17 лет, когда его учитель Ришар констатировал: "Галуа работает только в высших областях математики". Ему было неполных 18 лет, когда была опубликована его первая работа. И в те же годы Галуа два раза подряд не удается сдать экзамены в Политехническую школу, самое престижное учебное заведение того времени. В 1830 г. Он был принят в привилегированную Высшую нормальную школу, готовившую преподавателей. За год учебы в этой школе Галуа написал несколько работ; одна из них, посвящена теории чисел, представляла исключительный интерес.

Бурные июльские дни 1830 г. Застали Галуа в стенах Нормальной школы. Его все более захватывает новая страсть - политика. Галуа присоединяется к набиравшей силы республиканской партии - Обществу друзей народа, - недовольной политикой Луи-Филиппа. Возникает конфликт с директором школы, всеми силами противодействовавшим росту политических интересов у учащихся, и в январе 1831 г. Галуа исключают из школы. В январе 1831 г. Галуа передал в Парижскую академию наук рукопись своего исследования о решении уравнений в радикалах. Однако академия отвергла работу Галуа - слишком новы были изложенные там идеи. В это время Галуа находился в тюрьме Сент-Пелажи после попытки организовать манифестацию 14 июля (в годовщину взятия Бастилии), на сей раз Галуа приговорен к 9 месяцам тюрьмы. За месяц до окончания срока заключения Галуа переводят в больницу. В тюрьме он встретил свое двадцатилетие.

апреля он выходит на свободу, но ему было суждено прожить лишь только один месяц. 30 мая он был тяжело ранен на дуэли. На следующий день он умер. В день перед дуэлью Галуа написал своему другу Огюсту Шевалье письмо: "Публично обратись к Якоби или Гауссу с просьбой дать мнение не об истинности, а о значении тех теорем, развернутого доказательства которых я не даю, и тогда, надеюсь, кто-нибудь сочтет полезным разобраться во всей этой путанице". Работы Галуа содержали окончательное решение проблемы о разрешимости алгебраических уравнений в радикалах, то, что сегодня называется теорией Галуа и составляет одну из самых глубоких глав алгебры. Другое направление в его исследованиях связано с так называемыми абелевыми интегралами и сыграло важную роль в математическом анализе XIX века. Работы Галуа были опубликованы лишь в 1846 г. Ж. Лиувиллем, а признание к ним пришло еще позже, когда с 70-х годов понятие группы постепенно становится одним из основных математических объектов.

8.9 Куммер, Эрнст Эдуард

Эрнст Эдуард Куммер (нем. Ernst Eduard Kummer; 29 января 1810 - 14 мая 1893) - немецкий математик, наиболее значительные труды относятся к алгебре и теории чисел. Член Берлинской академии наук (1855), иностранный член Парижской Академии наук (1868), Лондонского Королевского общества (1863) и Петербургской Академии наук (1862).

Куммер родился в прусском городе Зорау (сейчас это город Жары в Польше), в семье врача. В раннем возрасте лишился отца, но героические усилия матери помогли талантливому юноше получить образование.

: Куммер поступает в университет Галле, где изучает математику, теологию и философию.

: заканчивает университет. За одну из работ по математическому анализу университет сразу присуждает ему докторскую степень.

Следующие 10 лет Куммер преподаёт математику и физику в высшей гимназии Лигница (ныне Лигнице). Среди его учеников был Кронекер, дружбу с которым он сохранил на всю жизнь.

В это время Куммер обращает на себя внимание научного мира публикацией нескольких работ по гипергеометрическим рядам. В 1839 году его избирают в Берлинскую Академию наук.

: женится на двоюродной сестре Дирихле.

: по рекомендации Дирихле и Якоби получает кафедру профессора математики в Бреслау (ныне Вроцлав).

: умирает жена Куммера.

: переезжает в Берлин, где преподаёт в Берлинском университете. Помогает перебраться туда Вейерштрассу. С этого момента берлинская математическая школа становится одной из ведущих в Европе.

: уходит в отставку и 3 года спустя умирает.

Среди учеников Куммера, кроме упомянутого Кронекера, были такие известные математики, как П. Дюбуа-Реймон (англ.), П. Гордан, К. Г. А. Шварц и Г. Кантор.

Куммер внёс вклад в анализ, теорию алгебраических чисел, геометрию, теоретическую механику.

В анализе он продолжил работы Гаусса по гипергеометрическим рядам. Его имя носит известный признак сходимости.

В теории чисел он с 1837 года много занимался Великой теоремой Ферма и доказал её для целого класса простых показателей. Проблему он не решил, но в ходе исследования получил множество ценных результатов, например, открыл идеальные числа и описал их необычные свойства (1846). За эти работы он получил Большой приз Парижской Академии наук (1857).

Куммер также доказал закон взаимности для всех степенных вычетов с простым показателем. Продвинуться дальше удалось только Гильберту спустя несколько десятилетий.

8.10 Кронекер, Леопольд

Леопо́льд Кро́некер (нем. Leopold Kronecker; 7 декабря 1823, Лигниц, Германия, ныне Легница, Польша - 29 декабря 1891, Берлин, Германия) - немецкий математик. Брат известного физиолога Гуго Кронекера (1830-1914). Родился в еврейской семье, за год до смерти принял христианство.

Иностранный член-корреспондент Петербургской Академии наук (1872), член Берлинской АН (1861), профессор университета в Берлине. Основные труды по алгебре и теории чисел, где он продолжил работы своего учителя Э. Куммера по теории квадратичных форм и теории групп. Большое значение имеют его исследования по арифметической теории алгебраических величин.

Был сторонником «арифметизации» математики, которая по его мнению, должна быть сведена к арифметике целых чисел; только последняя, как он утверждал, обладает подлиной реальностью. Защищая эти взгляды, вёл упорную дискуссию с принципами теоретико-функциональной школы К. Вейерштрасса и теоретико-множественной школы Г. Кантора. Следующее его выражение стало знаменитым: Бог создал натуральные числа, всё остальное - создание человека.

Написал свыше 120 больших и малых мемуаров, печатавшихся в специальных журналах. В своих исследованиях Кронекер, путём применения эллиптических функций, получил ряд новых данных для теории чисел. Его «Grundzüge einer arithmet. Theorie der algebraischen Grössen» изданы, вместе с перепечаткой его докторской диссертации «De unitatibus complexis», в качестве юбилейного издания в честь Куммера (Б., 1882), а мемуары «Ueber den Zahlenbegriff» появились в «Philosoph. Aufsätze» (Лейпциг, 1887), изданных к 50-летнему докторскому юбилею Эдуарда Целлера.

По поручению Берлинской академии наук Кронекер приступил к изданию сочинений своего учителя Дирихле (т. I, Б., 1890); переписку последнего с Кронекером издал Шеринг в «Göttinger Nachrichte» 1885. При содействии Вейерштрасса, Гельмгольца, Шретера и Фукса, Кронекер продолжал издание «Journal für Mathematik», основанного Креллем.

8.11 Кэли, Артур

А́ртур Кэ́ли (другие варианты написания фамилии Кейли, Кэйлей; англ. Arthur Cayley; (16 августа 1821, Ричмонд - 26 января 1895)

Артур Кэли родился в Ричмонде (Лондон), Англия. Его отец Генри Кэли был дальним родственником сэра Джорджа Кэли - новатора в авиации, который ведёт род от старинной семьи графства Йоркшир. Он торговцем поселился в Санкт-Петербурге (Россия). Его мать, Мария Антония Доти, была дочерью Вильяма Доти. Согласно некоторым источникам, она была русской, хотя имя отца говорит об английском происхождении. Его брат, Чарльз Багот Кэли, был лингвистом.

Артур провёл свои первые восемь лет в Санкт-Петербурге. В 1829 году его родители переехали в Блэкхис (англ. Blackheath) вблизи Лондона (ныне район Большого Лондона). Артур пошёл в частную школу.

Ещё когда Кэли был ребёнком, он решал сложные математические задачи ради забавы.

В 14 лет он пошёл в школу Кингс-колледж. Школьный учитель увидел в мальчике гения и посоветовал отцу не учить своему бизнесу, как он(отец) намеревался, а готовить к поступлению в Кембриджский университет.

В необыкновенно раннем возрасте 17 лет Кэли поступил в кембриджский Тринити-колледж. В то время Аналитическое общество (Analytical Society) процветало, и Грегори и Лесли Еллис основали Кембриджский математический журнал. В возрасте 20 лет Кэли передал этому журналу три рукописи на темы навеянные чтением Mécanique analytique Лагранжа и некоторыми работами Лапласа.

Его наставником в кембридже был Джордж Пикок, а его личным наставником был Вильям Хопкинс.

Кэли закончил свое студенческое образование лучшим студентом курса (англ. Senior Wrangler) и также получил первый из двух призов Смита, присуждаемых ежегодно за студенческие научные исследования. Его следующим шагом было получение степени Master of Arts (MA degree), и получение должности в университете по конкурсу. Он остался в Кембридже в течение 4 лет. В это время он взял себе несколько учеников, но его основной работой была подготовка 28 мемуаров для Кембриджского математического журнала.

В связи с тем, что его должность была с ограниченным сроком пребывания, было необходимо выбирать профессию. Как и Морган, Кэли выбрал профессию адвоката, и в возрасте 25 лет стал членом лондонского судебного инна Линкольна. Он выбрал специальность связанную с транспортировкой. Когда он был учеником, и сдавал адвокатский экзамен, он ездил в Дублин слушать лекцию Гамильтона про кватернионы.

Его друг Сильвестр был тогда актуарием. У них было привычкой гулять вместе вокруг судебного инна Линкольна, обсуждая теорию инвариантов и ковариантов. В течение этого периода его жизни, длящегося примерно 14 лет, Кэли выпустил от 200 до 300 работ.

В Кембриджском университете с давних времён профессор чистой математики назывался Лукасовским профессором, эту должность некогда занимал Исаак Ньютон. Примерно в 1860 году несколько фондов, завещанных Лэди Сэдлер университету, стали бесполезными для их настоящей цели и были использованы для основания ещё одной именной профессуры. В обязанности Сэдлеровского профессора входило объяснять и обучать принципам чистой математики, и заниматься продвижением науки. На эту должность Кэли был избран, когда ему было 42 года. Он оставил доходную практику ради скромной зарплаты, но никогда об этом не жалел.

Должность профессора позволила ему прекратить разделять верность к юриспруденции с верностью к математике и полностью заняться любимым делом. Сразу же после этого Кэли женился и поселился в Кембридже.

Более удачно чем у Гамильтона, дом Кэли был полон счастья. Его друг и приятель, исследователь Сильвестр, однажды отметил, что Кэли более удачлив, чем он сам; они оба были холостяками и вместе жили в Лондоне, но Кэли женился и поселился в Кембридже с его тихой и мирной жизнью, а Сильвестр так и не женился и сражался со всем миром всю свою жизнь.

Кэли - один из плодовитейших учёных XIX века, написавший более 700 работ. Большая часть его работ относится к линейной алгебре, дифференциальным уравнениям и эллиптическим функциям. В частности, он доказал теорему Гамильтона-Кэли о том, что каждая квадратная матрица является корнем своего характеристического многочлена.

Он был первым, кто сформулировал определение группы в том виде, как она определяется сегодня - множество с бинарной операцией, удовлетворяющей определённым законам. Прежде же, когда математики говорили о группе, они подразумевали группу перестановок.

В 1882 Лондонское королевское общество присудило ему Медаль Копли.

8.12 Жордан Мари Энмон Камиль (05.01.1838 - 21.01.1922)

Жордáн Мари Энмон Камиль (Jordan Marie Ennemond Camille), род. 5.1.1838, Лион - ум. 21.1.1922, Париж.

Французский математик, иностранный чл.-корр. Петербургской АН (с 2.12.1895), член Парижской АН (1881). Издатель "Journal de mathématiques pures et appliquées" (1885-1921). Основные труды по алгебре, теории функций, а также топологии и кристаллографии. С именем Жордана связаны: теорема Жордана - Гёльдера о композиционных рядах групп, нормальная (жорданова) форма матриц, кривая Жордана; им введено понятие функции с ограниченным изменением. Жордану принадлежат первый систематический курс теории групп и теории Галуа (1870) и трёхтомный курс анализа (1882-87).

8.13 Ли Мариус Софус

Ли Мариус Софус (17.XII.1842 - 18.II.1899) - норвежский математик. Родился в Эйд (близ Норфьордейде). В 1865 году окончил университет в Христиании. За работу "О представлении мнимых чисел в геометрии" получил (1869 г.) стипендию для поездки в европейские научные центры (Берлин, Париж).

В 1871 г. за работу "Об одном классе геометрических преобразований" присуждена ученая степень доктора философии.

В 1877 - 1886 гг. профессура в университете Христиании. С 1886 г. - профессор Лейпцигского университета.

Работы посвящены теории групп и дифференциальной геометрии. Создатель классической. теории непрерывных групп (называемой теорией групп Ли), развитой впоследствии в общую теорию непрерывных групп. Первые работы (1871-72гг.) относились к чисто геометрическим вопросам. Однако уже в 1872г. Ли обратился к теории дифференциальных уравнений, ввел в нее понятия и методы n-мерной геометрии.

Теория групп Ли, возникшая из стремления внести об'единяющее начало и установить общие точки зрения в самых разнообразных отделах математики, оказала глубокое влияние на дальнейшее развитие теории дифференциальных уравнений, алгебры, оснований геометрии, топологии и теоретической физики. В результате работ Ли (и Ф. Клейна) геометрия была перестроена на основе теоретико-групповых преобразований.

Международная премия им. Н.И.Лобачевского присуждена в 1897 году за работу по применению теории групп для обоснования геометрии Лобачевского.

8.14 Феликс Христиан Клейн

Феликс Христиан Клейн (нем. Felix Christian Klein; 1849-1925) - немецкий математик и педагог. Член Берлинской академии наук (1913), иностранный член-корреспондент Петербургской академии наук (1895).

Феликс Клейн родился в Дюссельдорфе, в семье чиновника. Закончил гимназию в Дюссельдорфе, потом учился математике и физике в Боннском университете. Вначале планировал стать физиком. В это время Юлиус Плюккер заведовал отделением математики и экспериментальной физики в Бонне, и Клейн стал его ассистентом. Однако главным интересом Плюккера была геометрия. Под его руководством Клейн стал доктором в 1868 году.

: Плюккер умер. Клейн совершает поездку по Германии, знакомится с Клебшем и другими крупными математиками. Особенное влияние на него оказал Софус Ли.

: в самое неудачное время (назревает франко-прусская война) вместе с Ли приезжает в Париж, где знакомится с Дарбу и Жорданом. После начала войны возвращается в Германию, где чуть не становится жертвой спутника войны - эпидемии тифа.

: профессор Эрлангенского университета, по рекомендации Клебша. Публикует знаменитую «Эрлангенскую программу» и сразу приобретает общеевропейскую известность.

: профессор Высшей технической школы в Мюнхене. Женится на Анне Гегель, внучке знаменитого философа.

: совместно с Адольфом Майером становится главным редактором журнала «Mathematische Annalen».

: переходит в Лейпцигский университет.

-1884: серьёзная болезнь по причине переутомления. Клейн переориентирует свою гигантскую энергию на педагогическую и общественную работу.

: профессор Гёттингенского университета. Ведёт яркие, глубокие и содержательные факультативные курсы по самым разнообразным предметам, от теории чисел до технической механики. Слушатели его курсов приезжали со всех концов мира.

В начале XX века Клейн принял активное участие в реформе школьного образования, автор и инициатор ряда исследований состояния дел с преподаванием математики в разных странах.

Клейн способствовал созданию при Гёттингенском университете системы научно-исследовательских институтов для прикладных исследований в самых разных технических областях. Участвовал в издании полного собрания сочинений Гаусса и первой Математической энциклопедии. Представлял Гёттингенский университет в парламенте. Надо отметить, что с началом Первой мировой войны Клейн не участвовал в многочисленных тогда шовинистических акциях.

: широко отмечается 75-летие Клейна. В следующем году те же газеты опубликовали его некролог.

8.15 Артин, Эмиль

Э́миль А́ртин (нем. Emil Artin, 3 марта 1898, Вена, Австро-Венгрия - 20 декабря 1962, Гамбург, ФРГ) - выдающийся математик. Уроженец Австро-Венгрии, университетское образование получил в Германии, научной деятельностью занимался в университетских центрах Германии и США.

Родился в Вене, вырос в Райхенберге (ныне Либерец в Чехии). Родители будущего математика - Эмиль Артин[1], торговец предметами искусства (умер в 1906 году), и Эмма Лаура-Артин, до своего второго замужества - певица в оперетте. Фамилию свою Эмиль Артин унаследовал от деда-армянина, торговца коврами[2], который перебрался в Вену в XIX веке[3].

По утверждению Майкла, сына Артина, фамилия «Артин» происходит от армянской фамилии «Артинян» (Artinian), которую, по его словам, «укоротили» в Германии и США[4].

В 1916 году Эмиль поступил в Венский университет (здесь он проучился всего один семестр, после чего был призван в армию), а в 1919 году продолжил учёбу в Лейпциге (Германия). По окончании преподавал в немецких университетах, в основном в Гамбурге. В 1929 году женился на своей студентке, Natalie (Natascha) Jasny, которую родители после революции вывезли из России. Она была наполовину еврейкой[5], и после прихода нацистов к власти и принятия антиеврейских законов Артин в 1937 году был уволен из Гамбургского университета[3] и эмигрировал в США, где работал в Индианском (1938-1946) и Принстонском университете (1946-1958), после чего вновь вернулся в Гамбург.

Артин имел работы во многих областях математики - можно указать на аксиоматическое определение Γ-функции, работы по проективной геометрии или теорию кос, связанную с топологией, - но главный интерес для него представляла алгебра. Совместно с Э. Нётер Артин создал современную общую алгебру. Его работы составляют значительную часть знаменитой «Современной алгебры» (ныне просто «Алгебры») ван дер Вардена. В особенности важен его вклад в теорию полей, где он совместно с О. Шрайером создал теорию вещественных полей, а затем решил знаменитую 17-ю проблему Гильберта. Не менее важны его работы в алгебраической теории чисел, главным образом в теории полей классов, где он применил аппарат когомологий Галуа.

Сформулировал закон взаимности.

Среди учеников Эмиля Артина - Серж Ленг и Джон Тэйт; его сын Майкл Артин - также известный математик.

8.16 Фердина́нд Гео́рг Фробе́ниус

Фердина́нд Гео́рг Фробе́ниус (нем. Ferdinand Georg Frobenius; 26 октября 1849, Берлин - 3 августа 1917, Шарлоттенбург) - немецкий математик.

В 1867 году один семестр посещал занятия в Гёттингенском университете, затем продолжил обучение в университете Гумбольдта в Берлине, в 1870 году защитил там диссертацию под руководством Карла Вейерштрасса и Эрнста Эдуарда Куммера. Некоторое время преподавал в берлинской гимназии, в 1874 году, без обычной для этого хабилитации, был принят на должность профессора в Берлинский университет. На следующий год перешел в Цюрихский Политехникум, в 1892 году вернулся в Берлинский Университет, заняв место умершего Леопольда Кронекера.

Член Прусской академии наук (1893). Вместе с Кронекером, Лазарусом Иммануэлем Фуксом и Германом Амандусом Шварцем принадлежал к узкому кругу известнейших берлинских математиков своего времени.

Основные работы Фробениуса относятся к теории групп, в частности, к теории представлений

Он первым доказал, что алгебры с делением над R существуют только в пространствах размерности один (вещественные числа), два (комплексные числа) и четыре (кватернионы). (Теорема Фробениуса)

8.17 Нётер, Эмми

Ама́лия Э́мми Нётер (нем. Amalie Emmy Noether ; 23 марта 1882, Эрланген, Германия - 14 апреля 1935, Брин-Мор, Пенсильвания, США) - выдающийся немецкий математик, «самая крупная женщина-математик, когда-либо существовавшая».

Отметим, что Эмми - не сокращение от «Амалии», как часто полагают, а второе имя Нётер.

Родилась в еврейской семье математика Макса Нётера в Эрлангене, где была старшей из 4 детей. Первоначально изучала языки, планируя стать преподавателем английского и французского . С этой целью добилась разрешения посещать лекции в Эрлангенском университете, где работал её отец, вначале вольнослушательницей (1900), а с 1904 года, когда разрешили женское обучение, зачислена официально. Однако в университете лекции по математике привлекали Эмми больше, чем любые другие. Она стала ученицей математика Пауля Гордана, под руководством которого защитила в 1907 году диссертацию по теории инвариантов.

Уже в 1915 году Нётер внесла вклад в разработку Общей теории относительности; Эйнштейн в письме к мировому лидеру математиков Давиду Гильберту выразил восхищение «проницательным математическим мышлением» Нётер.

В 1916 году Нётер переехала в Гёттинген, где знаменитые математики Давид Гильберт и Феликс Клейн продолжали работы по теории относительности, и знания Нётер в области теории инвариантов были им нужны. Гильберт оказал на Нётер огромное влияние, сделав её сторонницей аксиоматического метода. Он пытался сделать Нётер приват-доцентом Гёттингенского университета, но все его попытки провалились из-за предрассудков профессуры, в основном в области гуманитарных наук. Стала известна фраза Гильберта:

«Не понимаю, почему пол кандидата служит доводом против избрания её приват-доцентом. Ведь здесь университет, а не мужская баня.»

Нётер тем не менее, не занимая никакой должности, часто читала лекции за Гильберта. Лишь по окончании Первой мировой войны она смогла стать приват-доцентом в 1919 году, затем сверхштатным профессором (1922).

Самый плодотворный период научной деятельности Нётер начинается около 1920 года, когда она создаёт целое новое направление в абстрактной алгебре. С 1922 года она работает профессором Гёттингенского университета, возглавляет авторитетную и быстро растущую научную школу.

Современники описывают Нётер как на редкость умную, обаятельную и приветливую женщину. Её женственность проявлялась не внешне, а в трогательной заботе об учениках, всегдашней готовности помочь им и коллегам. В числе ее преданных друзей были ученые с мировым именем: Гильберт, Герман Вейль, Эдмунд Ландау, нидерландский математик Л. Брауэр, советские математики П. С. Александров, П. С. Урысон и многие другие.

Нётер придерживалась социал-демократических взглядов. На протяжении 10 лет жизни она сотрудничала с математиками СССР; в 1928-1929 учебном году читала лекции в Московском университете, где она оказала влияние на Л. С. Понтрягина и особенно на П. С. Александрова, до этого часто бывавшего в Гёттингене. П. С. Александров вспоминал:

Вершиной всего услышанного мною в это лето в Гёттингене были лекции Эмми Нётер по общей теории идеалов… Конечно, самое начало теории заложил Дедекинд, но только самое начало: теория идеалов во всём богатстве её идей и фактов, теория, оказавшая такое огромное влияние на современную математику, есть создание Эмми Нётер. Я могу об этом судить, потому что я знаю и работу Дедекинда, и основные работы Нётер по теории идеалов.

Лекции Нётер увлекли и меня, и Урысона. Блестящими по форме они не были, но богатством своего содержания они покоряли нас. С Эмми Нётер мы постоянно виделись в непринуждённой обстановке и очень много с ней говорили, как на темы теории идеалов, так и на темы наших работ, сразу же её заинтересовавших.

Наше знакомство, живо завязавшееся этим летом, очень углубилось следующим летом, а затем, после смерти Урысона, перешло в ту глубокую математическую и личную дружбу, которая существовала между Эмми Нётер и мною до конца её жизни. Последним проявлением этой дружбы с моей стороны была речь памяти Эмми Нётер на собрании Московской международной топологической конференции в августе 1935 года[4].

В 1932 году Нётер, совместно со своим учеником Эмилем Артином, получает премию Аккермана-Тёбнера за достижения в математике.

После прихода нацистов к власти в 1933 году Нётер, как еврейке, пришлось эмигрировать в США, где она стала преподавателем женского колледжа в Брин-Море (Пенсильвания) и приглашённым преподавателем Института перспективных исследований в Принстоне. Младший брат Эмми, одарённый математик Фриц Нётер, уехал в СССР, где был расстрелян в сентябре 1941 года за «антисоветские настроения».

Несмотря на блестящие математические достижения, личная жизнь Нётер не сложилась. Непризнание, изгнание, одиночество на чужбине, казалось бы, должны были испортить её характер. Тем не менее, она почти всегда выглядела спокойной и доброжелательной. Герман Вейль писал, что даже счастливой.

В 1935 году Эмми Нётер умерла после неудачной операции по удалению раковой опухоли.

Академик П. С. Александров писал:

«Если развитие математики сегодняшнего дня несомненно протекает под знаком алгебраизации, проникновения алгебраических понятий и алгебраических методов в самые различные математические теории, то это стало возможным лишь после работ Эмми Нётер.»

А. Эйнштейн в заметке на её смерть отнёс Нётер к величайшим творческим гениям математики.

В основном труды Нётер относятся к алгебре, где они способствовали созданию нового направления, известного под названием абстрактной алгебры. В эту область Нётер внесла решающую роль (наряду с Эмилем Артином и её учеником Б. Л. ван дер Варденом). Герман Вейль писал:

Значительная часть того, что составляет содержание второго тома «Современной алгебры» (Теперь просто «Алгебры») ван дер Вардена, должно принадлежать Эмми Нётер

Термины «нётерово кольцо», «нётеров модуль», теоремы о нормализации и теорема Ласкера-Нётер о разложении идеала теперь являются основополагающими.

Большой вклад внесла Нётер в математическую физику, где её именем называется фундаментальная теорема теоретической физики (опубликована в 1918 году), связывающая законы сохранения с симметриями системы (например, однородность времени влечет закон сохранения энергии). На этом плодотворном подходе основана знаменитая серия книг «Теоретической физики» Ландау-Лифшица. Особенно важное значение имеет теорема Нётер в квантовой теории поля, где законы сохранения, вытекающие из существования определенной группы симметрии, обычно являются главным источником информации о свойствах исследуемых объектов.

Идеи и научные взгляды Нётер оказали огромное влияние на многих учёных-математиков и физиков. Она воспитала ряд учеников, которые стали учёными мирового класса и продолжили открытые Нётер новые направления.

8.18 Колмогоров Андрей Николаевич (1903-1987)

Русский математик. Родился 12(25) апреля 1903 в Тамбове. После смерти матери воспитывался и был усыновлен ее сестрой. Раннее детство провел в родовом имении родителей матери в Ярославской губернии. В 1910, после переезда в Москву, поступил в частную гимназию Е.А.Репман, организованную кружком радикально настроенной интеллигенции. Здесь совместно обучались мальчики и девочки по программе мужской гимназии, явление уникальное в то время. Отличные успехи по математике позволили будущему ученому заниматься по этому предмету на класс старше, однако на время интерес к другим наукам взял верх, и первый научный доклад, который 17-летний Колмогоров сделал в МГУ, был посвящен вовсе не математике: на семинаре С.В.Бахрушина он выступил с сообщением о Новгородском землевладении. Впрочем, при анализе писцовых книг 15-16 вв. им были использованы элементы математической теории вероятностей.

В 1920 А.Н.Колмогоров поступил на математическое отделение университета (куда в то время принимали всех желающих без экзаменов) и одновременно - на металлургический факультет Менделеевского института. Но скоро интерес к математике перевесил все остальное. С 1922 параллельно с занятиями в университете он преподавал математику в средней школе. В том же году под руководством проф. В.В.Степанова начал заниматься теорией тригонометрических рядов, несколько позднее стал учеником Н.Н.Лузина. Ко времени окончания университета у Колмогорова было уже около 15 статей по теории функций действительного переменного.

Окончив в 1925 университет, поступил в аспирантуру. Продолжая заниматься под руководством Н.Н.Лузина теорией функций действительного переменного, начал (совместно с А.Я.Хинчиным) работать в области теории вероятностей, ставшей потом его основной узкой специальностью. После аспирантуры работал в НИИ математики и механики МГУ (в 1933-1939 и 1951-1953 был его директором).

В 1930-1931 в течение девяти месяцев стажировался в университетах Гёттингена, Мюнхена и Парижа, где познакомился с Р. Курантом, Г. Вейлем, Д. Гильбертом и др. С 1931 Колмогоров - профессор МГУ. В 1954-1956, а затем с 1978 и до конца жизни - заведующий отделением математики механико-математического факультета МГУ, с 1954 по 1956 - декан факультета.

Широта научных интересов Колмогорова беспрецендентна: их спектр простирается от метеорологии (Колмогоров был почетным членом Американского метеорологического общества) до теории стиха (вышел сборник его стиховедческих работ под редакцией Д.С. Лихачева). В известной хрестоматии ван Хейеноорта (Van Heijenoort J) она входит в серию, каждая из книг которой представляет собой сборник статей, определивших структуру той или иной науки, посвященной математической логике, помещена статья 22-летнего Колмогорова. Составитель характеризует ее как «первое систематическое изучение интуиционной логики». Галерея портретов ученых в области классической механики, приведенная в классической монографии Абрахама и Марсдена Основания механики, содержит наряду с портретом Архимеда и портрет Колмогора, а его доклад Общая теория динамических систем и классическая механика на Международном математическом конгрессе 1954 в Амстердаме полностью воспроизведен в монографии. Помимо классической механики, Колмогоров внес выдающийся вклад в аэродинамику (теория турбулентности).

Однако основной сферой деятельности Колмогорова была математика. Перечень лишь некоторых областей математики, где он оставил глубокий след, включает теорию функций (где студенческая работа 19-летнего автора, устанавливающая существование почти всюду расходящегося ряда Фурье, сразу сделала его знаменитым); теорию множеств; топологию (где он разделил авторство теории гомологий с П.С. Александровым); теорию информации (где он вместе с Шенноном построил основание этой науки); теорию алгоритмов. И наконец, теорию вероятностей, признанным во всем мире главой которой он был. Применив здесь методы теории функций действительного переменного, он построил (совместно с А.Я.Хинчиным) систему аксиоматического обоснования этой науки (1933). Работы Колмогорова по предельным теоремам, общей теории случайных процессов и теории марковских процессов продолжают играть важную роль в современной теории вероятностей, а его труд Основные понятия теории вероятностей (1933) считается классическим. Используя теорию вероятностей, Колмогоров разработал метод, позволяющий строить прогнозы на основе наблюдения случайных событий. Этот метод нашел применение при решении широкого круга проблем, таких, например, как задача о посадке самолета на палубу авианосца в открытом море, сводящаяся к вычислению наиболее вероятного места нахождения авианосца в данный момент.

Глубину исследований Колмогорова иллюстрирует то, что значение введенных им понятий со временем лишь возрастает. Так, в начале 1954 им была предложена общая идея нумерации и понятие сводимости нумераций. Сейчас основанная на этих представлениях теория нумераций составляет важную ветвь теории алгоритмов, ей посвящаются монографии и конференции. Пионерскими были и многие предложенные Колмогоровым методы. Так, при исследовании знаменитой проблемы Гильберта о суперпозициях он не только показал возможность представления любой непрерывной функции в виде суперпозиции непрерывных же функций трех переменных, но и создал метод, позволивший его ученику В.И.Арнольду в 1957 понизить число переменных до двух и тем самым решить упомянутую проблему.

Колмогорову принадлежит первое место среди отечественных математиков по числу иностраннх академий и научных обществ, избравших его своим членом, а также университетов, сделавших его своим почетным доктором. Среди них: Парижская АН, Лондонское королевское общество, Германская АН «Леопольдина», Лондонской математическое общество, Национальная академия США и т.д.

Колмогоров внес уникальный вклад в дело распространения математических знаний. Он автор школьных учебников и многочисленных научно-популярных статей, инициатор издания физико-математического журнала для юношества «Квант». Ему же принадлежит идея создания знаменитого интерната при МГУ для одаренных в физике и математике иногородних школьников. Многие ученики Колмогорова стали крупными учеными в разных областях математики, среди них - В.И.Арнольд, И.М.Гельфанд, М.Д.Миллионщиков, Ю.В.Прохоров и др.

Умер Колмогоров в Москве 20 октября 1987.

8.19 Отто Юльевич Шмидт

Отто Юльевич Шмидт (30 сентября 1891 - 7 сентября 1956) - российский ученый, государственный деятель, один из организаторов освоения Северного морского пути, академик (1935), вице-президент АН СССР (1939-42), академик АН Украины (1934), Герой Советского Союза (1937). В 1918-22 в Наркомпроде, Наркомфине, Наркомпросе.

В 1932-39 начальник Главсевморпути. Руководитель экспедиций на «Седове» (1929-30), «Сибирякове» (1932), «Челюскине» (1933-1934), воздушной экспедиции по организации дрейфующей станции «СП-1» (1937). Разрабатывал космогоническую гипотезу образования тел Солнечной системы в результате конденсации околосолнечного газово-пылевого облака. Труды по высшей алгебре (теории групп). Один из основателей и главный редактор Большой Советской Энциклопедии (1924-42).

В русском подданстве предки Шмидтов состояли с XVIII века. В семье говорили на русском, латышском и немецком языках, хотя Отто Юльевич и отмечал, что согласно "своему самосознанию по паспорту он является русским". Его отец по происхождению был немцем, а мать латышкой.

Отец служил в Могилеве и Одессе мелким торговым служащим. Отто родился 18 (30) сентября 1891 года в Могилеве. Детские годы Отто Шмидта прошли здесь же. В семье, кроме него, было еще четверо детей.

Шмидты жили бедно, поэтому дети не могли получить приличного образования. Однако Отто, старший сын, рано обнаружил способности, одаренность, любознательность, стремление к знаниям. Поэтому на семейном совете было принято решение помочь ему получить образование.

Отец не был слишком удачлив в торговле, а потому материальное неблагополучие заставляло Шмидтов переезжать из города в город в поисках лучшей жизни. Отто Шмидт начал свое образование в 1900 году в классической гимназии Могилева, куда был принят сразу во второй класс. Учебу он продолжил в одесской гимназии.

Но, конечно, такой способный мальчик, каким был Отто, не мог довольствоваться программной гимназии. Шмидт решил расширить свою учебную программу: начал читать произведения отечественных и зарубежных классиков, изучал иностранные языки. Уже в одесской гимназии он увлекся древними языками. Наряду с обязательным латинским он добился у директора гимназии разрешения изучать еще и древнегреческий язык.

В 1907 году Шмидты переехали в Киев, где находилась 2-я мужская классическая гимназия. Отто поступил сразу во второй класс. В 1909 году он окончил ее, получив среднее образование, и за хорошую учебу Отто Юльевич Шмидт был награжден золотой медалью".

Отто Шмидт скончался 7 сентября 1956 года.

8.20 Курош, Александр Геннадиевич

Алекса́ндр Генна́диевич Ку́рош (Александр Геннадьевич Курош; 6 (19) января 1908, село Ярцево (ныне город), Смоленская губерния - 18 мая 1971, Москва) - выдающийся советский математик-алгебраист, доктор физико-математических наук, профессор МГУ. Автор многочисленных работ, монографий и учебников, сохраняющих ценность и в наши дни. За свою деятельность был удостоен премии имени П. Л. Чебышева (1945), Государственной премии СССР (посмертно). Награждён также орденами Трудового Красного Знамени, «Знак Почета» и медалями.

А. Г. Курош окончил Смоленский университет (1928) и был направлен в Саратовский университет, где создал и возглавил кафедру алгебры.

С 1930 года и до конца жизни работал в Московском университете, которому посвятил более 40 лет. Протестовал против репрессий в отношении Д. Ф. Егорова, за что был исключён из комсомола (1930). В 1936 году защитил докторскую диссертацию под научным руководством академика П. С. Александрова. Профессор МГУ с 1937 года. Жена - Зоя Михайловна Кишкина (1917-1987), преподаватель МГУ.

В 1949 году А. Г. Курош возглавил кафедру высшей алгебры МГУ. Высокий престиж московской алгебраической школы - в немалой степени его личная заслуга.

Подпись А. Г. Куроша была под известным «письмом 99 математиков» (1968) в защиту арестованного А. С. Есенина-Вольпина[1], однако вскоре в советской печати появилось заявление А. Г. Куроша о том, что он не подписывал данное письмо[2].

А.Г. Курош был главным редактором биографически-библиографического двухтомного справочника:

«Математика в СССР за сорок лет. 1917-1957»

«Математика в СССР. 1958-1967»

С 28 мая по 3 июня 2008 года на мехмате МГУ прошла Международная алгебраическая конференция, посвященная 100-летию со дня рождения профессора Куроша.

8.21 Понтрягин Лев Семёнович

Лев Семё́нович Понтря́гин (1908-1988) - советский математик, академик АН СССР (1958; член-корреспондент 1939). Герой Социалистического Труда (1969). Лауреат Ленинской премии (1962), Сталинской премии второй степени (1941) и Государственной премии СССР (1975).

Л. С. Понтрягин родился 21 августа (3 сентября) 1908 года в Москве. В 14 лет потерял зрение в результате несчастного случая. Окончил Московский университет (1929). С 1939 года заведующий отделом МИАН имени В. А. Стеклова, одновременно с 1935 года профессор МГУ. Последние 8 лет был вегетарианцем.

В топологии открыл общий закон двойственности и в связи с этим построил теорию характеров непрерывных групп; получил ряд результатов в теории гомотопий (классы Понтрягина). В теории колебаний главные результаты относятся к асимптотике релаксационных колебаний. В теории управления - создатель математической теории оптимальных процессов, в основе которой лежит т. н. принцип максимума Понтрягина (см. Оптимальное управление); имеет фундаментальные результаты по дифференциальным играм. Работы школы Понтрягина оказали большое влияние на развитие теории управления и вариационного исчисления во всём мире. Его учениками являются известные математики Д. В. Аносов, В. Г. Болтянский, Р. В. Гамкрелидзе, М. И. Зеликин, Е. Ф. Мищенко, М. М. Постников, Н. Х. Розов, В. А. Рохлин.

Понтрягин написал подробные мемуары «Жизнеописание Л. С. Понтрягина, математика, составленное им самим», в которых дал оценки многим учёным и событиям, свидетелем и участником которых он был, в частности, кампании против Н. Н. Лузина.

За рубежом Понтрягина часто называли антисемитом, в частности, за такие высказывания, как:

"Я упорно сопротивлялся давлению международного сионизма, стремящегося усилить свое влияние на деятельность Международного союза математиков. И этим вызвал озлобление сионистов против себя”.

Л. С. Понтрягин является автором следующих популярных книг по математике: "Знакомство с высшей математикой. Анализ бесконечно малых.", М., "Наука", 1980, "Знакомство с высшей математикой. Алгебра.", М., "Наука", 1987.

Л. С. Понтрягин умер 3 мая 1988 года. Похоронен в Москве на Новодевичьем кладбище (участок № 10).

Список литературы

1. Ф.Клейн Лекции о развитии математики в XIX столетии.-М.:Наука,1989.

. Каргаполов М.И. Мерзляков Ю.И. Основы теории групп 1982

. Дж. Стиллвелл «Математика и её история».

. П.С. Александров «Введение в теорию групп».

. «Математика XIX века. Математическая логика. Алгебра. Теория чисел. Теория вероятностей» / Под ред. Колмогорова А.Н., Юшкевичка А.П. -М.,1978.

. Рыбников К.А. История математики. -М.: Изд-во МГУ, 1994.

. Даан-Дальмедико А.Б., Пейффер Ж. Пути и лабиринты. Очерки об истории математики, М.,Мир, 1987.

. Курош А.Г. Теория Групп

. Желобенко Д.П. Компактные группы Ли и их представления

. Магнус В., Чандлер Б. Развитие комбинаторной теории групп

. «Математика в СССР за 40 лет»/ Под ред. Куроша А.Г.

. Матвеев С. В. Фундаментальная группа: Лекции по курсу «Топология». Челябинск: ЧелГУ, 2001. - 16 с.

. Гельфанд И.М., Граев М.И., Пятецкий-Шапиро И.И. «Теория представлений и автоморфные функции»

. Алешин С.В. Алгебраические конструкции в теории автоматов

. Бутырский Е.Ю., Кувалдин И.А., Чалкин В.П. Об одном походе к обобщению теории сигналов и систем

. М. Ричардсон «Распознавание образов и теория групп»

. Алферров А.П., А.Ю. Зубов, А.С. Кузьмин, А.В.Черемушкин «Основы криптографии»

. Гелашвили Д.Б., Чупрунов Е.В., Марычев М.О. Приложение теории групп к описанию псевдосимметрии биологических объектов.