Метод Милна
Метод Милна
Одним из наиболее простых и
практически удобных методов численного решения дифференциальных уравнений
является метод Милна. Метод Милна относится к многошаговым методам и
представляет один из методов прогноза и коррекции. Решение в следующей точке
находится в два этапа. На первом этапе осуществляется по специальной формуле
прогноз значения функции, а затем на втором этапе - коррекция полученного
значения. Если полученное значение у после коррекции существенно отличается от
спрогнозированного, то проводят еще один этап коррекции. Если опять имеет место
существенное отличие от предыдущего значения (т.е. от предыдущей коррекции), то
проводят еще одну коррекцию и т.д. Однако очень часто ограничиваются одним
этапом коррекции.
Пусть дано уравнение:
'= f (x, y) (1)
с начальным условием(x0)=y0 (2)
Выбрав, шаг h положим
xi=x0
+ ih, yi = y(xi), 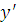
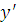 =f (x, y) (i = 0, 1, 2,
…).
=f (x, y) (i = 0, 1, 2,
…).
Первые 4 значения
начального отрезка y0, y1, y2, y3 находим, применив метод Рунге-Кутта. Тем
самым будут известны y'i (i = 0, 1, 2, 3).
Дальнейшие значения yi =
y(xi) (i = 4, 5, 6, …) определяются по следующей схеме:
) вычисляем
первое приближение 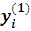
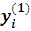 по формуле
по формуле

 (i = 4, 5, 6, …) (3)
(i = 4, 5, 6, …) (3)
) значение 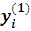
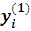 подставляем в (1) и
определяем
подставляем в (1) и
определяем 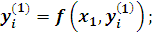
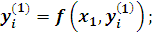
) находим второе
приближение 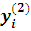
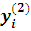 по формуле
по формуле
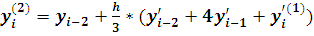
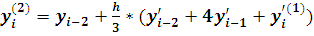 (i = 4, 5, 6, …) (4)
(i = 4, 5, 6, …) (4)
милн прогноз коррекция ошибка
Милн показал, что
абсолютная погрешность значения 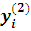
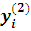 приближенно pавна:
приближенно pавна:
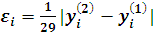
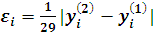 (5)
(5)
Поэтому, если 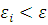
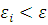 , где ε
- заданная предельная погрешность решения, то можно положить
, где ε
- заданная предельная погрешность решения, то можно положить 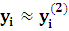
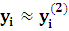 и
и
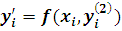
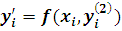 .
.
Далее переходим к
вычислению следующего значения 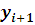
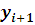 , повторяя указанную
выше схему. В случае, если точность ε не
обеспечена, следует уменьшить шаг h и сделать пересчет.
, повторяя указанную
выше схему. В случае, если точность ε не
обеспечена, следует уменьшить шаг h и сделать пересчет.
Замечания:
Суммарная ошибка метода
Милна есть величина порядка 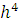
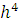 Метод Милна не обладает
устойчивостью, поэтому его рекомендуют использовать, когда предполагаемое число
шагов не велико.
Метод Милна не обладает
устойчивостью, поэтому его рекомендуют использовать, когда предполагаемое число
шагов не велико.
Дано уравнение 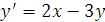
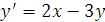 с начальным условием
с начальным условием 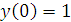
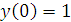 . Найдем методом Милна
приближенное значение решения
. Найдем методом Милна
приближенное значение решения 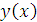
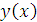 в точке
в точке 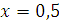
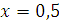 с точностью до
с точностью до 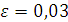
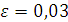
Решение
Метод Милна имеет
глобальную ошибку 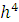
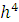 , это значит, что взяв
, это значит, что взяв 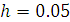
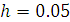 , получим погрешность
результата порядка
, получим погрешность
результата порядка 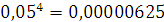
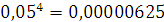 , таким образом,
заданная точность практически достигается.
, таким образом,
заданная точность практически достигается.
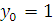
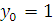 (из начального условия)
(из начального условия)
Значения 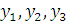
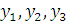 найдем явным методом
Эйлера.
найдем явным методом
Эйлера.
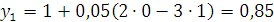
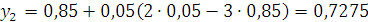
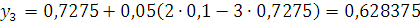
Найдем значения 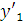
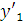 ,
, 
 и
и 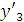
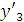
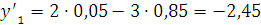
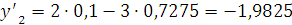
Далее используем метод
Милна.
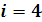
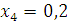
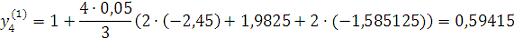
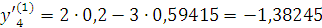
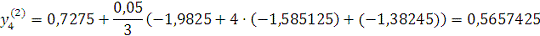
Проверка:
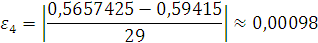
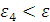
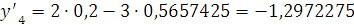
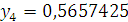
Будем заносить
результаты расчетов в таблицу
|
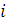
|
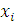
|
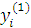
|
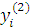
|
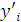
|
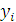
|
|
0
|
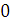
|
-
|
-
|
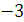
|
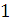
|
|
1
|
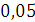
|
-
|
-
|
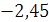
|

|
|
2
|
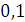
|
-
|
-
|
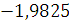
|
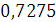
|
|
3
|
-
|
-
|
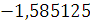
|
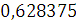
|
|
4
|
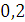
|
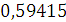
|
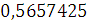
|
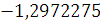
|
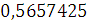
|
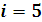
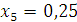
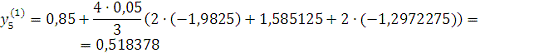
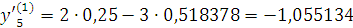
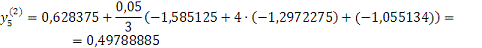
Проверка:
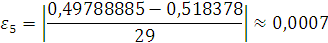
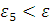
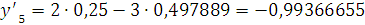
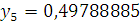
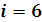
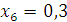
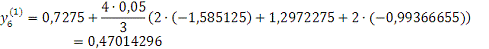
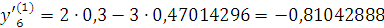
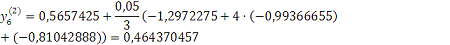
Проверка:
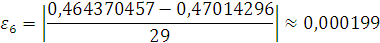
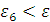
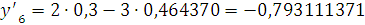
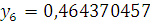

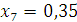
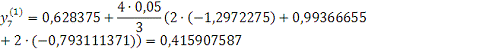
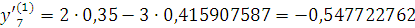
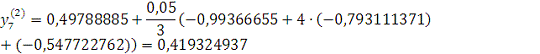
Проверка:
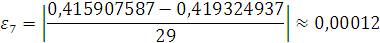
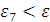
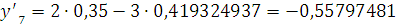
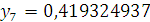
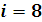
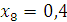
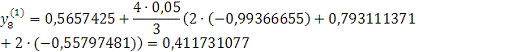
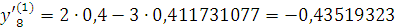
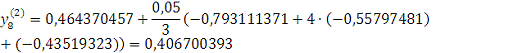
Проверка:
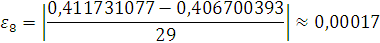
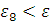
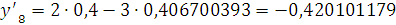
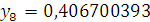
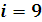
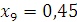
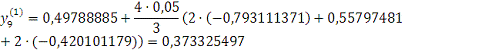
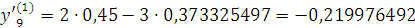
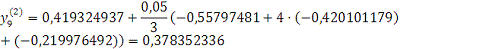
Проверка:
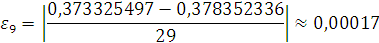
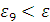
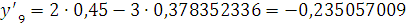
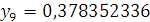
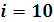
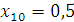
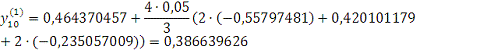
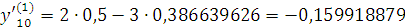
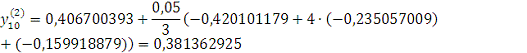
Проверка:
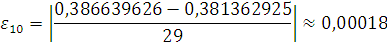
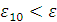
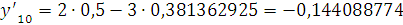
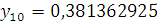
|
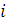
|
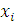
|
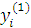
|
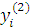
|
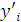
|
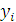
|
|
0
|
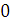
|
-
|
-
|
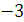
|
|
1
|
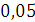
|
-
|
-
|
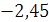
|

|
|
2
|
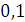
|
-
|
-
|
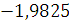
|
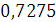
|
|
3
|
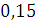
|
-
|
-
|
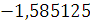
|
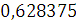
|
|
4
|
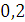
|
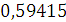
|
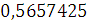
|
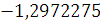
|
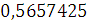
|
|
5
|
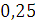
|
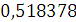
|
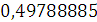
|
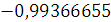
|
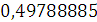
|
|
6
|
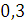
|
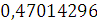
|
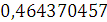
|
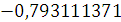
|
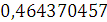
|
|
7
|
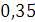
|
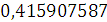
|
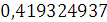
|
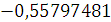
|
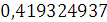
|
|
8
|
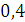
|
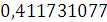
|
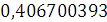
|
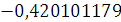
|
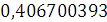
|
|
9
|
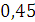
|
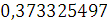
|
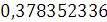
|

|
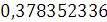
|
|
10
|
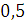
|
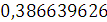
|
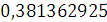
|
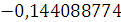
|
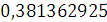
|
Напомним, что точное решение
заданного уравнения:
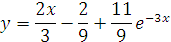
Найдем точное значение 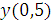
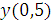 :
:
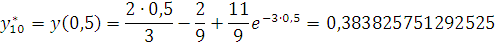
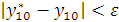
Заданная точность
достигнута.
Метод требует несколько
меньшего количества вычислений (например, достаточно только два раза вычислить
f (x, y), остальные запомнены с предыдущих этапов), но требует дополнительного
«расхода» памяти. Кроме этого, как уже указывалось выше, невозможно «запустить»
метод для этого необходимо предварительно получить одношаговыми методами первые
три точки.