Разработка и реализация алгоритма Флойда и Беллмана-Форда для поиска кратчайшего пути между всеми вершинами графа

Разработка и реализация алгоритма Флойда и Беллмана-Форда для поиска кратчайшего пути между всеми вершинами графа

Содержание

Введение

Разработка блок-схемы алгоритмов

Разработка псевдокода алгоритмов

Анализ трудоемкости роста функции

Программа реализации алгоритмов

Тестирование программ реализации алгоритмов

.1 Тестирование правильности

.2 Анализ по времени

Анализ результатов

Заключение

Список использованных источников

Приложение А Код программы по алгоритму Флойда

Приложение Б Код программы по алгоритму Беллмана-Форда

Введение

Алгоритм Флойда поиска кратчайших путей между всеми парами вершин.

Граф - это совокупность множества вершин и множества пар вершин (связей между вершинами, дуг).

Алгоритм Флойда - Уоршелла - алгоритм для нахождения кратчайших расстояний между всеми вершинами взвешенного графа без циклов с отрицательными весами с использованием метода динамического программирования.

Этот алгоритм был одновременно опубликован в статьях Роберта Флойда (Robert Floyd <#"600184.files/image001.gif"> до всех остальных вершин. В, случае, когда в графе 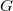 содержатся отрицательные циклы, достижимые из , алгоритм сообщает, что кратчайших путей не существует.

1. Разработка блок-схемы алгоритмов

На рисунке 1 представлена разработанная блок-схема алгоритма Флойда, где показано, каким образом, работает этот алгоритм. i, j, k, - аргументы прохода по циклу, N - размер массива расстояний, D[N][N] - массив расстояний.

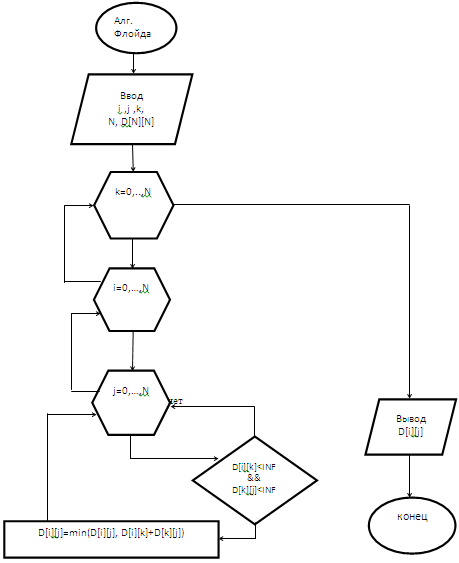
Рисунок 1 - Блок-схема алгоритма Флойда

На рисунке 2 представлена разработанная блок-схема алгоритма Беллмана-Форда, где показано, каким образом, работает этот алгоритм. Smej - матрица смежности графа, start_v - начальная вершина, mRast - массив существующих в графе дуг, rez - массив кратчайших расстояний, RELAX(rez[mRast[j].to]) - улучшение пути между начальной и j-ой вершиной графа.

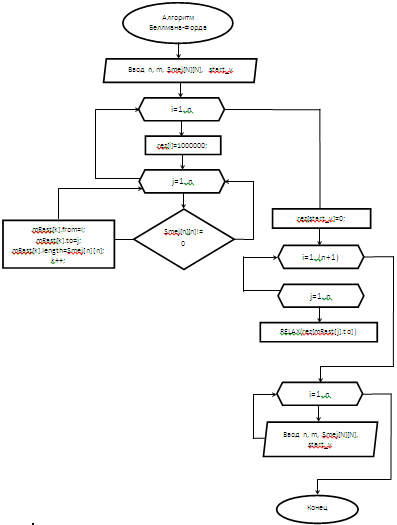
Рисунок 2 - Блок-схема алгоритма Беллмана-Форда

2. Разработка псевдокода

Алгоритм Флойда.

На рисунке 3 приведена часть псевдокода, где описан процесс ввода матрицы смежности заданного графа, где i, j - аргументы порхода по циклу. Тут же зануляется главныя диогональ при помощи условия - if(i==j), SizeMatr - размер матрицы(количество вешин в графе).

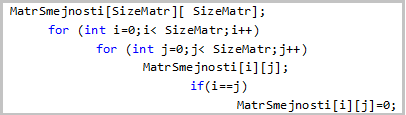
Рисунок 3 - Ввод матрицы смежности

На рисунке 4 приведена часть псевдокода, где описано вычисление матрицы кратчаших путей; будем улучшать путь через k-ю вершину, если пойти из i в k, а из k в j выгоднее, чем пойти напрямую из i в j, то запоминаем этот путь.

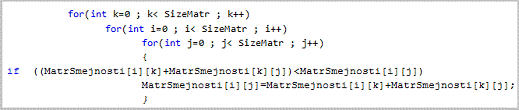
Рисунок 4 - Алгоритм Флойда

На рисунке 5 приведена часть псевдокода, где описан вывод получившейся матрицы.

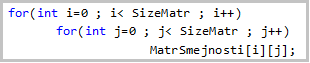
Рисунок 5 - Вывод матрицы

Алгоритм Беллмана-Форда.

На рисунке 6 приведена часть псевдокода, где производится ввод n - количество вершин в графе, m - количество дуг в графе, start_v - начальная вершина, Smej - матрица смежности графа G(n,m).

Рисунок 6 - Ввод матрицы смежности

На рисунке 7 приведена часть псевдокода, где mRast - массив типа struct, в котором регистрируются from - начальная вершина дуги, to - конечная вершина дуги и length - длина этой дуги.

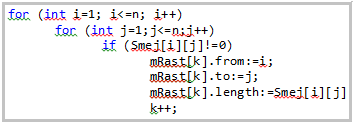
Рисунок 7 - Массив длинн

Ниже, на рисунке 8, заполняется массив кратчайших путей до вершины i, изначально путь равен «бесконечности». Здесь бесконечность - это некоторое значение, заведомо превосходящее все возможные расстояния. Длина дуги к start_v приравнивается нулю.

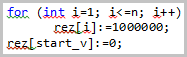
Рисунок 8 - Заполнение массива

На рисунке 9 реализован, непосредственно алгоритм Беллмана-Форда. Здесь rez[mRast[j].from] - длина пути из начальной вершины до вершины, от которой начинается текущая дуга, mRast[j].length - длина текущей дуги, rez[mRast[j].to] - текущее кратчайшее расстояние из start_v до j-ой вершины.

Рисунок 9 - Алгоритм Беллмана-Форда

В последней части псевдокода, рисунок 10, осуществляется вывод кратчайших расстояний, при этом, в случае если rez[i]=100000 путь до j-ой вершины не определен.

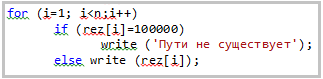
Рисунок 10 - Вывод кратчайших расстояний

3. Анализ трудоемкости роста функции

Время выполнения программы по алгоритму Флойда состовляет O(n^3), так как в ней нет практически ничего, кроме 3 вложенных друг в друга циклов.

Наилучшим случаем для алгоритма станет граф в котором всего нет улучшения пути, т. е. вводимая матрица расстояний не изменится после выполнения программы. В этом случае время выполнения программы составит O(n^3).

Наихудшим случаем для алгоритма станет граф с отрицательным циклом. Если в графе есть циклы отрицательного веса, то формально алгоритм Флойда к такому графу неприменим. Но на самом деле алгоритм корректно сработает для всех пар, пути между которыми никогда не проходят через цикл негативной стоимости, а для остальных мы получим какие-нибудь числа, возможно сильно отрицательные. Алгоритм можно научить выводить для таких пар некое значение, соответствующее -∞.

В среднем случае алгоритм не будет иметь отрицательных циклов и улучшит почти все пути. Таким образом он не превысит an^3+bn^2+cn+d операций. алгоритм флойд беллман псевдокод

Анализ алгоритма Беллмана-Форда.

Время выполнения программы, имеет порядок O(nm), где n - это количество вершин, а m - это количество дуг.

Наилучшим случаем для алгоритма станет граф в котором 2 вершины и отсутствуют дуги, т. е. вводимая матрица расстояний состоит из нулей.

4. Программа реализации алгоритмов

Ниже проиллюстрирована работа алгоритма Флойда, а сам код написан в Приложении А. Заполнение матрицы расстояний осуществляем при помощи чтения текстового файла «algF .txt», заполненная матрица представлена на рисунке 11.

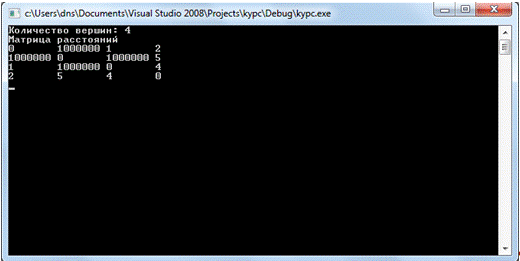
Рисунок 11 - Ввод матрицы из файла

На рисунке 12 представлен вывод матрицы кратчайших расстояний заданного графа, помимо матрицы показано время работы программы в секундах.

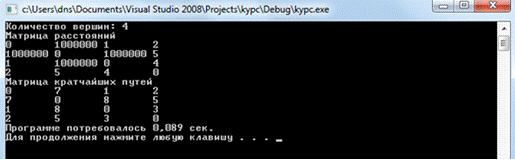
Рисунок 12 - Вывод результатов работы программы по алгоритму Флойда

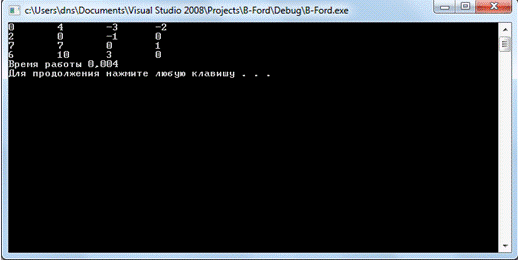
На рисунке 13 показана матрица кратчайших путей, программа реализована с помощью алгоритма Беллмана-Форда. Заполнение матрицы расстояний осуществляем при помощи чтения текстового файла «algBF .txt» В том же рисунке показано время работы программы. Полный код программы находится в Приложении Б. В реализации этого алгоритма пришлось добавить внешний цикл, в котором будут пробегать все вершины: for(start_v=1;start_v<=n;start_v++), таким образом этот алгоритм теперь находит не от одной вершины до всех остальных, а от каждой вершины до всех остальных.

5. Тестирование программ реализации алгоритмов

.1 Тестирование правильности

Протокол тестирования правильности работы программы по алгоритму Флойда содержится в таблице 1. В входных данных вводится матрица расстояний, так же матрицу ожидаем получить и в выходных данных. Будем считать, что несуществующее ребро между двумя вершинами будет равняться inf = 1000. Первый пример характеризует ориентированный граф, второй же неориентированный. В 3 - м случае граф состоит из 6 вершин. В 4 и 5 примерах используются ребра отрицательного веса, где последний задает граф с циклом отрицательного веса.

Таблица 1 - Тестирование правильности алгоритма Флойда

Протокол тестирования правильности работы программы по алгоритму Беллмана-Форда содержится в таблице 2. В входных данных вводится матрица расстояний, так же матрицу ожидаем получить и в выходных данных. Будем считать, что несуществующее ребро между двумя вершинами будет равняться inf = 1000. Первый пример характеризует ориентированный граф, второй же неориентированный. В 3 - м случае граф состоит из 6 вершин. В 4 и 5 примерах используются ребра отрицательного веса, где последний задает граф с циклом отрицательного веса.

Таблица 2 - Тестирование правильности алгоритма Беллмана-Форда

Проанализировав оба протокола мы увидим, что обе программы работают корректно и выводят одно и тоже правильное решение.

5.2 Анализ по времени

Анализ по времени проводится функцией clock() из стандартной библиотеки <time.h>. Длины ребер задаем с помощью функции rand() из той же библиотеки <time.h>, длины этих ребер будут варьироваться от 0 до 99. Ниже на рисунке 14 представлена диаграмма роста функции f(t)=N, где t - время работы программы в секундах, а N - количество вершин. «Жирным» выделен график роста функции алгоритма Флойда, а «тонким» выделен график роста функции алгоритма Беллмана-Форда.

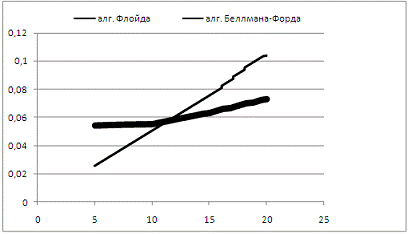
Рисунок 14 - Диаграмма роста функции f(t)=N

6. Анализ результатов

Проанализируем результаты, алгоритмы Флойда и Беллмана-Форда очень похожи по своей структуре и поиску кратчайших путей, они различаются по хранению промежуточной информации о кратчайших путях. Исходя из этого, они различаются и в скорости роста функции f(t)=N. Как показали тесты, эти два алгоритма схожи и в работе с ребрами отрицательного веса.

Заключение

Для достижения поставленной цели потребовалось реализовать алгоритмы Флойда и Беллмана-Форда в среде (программе) Microsoft Visual Studio. При создание кода программы использовалась программа Microsoft Visual Studio 2008. В результате при помощи созданной программы была получена возможность нахождения минимального расстояния между всеми вершинами, при случайном распределении длин ребер, при ручном вводе и вводе при помощи файла. Так же был изменен код алгоритма Беллмана-Форда, для того, чтобы этот алгоритм находил кратчайшие пути между всеми вершинами графа, а не от одной вершины до всех остальных. Проанализирована работа алгоритмов Флойда и Беллмана-Форда, после чего составлены диаграммы тестирования скорости работы, по которым можно сравнить работу алгоритмов.

Можно добавить, что поиск пути не тривиальная задача, существует несколько хороших, надежных, и всем известных алгоритмов, которые заслуживают должного внимания в сообществе разработчиков. Помимо представленных выше алгоритмов, хорошо известны такие алгоритмы как алгоритм Дейкстры, алгоритм Джонсона, все они решают одни и те же задачи, но подходы к решению отличаются.

Некоторые алгоритмы поиска пути не очень эффективны, но их изучение позволяет постепенно вводить концепции. Так можно понять, как решаются различные проблемы.

Список использованных источников

1       ГОСТ 7.32-2001. Отчёт о научно-исследовательской работе. Структура и правила оформления [Текст]. - Взамен ГОСТ 7.32-91 ; введ. 2001-07-01. - Минск : Межгос. совет по стандартизации, метрологии и сертификации ; М. : Изд-во стандартов, 2001. - 16 с. - (Система стандартов по информации, библиотечному и издательскому делу).

         ГОСТ 7.1-2003. Библиографическая запись. Библиографическое описание. Общие требования и правила составления [Текст]. - Взамен ГОСТ 7.1-84, ГОСТ 7.16-79, ГОСТ 7.18-79, ГОСТ 7.34-81, ГОСТ 7.40-82 ; введ. 2004-07-01. - М. : Изд-во стандартов, 2004. - 116 с. - (Система стандартов по информации, библиотечному и издательскому делу).

         Левитин А. В. Алгоритмы: ввдение в разработку и анализ. / А. В. Левитин ; пер. с англ. под общ. ред. С. Г. Тригуб. - М. : Издательский дом «Вильямс», 2006. - 576 с.

         Макконелл Дж. Основы современных алгоритмов / Дж. Макконелл ; пер. с англ. под общ. ред. С. К. Ландо. - М. : Издательство ЗАО РИЦ «Техносфера», 2004. - 368 с.

Приложение А

Код программы по алгоритму Флойда

#include <iostream>

#include <stdio.h>

#include <fstream>

#include <time.h>namespace std;main()

{*f = fopen("algF.txt","r");int inf = 1000000;ch = 0;count = 0, i = 0, N;loc("russian");::global(loc);_t t;= clock();(time(NULL));(f,"%d",&N);**MatrS = new int *[N];(int i = 0; i < N; i++)

{[i] = new int[N];

}("\n%d\n",N);("Матрица расстояний\n");(!feof(f))

{(int i=0;i<N;i++)

{(int j=0;j<N;j++)

{(f,"%d",&MatrS[i][j]);(i==j)[i][j] = 0;("%d ",MatrS[i][j]);

}("\n");

}

}(f);(int k=0 ; k<N ; k++)

{(int i=0 ; i<N ; i++)

{(int j=0 ; j<N ; j++)

{((MatrS[i][k] + MatrS[k][j]) < MatrS[i][j])[i][j] = MatrS[i][k] + MatrS[k][j];

}

}

}(int i = 0; i < N; i++)[] MatrS[i];[] MatrS;("Матрица кратчайших путей\n");(int i=0 ; i<N ; i++)

{(int j=0 ; j<N ; j++)

{("%d ",MatrS[i][j]);

}("\n");

}("Программе потребовалось %.3f сек.\n",((float)t)/CLOCKS_PER_SEC);("pause");

}

Приложение Б

Код программы по алгоритму Беллмана-Форда

#include <stdio.h>

#include <iostream>

#include <time.h>namespace std;int inf=1E9;n,m,i,*rez,j,start_v,k=1;Duga

{from,to,length;

}*mRast;main()

{*f = fopen("algBF.txt","r");loc("russian");::global(loc);(f,"%d %d",&n,&m);_t t;=clock();**Smej=new int *[n];= new Duga [m];(i=1; i<=n; i ++)

{[i]=new int [n];(j=1; j<=n; j++)

{(f,"%d",&Smej[i][j]);(Smej[i][j]!=0)

{[k].from=i;[k].to=j;[k].length=Smej[i][j];++;

}

}

}(int i = 0; i < N; i++)[] Smej[i];[] Smej;(f);(start_v=1;start_v<=n;start_v++)

{=new int [n];(i=1;i<=n;++i)[i]=inf;[start_v]=0;(i=1;i<=(n+1);i++)

{(j=1;j<=m;j++)

{(rez[mRast[j].from]<inf && rez[mRast[j].from]+mRast[j].length<rez[mRast[j].to])(i==(n+1))

{("В графе есть цикл отрицательного веса");("pause");0;

}[mRast[j].to]=rez[mRast[j].from]+mRast[j].length;

}

}(i=1;i<=n;++i)

{(rez[i]==inf) printf("нет пути\n"); else printf("%d ",rez[i]);

}("\n");

}=clock()-t;("Время работы %f", (double)t/CLOCKS_PER_SEC);[] mRast;[] rez;("pause");

}