Исследование стационарных движений механической системы на устойчивость
РЕФЕРАТ
В данной работе проведено исследование стационарных движений механической
системы на устойчивость. Составлены уравнения движения системы, с помощью
уравнений Лагранжа второго рода. Получены уравнения первого приближения. На
основании метода Четаева получена функция Ляпунова. Составлена функция Рауса. С
помощью различных методов теории устойчивости, определены устойчивые и
неустойчивые положения равновесия.
СОДЕРЖАНИЕ
Введение
1. ПОСТРОЕНИЕ
УРАВНЕНИЙ ВОЗМУЩЕННОГО ДВИЖЕНИЯ МЕХАНИЧЕСКОЙ СИСТЕМЫ
.1 Построение
уравнений движения системы в виде уравнений Лагранжа второго рода
.2
Определение стационарных движений механической системы
.3 Вывод
уравнений возмущенного движения механической системы
.
ИССЛЕДОВАНИЕ УСТОЙЧИВОСТИ ДВИЖЕНИЯ МЕХАНИЧЕСКОЙ СИСТЕМЫ
.1
Исследование устойчивости движения по уравнениям первого приближения
.2
Исследование устойчивости движения с помощью функции Ляпунова
.3
Исследование устойчивости стационарных движений методом Рауса
Заключение
Список использованной литературы
Введение
В курсовой работе проводиться комплексный анализ устойчивости
стационарных движений механической системы с двумя степенями свободы,
различными методами теории устойчивости.
В первой части курсовой работы составляются уравнения движения системы в
форме уравнений Лагранжа второго рода. Определяется множество стационарных
движений рассматриваемой системы. Составляются уравнения возмущенного движения
в окрестности стационарных движений.
Во второй части работы на основе классических методов теории устойчивости,
проводится исследование на устойчивость стационарных движений механической
системы, а именно:
по первому приближению;
с помощью функции Ляпунова;
методом Рауса.
1. ПОСТРОЕНИЕ УРАВНЕНИЙ ВОЗМУЩЕННОГО ДВИЖЕНИЯ МЕХАНИЧЕСКОЙ
СИСТЕМЫ
.1 Построение уравнений движения системы в виде
уравнений Лагранжа второго рода
Рассмотрим
механическую систему, состоящую из пластины массы 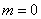 , длины
, длины  и ширины
и ширины 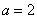 , находящуюся под действием потенциальных сил (Рисунок
1). Рассматриваемая система имеет две степени свободы. Пластина может вращаться
вокруг вертикальной оси со скоростью
, находящуюся под действием потенциальных сил (Рисунок
1). Рассматриваемая система имеет две степени свободы. Пластина может вращаться
вокруг вертикальной оси со скоростью 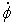 , и
отклонятся от вертикальной оси на угол
, и
отклонятся от вертикальной оси на угол 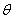 .
.
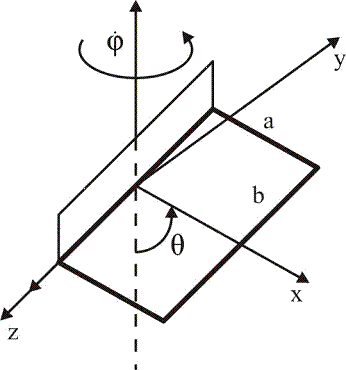
Рисунок
1 - Механическая система
Составим
уравнения движения механической системы, для этого используем уравнения
Лагранжа 2-го рода:
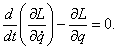 (1.1)
(1.1)
Выберем
в качестве обобщенных координат:  .
.
Определим
кинетическую энергию системы:
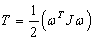 ,
,
где
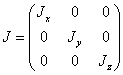 - тензор
инерции, его компоненты:
- тензор
инерции, его компоненты:
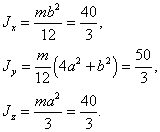
Определим
угловую скорость:
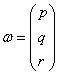 ,
,
где
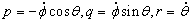 .
.
Подставляя,
получим полную кинетическую энергию:
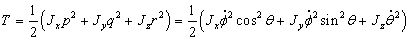 .
.
Потенциальная
энергия системы
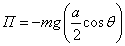 .
.
Запишем
Лагранжиан системы:
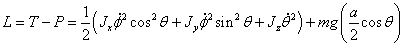 .
(1.2)
.
(1.2)
Подставляя
(1.2) в (1.1) получим систему дифференциальных уравнений, описывающую движение
механической системы:
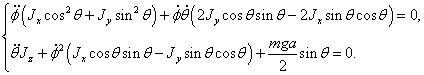 (1.3)
(1.3)
механический уравнение равновесие лагранж
1.2 Определение стационарных движений механической системы
Определим стационарные движения системы, для этого согласно определению,
сделаем подстановку
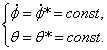
система
(1.3) примет вид:
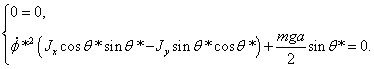 (1.4)
(1.4)
Из
системы (1.4) получается уравнение
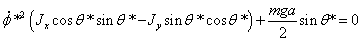 ,
,
Уравнение
распадается на два уравнения:
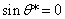 и
и 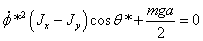 .
.
Из
первого уравнения следует 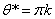 и
и 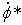 - любое.
- любое.
Найдем
решение второго уравнения,
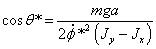 ,
, 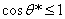 или
или 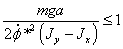
Сделав
преобразования,
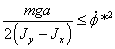 получим
что при выполнении условия
получим
что при выполнении условия 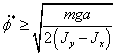 , или с
учетом численных значений параметров системы
, или с
учетом численных значений параметров системы 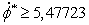 ,
существуют решения
,
существуют решения
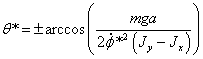
Обозначим
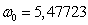 .
.
Множество
стационарных движений изображено на рисунке 2.
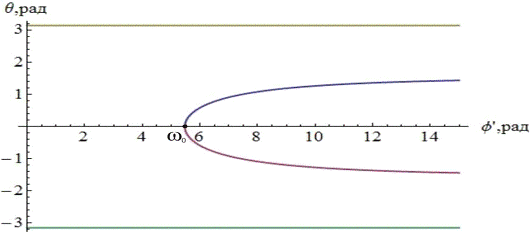
Рисунок
2 - Множество стационарных движений
Точки
прямой 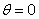 соответствуют вращению пластины вокруг вертикальной
оси в нижнем положении. Точки
соответствуют вращению пластины вокруг вертикальной
оси в нижнем положении. Точки 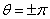 ,
соответствуют одним и тем же движениям, вращению пластины вокруг вертикальной
оси в верхнем положении. Точки кривых
,
соответствуют одним и тем же движениям, вращению пластины вокруг вертикальной
оси в верхнем положении. Точки кривых 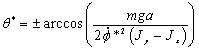 , обозначают
вращение пластины с различными угловыми скоростями
, обозначают
вращение пластины с различными угловыми скоростями 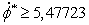 , при соответствующем постоянном угле отклонения от
вертикальной оси.
, при соответствующем постоянном угле отклонения от
вертикальной оси.
Будем
рассматривать три стационарных движения:
.
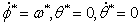 (1.5)
(1.5)
.
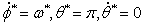 (1.6)
(1.6)
.
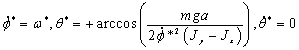 (1.7)
(1.7)
1.3 Вывод уравнений возмущенного движения механической
системы
Разрешим систему (1.3) относительно вторых производных:
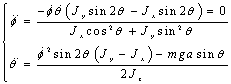 (1.8)
(1.8)
Запишем
её в нормальном виде, для этого введем обозначения:
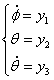 (1.9)
(1.9)
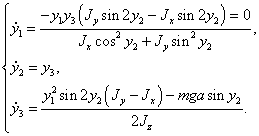 (1.10)
(1.10)
Рассмотрим
первое невозмущенное движение системы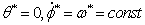 .
Определим отклонения следующими равенствами:
.
Определим отклонения следующими равенствами:
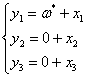 (1.11)
(1.11)
Перейдем
от системы (1.10) к уравнениям возмущенного движения:
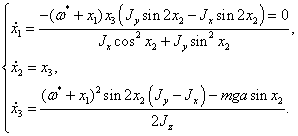 (1.12)
(1.12)
Рассмотрим
второе невозмущенное движение: 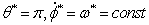 . Введем
отклонения:
. Введем
отклонения:
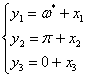 (1.13)
(1.13)
Подставляя
(1.13) в систему (1.10), получим уравнения возмущенного движения:
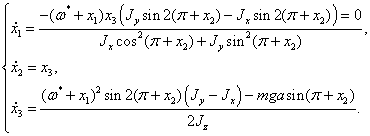
Использую
формулы приведения, полученную систему можно переписать в виде:
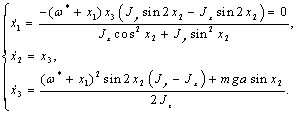 (1.14)
(1.14)
Рассмотрим
третье невозмущенное движение: 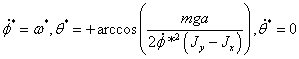
Введем
обозначения: 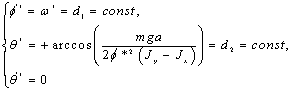
Запишем
отклонения:
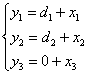 (1.15)
(1.15)
Подставляя
(1.15) в систему (1.10), получим уравнения возмущенного движения для третьего
невозмущенного движения:
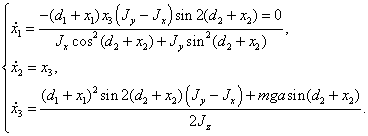 (1.16)
(1.16)
2. ИССЛЕДОВАНИЕ УСТОЙЧИВОСТИ ДВИЖЕНИЯ МЕХАНИЧЕСКОЙ СИСТЕМЫ
.1 Исследование устойчивости движения по уравнениям первого
приближения
Рассмотрим систему (1.12), представляющую собой уравнения возмущенного
движения механической системы, и исследуем её на устойчивость по первому
приближению.
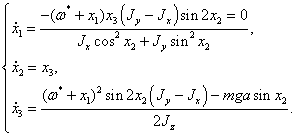
Запишем
уравнения первого приближения, для этого разложим правые части системы (1.12) в
ряд по степеням отклонений в окрестности невозмущенного движения и оставим
только члены первого порядка:
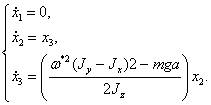 (2.1)
(2.1)
Запишем
характеристическое уравнение системы:
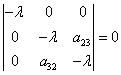 , где
, где 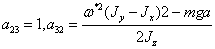 (2.2)
(2.2)
Вычислим
его корни:
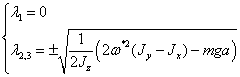 (2.3)
(2.3)
Выражение
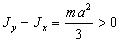 . Выражение под корнем будет больше 0 при выполнении
условия
. Выражение под корнем будет больше 0 при выполнении
условия
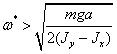 . (2.4)
. (2.4)
Таким
образом, при выполнении условия (2.4) все три корня характеристического
уравнения (2.2) действительные числа, и среди них есть корень 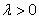 . Поэтому на основе утверждения теоремы Ляпунова о
неустойчивости по первому приближению можно сделать вывод: стационарное
движение
. Поэтому на основе утверждения теоремы Ляпунова о
неустойчивости по первому приближению можно сделать вывод: стационарное
движение 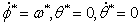 , при выполнении условия (2.4) неустойчиво по первому
приближению.
, при выполнении условия (2.4) неустойчиво по первому
приближению.
Если
выражение  имеет отрицательное значение, то есть
имеет отрицательное значение, то есть 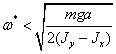 , то все три корня характеристического уравнения (2.2)
имеют действительные части равные 0, и на основании теоремы Ляпунова о
неустойчивости и неустойчивости стационарного движения по первому приближению
нельзя сделать вывод об устойчивости или неустойчивости рассматриваемого
движения. Требуются дополнительные исследования.
, то все три корня характеристического уравнения (2.2)
имеют действительные части равные 0, и на основании теоремы Ляпунова о
неустойчивости и неустойчивости стационарного движения по первому приближению
нельзя сделать вывод об устойчивости или неустойчивости рассматриваемого
движения. Требуются дополнительные исследования.
Рассмотрим
второе стационарное движение 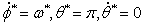 .
Уравнения возмущенного движения определены системой (1.14):
.
Уравнения возмущенного движения определены системой (1.14):
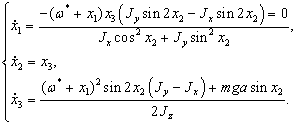
Аналогично
первому движению, запишем уравнения первого приближения:
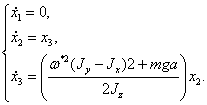 (2.5)
(2.5)
Характеристическое
уравнение имеет вид:
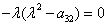 , где
, где
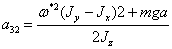 .(2.6)
.(2.6)
Его
решение:
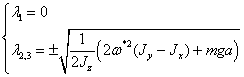 (2.7)
(2.7)
Выражение
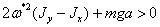 , при любых значениях
, при любых значениях 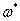 .
Следовательно, все корни характеристического уравнения (2.6) действительные.
Причем один из корней
.
Следовательно, все корни характеристического уравнения (2.6) действительные.
Причем один из корней 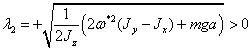 , поэтому на основании теоремы Ляпунова о
неустойчивости по первому приближению, можно сделать вывод: что стационарное
движение
, поэтому на основании теоремы Ляпунова о
неустойчивости по первому приближению, можно сделать вывод: что стационарное
движение 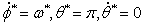 неустойчиво по первому приближению.
неустойчиво по первому приближению.
Рассмотрим
третье стационарное движение
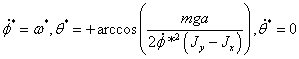
Уравнения
возмущенного движения определены системой (1.16):
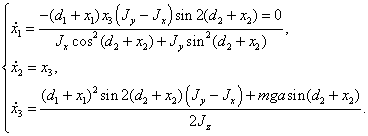
Аналогично
первому движению, запишем уравнения первого приближения для системы (1.16):
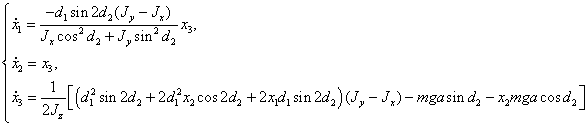 (2.8)
(2.8)
Введем
обозначения:
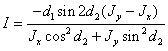 ,
,
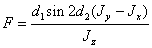 , (2.9)
, (2.9)
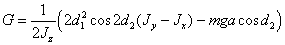 .
.
Составим
характеристическое уравнение:
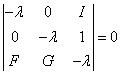 (2.10)
(2.10)
Корни
уравнения (2.10) имеют нулевую действительную часть (критический случай),
поэтому по уравнениям первого приближения нельзя сделать вывод об устойчивости
или неустойчивости стационарных движений:
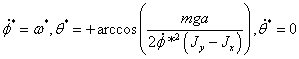
Найдем
численные значения корней 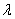 , соответствующих характеристических уравнений для
стационарных движений с различной угловой скоростью и при различных значениях
, соответствующих характеристических уравнений для
стационарных движений с различной угловой скоростью и при различных значениях 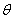 . Результаты запишем в таблицу 1.
. Результаты запишем в таблицу 1.
Таблица
1
|
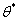 , рад , рад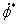 , рад/с , рад/с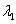 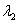 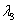 Движения Движения
|
|
|
|
|
|
|
0
|
5
|
0
|
-1,11803i
|
1,11803i
|
Критический случай
|
|
0
|
6
|
0
|
-1,22474
|
1,22474
|
неустойчиво
|
|
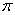 100-5,700885,70088неустойчиво 100-5,700885,70088неустойчиво
|
|
|
|
|
|
|
1,2661
|
0
|
-4,94146i
|
4, 94146i
|
Критический случай
|
Проиллюстрируем
неустойчивость полученных стационарных движений графически. Для этого приведем
графики отклонений для значений 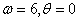 и
и 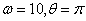 . Из рисунков видно, что в обоих случаях значения
отклонений
. Из рисунков видно, что в обоих случаях значения
отклонений 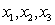 сильно растут с течением времени при выборе
достаточно малых значений.
сильно растут с течением времени при выборе
достаточно малых значений.
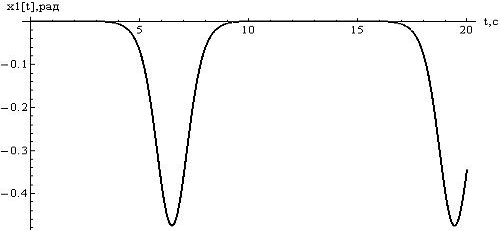
Рисунок
3 - отклонения 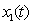 , при
, при 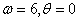
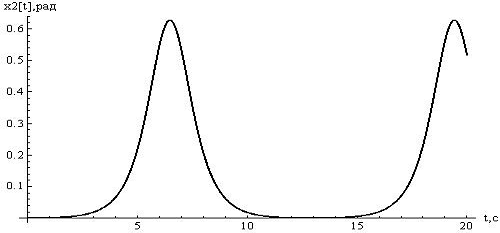
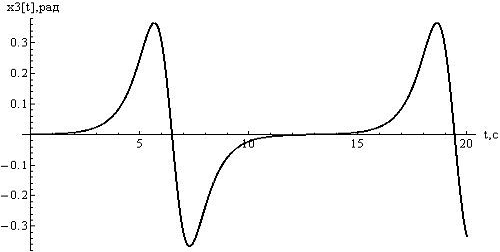
Рисунок
4 - отклонения 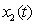 ,, при
,, при 
Рисунок
5 - отклонения  , при
, при 
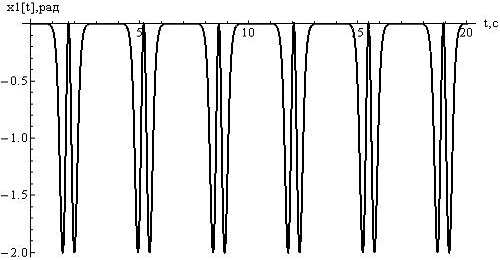
Рисунок
6 - отклонения 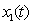 , при
, при 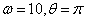
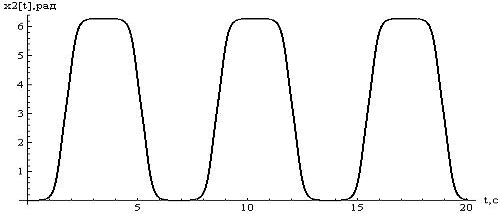
Рисунок
7 - отклонения 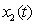 , при
, при 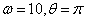
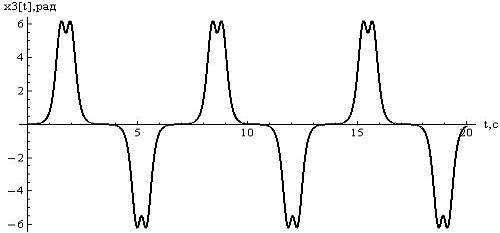
Рисунок
8 - отклонения 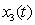 , при
, при 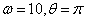
Вывод:
при исследовании на устойчивость по первому приближению стационарных движений
механической системы, вращения пластины вокруг вертикальной оси в наивысшем
положении при любых угловых скоростях и в наинизшем положении, при угловых
скоростях больших чем 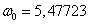 , неустойчивы. Для остальных движений требуются
дополнительные исследования другими методами.
, неустойчивы. Для остальных движений требуются
дополнительные исследования другими методами.
2.2 Исследование устойчивости движения с помощью функции
Ляпунова
Исследуем устойчивость стационарных движений механической системы вторым
методом Ляпунова.
Построим, функцию Ляпунова используя метод Четаева - метод связки
интегралов.
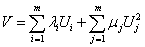 .
.
Для
этого запишем первые интегралы рассматриваемой системы.
Интеграл
энергии:
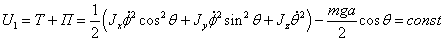 (2.11)
(2.11)
Интеграл
кинетического момента:
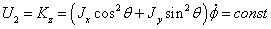 (2.12)
(2.12)
Исследуем
устойчивость первого стационарного движения: 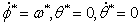
Используем
отклонения (1.11), подставим их в интегралы.
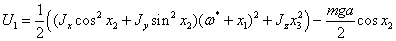
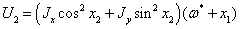
Разложим
интегралы в ряд по степеням отклонений, и отбросим слагаемые старше второй
степени:
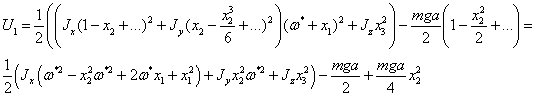
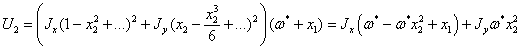
Для
того чтобы избавиться от констант вычтем из интегралов интегралы от нулей:
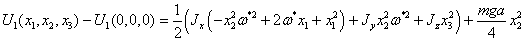
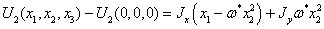
Составим
функцию Ляпунова в виде 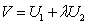 , положим
, положим 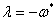 :
:
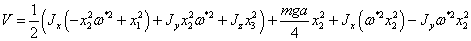 (2.13)
(2.13)
Приводя
подобные слагаемые, получим:
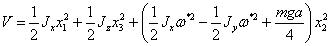 (2.14)
(2.14)
Для
того чтобы функция 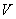 была определенно положительной необходимо чтобы
выражение
была определенно положительной необходимо чтобы
выражение 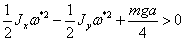 ,
,
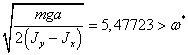 (2.15)
(2.15)
Получаем
что при выполнении условия (2.15), функция 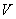 будет
определенно положительной, а её производная
будет
определенно положительной, а её производная 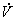 будет
тождественно равна нулю.
будет
тождественно равна нулю.
Следовательно,
рассматриваемое движение будет устойчивым для всех 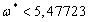
Для
всех 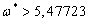 , функция
, функция 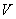 будет
знакопеременной, и сделать вывод об устойчивости или неустойчивости нельзя.
будет
знакопеременной, и сделать вывод об устойчивости или неустойчивости нельзя.
Исследуем
второе стационарное движение: 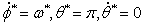 .
Используем отклонения (1.13), подставим их впервые интегралы:
.
Используем отклонения (1.13), подставим их впервые интегралы:
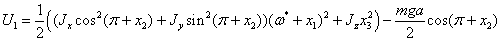
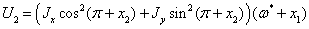
Используя
формулы приведения, получим:
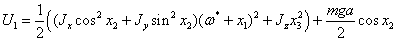
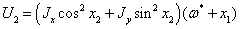
Разложим
интегралы в ряд по степеням отклонений, и отбросим слагаемые старше второй
степени:
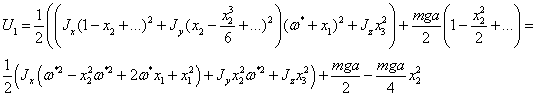
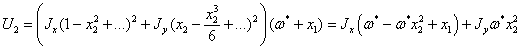
Избавимся
от констант:
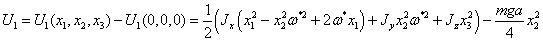
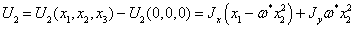
Составим
функцию Ляпунова:
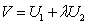
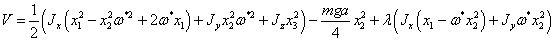
Выберем
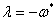 , получим
, получим
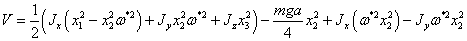 .
.
Приведем
подобные слагаемые:
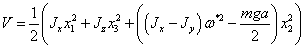 (2.16)
(2.16)
Рассмотрим
коэффициент, стоящий перед 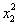 :
:
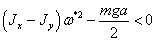 , для
любых
, для
любых 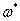 . (2.17)
. (2.17)
Таким
образом, функция (2.16) является знакопеременной, а её производная 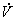 будет тождественно равна нулю.
будет тождественно равна нулю.
Вывод:
на основании данного метода сделать вывод об устойчивости или неустойчивости
второго стационарного движения нельзя.
Для
подтверждения и иллюстрации полученных результатов, построим графики отклонений
в окрестности устойчивого стационарного движения. Выберем 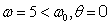
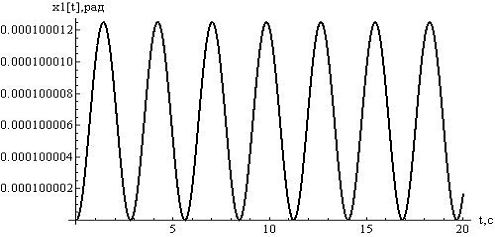
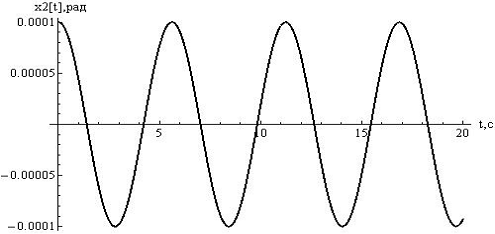
Рисунок
10 - отклонения 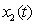 , при
, при 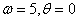
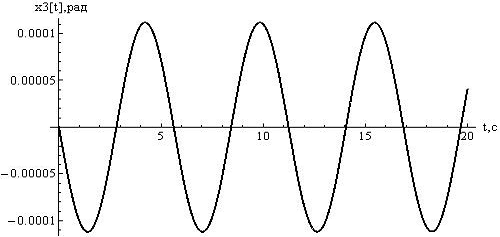
Рисунок
11 - отклонения 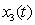 , при
, при 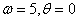
Вывод:
вращение пластины вокруг вертикальной оси в наинизшем положений с угловой
скоростью 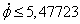 , устойчиво.
, устойчиво.
2.3 Исследование устойчивости стационарных движений методом
Рауса
Исследуем стационарные движения механической системы с помощью функции
Рауса:
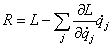
где
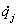 - циклическая координата.
- циклическая координата.
Для
рассматриваемой системы 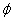 - является циклической координатой, функция Рауса
примет вид:
- является циклической координатой, функция Рауса
примет вид:
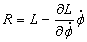 (2.18)
(2.18)
Выпишем Лагранжиан системы, для этого используем полученную ранее формулу
(1.2)
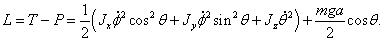
Найдем
циклический интеграл:
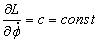 ,
подставляя Лагранжиан (1.2) получим:
,
подставляя Лагранжиан (1.2) получим:
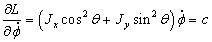
Выразим
величину 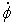 :
:
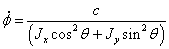 ,
(2.19)
,
(2.19)
подставим
полученное значение в функцию Рауса, получим
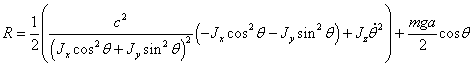 (2.20)
(2.20)
Представим
функцию (2.20) в виде суммы квадратичной, линейной и нулевой форм относительно
степеней обобщенной скорости 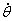
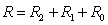
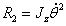 ,
,
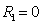 ,
,
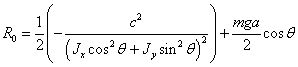 (2.21)
(2.21)
Приведенная
потенциальная энергия системы будет равна 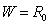
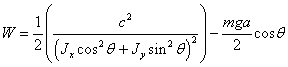 (2.22)
(2.22)
Положения,
в которых вторая производная от приведенной потенциальной энергии по координате
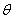 имеет положительный знак, являются устойчивыми.
Соответственно положения, в которых она имеет отрицательный знак, являются
неустойчивыми. Исследуем на устойчивость стационарные движения (1.5) - (1.7) на
устойчивость. Для этого продифференцируем дважды (2.22) по координате
имеет положительный знак, являются устойчивыми.
Соответственно положения, в которых она имеет отрицательный знак, являются
неустойчивыми. Исследуем на устойчивость стационарные движения (1.5) - (1.7) на
устойчивость. Для этого продифференцируем дважды (2.22) по координате 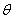 :
:
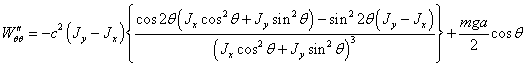 (2.23)
(2.23)
Подставим
в (2.23) циклический интеграл определяющий константу 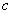 :
:
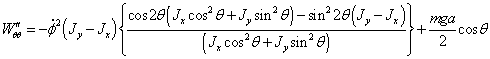 (2.24)
(2.24)
Рассмотрим
первое стационарное движение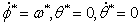 :
:
Подставим
значения в (2.24):
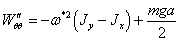 (2.25)
(2.25)
Для
устойчивости рассматриваемого движения необходимо чтобы (2.25) была больше
нуля.
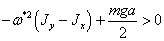
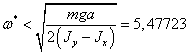 (2.26)
(2.26)
Получаем
что при выполнение условия (2.26) функция (2.24) положительная, следовательно,
для 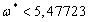 , стационарное движение будет устойчивым. Для
, стационарное движение будет устойчивым. Для 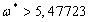 , движение неустойчиво.
, движение неустойчиво.
Рассмотрим
второе стационарное движение 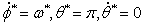 :
:
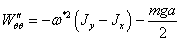 ,
,
полученное
выражение всегда меньше нуля, следовательно, можно сделать вывод: Стационарное
движение системы 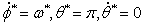 , неустойчиво.
, неустойчиво.
Рассмотрим
третье стационарное движение
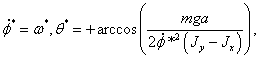
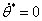 :
:
Выразим
значение 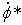 :
:
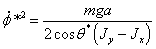 ,
подставим полученное значение в (2.24), получим
,
подставим полученное значение в (2.24), получим
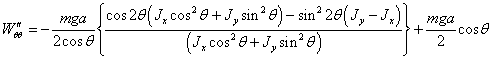 (2.27)
(2.27)
Преобразуем
выражение (2.27):
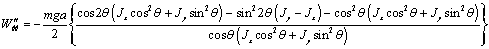
Использую
формулу тригонометрии 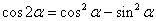 , перепишем предыдущее соотношение,
, перепишем предыдущее соотношение,
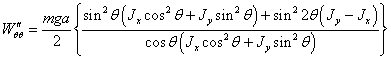 (2.28)
(2.28)
Так
как 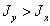 , то выражение
, то выражение 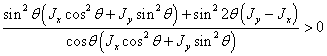 , для
любых
, для
любых 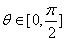 . Это означает что, выражение (2.28) всегда больше
нуля, для рассматриваемого движения. Следовательно, стационарное движение
. Это означает что, выражение (2.28) всегда больше
нуля, для рассматриваемого движения. Следовательно, стационарное движение
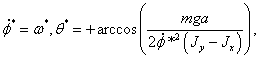
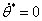 будет
устойчивым.
будет
устойчивым.
Численные
значения второй производной от приведенной потенциальной энергии,
соответствующие исследуемым стационарным движениям, приведены в таблице 2.
Таблица 2
|
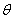 , рад , рад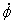 , рад/с , рад/с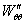
|
|
|
|
0
|
5
|
16,67
|
|
0
|
6
|
-20
|
|
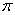 10-433,3 10-433,3
|
|
|
|
1,2661
|
10
|
325,27
|
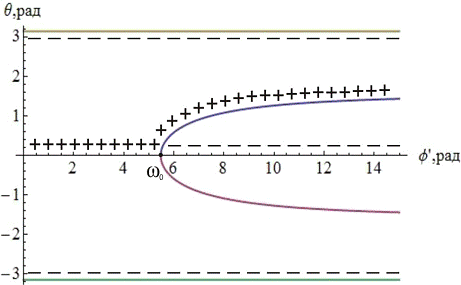
Рисунок 12 - Множество стационарных движений системы
Подтвердим
и проиллюстрируем полученные теоретические результаты. Для этого построим
графики отклонений для значений 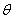 и
и 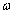 , не исследованных ранее, то есть лежащих на одной из
веток кривой, которая соответствует устойчивым стационарным движениям для
, не исследованных ранее, то есть лежащих на одной из
веток кривой, которая соответствует устойчивым стационарным движениям для 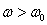 . Возьмем
. Возьмем 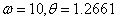 :
:
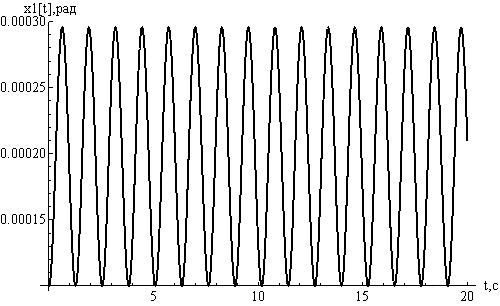
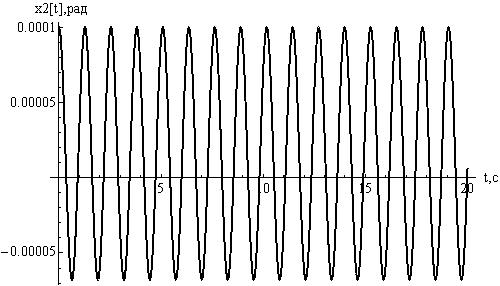
Рисунок
14 - отклонения 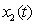 , при
, при 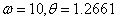
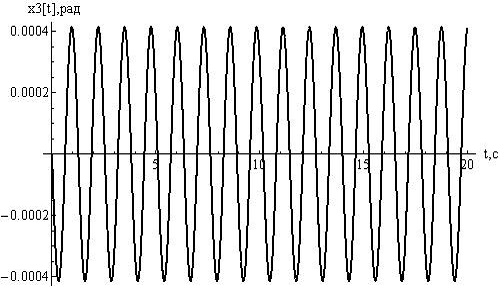
Рисунок
15 - отклонения 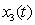 , при
, при 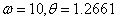
Заключение
В данной работе проведено комплексное исследование свойств устойчивости
различных стационарных движений механической системы. Составлены уравнения
движения, уравнения возмущенного движения и уравнения их линейного приближения.
Получено и проанализировано множество всех стационарных движений. С помощью
различных методов теории устойчивости были выделены подмножества устойчивых и
неустойчивых положений относительного равновесия системы и получены условия их
устойчивости и неустойчивости. Проведен анализ применимости каждого метода, и
их сравнение. В каждом разделе приведены графики и выводы по проделанной
работе.
Список использованной литературы
1. Авраменко,
А.А. Исследование устойчивости движений механических систем[Текст] Методические
указания к курсовой работе по теории устойчивости и управления. Часть
1/А.А.Авраменко, С.П.Безгласный.- Самара:СГАУ, 2008. - 68 с.
. Ярошевский,
В.А. Лекции по теоретической механике [Текст]: учебное пособие / В.А.Ярошевский.
- М.: МФТИ, 2001. - 244 с.
. Барбашин,
Е.А. Введение в теорию устойчивости[Текст]: учебное пособие/Е.А.Барбашин. - М.:
Наука, 1967. -223 с.