Использование экономико-математического моделирования в животноводстве

Использование экономико-математического моделирования в животноводстве

Задание 1

Постановка задачи, критерий оптимальности и матрица ЭММ распределения и использования удобрений.

Все модели по расчетам оптимальных рационов кормления скота и птицы, применяемые на практике с использованием экономико-математических методов и ЭВМ, можно свести к трем основным:

-   модель оптимальных рационов кормления скота;

-   модель планирования оптимальных кормовых смесей с учетом всех ингредиентов питания;

-   модель оптимального плана использования (распределения) заготовленных кормов в сельскохозяйственном предприятии.

Для успешного развития животноводства важное значение имеет организация кормовой базы. В себестоимости продукции животноводства затраты на корма занимают наибольший удельный вес (до 50% и более). Поэтому одним из основных путей снижения себестоимости животноводческой продукции является удешевление рационов кормления при высокой их питательной ценности.

Животные должны получать полноценные рационы, сбалансированные по содержанию кормовых единиц, переваримого протеина, каротина и других элементов питания, а также аминокислот и микроэлементов. Кормовые рационы должны не только полностью удовлетворять потребности животных в питательных веществах, но и быть наиболее дешевыми, то есть оптимальными.

Рассчитать оптимальный кормовой рацион, учитывающий зоотехнические и экономические требования, при помощи традиционных методов подбора кормов практически невозможно. Поэтому для этих целей все чаще используют экономико-математические методы и ЭВМ.

Цель задачи можно выразить следующим образом:

из имеющихся в сельскохозяйственном предприятии кормов составить такой рацион кормления, который полностью отвечал бы требованиям животных по содержанию в нем питательных веществ, соотношению отдельных видов и групп кормов и одновременно был самым дешевым для хозяйства. Критерием оптимальности чаще всего служит минимум стоимости (точнее себестоимости) рациона.

Основными переменными в экономико-математической задаче являются корма, имеющиеся в хозяйстве, а также корма, кормовые и минеральные добавки, которые хозяйство может приобрести. Единицами измерения этих переменных являются весовые единицы (кг, ц) в зависимости от периода, на который составляется рацион (сутки, год).

В экономико-математической задаче, кроме основных, могут быть также и вспомогательные переменные. Они чаще всего выражают суммарное количество кормовых единиц или переваримого протеина в рационе. С помощью этих переменных записывают условия по структуре рациона (удельному весу отдельных групп кормов).

Основные ограничения необходимы для записи условий по балансу питательных веществ. Технико-экономические коэффициенты в этих ограничениях обозначают содержание соответствующих питательных веществ в единице корма (в 1 кг, 1 ц). Константы (объемы ограничений) показывают количество питательных веществ, которое должно содержаться в рационе.

С помощью дополнительных ограничений в задаче записывают условия по соотношению отдельных групп кормов в рационе и отдельных видов кормов внутри групп. Если эти соотношения выражены в весовых единицах, то технико-экономическими коэффициентами по основным переменным соответствующих групп кормов являются единицы или величины, характеризующие удельный вес данного вида или группы корма в рационе (коэффициенты пропорциональности). Константы в данном случае обозначают минимальное или максимальное зоотехнически допустимое весовое количество рассматриваемой группы кормов в рационе. .

Если дополнительные ограничения измеряются в кормовых единицах (или других единицах питательных веществ), то технико-экономические коэффициенты по основным переменным обозначают содержание этого питательного вещества в единице корма, а по вспомогательным переменным - удельный вес (в долях от единицы) данной группы или вида корма в рационе. Константами в этих ограничениях служат нули.

С помощью вспомогательных ограничений записывают условия по суммарному количеству кормовых единиц и переваримого протеина. Технико-экономические коэффициенты по основным переменным (так же, как и в основных ограничениях) отражают содержание питательных веществ в единице корма или кормовых добавок, а по вспомогательным переменным равны -1. Константами в этих ограничениях являются нули.

Исходная информация и расчет технико-экономических коэффициентов и констант. Для составления экономико-математической модели оптимального рациона кормления скота (птицы) необходимы следующие данные:

. Вид или половозрастная группа скота (птицы), для которой рассчитывается рацион (кормовая смесь);

период (сутки, месяц, год); живая масса одной головы;

планируемая продуктивность. Эти данные берутся в хозяйстве.

. Требуемое содержание питательных веществ в рационе, или потребность животного в зависимости от его продуктивности, живой массы, физиологического состояния. Эти нормативные данные содержатся в справочниках.

. Предельные нормы скармливания отдельных видов и групп кормов данному виду скота (птицы) или допустимые зоотехнические нормы потребления кормов. Эти данные также берут из справочной литературы.

. Виды кормов и кормовых добавок, из которых могут быть составлены кормовые рационы (смеси). Эти данные имеются в хозяйстве.

. Содержание питательных веществ в единице корма или кормовых добавок по всем учитываемым в задаче видам питательных веществ. Эти данные получают на основе результатов анализа кормов, проведенного в агрохимлаборатории, или из справочных таблиц по питательности кормов.

. Стоимость (себестоимость) весовой единицы корма и добавок. Эти данные также берут в хозяйстве.

Рацион должен полностью удовлетворять потребность животного во всех перечисленных питательных веществах при заданном соотношении отдельных видов и групп кормов и одновременно иметь минимальную себестоимость.

Система переменных. В соответствии с перечисленными условиями задачи определим перечень переменных. Количество кормов, которое может войти в рацион коровы, обозначим символами: х1-комбикорм, х2- отруби ячменные, х3-сено клеверо-тимофеечное, х4- сено луговое, x5-сенаж вико-овсяный, х6-солома ячменная, x7-силос кукурузный, X8-силос подсолнечниковый, Х9-кормовая свекла, Х10--картофель.

Система ограничений. Основными ограничениями в данной модели будут условия по балансам всех питательных веществ: кормовых единиц, переваримого протеина, каротина и сухого вещества.

Математическая запись первой группы ограничений - по балансу питательных веществ - показывает, что рацион должен содержать питательных веществ не менее допустимого количества:

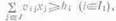
где j - индекс переменной;

J - множество, включающее в себя номера .переменных по видам кормов в рационе;

I - индекс ограничения;

I1 - множество, включающее номера ограничений по содержанию питательных веществ;

X j- количество корма j-вида, входящего в рацион:

vij - содержание i-элемента питания в единице j-корма;

bi - допустимое количество ('-питательного вещества в рационе.

Вторая группа ограничений обеспечивает содержание сухого вещества в рационе не более допустимого количества. Математическая запись при этом имеет такой вид:

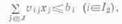
где I2 - множество, включающее номера ограничений по содержанию сухого вещества в рационе.

Третья группа ограничений обеспечивает удельный вес отдельных групп кормов в зоотехнически допустимых пределах. Математическая запись этой группы условий имеет вид:

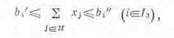
где Н - множество, включающее номера переменных по видам кормов одной группы;

bi’ и bi"- минимально и максимально допустимое количество кормов данной группы в рационе;

Iз - множество, включающее номера ограничений по содержанию отдельных групп кормов в рационе.

Четвертая группа ограничений-по удельному весу отдельных видов кормов внутри этих групп. Их записывают с помощью коэффициентов пропорциональности.

Эта группа ограничений обеспечивает определенный удельный вес отдельных видов кормов внутри соответствующих групп кормов. Общая математическая запись имеет вид:

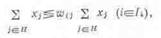
где wij - коэффициент пропорциональности;

I4 - множество, включающее номера ограничений по удельному весу отдельных видов кормов внутри групп.

Пятая группа ограничений - неотрицательность переменных величин:

 ≥0

Задание 2

В четырех пунктах отправления имеется груз в следующем количестве: первый пункт отправления - 110, второй - 180, третий - 230, четвертый - 310 тонн. Его необходимо доставить в четыре пункта назначения в следующем количестве: первый пункт назначения - 160, второй - 210, третий - 250, четвертый - 300 тонн. Требуется составить план грузоперевозок с минимумом затрат на транспортировку. Расстояния между пунктами отправления и назначения в км приведены в таблице:

Стоимость доставки единицы груза из каждого пункта отправления в соответствующие пункты назначения задана матрицей тарифов

Проверим необходимое и достаточное условие разрешимости задачи.

∑ a = 160 + 210 + 250 + 300 = 830

∑ b = 110 + 180 + 230 + 310 = 920

Как видно, суммарная потребность груза в пунктах назначения превышает запасы груза на базах. Следовательно, модель исходной транспортной задачи является открытой. Чтобы получить закрытую модель, введем дополнительную (фиктивную) базу с запасом груза, равным 90 (920-830). Тарифы перевозки единицы груза из базы во все магазины полагаем, равны нулю.

Занесем исходные данные в распределительную таблицу.

. Используя метод наименьшей стоимости, построим первый опорный план транспортной задачи.

В результате получен первый опорный план, который является допустимым, так как все грузы из баз вывезены, потребность магазинов удовлетворена, а план соответствует системе ограничений транспортной задачи.

. Подсчитаем число занятых клеток таблицы, их 8, а должно быть

+ n - 1 = 8.

Следовательно, опорный план является невырожденным.

. Проверим оптимальность опорного плана. Найдем потенциалы ui, vi. по занятым клеткам таблицы, в которых ui + vi = cij, полагая, что u1 = 0.

+ v3 = 3; 0 + v3 = 3; v3 = 3+ v3 = 4; 3 + u3 = 4; u3 = 1+ v4 = 5; 1 + v4 = 5; v4 = 4+ v4 = 4; 4 + u4 = 4; u4 = 0+ v1 = 2; 0 + v1 = 2; v1 = 2+ v5 = 0; 1 + v5 = 0; v5 = -1

u2 + v5 = 0; -1 + u2 = 0; u2 = 1+ v2 = 1; 1 + v2 = 1; v2 = 0

Опорный план не является оптимальным, так как существуют оценки свободных клеток, для которых

+ vi > cij

(1;4): 0 + 4 > 3; ∆14 = 0 + 4 - 3 = 1

Выбираем максимальную оценку свободной клетки (1;4): 3

Для этого в перспективную клетку (1;4) поставим знак «+», а в остальных вершинах многоугольника чередующиеся знаки «-», «+», «-». Цикл приведен в таблице.

Из грузов хij стоящих в минусовых клетках, выбираем наименьшее, т.е.

у = min (3, 4) = 120. Прибавляем 120 к объемам грузов, стоящих в плюсовых клетках и вычитаем 120 из Хij, стоящих в минусовых клетках. В результате получим новый опорный план.

. Проверим оптимальность опорного плана. Найдем потенциалы ui, vi. по занятым клеткам таблицы, в которых ui + vi = cij, полагая, что u1 = 0.

+ v3 = 3; 0 + v3 = 3; v3 = 3+ v3 = 4; 3 + u3 = 4; u3 = 1+ v5 = 0; 1 + v5 = 0; v5 = -1+ v5 = 0; -1 + u2 = 0; u2 = 1+ v2 = 1; 1 + v2 = 1; v2 = 0+ v4 = 3; 0 + v4 = 3; v4 = 3

u4 + v4 = 4; 3 + u4 = 4; u4 = 1+ v1 = 2; 1 + v1 = 2; v1 = 1

Опорный план является оптимальным.

Затраты составят:(x) = 3*40 + 3*120 + 1*180 + 0*30 + 4*190 + 0*60 + 2*110 + 4*190 = 2400

Задание 3

Площадь пашни в сельскохозяйственной организации составляет 3500 га, сенокосов - 1200 га, пастбищ -650га. В хозяйстве возделываются пшеница, озимая рожь, овес, свекла и картофель, животноводческий подкомплекс включает коров, молодняк КРС и овец. Для содержания одной коровы требуется 2 га пашни, 0,5 га сенокосов и 0,2 га пастбищ, молодняка КРС - 1 га пашни, 0,5 га сенокосов, 0,1 га пастбищ, овец - 0,3 га пашни, 0,09 га сенокосов, 0,05 га пастбищ. Площадь посевов озимой ржи и овса не должна превышать 67% в площади посевов зерновых. Поголовье овец должно быть не менее 700 голов. Хозяйство располагает трудовыми ресурсами в размере 200 тыс. чел.-ч. Затраты труда составляют на 1 га посевов пшеницы - 3 чел.-ч., озимой ржи - 2, овса - 2,1 , свеклы - 80, картофеля - 95 чел.-ч., а на одну голову молодняка КРС - 95, корову - 205, голову овец - 8 чел.-ч. Объем производства молока в хозяйстве должен быть не менее 5700, мяса - не менее 580 ц, шерсти - не менее 6 ц. Продуктивность животных на одну голову: овец - 0,3 ц мяса, 0,03 ц шерсти, коров - 28 ц молока, молодняка КРС - 1,6 ц мяса. Поголовье коров КРС в структуре стада КРС должно быть не более 69%. Себестоимость товарной продукции составляет с 1 га пшеницы - 3,9, озимой ржи - 3,4 , овса - 3,6, свеклы - 5,5, картофеля - 5,9 тыс. руб., с одной головы овцы - 2,9, коров - 6,7, молодняка КРС - 4,6 тыс. руб. Требуется разработать экономико-математическую модель производственно-отраслевой структуры организации и ее матрицу. Критерий оптимальности - минимум себестоимости товарной продукции.

Система переменных.

х1 - площадь пшеницы;

х2 - площадь озимой ржи;

х3 - площадь овса;

х4 - площадь свеклы;

х5 - площадь картофеля;

х6 - поголовье коров;

х7 - поголовье молодняка КРС;

х8 - поголовье овец;

х9 - площадь сенокосов;

х10 - площадь пастбищ;

Содержание животноводства

Затраты труда

Продуктивность, ц

Себестоимость

Система ограничений. Блок ограничений по использованию производственных ресурсов:

) Пашня

х1 + х2 + х3 + х4 + х5 £ 3500 га

) Сенокосы

х9 £ 1200 га

) Пастбища

х10 £ 650 га

4) Трудовые ресурсы

х1 + 2х2 + 2,1х3 + 80х4 + 95х5 + 205х6 + 95х7 + 8х8 £ 200000

. Блок ограничений по дополнительным требованиям к отраслям:

) Площадь посевов озимой ржи и овса не должна превышать 67% посевов зерновых.

х2 +х3 £ 0,67(х1+х2+х3)

преобразим и приведем к нулю: -0,67х1 + 0,33х2 + 0,33х3 £ 0

) Поголовье молодняка в структуре стада КРС должно быть не более 69%

,69(х6 + х7) ³ х7

преобразим и приведем к нулю:

,69х6 - 0,31х7 £ 0

) Поголовье овец должно быть не менее 700 голов.

х8 ³ 700

. Блок ограничений по содержанию животноводства :

) Коровы

х6 = 2(х1 + х2 + х3 + х4 + х5) + 0,5х9 + 0,2х10

х1 + 2х2 + 2х3 + 2х4 + 2х5 + 0,5х9 + 0,2х10 - х6 = 0

) Молодняк КРС

х7 = (х1 + х2 + х3 + х4 + х5) + 0,5х9 + 0,1х10

х1 + х2 + х3 + х4 + х5 + 0,5х9 + 0,1х10 - х7 = 0

10) Овцы

х8 = 0,3(х1 + х2 + х3 + х4 + х5) + 0,09х9 + 0,05х10

0,3х1 + 0,3х2 + 0,3х3 + 0,3х4 + 0,3х5 + 0,09х9 + 0,05х10 - х8 = 0

. Блок ограничений по производству:

) Молоко

х6 ³ 5700

) Мясо

,6х7 + 0,3х8 ³ 580

) Шерсть

,035х8 ³ 6- Целевая функция:

= 3,9х1 + 3,4х2 + 3,6х3 + 5,5х4 + 5,9х5 + 6,7х6 + 4,6х7 + 2,9х8 → min

экономический математический ограничение оптимальность

Матрица

Задание 4

Разработать рацион кормления коров с минимальной себестоимостью.

Содержание картофеля в рационе не должно быть менее 20% его веса.

Содержание сена в рационе не должно быть менее 50% питательного рациона.

Решение:

х1- сено

х2 - картофель

Ограничения по потребности

,45х1 + 0,3х2 ³ 24

х1 + 10х2 ³ 3000

х1 + 2х2 ³ 1200

х1³ 0, х2 ³ 0

Ограничение по составу

х2 ³ 0,2(х1 + х2) или 0,2х1 - 0,8х2 £ 0

х1 ³ 0,5(х1 + х2) или -0,5х1 + 0,5х2 £ 0

Целевая функция

,5х1 + 0,9х2 → min

Наносим на график уравнения ограничения.

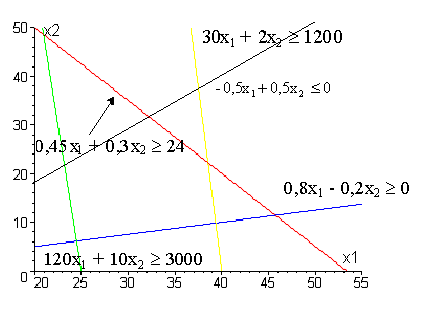
После этого определяем область допустимых значения.

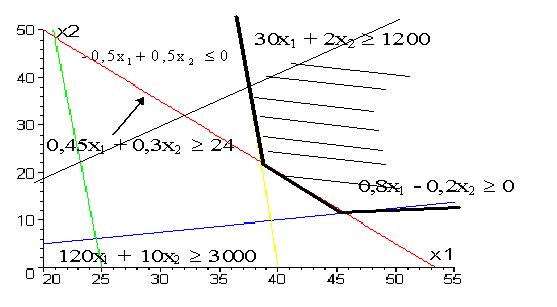
Чертим вектор с координатами (1,5; 0,9) и линии уровня, перпендикулярные ему. Видим, что линия уровня пересекает область в точке (1).

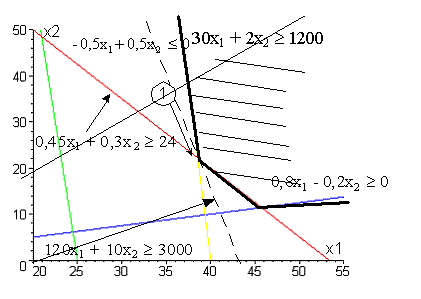
Найдем координаты точки (1). Это точка пересечения прямых

,45х1 + 0,3х2 = 24 и 30х1 + 2х2 = 1200

х1 = (24-0,3*x2)/0,3

Подставим во второе уравнение.

*(24-0,3*x2)/0,3 + 2x2 = 1200

Откуда х2 = 22,22 кг

х1 = 38,52 кг

Себестоимость: Z = 1,5*38,52+ 0,9*22,22 = 77,78 руб.

Задание 5

Дана математическая запись модели:

x1 - 5x2 + 3х3 = 4;

x1 + 5x2 - 3х3 ≥ 2;

х1 + 4х2 ≥ -4;(x)= -5x1 + х2 - 2х3 → max.

Решить задачу оптимизации модели модифицированным симплексным методом.

Решение:

Решим прямую задачу линейного программирования модифицированным симплексным методом.

Определим максимальное значение целевой функции F(X) = -5x1+x2-2x3 при следующих условиях - ограничений.

x1-5x2+3x3=4

x1+5x2-3x3≥2

x1+4x2≥-4

Для построения первого опорного плана систему неравенств, приведем к системе уравнений путем введения дополнительных переменных (переход к канонической форме).

x1-5x2 + 3x3 + 0x4 + 0x5 = 4

x1 + 5x2-3x3-1x4 + 0x5 = 2

x1 + 4x2 + 0x3 + 0x4-1x5 = -4

Введем искусственные переменные x.

x1-5x2 + 3x3 + 0x4 + 0x5 + 1x6 + 0x7 + 0x8 = 4

x1 + 5x2-3x3-1x4 + 0x5 + 0x6 + 1x7 + 0x8 = 2

x1 + 4x2 + 0x3 + 0x4-1x5 + 0x6 + 0x7 + 1x8 = -4

Поскольку в начальном плане присутствуют отрицательные значения bi < 0, то с помощью двойственного симплекс-метода устраняем отрицательные значения.

Полагая, что свободные переменные равны 0, получим первый опорный план:

= (0,0,0,0,0,4,2,-4)= 0= -1+x1+5x2-3x3= 2-2x1-5x2+3x3+x4= 2-2x1-4x2+x5

Среди свободных членов в системе уравнений есть отрицательные элементы. Используем двойственный симплекс-метод. Выберем из них наибольший по модулю, а в его уравнении - любой отрицательный.

Чтобы теперь выразить все переменные через небазисные, в выражении для x8 выразим x5 и подставим полученное выражение во все остальные равенства.

= 0-5x1+x2-2x3= 4+x1+5x2-3x3= 2-2x1-5x2+3x3+x4= 4+2x1+4x2+x8

Переходим к первому этапу модифицированного симплекс-метода.

Первый этап. Для нахождения начальной допустимой базы воспользуемся методом искусственного базиса.

Имеем:

Матрица коэффициентов A = aij

Матрица b.

Итерация №1.

<X> = (6, 7, 5)

Матрица c.

c = (0, 0, 0, 0, 0, 1, 1, 0)= (1, 1, 0)= (0, 0, 0, 0, 0)

Вычисляем:

Матрицу B-1 вычисляем через алгебраические дополнения.

= cBB-1 = (1, 1, 0)

c* = cN - uN = (-1, 0, 0, 1, 0)

Откуда s = 1

Откуда r = 2

Итерация №2.

<X> = (6, 1, 5)

Матрица c.

= (-1, 0, 0, 1, 0, 0, 0, 0)= (0, -1, 0)= (0, 0, 1, 0, 0)

Вычисляем:

= cBB-1 = (0, -0.5, 0)

c* = cN - uN = (2.5, -1.5, 0.5, 0.5, 0)

Откуда s = 2

Откуда r = 1

Итерация №3.

<X> = (3, 1, 5)

Матрица c.

= (0, 2.5, -1.5, 0.5, 0, 0, 0.5, 0)= (-1.5, 0, 0)= (2.5, 0.5, 0, 0.5, 0)

Вычисляем:

= cBB-1 = (-1, -0.5, 0)

* = cN - uN = (-0, 0, 1, 1, 0)

Нулевая строка симплексной таблицы неотрицательна. Первый этап симплекс-метода завершен.

Второй этап. Удаляем столбцы с искусственными переменными. Заменим вектор оценок С на целевую функцию.

Выразим базисные переменные:= 3.33-1.67x2-0.3333x4= 6-1x4

которые подставим в целевую функцию:

(X) = 5(6-1x4)-x2 + 2(3.33-1.67x2-0.3333x4)

или(X) = 36.67+2.33x2+5.67x4

Имеем:

Матрица коэффициентов A = aij

Матрица b.

Итерация №1.

<X> = (3, 1, 5)

Матрица c.

= (0, -2.3333, 0, -5.6667, 0)= (0, 0, 0)= (-2.3333, -5.6667, 0, 0, 0)

Вычисляем:

Матрицу B-1 вычисляем через алгебраические дополнения.

= cBB-1 = (0, 0, 0)

c* = cN - uN = (-2.3333, -5.6667, 0, 0, 0)

Откуда s = 2

Выводимую переменную r найти невозможно. Прерываем процесс поиска первого опорного плана.

Вектор результатов X = (6, 0, 3.33)T

Значение целевой функции F(X) = bc = -36.67