Особенности движения истребителя
Оглавление
1. Постановка задачи
. Теоретические сведения
2.1. Динамика пространственного движения самолета
.2. Оптимальное управление дискретными системами
.3. Полная управляемость системы по состоянию
3. Начальные данные
. Ход решения задачи
. Результаты вычислений
. Графики
Выводы
Список использованной литературы
Приложение (текст программы - 1 случай) [Mathcad 14]
Постановка задачи
Дано:
Система дифференциальных уравнений, описывающая движение
высокоманевренного фронтового истребителя:
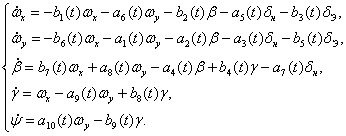
Фазовые
координаты: 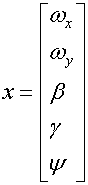 , управление:
, управление: 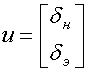 .
.
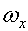 -
угловая скорость крена;
-
угловая скорость крена;
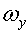 -
угловая скорость рыскания;
-
угловая скорость рыскания;
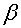 - угол
скольжения;
- угол
скольжения;
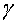 - угол
крена;
- угол
крена;
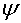 - угол
рыскания;
- угол
рыскания;
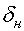 -
управление углом
-
управление углом 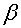 ;
;
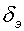 -
управление креном.
-
управление креном.
СДУ
представима в виде: 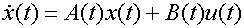 ,
,
где
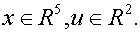
Функционал
качества управления:
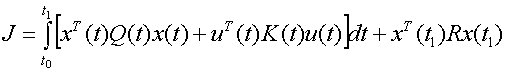 .
.
Требуется:
1).
От системы ДУ, используя метод Эйлера перейти к разностной схеме, шаг при
переходе - 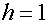 сек., время -
сек., время - 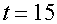 сек.
сек.
).
Проверить систему на управляемость.
).
Построить графики: 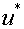 ,
,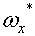 ,
,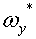 ,
,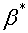 ,
,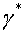 ,
,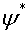 .
.
).
При заданных матрицах 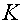 и
и 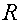 - проверить влияния матрицы
- проверить влияния матрицы 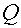 .
.
1.
Теоретические сведения
.1 Динамика
пространственного движения самолета
Угол рыскания - угол поворота корпуса самолёта в горизонтальной
плоскости, отсчитываемый от направления на север. Этот угол сходен с курсом, но
отсчитывается строго в соответствии с выбранной системой координат.
Угол крена - угол, характеризующий поворот самолёта вокруг его продольной
оси.
Угол скольжения - угол между воздушной скоростью самолета и плоскостью
симметрии самолета.
Управление
углом крена самолета осуществляется элеронами, управление углом 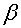 и углом
рыскания - рулем направления.
и углом
рыскания - рулем направления.
1.2 Оптимальное
управление дискретными системами
Пусть математическая модель объекта управления описывается разностным
уравнением:
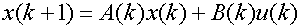 ,
, 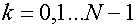 ,
,
с
начальным условием: 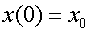 ,
,
а
функционал качества управления имеет вид:
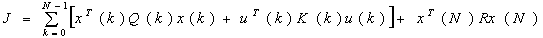 ,
,
где:
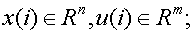
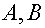 -
матрицы размера
-
матрицы размера 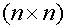 и
и 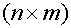 ;
;
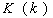 -
симметричная, положительно определенная матрица
-
симметричная, положительно определенная матрица 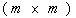 ,
,
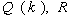 -
симметричные, неотрицательно определенные матрицы
-
симметричные, неотрицательно определенные матрицы 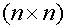 .
.
Требуется,
зная начальное состояние, выбрать такое допустимое управление для системы,
которое придаёт функционалу минимальное значение, т.е. в задаче ищется 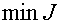 .
.
Алгоритм
поиска оптимального управления дискретной системой:
).
Обратный ход алгоритма (вычисляются вспомогательные матрицы):
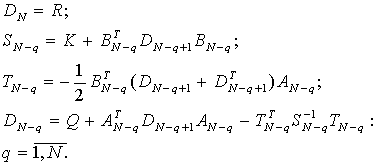
).
Прямой ход алгоритма (вычисляются фазовые координаты и управление):
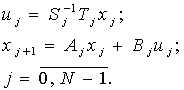
1.3 Полная
управляемость системы по состоянию
Теорема 1: Линейная нестационарная система
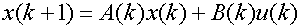 ,
,
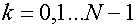 является
полностью управляемой по состоянию только в том случае, если матрица
является
полностью управляемой по состоянию только в том случае, если матрица 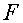 имеет ранг
имеет ранг 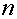 :
:
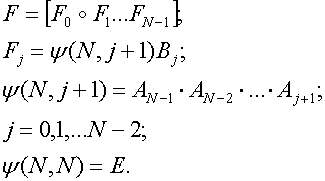
2
Начальные данные
Вариант № 2, Режим № 8.
1).
Коэффициенты 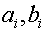 для 11 режима полета высокоманевренного фронтового
истребителя.
для 11 режима полета высокоманевренного фронтового
истребителя.
|
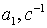 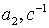 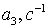 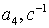 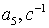 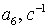 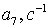 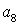 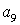 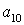
|
|
|
|
|
|
|
|
|
|
|
0,0919
|
3,1215
|
2,1499
|
0,014
|
0,8929
|
0,3877
|
0,0279
|
0,9998
|
0,59
|
0,13
|
|
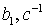 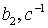 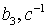 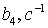 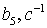 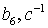 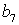 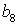 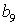
|
|
|
|
|
|
|
|
|
|
|
1,9603
|
21,6404
|
17,3369
|
0,0298
|
-0,3603
|
-0,0753
|
0,022
|
0,01
|
0,12
|
|
2). Вектор начальных значений фазовых координат.
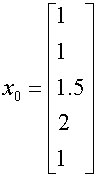 .
.
).
Матрицы функционала качества управления (для 6 различных случаев).
А).
 ,
, 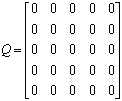 .
.
Б).
 ,
, 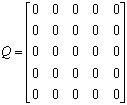 .
.
В).
 ,
, 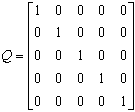 .
.
Г).
 ,
, 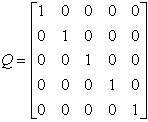 .
.
Д).
 ,
,  .
.
Е).
 ,
,  .
.
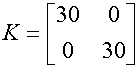 (одинакова для всех случаев).
(одинакова для всех случаев).
3
Ход решения задачи
1).
От системы ДУ 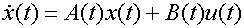 перейдем к
разностной системе, используя метод Эйлера с шагом
перейдем к
разностной системе, используя метод Эйлера с шагом 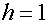 сек.
сек.
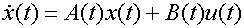 =>
=>
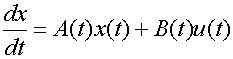 =>
=>
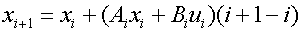 =>
=>
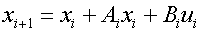 =>
=>
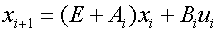 =>
=>
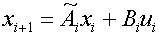 , где
, где 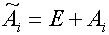 .
.
).
Запишем матрицы 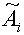 ,
, 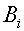 .
.
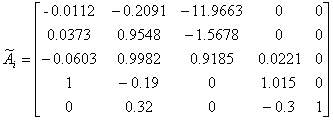 ,
,
 .
.
).
Запишем функционал качества управления для дискретной системы.
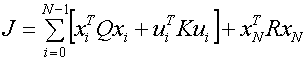 .
.
).
Найдем оптимальное управление и соответствующие фазовые координаты, исходя из
условия 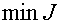 , по вышеизложенному алгоритму с помощью уравнения
Беллмана.
, по вышеизложенному алгоритму с помощью уравнения
Беллмана.
).
Проверим систему на управляемость.
Согласно
теореме 1, найдем матрицу 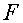 и вычислим ее ранг.
и вычислим ее ранг.
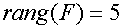 =>
=>
система
- полностью управляема по состоянию.
4
Результаты вычислений
1 случай.
|
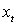
|
|
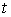 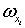 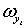 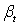 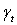 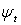
|
|
|
|
|
|
|
0
|
1
|
1
|
1.5
|
2
|
1
|
|
1
|
6.614928
|
-2.349614
|
2.544569
|
2.43
|
0.89
|
|
2
|
-29.285287
|
-1.219423
|
0.202584
|
10.4555
|
0.29295
|
|
3
|
12.681284
|
0.398913
|
-0.010775
|
-18.005772
|
-1.120235
|
|
4
|
-5.185979
|
0.524958
|
-0.436129
|
-5.739904
|
1.092316
|
|
5
|
10.923501
|
0.440143
|
0.024031
|
-11.293008
|
1.84935
|
|
6
|
-3.20727
|
0.14413
|
-0.123873
|
-0.742121
|
3.261729
|
|
7
|
5.78447
|
0.106238
|
0.068243
|
-4.041849
|
3.369521
|
|
8
|
-2.318427
|
0.020945
|
-0.076765
|
1.639523
|
3.868353
|
|
9
|
3.960249
|
2.608373e-3
|
0.044087
|
-0.674866
|
3.674333
|
|
10
|
-2.123644
|
-0.058426
|
-0.063303
|
3.277095
|
3.755656
|
|
11
|
3.450588
|
-0.08655
|
0.022636
|
1.220694
|
3.35481
|
|
12
|
-2.516761
|
7.266306e-3
|
-0.104745
|
4.734553
|
3.197075
|
|
13
|
4.311572
|
0.151688
|
0.100444
|
2.260851
|
2.629873
|
|
14
|
-6.25145
|
0.157603
|
0.22336
|
6.505535
|
2.37829
|
|
15
|
0.172774
|
-0.938737
|
0.710059
|
0.226154
|
1.618115
|
|
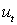
|
|
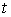 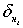 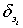
|
|
|
|
0
|
-1.009625
|
-2.279648
|
|
1
|
-4.154053
|
-1.586928
|
|
2
|
-1.892681
|
0.762542
|
|
3
|
0.314581
|
-0.414966
|
|
4
|
0.496131
|
0.164278
|
|
5
|
0.386169
|
-0.479789
|
|
6
|
0.077545
|
-8.593071e-3
|
|
7
|
0.091896
|
-0.278968
|
|
8
|
0.036791
|
-6.552785e-3
|
|
9
|
0.076844
|
-0.155915
|
|
10
|
0.032647
|
-2.760504e-3
|
|
11
|
0.035632
|
-0.074116
|
|
12
|
1.448854e-5
|
0.021294
|
|
13
|
-5.190081e-3
|
-6.736298e-3
|
|
14
|
-0.030735
|
0.05556
|
случай.
|
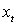
|
|
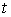 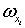 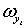 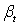 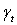 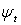
|
|
|
|
|
|
|
0
|
1
|
1
|
1.5
|
2
|
1
|
|
1
|
6.129498
|
-2.352163
|
2.544406
|
2.43
|
0.89
|
|
2
|
-29.461477
|
-1.214119
|
0.210944
|
9.971574
|
0.292619
|
|
3
|
12.378299
|
0.409608
|
-7.269674e-3
|
-18.673857
|
-1.061805
|
|
4
|
-5.389253
|
0.549299
|
-0.43471
|
-6.723965
|
1.232306
|
|
5
|
10.897833
|
0.46917
|
0.025207
|
-12.504544
|
2.110591
|
|
6
|
-3.413099
|
0.183854
|
-0.129039
|
-2.008567
|
3.672129
|
|
7
|
6.059615
|
0.147011
|
0.069701
|
-5.550226
|
3.937058
|
|
8
|
-2.616786
|
0.071337
|
-0.085597
|
0.36715
|
4.622196
|
|
9
|
4.563664
|
0.03877
|
0.054257
|
-2.288053
|
4.587412
|
|
10
|
-2.738081
|
-0.034631
|
-0.078708
|
2.229856
|
4.867018
|
|
11
|
4.672202
|
-0.096584
|
0.013198
|
-0.465494
|
4.594934
|
|
12
|
-3.109424
|
0.077723
|
-0.201646
|
4.259039
|
4.638237
|
|
13
|
7.416524
|
0.421896
|
0.073672
|
1.146348
|
4.137256
|
|
14
|
-8.223066
|
0.364966
|
8.325416
|
4.054541
|
|
15
|
-0.573415
|
-1.14173
|
1.449207
|
-0.203998
|
3.141336
|
|
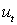
|
|
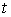 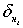 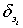
|
|
|
|
0
|
-1.003797
|
-2.251949
|
|
1
|
-4.16799
|
-1.548899
|
|
2
|
-1.910772
|
0.780156
|
|
3
|
0.296237
|
-0.390129
|
|
4
|
0.48557
|
0.175247
|
|
5
|
0.379277
|
-0.468258
|
|
6
|
0.075848
|
-7.415338e-3
|
|
7
|
0.093061
|
-0.279792
|
|
8
|
0.042178
|
-0.015212
|
|
9
|
0.08542
|
-0.167842
|
|
10
|
0.045132
|
-0.021135
|
|
11
|
0.051377
|
-0.096403
|
|
12
|
0.019353
|
-6.590723e-3
|
|
13
|
0.017352
|
-0.038783
|
|
14
|
-4.833736e-3
|
0.018476
|
3 случай.
|
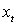
|
|
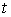 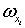 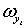 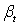 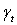 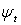
|
|
|
|
|
|
|
0
|
1
|
1
|
1.5
|
2
|
1
|
|
1
|
-1.40575
|
-2.175387
|
2.544666
|
2.43
|
0.89
|
|
2
|
-3.585641
|
-0.968779
|
0.567121
|
2.332029
|
0.3156
|
|
3
|
-0.146883
|
0.062133
|
-0.220434
|
-0.658712
|
-0.090185
|
|
4
|
0.714608
|
0.200054
|
-0.179604
|
-0.848841
|
-3.062246e-3
|
|
5
|
0.374294
|
0.066533
|
-0.028215
|
-0.260753
|
0.124806
|
|
6
|
0.042724
|
-9.658054e-3
|
0.020249
|
0.071679
|
0.164745
|
|
7
|
-0.043445
|
-0.016175
|
0.012297
|
0.120819
|
0.154888
|
|
8
|
-0.02862
|
-6.045082e-3
|
1.207221e-3
|
0.088125
|
0.138287
|
|
9
|
-0.012492
|
-1.251925e-3
|
-1.471402e-3
|
0.063953
|
0.126926
|
|
10
|
-0.010254
|
-9.986284e-4
|
-5.81666e-4
|
0.052839
|
0.119089
|
|
11
|
-0.011975
|
-1.349416e-3
|
1.99818e-4
|
0.043703
|
0.112619
|
|
12
|
-0.012153
|
-1.259356e-3
|
4.275548e-4
|
0.032961
|
0.107199
|
|
13
|
-0.0105
|
-1.596758e-3
|
4.315781e-4
|
0.02188
|
0.10308
|
|
14
|
-3.895641e-3
|
-3.085415e-3
|
-2.828136e-4
|
0.012542
|
0.100247
|
|
15
|
1.813073e-3
|
-1.926203e-3
|
-2.902997e-3
|
0.010592
|
0.098341
|
|
|
|
|
|
|
|
0
|
-1.013102
|
-1.816833
|
|
1
|
-4.648489
|
-2.603578
|
|
2
|
-1.454854
|
-0.40422
|
|
3
|
0.28597
|
0.225952
|
|
4
|
0.362794
|
0.139856
|
|
5
|
0.087679
|
6.018131e-3
|
|
6
|
-0.02839
|
-0.023457
|
|
7
|
-0.025013
|
-9.642615e-3
|
|
8
|
-4.530623e-3
|
1.167433e-3
|
|
9
|
2.143613e-3
|
3.037628e-3
|
|
10
|
1.018819e-3
|
1.954631e-3
|
|
11
|
-4.975721e-4
|
1.17068e-3
|
|
12
|
-7.000244e-4
|
8.093026e-4
|
|
13
|
-1.812931e-4
|
3.126241e-4
|
|
14
|
-4.338739e-5
|
5.354513e-4
|
 4
случай.
4
случай.
|
|
|
  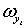 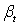 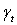 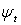
|
|
|
|
|
|
|
0
|
1
|
1
|
1.5
|
2
|
1
|
|
1
|
-1.406688
|
-2.175398
|
2.544665
|
2.43
|
0.89
|
|
2
|
-3.585999
|
-0.968767
|
0.567132
|
2.331097
|
0.315598
|
|
3
|
-0.147074
|
0.062164
|
-0.220431
|
-0.660018
|
-0.090073
|
|
4
|
0.714508
|
0.200096
|
-0.179605
|
-0.850368
|
-2.789661e-3
|
|
5
|
0.374221
|
0.066581
|
-0.028216
|
-0.262421
|
0.125267
|
|
6
|
0.042649
|
-9.606914e-3
|
0.020248
|
0.069893
|
0.165413
|
|
7
|
-0.043531
|
-0.016121
|
0.012296
|
0.11891
|
0.155777
|
|
8
|
-0.028713
|
-5.985575e-3
|
1.204766e-3
|
0.086079
|
0.139412
|
|
9
|
-0.012581
|
-1.18331e-3
|
-1.47311e-3
|
0.061759
|
0.128304
|
|
10
|
-0.01032
|
-9.287444e-4
|
-5.781063e-4
|
0.050493
|
0.12074
|
|
11
|
-0.011959
|
-1.316016e-3
|
2.045864e-4
|
0.041226
|
0.11456
|
|
12
|
-0.011813
|
-1.302918e-3
|
3.908352e-4
|
0.030456
|
0.109441
|
|
13
|
-9.239351e-3
|
-1.594063e-3
|
2.686431e-4
|
0.019716
|
0.105617
|
|
14
|
-2.017104e-4
|
-2.616401e-3
|
-5.343933e-4
|
0.011614
|
0.103044
|
|
15
|
5.158174e-3
|
-5.520453e-4
|
-2.79208e-3
|
0.013072
|
0.10131
|
|
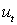
|
|
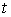 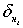 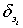
|
|
|
|
0
|
-1.013088
|
-1.81678
|
|
1
|
-4.648518
|
-2.603503
|
|
2
|
-1.454888
|
-0.404201
|
|
3
|
0.285953
|
0.225964
|
|
4
|
0.362789
|
0.139867
|
|
5
|
0.087677
|
6.027394e-3
|
|
6
|
-0.028393
|
-0.023448
|
|
7
|
-0.025017
|
-9.631605e-3
|
|
8
|
-4.535048e-3
|
1.179696e-3
|
|
9
|
2.141039e-3
|
3.047115e-3
|
|
10
|
1.024712e-3
|
1.95105e-3
|
|
11
|
-4.74313e-4
|
1.142275e-3
|
|
12
|
-6.6228e-4
|
7.626443e-4
|
|
13
|
-1.313613e-4
|
2.304926e-4
|
|
14
|
-5.877152e-6
|
4.395042e-4
|
5 случай.
|
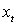
|
|
|
|
|
|
|
0
|
1
|
1
|
1.5
|
2
|
1
|
|
1
|
-2.635432
|
-1.385632
|
2.36552
|
2.84
|
0.72
|
|
2
|
-1.066552
|
-0.868977
|
1.050402
|
0.510438
|
-0.575402
|
|
3
|
-0.269815
|
-0.206133
|
0.193252
|
-0.383352
|
-1.006606
|
|
4
|
0.053727
|
0.043633
|
-0.015822
|
-0.619752
|
-0.957563
|
|
5
|
0.134098
|
0.056636
|
0.011988
|
-0.583612
|
-0.757675
|
|
6
|
0.125795
|
0.022357
|
0.046545
|
-0.469028
|
-0.564468
|
|
7
|
0.099627
|
4.143416e-3
|
0.047715
|
-0.354516
|
-0.416605
|
|
8
|
0.076494
|
9.458446e-4
|
0.034827
|
-0.260994
|
-0.308925
|
|
9
|
0.058871
|
1.972175e-3
|
0.023091
|
-0.188595
|
-0.230324
|
|
10
|
0.045537
|
2.644084e-3
|
0.015818
|
-0.132927
|
-0.173114
|
|
11
|
0.035239
|
2.999704e-3
|
0.01173
|
-0.089886
|
-0.13239
|
|
12
|
0.026461
|
3.724759e-3
|
9.842419e-3
|
-0.056564
|
-0.104465
|
|
13
|
0.016417
|
3.013809e-3
|
0.010058
|
-0.03166
|
-0.086303
|
|
14
|
-5.100463e-4
|
-5.295647e-3
|
0.01065
|
-0.01629
|
-0.075841
|
|
15
|
-0.030356
|
-0.026497
|
4.170728e-3
|
-0.016038
|
-0.072649
|
|
|
|
|
|
|
|
0
|
-0.683168
|
-1.105911
|
|
1
|
-4.714311
|
-1.947149
|
|
2
|
-2.443037
|
-0.878414
|
|
3
|
-0.559008
|
-0.169137
|
|
4
|
0.011766
|
3.324338e-3
|
|
5
|
1.880721e-3
|
-0.019994
|
|
6
|
-0.071931
|
-0.047549
|
|
7
|
-0.08527
|
-0.046727
|
|
8
|
-0.064922
|
-0.034317
|
|
9
|
-0.04315
|
-0.023241
|
|
10
|
-0.029561
|
-0.01623
|
|
11
|
-0.022318
|
-0.012079
|
|
12
|
-0.017532
|
-9.730539e-3
|
|
13
|
-0.011198
|
-8.641283e-3
|
|
14
|
-4.790906e-4
|
-6.800006e-3
|
6 случай.
|
|
|
  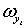 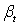 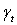 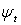
|
|
|
|
|
|
|
0
|
1
|
1
|
1.5
|
2
|
1
|
|
1
|
1.863665
|
-1.529179
|
2.366237
|
2.84
|
0.72
|
|
2
|
-5.992367
|
-1.349428
|
0.631161
|
5.036809
|
-0.621337
|
|
3
|
-2.453521
|
-0.212276
|
-0.277259
|
-0.623614
|
-2.564197
|
|
4
|
0.799325
|
0.318411
|
-0.332155
|
-3.046156
|
-2.445041
|
|
5
|
1.457799
|
0.276979
|
-0.107615
|
-2.353022
|
-1.429303
|
|
6
|
0.788232
|
0.089476
|
0.03486
|
-0.983144
|
-0.634763
|
|
7
|
0.151516
|
-0.013606
|
0.051799
|
-0.226659
|
-0.311188
|
|
8
|
-0.061327
|
-0.024025
|
0.0205
|
-0.075958
|
-0.247544
|
|
9
|
-0.025713
|
-3.698787e-3
|
-2.68783e-3
|
-0.13386
|
-0.232444
|
|
10
|
0.040388
|
9.300063e-3
|
-7.500846e-3
|
-0.160878
|
-0.19347
|
|
11
|
0.058238
|
0.010685
|
-3.685949e-3
|
-0.124671
|
-0.14223
|
|
12
|
0.041502
|
7.814105e-3
|
9.426781e-4
|
-0.070333
|
-0.10141
|
|
13
|
0.0171
|
3.434638e-3
|
4.592589e-3
|
-0.031371
|
-0.07781
|
|
14
|
-6.42921e-3
|
-5.309767e-3
|
5.927134e-3
|
-0.015394
|
-0.067299
|
|
15
|
-0.030521
|
-0.016636
|
1.922601e-4
|
-0.021045
|
-0.06438
|
|
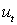
|
|
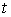 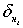 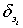
|
|
|
|
0
|
-0.769522
|
-1.425241
|
|
1
|
-4.074031
|
-1.594848
|
|
2
|
-2.092241
|
-0.354487
|
|
3
|
-0.028395
|
0.183173
|
|
4
|
0.584274
|
0.177939
|
|
5
|
0.345655
|
0.033112
|
|
6
|
0.033454
|
-0.041927
|
|
7
|
-0.078179
|
-0.040145
|
|
8
|
-0.053699
|
-0.015611
|
|
9
|
-8.176453e-3
|
-5.781337e-4
|
|
10
|
0.010717
|
2.155128e-3
|
|
11
|
8.463548e-3
|
5.353241e-5
|
|
12
|
1.976135e-3
|
-2.141087e-3
|
|
13
|
-5.804217e-4
|
-3.505654e-3
|
|
14
|
-1.116794e-4
|
-2.778321e-3
|
5
Графики
1 случай.
Оптимальное управление.
Управление
углом 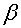 :
:
[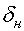 ]
]
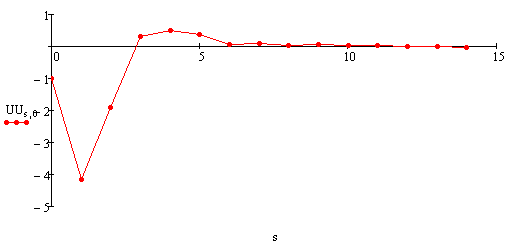
Управление креном:
[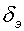 ]
]
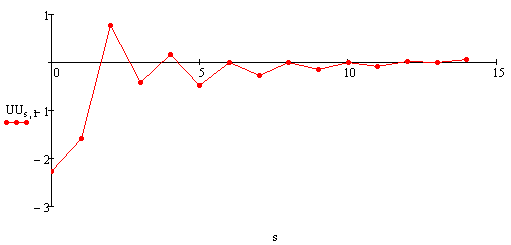
Фазовые координаты.
Угловая скорость крена:
[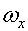 ]
]
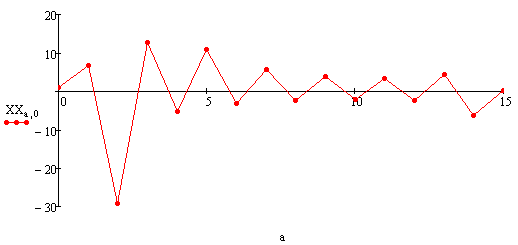
Угловая скорость рыскания:
[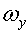 ]
]
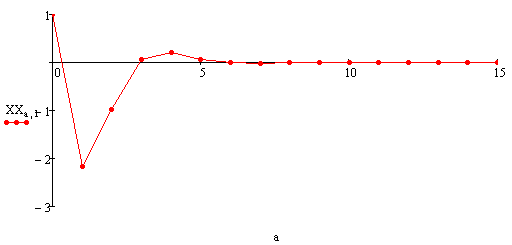
Угол скольжения:
[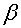 ]
]
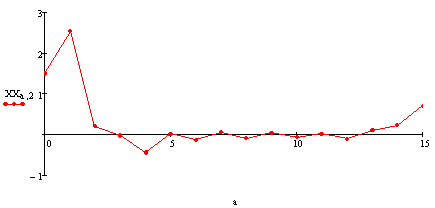
Угол крена:
[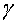 ]
]
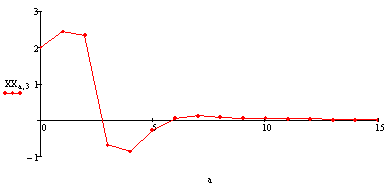
Угол рыскания:
[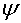 ]
]
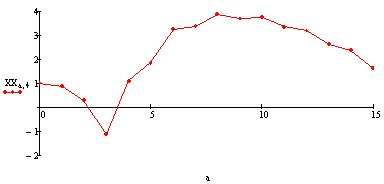
2 случай.
Оптимальное управление.
Управление
углом 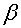 :
:
[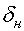 ]
]
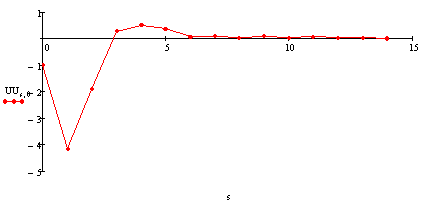
Управление креном:
[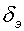 ]
]
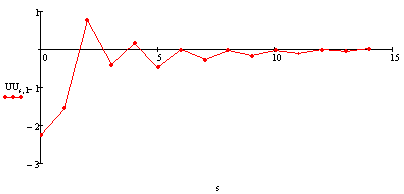
Фазовые координаты.
Угловая скорость крена:
[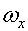 ]
]
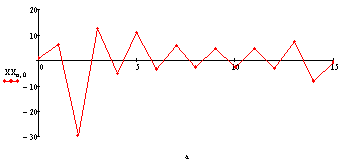
Угловая скорость рыскания:
[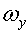 ]
]
Угол скольжения:
[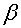 ]
]
Угол крена:
[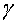 ]
]
Угол рыскания:
[ ]
]
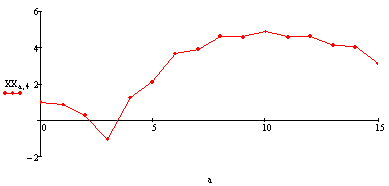
3 случай.
Оптимальное управление.
Управление
углом 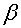 :
:
[ ]
]
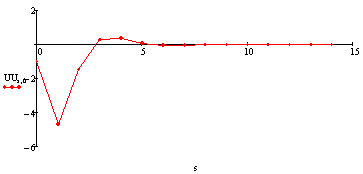
Управление креном:
[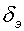 ]
]
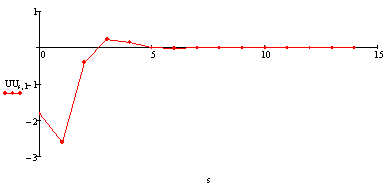
Фазовые координаты.
Угловая скорость крена:
[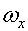 ]
]
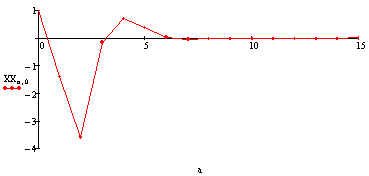
[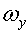 ]
]
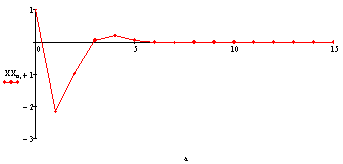
Угол скольжения:
[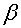 ]
]
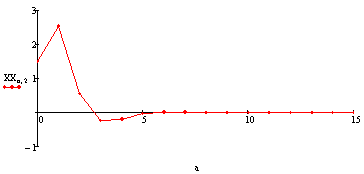
Угол крена:
[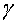 ]
]
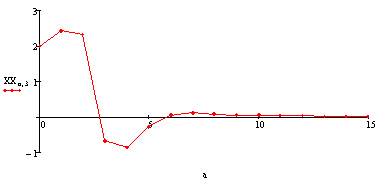
Угол рыскания:
[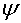 ]
]
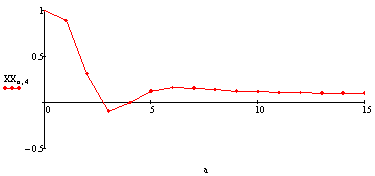
4 случай.
Оптимальное управление.
Управление
углом 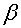 :
:
[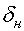 ]
]
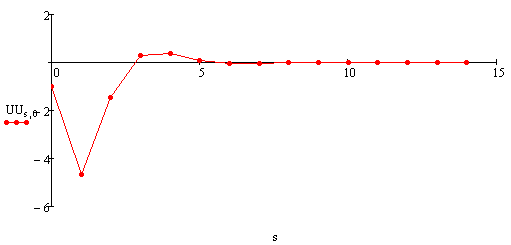
Управление креном:
[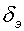 ]
]
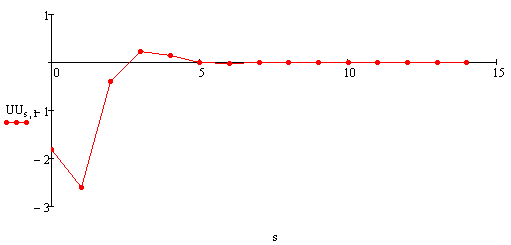
Фазовые координаты.
Угловая скорость крена:
[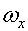 ]
]
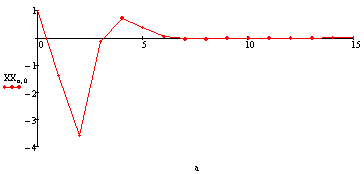
Угловая скорость рыскания:
[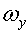 ]
]
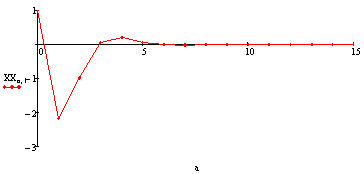
Угол скольжения:
[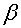 ]
]
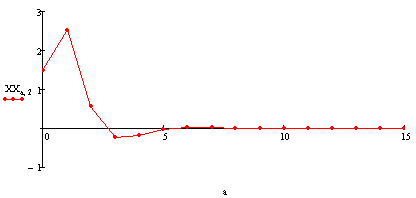
Угол крена:
[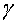 ]
]
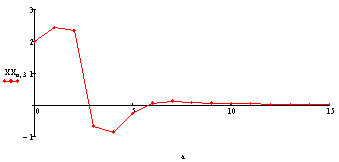
Угол рыскания:
[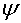 ]
]
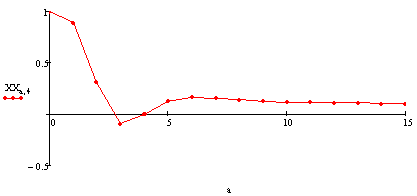
5 случай.
Оптимальное управление.
Управление
углом 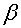 :
:
[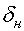 ]
]
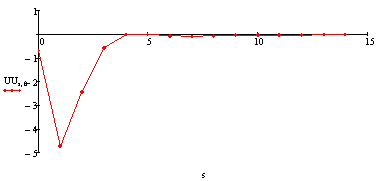
Управление креном:
[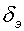 ]
]
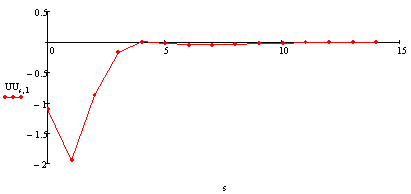
Фазовые координаты.
Угловая скорость крена:
[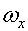 ]
]
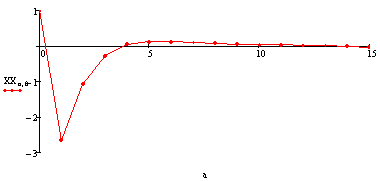
Угловая скорость рыскания:
[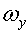 ]
]
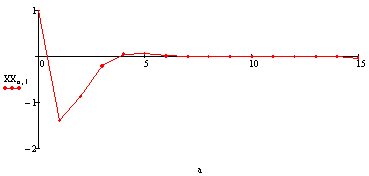
Угол скольжения:
[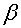 ]
]
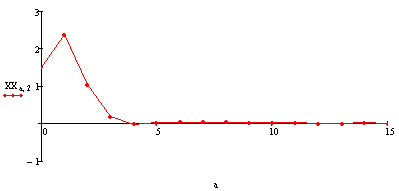
Угол крена:
[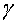 ]
]
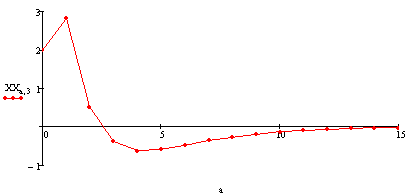
Угол рыскания:
[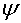 ]
]
6 случай.
Оптимальное управление.
Управление
углом 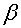 :
:
[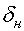 ]
]
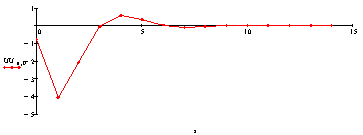
Управление креном:
[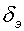 ]
]
Фазовые координаты.
Угловая скорость крена:
[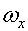 ]
]
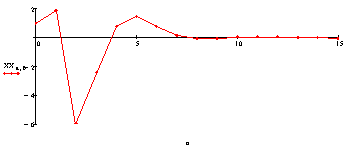
Угловая скорость рыскания:
[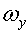 ]
]
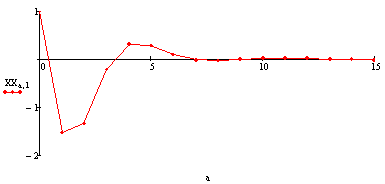
Угол скольжения:
[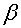 ]
]
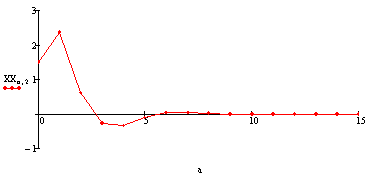
Угол крена:
[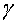 ]
]
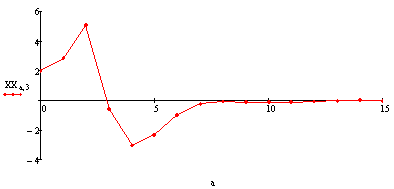
Угол рыскания:
[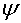 ]
]
истребитель управление функционал качество
Выводы
В данной работе проводилось исследование бокового движения
высокоманевренного фронтового истребителя. Требовалось найти оптимальное
управление, с помощью минимизации функционала качества управления.
При анализе системы, которой описывается движение истребителя, было
установлено, что система - полностью управляема по состоянию.
Было рассмотрено 6 различных случаев функционалов качества управления.
Исследование параметров задачи привело к следующим результатам:
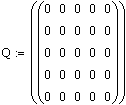
· Матрица Q
накладывает ограничения на поведение фазовых координат в данный момент времени,
т.е. учитывает ошибки управления в каждый момент времени. Ее изменение
существенно влияет на результаты. Замечена прямая зависимость между значениями
элементов матрицы и ограничением на значения фазовых координат. Т.е. с
увеличением значений элементов матрицы Q, ошибка управления корректируется больше.
· Матрица R
накладывает ограничения на поведение фазовых координат в конечный момент
времени. Чем больше значение СЗ матрицы R, тем большие ограничения накладываются на фазовые координаты
в конечный момент времени, т.е. происходит большая коррекция ошибки управления
в конечный момент времени.
· Матрица K -
есть матрица ограничения управления, в данной работе она не изменялась и
соответствует возможностям системы управления истребителя.
В силу вышеизложенного стоит отменить, что в случаях 3,4,5,6 -
стабилизация полета происходить приблизительно к 10-13 секундам, а в случае 1,2
- даже к 15 секунде не наблюдается стабилизации полета в силу того, что матрица
Q - нулевая и ограничения на фазовые
координаты - нет, и ошибки управления не учитываются в течение всего времени,
кроме конечного момента.
Список
использованной литературы
1. Пантелеев
А.В. Бортаковский А.С. Теория управления в примерах и задачах.
. Бюшгенс
Г.С. Студнев Р.В. Динамика самолета. Пространственное движение.
. Б. Куо.
Теория и проектирование цифровых систем управления.
Приложение (текст программы - 1
случай) [Mathcad 14]
. Исходные данные.
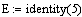
единичная матрица размера 5х5.
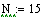
число шагов.


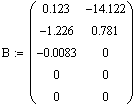

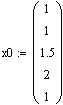
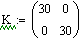
2. Проверка матриц на неотрицательную и
положительную определенность.
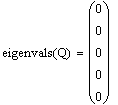
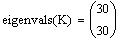
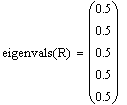
собственные значения матрицы К >0 => матрица К -
положительно определенная
собственные значения матриц Q,R >= 0 => матрицы Q, R-
неотрицательно определенные
3. Реализация алгоритма поиска оптимального
управления дискретной системой.
а). Обратный ход
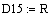
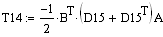
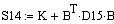
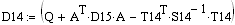

. . . . .

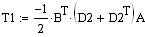
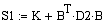
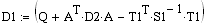

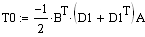
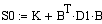
б). Прямой ход
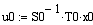
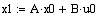

. . . . .

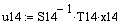
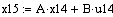

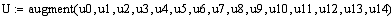
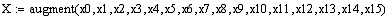
Оптимальное управление:
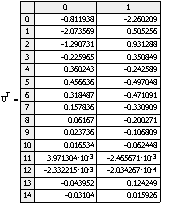
Фазовые координаты:
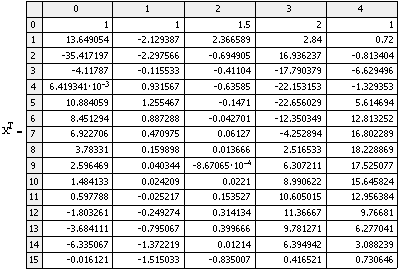
5. Проверка системы на управляемость по состоянию.
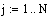
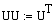
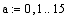
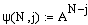
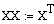
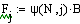
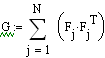
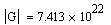
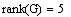
=> система полностью управляема по состоянию
6. Графики оптимальных управлений и фазовых
координат.