Электротехника и основы электроники
Федеральное
агентство по образованию
Государственное
учреждение
высшего
профессионального образования
Тульский
государственный университет
Кафедра
электротехники и электрооборудования
Стрекалов НА
Электротехника
и основы электроники
Методические
указания и контрольные задания
Тула 2009г.
ВВЕДЕНИЕ
Материал предназначен для студентов заочного обучения всех не
электрических специальностей. В его состав входят - программы изучения курса,
общие методические указания к выполнению контрольных работ, условия задач к
двум контрольным работам с методическими указаниями и примерами расчета.
Методические указания к третьей контрольной, в которой рассматривается расчет
полупроводниковых выпрямителей, изданы ранее и служат дополнением к данной работе.
Могут быть использованы только теми студентами, которые согласно учебному
плану должны выполнять три контрольные работы.
Если по учебному плану должна выполняться только одна контрольная работа,
то она составляется из задач /не всех/ первых двух контрольных работ и
оформляется как одна контрольная работа.
Материал включает контрольные работы по следующим разделам курса:
электрические и магнитные цепи постоянного тока; однофазные цепи
синусоидального тока; трехфазные цепи; трансформаторы; асинхронно трехфазные
цепи; двигатели постоянного тока параллельного возбуждения.
Методические указания и контрольные задания выдаются кафедрой каждому
студенту на период выполнения контрольных работ и подлежат обязательному
возврату на кафедру вместе с последнее контрольной работой.
Электрическая энергия, ее особенности и области применения. Значение и
электрификации в научно-технической революции и создание
материально-технической базы страны. Значение электротехнической подготовки для
инженеров не электротехнических специальностей.
ЭЛЕКТРИЧЕСКИЕ ЦЕПИ ПОСТОЯННОГО ТОКА
ЛИНЕЙНЫЕ ЦЕПИ. Условные обозначения элементов электрических цепей.
Направление токов, напряжений и ЭДС. Единицы их измерений. Законы Ома и
Кирхгофа. Цепи с одним источником питания с последовательным. параллельным и
смешанным соединением резистивных элементов. Преобразование треугольника
резистивных элементов в эквивалентную звезду и обратное преобразование.
Разветвленная цепь с несколькими источниками ЭДС: схема цепи, расчет путем
применения законов Кирхгофа; уравнение баланса мощностей. Двухполюсники
пассивные и активные: определения, условные обозначения, внутреннее (входное)
сопротивление пассивного двухполюсника и напряжение холостого хода активного
двухполюсника и способы их определения, расчет цепи методом активного
двухполюсника (эквивалентного генератора).
НЕЛИНЕЙНЫЕ ЦЕПИ. Определения нелинейного элемента и цепи. Вольт-амперные
характеристики (ВАХ) нелинейных и линейных элементов. Методы расчета
последовательной и параллельной цепей с двумя нелинейными элементами путем
сложения ВАХ этих элементов. Расчет последовательной цепи, состоящей из
линейного и нелинейного элементов, методом пересечения характеристик.
ЭЛЕКТРИЧЕСКИЕ ЦЕПИ ПЕРЕМЕННОГО ТОКА.
ЦЕПИ ОДНОФАЗНОГО СИНУСОИДАЛЬНОГО ТОКА.
Синусоидальные электрические величины, представление синусоидальными
функциями и графиками (синусоидами), мгновенные и амплитудные значения, фазы и
начальные фазы. Частота, период и угловая частота синусоидальной электрической
величины. Действующие значения синусоидального тока, напряжения и ЭДС.
Представление синусоидальных электрических величин вращающимися векторами и
комплексными числами.
Одноэлементные цепи: активная, индуктивная и емкостная. Схемы цепей;
уравнения мгновенных значений тока, напряжения и мощности, графики этих
значений; активное, индуктивное и емкостное сопротивления; векторная диаграмма
тока и напряжения; углы сдвига фаз между напряжением и током; закон Ома;
формулы мощности; понятие об активной и реактивной мощностях; единицы измерения
этих мощностей.
Последовательная цепь с резистивным, индуктивным и емкостным элементами:
схема цепи; уравнение напряжений (второй закон Кирхгофа); векторная диаграмма
тока и напряжений; угол сдвига фаз между напряжением на зажимах цепи и током, и
его зависимость от параметров цепи; резонанс напряжений; закон Ома; активное,
реактивное и полное сопротивления цепи, треугольник сопротивлений; активная,
реактивная и полная мощность цепи, треугольник мощностей, единицы измерения
мощностей.
Цепь с параллельным соединением ветвей: схема цепи; уравнение токов
(первый закон Кирхгофа); векторная диаграмма напряжения и токов; активная,
реактивная и полная проводимости ветвей и всей цепи, треугольник проводимостей;
угол сдвига фаз между напряжением и общим током, и его зависимость от проводимостей
цепи; резонанс токов; методы расчета.
Цепь со смешанным соединением ветвей: схема цепи; расчет цепи
символическим методом; векторная диаграмма напряжений и токов.
ТРЕХФАЗНЫЕ ЦЕПИ. Области применения трехфазных цепей и из преимущество
перед однофазными. Простейший трехфазный генератор: устройство и принцип
действия; уравнения и графики мгновенных значений фазных ЭДС; векторная
диаграмма фазных ЭДС генератора; представление векторов фазных ЭДС комплексными
числами. Симметричные и несимметричные трехфазные системы электрических
величин. Схемы трехфазных цепей. Симметричные и несимметричные трехфазные
приемники и цепи.
Четырехпроводная цепь, соединенная звездой: схема цепи; фазные и линейные
напряжения и токи; фазные напряжения приемника в комплексной форме; выражение
векторов линейных напряжений через фазные; векторная диаграмма фазных и
линейных напряжений приемники; количественное соотношение между фазным и
линейным напряжениями; ток в нейтральном проводе и его выражение через фазные
токи приемника; векторные диаграмы напряжений и токов для симметричного и
несимметричного режимов.
Трехпроводная цепь, соединенная звездой: схема цепи; напряжение смещения
нейтрали (определение, условное обозначение, расчетная формула), выражение
фазных напряжений приемника через фазные напряжения источника и напряжение
смещения нейтрали. векторная диаграмма напряжений и токов при несимметричном
режиме работы.
Трехпроводная цепь, приемник которой соединен треугольником: схема цепи,
фазные напряжения приемника в комплексной форме. выражение векторов линейных
токов через фазные, векторные диаграммы напряжений и токов для симметричной и
несимметричной цепей.
Мощности симметричной и несимметричной трехфазных цепей.
ЦЕПИ НЕСИНУСОИДАЛЬНОГО ТОКА. Причины возникновения периодических несинусоидальных
токов и напряжений. Представление периодических несинусоидальных функций рядами
Фурье. Максимальное, среднее и действующие значения периодической
несинусоидальной величины. Активная и полная мощности. Метод расчета линейных
электрических цепей при несинусоидальном напряжении источника питания.
МАГНИТНЫЕ ЦЕПИ
МАГНИТНЫЕ ЦЕПИ С ПОСТОЯННОЙ МДС. Устройство магнитных цепей и их
разновидности. Однородная и неоднородная неразветвленные цепи. Основные
величины, используемые при расчете магнитных цепей: магнитная индукция,
напряженность магнитного поля, магнитная проницаемость, магнитный поток, и их
взаимосвязь. Закон полного тока в интегральной форме для неразветвленной
однородной и неоднородной магнитной цепи. Ферромагнитные материалы и их свойства.
Кривые намагничивания ферромагнитных материалов и их использование при расчете
магнитных цепей. Методы расчета неразветвленных цепей.
МАГНИТНЫЕ ЦЕПИ С ПЕРЕМЕННОЙ МДС
Особенности электромагнитных процессов в магнитных цепях с переменной
МДС. Магнитные потери. Вольт-амперные характеристики и индуктивное
сопротивление намагничивающей обмотки при синусоидальном напряжении. Уравнение
электрического состояния и векторная диаграмма намагничивающей обмотки.
ТРАНСФОРМАТОРЫ И ЭЛЕКТРИЧЕСКИЕ МАШИНЫ
ТРАНСФОРМАТОРЫ. Назначение и области применения. Однофазный
трансформатор: устройство и принцип действия; схема электрической цепи и
основные уравнения трансформатора; опыты холостого хода и короткого замыкания
(определение, назначение и порядок проведения); потери энергии и КПД; изменение
вторичного напряжения при нагрузке и внешняя характеристика. Трехфазный
трансформатор: устройство и принцип действия: группы соединения обмоток.
Автотрансформаторы: устройство, принцип действия, области применения.
МАШИНЫ ПОСТОЯННОГО ТОКА. Назначение, устройство, области применения.
Принцип действия в режиме генератора и двигателя. Уравнения ЭДС якоря и
электромагнитного момента. Реакция якоря. Классификация машин постоянного тока
по способу возбуждения. Генераторы постоянного тока по способу возбуждения.
Генераторы постоянного тока независимого, параллельного и смешанного
возбуждения: схемы электрических цепей, уравнения электрического состояния
цепей якоря, внешние характеристики, сущность самовозбуждения, роль остаточного
намагничивания в самовозбуждении генераторов. Двигатель параллельного
возбуждения: схема электрической цепи, уравнение электрического состояния цепи
якоря, назначение пускового реостата и порядок пуска, естественная и
искусственные механические характеристики, способы регулирования частоты
вращения. Двигатель последовательного возбуждения: схема электрической цепи,
естественная механическая характеристики ее особенности, способы регулирования
частоты вращения, области применения. Двигатель смешанного возбуждения: схема
электрической цепи, естественная механическая характеристика.
АСИНХРОННЫЕ ДВИГАТЕЛИ. Асинхронный трехфазный двигатель с
короткозамкнутым ротором: устройство, формула частоты вращения поля статора,
принцип действия, скольжение, схема замещения, зависимость электромагнитного
момента от скольжения, скольжение при холостом ходе и в начале пуска,
номинальное и критическое скольжения, номинальный, максимальный пусковой
моменты, механическая характеристика, пуск и регулирование частоты вращения. А
синхронный двигатель с фазным ротором: устройство, схема электрической цепи с
пусковым реостатом, назначение пускового реостата, процесс пуска, естественная
и искуственная механические характеристики и их использование при пуске и
регулировании частоты вращения. Однофазные асинхронные двигатели с пульсирующим
полем, конденсаторные, с экранированными полюсами статора.
СИНХРОННЫЕ МАШИНЫ. Назначение и области применения. Устройство. Принцип
действия в режиме генератора и двигателя. Механическая характеристика и способы
пуска двигателя.
ОСНОВЫ ЭЛЕКТРОНИКИ.
Электропроводность полупроводников. Образование и свойства
электронно-дырочного перехода. Полупроводниковые диоды: выпрямительные
(точечные и плоскостные), стабилитроны. Биполярные транзисторы: структура,
условное обозначение на схемах, конструктивное устройство, движение носителей
заряда в транзисторе, уравнение токов эммитера, базы и коллектора. Включение
транзистора по схеме с общим эмиттером: схема цепи, выходные и входные
характеристики, коэффициент передачи тока, рабочая область выходных
характеристик. Полевые транзисторы: разновидности и условные графические
обозначения, структура и схема включения, принцип действия, передаточная и
выходные характеристики. Тиристоры: разновидности и условные графические
обозначения, структура и вольт-амперные характеристики триодного тиристора,
области применения. Интегральные микросхемы: определения, классификация по
степени интеграции, полупроводниковые и гибридные микросхемы, параметры
интегральных микросхем, достоинства и области применения.
Выпрямители: назначение, классификация, структурная схема. Однофазные
однополупериодный и мостовой двухполупериодный выпрямители: схема электрических
цепей, принцип действия, временные диаграммы напряжений и токов, основные
электрические параметры. Сглаживающие фильтры. Внешние характеристики
выпрямителей.
Усилители: назначение, классификация и основные характеристики.
Усилительный каскад с общим эммитером: схема электрической цепи, графический
анализ работы, основные параметры, температурная стабилизация режима работы.
Усилительные каскады на полевых транзисторах. Двухкаскадный усилитель
напряжения с резистивно-емкостной связью на биполярных транзисторах: схема
электрической цепи, принцип действия, коэффициент усиления,
амплитудно-частотная и фазочастотная характеристики. Усилители напряжения с
резистивно-емкостной связью на интегральных микросхемах.
Стабилизаторы напряжения и тока.
ЭЕЛЕКТРИЧЕСКИЕ ИЗМЕРЕНИЯ И ИЗМЕРИТЕЛЬНЫЕ ПРИБОРЫ.
Погрешности в электрических измерениях. Устройство, принцип действия, основные
свойства и области применения приборов магнитоэлектрической, электромагнитной,
электродинамической и выпрямительной систем. Измерение токов, напряжений,
сопротивлений, мощностей и энергии. Электронный осциллограф: функциональная
схема, принцип действия, использование в технике.
ОСНОВЫ ЭЛЕКТОРПРИВОДА.
Основы механики электропривода. Задачи выбора электродвигателя.
Нагревание и охлаждение электродвигателей. Расчет мощности и выбор
электродвигателя для длительного, повторно-кратковременного и кратковременного
режимов работы. Электрическое торможение двигателей. Определение времени
ускорения и замедления электропривода.
Принципа автоматизации пуска, защиты и торможения электродвигателей.
ОБЩИЕ МЕТОДИЧЕСКИЕ УКАЗАНИЯ
При выполнении контрольных работ следует иметь в виду, что решение данных
задач может несколько отличаться от решенных примеров.
Оформление контрольных работ осуществляется в ученических тетрадях в
клетку, чернилами или пастой. Все чертежи и схемы выполняются с применением
чертежных инструментов в соответствии с действующими ГОСТами. Сокращения и
исправления в текстах не допускаются. Расчеты производятся с точностью то
третьей значащей цифры. Более высокая точность в большинстве расчетов не
требуется.
Каждая работы выполняется в отдельной тетради, на обложке которой должны
быть написаны: имя, фамилия и отчество студента, его домашний адрес, шифр
(номер) группы, номера личного и группового вариантов, полное наименование
учебного заведения, дата выполнения контрольной работы.
Номер личного варианта представляет собой порядковый номер фамилии
студента в групповом журнале.
Номер группового варианта, а также номера задач из данных методических
указания, подлежащие выполнению, указывает преподаватель, проводящий занятия в
группе.
КОНТРОЛЬНЫЕ ЗАДАНИЯ, МЕТОДИЧЕСКИЕ УКАЗАНИЯ К ИХ ВЫПОЛНЕНИЮ, ПРИМЕРЫ
РАСЧЕТА
ЗАДАЧА 1. расчет линейной цепи постоянного тока
методом двух законов Кирхгофа и предварительным преобразование треугольника
резисторов в эквивалентную звезду
В цепи, схема которой приведена на рисунке 1, требуется:
1.
Преобразовать треугольник резисторов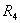 ,
,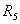 ,
,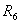 в эквивалентную звезду и затем методом двух законов
Кирхгофа определить токи в ветвях преобразованной цепи
в эквивалентную звезду и затем методом двух законов
Кирхгофа определить токи в ветвях преобразованной цепи
.
Определить напряжения 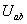 ,
,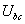 ,
,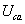 и токи
и токи 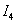 ,
,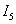 ,
,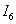 исходной цепи
исходной цепи
.
Составить уравнение баланса мощностей для исходной цепи с целью проверки
правильности расчета токов (расхождение баланса мощностей не должно превышать 3
%). Номер схемы и чистовые данные к расчету определяются по таблице 1 и 2.
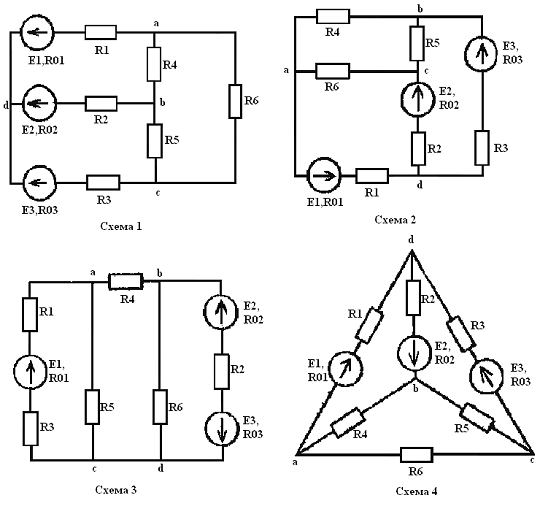
Рисунок
1
Таблица
1
|
Номер личного варианта
|
Номер схемы
|
Параметры источника ЭДС
|
|
|
E1,B
|
R01,Oм
|
Е2,В
|
R02,Ом
|
Е3, В
|
R03,Ом
|
|
1
|
2
|
3
|
4
|
5
|
6
|
7
|
8
|
|
1
|
1
|
24
|
1
|
36
|
2
|
48
|
1
|
|
2
|
2
|
48
|
2
|
24
|
1
|
36
|
1
|
|
3
|
3
|
36
|
1
|
48
|
1
|
24
|
2
|
|
4
|
4
|
24
|
1
|
36
|
2
|
48
|
1
|
|
5
|
5
|
48
|
2
|
24
|
1
|
36
|
1
|
|
6
|
6
|
36
|
1
|
48
|
1
|
24
|
2
|
|
7
|
1
|
24
|
1
|
48
|
2
|
36
|
1
|
|
8
|
2
|
48
|
2
|
36
|
1
|
24
|
1
|
|
9
|
3
|
36
|
1
|
24
|
1
|
48
|
2
|
|
10
|
4
|
24
|
1
|
48
|
2
|
36
|
1
|
|
11
|
5
|
48
|
2
|
36
|
2
|
24
|
1
|
|
12
|
6
|
36
|
1
|
24
|
1
|
48
|
1
|
|
13
|
1
|
20
|
1
|
40
|
2
|
30
|
2
|
|
14
|
2
|
50
|
2
|
25
|
1
|
40
|
2
|
|
15
|
3
|
48
|
2
|
38
|
2
|
24
|
1
|
|
16
|
4
|
36
|
1
|
48
|
1
|
24
|
2
|
|
17
|
5
|
36
|
1
|
48
|
2
|
24
|
1
|
|
18
|
6
|
48
|
2
|
24
|
1
|
36
|
1
|
|
19
|
1
|
20
|
2
|
30
|
2
|
20
|
1
|
|
20
|
2
|
25
|
1
|
50
|
2
|
40
|
2
|
|
21
|
3
|
48
|
2
|
36
|
1
|
24
|
1
|
|
22
|
4
|
48
|
2
|
36
|
1
|
24
|
1
|
|
23
|
5
|
24
|
1
|
48
|
2
|
36
|
1
|
|
24
|
6
|
40
|
2
|
30
|
2
|
20
|
1
|
|
25
|
1
|
30
|
2
|
48
|
2
|
20
|
1
|
Таблица 2
|
Номер группового варианта
|
Сопротивления резисторов,
Ом
|
|
R1
|
R2
|
R3
|
R4
|
R5
|
R6
|
|
1
|
9
|
7
|
5
|
2
|
3
|
5
|
|
2
|
7
|
5
|
8
|
6
|
4
|
2
|
|
3
|
3
|
4
|
6
|
3
|
9
|
6
|
|
4
|
5
|
3
|
2
|
10
|
4
|
6
|
|
5
|
12
|
10
|
8
|
1
|
3
|
2
|
МЕТОДИЧЕСКИЕ УКАЗАНИЯ И ПРИМЕР РАСЧЕТА.
Решение
данной задачи рассматривается на примере цепи, представленной на рисунке 2, в
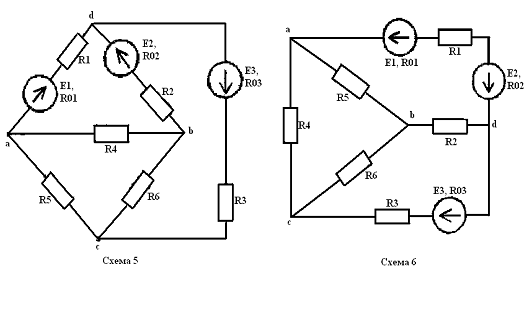
которой 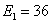 ,
, 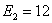 ,
, 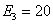 В;
В; 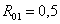 ,
,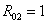 ,
,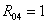 ,
,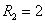 ,
, 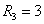 ,
, 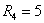 ,
, 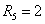 ,
,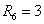 Ом.
Ом.
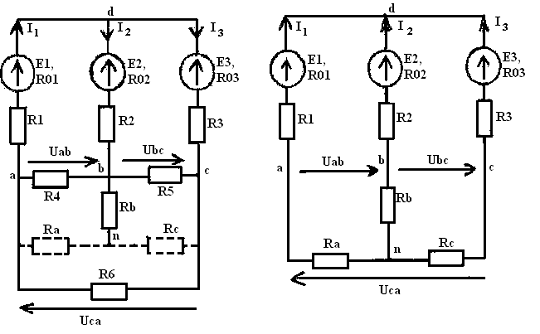
Рисунок
2 Рисунок 3
Замена
треугольника резисторов 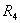 ,
,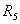 ,
,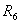 эквивалентной звездой резисторов
эквивалентной звездой резисторов 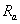 ,
,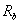 ,
,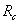 осуществляется следующим образом. К узловым точкам a, b, c или
к проводам, связанным с этими точками, подключается эквивалентная звезда
резисторов (на рисунке 2 она показана штриховыми линиями). Определяются
сопротивления резисторов эквивалентной звезды:
осуществляется следующим образом. К узловым точкам a, b, c или
к проводам, связанным с этими точками, подключается эквивалентная звезда
резисторов (на рисунке 2 она показана штриховыми линиями). Определяются
сопротивления резисторов эквивалентной звезды:
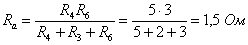 ;
;
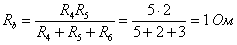 ;
;
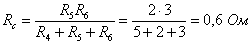
Вычерчивается
схема цепи (рисунок 3), получившаяся после замены треугольника резисторов
эквивалентной звездой.
Токи
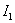 ,
,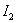 ,
,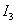 определяются на основе преобразованной цепи в
следующем порядке. На схему наносятся произвольные направления исходных токов
(здесь все три тока направлены к узлу d). Задается направление обхода
по контурам (оно здесь принято совпадающим с направлением движения часовой
стрелки). Составляется система уравнений по законам Кирхгофа:
определяются на основе преобразованной цепи в
следующем порядке. На схему наносятся произвольные направления исходных токов
(здесь все три тока направлены к узлу d). Задается направление обхода
по контурам (оно здесь принято совпадающим с направлением движения часовой
стрелки). Составляется система уравнений по законам Кирхгофа:
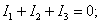
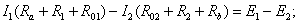
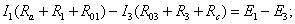
Подставив
в данную систему уравнений числовые значения и решив ее, получаем 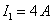 ;
; 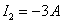 ;
; 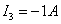 . Знак минус у значений токов
. Знак минус у значений токов 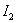 и
и 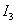 означает,
что их истинные направления противоположны направлениям, принятым на рисунке 3,
т.е. они направлены от узла d. На схеме (рисунок 2) нанесены истинные направления
этих токов.
означает,
что их истинные направления противоположны направлениям, принятым на рисунке 3,
т.е. они направлены от узла d. На схеме (рисунок 2) нанесены истинные направления
этих токов.
Напряжения
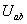 ,
,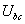 ,
,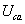 определяются из решений уравнений, составленных по
второму закону Кирхгофа для контуров abna, bcnb, canc:
определяются из решений уравнений, составленных по
второму закону Кирхгофа для контуров abna, bcnb, canc:
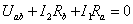 ;
; 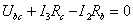 ;
; 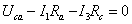
Подставив
в данные уравнения числовые значения и решив их, получаем: 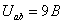 ,
, ,
,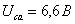 .
.
Токи
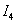 ,
,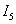 ,
,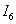 в исходной цепи (рисунок 2) определяются по закону
Ома
в исходной цепи (рисунок 2) определяются по закону
Ома
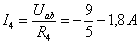 ;
; 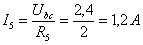 ;
; 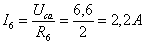
Знак
минус у значения тока 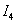 означает, что этот ток направлен от узла b к
узлу a.
означает, что этот ток направлен от узла b к
узлу a.
Уравнение
баланса мощностей для исходной цепи (рисунок 2) имеет следующий вид:
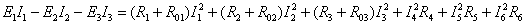 .
.
ЗАДАЧА 2. Расчет линейной цепи постоянного тока
методом активного двухполюсника (эквивалентного генератора)
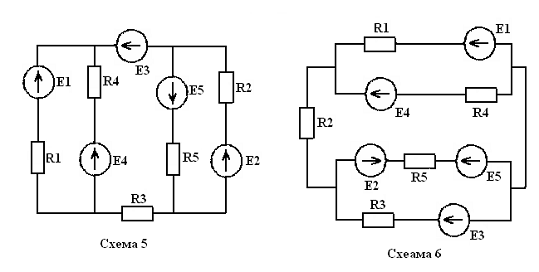
Методом
активного двухполюсника определить ток, протекающий через один из резисторов
цепи, схема которой представлена на рисунке 4. Номер схемы и числовые данные к
расчету приведены в таблице 4. Наименование резистора, ток которого подлежит
определению, приведено в таблице 4.
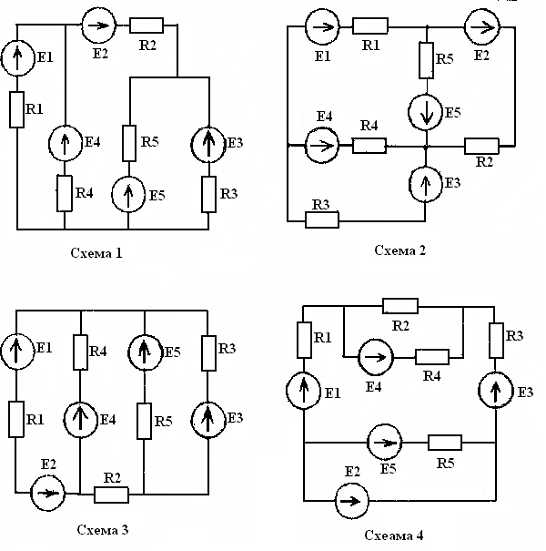
Рисунок
4
Таблица
3
|
Номер личного варианта
|
Номер схемы
|
Значения ЭДС, В
|
Сопротивления, Ом
|
|
|
E1
|
E2
|
E3
|
E4
|
E5
|
R1
|
R2
|
R3
|
R4
|
R5
|
|
1
|
2
|
3
|
4
|
5
|
6
|
7
|
8
|
9
|
10
|
11
|
12
|
|
1
|
1
|
8
|
12
|
16
|
20
|
24
|
1
|
2
|
3
|
4
|
5
|
|
2
|
2
|
12
|
16
|
20
|
24
|
8
|
2
|
3
|
4
|
5
|
1
|
|
3
|
3
|
16
|
20
|
24
|
8
|
12
|
3
|
4
|
5
|
1
|
2
|
|
4
|
4
|
20
|
24
|
8
|
12
|
16
|
4
|
5
|
1
|
2
|
3
|
|
5
|
5
|
24
|
8
|
12
|
16
|
20
|
5
|
1
|
2
|
3
|
4
|
|
6
|
6
|
12
|
16
|
20
|
24
|
28
|
2
|
3
|
4
|
5
|
4
|
|
7
|
1
|
16
|
20
|
24
|
28
|
12
|
3
|
4
|
5
|
4
|
2
|
|
8
|
2
|
20
|
24
|
28
|
12
|
16
|
4
|
5
|
4
|
2
|
3
|
|
9
|
3
|
24
|
28
|
12
|
16
|
20
|
5
|
4
|
2
|
3
|
4
|
|
10
|
4
|
28
|
12
|
16
|
20
|
24
|
4
|
2
|
3
|
4
|
5
|
|
11
|
5
|
16
|
20
|
24
|
28
|
32
|
2
|
3
|
4
|
6
|
2
|
|
12
|
6
|
20
|
24
|
28
|
32
|
16
|
3
|
4
|
6
|
2
|
2
|
|
13
|
1
|
24
|
28
|
32
|
16
|
20
|
4
|
6
|
2
|
2
|
3
|
|
14
|
2
|
38
|
32
|
16
|
20
|
24
|
6
|
4
|
2
|
2
|
3
|
|
15
|
3
|
32
|
16
|
20
|
24
|
28
|
2
|
2
|
3
|
4
|
6
|
|
16
|
4
|
20
|
24
|
28
|
32
|
36
|
2
|
3
|
2
|
4
|
6
|
|
17
|
5
|
24
|
28
|
32
|
36
|
20
|
3
|
2
|
4
|
6
|
2
|
|
18
|
6
|
28
|
32
|
36
|
20
|
24
|
2
|
4
|
6
|
2
|
3
|
|
19
|
1
|
32
|
36
|
40
|
24
|
28
|
4
|
6
|
8
|
3
|
2
|
|
20
|
2
|
36
|
40
|
24
|
30
|
32
|
6
|
8
|
3
|
2
|
4
|
|
21
|
3
|
40
|
24
|
28
|
32
|
36
|
8
|
3
|
2
|
4
|
6
|
|
22
|
4
|
24
|
28
|
32
|
36
|
40
|
3
|
2
|
4
|
6
|
8
|
|
23
|
5
|
28
|
32
|
36
|
40
|
24
|
2
|
4
|
6
|
8
|
3
|
|
24
|
6
|
10
|
20
|
40
|
50
|
60
|
5
|
9
|
8
|
7
|
6
|
|
25
|
1
|
20
|
40
|
30
|
25
|
10
|
9
|
8
|
7
|
6
|
5
|
Таблица 4
|
Номер группового варианта
|
1
|
2
|
3
|
4
|
5
|
|
Резистор, в котором требуется
определить ток
|
R1
|
R2
|
R3
|
R4
|
R5
|
МЕТОДИЧЕСКИЙ УКАЗАНИЯ И ПРИМЕР РАСЧЕТА
Решение
данной задачи рассматривается на примере цепи, представленной на рисунке 5, в
которой 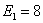 ,
, 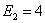 ,
, 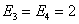 ,
, 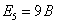 ;
; 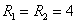 ,
, 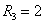 ,
, 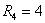 ,
, 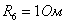 .
Требуется определить ток в резисторе
.
Требуется определить ток в резисторе 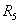 .
.
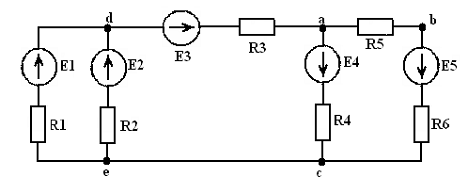
Рисунок
5
Решение
данной задачи осуществляется в 4 этапа:
. Определяется
напряжение холостого хода 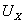 на зажимах активного двухполюсника;
на зажимах активного двухполюсника;
. Определяется
входное сопротивление 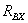 пассивной части активного двухполюсника;
пассивной части активного двухполюсника;
. Определяется
искомый ток 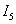 , протекающий через резистор
, протекающий через резистор 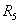 .
.
Напряжение
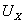 определяется в следующем порядке. Вычерчивается схема
активного двухполюсника при холостом ходе (рисунок 6). Определяются тока
холостого хода
определяется в следующем порядке. Вычерчивается схема
активного двухполюсника при холостом ходе (рисунок 6). Определяются тока
холостого хода 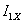 ,
,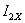 ,
,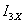 активного двухполюсника методом двух законов
Кирхгофа. Для этого составляется и решается система трех уравнений и
неизвестными точками
активного двухполюсника методом двух законов
Кирхгофа. Для этого составляется и решается система трех уравнений и
неизвестными точками 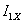 ,
,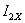 ,
,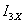 :
:
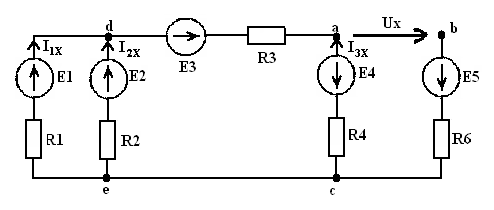
Рисунок
6
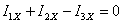 ;
;
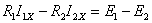 ;
;
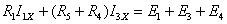 .
.
Подставив
в данную систему уравнений числовые значения и решив ее, получаем: 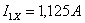 ;
; 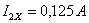 ;
; 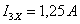 . Определяется напряжение
. Определяется напряжение 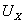 из решения уравнения, которое составляется по второму
закону Кирхгофа для контура abca:
из решения уравнения, которое составляется по второму
закону Кирхгофа для контура abca: 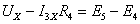 ;
; 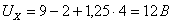 .
.
Сопротивление
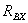 определяется в следующем порядке. Вычерчивается схема
пассивной части активного двухполюсника (рисунок 7), которая получается из
схемы активного двухполюсника путем исключения из нее источников ЭДС.
Сопротивление
определяется в следующем порядке. Вычерчивается схема
пассивной части активного двухполюсника (рисунок 7), которая получается из
схемы активного двухполюсника путем исключения из нее источников ЭДС.
Сопротивление 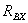 представляет собой эквивалентное сопротивление цепи,
схема которой приведена на рисунке 7.
представляет собой эквивалентное сопротивление цепи,
схема которой приведена на рисунке 7.

Рисунок 7
Оно определяется в 2 этапа:
1. Определяется
эквивалентное сопротивление 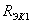 части
цепи, расположенной слева от узлов a и c:
части
цепи, расположенной слева от узлов a и c:
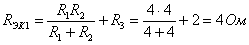
. Определяется
сопротивление 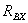 :
:
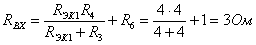
Искомый
ток 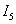 определяется по формуле:
определяется по формуле:
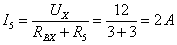
ЗАДАЧА 3. Расчет последовательной нелинейной цепи постоянного
тока
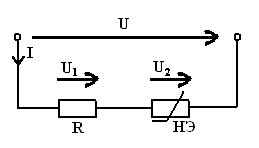
Рисунок
8
В
цепи, общая схема которой приведена рисунке 8, по заданному напряжению 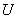 на зажимах цепи определить ток
на зажимах цепи определить ток 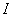 и напряжение
и напряжение 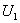 и
и 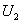 на элементах. Задачу решить методами сложения и
пересечения характеристик. Схема конкретной цепи, подлежащей расчету,
получается из общей схемы путем замены в ней резистора R и нелинейного
элемента НЭ конкретными элементами согласно данным таблицы 5. Числовые значения
сопротивлений резисторов и вольт-амперных характеристик (ВАХ) нелинейных
элементов приведены в таблице 6 и 7.
на элементах. Задачу решить методами сложения и
пересечения характеристик. Схема конкретной цепи, подлежащей расчету,
получается из общей схемы путем замены в ней резистора R и нелинейного
элемента НЭ конкретными элементами согласно данным таблицы 5. Числовые значения
сопротивлений резисторов и вольт-амперных характеристик (ВАХ) нелинейных
элементов приведены в таблице 6 и 7.
Таблица
5
|
Номер личного варианта
|
Последовательная цепь
|
Параллельная цепь
|
|
U, B
|
R
|
НЭ
|
I, A
|
НЭ*
|
НЭ**
|
|
1
|
2
|
3
|
4
|
5
|
6
|
7
|
|
1
|
9
|
R1
|
НЭ2
|
8
|
НЭ10
|
НЭ9
|
|
2
|
10
|
R1
|
НЭ3
|
10
|
НЭ10
|
НЭ8
|
|
3
|
11
|
R1
|
НЭ4
|
11
|
НЭ10
|
НЭ7
|
|
4
|
12
|
R1
|
НЭ5
|
12
|
НЭ10
|
НЭ6
|
|
5
|
14
|
R1
|
НЭ6
|
9
|
НЭ10
|
НЭ5
|
|
6
|
10
|
R2
|
НЭ1
|
8
|
НЭ10
|
НЭ4
|
|
7
|
11
|
R2
|
НЭ2
|
12
|
НЭ9
|
НЭ8
|
|
8
|
12
|
R2
|
НЭ3
|
13
|
НЭ9
|
НЭ7
|
|
9
|
13
|
R2
|
НЭ4
|
14
|
НЭ9
|
НЭ6
|
|
10
|
16
|
R2
|
НЭ5
|
11
|
НЭ9
|
НЭ5
|
|
11
|
17
|
R2
|
НЭ6
|
10
|
НЭ9
|
НЭ4
|
|
12
|
12
|
R3
|
НЭ1
|
15
|
НЭ8
|
НЭ7
|
|
13
|
13
|
R3
|
НЭ2
|
16
|
НЭ8
|
НЭ6
|
|
14
|
14
|
R3
|
НЭ3
|
13
|
НЭ8
|
НЭ5
|
|
15
|
15
|
R3
|
НЭ4
|
12
|
НЭ8
|
НЭ4
|
|
16
|
18
|
R3
|
НЭ5
|
18
|
НЭ7
|
НЭ6
|
|
17
|
14
|
R4
|
НЭ1
|
15
|
НЭ7
|
НЭ5
|
|
18
|
15
|
R4
|
НЭ2
|
14
|
НЭ7
|
НЭ4
|
|
19
|
16
|
R4
|
НЭ3
|
15
|
НЭ6
|
НЭ5
|
|
20
|
18
|
R4
|
НЭ4
|
14
|
НЭ6
|
НЭ4
|
|
21
|
16
|
R5
|
НЭ1
|
11
|
НЭ5
|
НЭ4
|
|
22
|
17
|
R5
|
НЭ2
|
8
|
НЭ4
|
НЭ3
|
|
23
|
19
|
R5
|
НЭ3
|
9
|
НЭ5
|
НЭ3
|
|
24
|
18
|
R5
|
НЭ1
|
11
|
НЭ6
|
НЭ3
|
|
25
|
20
|
R5
|
НЭ2
|
12
|
НЭ7
|
НЭ3
|
Таблица 6
|
Сопротивления резисторов,
Ом
|
|
R1
|
R2
|
R3
|
R4
|
R5
|
R6
|
|
0,35
|
0,5
|
0,6
|
0,75
|
0,9
|
1,0
|
Таблица 7
|
Вольтамперные
характеристики нелинейных элементов
|
|
U, В
|
Токи, А
|
|
НЭ1
|
НЭ2
|
НЭ3
|
НЭ4
|
НЭ5
|
НЭ6
|
НЭ7
|
НЭ8
|
НЭ9
|
НЭ10
|
|
1
|
2
|
3
|
4
|
5
|
6
|
7
|
8
|
9
|
10
|
11
|
|
1
|
0,1
|
0,2
|
0,2
|
2,5
|
4,0
|
6,7
|
0,4
|
3,3
|
2,2
|
1,4
|
|
2
|
0,2
|
0,7
|
0,5
|
4,2
|
5,9
|
7,8
|
1,5
|
5,6
|
3,8
|
2,1
|
|
3
|
4,5
|
1,5
|
0,8
|
4,3
|
6,1
|
8,0
|
9,1
|
6,2
|
4,4
|
2,6
|
|
4
|
16,0
|
2,7
|
1,3
|
4,3
|
6,2
|
8,1
|
9,4
|
6,8
|
4,9
|
2,9
|
|
5
|
-
|
4,3
|
1,8
|
4,4
|
6,2
|
8,1
|
9,5
|
7,2
|
5,2
|
3,2
|
|
6
|
-
|
16,0
|
2,7
|
4,4
|
6,3
|
8,2
|
9,5
|
7,4
|
5,4
|
3,4
|
|
7
|
-
|
-
|
4,5
|
4,5
|
6,4
|
8,2
|
9,6
|
7,6
|
5,6
|
3,5
|
|
8
|
-
|
-
|
16,0
|
4,8
|
6,4
|
8,3
|
9,6
|
7,7
|
5,7
|
3,6
|
|
9
|
-
|
-
|
-
|
10,0
|
6,7
|
8,4
|
7,7
|
5,7
|
3,7
|
|
10
|
-
|
-
|
-
|
16,0
|
10,0
|
8,4
|
9,7
|
7,8
|
5,7
|
3,7
|
|
11
|
|
-
|
-
|
-
|
16,0
|
9,3
|
9,8
|
7,8
|
5,8
|
3,8
|
|
12
|
-
|
-
|
-
|
-
|
-
|
16,0
|
9,8
|
7,8
|
5,8
|
3,8
|
|
13
|
-
|
-
|
-
|
-
|
-
|
-
|
9,8
|
7,9
|
5,9
|
3,8
|
|
14
|
-
|
-
|
-
|
-
|
-
|
-
|
9,9
|
7,9
|
5,9
|
3,9
|
|
15
|
-
|
-
|
-
|
-
|
-
|
-
|
9,9
|
7,9
|
5,9
|
3,9
|
|
16
|
-
|
-
|
-
|
-
|
-
|
-
|
10,0
|
8,0
|
6,0
|
4,0
|
МЕТОДИЧЕСКИЕ УКАЗАНИЯ И ПРИМЕР РАСЧЕТА
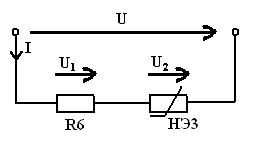
Рисунок 9
Решение
данной задачи рассматривается на примере цепи, приведенной на рисунке 9,
элементами которой являются резистор 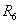 и
нелинейный элемент НЭ3. Согласно таблице 6 сопротивление
и
нелинейный элемент НЭ3. Согласно таблице 6 сопротивление 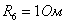 . Напряжение
. Напряжение 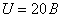 .
.
Сущность
метода сложения характеристик состоит в следующем. В осях координат 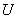 ,
, 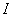 строятся
ВАХ элементов цепи
строятся
ВАХ элементов цепи 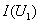 и
и 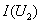 и ВАХ
всей цепи
и ВАХ
всей цепи 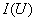 (рисунок 10).
(рисунок 10).
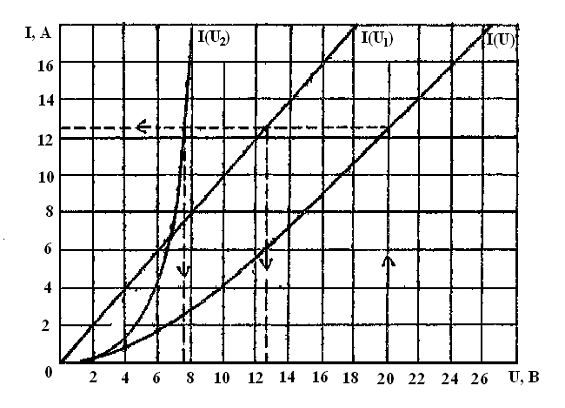
Рисунок
10
Затем
используя эти характеристики, графическим путем по заданной величине определяют
искомые величины.
ВАХ
резистора 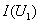 представляет собой прямую линию, проходящую через
начало координат. Вторая, вспомогательная, точка (точка B)
этой прямой определяется с помощью закона Ома. Для этого в пределах оси
представляет собой прямую линию, проходящую через
начало координат. Вторая, вспомогательная, точка (точка B)
этой прямой определяется с помощью закона Ома. Для этого в пределах оси 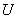 задается абсцисса
задается абсцисса 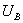 этой
точки, а затем определяется ордината
этой
точки, а затем определяется ордината 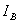 этой
точки по закону Ома
этой
точки по закону Ома
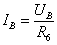
ВАХ
нелинейного элемента 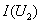 строится по значениям, приведенным в таблице 7.
строится по значениям, приведенным в таблице 7.
Характеристики
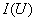 строится на основе второго закона Кирхгофа
строится на основе второго закона Кирхгофа
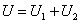
Это
уравнение в данном случае следует понимать так: для каждого фиксированного
значения тока напряжение на зажимах цепи равно сумме падений напряжений на
элементах цепи. А это значит, что для построения кривой 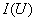 следует задать ряд значений тока (8-10 значений в
пределах оси ординат) и для каждого тока тока найти значение напряжения путем
сложения абсцисс кривых
следует задать ряд значений тока (8-10 значений в
пределах оси ординат) и для каждого тока тока найти значение напряжения путем
сложения абсцисс кривых 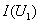 и
и 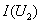 . При
этом на плоскости координат будет получен ряд точек, при соединении которых
получится искомая кривая
. При
этом на плоскости координат будет получен ряд точек, при соединении которых
получится искомая кривая 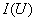 .
.
В
рассматриваемом примере 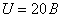 . Согласно кривой
. Согласно кривой 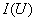 данному
значению напряжения соответствует ток, равный 12,4 А. Согласно кривым
данному
значению напряжения соответствует ток, равный 12,4 А. Согласно кривым 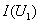 и
и 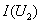 данному
значению тока соответствуют следующие напряжения на элементах цепи:
данному
значению тока соответствуют следующие напряжения на элементах цепи: 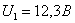 ;
; 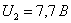 .
.
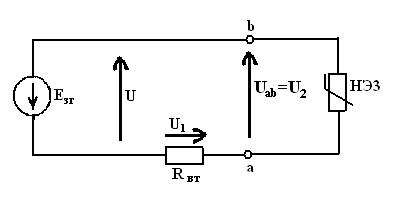
Рисунок
11
Расчет
данной цепи методом пересечения характеристик осуществляется следующим образом.
Заданная цепь представляется состоящей из двух частей: в первую часть входят
источник напряжения 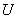 и резистор
и резистор 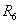 , во вторую
- нелинейный элемент НЭЗ. Первая часть заменяется эквивалентным генератором в
параметрами
, во вторую
- нелинейный элемент НЭЗ. Первая часть заменяется эквивалентным генератором в
параметрами
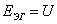 ;
;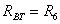 ;
; 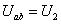
где
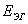 ,
, 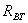 ,
, 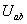 - ЭДС, внутреннее сопротивление , выходное напряжение
эквивалентного генератора. Нелинейный элемент рассматривается как нагрузка
эквивалентного генератора (рисунок 11). Уравнение внешней характеристики
данного эквивалентного генератора, полученное на основании второго закона
Кирхгофа, имеет следующий вид
- ЭДС, внутреннее сопротивление , выходное напряжение
эквивалентного генератора. Нелинейный элемент рассматривается как нагрузка
эквивалентного генератора (рисунок 11). Уравнение внешней характеристики
данного эквивалентного генератора, полученное на основании второго закона
Кирхгофа, имеет следующий вид
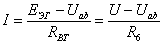
Рисунок
12
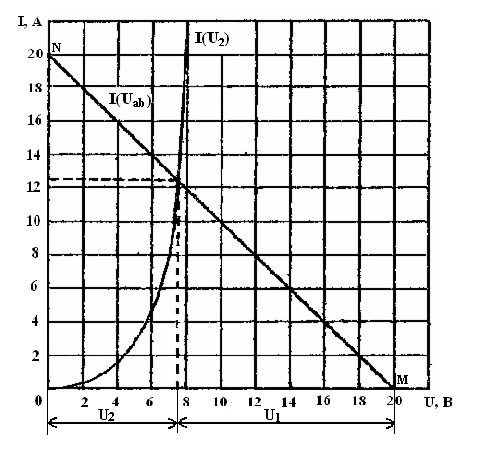
Согласно
этому уравнению в осях 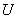 ,
,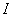 (рисунок 12) строится график этой характеристики
(рисунок 12) строится график этой характеристики 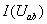 . Он представляет собой прямую линию, пересекающую оси
координат в точках M и N.
. Он представляет собой прямую линию, пересекающую оси
координат в точках M и N.
Координаты
точки M определяются из опыта холостого хода, а точки N из
опыта короткого замыкания эквивалентного генератора. При холостом ходе  , а
, а 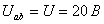 . Из
этого следует, что абсцисса точки М равна 20, а ордината - нулю. При опыте
короткого замыкания
. Из
этого следует, что абсцисса точки М равна 20, а ордината - нулю. При опыте
короткого замыкания 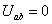 , а
, а 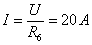 . Из
этого следует, что абсцисса точки N равна нулю, а ордината - 20.
. Из
этого следует, что абсцисса точки N равна нулю, а ордината - 20.
В
этих же осях координат строится ВАХ нелинейного элемента по значениям, приведенным
в таблице 7.
Искомые
ток и напряжения 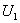 и
и 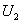 определяются
точкой пересечения прямой
определяются
точкой пересечения прямой 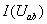 и кривой
и кривой 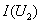 (точкой A).
Ордината этой точки равна искомому току, а ее абсцисса разделяет отрезок OM на
две части. Одна часть численно равна
(точкой A).
Ордината этой точки равна искомому току, а ее абсцисса разделяет отрезок OM на
две части. Одна часть численно равна 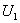 , а
другая
, а
другая 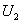 (рисунок 12).
(рисунок 12).
ЗАДАЧА 4. Расчет параллельной нелинейной цепи постоянного
тока
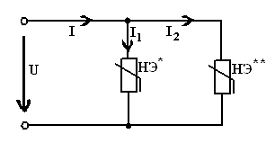
Рисунок
13
В
цепи, общая схема которой приведена на рисунке 13 по заданному значению тока 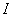 определить напряжение и токи
определить напряжение и токи 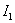 ,
, 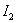 конкретной
цепи. Схема конкретной цепи, подлежащая расчету, получается из общей схемы
(рисунок 13) путем замены в ней нелинейных элементов НЭ* и НЭ** конкретными
нелинейными элементами согласно данным таблицы 5. Числовые значения ВАХ
нелинейных элементов приведены в таблице 7.
конкретной
цепи. Схема конкретной цепи, подлежащая расчету, получается из общей схемы
(рисунок 13) путем замены в ней нелинейных элементов НЭ* и НЭ** конкретными
нелинейными элементами согласно данным таблицы 5. Числовые значения ВАХ
нелинейных элементов приведены в таблице 7.
МЕТОДИЧЕСКИЕ
УКАЗАНИЯ И ПРИМЕР РАСЧЕТА
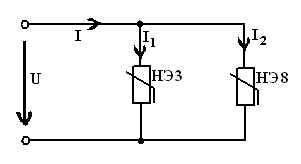
Рисунок
14
Решение
данной задачи рассматривается на примере уепи с нелинейными элементами НЭ3 и
НЭ8, схема которой приведена на рисунке 14. Ток 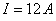 . Данная
задача решается следующим образом.
. Данная
задача решается следующим образом.
В
осях координат 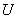 ,
, 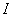 строится
ВАХ нелинейных элементов
строится
ВАХ нелинейных элементов 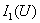 и
и 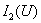 ,
согласно данным таблицы 7 и ВАХ всей цепи
,
согласно данным таблицы 7 и ВАХ всей цепи 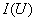 (рисунок
15).
(рисунок
15).
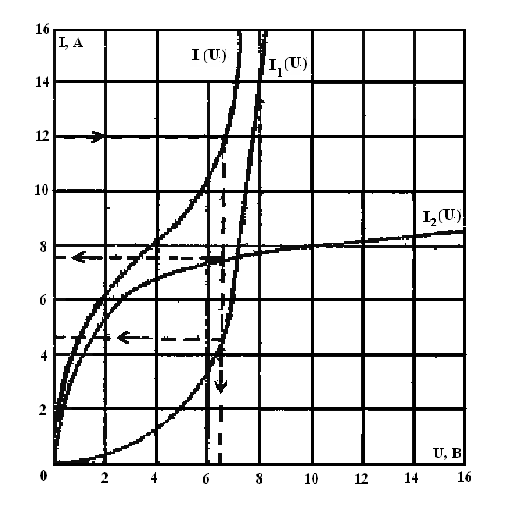
Рисунок
15
Характеристика
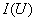 строится на основе первого закона Кирхгофа:
строится на основе первого закона Кирхгофа:
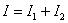
В
данном случае это уравнение следует понимать так: для каждого фиксированного
значения напряжения 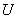 значение общего тока
значение общего тока 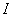 равно
сумме токов в ветвях. А это значит, что для построения кривой
равно
сумме токов в ветвях. А это значит, что для построения кривой 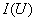 следует задать ряд значений напряжения
следует задать ряд значений напряжения 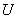 (8-10 значений в пределах оси абсцисс) и для каждого
значения напряжения найти значение общего тока
(8-10 значений в пределах оси абсцисс) и для каждого
значения напряжения найти значение общего тока 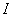 путем
сложения ординат характеристик
путем
сложения ординат характеристик 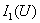 и
и 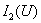 .
.
При
этом на плоскости координат будет получено множество точек, при соединении
которых получиться кривая 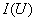 .
.
В
рассматриваемом примере 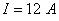 . Согласно кривой
. Согласно кривой 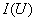 данному
значению тока соответствует напряжения
данному
значению тока соответствует напряжения 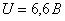 .
Согласно кривым
.
Согласно кривым 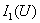 и
и 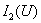 данному
значению напряжения соответствуют следующие значения токов в ветвях цепи:
данному
значению напряжения соответствуют следующие значения токов в ветвях цепи: 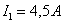 ;
; 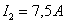 .
.
ЗАДАЧА 5. Расчет неразветвленной неоднородной
магнитной цепи с постоянной магнитодвижущей силой
В
цепи, эскиз которой приведен на рис. 16, по заданному значению магнитной
индукции в воздушном зазоре B0 определить магнитный поток и магнитодвижущую силу
(МДС). Размеры магнитопровода приведены в табл. 8. Наименования ферромагнитных
материалов, из которых изготовлен магнитопровод, и заданное значение B0
приведены в табл. 9. Числовые значения кривых намагничивания ферромагнитных
материалов приведены в табл. 10.
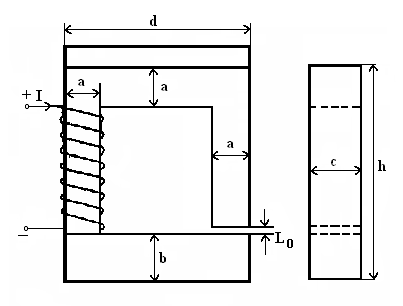
Рисунок
16
Таблица 8
|
Номер личного варианта
|
Размеры магнитопровода, мм
|
|
a
|
b
|
c
|
d
|
h
|
l0
|
|
1
|
2
|
3
|
4
|
5
|
6
|
7
|
|
1
|
32
|
36
|
30
|
160
|
160
|
1,30
|
|
2
|
36
|
42
|
40
|
140
|
160
|
1,30
|
|
3
|
40
|
36
|
36
|
160
|
180
|
1,20
|
|
4
|
36
|
32
|
40
|
160
|
180
|
1,15
|
|
5
|
34
|
40
|
30
|
160
|
180
|
1,15
|
|
6
|
32
|
36
|
30
|
140
|
200
|
1,15
|
|
7
|
38
|
48
|
40
|
140
|
220
|
1,10
|
|
8
|
40
|
40
|
40
|
160
|
160
|
1,30
|
|
9
|
36
|
40
|
30
|
140
|
160
|
1,40
|
|
10
|
48
|
40
|
40
|
180
|
200
|
1,00
|
|
11
|
42
|
50
|
42
|
200
|
180
|
0,95
|
|
12
|
30
|
32
|
30
|
120
|
140
|
1,40
|
|
13
|
32
|
30
|
30
|
120
|
180
|
1,25
|
|
14
|
34
|
40
|
36
|
120
|
160
|
1,40
|
|
15
|
42
|
36
|
40
|
180
|
200
|
0,90
|
|
16
|
48
|
48
|
38
|
200
|
200
|
0,70
|
|
17
|
36
|
40
|
40
|
160
|
220
|
0,50
|
|
18
|
42
|
50
|
50
|
160
|
240
|
0,40
|
|
19
|
48
|
48
|
48
|
200
|
260
|
0,30
|
|
20
|
42
|
48
|
40
|
200
|
280
|
0,20
|
|
21
|
20
|
24
|
24
|
100
|
140
|
1,45
|
|
22
|
28
|
34
|
30
|
100
|
140
|
1,50
|
|
23
|
26
|
32
|
40
|
100
|
140
|
1,45
|
|
24
|
30
|
36
|
30
|
120
|
120
|
1,50
|
|
25
|
30
|
30
|
30
|
120
|
100
|
1,55
|
Таблица 9
|
Номер группового варианта
|
Материал
|
В0,Тл
|
|
верхней П-образной части
магнитопровода
|
нижней части магнитопровода
|
|
|
1
|
Эл.техн. Сталь ЭЗ10
|
Пермаллой
|
1,5
|
|
2
|
Пермаллой
|
Эл.техн. Сталь Э42
|
1,4
|
|
3
|
Эл.техн. Сталь Э42
|
Литая сталь
|
1,3
|
|
4
|
Литая сталь
|
Чугун
|
0,65
|
|
5
|
Пермендюр
|
Эл.техн. Сталь ЭЗ10
|
1,6
|
Таблица 10
|
Напряженность магнитного
поля, А/м
|
Магнитная индукция, Тл
|
|
Чугун
|
Литая сталь
|
Эл.техн. сталь ЭЗ10
|
Эл.техн. сталь Э42
|
Пермендюр
|
|
1
|
2
|
3
|
4
|
5
|
6
|
7
|
|
50
|
0,03
|
0,12
|
0,50
|
0,28
|
0,95
|
0,50
|
|
100
|
0,06
|
0,22
|
1,00
|
0,43
|
1,00
|
1,00
|
|
150
|
0,08
|
0,33
|
1,22
|
0,61
|
1,16
|
1,42
|
|
200
|
0,11
|
0,43
|
1,25
|
0,70
|
1,21
|
1,60
|
|
300
|
0,16
|
0,60
|
1,33
|
0,85
|
1,27
|
1,84
|
|
400
|
0,20
|
0,72
|
1,37
|
0,96
|
1,31
|
1,95
|
|
600
|
0,27
|
0,90
|
1,44
|
1,12
|
1,37
|
2,08
|
|
1000
|
0,38
|
1,10
|
1,52
|
1,25
|
1,46
|
2,20
|
|
2000
|
0,55
|
1,33
|
1,60
|
1,38
|
1,55
|
2,31
|
|
3000
|
0,65
|
1,45
|
1,66
|
1,44
|
1,60
|
2,33
|
|
4000
|
0,70
|
1,53
|
1,71
|
1,49
|
1,65
|
2,36
|
|
5000
|
0,73
|
1,60
|
1,77
|
1,55
|
1,70
|
2,43
|
|
6000
|
0,75
|
1,61
|
1,82
|
1,60
|
1,75
|
2,45
|
МЕТОДИЧЕСКИЕ УКАЗАНИЯ И ПРИМЕР РАСЧЕТА
Решение данной задачи рассматривается при следующих исходных данных: a = 40, b = 50, c =
30, d = 160, h = 180, l0 =
1,2 мм; материал верхней П-образной части магнитопровода - пермендюр, нижней -
эл. техн. сталь Э310; B0 =
1,6 Тл.
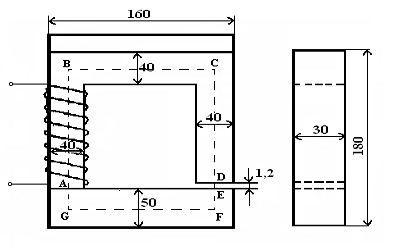
Рисунок 17
Расчет данной цепи производится следующим образом.
Вычерчивается магнитопровод цепи (рис. 17) с учетом его размеров.
Определяются длины верхнего lв и нижнего lн участков
магнитопровода (по средней линии магнитопровода):
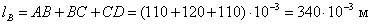
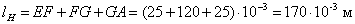
Определяются
поперечные сечения верхнего SB и нижнего SH участков магнитопровода:
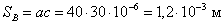
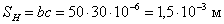
Поперечное
сечение воздушного зазора S0 принимается равным поперечному сечению верхней части
магнитопровода.
Определяется
магнитный поток:
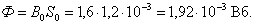
Определяется
магнитная индукция в нижней части магнитопровода:
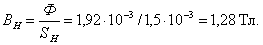
Определяется
напряженность магнитного поля в воздушном зазоре:
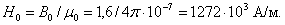
Рисунок
18
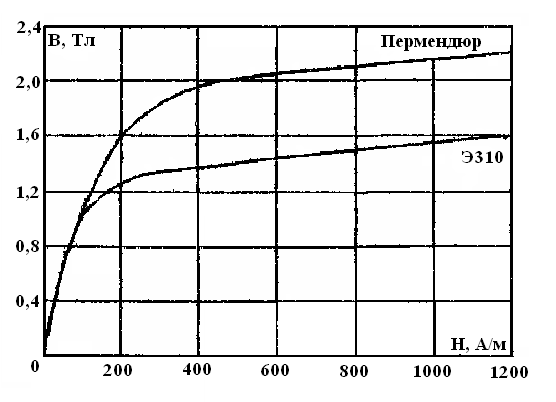
Строятся
кривые намагничивания (рис. 18) ферромагнитных материалов, из которых
изготовлен магнитопровод.
По
кривым намагничивания определяются напряженности магнитного поля в верхней и
нижней частях магнитопровода. В результате получается: HB = 200 А/м; HH =
230 А/м.
По
закону полного тока определяется магнитодвижущая сила цепи:
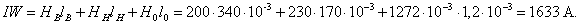
ЗАДАЧА 6. Расчет последовательной цепи
синусоидального тока
В
цепи, схема которой приведена на рис. 19, требуется:
.
Определить: действующее I и амплитудное Im значение
тока; действующие значения напряжений на элементах цепи UR, UL, UC;
действующее U и амплитудное Um значения
напряжения на зажимах цепи; угловую частоту 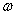 ; угол
сдвига фаз между напряжением и током
; угол
сдвига фаз между напряжением и током 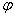 ;
начальную фазу напряжения на зажимах цепи
;
начальную фазу напряжения на зажимах цепи 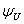 ;
мощности элементов цепи P, QL, QC; полную S и реактивную Q
мощности цепи; коэффициент мощности цепи
;
мощности элементов цепи P, QL, QC; полную S и реактивную Q
мощности цепи; коэффициент мощности цепи 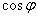 . Одна из
этих величин может оказаться заданной.
. Одна из
этих величин может оказаться заданной.
.
Составить уравнения мгновенных значений тока 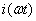 и
напряжения
и
напряжения 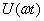 и построить синусоиды, соответствующие этим
уравнениям.
и построить синусоиды, соответствующие этим
уравнениям.
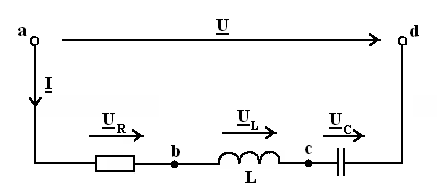
Рисунок
19
.
Построить векторную диаграмму тока  и
напряжений
и
напряжений 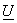 ,
, 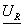 ,
, 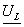 ,
, 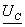 и
треугольник мощностей.
и
треугольник мощностей.
Исходные
данные к расчету приведены в табл. 11 и 12. Частота f = 50 Гц.
Таблица 11
|
Номер личного варианта
|
R, Ом
|
L, МГн
|
С, мкФ
|
Ψi,
град
|
Номер личного варианта
|
R, Ом
|
L, МГн
|
С, мкФ
|
Ψi,
град
|
|
1
|
2
|
3
|
4
|
5
|
1
|
2
|
3
|
4
|
5
|
|
1
|
2
|
9,6
|
796
|
0
|
14
|
2
|
15,9
|
1061
|
70
|
|
2
|
2
|
12,7
|
1061
|
10
|
15
|
4
|
6,4
|
531
|
-30
|
|
3
|
2
|
9,6
|
531
|
-90
|
16
|
3
|
6,4
|
637
|
80
|
|
4
|
3
|
12,7
|
1592
|
20
|
17
|
4
|
19,1
|
1592
|
-20
|
|
5
|
2
|
19,1
|
1061
|
-80
|
18
|
3
|
15,9
|
1592
|
90
|
|
6
|
3
|
6,4
|
796
|
30
|
19
|
4
|
9,6
|
637
|
-10
|
|
7
|
3
|
19,1
|
1592
|
-70
|
20
|
4
|
15,9
|
1061
|
15
|
|
8
|
2
|
6,4
|
796
|
40
|
21
|
4
|
9,6
|
455
|
-45
|
|
9
|
3
|
6,4
|
531
|
-60
|
22
|
4
|
9,6
|
531
|
25
|
|
10
|
2
|
12,7
|
1592
|
50
|
23
|
4
|
15,9
|
455
|
-35
|
|
11
|
2
|
12,7
|
531
|
-50
|
24
|
4
|
19,1
|
1061
|
35
|
|
12
|
2
|
9,6
|
637
|
60
|
25
|
4
|
22,3
|
637
|
-25
|
|
13
|
2
|
19,1
|
796
|
-40
|
|
|
|
|
|
Таблица 12
|
Номер группового варианта
|
1
|
2
|
3
|
4
|
5
|
|
Дано
|
U = 12 B
|
S = 100 B·A
|
Q = 72 вар.
|
Uac = 10 B
|
Ubc = 4 B
|
МЕТОДИЧЕСКИЕ УКАЗАНИЯ И ПРИМЕР РАСЧЕТА
Решение
данной задачи рассматривается при следующих исходных данных: R = 3
Ом, L = 15,9 мГн; C = 255 мкФ; 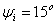 ; Q = 72 вар.
; Q = 72 вар.
Расчет
данной цепи осуществляется в следующем порядке.
Определяются
индуктивное XL, емкостное XC, реактивное X и
полное Z сопротивления цепи: 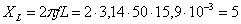 Ом;
Ом;
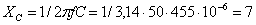 Ом;
Ом; 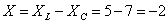 Ом;
Ом; 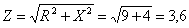 Ом.
Ом.
Определяются
действующие и амплитудные значения тока и общего напряжения: 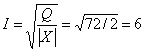 А;
А;  А; U = Z I = 3,6 ∙ 6 = 21,6 В;
А; U = Z I = 3,6 ∙ 6 = 21,6 В; 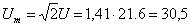 В.
В.
Определяются
действующие значения напряжений на резистивном, индуктивном и емкостном
элементах цепи: UR = R I = 3 ∙ 6 = 18 В; UL = XL I = 5 ∙ 6 = 30 В; UC = XC I = 42 В.
Определяются
мощности резистивного, индуктивного и емкостного элементов и полная мощность
цепи: P = I2 R = 62 ∙ 3 = 108 Вт; QL = XL I2 = 5 ∙ 62 = 180 вар; QC = XC I2 = 7 ∙ 62 = 252 вар; S = U I = 21,6 ∙ 6 = 129,6 В∙А.
Определяются
угловая частота 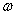 , угол сдвига фаз между напряжением и током
, угол сдвига фаз между напряжением и током 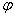 , начальная фаза общего напряжения
, начальная фаза общего напряжения 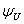 и коэффициент мощности цепи
и коэффициент мощности цепи 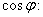
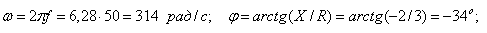
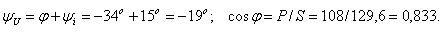
Составляются
уравнения мгновенных значений тока 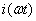 и общего
напряжения
и общего
напряжения 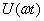 :
:
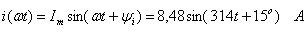 ;
;
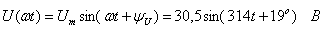
Строятся временная (синусоидальная) диаграмма мгновенных значений тока и
напряжения (рис. 20), векторная диаграмма тока и напряжений (рис. 21) и
треугольник мощностей (рис. 22).
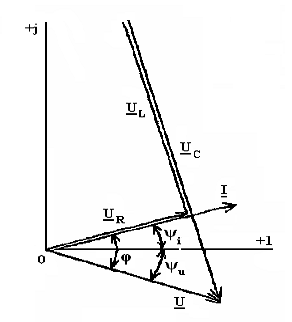
Рисунок 20
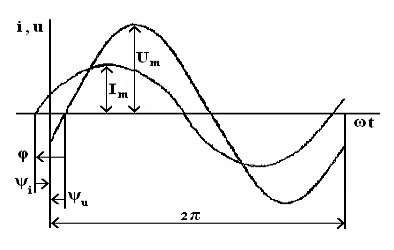
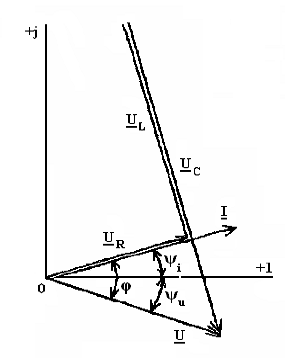
Рисунок 21
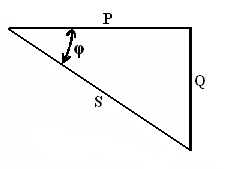
Рисунок 22
В
данном примере рассмотрено решение задачи, относящейся к третьему групповому
варианту. При решении задач, относящихся к остальным групповым вариантам,
действующие значения токов определяются по формулам: для первого группового
варианта 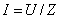 , для второго
, для второго 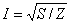 , для
четвертого
, для
четвертого 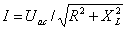 , для пятого
, для пятого 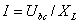 .
.
ЗАДАЧА 7. Расчет параллельной цепи синусоидального
тока
Определить
токи и построить векторную диаграмму напряжения и токов цепи, общая схема
которой приведена на рис. 23. Данная схема соответствует первому групповому
варианту. Схемы для остальных групповых вариантов получаются путем исключения
из общей схемы одного из элементов согласно табл. 13. Исходные данные расчету
приведены в табл. 14.
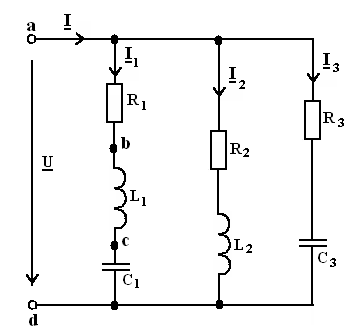
Рисунок 23
Таблица 13
|
Номер группового варианта
|
Элемент, исключаемый из
общей схемы
|
|
1
|
-
|
|
2
|
L2
|
|
3
|
R2
|
|
4
|
R3
|
|
5
|
C3
|
Таблица 14
|
Номер личного варианта
|
Одна из заданных величин
|
Сопротивления, Ом
|
|
|
R1
|
XL1
|
XC1
|
R2
|
XL2
|
R3
|
XC3
|
|
1
|
2
|
3
|
4
|
5
|
6
|
7
|
8
|
9
|
U = 20 B
|
3
|
6
|
2
|
8
|
6
|
5
|
5
|
|
2
|
Uab = 40 B
|
8
|
4
|
10
|
10
|
20
|
16
|
10
|
|
3
|
Ubc = 50 B
|
12
|
10
|
5
|
24
|
18
|
21
|
24
|
|
4
|
Ucd = 36 B
|
9
|
6
|
18
|
10
|
15
|
10
|
10
|
|
5
|
Uac = 45 B
|
5
|
10
|
5
|
6
|
8
|
12
|
7
|
|
6
|
Ubd = 21 B
|
4
|
3
|
10
|
4
|
6
|
8
|
6
|
|
7
|
P1 = 200 Вт
|
8
|
8
|
4
|
9
|
5
|
15
|
9
|
|
8
|
QL1 = 8 вар
|
9
|
2
|
10
|
4
|
3
|
8
|
8
|
|
9
|
QC1 = 136 вар
|
15
|
15
|
7
|
15
|
20
|
10
|
15
|
|
10
|
Q1 = 600 вар
|
10
|
5
|
20
|
9
|
6
|
12
|
4
|
|
11
|
S1 = 320 B·A
|
12
|
20
|
4
|
8
|
16
|
20
|
10
|
|
12
|
U = 35 B
|
5
|
5
|
10
|
5
|
7
|
15
|
8
|
|
13
|
Uab = 42 B
|
7
|
5
|
12
|
12
|
15
|
10
|
10
|
|
14
|
Ubc = 80 B
|
10
|
20
|
10
|
8
|
7
|
15
|
20
|
|
15
|
Ucd = 30 B
|
20
|
25
|
10
|
15
|
15
|
10
|
20
|
|
16
|
Uac = 36 B
|
4
|
6
|
3
|
5
|
5
|
7
|
4
|
|
17
|
Ubd = 32 B
|
6
|
2
|
10
|
10
|
8
|
16
|
12
|
|
18
|
P1 = 180 Bт
|
5
|
20
|
8
|
10
|
15
|
13
|
13
|
|
19
|
QL1 = 150 вар
|
12
|
6
|
15
|
15
|
10
|
20
|
20
|
|
20
|
QC1 = 40 вар
|
5
|
15
|
10
|
7
|
7
|
4
|
8
|
|
21
|
Q1 = 144 вар
|
7
|
6
|
10
|
3
|
8
|
4
|
6
|
|
22
|
S1 = 225 B·A
|
4
|
10
|
2
|
9
|
5
|
15
|
10
|
|
23
|
U = 72 B
|
8
|
6
|
15
|
18
|
24
|
12
|
18
|
|
24
|
Uac = 86 B
|
8
|
20
|
5
|
12
|
16
|
15
|
10
|
|
25
|
Ubd = 70 B
|
15
|
10
|
20
|
26
|
25
|
12
|
16
|
МЕТОДИЧЕСКИЕ УКАЗАНИЯ И ПРИМЕР РАСЧЕТА
Решение данной задачи рассматривается на примере цепи, представленной на
рис. 24, при следующих исходных данных: U = 180 В; R1 =
20; R2 = 6; XC2 = 8; R3 =
10; XL3 = 30; XC3 = 15 Ом.
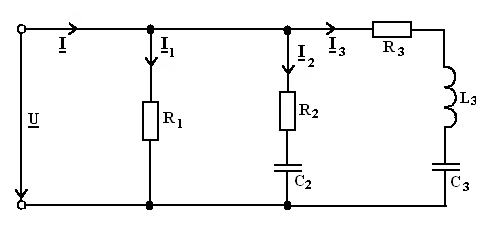
Рисунок 24
Расчет данной цепи осуществляется символическим методом в следующем
порядке.
Составляются комплексные сопротивления ветвей цепи
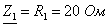 ;
; 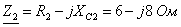 ;
;
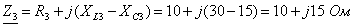 .
.
Начальная
фаза напряжения 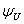 принимается равной нулю. Поэтому U = U =
180 В.
принимается равной нулю. Поэтому U = U =
180 В.
Определяются
комплексные и действующие значения токов в ветвях цепи
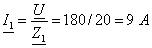 ;
; 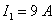 ;
;
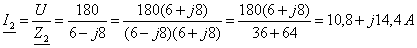 ;
;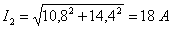 ;
; 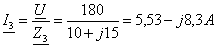 ;
; 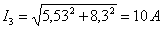 .
.
Определяются
комплексное и действующее значения общего тока:
 ;
;
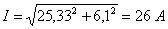 .
.
Определяются
начальные фазы токов по формуле 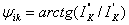 , где
, где 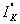 и
и 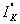 -
вещественная часть и числовое значение мнимой части комплексного числа,
определяющего k-й комплексный ток. Начальная фаза общего тока
-
вещественная часть и числовое значение мнимой части комплексного числа,
определяющего k-й комплексный ток. Начальная фаза общего тока
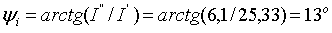
Начальные
фазы токов в ветвях
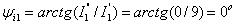 ;
; 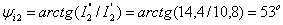 ;
;
 .
.
Строится
векторная диаграмма напряжения и токов (рис. 25).
цепь ток трехфазный двигатель
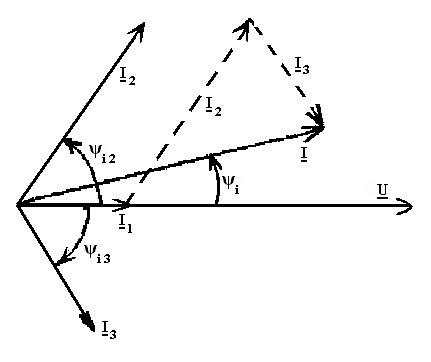
Рисунок 25
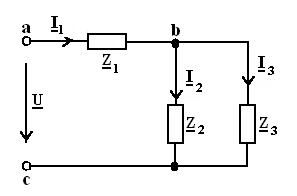
Рисунок 26
ЗАДАЧА 8. Расчет смешанной цепи синусоидального
тока
Пользуясь общей схемой цепи (рис. 26), и данными табл. 15, составить
схему цепи, подлежащую расчету. В составленной цепи определить токи I1, I2, I3,
напряжение на зажимах U,
напряжения на ветвях Uab, Ubc и напряжения на элементах цепи.
(Одна из этих величин известна, т.е. задана в качестве исходной данной в табл.
15.) Построить векторную диаграмму токов и напряжений.
Таблица 15
|
Номер личного варианта
|
Комплексное сопротивление
ветвей цепи, Ом
|
Номера групповых вариантов
и исходные данные к ним
|
|
Z1
|
Z2
|
Z3
|
1
|
2
|
3
|
4
|
5
|
|
|
|
|
U, B
|
I1, A
|
Uab, B
|
I2, A
|
Ubc, B
|
|
1
|
2
|
3
|
4
|
5
|
6
|
7
|
8
|
9
|
|
1
|
- j2,4
|
4
|
2+j2
|
12
|
5
|
9,6
|
8
|
8
|
|
2
|
2+j10
|
5
|
- j10
|
20
|
3
|
24,0
|
4
|
20
|
|
3
|
- j2,8
|
4
|
4+j4
|
12
|
3
|
5,6
|
2
|
10
|
|
4
|
2+j14
|
10
|
- j20
|
28
|
2
|
25,0
|
4
|
36
|
|
5
|
- j3,6
|
6
|
3+j3
|
10
|
2
|
7,2
|
3
|
6
|
|
6
|
4+j24
|
15
|
- j30
|
48
|
2,5
|
48,0
|
4
|
40
|
|
7
|
- j4,8
|
6
|
6+j6
|
20
|
3
|
9,6
|
2
|
15
|
|
8
|
6+j20
|
20
|
- j40
|
50
|
4
|
41,0
|
3
|
54
|
- j5,4
|
8
|
4+j4
|
24
|
4
|
5,4
|
2,5
|
18
|
|
10
|
6+j25
|
25
|
- j50
|
60
|
3
|
52,0
|
6
|
45
|
|
11
|
- j6,6
|
8
|
8+j8
|
28
|
3
|
13,2
|
2
|
20
|
|
12
|
3+j25
|
30
|
- j60
|
90
|
2
|
100,0
|
2
|
130
|
|
13
|
- j5
|
10
|
5+j5
|
20
|
4
|
15,0
|
3
|
18
|
|
14
|
12+j23
|
35
|
- j70
|
82
|
5
|
127,0
|
4
|
127
|
|
15
|
- j10
|
10
|
10+j10
|
30
|
3,6
|
40,0
|
2,4
|
24
|
|
16
|
8+j25
|
40
|
- j80
|
127
|
4
|
110,0
|
3
|
72
|
|
17
|
- j6
|
12
|
6+j6
|
24
|
5
|
30,0
|
1,5
|
16
|
|
18
|
6+j10
|
10
|
- j5
|
30
|
2
|
48,0
|
2
|
15
|
|
19
|
- j10
|
12
|
12+j12
|
36
|
2,4
|
30,0
|
2
|
18
|
|
20
|
6+j18
|
20
|
- j10
|
42
|
3
|
56,0
|
1
|
18
|
|
21
|
- j11
|
15
|
10+j10
|
40
|
2
|
44,0
|
4
|
20
|
|
22
|
10+j30
|
30
|
- j15
|
60
|
1,5
|
64,0
|
2
|
27
|
|
23
|
- j11
|
15
|
15+j15
|
48
|
3
|
22,0
|
2
|
30
|
|
24
|
14+j28
|
40
|
- j20
|
100
|
2
|
36,0
|
1,5
|
36
|
|
25
|
- j7,2
|
18
|
9+j9
|
30
|
4
|
21,6
|
1,5
|
24
|
МЕТОДИЧЕСКИЕ УКАЗАНИЯ И ПРИМЕР РАСЧЕТА
Решение
данной задачи рассматривается при следующих исходных данных: 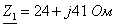 ;
; 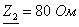 ;
; 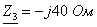 ; I1 = 3 A и осуществляется в следующем порядке.
; I1 = 3 A и осуществляется в следующем порядке.
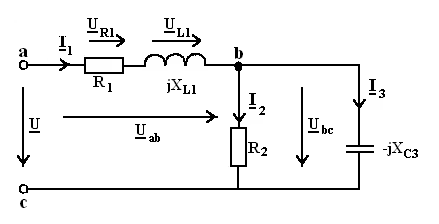
Рисунок
27
Составляется
подлежащая расчету схема цепи с учетом заданных комплексных сопротивлений (рис.
27).
Определяется
комплексное сопротивление разветвленной части цепи:
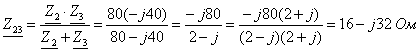
Определяется
комплексное сопротивление всей цепи
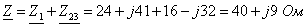
Начальная
фаза тока первой ветви 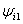 принимается равной нулю, поэтому
принимается равной нулю, поэтому 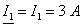 .
.
Определяются
комплексные и действующие значения напряжений на зажимах цепи и на ветвях цепи
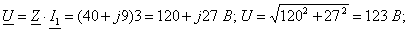
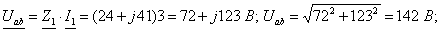
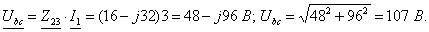
Определяются
комплексные и действующие значения токов во второй и третьей ветвях
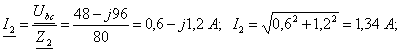
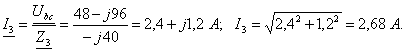
Определяются
комплексные и действующие значения напряжений на элементах цепи: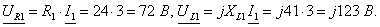
Определяются
начальные фазы напряжений и токов, которые необходимы для построения векторной
диаграммы: 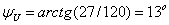 ;
; 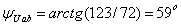 ;
; 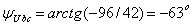 ;
; 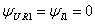 , так как
, так как
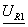 совпадает по фазе с
совпадает по фазе с 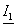 ;
; 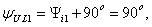 так как
так как 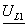 опережает
опережает
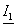 на 90o;
на 90o; 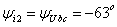 , так как
, так как
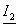 совпадает по фазе с
совпадает по фазе с 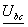 ;
;  , так как
, так как 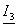 опережает
опережает
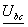 на 90o.
на 90o.
Строится
векторная диаграмма напряжений и токов (рис. 28).
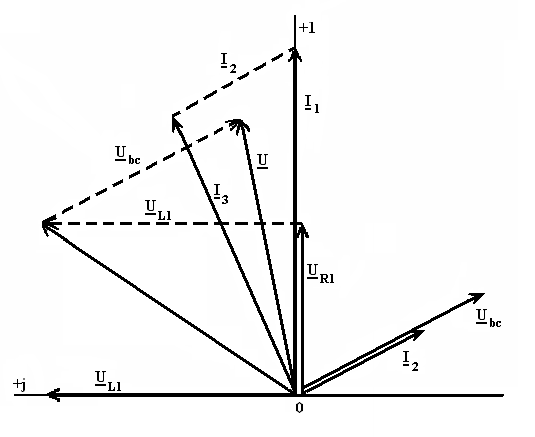
Рисунок
28
ЗАДАЧА 9. Расчет трехфазной четырехпроводной цепи,
соединенной звездой
Комплексные
сопротивления фаз приемника 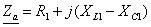 ;
; 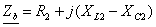 ;
; 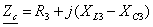 .
Числовые значения R1, XL1, … , XC3 даны в табл. 16. Значение линейного напряжения UЛ
сети, к которой подключен приемник, приведено в табл. 17. Сопротивление
нейтрального провода принимается равным нулю.
.
Числовые значения R1, XL1, … , XC3 даны в табл. 16. Значение линейного напряжения UЛ
сети, к которой подключен приемник, приведено в табл. 17. Сопротивление
нейтрального провода принимается равным нулю.
Начертить
схему цепи и показать на ней условно положительные направления линейных и
фазных напряжений, линейных токов и тока в нейтральном проводе. (Элементы цепи,
сопротивления которых равны нулю, на схеме не показывать.)
Определить:
линейные токи Ia, Ib, Ic и ток в нейтральном проводе IN; комплексные
мощности фаз приемника 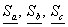 и всех трех фаз
и всех трех фаз 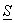 ; углы
сдвига между фазными напряжениями и токами φa, φb,
φc.
; углы
сдвига между фазными напряжениями и токами φa, φb,
φc.
Построить векторную диаграмму напряжений и токов.
Таблица 16
|
Номер личного варианта
|
Сопротивления, Ом
|
|
R1
|
XL1
|
XC1
|
R2
|
XL2
|
XC2
|
R3
|
XL3
|
XC3
|
|
1
|
2
|
3
|
4
|
5
|
6
|
7
|
8
|
9
|
10
|
|
1
|
3
|
8
|
4
|
4
|
3
|
4
|
0
|
18
|
6
|
|
2
|
4
|
7
|
4
|
4
|
3
|
0
|
10
|
6
|
6
|
|
3
|
3
|
8
|
4
|
3
|
4
|
0
|
0
|
12
|
2
|
|
4
|
4
|
7
|
4
|
4
|
3
|
0
|
0
|
5
|
15
|
|
5
|
6
|
4
|
12
|
6
|
0
|
8
|
9
|
12
|
0
|
|
6
|
8
|
4
|
10
|
8
|
0
|
6
|
15
|
8
|
8
|
|
7
|
6
|
4
|
12
|
6
|
0
|
8
|
0
|
25
|
10
|
|
8
|
8
|
4
|
10
|
8
|
0
|
6
|
10
|
10
|
25
|
|
9
|
4
|
6
|
9
|
4
|
7
|
4
|
12
|
0
|
16
|
|
10
|
4
|
9
|
12
|
4
|
4
|
7
|
20
|
25
|
5
|
|
11
|
4
|
12
|
9
|
4
|
7
|
4
|
0
|
28
|
8
|
|
12
|
4
|
9
|
12
|
4
|
4
|
7
|
10
|
10
|
20
|
|
13
|
9
|
17
|
5
|
9
|
12
|
0
|
8
|
10
|
16
|
|
14
|
12
|
14
|
5
|
12
|
9
|
0
|
10
|
10
|
10
|
|
15
|
9
|
17
|
5
|
9
|
12
|
0
|
0
|
15
|
|
16
|
12
|
14
|
5
|
12
|
9
|
0
|
0
|
6
|
16
|
|
17
|
12
|
6
|
12
|
10
|
26
|
16
|
16
|
12
|
0
|
|
18
|
16
|
6
|
6
|
18
|
16
|
10
|
22
|
20
|
8
|
|
19
|
12
|
6
|
22
|
12
|
10
|
26
|
0
|
28
|
8
|
|
20
|
16
|
6
|
18
|
16
|
10
|
22
|
0
|
12
|
32
|
|
21
|
15
|
25
|
5
|
15
|
20
|
0
|
21
|
10
|
28
|
|
22
|
20
|
20
|
15
|
20
|
15
|
0
|
35
|
10
|
10
|
|
23
|
15
|
25
|
5
|
15
|
20
|
0
|
0
|
45
|
10
|
|
24
|
20
|
20
|
15
|
20
|
15
|
0
|
0
|
10
|
45
|
|
25
|
18
|
4
|
28
|
18
|
0
|
24
|
24
|
32
|
0
|
Таблица 17
|
Номер группового варианта
|
1
|
2
|
3
|
4
|
5
|
|
Линейное напряжение сети, В
|
660
|
380
|
220
|
690
|
400
|
МЕТОДИЧЕСКИЕ УКАЗАНИЯ И ПРИМЕР РАСЧЕТА
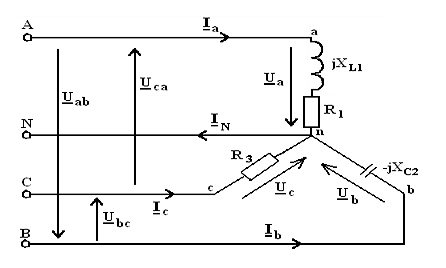
Рисунок 29
Решение данной задачи рассматривается при следующих исходных данных: UЛ = 380 В; R1 = 11, XL1 =
19, XC2 = 44, R3 = 22 Ом; сопротивления XC1, R2, XL2, XC3 равны нулю. Это решение осуществляется в следующем порядке.
Составляется подлежащая расчету схема цепи с учетом исходных данных.
Определяется действующее значение фазного напряжения приемника:
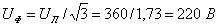
Составляется
симметричная система фазовых комплексных напряжений приемника:
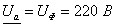 ;
;
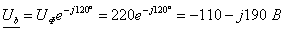 ;
;
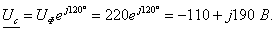
Составляются
комплексные сопротивления фаз приемника
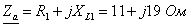 ;
; 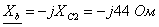 ;
; 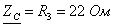 .
.
Определяются
комплексные и действующие значения линейных токов и тока в нейтральном проводе
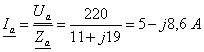 ;
; 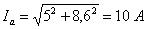 ;
;
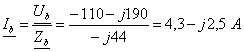 ;
; 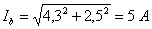 ;
;
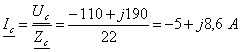 ;
; 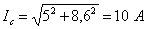 ;
;
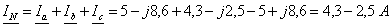 ;
; 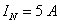
(В
данной цепи ток 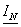 случайно оказался равным току
случайно оказался равным току 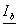 .)
.)
Определяются
углы сдвига фаз между фазными напряжениями и токами: 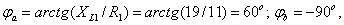 так как приемник фазы b емкостный,
так как приемник фазы b емкостный, 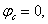 так как приемник фазы с - резистивный.
так как приемник фазы с - резистивный.
Определяются
комплексные мощности фаз и всей цепи:
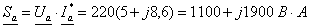 ;
;
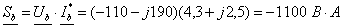 ;
;
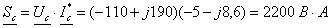 ;
;
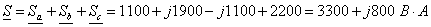 .
.
Строится
векторная диаграмма напряжений и токов (рис. 30).
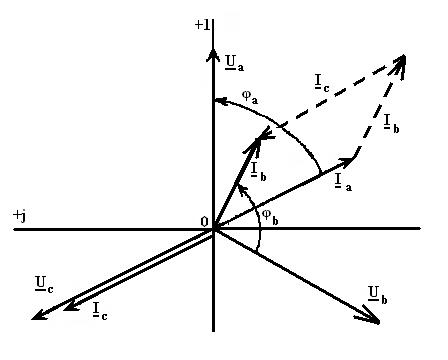
Рисунок
30
ЗАДАЧА 10. Расчет трехфазной цепи, соединенной
треугольником
Комплексные
сопротивления фаз приемника определяются выражениями: 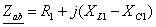 ;
; 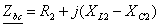 ;
; 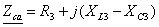 . Числовые значения сопротивлений R1, XL1,
…, XC3 даны в табл. 16. Значение линейного напряжения сети UЛ, к
которой подключен приемник, приведено в табл. 17.
. Числовые значения сопротивлений R1, XL1,
…, XC3 даны в табл. 16. Значение линейного напряжения сети UЛ, к
которой подключен приемник, приведено в табл. 17.
Начертить
схему цепи и показать на ней условно положительные направления линейных
напряжений, линейных и фазных токов. (Элементы цепи, сопротивления которых
равны нулю, на схеме не показывать.)
Определить:
фазные Iab, Ibc, Ica и линейные Ia, Ib, Ic
токи; углы сдвига фаз между фазными напряжениями и токами φa, φb, φc.
Построить
векторную диаграмму напряжений и токов.
МЕТОДИЧЕСКИЕ
УКАЗАНИЯ И ПРИМЕР РАСЧЕТА
Решение
данной задачи рассматривается при следующих исходных данных: UЛ =
660 В; R1 = 22, XC2 = 10, XL3 = 33 Ом; сопротивления XL1, XC1, R2, XL2, R3, XC3
равны нулю. Это решение осуществляется в следующем порядке.
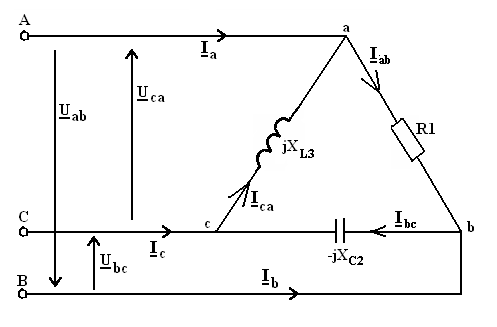
Рисунок
31
Составляется
подлежащая расчету схема цепи с учетом исходных данных (рис. 31).
Составляется
симметричная система фазных комплексных напряжений приемника
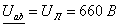 ;
;
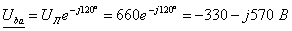 ;
;
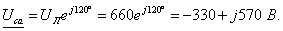
Составляются
комплексные сопротивления фаз приемника:
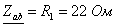 ;
; 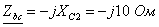 ;
; 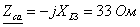
Определяются
комплексные и действующие значения фазных и линейных токов
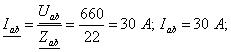
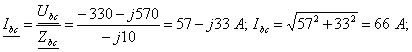
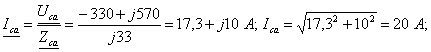
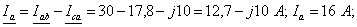
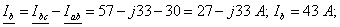
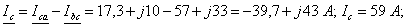
Определяются
углы сдвига фаз между фазными напряжениями и токами: 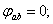
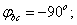
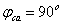 , так как приемник фазы ab резистивный,
фазы bc - емкостный, фазы ca -
индуктивный.
, так как приемник фазы ab резистивный,
фазы bc - емкостный, фазы ca -
индуктивный.
Определяются
комплексные мощности фаз и всей цепи:
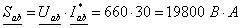 ;
;
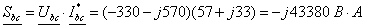 ;
;
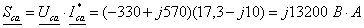 ;
;
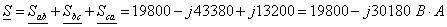
Строится
векторная диаграмма напряжений и токов (рис. 32).
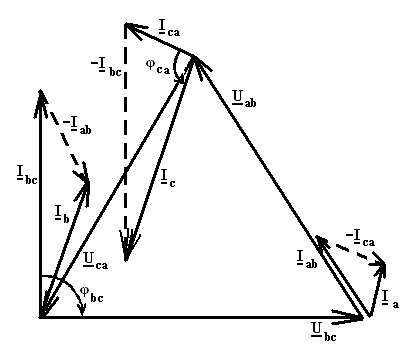
Рисунок
32
ЗАДАЧА 11. Расчет характеристик трехфазного
трансформатора
Исходные
данные к расчету приведены в табл. 18 и 19. Этими данными являются: номинальная
мощность Sном; номинальные первичное и вторичное напряжения U1ном,
U2ном; мощности потерь при опыте холостого хода Px и
при опыте короткого замыкания Pк; угол сдвига фаз φ2 между фазным напряжением и током вторичной обмотки; коэффициент
нагрузки β;
напряжение короткого замыкания Uк в
процентах от U1ном; группа соединения обмоток трансформатора.
Требуется:
начертить схему электрической цепи нагруженного трансформатора; определить
коэффициенты трансформации фазных и линейных напряжений и значения фазных и
линейных номинальных токов; рассчитать и построить внешнюю характеристику
трансформатора и зависимость коэффициента полезного действия трансформатора от
коэффициента нагрузки β.
При этом принять β = 0,1;
0,2; 0,4; 0,6; 0,8; 1,0; 1,2.
Таблица 18
|
Номер личного варианта
|
Sном, кВ·А
|
U1ном, кВ
|
U2ном, кВ
|
Px, кВт
|
Pк, кВт
|
φ2,
град
|
|
1
|
25
|
10
|
380
|
0,3
|
1
|
0
|
|
2
|
40
|
15
|
380
|
0,4
|
1
|
10
|
|
3
|
63
|
10
|
380
|
0,6
|
2
|
20
|
|
4
|
63
|
20
|
660
|
0,7
|
2
|
30
|
|
5
|
100
|
10
|
660
|
1,0
|
3
|
40
|
|
6
|
100
|
35
|
660
|
0,9
|
3
|
-10
|
|
7
|
160
|
10
|
3000
|
1,5
|
4
|
-20
|
|
8
|
160
|
35
|
3000
|
1,6
|
5
|
-30
|
|
9
|
250
|
10
|
230
|
2,5
|
5
|
-40
|
|
10
|
250
|
35
|
380
|
2,4
|
6
|
15
|
|
11
|
400
|
10
|
660
|
4,0
|
12
|
-15
|
|
12
|
400
|
35
|
3150
|
3,8
|
11
|
25
|
|
13
|
630
|
10
|
230
|
6,3
|
20
|
-25
|
|
14
|
630
|
35
|
400
|
6,0
|
18
|
35
|
|
15
|
1000
|
10
|
690
|
10,0
|
30
|
-35
|
|
16
|
1000
|
35
|
3150
|
9,0
|
30
|
37
|
|
17
|
1600
|
10
|
3300
|
16,0
|
50
|
-37
|
|
18
|
1600
|
35
|
690
|
15,0
|
45
|
26
|
|
19
|
2500
|
10
|
6300
|
25,0
|
75
|
-26
|
|
20
|
2500
|
35
|
3300
|
24,0
|
60
|
18
|
|
21
|
4000
|
10
|
6600
|
40,0
|
100
|
-18
|
|
22
|
4000
|
35
|
6600
|
38,0
|
100
|
24
|
|
23
|
6300
|
10
|
380
|
63,0
|
200
|
28
|
|
24
|
6300
|
35
|
400
|
60,0
|
150
|
|
25
|
9000
|
35
|
6000
|
100,0
|
250
|
38
|
Таблица 19
|
Номер группового варианта
|
1
|
2
|
3
|
4
|
5
|
|
Uк, %
|
8
|
9
|
10
|
7
|
6
|
|
Группы соединения обмоток
|
Y/Y - 0
|
Y/Δ
- 11
|
Y/Y - 0
|
Y/Δ
- 11
|
Y/Y - 0
|
МЕТОДИЧЕСКИЕ УКАЗАНИЯ И ПРИМЕР РАСЧЕТА
Решение данной задачи рассматривается при следующих исходных данных: Sном = 630 кВ∙А; U1ном = 10 кВ; U2ном = 400 В; Px = 1,8 кВт; Pк = 8,4 кВт; Uк =
5%; φ2
= 37o; группа соединения обмоток Y/Y - 6. Это решение осуществляется в следующем порядке.
Составляется схема электрической цепи нагруженного трансформатора (рис.
33).
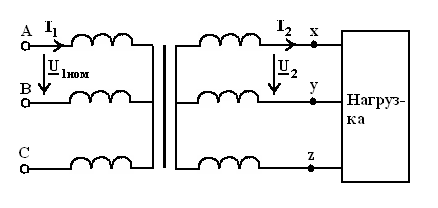
Рисунок 33
Определяется
коэффициент трансформации. Так как обе обмотки соединены звездой, то линейный nЛ и
фазный nФ коэффициенты трансформации равны: 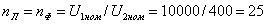 .
.
Определяются
фазные номинальные напряжения первичной и вторичной обмоток
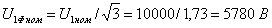 ;
; 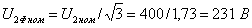
Определяются
значения номинальной мощности и мощностей потерь при опытах холостого хода и
короткого замыкания, приходящиеся на одну фазу
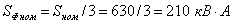 ;
; 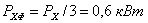 ;
;
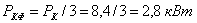 .
.
Определяются
номинальные токи первичной и вторичной обмоток. Так как обмотки соединены
звездой, то линейный и фазный токи равны: I1ном = I1Ф
ном = SФ ном / U1Ф ном = 210000 / 5780 = 36 A. I2ном
= I2Ф ном = SФ ном / U2Ф ном = 210000
/ 231 = 909 A.
Определяются
внешняя характеристика трансформатора, представляющая зависимость вторичного
напряжения U2 от тока нагрузки I2 или от
величины β,
которая пропорциональна току нагрузки (β = I2 / I2ном).
Зависимость U2(β) определяется в следующем порядке. Определяются активная Uак и
реактивная Uрк составляющие напряжения короткого замыкания в
процентах от U1Ф ном
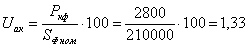 ;
;
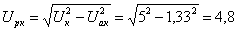 .
.
Определяется
зависимость относительного изменения вторичного напряжения 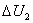 от коэффициента нагрузки β по формуле
от коэффициента нагрузки β по формуле
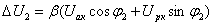
При
β
= 0,6 и φ2 = 37o
получаем:  . Значения
. Значения 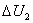 для
остальных значений β
приведены в табл. 20.
для
остальных значений β
приведены в табл. 20.
Определяется
зависимость 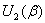 по формуле
по формуле
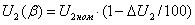
При
β
= 0,6 получаем 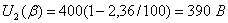 . Значения
. Значения 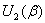 для
остальных значений β
приведены в табл. 20.
для
остальных значений β
приведены в табл. 20.
Определяется
зависимость коэффициента полезного действия трансформатора от коэффициента
нагрузки β
по формуле:
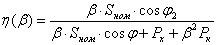 .
.
При
β
= 0,6 получаем
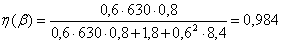 .
.
Значения
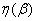 для остальных значений β приведены в табл. 20.
для остальных значений β приведены в табл. 20.
Таблица 20
|
β
|
0
|
0,1
|
0,2
|
0,4
|
0,6
|
0,8
|
1,0
|
1,2
|
|
ΔU2, %
|
0
|
0,39
|
0,78
|
1,56
|
2,36
|
3,15
|
3,94
|
4,73
|
|
U2(β),
B
|
400
|
398
|
396
|
393
|
390
|
387
|
384
|
381
|
|
η(β)
|
0
|
0,964
|
0,979
|
0,984
|
0,983
|
0,982
|
0,980
|
0,977
|
На
основании данных табл. 20 строятся графики зависимостей 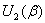 и
и  (рис. 34
и 35).
(рис. 34
и 35).
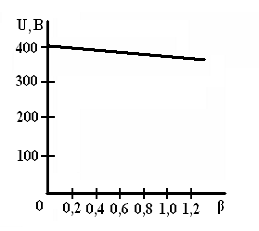
Рисунок
34
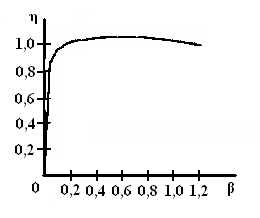
Рисунок 35
ЗАДАЧА 12. Расчет характеристик асинхронного
трехфазного двигателя с короткозамкнутым ротором
Исходные
данные к расчету приведены в табл. 21 и 22. Этими данными являются: номинальная
мощность двигателя Pном, номинальная частота вращения ротора nном,
номинальный коэффициент полезного действия  ,
номинальный коэффициент мощности cosφном, кратность максимального момента Mmax / Mном,
кратность пускового тока Iп / Iном, номинальное напряжение Uном, число пар
полюсов обмотки статора p, схема соединения обмоток статора. Двигатель получает
электроэнергию от сети с частотой напряжения 50 Гц.
,
номинальный коэффициент мощности cosφном, кратность максимального момента Mmax / Mном,
кратность пускового тока Iп / Iном, номинальное напряжение Uном, число пар
полюсов обмотки статора p, схема соединения обмоток статора. Двигатель получает
электроэнергию от сети с частотой напряжения 50 Гц.
Требуется:
определить номинальную мощность, потребляемую двигателем от сети, номинальный и
пусковой токи статора, номинальное и критическое скольжения, номинальный,
максимальный и пусковой моменты; рассчитать и построить зависимость момента от
скольжения и механическую характеристику; начертить схему подключения двигателя
к сети посредством магнитного пускателя, обеспечивающего двигателю
реверсирование, максимальную и тепловую защиту.
Таблица 21
|
Номер личного варианта
|
PНОМ, кВт
|
nном, об/мин
|
ηном, %
|
cosφном
|
Mmax/Mном
|
Iн/Iном
|
p
|
|
1
|
17
|
2900
|
88
|
0,88
|
2,2
|
7
|
1
|
|
2
|
22
|
2900
|
89
|
0,88
|
2,2
|
7
|
1
|
|
3
|
30
|
2900
|
90
|
0,90
|
2,2
|
7
|
1
|
|
4
|
40
|
2900
|
89
|
0,90
|
2,2
|
7
|
1
|
|
5
|
55
|
2900
|
91
|
0,90
|
2,2
|
7
|
1
|
|
6
|
75
|
2900
|
92
|
0,90
|
2,2
|
7
|
1
|
|
7
|
100
|
2920
|
91
|
0,89
|
2,2
|
7
|
1
|
|
8
|
13
|
1450
|
87
|
0,87
|
2,0
|
7
|
2
|
|
9
|
17
|
1460
|
88
|
0,88
|
2,0
|
7
|
2
|
|
10
|
22
|
1470
|
89
|
0,89
|
2,0
|
6
|
2
|
|
11
|
30
|
1460
|
87
|
0,86
|
1,8
|
6
|
2
|
|
12
|
40
|
1455
|
88
|
0,88
|
1,9
|
7
|
2
|
|
13
|
55
|
1460
|
89
|
0,90
|
2,1
|
6
|
2
|
|
14
|
75
|
1470
|
90
|
0,89
|
2,0
|
7
|
2
|
|
15
|
10
|
965
|
88
|
0,86
|
1,8
|
6
|
3
|
|
16
|
13
|
970
|
87
|
0,86
|
1,8
|
5,5
|
3
|
|
17
|
17
|
975
|
88
|
0,87
|
1,9
|
6
|
3
|
|
18
|
22
|
965
|
89
|
0,87
|
1,8
|
7
|
3
|
|
19
|
30
|
970
|
90
|
0,88
|
1,7
|
6,5
|
3
|
|
20
|
40
|
965
|
91
|
0,89
|
1,8
|
7
|
3
|
|
21
|
55
|
980
|
92
|
0,89
|
1,9
|
6,5
|
3
|
|
22
|
8
|
725
|
85
|
0,78
|
1,7
|
6
|
4
|
|
23
|
10
|
730
|
86
|
0,79
|
1,6
|
7
|
4
|
|
24
|
13
|
725
|
87
|
0,82
|
1,7
|
6,6
|
4
|
|
25
|
17
|
730
|
88
|
0,82
|
1,6
|
6
|
4
|
Таблица 22
|
Номер группового варианта
|
1
|
2
|
3
|
4
|
5
|
|
Схема соединения обмоток
статора
|
|
|
|
|
|
|
Номинальное напряжение
|
380
|
220
|
660
|
220
|
127
|
МЕТОДИЧЕСКИЕ УКАЗАНИЯ И ПРИМЕР РАСЧЕТА
Решение
данной задачи рассматривается при следующих исходных данных: Pном
= 40 кВт; Пном = 730 об/мин; 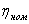 = 0,91; cos φном = 0,83; Mmax / Mном = 1,8; Iп / Iном = 6; Uном
= 220 В; p = 4; обмотка статора соединена в треугольник. Это
решение осуществляется в следующем порядке.
= 0,91; cos φном = 0,83; Mmax / Mном = 1,8; Iп / Iном = 6; Uном
= 220 В; p = 4; обмотка статора соединена в треугольник. Это
решение осуществляется в следующем порядке.
Определяется
номинальная мощность, потребляемая двигателем:
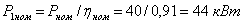
Определяются
номинальный и пусковой токи
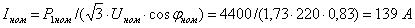 ;
;
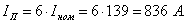
Определяются
частота вращения поля статора n1, номинальное Sном и
критическое Sкр скольжения
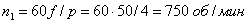 ;
;
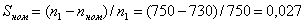 или 2,7 %
или 2,7 %
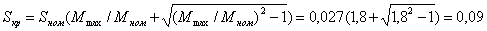 или 9%.
или 9%.
Определяются
номинальный и максимальный моменты на валу двигателя
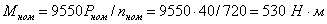 ;
;
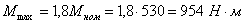
Зависимость
момента от скольжения M(S) и механическая характеристика n(M)
рассчитываются в следующем порядке. Для заданного ряда значений S (он
приведен в табл. 23) определяются значения частоты вращения ротора n и
момента на валу M по формулам
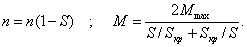
При
S = 0,2 получаем: n = 750(1 - 0,2)
= 600 об / мин;
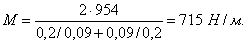
Значения
n и M для остальных значений S приведены в
табл. 23.
Таблица 23
|
S
|
0
|
0,027
|
0,09
|
0,2
|
0,4
|
0,6
|
0,8
|
1
|
|
n, об/мин
|
730
|
682
|
600
|
450
|
300
|
150
|
0
|
|
М, H·м
|
0
|
530
|
954
|
715
|
409
|
279
|
212
|
170
|
Первая графа этой таблицы соответствует холостому ходу двигателя, при
котором момент на валу Mx =
0, скольжение Sx ≈ 0, частота вращения ротора nx = n1 = 750 об / мин. Вторая и третья графы соответствуют
номинальному и критическому скольжениям Последняя графа соответствует началу
пуска двигателя.
Из нее следует, что пусковой момент двигателя MП = 170 Н∙м.
По данным табл. 23 строятся графики зависимостей M(S) и n(M) (рис. 36 и 37).
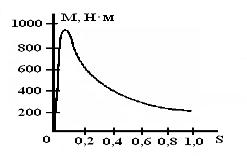
Рисунок 36
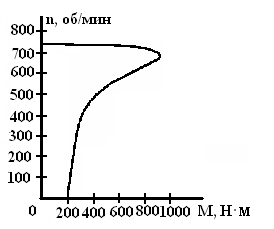
Рисунок 37
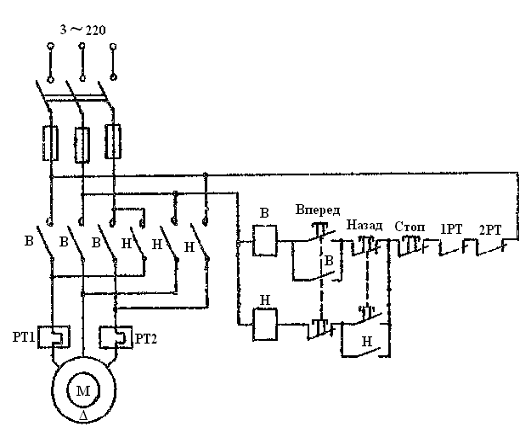
Рисунок 38
ЗАДАЧА 13 Расчет характеристик асинхронного
двигателя с фазным ротором
Рассчитать
и построить зависимости момента от скольжения (характеристики  ), указано таблице 24.
), указано таблице 24.
Схема
электрической цепи двигателя приведена на рисунке 39. Исходные данные к расчету
даны в таблицах 25 и 26. Знак “X” в таблице 24 означает, что данный контакт замкнут.
При расчете пользоваться упрощенной схемой замещения. Активное сопротивление
обмотки статора R1 при расчете принять равным нулю. Двигатель работает
от сети частотой 50 Гц. Критической скольжение характеристики M(S)1
должно равняться единице: Sкр1=1. Критическое скольжение Sкр2
характеристики M(S)2 должно равняться среднему арифметическому от Sкр и
Sкр1, где Sкр - критическое скольжение,
относящееся к единственной характеристике. Обмотка ротора соединена звездой.
Определить
значения пусковых моментов и токов, которые будет иметь двигатель на каждой
характеристике, значения сопротивлений пусковых реостатов RП1 и
RП2.
Используя
графики M(S)1 и M(S)2, определить скольжение Sном1 и Sном2,
частоты вращения nном1 и nном2, токи статора Iном1 и Iном2
при моменте вращения на валу, равном номинальному.
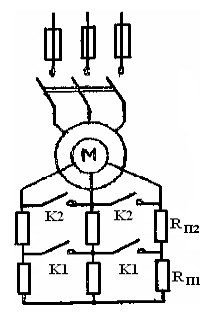
Рисунок 39
Таблица 25
|
Номер личного варианта
|
Схема соедин. обмоток
статора
|
p
|
Номинальные значения
|
Mmax/Mном
|
|
|
|
U, В
|
Р, кВт
|
η
|
cos
φ
|
U2,B
|
|
|
1
|
2
|
3
|
4
|
5
|
6
|
7
|
8
|
9
|
|
1
|
Y
|
3
|
380
|
21
|
0,86
|
0,83
|
114
|
3,2
|
|
2
|
∆
|
3
|
220
|
28
|
0,88
|
0,82
|
147
|
3,4
|
|
3
|
Y
|
4
|
380
|
18
|
0,84
|
0,75
|
101
|
2,8
|
|
4
|
∆
|
4
|
220
|
22
|
0,85
|
0,74
|
138
|
3,0
|
|
5
|
Y
|
3
|
380
|
36
|
0,89
|
0,83
|
171
|
3,2
|
|
6
|
∆
|
3
|
220
|
52
|
0,90
|
0,84
|
220
|
3,5
|
|
7
|
Y
|
4
|
380
|
31
|
0,88
|
0,78
|
150
|
2,8
|
|
8
|
∆
|
4
|
220
|
42
|
0,89
|
0,79
|
220
|
3,3
|
|
9
|
Y
|
2
|
380
|
100
|
0,91
|
0,89
|
540
|
3,1
|
|
10
|
∆
|
2
|
220
|
120
|
0,90
|
0,90
|
635
|
3,2
|
|
11
|
Y
|
3
|
380
|
70
|
0,91
|
0,84
|
432
|
3,0
|
|
12
|
∆
|
3
|
220
|
90
|
0,91
|
0,87
|
500
|
3,5
|
|
13
|
Y
|
4
|
380
|
55
|
0,90
|
0,79
|
367
|
2,8
|
|
14
|
∆
|
4
|
220
|
70
|
0,91
|
0,81
|
430
|
4,1
|
|
15
|
Y
|
4
|
380
|
55
|
0,88
|
0,77
|
171
|
2,2
|
|
16
|
∆
|
4
|
220
|
70
|
0,89
|
0,77
|
218
|
2,1
|
|
17
|
Y
|
4
|
380
|
80
|
0,89
|
0,77
|
265
|
2,3
|
|
18
|
∆
|
4
|
220
|
95
|
0,89
|
0,78
|
285
|
2,2
|
|
19
|
Y
|
4
|
380
|
130
|
0,90
|
0,80
|
320
|
2,6
|
|
20
|
∆
|
4
|
220
|
160
|
0,91
|
0,80
|
405
|
2,5
|
|
21
|
Y
|
2
|
660
|
120
|
0,90
|
0,89
|
635
|
3,2
|
|
22
|
∆
|
2
|
380
|
100
|
0,89
|
0,88
|
540
|
3,0
|
|
23
|
Y
|
3
|
660
|
52
|
0,83
|
0,84
|
380
|
3,4
|
|
24
|
∆
|
3
|
380
|
38
|
0,84
|
0,83
|
220
|
3,1
|
|
25
|
Y
|
3
|
660
|
28
|
0,85
|
0,83
|
250
|
3,3
|
Таблица 26
|
Номер группового варианта
|
1
|
2
|
3
|
4
|
5
|
|
Sном, %
|
2,5
|
3,5
|
3
|
4
|
4,5
|
МЕТОДИЧЕСКИЕ УКАЗАНИЯ И ПРИМЕР РАСЧЕТА
Решение данной задачи рассматривается при следующих исходных данных: Pном=21 кВт; Uном=380 В; 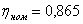 ;
; 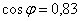 ;
; 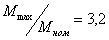 ; U2ном=114 В; Sном=0,025; p=3, обмотка статора соединена звездой. Это решение
осуществляется следующим образом.
; U2ном=114 В; Sном=0,025; p=3, обмотка статора соединена звездой. Это решение
осуществляется следующим образом.
Определяются критические скольжения, относящиеся к естественной и второй
искусственной характеристикам. Критическое скольжение, относящееся к
естественной характеристике.
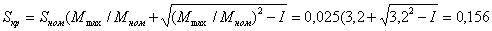
Критическое
скольжение, относящееся к второй искусственной характеристике, 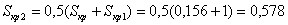 .
.
Определяются
частота вращения поля статора и номинальная частота вращения ротора
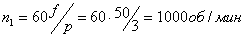 ;
;
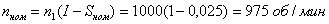
Определяются
номинальный и максимальный моменты на валу
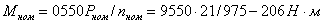 ;
;
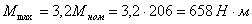 .
.
Определяется
номинальные фазные напряжения и ток статора:
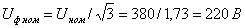 ;
;
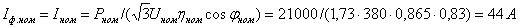
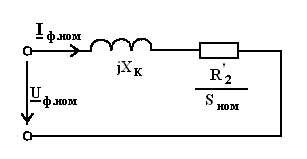
Рисунок
40
Составляется
схема замещения двигателя при номинальном режиме работы (рисунок 40) и на
основе ее определяются приведенное активное сопротивление 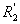 и индуктивное сопротивление двигателя при опыте
короткого замыкания
и индуктивное сопротивление двигателя при опыте
короткого замыкания 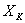 .
.
Полное
сопротивление 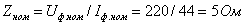 . Полное сопротивление Zном,
индуктивное сопротивление XК и активное сопротивление
. Полное сопротивление Zном,
индуктивное сопротивление XК и активное сопротивление 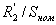 связаны уравнением
связаны уравнением 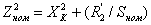 ,
учитывая, что для упрощенной схемы замещения
,
учитывая, что для упрощенной схемы замещения 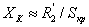 ,
получаем:
,
получаем: 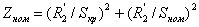 . После подстановки числовых значений данное уравнение
принимает вид:
. После подстановки числовых значений данное уравнение
принимает вид: 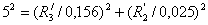 . Решив данное уравнение получаем:
. Решив данное уравнение получаем: 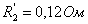 . В связи с этим
. В связи с этим 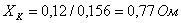 .
.
Составляется
схема замещения двигатель с пусковым реостатом (рисунок 41) и на ее основе
определяются приведенные сопротивления пусковых резисторов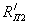 и
и 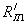 . При
включении в цепь ротора верхней ступени пускового реостата (рисунок 39) в схему
замещения добавляется резистор
. При
включении в цепь ротора верхней ступени пускового реостата (рисунок 39) в схему
замещения добавляется резистор 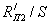 (рисунок
41). Данному состоянию схемы соответствует уравнение
(рисунок
41). Данному состоянию схемы соответствует уравнение 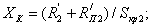
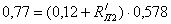 , решив
второе уравнение получаем
, решив
второе уравнение получаем 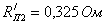 . При включении в цепь ротора обеих ступеней реостата
в схему замещения добавляются два резистора:
. При включении в цепь ротора обеих ступеней реостата
в схему замещения добавляются два резистора: 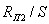 ,
, 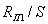 . Данному состоянию системы соответствует уравнение:
. Данному состоянию системы соответствует уравнение: 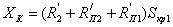 ;
; 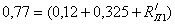 , решив
которое получаем
, решив
которое получаем 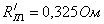 .
.
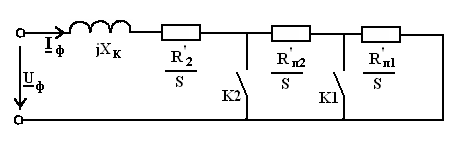
Рисунок 41
Определяются
фазное напряжение обмотки ротора 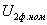 ,
коэффициент трансформации двигателя K и сопротивление пусковых
реостатов
,
коэффициент трансформации двигателя K и сопротивление пусковых
реостатов 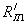 и
и 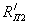 :
:
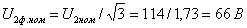 ;
; 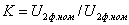 =220/66=1,93;
=220/66=1,93;
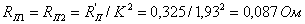
Определяются
пусковые токи и моменты для каждой характеристики
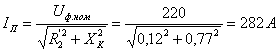 ;
;
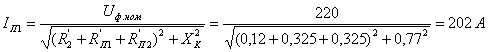 ;
;
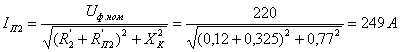 ;
;
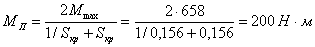 ;
;
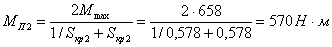 ;
;
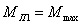
Строятся
графики зависимостей M(S) (рисунок 42).
Графическим
путем определяются скольжения Sном1 и Sном2, которые будет иметь двигатель, работая согласно
характеристикам M(S)1 и M(S)2 с моментом на валу, равным номинальному. При этом
получилось: Sном1=0,32; и Sном2=0,17.
Определяются
частоты вращения nном1, nном2 и тока статора Iном1, Iном2,
соответствующие скольжениям Sном1 и Sном2:
 ;
;
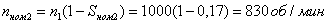 ;
;
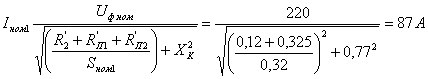 ;
;
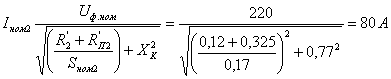 ;
;
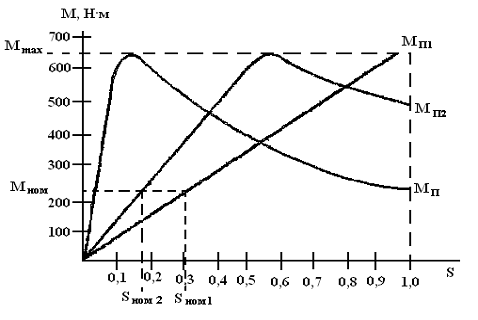
Рисунок 42
Для удобства анализа и использования значения найденных в процессе
решения задачи величин приводятся в таблице 27.
Таблица 27
|
Наименования величин, их
обозначения и единицы измерения
|
Характеристики М в значения
величин, относящихся к ним
|
|
M(S)1
|
M(S)2
|
M(З)
|
|
Критические скольжения
Sкр1, Sкр2, Sкр
|
1
|
0,578
|
0,156
|
|
Пусковые моменты Mп1, Mп2,
Mп, Н·м
|
658
|
570
|
200
|
|
Пусковые токи Iп1, Iп2, Iп,
А
|
202
|
249
|
282
|
|
Величины, соответствующие
номинальному моменту на валу :
|
0,32
|
0,17
|
0,025
|
|
б) частоты вращения ротора
nном1, nном2, nном, об/мин
|
680
|
830
|
975
|
|
в) токи статора Iном1,
Iном2, Iном, А
|
87
|
80
|
45,2
|
ЗАДАЧА 14. Расчет характеристик двигателя
постоянного тока параллельного возбуждения
Рассчитать и построить механические характеристики двигателя, указанные в
таблице 28. Знак «Х» в ней означает, что данный контакт замкнут. Схема электрической
цепи двигателя приведена на рисунке 43. Исходные данные к расчету приведены в
таблицах 29 и 30.
Этими
данными являются: напряжение двигателя  ,
номинальная мощность
,
номинальная мощность  , номинальная частота вращения якоря
, номинальная частота вращения якоря 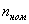 , номинальный коэффициент полезного действия
, номинальный коэффициент полезного действия 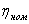 , сопротивление обмотки якоря
, сопротивление обмотки якоря 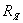 , сопротивление обмотки возбуждения
, сопротивление обмотки возбуждения 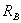 , кратность пускового момента
, кратность пускового момента 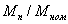 , ток возбуждения
, ток возбуждения 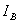 в
процентах от
в
процентах от 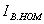 , поток возбуждения
, поток возбуждения 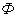 в
процентах от
в
процентах от 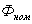 . Естественная характеристика
. Естественная характеристика 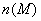 получается при номинальном возбуждении:
получается при номинальном возбуждении: 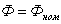 . Первая реостатная механическая характеристика
. Первая реостатная механическая характеристика 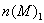 должна обеспечивать пусковой момент, значение
которого указанно в таблице 30.
должна обеспечивать пусковой момент, значение
которого указанно в таблице 30.
Вторая
реостатная механическая характеристика 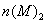 должна
занимать среднее положение между характеристиками
должна
занимать среднее положение между характеристиками 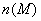 и
и 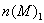 . Первая
полюсная механическая характеристика
. Первая
полюсная механическая характеристика 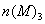 получается
при
получается
при 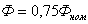 , а вторая
, а вторая 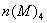 при
при 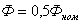 . При определении тока возбуждения по заданному
магнитному потоку следует пользоваться вебер-амперной характеристикой магнитной
цепи двигателя, приведенной в таблице 31. График этой характеристики необходимо
представить в данной работе.
. При определении тока возбуждения по заданному
магнитному потоку следует пользоваться вебер-амперной характеристикой магнитной
цепи двигателя, приведенной в таблице 31. График этой характеристики необходимо
представить в данной работе.
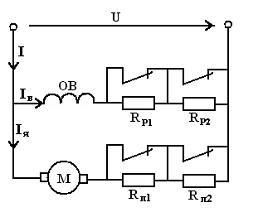
Рисунок 43
При расчете реакцией якоря следует пренебречь.
Пуск
двигателя начинается согласно первой реостатной характеристике, т.е. 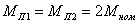 .
.
Таблица 28
|
Условное обозначение и
наименование характеристики
|
Контакты и их положение
|
|
K1
|
K2
|
K3
|
K4
|
|
n(M) - естественная
механическая характеристика
|
X
|
X
|
X
|
X
|
|
n(M)1 - первая реостатная
механическая характеристика
|
|
|
X
|
X
|
|
n(M)2 - вторая реостатная механическая
характеристика
|
X
|
|
X
|
X
|
|
n(M)3 - первая полюсная
механическая характеристика
|
X
|
X
|
|
X
|
|
n(M)4 - вторая полюсная
механическая характеристика
|
X
|
X
|
|
|
Таблица 29
|
Номер личного варианта
|
Uном, В
|
Pном, кВт
|
nном, об/мин
|
ηном, %
|
Rя, Ом
|
Rв, Ом
|
|
1
|
110
|
1,0
|
3000
|
77
|
1,20
|
220
|
|
2
|
110
|
1,5
|
3000
|
76
|
0,80
|
160
|
|
3
|
110
|
2,2
|
3000
|
80
|
0,48
|
110
|
|
4
|
110
|
3,2
|
3000
|
78
|
0,34
|
80
|
|
5
|
110
|
4,5
|
1500
|
80
|
0,23
|
70
|
|
6
|
220
|
6,0
|
1500
|
82
|
0,62
|
220
|
|
7
|
220
|
8,0
|
3000
|
83
|
0,44
|
110
|
|
8
|
220
|
11,0
|
1500
|
84
|
0,31
|
185
|
|
9
|
220
|
14,0
|
1500
|
86
|
0,21
|
135
|
|
10
|
220
|
19,0
|
1500
|
84
|
0,16
|
110
|
|
11
|
220
|
3,8
|
1025
|
86
|
1,20
|
180
|
|
12
|
220
|
13,5
|
1225
|
86
|
0,21
|
33
|
|
13
|
115
|
14,0
|
1000
|
82
|
0,11
|
50
|
|
14
|
110
|
34,5
|
1100
|
86
|
0,04
|
27
|
|
15
|
220
|
4,3
|
1025
|
84
|
1,16
|
75
|
|
16
|
110
|
1,0
|
1240
|
85
|
0,80
|
210
|
|
17
|
220
|
5,2
|
960
|
83
|
1,50
|
150
|
|
18
|
110
|
4,5
|
1400
|
86
|
0,60
|
60
|
|
19
|
220
|
8,1
|
1600
|
86
|
0,94
|
120
|
|
20
|
220
|
8,6
|
1100
|
87
|
0,45
|
110
|
|
21
|
110
|
1,2
|
850
|
85
|
1,90
|
200
|
|
22
|
110
|
2,6
|
940
|
84
|
0,70
|
80
|
|
23
|
220
|
3,8
|
1350
|
85
|
0,82
|
200
|
|
24
|
110
|
1,1
|
1450
|
83
|
1,40
|
220
|
|
25
|
220
|
5,2
|
1025
|
86
|
0,74
|
258
|
Таблица 30
|
Номер группового варианта
|
1
|
2
|
3
|
4
|
5
|
|
Кратность пускового момента
Мп/Мном
|
2,0
|
2,4
|
1,8
|
2,2
|
1,6
|
Таблица 31
|
Ток возбуждения Iв
в процентах от Iном.в
|
0
|
20
|
40
|
60
|
80
|
100
|
120
|
150
|
|
Поток возбуждения Ф в
процентах от Фном
|
5
|
45
|
73
|
88
|
95
|
100
|
103
|
107
|
МЕТОДИЧЕСКИЕ УКАЗАНИЯ И ПРИМЕР РАСЧЕТА
Решение
данной задачи рассматривается при следующих исходных данных: 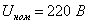 ;
; 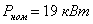 ;
; 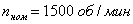 ;
; 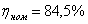 ;
; 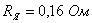 ;
; 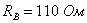 ;
; 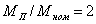 . Это решение осуществляется следующим образом.
. Это решение осуществляется следующим образом.
Определяются
величины, относящиеся к естественной характеристике двигателя при номинальном
режиме работы, а именно: номинальная мощность, потребляемая двигателем от сети
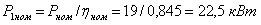 ;
номинальный ток двигателя
;
номинальный ток двигателя
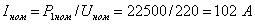 ;
номинальный ток возбуждения
;
номинальный ток возбуждения
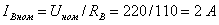 ;
номинальный ток якоря
;
номинальный ток якоря
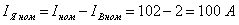 ;
номинальное напряжение ЭДС
;
номинальное напряжение ЭДС
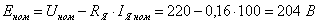 ;
номинальный момент на валу
;
номинальный момент на валу
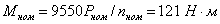
Определяются
числовые значения величин CeФном, СмФном и СеСмФном2, которые широко используются
как вспомогательные величины при дальнейшем решении задачи. Величина CeФном
определяется из уравнения номинальной ЭДС: 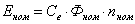 , из
которого получаем:
, из
которого получаем: 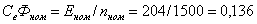 .
.
Величина
CмФном определяется из уравнения номинального момента 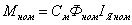 , из которого получаем:
, из которого получаем: 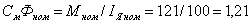 .
Величина
.
Величина 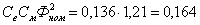 .
.
Так
как характеристики n(M), n(M)1, n(M)2 получаются при одном и том же потоке возбуждения
Фном, то частоты вращения якоря при холостом ходе двигателя nx, nx1, nx2,
относящиеся к этим характеристикам, оказываются равными. Частота вращения nx
определяется из уравнения естественной механической характеристики при холостом
ходе двигателя: 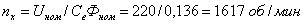 .
.
График
естественной механической характеристики n(M)
проходит через точку nx и точку с координатами Mном, nном
(рис. 44).
График
первой реостатной механической характеристики n(M)1
проходит через точку nx и точку MП, так как пуск двигателя
начинается согласно этой характеристике: 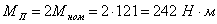 . По
этому графику определяется частота вращения якоря nном1, которую
будет иметь двигатель, работая согласно данной характеристике с моментом на
валу, равным номинальному. Получилось
. По
этому графику определяется частота вращения якоря nном1, которую
будет иметь двигатель, работая согласно данной характеристике с моментом на
валу, равным номинальному. Получилось 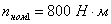 .
.
График
второй реостатной механической характеристики n(M)2
проходит через точку nx и по условию задачи занимает среднее положение между
характеристиками n(M) и n(M)1. При этом условии частота вращения nном2,
которую будет иметь двигатель, работая согласно характеристике n(M)2 с
моментом на валу, равным номинальному, определяется как среднее арифметическое
от nном и nном1:
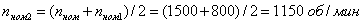
График первой полюсной механической характеристики n(M)3 проходит через точку nх3 и точку с координатами Mном; nном3.
Частота вращения якоря nx3,
которую будет иметь двигатель, работая на холостом ходу согласно данной
характеристике, определяется по формуле
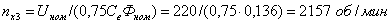
Частота
вращения якоря nном3, которую будет иметь двигатель, работая согласно
данной характеристике с моментом на валу, равным номинальному, определяется из
уравнения данной механической характеристики
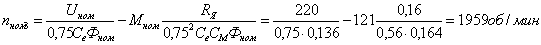
График
второй полюсной механической характеристики 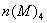 проходит
через точку
проходит
через точку 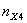 и точку с координатами
и точку с координатами 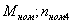 .
.
Частота
вращения якоря 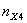 , которую имеет двигатель, работая на холостом ходу
согласно данной характеристике определяется по формуле
, которую имеет двигатель, работая на холостом ходу
согласно данной характеристике определяется по формуле 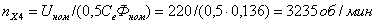 . Частота вращения якоря
. Частота вращения якоря 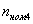 , которую будет иметь двигатель, работающий согласно
этой характеристике с моментом на валу, равным номинальному, определяется из
уравнения данной механической характеристики
, которую будет иметь двигатель, работающий согласно
этой характеристике с моментом на валу, равным номинальному, определяется из
уравнения данной механической характеристики
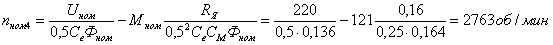
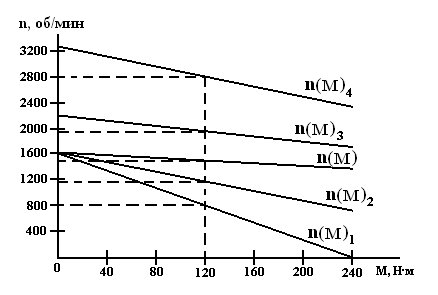
Рисунок 44
Графики механических характеристик, построенные согласно полученным
данным, приведены на рисунке 44.
Сопротивление пускового резистора RП2 определяется из уравнения второй реостатной механической
характеристики двигателя при моменте на валу, равном нмоинальному
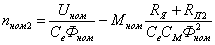 ;
; 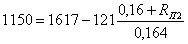 ;
;
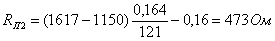 .
.
Сопротивление
пускового реостата RП1 определяется из уравнения первой реостатной
механической характеристики двигателя при моменте на валу, равном номинальному
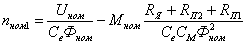 ;
; 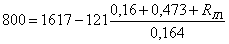 ;
;
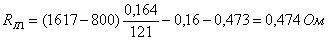
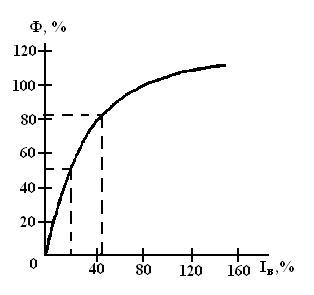
По
данным таблице 31 строится вебер-амперная характеристика двигателя (рисунок 45)
и посредством ее определяются значения токов возбуждения IВ3 и
IВ4 в процентах от IВ.НОМ при
работе двигателя согласно характеристикам n(M)3 и
n(M)4. Они получились равными 44 и 22% соответсвтенно.
Значения этих токов в амперах равны: IВ3=0,84 А и IВ4=0,44
А.
Сопротивление
резистора RП1 определяется из уравнения электрического состояния
цепи возбуждения, относящегося к первой полюсной характеристике: 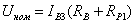 , из которого получается:
, из которого получается: 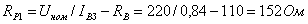 .
.
Сопротивление
резистора RР2 определяется из уравнения электрического состояния
, относящегося ко второй полюсной характеристике:  , из которого получается:
, из которого получается: 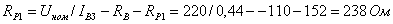 .
.
Библиографический список
1. Болынский
Б.А., Зейн Е.Н., Шатерников В.Е. Электротехника. - М.: Энергоатомиздат, 1987. -
528 с.
2. Электротехника
/ под ред. Е.Г. Герасимова. - М.: Высш. Школа, 1985. - 480 с.
. Борисов
Ю.М., Липатов Д.Н., Зорин Ю.Н. Электротехника. - М.: Энергоатомиздат, 1985 -
550 с.
. Сборник
задач по электротехнике и основам электроники /Под ред. В.Г. Герасимова. - М.:
Высш. Школа, 1987. - 286 с.