Методы оценок неизвестных параметров распределения

Федеральное агентство по образованию РФ

Дагестанский Государственный Университет

Математический факультет

Кафедра информатики и вычислительной техники

Курсовая работа

На тему:

"Методы оценок неизвестных параметров распределения"

Выполнила: студентка 3 курса 5 группы

Тажудинова П.Г.

Руководитель: Магомедов И.И.

Махачкала 2008 г.

Содержание

Введение

1. Нормальное распределение на прямой

2. Нормальная кривая

3. Влияние параметров нормального распределения на форму нормальной кривой

4. Вероятность отклонения в заданный интервал нормальной случайной величины

5. Вычисление вероятности заданного отклонения

6. Правило трех сигм

7. Равномерное распределение

8. Задачи

Литература

Введение

Исходным объектом статистических исследований является выборка

 ,

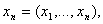
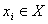Из распределения 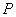, которое полностью или частично неизвестно.

В математической статистике традиционно выделяют в качестве основных два следующих класса задач:

1.       Оценка неизвестных параметров.

2.       Проверка статистических гипотез.

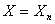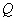Задачи первого класса возникают, когда по выборке  нужно оценить какую-нибудь неизвестную числовую характеристику  распределения Р (оно ведь неизвестно).

То есть, для заданного функционала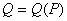

От распределения Р мы должны указать функцию от выборки (или, что то же, статистику)

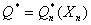
Предназначенную для использования вместо параметра 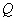 в качестве его приближения.

Статистику 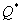 называют оценкой параметра 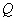. Разумеется, оценок для параметра  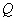может быть очень много. Для оценки функционал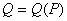а  вида

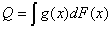
естественно использовать статистику

.

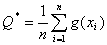Но можно, конечно, рассматривать и другие оценки, скажем,

,

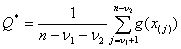где  - элементы вариационного ряда и т.д. в качестве 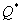 можно брать и значения, не зависящие от выборки.

Часто в постановке задач об оценивании содержится указания на то, каким является множество 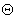возможных значений параметра 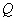. Например, если оценивается доля  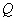какого-нибудь минерала в руде, то ясно, что.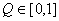

Качественной разницы между задачами первого класса (теории оценок) и второго класса (проверка статистических гипотез) не существует.

Основные законы распределения:

1.       Биномиальный закон распределения.

Определение. Дискретная случайная величина Х имеет биномиальный закон

Распределения с параметрами n и p, если она принимает

значения 0,1,2,…,m,…,n с вероятностями

,

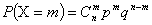где 0<p<1, .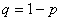

. Закон распределения Пуассона

Определение. Дискретная случайная величина Х имеет закон распределения

Пуассона с параметром 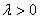, если она принимает значения

,1,2,…,m,… (бесконечное но счетное множество значений) с

вероятностями

.

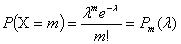. Геометрическое распределение

Определение. Дискретная случайная величина Х=m имеет геометрическое

распределение с параметром 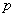, если она принимает значения

,2,…,m… (бесконечное, но счетное множество значений) с

вероятностями

,

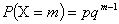где 0<p<1, .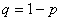

. Гипергеометрическое распределение

Определение. Дискретная случайная величина Х имеет гипергеометрическое

распределение с параметрами n, M, N, если она принимает

значения 0,1,2,…,m,…, min (n,M) с вероятностями

,

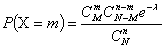где 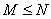, ; n,M,N - натуральные числа.

. Равномерный закон распределения

Определение. Непрерывная случайная величина Х имеет равномерный закон

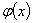 постоянна на этом отрезке и равна нулю вне его, т.е.

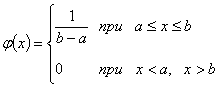
. Показательный (экспоненциальный) закон распределения

Определение. Непрерывная случайная величина Х имеет показательный (экспоненциальный) закон распределения с параметром 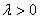, если ее плотность вероятности имеет вид:

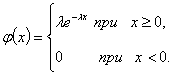
. Нормальный закон распределения

Определение. Непрерывная случайная величина Х имеет нормальный закон распределения (закон Гаусса) с параметрам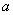и  и 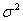, если ее плотность вероятности имеет вид:

.

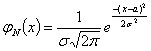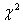.  - распределение.

Определение. Распределением 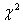 (хи-квадрат) с 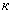степенями свободы называется распределение суммы квадратов 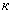независимых случайных величин, распределенных по стандартному нормальному закону, т.е.

,

где 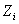 (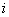=1,2,… ) имеет нормальное распределение N (0;1).

. Распределение Стьюдента.

Определение. Распределение Стьюдента (или t-распределением) называется распределение случайной величины

,

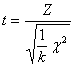где Z - случайная величина, распределенная по стандартному нормальному закону, т.е. N (0; 1);

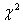 - независимая от Z случайная величина, имеющая 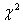 - распределение с 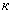степенями свободы.

. Распределение Фишера-Снедекора.

Определение. Распределение Фишера-Снедекора (или F-распределением) называемся распределение случайной величины

,

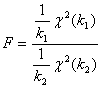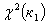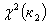где  и  - случайные величины, имеющие 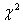-распределение соответственно с  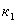и 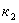 степенями свободы.

параметр распределение нормальная кривая

1. Нормальное распределение на прямой

Нормальным называют распределение вероятностей непрерывной случайной величины, которое описывается плотностью

.

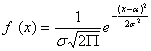Нормальное распределение определяется двумя параметрам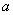и:  и 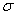. Достаточно знать эти параметры, чтобы задать нормальное распределение. Покажем, что вероятностный смысл этих параметров таков: 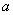 есть математическое ожидание,  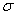- среднее квадратическое отклонение нормального распределения.

а) По определению математического ожидания непрерывной случайной величины,

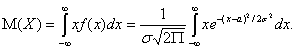
Введем новую переменную 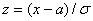. Отсюда 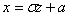, 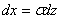. Приняв во внимание, что новые пределы интегрирования равны старым, получим

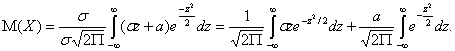
Первое из слагаемых равно нулю (под знаком интеграла нечетная функция; пределы интегрирования симметричны относительно начала координат). Второе из слагаемых равно 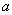 (интеграл Пуассона ).

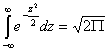Итак, 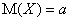, т.е. математическое ожидание нормального распределения равно параметру .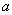

б) По определению дисперсии непрерывной случайной величины, учитывая, что 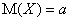, имеем

.

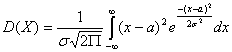Введем новую переменную 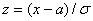. Отсюда 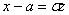, 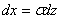. Приняв во внимание, что новые пределы интегрирования равны старым, получим

.

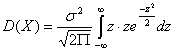Интегрирую по частям, положив 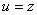, , 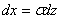найдем

.

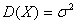Следовательно,

.

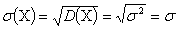Итак, среднее квадратическое отклонение нормального распределения равно параметру .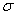

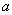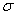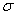Общим называют нормальное распределение с произвольными параметрами  и  (>0).

Нормированным называют нормальное распределение с параметрами  и .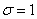

Плотность нормированного распределения

.

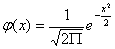Функция 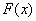общего нормального распределения

,

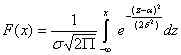А функция нормированного распределения

.

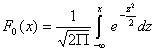Вероятность попадания нормированной нормальной величины X в интервал (0,x) можно найти, пользуясь функцией Лапласа

.

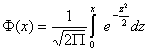Действительно

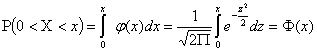
Учитывая, что 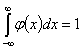 и, следовательно, в силу симметрии  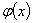относительно нуля 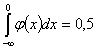, а значить, и ,

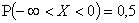Легко получить, что .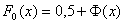

Действительно,

.

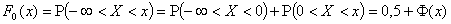2. Нормальная кривая

График плотности нормального распределения называют нормальной кривой (кривая Гаусса).

Исследуем функцию

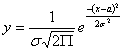
Методами дифференциального исчисления.

1.       Очевидно, функция определена на всей оси .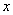

2.       При всех значениях 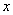 функция принимает положительные значения, т.е. нормальная кривая расположена над осью .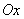

.        Предел функции при неограниченном возрастании 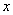 (по абсолютной величине) равен нулю: 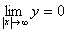, т.е. ось  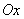служит горизонтальной асимптотой графика.

.        Исследуем функции на экстремум. Найдем первую производную:

.

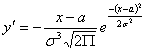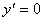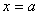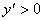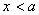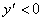Легко видеть, что  при ,  при ,  при .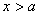

Следовательно, при 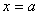функция имеет максимум равный .

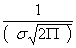.        Равность 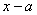содержится в аналитическом выражении функции в квадрате, т.е. график функции симметричен относительно прямой .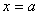

.        Исследуем функцию на точки перегиба. Найдем вторую производную:

Легко видеть, что пр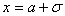и  и 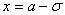 вторая производная равна нулю, а при переходе через эти точки она меняет знак (в обеих этих точках значение функции равно 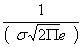). Таким образом, точки графика  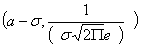и 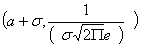 является точками перегиба.

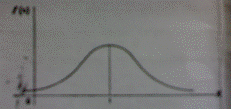
На рис. изображена нормальная кривая пр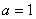и  и .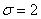

3. Влияние параметров нормального распределения на форму нормальной кривой

График функци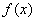и  и 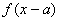 имеют одинаковую форму; сдвинув график  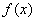в положительном направлении оси  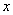на 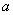 единиц масштаба при  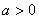или в отрицательном направлении при 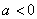, получим график 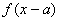. Отсюда следует, что изменение величины параметра 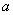 (математического ожидания) не изменяет формы нормальной кривой, а приводить лишь к ее сдвигу вдоль оси 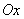: вправо, если  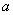возрастает, и влево, если  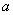убывает.

По иному обстоит дело, если изменяется параметр 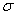 (среднее квадратическое отклонение). Максимум дифференциальной функции нормального распределения равен

.

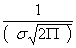Отсюда следует, что с возрастанием 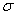 максимальная орбита нормальной кривой убывает, а сама кривая становится более пологой, т.е. сжимается к оси 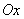; при убывании  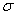нормальная кривая становится более "островершинной" и растягивается в положительном направлении оси .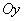

При любых значениях параметра 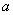 и о площадь, ограниченная нормальной кривой и осью 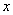, остается равной единице.

На рис. изображены нормальные кривые при различных значениях 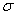 и . Чертеж наглядно иллюстрирует, как изменение параметра 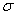 сказывается на форме нормальной кривой.

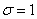При  и  нормальную кривую

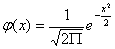
называют нормированной.

4. Вероятность отклонения в заданный интервал нормальной случайной величины

Если случайная величина X задана плотностью распределения 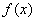, то вероятность того, что X примет значение, принадлежащее интервалу 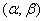, такова:

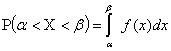
Пусть случайная величина X распределена по нормальному закону. Тогда вероятность того, что X примет значение, принадлежащее интервалу 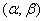, равна

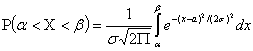
Можно преобразовать эту формулу так, чтобы можно было пользоваться готовыми таблицами. Введем новую переменную 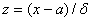. Отсюда 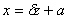, 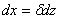. Найдем новые пределы интегрирования. Если 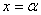, то 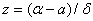; если 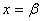, то .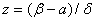

Таким образом, имеем

Пользуясь функцией Лапласа

,

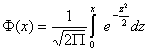окончательно получим

.

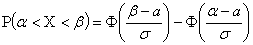5. Вычисление вероятности заданного отклонения

Часто требуется вычислить вероятность того, что отклонение нормально распределенной случайной величины X по абсолютной величине меньше заданного положительного числа 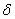, т.е. требуется найти вероятность осуществления неравенства .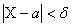

Заметим это неравенство равносильным ему двойным неравенством

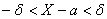, или .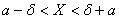

Пользуясь формулой

,

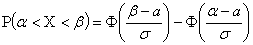получим

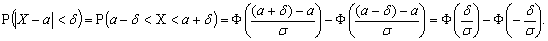
Приняв во внимание равенство 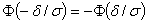 (функция Лапласа - нечетная), окончательно имеем

.

В частности, при

.

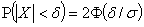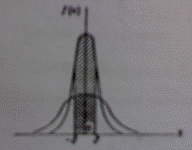
На рисунке наглядно показано, что если две случайные величины нормально распределены и , то вероятность принять значение, принадлежащее интервалу 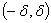, больше у той величины, которая имеет меньшее значение 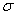. Этот факт полностью соответствует вероятностному смыслу параметра 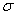 ( 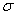есть среднее квадратическое отклонение; оно характеризует рассеяние случайной величины вокруг ее математического ожидания).

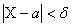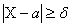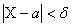События состоящие в осуществлении неравенства  и , - противоположные. Поэтому, если вероятность осуществления неравенства  равна 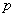, то вероятность неравенств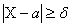а  равна .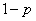

6. Правило трех сигм

Преобразуем формулу

,

положив 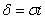. В итоге получим

.

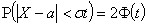Если 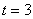 и, следовательн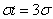о, , то

,

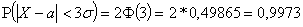т.е. вероятность то, что отклонение по абсолютной величине будет меньше утроенного среднего квадратического отклонения, равна 0,9973.

Другими словами, вероятность того, что абсолютная величина отклонения превысит утроенное среднее квадратическое отклонение, очень мала, а именно равна 0,0027. это означает, что лишь в 0,27% случаев так может произойти. Такие события исходя из принципов невозможности маловероятных событий можно считать практически невозможными. В этом и состоит сущность правила тих сигм: если случайная величина распределена нормально, то абсолютная величина ее отклонения от математического ожидания не превосходит утроенного среднего квадратического отклонения.

На практике правило трех сигм применяются так: если распределение изучаемой случайной величины неизвестно, но условие, указанное приведенном правиле, выполняются, то есть основание предполагать, что изучаемая величина распределена нормально; в противном случае она не распределена нормально.

7. Равномерное распределение

Определение. Непрерывная случайная величина Х имеет равномерный закон распределения на отрезке 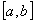, если ее плотность вероятности  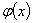постоянна на этом отрезке и равна нулю вне его, т.е.

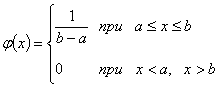
Функция распределения случайной величины Х, распределенной по равномерному закону, есть

 (*)

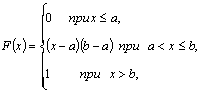ее математическое ожидание

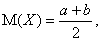
а дисперсия

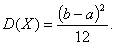
При 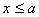 функция распределения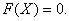

При 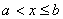 получим

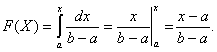
При 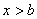 очевидно, что

т.е. формула (*) доказана.

Математическое ожидание случайной величины Х с учетом его механической интерпретации как центра массы равно абсциссе середины отрезка, т.е.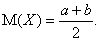

Тот же результат получается если вычислить интеграл:

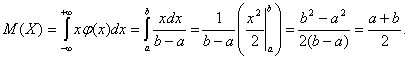
А для дисперсии имеем:

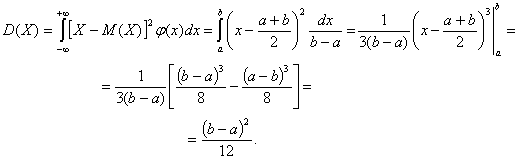
Равномерный закон распределения используется при анализе ошибок округления при проведении числовых расчетов (например, ошибка округления числа до целого распределена равномерно на отрезке [-0,5; +0,5]), в ряде задач массового обслуживания, при статистическом моделировании наблюдений, подчиненных заданному распределению. Так, случайная величина Х, распределена по равномерному закону на отрезке [0,1], называемая "случайным числом от 0 до 1", служит исходным материалом для получения случайных величин с любым законом распределения.

8. Задачи

1.       Производится измерение диаметра вала без систематических (одного знака) ошибок. Случайные ошибки измерения X подчинены нормальному закону со средним квадратическим отклонение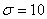м мм. Найти вероятность того, что измерение будет произведено с ошибкой, не превосходящей по абсолютной величине 15мм.

Решение.

Математическое ожидание случайных ошибок равно нулю, поэтому применима формула

По таблице находим 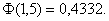 Искомая вероятность

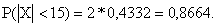
.        Автомат изготавливает шарики. Шарик считается годным, если отклонение X диаметра шарика от проектного размера по абсолютной величине меньше 0,7мм. Считая, что случайная величина X распределена нормально со средним квадратическим отклонением 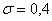мм, найти, сколько в среднем будет годных шариков среди ста изготовленных.

Решение.

Так как X - отклонение (диаметра шарика от проектного размера), то

.

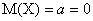Воспользовавшись формулой

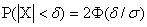, подставив 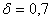, , 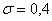получим

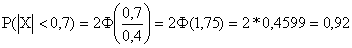
Таким образом, вероятность отклонения, меньшего 0,7мм, равна 0,92. Отсюда следует, что примерно 92 шарика из 100 окажутся годными.

.        Диаметр круга 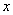 измерен приближенно, причем 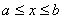,  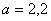и . Рассматривая диаметр как случайную величину Х, распределенную равномерно в интервале 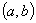, найти математическое ожидание и дисперсию площади круга.

Решение.

1. Математическое ожидание площади круга - случайной величины 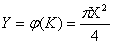 находим по формуле

.

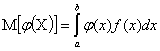Подставив 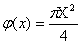, , 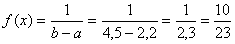получим

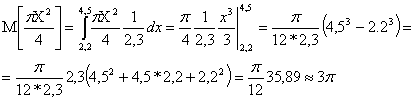
. Дисперсию площади круга находим по формуле

Подставив 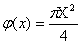, , 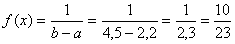получим

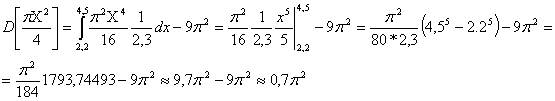
.        Полагая, что рост мужчин определенной возрастной группы есть нормально распределенная случайная величина Х с параметрам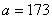и  и 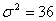, найти случайную величину Х.

Решение.

Практически достоверно, что рост мужчин данной возрастной группы заключен в границах от 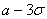 до . Найдем эти границы:

,

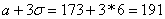 (см),

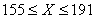т.е.  (см).

Литература

1. "Теория вероятностей и математическая статистика".В.Е. Гмурман Москва: "Высшая школа" 1998 г.

. "Руководство к решению задач по теории вероятностей и математической статистике" В.Е. Гмурман Москва: "Высшая школа" 2002 г.

. "Теория вероятностей и математическая статистика".Н.Ш. Кремер Москва: "Юнити-Дана", 2004 г.

. "Математическая статистика. Оценка параметров. Проверка гипотез". А.А. Боровков Москва: изд. "Наука" 1996 г.