Чувствительность систем управления
Содержание
1. Построение МТЧ НОУ. Ранжирование параметров
2. Построение МТЧ ДОУ к вариации интервала дискретности
3. Построение МТЧ спроектированной системы по каждому из параметров
и для значения 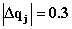 выделение
доминирующих параметров по степени их влияния на величину
выделение
доминирующих параметров по степени их влияния на величину 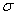 перерегулирования
и длительность
перерегулирования
и длительность 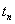 переходного
процесса
переходного
процесса
4. Построение матрицы функций модальной чувствительности и
выделение неблагоприятного сочетания вариаций параметров
5. Вычисление матриц Кg и К методом модального управления, базовый
алгоритм которого дополняется контролем нормы 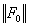 медианной составляющей
интервальной матрицы
медианной составляющей
интервальной матрицы 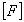 спроектированной
системы с последующим вычислением оценки
спроектированной
системы с последующим вычислением оценки 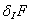
Вывод
Литература
1.
Построение МТЧ НОУ. Ранжирование параметров
Дана передаточная функция "вход-выход (ВВ)" НОУ:
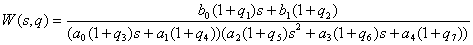 ,
,
Номинальные значения параметров: 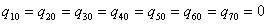
Заданные коэффициенты ПФ: 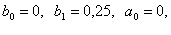
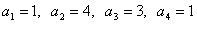 . Передаточная функция вход-выход НОУ:
. Передаточная функция вход-выход НОУ:
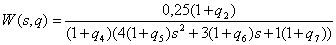
Используя канонический наблюдаемый базис векторно-матричного
описания ВСВ НОУ, получим:
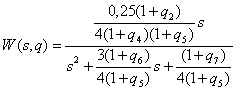
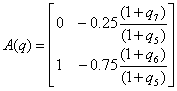 ,
,  ,
, 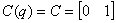 .
.
Матрицы номинального объекта управления имеют реализации:
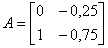 ,
, 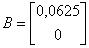 ,
, 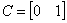 .
.
Построим семейство моделей траекторной чувствительности.
Для j-ой модели траекторной чувствительности
получим представление:
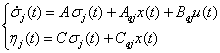
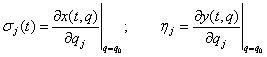
Матрицы моделей траекторной чувствительности - реализации:
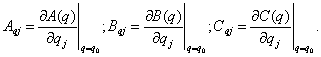
И затем, сформируем семейство агрегированных систем:
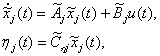 , где
, где 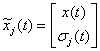 ,
, 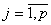 ,
,
Матрицы агрегированной системы представлены как:
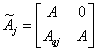 ,
, 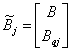 ,
, 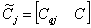 .
.
Получим:
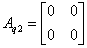 ,
, 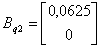 ,
,  ,
, 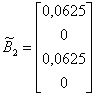 ;
;
 ,
, 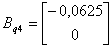 ,
,  ,
, 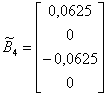 ;
;
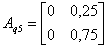 ,
, 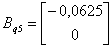 ,
,  ,
, 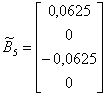 ;
;
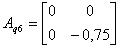 ,
, 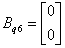 ,
,  ,
, 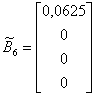 ;
;
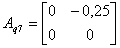 ,
, 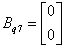 ,
,  ,
, 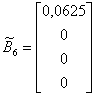 ;
;
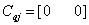 ,
, 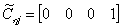
Проверим управляемость агрегированных систем по выходу 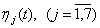 с помощью матриц управляемости
с помощью матриц управляемости 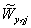 :
:
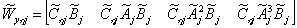 ,
,
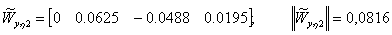
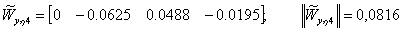
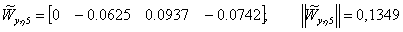
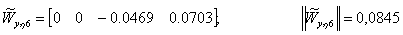
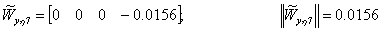
С использованием матрицы управляемости агрегированной системы
проранжируем параметры 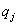 по потенциальной чувствительности:
по потенциальной чувствительности:
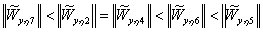
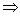
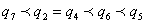
Для достижения нулевой чувствительности q5 - го параметра потребуется наименьшее число затрат; для
достижения нулевой чувствительности q7 - го
параметра - наибольшее число затрат.
Т.е. чем выше норма, тем меньше затрат на управление, и наоборот.
2. Построение
МТЧ ДОУ к вариации интервала дискретности
Задан интервал дискретности 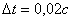 , метод перехода к дискретному векторно-матричному ВСВ описанию
объекта управления (ДОУ) - произвольный (заменой производной отношением
конечных малых.)
, метод перехода к дискретному векторно-матричному ВСВ описанию
объекта управления (ДОУ) - произвольный (заменой производной отношением
конечных малых.)
Переход к дискретному описанию ОУ осуществляется по формулам:
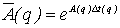 ,
, 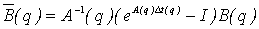 ,
, 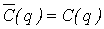 ,где
,где
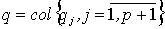 ,
,  ,
, 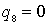 .
.
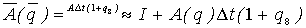 ,
, 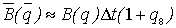 ,
,
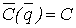 ,
,
откуда при 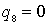 имеем:
имеем:
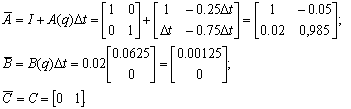
Построим модель траекторной чувствительности к вариации
интервала дискретности.
Для модели траекторной чувствительности получим
представление:
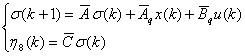
где 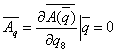 ,
, 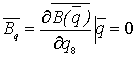 ,
,
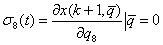 ,
, 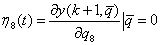 .
.
Получим:
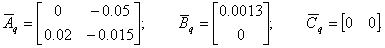
Получим агрегированную систему вида:
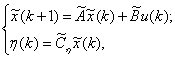 , где
, где 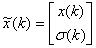 .
.
Матрицы агрегируемой системы имеют представления:
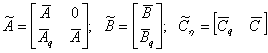 .
.
 ;
; 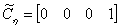 .
.
Проверим управляемость агрегированной системы по выходу 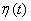 с помощью матрицы управляемости:
с помощью матрицы управляемости:
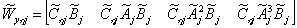 ,
,
Так как норма не равна нулю, то в данной системе существуют
структурные возможности к минимизации чувствительности неадаптивными методами
(алгоритмами) управления.
3.
Построение МТЧ спроектированной системы по каждому из параметров и для значения
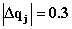 выделение доминирующих
параметров по степени их влияния на величину
выделение доминирующих
параметров по степени их влияния на величину 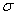 перерегулирования и
длительность
перерегулирования и
длительность 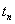 переходного процесса
переходного процесса
Закон управления (ЗУ) 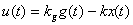 должен доставлять системе
должен доставлять системе
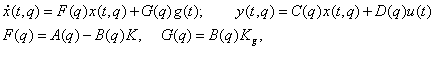
образованной соединением НОУ и ЗУ, с помощью:
матрицы 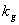 прямой связи по входу
прямой связи по входу 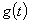 равенство входа
равенство входа 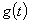 и выхода
и выхода 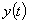 в неподвижном состоянии при номинальных значениях параметров;
в неподвижном состоянии при номинальных значениях параметров;
матрицы 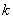 обратной связи по состоянию
обратной связи по состоянию 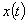 при номинальных значениях параметров
распределение мод Баттерворта с характеристической частотой
при номинальных значениях параметров
распределение мод Баттерворта с характеристической частотой 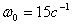 .
.
Построить МТЧ спроектированной системы по каждому из параметров и
для значения 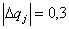 выделить доминирующие параметры по
степени их влияния на величину
выделить доминирующие параметры по
степени их влияния на величину 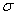 перерегулирования и длительность
перерегулирования и длительность 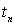 переходного процесса. Построить матрицу функций модальной
чувствительности и выделить неблагоприятное сочетание вариаций параметров.
переходного процесса. Построить матрицу функций модальной
чувствительности и выделить неблагоприятное сочетание вариаций параметров.
ОУ (из пункта 1):
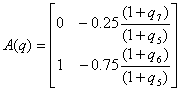 ,
, 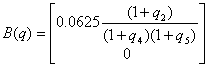 ,
, 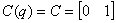 .
.
Закон управления имеет вид:
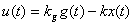 .
.
Для нахождения матриц обратной и прямой связи 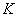 и
и 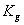 , решим матричное уравнение Сильвестра:
, решим матричное уравнение Сильвестра:
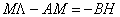 ,
,
в котором:
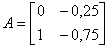 ,
, 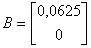 ,
, 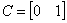 .
.
Для целей обеспечения гарантированной вычислительной устойчивости
матричных процедур решения уравнения Сильвестра матрицу 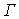 следует задавать в диагональной (блочно
диагональной) форме
следует задавать в диагональной (блочно
диагональной) форме
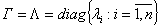 .
.
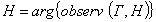
По требуемым показателям выбираем
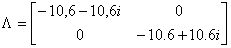 ,
, 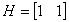
Решая матричное уравнение типа Сильвестра получаем матрицы:
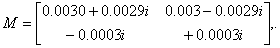
Тогда матрицу ЛСОС можно определить как:
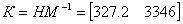

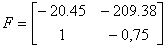
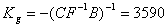
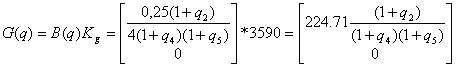
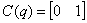 .
.
Номинальные матрицы спроектированной системы имеют реализации:

Теперь построим семейство МТЧ и агрегированных систем.
Для j-ой модели траекторной чувствительности получим
представление:
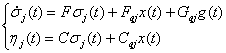 , где
, где
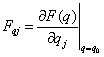 ,
, 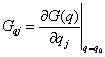 ,
, 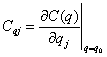
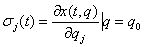 ,
, 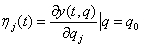 .
.
И семейство агрегированных систем:
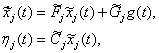 , где
, где
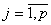 ,
, 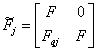 ,
, 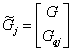 ,
, 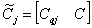 .
.
В результате расчетов сформировано:
чувствительность система управление
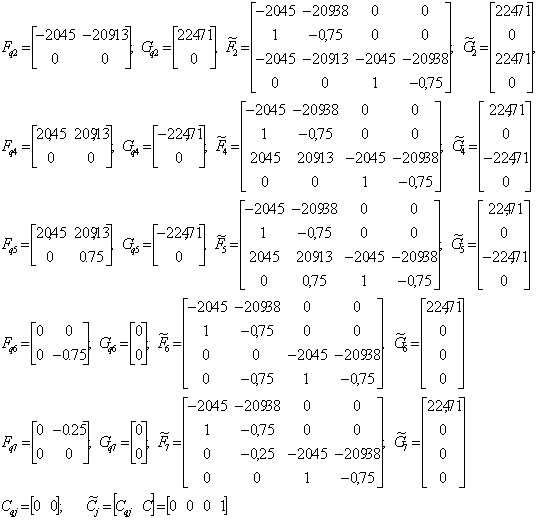
Сформируем спроектированную систему по каждому из параметров при 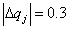 в форме:
в форме:
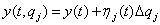 .
.
Схема моделирования агрегированной системы представлена на рисунке
3.1.
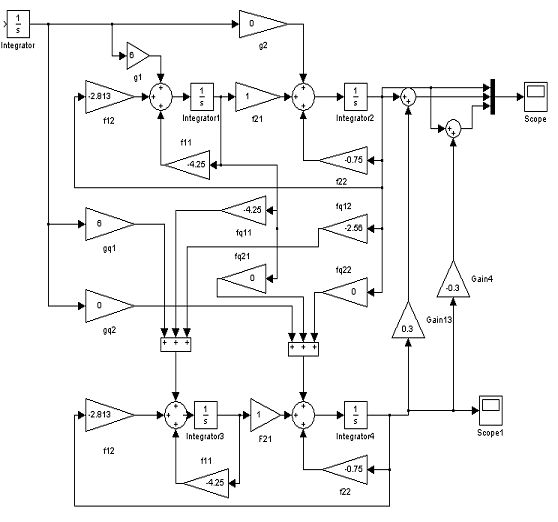
Рисунок 3.1 - схема моделирования агрегированной системы:
номинального объекта управления и модели траекторной чувствительности к
вариации одного из параметров (q2)
Исследуем влияние вариации каждого из параметров по графикам,
на которых приведем переходные характеристики номинальной и возмущенной систем.
Графики представлены на рисунке 3.2 - 3.5.
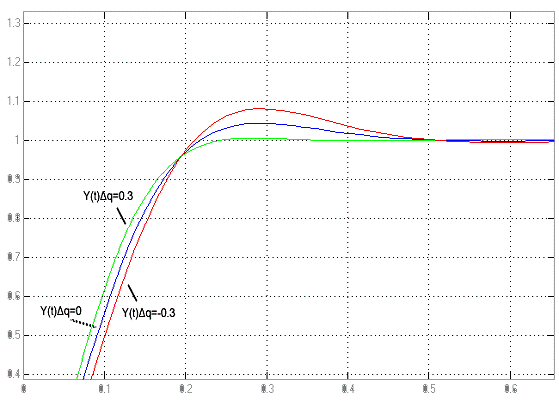
Рисунок 3.2 - Графики переходных процессов системы при 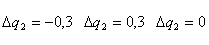
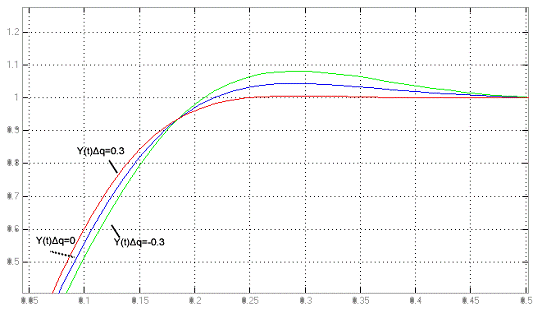
Рисунок 3.3 - Графики переходных процессов системы при 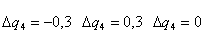
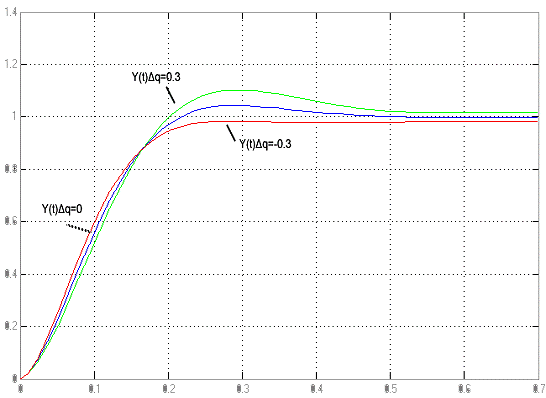
Рисунок 3.4 - Графики переходных процессов системы при 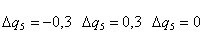
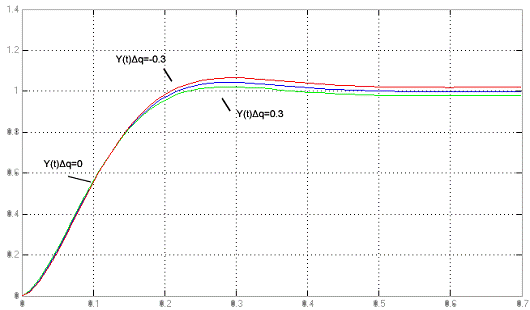
Рисунок 3.5 - Графики переходных процессов системы при 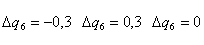
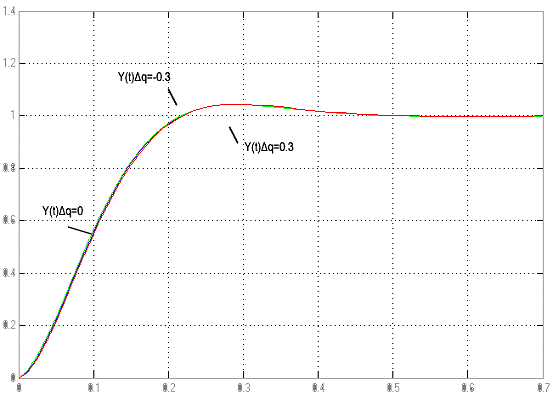
Рисунок 3.6 - Графики переходных процессов системы при 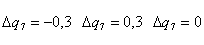
Обозначим:
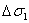 - разница между
- разница между  и
и 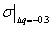 ;
;
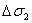 - разница между
- разница между  и
и 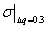 ;
;
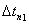 - разница между
- разница между 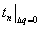 и
и 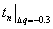 ;
;
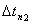 - разница между
- разница между 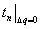 и
и 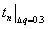 .
.
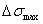 ,
, 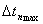 - максимальные из этих значений.
- максимальные из этих значений.
Определим степень влияния каждого из параметров на качественные
характеристики переходных процессов:
j=2: 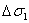 =5%;
=5%; 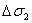 =4%;
=4%; 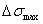 =5%;
=5%; 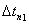 =0.05с;
=0.05с; 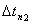 =0.2с;
=0.2с; 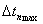 =0.2с.
=0.2с.
j=4: 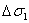 =5%;
=5%; 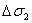 =4%;
=4%; 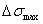 =5%;
=5%; 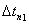 =0.02с;
=0.02с; 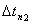 =0.2;
=0.2; 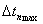 =0.2с.
=0.2с.
j=5: 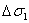 =6%;
=6%; 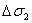 =4%;
=4%; 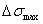 =6%;
=6%; 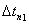 =0.03с;
=0.03с; 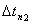 =0.2;
=0.2; 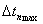 =0.2с.
=0.2с.
j=7: - отличия отсутствуют
Доминирующими параметрами по степени влияния на величину
перерегулирования σ являются параметры 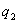 и
и 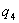 .
.
Доминирующим параметром на длительность переходного процесса 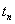 является параметр
является параметр 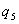 .
.
4. Построение
матрицы функций модальной чувствительности и выделение неблагоприятного
сочетания вариаций параметров
Получим спектр собственных значений
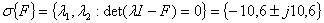 .
.
Составим матрицу Вандермонда:
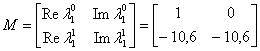 .
.
Вычислим функции модальной чувствительности 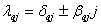 (
(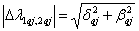 ) с помощью соотношений:
) с помощью соотношений:
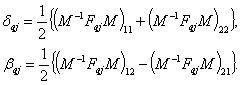
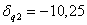 ,
,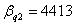 ;
;
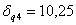 ,
,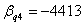 ;
;
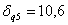 ,
,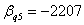 ;
;
 ,
,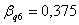 ;
;
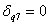 ,
,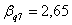 .
.
Сконструируем матрицу функций модальной чувствительности в виде
функций чувствительности вещественной и мнимой частей:
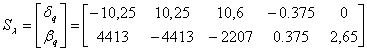 , где
, где 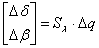
По нормам столбцов выделяем доминирующие параметры:
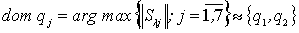
Для выделения неблагоприятного сочетания вариаций параметров
воспользуемся сингулярным разложением матрицы модальной чувствительности:
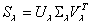
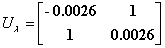 ,
,  ,
,
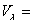
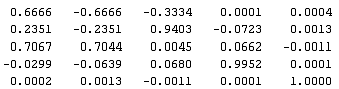
Вектор наиболее неблагоприятного сочетания параметров может быть
сформирован так:
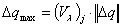 , где
, где 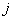 -й столбец матрицы
-й столбец матрицы  соответствует максимальному сингулярному
числу.
соответствует максимальному сингулярному
числу.
Таким образом:
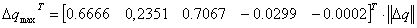
5. Вычисление матриц Кg и К методом модального управления, базовый
алгоритм которого дополняется контролем нормы 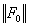 медианной составляющей
интервальной матрицы
медианной составляющей
интервальной матрицы 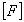 спроектированной системы с последующим вычислением
оценки
спроектированной системы с последующим вычислением
оценки 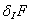
Дано ВМО ВСВ НОУ с интервальными матричными компонентами в
форме:
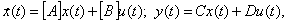
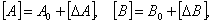
получаемое с использованием интервальной арифметики на основе
интервальной реализации параметров 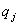 , записываемых в форме
, записываемых в форме
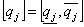
при следующих граничных (угловых) значениях: 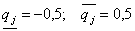
Закон управления (ЗУ): 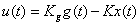 должен доставлять системе с интервальными матричными компонентами
должен доставлять системе с интервальными матричными компонентами
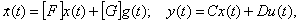
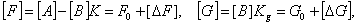
образованной объединением НОУ и ЗУ, с помощью:
матрицы 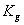 прямой связи по входу
прямой связи по входу 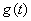 равенство входа
равенство входа 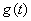 и выхода
и выхода 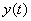 в неподвижном состоянии при медианных значениях параметров;
в неподвижном состоянии при медианных значениях параметров;
матрицы 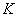 обратной связи по состоянию
обратной связи по состоянию 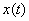 при медианных значениях параметров
распределение мод Баттерворта с характеристической частотой
при медианных значениях параметров
распределение мод Баттерворта с характеристической частотой 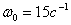 , которая гарантирует достижение оценки
относительной интервальности матрицы состояния системы
, которая гарантирует достижение оценки
относительной интервальности матрицы состояния системы
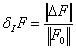
не больше заданной 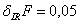 . Методом модального управления, базовый алгоритм которого,
опирающийся на решение матричного уравнения Сильвестра и примененный к
медианным составляющим интервальных матричных компонентов ВМО ВСВ НОУ,
дополняется контролем нормы
. Методом модального управления, базовый алгоритм которого,
опирающийся на решение матричного уравнения Сильвестра и примененный к
медианным составляющим интервальных матричных компонентов ВМО ВСВ НОУ,
дополняется контролем нормы 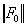 медианной составляющей интервальной матрицы
медианной составляющей интервальной матрицы 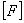 спроектированной системы с последующим
вычислением оценки
спроектированной системы с последующим
вычислением оценки 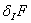 , вычислить матрицы
, вычислить матрицы 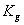 и
и 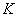 . ВМО ВСВ интервального ОУ (из пункта 1):
. ВМО ВСВ интервального ОУ (из пункта 1):
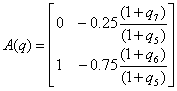 ,
, 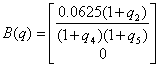 ,
, 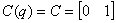 .
.
В примечании к заданию рекомендуется преобразовать систему так,
чтобы интервальной была бы только матрица состояния.
Для этого введем третью переменную состояния 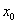 и новое входное воздействие
и новое входное воздействие 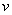 :
:
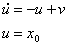
Изначально:
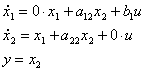
После преобразования:
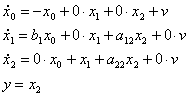
Таким образом, матрицы описания ОУ принимают вид:
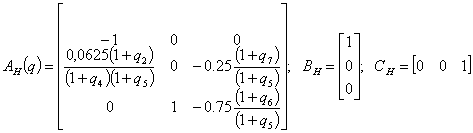
Определим угловые значения матрицы 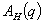 . Очевидно, что элементы матрицы
. Очевидно, что элементы матрицы 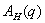 примут: максимальные значения при:
примут: максимальные значения при: 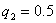 и
и 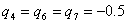 , минимальные значения при:
, минимальные значения при: 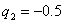 и
и 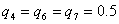 .
.
Остается лишь сравнить значения матрицы при 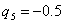 и
и 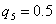 .
.
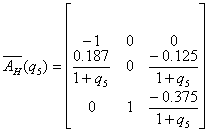 при
при 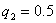 ,
, 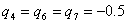
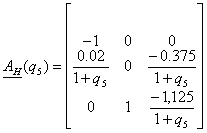 при
при 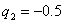 ,
, 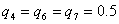
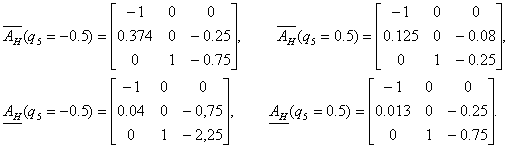
Граничные значения матрицы 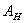 получим, скомпоновав экстремальные значения каждой составляющей
матрицы
получим, скомпоновав экстремальные значения каждой составляющей
матрицы 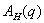 :
:
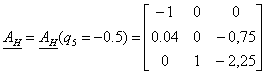 ,
, 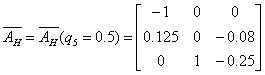 .
.
Необходимо отметить, что полученные граничные значения
интервальной матрицы 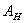 физически не реализуемы, то есть элементы
матрицы не могут принять одновременно указанные экстремальные значения. Другими
словами, здесь неизбежно закладывается избыточность в задании матрицы.
физически не реализуемы, то есть элементы
матрицы не могут принять одновременно указанные экстремальные значения. Другими
словами, здесь неизбежно закладывается избыточность в задании матрицы.
Это сделано формально с тем, чтобы все реализации матрицы
ограничивались указанными значениями.
Далее, найдём медианное значение как среднее арифметическое
угловых значений:
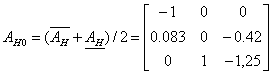
Найдем также абсолютную разность между угловым и медианным
значением для последующего расчета относительной интервальности:
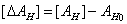 .
.
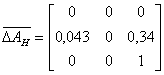 ,
,  .
.
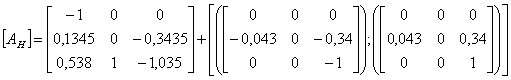 .
.
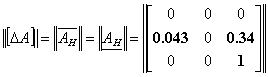
Теперь можем сформировать медианное модальное управление.
Матрицы эталонной модели с учетом требования к выбору корней
полинома Баттерворта (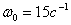 ) имеют вид:
) имеют вид:

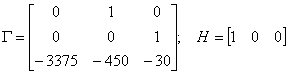
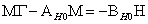
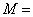
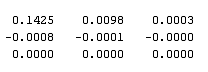 -1=
-1=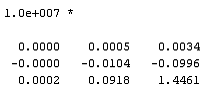
Тогда медианная составляющая матрицы 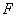 замкнутой системы имеет вид:
замкнутой системы имеет вид:
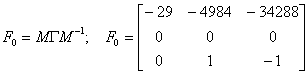
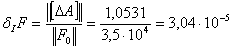
Таким образом, на частоте среза 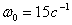 достигается требуемая относительная интервальность матрицы
состояния системы.
достигается требуемая относительная интервальность матрицы
состояния системы.
Сформируем закон управления:
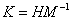 ,
,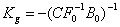 .
.
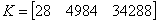 ,
,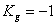
Закон управления имеет вид:
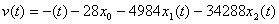 .
.
Вывод
В реальных условиях на работу системы могут влиять изменения
различных параметров (к примеру изменение направления и силы ветра, амплитуда
внешних шумов, изменение напряжения в сети питания и т.д.). Такие изменения,
для повышения надежности и соответствию необходимым паказателям качества,
необходимо учитывать при разработке или усовершенствовании системы.
В данной работе были проделаны исследования над системами,
функционирующими в условиях неопределенности. Для них можно оценить степень
влияния каждого варьируемого параметра на внутренние связи системы, ее корни и
собственные векторы, длительность переходных процессов и перерегулирование. При
такой оценке строятся модели траекторной чувствительности системы к вариации
параметров. Также для объекта, заданного в интервальном представлении, возможно
сформировать закон управления методом модального управления.
Литература
1.
Мирошник И.В. "Теория автоматического управления. Линейные системы"
.
Никифоров В.О., Ушаков А.В. "Управление в условиях неопределенности:
чувствительность, адаптация, робастность." - СПб.: СПб ГИТМО (ТУ), 2002.
.
Конспект лекций по курсу "Адаптивное и робастное управление".
.
Квакернаак Х., Сиван Р. "Линейные оптимальные системы управления". -
М.: Мир, 1977.