Организация использования транспортных средств при комплексной механизации дорожных работ

Организация использования транспортных средств при комплексной механизации дорожных работ

Министерство образования и науки Российской Федерации

ИРКУТСКИЙ ГОСУДАРСТВЕННЫЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ

Кафедра СДМ и ГС

ПОЯСНИТЕЛЬНАЯ ЗАПИСКА

к курсовому проекту

по дисциплине «Комплексная механизация, автоматизация и механовооруженность строительства»

«Организация использования транспортных средств при комплексной механизации дорожных работ»

Выполнил студент Ануфриев Н.Н.

Руководитель В.И.Крысенко

Иркутск 2012

СОДЕРЖАНИЕ

ВВЕДЕНИЕ

1. Постановка задачи и исходные данные

. Построение начального плана

. Проверка оптимальности полученного распределения

. Улучшение полученного распределения

. Определение эффективности от применения оптимального распределения

ЗАКЛЮЧЕНИЕ

Список литературы

ВВЕДЕНИЕ

Научная дисциплина «Комплексная механизация, автоматизация и механовооруженность строительства» представляет систему знаний в процессах функционирования средств механизации и совокупность методов для эффективного решения задач комплексной механизации, автоматизации и механовооруженности строительства. Основная задача данного курса - привести в необходимое соответствие средства механизации и выполнения работы.

В современных условиях возрастает разнообразие объектов и условий строительства, расширяется номенклатура строительных и дорожных машин и оборудования, повышается их уровень автоматизации, расширяется сфера использования, ускоряется темп сменяемости моделей машин и темп выполнения строительно-монтажных работ.

Курсовая работа ставит своей целью приобретение студентами навыков применения современных методов оптимизации при организации оптимального использования строительно-дорожных машин, излагаемых в курсе лекций «КОМПЛЕКСНАЯ МЕХАНИЗАЦИЯ, АВТОМАТИЗАЦИЯ И МЕХАНОВООРУЖЕННОСТЬ СТРОИТЕЛЬСТВА»

1.       Постановка задачи и исходные данные

Дорожно-строительная организация ведет строительство пяти автомобильных дорог, для которых поставляется песчано-гравийная смесь из четырех карьеров местных строительных материалов.

Расстояние между соответствующими карьерами и дорогами известно и обозначено L ij - расстояние от i -го карьера до j- ой дороги.

Расстояние между карьерами и строящимися дорогами Lij (км) приведено в табл. 1.1.

Таблица 1.1

Требуется определить оптимальное распределение объемов песчано- гравийной смеси между потребителями с учетом имеющихся ограничений, исходя из минимальных затрат транспортной работы, выраженной в [т км]

Таблица 1.2 Исходные данные:

В данном случае между карьером К₁ и дорогой Д₁, отсутствует подъездной путь и доставка этой дорогой груза из данного карьера невозможна.

Имеет место ограничения в т:

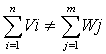
где n - число карьеров;

m - число дорог.

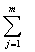600+600+500+200 < 100+500+600+600+300

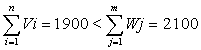
2. Построение начального плана

Т.к. отсутствует подъездной путь между поставщиком К₁ и потребителем Д₁ необходимо в клетку К₁Д₁ поставить вместо действительно расстояния на порядок больше самого большого расстояния в матрице и тем самым выполнить условие математической записи отсутствия проезда

К₁Д₁ = L₁₁ =8*10=80км → ∞

В данном случае объем разрабатываемой песчано-гравийной смеси меньше количества, необходимого для строительства дорог, поэтому в матрицу необходимо ввести так называемого «фиктивного» поставщика, для которого вводится отдельный столбец. Его наличие груза над суммарным объемом поставок. Вместо расстояния в клетках этого столбца матрицы записывается произвольное значение пути, обычно равное 0;

Из условий решаемой задачи известно, о превышении поставляемого объема разрабатываемой песчано-гравийной смеси над потребляемым, и об отсутствии подъездного пути между поставщиком К1 и потребителем Д1, тогда исходная матрица может быть записана в виде табл. 2.1.

Таблица 2.1

В рассматриваемой матрице расстояние L₃₄ выбирается значительно большим, чем действительное, с целью выполнения условия

К₁Д₁ = L₁₁ =8* 10=80км → ∞

Поскольку объем поставляемого груза меньше чем объем потребления, то вводим в матрицу столбец фиктивного поставщика К_ф с объемом потребления V_ф, равным

строительный машина транспортный распределение

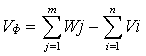
Vф=2100-1900=200 тн.

Таблица 2.2

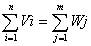
Проведем последовательное закрепление потребителей за поставщиками способом двойного предпочтения. Вначале выбираем и отличаем наименьшее расстояние в каждой строке. Затем тоже самое делаем по столбцам. Клетку, имеющую две отметки, загружаем, т.е. записываем в нее количество груза в первую очередь. Затем загружаем клетки с меньшим расстояниями, отмеченные один раз. Нераспределенный груз записывают в неотмеченные клетки, расположенные на пересечении неудовлетворенной строки и столбца. Количество груза, помещаемого в каждую клетку, определяется наименьшей величиной груза у соответствующего поставщика или потребностью в грузе соответствующего потребителя.

Клетки, в которых проставлено количество груза, называются загруженными.

Определим общий объем транспортных работ по формуле:

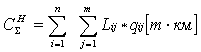
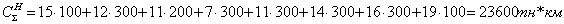
где q_ij - наличие груза в загруженной клетке, т;_ij - дороги, км.

3. Проверка оптимальности полученного распределения

Определение потенциалов

Для одного из столбцов (поставщиков) принимаем потенциал U_i = 0; приравниваем к нулю потенциал третьего столбца U₃ = 0, т.к. в нем имеется загруженная клетка с наибольшим расстоянием.

Для загруженной клетки разность между соответствующими этой клетке потенциалами должна быть равна указанному в ней расстоянию, т.е.

_j - U_i= L_ij

Остальные потенциалы определяют по загруженным клеткам, исходя из следующих зависимостей:

Для столбцов U_i = V_j - L_ij

Для строк V_j = U_i + L_ij

для определения всех потенциалов строк в матрице необходимо соблюдение правила:

N = m + n - 1

где N - число загруженных клеток.

В данном случае правило выполняется: 9 = 5 + 5 - 1

9 = 9₃=0₁ = U₃ + L₃₁ = 0 + 15=15;₄=U₃ + L₃₄ =0+16=16;₂=V₄ - L₂₄=16-14=2;₃ =U₂ + L₂₃ =2+11=13;₁=V₃ + L₁₃ =13-7=6;₂=U₁ + L₁₂=6+12=18;₄=V₂ -L₄₂ =18 - 11=7;₅ =U₃ + L₃₅ =0+19=19;

U_ф = V₅ - L_ф5 = 19-0=19;

Полученные значения потенциалов заносим в таблицу 3.1

Таблица 3.1

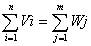
После определения потенциалов рассматриваем все незагруженные клетки и среди них отыскивают такие, для которых разность между соответствующим им потенциалам будет больше расстояния, указанного в этой клетке, т.е.:

Vj - Ui > Lij

V₁ - U₁=15-6 = 9 < 80;₁ - U₂=15-2= 13 ˃ 12;₁ - U₄=15-8 = 7 < 23;₂ - U₂=18-2 = 16 ˃ 10;₂ - U₃=18-0 = 18 > 14;₃ - U₃=13-0 = 13 < 19;₃ - U₄=13-7 = 6 < 14;₄ - U₁=16-6 = 10 < 23;₄ - U₄=16-7 = 9 < 18;₅ - U₁=19-6 = 13 < 17;₅ - U₂=19-2 = 17 < 20;₅ - U₄=19-7 = 12 < 20;

Для каждой такой клетки определяют число

D_ij = V_j - U_i - L_ij

Наличие Dij свидетельствует, что принятое нами в табл. 3.1 распределение не является оптимальным и его можно улучшить, то есть найти оптимальный вариант доставки грузов.

D₂₁ =V₁ -U₂ -L₂₁ =15-2-12=1;₂₂ =V₂ -U₂ -L₂₂ =18-2-10=6;₃₂ =V₂ -U₃ -L₃₂ =18-0-14=1;

4. Улучшение полученного распределения

Улучшения поставок приводят путем нахождения наибольшего значения Dij. В нашем случае число Dij присуще только одной клетке - К₂Д₂.

Начиная с этой клетки, строим «контур». Клеткам в вершинах контура попеременно присваивают знаки «+» и «-», начиная с выбранной клетки, которой присваивается знак «-» (см. таблицу 4.1).

Таблица 4.1

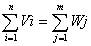
Из всех клеток, обозначенных знаком «+» выберем наименьшую цифру загрузки. Такой клеткой в матрице табл. 4.1 является К₁Д₂ и К₂Д₃, указанное в ней количество груза отнимем от загрузки, указанной в клетке со знаком «+», и прибавим в клетках со знаком «-». Полученные цифры запишем в новую матрицу - табл. 4.2.

Таблица 4.2

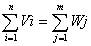
Определение потенциалов

В данном случае правило не выполняется:

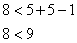
Т.к. N < m + n - 1, то искусственно загружаем недостающее количество клеток матрицы, и указываем количество груза равное 0, и в последующих расчетах оперируем этой клеткой как загруженной. Наличие клетки с нулевой загрузкой не повлияет на сбалансированность матрицы с точки зрения равенства поставляемого и потребляемого груза. Нулевую загрузку следует ставить в клетку, лежащую на пересечении строки и столбца, не имеющих потенциалов, со стрелкой или столбцом, для которых потенциалы уже определены. Искусственно загружаем клетку К₂Д₃

Для одного из столбцов (поставщиков) принимаем потенциал U_i = 0; приравниваем к нулю потенциал третьего столбца U₃ = 0, т.к. в нем имеется загруженная клетка с наибольшим расстоянием.

U ₃=0₁ =U₃ + L₃₁ = 0 + 15 = 15;₄=U₃ + L₃₄ =0+16 = 16;₂=V₄ - L₂₄=16-14 = 2;₂ = U₂ + L₂₂ =2+10 = 12;₄=V₂ -L₄₂ =12 - 11 = 1;₃ =U₂ + L₂₃ =2+11 = 13;₁=V₃ -L₁₃ =13 - 7 = 6;₅ = U₃ + L₃₅ =0+19 = 19;

U_ф = V₅ - L_ф5 = 19-0 = 19;

После определения потенциалов рассматриваем все незагруженные клетки и проверяем на условие:

Vj - Ui >Lij

V₁ - U₁=15-6 = 9 < 80;₁ - U₂= 15-2 = 13 > 12;₁ - U₄=15-1 = 14 < 23;₂ - U₁=12-6 = 6 < 12;₂ - U₃=12-0 = 12 < 14;₃ - U₃=13-0 = 13 < 19;₃ - U₄=13-1 = 12 < 14;₄ - U₁=16-6 = 10 > 23;₄ - U₄=16-1 = 15 < 18;₅ - U₁=19-6 = 13 < 17;₅ - U₂=19-2 = 17 < 20;₅ - U₄=19-1 =18 < 20;

Для каждой такой клетки определяют число

D_ij = V_j - U_i - L_ij

Наличие Dij свидетельствует, что принятое нами в табл. 4.2 распределение не является оптимальным и его можно улучшить, то есть найти оптимальный вариант доставки грузов.

D₂₁ =V₁ -U₂ -L₂₄ =15-2-12=1;

Улучшения поставок приводят путем нахождения наибольшего значения Dij. В нашем случае число Dij присуще только одной клетке - К₂Д₁.

Начиная с этой клетки, строим «контур». Клеткам в вершинах контура попеременно присваивают знаки «+» и «-», начиная с выбранной клетки, которой присваивается знак «-» (см. таблицу 5.1).

Таблица 5.1

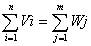
Из всех клеток, обозначенных знаком «+» выберем наименьшую цифру загрузки. Такой клеткой в матрице табл. 5.1 является К₃Д₁, указанное в ней количество груза отнимем от загрузки, указанной в клетке со знаком «+», и прибавим в клетках со знаком «-». Полученные цифры запишем в новую матрицу - табл. 5.2.

Таблица 5.2

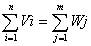
Определение потенциалов

В данном случае правило выполняется: 9 = 5+5-1

= 9

Для одного из столбцов (поставщиков) принимаем потенциал U_i = 0; приравниваем к нулю потенциал третьего столбца U₃ = 0, т.к. в нем имеется загруженная клетка с наибольшим расстоянием.

U ₃=0₄=U₃ + L₃₄ =0+16 = 16;₂=V₄ - L₂₄=16-14 = 2;₁ =U₂ + L₂₁ = 2 + 12 = 14;₂ = U₂ + L₂₂ =2+10 = 12;₄=V₂ -L₄₂ =12 - 11 = 1;₃ =U₂ + L₂₃ =2+11 = 13;₁=V₃ -L₁₃ =13 - 7 = 6;₅ = U₃ + L₃₅ =0+19 = 19;

U_ф = V₅ - L_ф5 = 19-0 = 19;

После определения потенциалов рассматриваем все незагруженные клетки и проверяем на условие:

Vj - Ui >Lij

V₁ - U₁=14-6 = 8 < 80;₁ - U₄=14-1 = 13 < 23;₂ - U₁=12-6 = 6 < 12;₂ - U₃=12-0 = 12 < 14;₃ - U₃=13-0 = 13 < 19;₃ - U₄=13-1 = 12 < 14;₄ - U₁=16-6 = 10 < 14;₄ - U₁=21-11 = 10 < 23;₄ - U₄=16-1 = 15 < 18;₅ - U₁=19-6 = 13 < 17;₅ - U₂=19-2= 17 < 20;

Так как выполняется условие Vj - Ui ≤ Lij, можно сделать вывод что оптимальный вариант найден.

Определим общий объем транспортных работ для оптимального распределения:

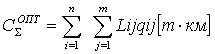
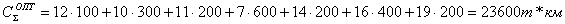
5. Определение эффективности от применения оптимального распределения

Проведём сравнения объёмов транспортной работы в первоначальном и оптимальном распределении

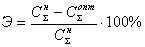м

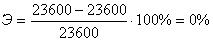
Полученные 0% снижения транспортной работы говорят о том, что эффект от применения оптимального плана использования комплекта машин при доставке материалов на строящиеся дороги не изменится, а следовательно первоначальное распределение грузов является оптимальным вариантом.

ЗАКЛЮЧЕНИЕ

В данной работе ставилась задача приобретения навыков применения современных методов оптимизации при организации оптимального использования строительно-дорожных машин.

В ходе выполнения курсовой работы устранялись ограничения поставок песчано-гравийной смеси между конкретными пунктами, а также уменьшалась несбалансированность в поставках и потреблении.

В результате проведения ряда операций, указанных в методических указаниях по выполнению курсовой работы, достигалось оптимальное распределение объемов песчано-гравийной смеси между потребителями и уменьшались затраты транспортной работы.

Применение оптимального плана использования комплекта машин при доставке материала на строящиеся дороги после перераспределения грузов не изменится и поэтому первоначально составленное распределение является оптимальным.

Список литературы

1. Крысенко В.И. Методическое указание по выполнению курсовой работы «Комплексная механизация, автоматизация и механовооруженность строительства». - ИрГТУ.