Рынок ценных бумаг. Оптимизация портфеля инвестиций
Введение
Корпорация или частная фирма, которой требуется
заем, может получить необходимые деньги, взяв кредит в банке или выпустив
долговые обязательства. Однако существует еще достаточно много способов
привлечения средств компанией. Одной из наиболее распространенных форм
финансирования собственного капитала компании является продажа части своих
активов путем выпуска долевых ценных бумаг. Такие ценные бумаги называются
акциями, а компания, их выпустившая, - акционерным обществом.
Среди корпораций, выпустивших акции, существуют
закрытые акционерные общества, акции которых распределяются среди их
учредителей, и открытые акционерные общества, акции которых продаются и
покупаются свободно. Совладельцем объединенного имущества открытого
акционерного общества может стать любой, кто приобрел хотя бы одну акцию.
Высшим органом управления акционерного общества является общее собрание
акционеров, на котором каждый акционер обладает правом голоса пропорционально
сумме имеющихся у него акций. Именно на общем собрании акционеров выбирается
правление корпорации, или совет директоров, которое руководит текущими делами
акционерного общества.
Существуют два основных вида акций,
различающихся по выплате дивидендов по ним и степени риска вложения капитала в
них. Это обыкновенная акция и привилегированная акция.
1. Основные понятия
Привилегированные акции являются в некотором
смысле смешанной формой финансирования, имеющие черты облигации и обыкновенной
акции. С одной стороны, они определяют фиксированный доход (дивиденды), который
должен выплачиваться через равномерные промежутки времени, чем напоминают
купонные облигации. С другой стороны, они не имеют определенного срока
погашения, поскольку могут быть выкуплены эмитентом в любое удобное для него
время. Таким образом, как и обыкновенные акции, их следует отнести к бессрочным
ценным бумагам.
Привилегированные акции получили свое название в
силу того, что в случае ликвидации фирмы претензии владельца привилегированной
акции удовлетворяются после претензий кредиторов, но раньше, чем обязательства
компании перед обыкновенными акционерами. При этом, как правило, обязательства
фирмы перед привилегированными акционерами удовлетворяются не более чем на
сумму номинальной стоимости акций, которыми они владеют. Более того, хотя оговорено,
что привилегированная акция приносит инвестору некий фиксированный дивиденд, в
действительности выплата этих дивидендов скорее производится по усмотрению
компании, чем является строгим обязательством, так как невыплата дивидендов не
является нарушением обязательств перед кредиторами и тем самым не ведет к
несостоятельности компании. Поэтому совет директоров имеет право принять
решение проигнорировать выплату дивидендов по привилегированным акциям. Таким
образом, хотя привилегированные акции и близки к облигациям, инвестиции в них
являются более рискованными.
Привилегированные акционеры не имеют права
голоса на общем собрании акционеров, в том числе и при избрании членов
правления. Поэтому они не могут оказывать существенное влияние на состояние дел
в компании за исключением той ситуации, когда компания на протяжении
определенного пери ода не выплачивает дивиденды по привилегированным акциям. В
этом случае привилегированные акционеры имеют право выбрать в правление
определенное число директоров.
Рисковый капитал, который позволяет новым фирмам
начинать свою деятельность, а существующим - расширяться, получается обычно
путем продажи обыкновенных акций. Обладатели обыкновенных акций компании, или
просто акционеры компании, являются ее владельцами. Поэтому они полностью
принимают риски, связанные с владением капитала данной компании, а в случае ее
ликвидации их претензии погашаются после полного удовлетворения требования
кредиторов и привилегированных акционеров. Это означает, что в случае
банкротства компании они несут убытки вместе с компанией и могут потерять часть
своего инвестированного капитал или даже весь. С другой стороны, их возможные
доходы ничем не ограничиваются. Если компания успешно ведет дело и цены на ее
акции растут, то инвестор может ожидать получения хороших дивидендов по акциям
этой компании, а также прибыль при продаже акций на рынке. Дивиденды на
обыкновенные акции являются распределением прибыли компании среди ее владельцев
и зависят от того, сколько заработала корпорация в текущем году и какой
является дивидендная политика правления компании. Так как обладатели
обыкновенных акций являются владельцами компании, они имеют право голоса при
избрании совета директоров и тем самым имеют возможность влиять на
экономическую политику и практическую деятельность компании.
Существуют и другие виды акций, оговаривающие
долю участия акционера, специальный способ выплаты ему дивидендов и т.п.
Многих инвесторов покупка акций привлекает не
дивидендами, а возможностью получать доход на колебаниях цен акций, покупая их
по низкой цене, перед тем как большинство участников фондового рынка начнут это
делать, и продавая по высокой цене, перед тем как другие будут это делать.
Рыночная цена акции данной фирмы во многом будет
зависеть от рискованности ее будущих доходов, от отношения акционеров к риску
и, конечно, от уровня процентных ставок по безрисковым ценным бумагам. Чтобы
оценить эту величину, требуется проанализировать достаточно большой объем
информации, влияние которой на значение цены акции или прибыли при инвестиции в
нее порой носит неопределенный характер. В условиях такой неопределенности
оценка требуемых величин может быть основана только на построении
стохастических математических моделей. Такого рода модели довольно часто
используются в экономике и основаны на логических принципах раздела математики,
называемого теорией вероятностей.
Удобный способ формализации
неопределенности состоит в использовании концепции «состояния мира». Состояние
полностью определяет все переменные, являющиеся внешними по отношению к рынку.
Например, состояние может включать спрос на продукцию фирмы, цены ресурсов и
полуфабрикатов и т. д. Представим себе всю экономику мира как некоторый
случайный эксперимент. Тогда множество исходов этого эксперимента и есть
множество состояний мира. В теории вероятностей такое множество называется
пространством элементарных событий и обозначается 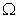 . Тогда
каждое элементарное событие
. Тогда
каждое элементарное событие 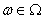 есть исход нашего эксперимента или
состояние мира. Принято различать пространство элементарных событий на два
типа: дискретное и непрерывное. Под дискретным множеством состояний понимается
конечное или счетное множество. Все остальные относятся к непрерывным.
есть исход нашего эксперимента или
состояние мира. Принято различать пространство элементарных событий на два
типа: дискретное и непрерывное. Под дискретным множеством состояний понимается
конечное или счетное множество. Все остальные относятся к непрерывным.
Численной оценкой шансов появления
того или иного случайного события А является его вероятность Р(А). Так как
любое случайное событие, связанное с экспериментом, можно разложить на
благоприятствующие ему исходы, то вероятность его появления однозначно
определяется, если нам заданы вероятности элементарных событий. В случае
дискретного вероятностного пространства это означает, что каждому возможному
исходу 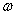 приписана
вероятность
приписана
вероятность 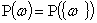 . Если же
множество исходов непрерывно, то будем предполагать, что на
. Если же
множество исходов непрерывно, то будем предполагать, что на 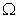 задана
некоторая числовая функция
задана
некоторая числовая функция 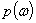 , являющаяся плотностью вероятности
Р. Тогда вероятность события А определяется по формулам:
, являющаяся плотностью вероятности
Р. Тогда вероятность события А определяется по формулам:
для дискретного случая
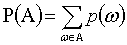 ,
,
для непрерывного случая
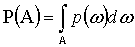 .
.
Вероятность принимает
неотрицательные значения и обладает свойством нормированности (т.е. 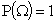 ), введенные
функции
), введенные
функции 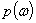 неотрицательны
и удовлетворяют следующим соотношениям в дискретном и непрерывном случаях
соответственно:
неотрицательны
и удовлетворяют следующим соотношениям в дискретном и непрерывном случаях
соответственно:
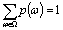 и
и 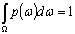
В условиях случайного эксперимента
любой числовой параметр является функцией 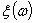 от возможного исхода
от возможного исхода 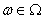 .
.
Такие функции в теории вероятностей
называются случайными величинами. Каждой случайной величине  ставятся в
соответствие ее числовые характеристики. Основными из них являются
математическое ожидание E
ставятся в
соответствие ее числовые характеристики. Основными из них являются
математическое ожидание E и дисперсия D
и дисперсия D . В случае
дискретного вероятностного пространства они находятся по формулам:
. В случае
дискретного вероятностного пространства они находятся по формулам:
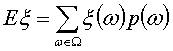 (1)
(1)

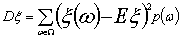 (2)
(2)
Если вероятность определяется
плотностью 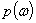 , то
, то
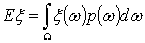 (3)
(3)
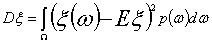 (4)
(4)
В силу неотрицательности
вероятностей 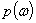 дисперсия D
дисперсия D есть
величина неотрицательная. Поэтому можно определить квадратный корень из
дисперсии:
есть
величина неотрицательная. Поэтому можно определить квадратный корень из
дисперсии:
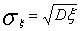
Величина 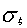 называется
средним квадратичным отклонением. Очевидно, что
называется
средним квадратичным отклонением. Очевидно, что 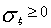 . Как принято, данная величина
характеризует стохастичность случайной величины
. Как принято, данная величина
характеризует стохастичность случайной величины  . Это означает, что, чем больше
. Это означает, что, чем больше 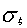 , тем более
случайной является функция
, тем более
случайной является функция 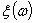 . В частности, если
. В частности, если 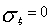 , то с
вероятностью 1
, то с
вероятностью 1 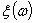 не зависит
от исходов эксперимента, то есть является неслучайной константой.
не зависит
от исходов эксперимента, то есть является неслучайной константой.
Нетрудно показать, что для заданных
констант А и В математическое ожидание и дисперсия случайной величины A +В
выражаются через числовые характеристики случайной величины
+В
выражаются через числовые характеристики случайной величины  следующим
образом:
следующим
образом:
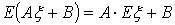 ,
, 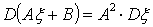 (5)
(5)
Если нам заданы две случайные
величины 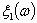 и
и 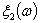 , то их
совместное распределение определяет ковариацию cov(
, то их
совместное распределение определяет ковариацию cov(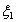 ,
,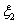 ) по
формулам:
) по
формулам:
в дискретном случае
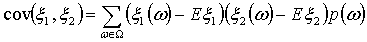 ,
,
в непрерывном случае
 .
.
Очевидно, что
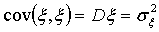
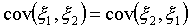 .
.
Большое значение при оценке
взаимовлияния случайных величин друг на друга имеет коэффициент корреляции
определяемый как
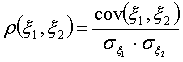 .
.
В некотором смысле он понимается как
косинус угла наклона между возможными направлениями двух случайных величин. Так
же, как обычный косинус некоторого угла, коэффициент корреляции принадлежит
отрезку [-1, 1], то есть 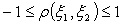 .
.
2. Портфель инвестиций
Чтобы все фирмы были в равных по
времени условиях, будем предполагать, что через единицу времени все фирмы
ликвидируются, а полученные доходы распределяются среди акционеров в качестве
дивидендов. Дивиденды, выплачиваемые на акции каждого типа, будем считать
случайными величинами. Другими словами, существует некоторое пространство
элементарных событий 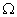 с заданной
на нем вероятностью Р.
с заданной
на нем вероятностью Р.
Через 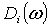 дивиденд, обозначим, выплачиваемый
на акцию
дивиденд, обозначим, выплачиваемый
на акцию 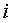 в состоянии
в состоянии 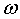 . Пусть S
. Пусть S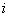 - цена
акции
- цена
акции 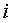 в начальное
время. Тогда
в начальное
время. Тогда
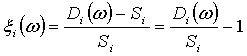
является доходностью акции 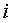 в состоянии
в состоянии
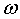 . Так как
это случайная величина, то ей можно поставить в соответствие математическое
ожидание
. Так как
это случайная величина, то ей можно поставить в соответствие математическое
ожидание 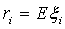 и дисперсию
и дисперсию
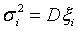 . Таким
образом, каждой акции
. Таким
образом, каждой акции 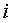 мы ставим в
соответствие ожидаемую доходность
мы ставим в
соответствие ожидаемую доходность 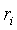 и среднее квадратическое отклонение
и среднее квадратическое отклонение
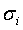 ,
, 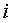 = 1, 2,..., N. Взаимная
зависимость акций определяется матрицей ковариации, каждый элемент которой
равен
= 1, 2,..., N. Взаимная
зависимость акций определяется матрицей ковариации, каждый элемент которой
равен
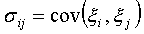 .
.
В частности,
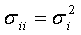 .
.
Рассмотрим теперь некоторого
инвестора, имеющего капитал W и желающего весь его инвестировать
в имеющиеся акции с целью получения дохода через единицу времени. Допустим, что
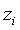 - число
акций типа
- число
акций типа 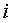 , купленных
в начальный период. Тогда
, купленных
в начальный период. Тогда
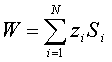 . (6)
. (6)
Обозначим через
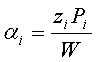 (7)
(7)
долю инвестиций в акции 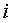 . Набор
действительных чисел
. Набор
действительных чисел
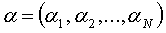 ,
,
удовлетворяющих условию
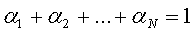 , (8)
, (8)
называется портфелем инвестиций. В
большом количестве примеров помимо ограничения (8) вводится условие
неотрицательности активов 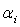 . Однако в
общем случае можно предположить, что у инвестора имеется возможность взять
взаймы любое количество акций
. Однако в
общем случае можно предположить, что у инвестора имеется возможность взять
взаймы любое количество акций 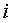 и продать их на рынке в начальный
момент времени. Такое действие называют открытием коротком позиции по акции
и продать их на рынке в начальный
момент времени. Такое действие называют открытием коротком позиции по акции 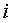 , и в этом
случае
, и в этом
случае 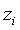 и
и 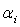 -
отрицательные числа. Через единицу времени инвестор обязан закрыть короткую
позицию, вернув своему кредитору соответствующие акции. Обычная покупка акций
-
отрицательные числа. Через единицу времени инвестор обязан закрыть короткую
позицию, вернув своему кредитору соответствующие акции. Обычная покупка акций 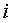 ,
естественно, понимается как открытие длинной позиции по данной акции. В
дальнейшем мы не будем ставить какие-либо ограничения на открытие короткой
позиции по акциям, если это не будет оговариваться в контексте. Вне зависимости
от коротких и длинных позиций по акциям будем считать, что балансовые уравнения
(6) - (8) всегда вы полнены. Это означает, что весь капитал инвестора
используется в портфеле инвестиций.
,
естественно, понимается как открытие длинной позиции по данной акции. В
дальнейшем мы не будем ставить какие-либо ограничения на открытие короткой
позиции по акциям, если это не будет оговариваться в контексте. Вне зависимости
от коротких и длинных позиций по акциям будем считать, что балансовые уравнения
(6) - (8) всегда вы полнены. Это означает, что весь капитал инвестора
используется в портфеле инвестиций.
Рассчитаем теперь случайную величину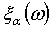 доходности
портфеля
доходности
портфеля 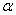 :
:
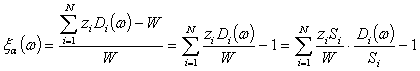 .
.
С учетом формул (6) - (8) получаем,
что
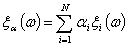 .
.
Тогда ожидаемая доходность портфеля
и его дисперсия находятся по формулам:
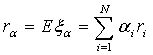 (9)
(9)
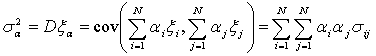 (10)
(10)
Полагая в качестве оценки риска
портфеля меру случайности доходности портфеля - среднее квадратическое
отклонение, для каждого допустимого портфеля на плоскости «риск-Доходность»
можно отметить точки, координаты которых равны среднему квадратическому
отклонению и ожидаемой доходности портфеля. В случае с запретом на открытие
коротких позиций, когда 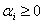 , это
приведет к рисунку 1. Данный рисунок показывает возможные соотношения между
риском и доходностью на данном рынке. Заметим, что каждая точка в
заштрихованной области соответствует портфелю инвестиций. Если инвестор
заинтересован в максимизации ожидаемой доходности и минимизации риска (в данном
случае среднего квадратического отклонения), то для него играет роль правило
левого верхнего угла. Суть этого правила состоит в том, что если выбрать
некоторый портфель
, это
приведет к рисунку 1. Данный рисунок показывает возможные соотношения между
риском и доходностью на данном рынке. Заметим, что каждая точка в
заштрихованной области соответствует портфелю инвестиций. Если инвестор
заинтересован в максимизации ожидаемой доходности и минимизации риска (в данном
случае среднего квадратического отклонения), то для него играет роль правило
левого верхнего угла. Суть этого правила состоит в том, что если выбрать
некоторый портфель 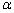 и на
соответствующей ему точке А
и на
соответствующей ему точке А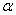 на плоскости «риск-доходность»
построить левый верхний угол, то любой портфель
на плоскости «риск-доходность»
построить левый верхний угол, то любой портфель 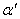 с соответствующей ему точкой А
с соответствующей ему точкой А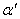 из
построенного угла является для инвестора более предпочтительным, чем
первоначально выбранный портфель
из
построенного угла является для инвестора более предпочтительным, чем
первоначально выбранный портфель 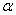 (см. рис. 1).
(см. рис. 1).
Для каждого допустимого значения
доходности  можно
выбрать граничную точку построенной области как точку, соответствующую портфелю
инвестиций с заданной ожидаемой доходностью и наименьшим значением риска.
можно
выбрать граничную точку построенной области как точку, соответствующую портфелю
инвестиций с заданной ожидаемой доходностью и наименьшим значением риска.
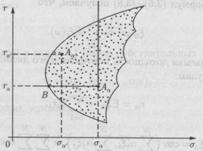
На рисунке 1 это точка В. Понятно,
что для инвестора координаты граничных точек и соответствующие им портфели
являются наиболее важными с точки зрения оптимального выбора инвестиций, так
как с учетом правила левого верхнего угла для любой внутренней точки области
всегда найдется более предпочтительная точка на границе. Форма границы в общем
виде имеет достаточно сложный вид, который в теории принято называть формой
пули.
Главное свойство этой кривой состоит
в том, что она является выпуклой влево. Этот факт основан на следующих
рассуждениях. Рассмотрим простейший случай, когда на рынке имеются два вида
акций, то есть N = 2. В этом случае область допустимых точек на плоскости
«риск-доходность» будет кривой, которую можно определить параметрически
следующим образом. Пусть t - параметр кривой. Положим 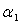 = t - доля
акций первого типа,
= t - доля
акций первого типа, 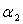 = 1 - t - доля
акций второго типа. Тогда допустимые портфели
= 1 - t - доля
акций второго типа. Тогда допустимые портфели 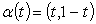 однозначно определяются параметром t. Нетрудно
увидеть, что ожидаемая доходность такого портфеля
однозначно определяются параметром t. Нетрудно
увидеть, что ожидаемая доходность такого портфеля
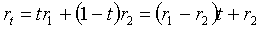
есть линейная функция от t.
Соответственно, дисперсия доходности портфеля 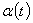 равна
равна
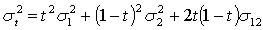
И является квадратным трехчленом от
параметра t. Поэтому
Множество точек 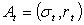 на
плоскости «риск-доходность» будет частью гиперболы, проходящей через точки
на
плоскости «риск-доходность» будет частью гиперболы, проходящей через точки 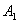 и
и 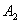 ,
определяющих риск и доходность акций первого и второго типов соответственно
(см. рис. 2). Для определенности на рисунке 2 рассмотрен частный случай, когда
,
определяющих риск и доходность акций первого и второго типов соответственно
(см. рис. 2). Для определенности на рисунке 2 рассмотрен частный случай, когда 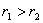 и
и
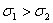 . Все другие возможные случаи
аналогичны.
. Все другие возможные случаи
аналогичны.
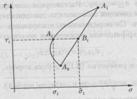

Рис. 2. Кривая «риск-доходность» портфеля из
двух акций
Рассмотрим теперь отрезок,
соединяющий вершины 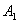 и
и 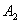 .
Параметрически каждая точка
.
Параметрически каждая точка 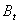 этого отрезка определяется
координатами
этого отрезка определяется
координатами 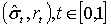 , где
, где
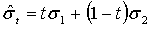 .
. (11)
(11)
Тогда для доказательства выпуклости
влево построенной кривой необходимо убедиться, что для любого 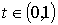 точка
точка 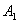 находится
левее точки
находится
левее точки 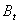 . Проверим,
что в действительности
. Проверим,
что в действительности
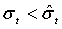 или
или 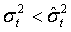
Для этого преобразуем формулу
дисперсии доходности портфеля 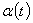 в следующем виде
в следующем виде
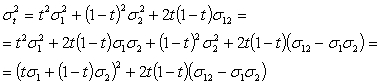
Тогда с учетом (11) получаем, что
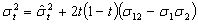 (12)
(12)
Так как параметр t берется из
интервала (0,1), знак второго слагаемого в правом выражении выписанного
равенства определяется разностью 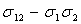 . Рассмотрим коэффициент корреляции
. Рассмотрим коэффициент корреляции 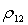 ,
определяющий зависимость доходностей акций первого и второго типов. По
определению, ковариация
,
определяющий зависимость доходностей акций первого и второго типов. По
определению, ковариация 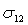 может быть
получена из коэффициента корреляции по следующей формуле:
может быть
получена из коэффициента корреляции по следующей формуле:
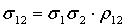 .
.
Подставляя это в равенство (12) и
взяв корень, находим, что
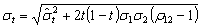 . (13)
. (13)
Так как коэффициент корреляции
удовлетворяет неравенствам 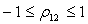 отсюда сразу следует, что
отсюда сразу следует, что 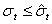 , причем
равенство здесь возможно только в том случае, если
, причем
равенство здесь возможно только в том случае, если 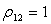 . Таким
образом, при
. Таким
образом, при 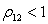 имеет место
строгое неравенство
имеет место
строгое неравенство 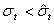 , и, значит,
выпуклость влево построенной кривой. Как уже было замечено, если коэффициент
корреляции
, и, значит,
выпуклость влево построенной кривой. Как уже было замечено, если коэффициент
корреляции 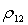 равен
единице, то
равен
единице, то 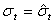 и
построенная кривая есть отрезок, соединяющий точки
и
построенная кривая есть отрезок, соединяющий точки 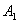 и
и 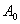 . В этом
вырожденном случае вероятностными методами нетрудно показать, что доходности
. В этом
вырожденном случае вероятностными методами нетрудно показать, что доходности 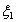 и
и 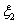 как
случайные величины связаны между собой линейной зависимостью почти наверное:
как
случайные величины связаны между собой линейной зависимостью почти наверное:
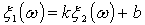 п.н., (14)
п.н., (14)
с положительным коэффициентом
линейной зависимости 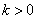 (здесь
константы
(здесь
константы 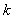 и
и 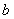 неслучайны).
Это означает, что рассматриваемые акции являются сильно зависимыми и риск
инвестиций в портфель из этих акций может быть уменьшен только пропорционально
уменьшению ожидаемой доходности портфеля. Противоположной данному случаю
является ситуация, когда коэффициент корреляции
неслучайны).
Это означает, что рассматриваемые акции являются сильно зависимыми и риск
инвестиций в портфель из этих акций может быть уменьшен только пропорционально
уменьшению ожидаемой доходности портфеля. Противоположной данному случаю
является ситуация, когда коэффициент корреляции 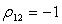 . В этом случае также имеет место
линейная зависимость (14). Если в результате доходность по одной акции оказалась
отрицательной, то доходность по другой обязательно положительна. Последнее дает
возможность снизить риски до минимального для этого вырожденного случая.
Рассмотрим вид допустимой кривой на плоскости «риск-доходность» при условии
. В этом случае также имеет место
линейная зависимость (14). Если в результате доходность по одной акции оказалась
отрицательной, то доходность по другой обязательно положительна. Последнее дает
возможность снизить риски до минимального для этого вырожденного случая.
Рассмотрим вид допустимой кривой на плоскости «риск-доходность» при условии 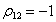 . Подставляя
это значение в формулы (11) и (13), получаем
. Подставляя
это значение в формулы (11) и (13), получаем
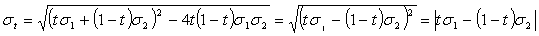
В силу свойств модуля, в итоге
имеем, что
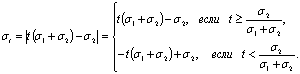
Следовательно, в этом случае кривая
будет представлять собой два прямых отрезка 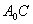 и
и 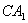 (см. рис. 3). Нетрудно увидеть,
что, при
(см. рис. 3). Нетрудно увидеть,
что, при 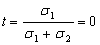 ,
, 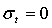 и портфель
и портфель 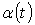 является безрисковой
инвестицией с неслучайной доходностью
является безрисковой
инвестицией с неслучайной доходностью 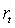 , равной
, равной
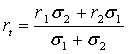
Это означает, что в рассматриваемой
вырожденной ситуации можно подобрать портфель акций таким образом, что риск
инвестиций в этот портфель станет нулевым.
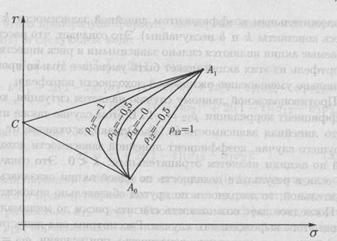
Рис. 3. Зависимость кривой
«риск-доходность» от коэффициента корреляции 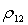
Таким образом, допустимые кривые на
плоскости «риск-доходность» являются дугами гиперболы с концами в точках 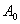 и
и 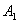 . Как видно
из рисунка, чем меньше коэффициент корреляции по акциям, тем более выпуклой
является дуга гиперболы, а значит, тем больше возможностей уменьшить риск по
портфелю инвестиций.
. Как видно
из рисунка, чем меньше коэффициент корреляции по акциям, тем более выпуклой
является дуга гиперболы, а значит, тем больше возможностей уменьшить риск по
портфелю инвестиций.
. Простейшая модель оптимизации
портфеля
привилегированный акция инвестиция
цена
Допустим, что у нас имеется две
возможности инвестирования. Первая - в безрисковый актив с доходностью 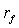 . Это
означает, что, инвестируя в этот актив, вне зависимости от случая мы всегда
будем иметь прибыль, равную
. Это
означает, что, инвестируя в этот актив, вне зависимости от случая мы всегда
будем иметь прибыль, равную 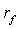 . Вторая возможность инвестирования
представляется некоторой акцией (или портфелем акций), доходность по которой
является случайной величиной
. Вторая возможность инвестирования
представляется некоторой акцией (или портфелем акций), доходность по которой
является случайной величиной 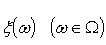 с математическим ожиданием
с математическим ожиданием 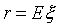 и средним
квадратическим отклонением
и средним
квадратическим отклонением 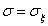 . Рискованность этого актива
предполагается условием, что
. Рискованность этого актива
предполагается условием, что 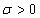 .
.
Портфель, состоящий из безрискового
и рискового актива, однозначно будет определяться долей t капитала,
инвестируемой в рисковый актив. Понятно, что оставшаяся часть капитала 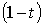 будет
вложена в безрисковый актив. Введем ограничения на открытие коротких позиций по
активам, предполагая, что
будет
вложена в безрисковый актив. Введем ограничения на открытие коротких позиций по
активам, предполагая, что 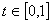 . Таким
образом, любое число t из отрезка
. Таким
образом, любое число t из отрезка 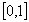 определяет
портфель
определяет
портфель 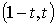 инвестиций
в безрисковый и рисковый активы. Для каждого такого портфеля его доходность
определяется по формуле:
инвестиций
в безрисковый и рисковый активы. Для каждого такого портфеля его доходность
определяется по формуле:
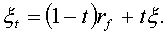
Тогда ожидаемая доходность и среднее
квадратическое отклонение по каждому портфелю равны, соответственно,
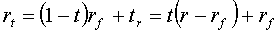 и
и 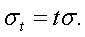
Каждая из этих функций является линейной
функцией от 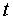 . Перед
каждым инвестором стоит выбор оптимального портфеля по каким-то собственным
критериям. Будем предполагать, что каждый инвестор интересуется только риском и
доходностью портфеля, оценивая риск при этом средним квадратическим отклонением
. Перед
каждым инвестором стоит выбор оптимального портфеля по каким-то собственным
критериям. Будем предполагать, что каждый инвестор интересуется только риском и
доходностью портфеля, оценивая риск при этом средним квадратическим отклонением
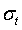 ,
Оптимальный портфель будет определяться каким-то конкретным значением
,
Оптимальный портфель будет определяться каким-то конкретным значением 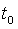 .
.
Рассмотрим несколько различных
вариантов оптимизационных задач, которые могут возникнуть перед инвестором.
. Максимум ожидаемой доходности.
Предположим вначале, что инвестор не интересуется риском и оптимизирует
портфель, стараясь получить максимум ожидаемой доходности. Тогда формально его
задача имеет следующий вид:
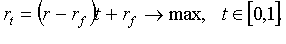 .
.
Решение этой задачи зависит от знака
линейного коэффициента 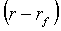 . В
зависимости от него имеется три возможных случая изменения ожидаемой доходности
. В
зависимости от него имеется три возможных случая изменения ожидаемой доходности
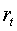 как функции
от пара метра
как функции
от пара метра 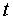 .
представлены на. В первом случае, когда
.
представлены на. В первом случае, когда 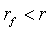 , функция
, функция 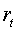 возрастает
и достигает своего максимума при
возрастает
и достигает своего максимума при  . Это означает, что оптимальным в
этом случае является портфель, когда все вкладывается в рисковый актив. Если
же, наоборот,
. Это означает, что оптимальным в
этом случае является портфель, когда все вкладывается в рисковый актив. Если
же, наоборот, 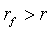 , то функция
, то функция
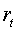 убывает,
убывает, 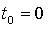 и
оптимальный портфель состоит из инвестиций только в безрисковый актив. Наконец,
в третьем случае, когда
и
оптимальный портфель состоит из инвестиций только в безрисковый актив. Наконец,
в третьем случае, когда 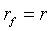 , функция
, функция 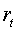 является
постоянной и любой портфель может быть оптимальным.
является
постоянной и любой портфель может быть оптимальным.
Следует заметить, что второй и
третий случаи являются очевидными с точки зрения инвестора. Действительно, если
ожидаемая доходность по рисковому активу не превосходит доходность по
безрисковому активу: 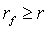 , то в любом
случае инвестор предпочтет безрисковый актив рисковому и полностью вложит весь
капитал в безрисковый актив:
, то в любом
случае инвестор предпочтет безрисковый актив рисковому и полностью вложит весь
капитал в безрисковый актив: 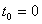 . Поэтому в дальнейшем будем
рассматривать только первый случай, когда
. Поэтому в дальнейшем будем
рассматривать только первый случай, когда 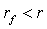 . В этом случае предпочтение
безрисковому активу не является очевидным.
. В этом случае предпочтение
безрисковому активу не является очевидным.
. Задача Марковица. Наиболее часто
встречаемая задача оптимизации портфеля была впервые описана Г. Марковичем и
имеет следующую постановку. Допустим, что задан некоторый уровень доходности 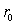 , ниже
которого инвестор не хотел бы иметь ожидаемую доходность. Тогда оптимальный
портфель выбирается среди всех возможных так, чтобы риск инвестиций,
определяемый дисперсией доходности портфеля, был минимальным. В нашем простейшем
случае задача Марковица может быть формализована следующим образом:
, ниже
которого инвестор не хотел бы иметь ожидаемую доходность. Тогда оптимальный
портфель выбирается среди всех возможных так, чтобы риск инвестиций,
определяемый дисперсией доходности портфеля, был минимальным. В нашем простейшем
случае задача Марковица может быть формализована следующим образом:
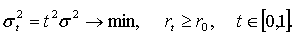
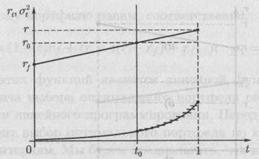
Рис. 4. Иллюстрация к задаче
Марковица
Естественно предположить, что 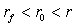 , иначе
задача либо не имеет решения, либо становится тривиальной. Так как
, иначе
задача либо не имеет решения, либо становится тривиальной. Так как 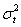 -
возрастающая функция на отрезке [0, 1], ее минимум достигается в минимально
возможном значении
-
возрастающая функция на отрезке [0, 1], ее минимум достигается в минимально
возможном значении 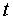 ,
определяемым условием
,
определяемым условием 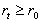 . В силу
того, что
. В силу
того, что 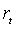 также
возрастает на [0, 1], минимальное возможное значение
также
возрастает на [0, 1], минимальное возможное значение 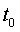 определяется
уравнением
определяется
уравнением 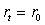 (см. рис.
4.). Таким образом, имеет место равенство
(см. рис.
4.). Таким образом, имеет место равенство
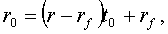
из которого находим значение 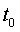 :
:

Соответственно,
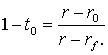
Таким образом, оптимальный портфель
в задаче Марковица в простейшем случае безрискового и рискового активов
определяется следующей парой:
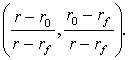
Нетрудно убедиться, что ожидаемая
доходность и среднее квадратическое отклонение по оптимальному портфелю в этом
случае находятся по формулам:
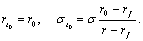
. Соотношение «риск-доходность».
Предпочтение инвестора определяется минимизацией некоторой функции, связывающей
риск и доходность каждого портфеля. Пусть, как и прежде, 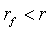 . Введем
функцию рискованности следующим образом:
. Введем
функцию рискованности следующим образом:
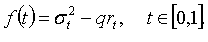
Здесь коэффициент q > 0
определяет предпочтение доходности перед риском для каждого инвестора. Если
инвестор в большей степени предпочитает определять свои вложения доходностью,
чем риском, то он выбирает коэффициент с большим значением. Если же для
инвестора более важным является риск, то он выберет коэффициент q маленьким.
В итоге задача оптимизации портфеля
в этом случае имеет следующий формальный вид:
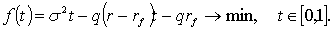
Как видно, функция 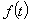 является
квадратным трехчленом с положительным старшим коэффициентом. Поэтому график
этой функции представляет параболу, ветви которой направлены вверх. Значит,
функция имеет глобальный минимум, определяемый вершиной параболы. Координата
является
квадратным трехчленом с положительным старшим коэффициентом. Поэтому график
этой функции представляет параболу, ветви которой направлены вверх. Значит,
функция имеет глобальный минимум, определяемый вершиной параболы. Координата 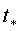 вершины
параболы равна
вершины
параболы равна
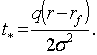 (15)
(15)
Так как 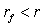 , координата
, координата
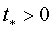 . Рассмотрим
два различных варианта выбора оптимального портфеля. Первый вариант возникает в
ситуации, когда
. Рассмотрим
два различных варианта выбора оптимального портфеля. Первый вариант возникает в
ситуации, когда 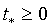 . Так как в
этом случае функция
. Так как в
этом случае функция 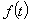 убывает на
всем отрезке [0, 1], ее минимум на отрезке [0, 1] достигается в точке
убывает на
всем отрезке [0, 1], ее минимум на отрезке [0, 1] достигается в точке 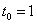 . Нетрудно
заметить, что неравенство
. Нетрудно
заметить, что неравенство 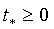 эквивалентно
условию
эквивалентно
условию
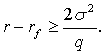
Это удобно переписать в следующем
виде:
Если это неравенство не выполнено и
имеет место следующее соотношение:
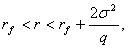
то 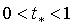 и минимум функции
и минимум функции 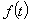 на отрезке
[0, 1] достигается в точке
на отрезке
[0, 1] достигается в точке 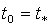 . Тогда оптимальный портфель
выбирается по второму варианту и равен
. Тогда оптимальный портфель
выбирается по второму варианту и равен 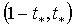 . В силу формулы (15) нетрудно
получить его окончательный вид:
. В силу формулы (15) нетрудно
получить его окончательный вид:
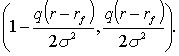 (17)
(17)
Ожидаемая доходность и среднее
квадратическое отклонение по оптимальному портфелю равны соответственно:
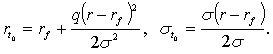
Важную роль играет так называемая
рисковая надбавка 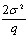 . Она будет
достаточно большой, если будет велика дисперсия доходности рискового актива или
коэффициент
. Она будет
достаточно большой, если будет велика дисперсия доходности рискового актива или
коэффициент  будет
достаточно мал. Другими словами, рисковая надбавка тем больше, чем больше риск
или чем он важнее для инвестора. Если ожидаемая доходность рискового актива не
меньше доходности безрискового актива плюс рисковая надбавка (16), то инвестор
предпочтет рискнуть и все вложить в рисковый актив. Если же рисковая надбавка
настолько велика, что неравенство (16) не выполнено, то инвестор распределяет
вложения в безрисковый и рисковый активы согласно формуле (17).
будет
достаточно мал. Другими словами, рисковая надбавка тем больше, чем больше риск
или чем он важнее для инвестора. Если ожидаемая доходность рискового актива не
меньше доходности безрискового актива плюс рисковая надбавка (16), то инвестор
предпочтет рискнуть и все вложить в рисковый актив. Если же рисковая надбавка
настолько велика, что неравенство (16) не выполнено, то инвестор распределяет
вложения в безрисковый и рисковый активы согласно формуле (17).
4. Модель ценообразования основных фондов
Рассмотрим множество точек на
плоскости «риск-доходность», соответствующих допустимым портфелям инвестиций в
акции, как показано на рисунке 5. Эффективная граница этого множества имеет
форму пули, и именно она представляет интерес с точки зрения инвестора.
Безрисковый актив на этой плоскости будет определяться точкой F на оси
ординат с координатой 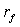 , так как
безрисковый актив имеет нулевую дисперсию.
, так как
безрисковый актив имеет нулевую дисперсию.
Наличие безрискового актива
расширяет возможности инвестора, так как он может комбинировать его с рисковыми
активами. Такая задача инвестирования уже обсуждалась нами. Покажем
геометрически, что для каждого инвестора, интересующегося только увеличением
ожидаемой доходности портфеля и уменьшением его среднего квадратического
отклонения, портфель инвестиций будет комплектоваться из некоторого
фиксированного портфеля акций и безрискового актива.
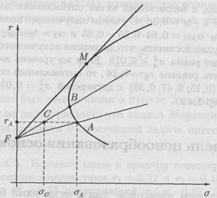
Рис.5. Плоскость «риск-доходность» с
добавлением безрискового актива
Для этого выберем на допустимой
эффективной границе произвольную точку А. Ей соответствует какой-то портфель
акций 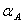 с ожидаемой
доходностью
с ожидаемой
доходностью 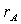 и средним
квадратическим отклонением
и средним
квадратическим отклонением 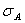 . Комбинация из портфеля акций
. Комбинация из портфеля акций 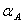 и
безрискового актива определяет на плоскости «риск-доходность» точку,
принадлежащую отрезку FA. Если прямая FA пересекает
эффективную границу, то на самой границе можно найти точку В такую, что прямая FB имеет
больший угол наклона, чем прямая FA. Тогда на отрезке FB найдется
точка С, ордината которой совпадает с ординатой точки А, а абсцисса
и
безрискового актива определяет на плоскости «риск-доходность» точку,
принадлежащую отрезку FA. Если прямая FA пересекает
эффективную границу, то на самой границе можно найти точку В такую, что прямая FB имеет
больший угол наклона, чем прямая FA. Тогда на отрезке FB найдется
точка С, ордината которой совпадает с ординатой точки А, а абсцисса 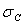 меньше
абсциссы
меньше
абсциссы 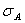 точки А.
Таким образом, портфель
точки А.
Таким образом, портфель 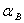 ,
соответствующий точке В на плоскости «риск-доходность», будет для инвестора
более предпочтительным, поскольку, комбинируя с безрисковым активом, он дает
возможность получать портфель инвестиций с такой же ожидаемой доходностью, но с
меньшим средним квадратическим отклонением. Продолжая увеличивать угол наклона
секущей линии, подойдем к крайней точке М на эффективной границе такой, что
прямая FM имеет
максимальный угол наклона среди всех возможных прямых такого рода. Так как для
точки М, с точки зрения инвестора, нет более предпочтительных точек на
эффективной границе, значит, М определяет наиболее предпочтительный для
инвестора портфель акций
,
соответствующий точке В на плоскости «риск-доходность», будет для инвестора
более предпочтительным, поскольку, комбинируя с безрисковым активом, он дает
возможность получать портфель инвестиций с такой же ожидаемой доходностью, но с
меньшим средним квадратическим отклонением. Продолжая увеличивать угол наклона
секущей линии, подойдем к крайней точке М на эффективной границе такой, что
прямая FM имеет
максимальный угол наклона среди всех возможных прямых такого рода. Так как для
точки М, с точки зрения инвестора, нет более предпочтительных точек на
эффективной границе, значит, М определяет наиболее предпочтительный для
инвестора портфель акций 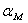 . Такой
портфель принято называть рыночным портфелем. Очевидно, что любой инвестор,
интересующийся только увеличением ожидаемой доходности портфеля и уменьшением
его среднего квадратического отклонения, будет выбирать комбинацию из рыночного
портфеля и безрискового актива, которой соответствует точка на прямой FM. Прямую FM принято
называть основной рыночной линией. Пусть, как и ранее,
. Такой
портфель принято называть рыночным портфелем. Очевидно, что любой инвестор,
интересующийся только увеличением ожидаемой доходности портфеля и уменьшением
его среднего квадратического отклонения, будет выбирать комбинацию из рыночного
портфеля и безрискового актива, которой соответствует точка на прямой FM. Прямую FM принято
называть основной рыночной линией. Пусть, как и ранее, 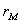 и
и 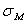 -
математическое ожидание и среднее квадратическое отклонение доходности
рыночного портфеля. Тогда нетрудно вычислить коэффициент k угла наклона
основной рыночной линии:
-
математическое ожидание и среднее квадратическое отклонение доходности
рыночного портфеля. Тогда нетрудно вычислить коэффициент k угла наклона
основной рыночной линии:
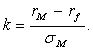 (18)
(18)
Коэффициент k в этом
случае равен доле снижения ожидаемой доходности по рыночному портфелю на
единицу уменьшения риска рыночного портфеля. Поэтому величину k можно
понимать как рыночную цену риска.
Рассмотрим портфель инвестирования
капитала в некоторую фиксированную акцию i и рыночный
портфель 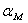 . Пусть t - доля
инвестирования в акцию. Тогда (1-t) - доля вложений в портфель.
Понимая рыночный портфель как отдельную акцию, изменяя t, получим
кривую на плоскости «риск-доходность», проходящую через точку М (см. рис.6.).
Эта кривая касается внешней границы в точке М, так как целиком лежит внутри множества
допустимых точек. С другой стороны, в силу предыдущих рассуждений, точка М
выбрана так, что прямая FM касается эффективной
границы. Отсюда следует, что FM является касательной и для
кривой, образованной комбинациями из акции i и рыночного
портфеля.
. Пусть t - доля
инвестирования в акцию. Тогда (1-t) - доля вложений в портфель.
Понимая рыночный портфель как отдельную акцию, изменяя t, получим
кривую на плоскости «риск-доходность», проходящую через точку М (см. рис.6.).
Эта кривая касается внешней границы в точке М, так как целиком лежит внутри множества
допустимых точек. С другой стороны, в силу предыдущих рассуждений, точка М
выбрана так, что прямая FM касается эффективной
границы. Отсюда следует, что FM является касательной и для
кривой, образованной комбинациями из акции i и рыночного
портфеля.

Рис.6. Иллюстрация к инвестированию
капитала в рыночный портфель и акцию
Ожидаемая доходность и среднее
квадратическое отклонение такой комбинации определяются но формулам
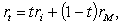
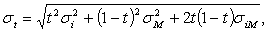
где 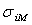 обозначает ковариацию доходностей
акции i и рыночного
портфеля. Продифференцируем по параметру t полученные
функции:
обозначает ковариацию доходностей
акции i и рыночного
портфеля. Продифференцируем по параметру t полученные
функции:
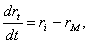
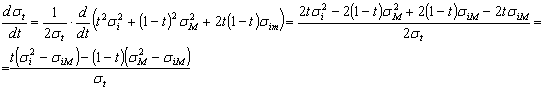
По этим формулам нетрудно вычислить
отношение полученных производных в точке t =0:
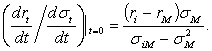
Так как основная рыночная линия
касается внутренней кривой, найденная величина и есть коэффициент k наклона
основной рыночной линии. Отсюда следует, что
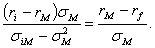
Преобразуя полученное равенство,
получаем
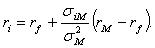 (19)
(19)
Обозначим через
 (20)
(20)
величину, которую принято называть
коэффициентом бета акции i. Тогда приведенное уравнение примет
следующий вид:
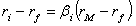 (21)
(21)
Уравнение в таком виде определяет
линейную функцию зависимости между ожидаемым доходом на акцию от ожидаемого
дохода на рыночный портфель. На соответствующей плоскости такая функция имеет
график в виде прямой линии, называемой характеристической линией (см. рис.7.).
Коэффициент бета выступает в данном случае в качестве коэффициента
пропорциональности избыточной доходности акции i, равной 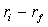 , по
отношению к избыточной доходности рыночного портфеля
, по
отношению к избыточной доходности рыночного портфеля 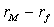 .
.
Уравнение (21) принято считать
основным выводом созданной В. Шарпом теории, называемой моделью ценообразования
основных фондов или САРМ-теорией.
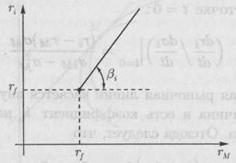
Рис.7. Характеристическая линия
доходности акций i
В основе этой теории ценообразования
рискованных финансовых активов в условиях рыночного равновесия заложены
принципы формирования инвестиционных портфелей, и состоящих в том, что каждый
инвестиционный портфель создается путем объединения двух конкретных типов
активов: безрискового актива и оптимального портфеля рискованных активов,
именуемого рыночным. Теоретически модель ценообразования основных активов
основана на двух предположениях. Во-первых, все инвесторы имеют рациональное
поведение на рынке и идентичны в отношении прогнозов по ожидаемым доходностям,
дисперсиям и корреляциям рисковых активов на финансовом рынке. Следовательно,
они формируют рисковый портфель в одинаковых пропорциях. Во-вторых, на
находящемся в равновесии финансовом рынке цена акции устанавливается таким
образом, что совокупный спрос на акцию равняется его совокупному предложению.
Два этих постулата позволяют сделать вывод, что фондовый рынок может находиться
в состоянии равновесия только в том случае, если оптимальные пропорции владения
рискованными ценными бумагами соответствуют пропорциям, в котором активы
представлены на рынке. Другими словами, оптимальный портфель акций, выбираемый
каждым участником рынка, состоит из пропорций, равных долям в общей
капитализации рынка. Состав такого оптимального портфеля отражает предложение
существующих финансовых активов, оцененных по текущим рыночным ценам. Отсюда и
название рыночного портфеля.
Покажем теперь, что точка М на рис.
6. в действительности определяет точку на плоскости «риск-доходность»,
соответствующую рыночному портфелю. Каждый инвестор будет выбирать точку на
плоскости «риск-доходность», лежащую на прямой FM. Это
означает, что каждая инвестиция комплектуется из рыночного портфеля 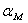 и
безрискового актива, причем пропорции, в которых данный инвестор будет
распределять свой капитал между безрисковым активом и рыночным портфелем,
определяются положением выбранной точки на прямой FM.
и
безрискового актива, причем пропорции, в которых данный инвестор будет
распределять свой капитал между безрисковым активом и рыночным портфелем,
определяются положением выбранной точки на прямой FM.
Если просуммировать все суммы денег,
вложенные в рыночный портфель, то мы получим суммарный капитал, инвестированный
в рисковый актив. Для каждой акции i можно
определить рыночную стоимость Vi фирмы i, перемножив
количество этих акций на рынке на их рыночную цену. Просуммировав рыночные
стоимости всех фирм на рынке, мы получим рыночную стоимость рискового актива.
Поскольку равновесие на рынке определяется равенством спроса и предложения,
суммарный капитал, вложенный всеми инвесторами на рынке в рыночный портфель,
должен быть равным рыночной стоимости рискового актива. Опишем это в следующих
терминах.
Обозначим через Yk капитал,
вложенный в рыночный портфель произвольным инвестором к. Тогда условие
равновесия определяется уравнением:
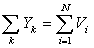 (22)
(22)
Пусть 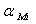 - доля актива i в рыночном
портфеле
- доля актива i в рыночном
портфеле 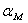 . Тогда
. Тогда 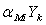 - капитал,
вложенный инвестором k в акцию i. Суммируя
по всем инвесторам, получим рыночную стоимость фирмы i:
- капитал,
вложенный инвестором k в акцию i. Суммируя
по всем инвесторам, получим рыночную стоимость фирмы i:
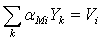
Так как 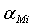 для всех k одинаково,
нетрудно отсюда получить, что
для всех k одинаково,
нетрудно отсюда получить, что
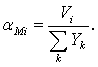
Подставляя уже полученное равенство
(22), находим, что
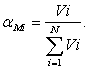
Последнее означает, что доля акций
фирмы i в рыночном
портфеле равна доле рыночной стоимости фирмы i в общей
рыночной стоимости рискового капитала. Таким образом, в условиях рационального
поведения инвесторов и равновесного рынка портфель 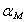 однозначно
определяется рынком. Это еще раз подтверждает его название - рыночный портфель.
однозначно
определяется рынком. Это еще раз подтверждает его название - рыночный портфель.
Таким образом, главным выводом
САРМ-теории является тот факт, что в условиях рыночного равновесия рискованные
активы в портфеле каждого из инвесторов будут формироваться в тех же
пропорциях, в каких они представлены на фондовом рынке. В соответствии с этим
основная рыночная линия FM на плоскости
«риск-доходность» (рис.6) в условиях рыночного равновесия представляет
лучшие из возможных для всех инвесторов комбинации «риск-доходность». Если в
случае неравновесной ситуации у инвесторов появляется возможность достижения
точек, лежащих над основной рыночной линией, то конкуренция на рынке будет
действовать в сторону понижения доходности рискового портфеля, в результате
чего восстановится равновесное состояние рынка и выбор инвесторов снова будет
характеризоваться точками, принадлежащими основной рыночной линии. Уравнение
основной рыночной линии имеет следующий вид:
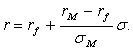
Как уже было замечено, коэффициент
наклона данной прямой 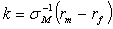 обычно
понимается как рыночная цена риска.
обычно
понимается как рыночная цена риска.
Так как рациональный инвестор не
выходит за пределы основной рыночной линии, можно сделать вывод, что инвесторы
получают вознаграждение, соответствующее более высокой ожидаемой доходности,
только при принятии на себя всего рыночного риска. В этом случае приведенное
уравнение показывает, как увеличится вознаграждение инвестора, если он
принимает на себя дополнительный риск.
Если теперь рассмотреть отдельно
взятую акцию i, то,
согласно САРМ-теории, вознаграждение за риск по данной акции пропорционально ее
вкладу в совокупный риск всего рыночного портфеля. Покажем это на следующем
рассуждении. Пусть
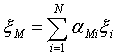
случайная величина доходности по
рыночному портфелю. Тогда нетрудно убедиться, что
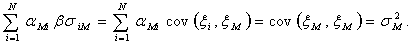
С другой стороны, избыточная
доходность по акции 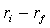 прямо
пропорциональна коэффициенту
прямо
пропорциональна коэффициенту 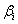 . Так как, коэффициент бета акции i равен
. Так как, коэффициент бета акции i равен 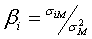 , его можно
интерпретировать как долю риска всего рыночного портфеля, принадлежащую акции i. Поэтому
вознаграждение за риск
, его можно
интерпретировать как долю риска всего рыночного портфеля, принадлежащую акции i. Поэтому
вознаграждение за риск 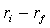 по акции i
пропорционально ее вкладу в совокупный риск всего рыночного портфеля
по акции i
пропорционально ее вкладу в совокупный риск всего рыночного портфеля 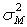 .
.
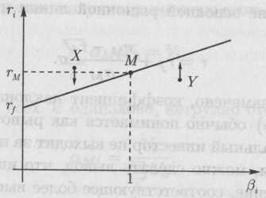
Рис.8. Линия рынка ценных бумаг
Согласно САРМ-теории уравнение
описывает так называемую линию рынка ценных, приведенную на рис.8. При этом
всем акциям, правильно оцененным по САРМ-теории, соответствуют только точки на
данной плоскости, принадлежащие линии рынка ценных бумаг. Предположим, что у
нас есть две акции - X и Y, которые
оценены неправильно, и соответствующие им точки не принадлежат линии рынка
ценных бумаг (см. рис.8). Так как точка X находится
выше линии рынка ценных бумаг, соответствующая ей акция X
обеспечивает более высокий уровень дохода. Инвесторы, видя возможность для
получения повышенного дохода при покупке акций X,
увеличивают спрос на эту акцию. Это поднимает вверх цену на акцию и
одновременно снижает ожидаемую доходность по акции. Тем самым происходит
движение точки X вниз к линии рынка ценных бумаг.
Аналогично, поскольку точка Y находится ниже линии рынка ценных
бумаг, ее ожидаемая доходность оказывается заниженной, а рыночная цена -
завышенной. В этом случае инвесторы могут улучшить свои портфели ценных бумаг,
уменьшая долю акций Y в них. Это приводит к
дополнительному предложению ценных бумаг Y, снижению
цены на акцию Y и повышению
ее доходности. Соответствующая ей точка Y на
плоскости произведет движение вверх к линии рынка ценных бумаг. Когда ожидаемый
доход по этим двум акциям оказывается на уровне, который соответствует точке
линии рынка ценных бумаг, снова восстанавливается равновесное состояние.
Формула (21) дает возможность
считать коэффициент бета акции i мерой чувствительности доходности
данной акции относительно изменений доходности всего рыночного портфеля. В
связи с этим акции, имеющие коэффициент бета больше 1, принято называть
«агрессивными» инвестициями, поскольку их доходность обладает более сильной
динамикой, чем доходность рыночного портфеля. Аналогично этому ценные бумаги,
имеющие коэффициент бета меньше 1, называются «защитными» инвестициями. В
некотором смысле они защищают рыночный портфель от риска. Сам рыночный портфель
имеет коэффициент бета, равный 1.
Следует заметить, что, согласно
математической статистике, коэффициент бета находится по формуле коэффициента
линейной регрессии доходности 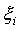 акции i на
доходность
акции i на
доходность 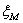 рыночного
портфеля. Уравнение линейной регрессии в этом случае имеет следующий вид:
рыночного
портфеля. Уравнение линейной регрессии в этом случае имеет следующий вид:
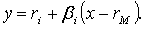
Подставляя вместо у случайную
величину 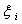 , а вместо х
-
, а вместо х
- 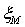 , образуем
случайную величину
, образуем
случайную величину 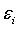 - ошибку
линейной регрессии:
- ошибку
линейной регрессии:
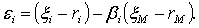
Нетрудно увидеть, что
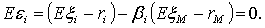
С другой стороны, в силу задания
коэффициента бета (20),
Тогда
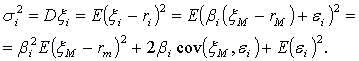
С учетом предыдущих равенств в итоге
получаем, что
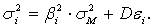
Это означает, что риск 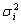 инвестирования
в акцию i равен сумме
двух рисков: систематического риска
инвестирования
в акцию i равен сумме
двух рисков: систематического риска 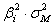 , определяемого рынком, и несистематического
риска
, определяемого рынком, и несистематического
риска 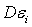 , присущего
непосредственно акции i.
, присущего
непосредственно акции i.
САРМ-теория имеет также важное
значение в силу того, что дает возможность оценивать настоящие стоимости
рисковых финансовых активов. Покажем, как уравнение (21) позволяет вычислить
ставку дисконтирования рисковых потоков наличности.
Рассмотрим акцию i. Ее
доходность за один период является случайной величиной и определяется по
формуле
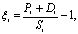
где 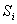 - текущая цена акции,
- текущая цена акции, 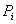 - будущая
цена,
- будущая
цена, 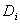 - дивиденд,
выплачиваемый по акции. Так как
- дивиденд,
выплачиваемый по акции. Так как 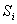 не является случайной величиной,
ожидаемая доходность по акции i равна
не является случайной величиной,
ожидаемая доходность по акции i равна
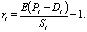
Преобразуя и воспользовавшись
уравнением (21), получаем равенство
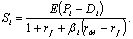 (23)
(23)
В этой формуле числитель равен
ожидаемым от акции платежам, а знаменатель равен единице плюс процентная
ставка, требуемая инвесторами. Чем больше риск по акции, тем больше требуется
ставка доходности и, следовательно, тем меньше цена при заданном уровне будущих
платежей. Таким образом, цена акции выражается с помощью коэффициента
дисконтирования, скорректированного с учетом риска. Поэтому формула (23)
определяет метод учета риска, который принято называть корректировкой
коэффициента дисконтирования.
Есть другой подход учета риска при
оценке текущей цены акции. Пусть
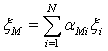
доходность рыночного портфеля. Тогда
ковариация 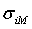 равна
равна
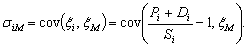
Отсюда, в силу свойств ковариации,
получаем, что
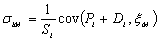
или, переписав,
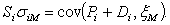
Воспользовавшись теперь формулой для
коэффициента 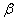 (20),
находим, что
(20),
находим, что
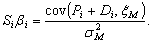
Преобразуем уравнение (23) в
следующем виде:
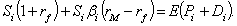
Подставив полученное в это
уравнение, в итоге имеем
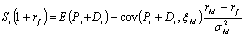
или, окончательно,
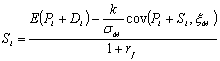
где k - цена
риска. В данной формуле риск учитывается при изменении числителя, а
дисконтирование проводится по безрисковой ставке. Такой скорректированный
числитель принято называть бездисковым эквивалентом. По этому и метод оценки
текущей стоимости акции является подходом с безрисковым эквивалентом.
. Модель формирования цены акции
Будем предполагать, что инвесторы
избегают риска и интересуются размером капитала на конец периода. Капитал
каждого инвестора в начале периода считается заданным. Выплаты по ценным
бумагам, в которые можно инвестировать капитал, являются стохастическими и
определяются набором случайных величин 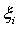 , i = 1, 2,...,n. Инвесторы
формируют портфели рисковых активов, и доходность по портфелю есть случайная
величина, получаемая как линейная комбинация случайных величин
, i = 1, 2,...,n. Инвесторы
формируют портфели рисковых активов, и доходность по портфелю есть случайная
величина, получаемая как линейная комбинация случайных величин 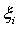 . Главным
предположением по отношению к каждому инвестору является то, что инвесторы
оценивают портфель по величине ожидаемой полезности будущего капитала. Это
означает, что каждый инвестор k определяет максимум ожидаемой
величины некоторой функции полезности
. Главным
предположением по отношению к каждому инвестору является то, что инвесторы
оценивают портфель по величине ожидаемой полезности будущего капитала. Это
означает, что каждый инвестор k определяет максимум ожидаемой
величины некоторой функции полезности 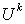 от будущего капитала
от будущего капитала 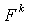 . При этом
будем считать, что данная функция
. При этом
будем считать, что данная функция 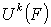 является квадратичной:
является квадратичной:
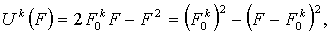 (24)
(24)
где 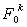 - величина капитала, максимально
возможного для инвестора k. В некотором смысле величину
- величина капитала, максимально
возможного для инвестора k. В некотором смысле величину 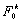 можно
понимать как величину капитала, к которой стремится инвестор k. График
этой функции является параболой. Следствием квадратичности функции полезности
будущего капитала является то, что инвесторы, формируя оптимальный портфель,
интересуются только его ожидаемой доходностью и дисперсией, но не другими
характеристиками портфеля.
можно
понимать как величину капитала, к которой стремится инвестор k. График
этой функции является параболой. Следствием квадратичности функции полезности
будущего капитала является то, что инвесторы, формируя оптимальный портфель,
интересуются только его ожидаемой доходностью и дисперсией, но не другими
характеристиками портфеля.
Инвесторы будут формировать портфель
так, чтобы максимизировать ожидаемую полезность при ограничениях по начальному
капиталу и по предложению бумаг на рынке. В рамках заданной модели будем
предполагать установление равновесных цен на финансовые активы в условиях
конкурентного рынка. Последнее означает, что инвесторы формируют портфели,
максимизирующие ожидаемую полезность капитала, и предложение активов каждого
вида равно спросу.
При построении модели конкурентного
равновесия в экономике с неопределенностью нами будут сделаны два шага.
Во-первых, при данных ценах мы докажем справедливость инвестировании в два
фонда. Во-вторых, мы определим равновесную стоимость каждой фирмы в экономике.
После этого легко подсчитываются равновесные цены на каждую акцию.
Напомним, что если инвесторы
интересуются только ожидаемой доходностью и дисперсией доходности портфеля, то
они будут формировать свой портфель как комбинацию только рыночного портфелям 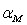 и
безрискового актива. Одним из следствий этого результата является факт, что
доля стоимости фирмы i, принадлежащая инвестору k, равна доле
фирмы j. Пусть
и
безрискового актива. Одним из следствий этого результата является факт, что
доля стоимости фирмы i, принадлежащая инвестору k, равна доле
фирмы j. Пусть 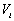 и
и 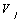 обозначают
рыночные стоимости этих фирм, a
обозначают
рыночные стоимости этих фирм, a 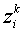 и
и 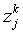 - доли
фирм, принадлежащих инвестору k, так что количество денег,
вложенных инвестором k в фирму i, равно
- доли
фирм, принадлежащих инвестору k, так что количество денег,
вложенных инвестором k в фирму i, равно 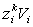 . Тогда
легко получить равенство
. Тогда
легко получить равенство 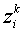 =
=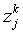 . Напомним,
что
. Напомним,
что 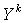 обозначает
количество денег, вложенных инвестором k в рисковые
активы, и
обозначает
количество денег, вложенных инвестором k в рисковые
активы, и 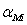 обозначает
долю фирмы i в рыночном
портфеле. Тогда стоимость фирмы i в портфеле инвестора k равна
обозначает
долю фирмы i в рыночном
портфеле. Тогда стоимость фирмы i в портфеле инвестора k равна  . Таким
образом, мы имеем
. Таким
образом, мы имеем 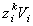 =
= 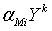 , так что
условие
, так что
условие 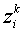 =
=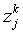 будет
выполнено, если
будет
выполнено, если 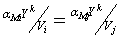 или
или 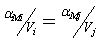 . Но
последнее равенство следует непосредственно из определения
. Но
последнее равенство следует непосредственно из определения 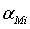 и
и 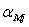 . Поскольку
. Поскольку 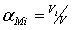 , где V - суммарная
рыночная стоимость всех фирм, мы получаем
, где V - суммарная
рыночная стоимость всех фирм, мы получаем 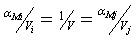 .
.
Для аналитического удобства спрос
каждого инвестора задается как желаемая (для владения) доля каждой фирмы. Мы
покажем, что из предположения о квадратичности функций полезности вытекает, что
каждый инвестор желает владеть одной и той же долей во всех фирмах. Этот факт
существенно используется при выводе основного уравнения для рыночной стоимости
фирмы. Оказывается, что стоимость каждой фирмы может рассматриваться как
текущая стоимость ее будущих доходов, скорректированных с учетом риска.
Введем следующие обозначения и
допущения. Как и ранее, будем считать, что 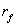 - безрисковый процент (кредиты
даются под данный процент). Пусть также каждая фирма j имеет
рыночную стоимость
- безрисковый процент (кредиты
даются под данный процент). Пусть также каждая фирма j имеет
рыночную стоимость 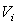 . Если
. Если 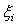 - доходность
по акциям фирмы j за единичный период, то
- доходность
по акциям фирмы j за единичный период, то 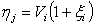 определяет
рыночную стоимость фирмы j в конце периода. Соответственно,
случайная величина
определяет
рыночную стоимость фирмы j в конце периода. Соответственно,
случайная величина 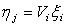 определяет
выплаты фирмы j своим
инвесторам на конец периода. Обозначим через
определяет
выплаты фирмы j своим
инвесторам на конец периода. Обозначим через 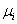 и
и 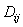 математическое ожидание случайной
величины
математическое ожидание случайной
величины 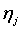 и
ковариацию случайных величин
и
ковариацию случайных величин 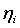 и
и 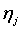 соответственно. Пусть, как и ранее,
соответственно. Пусть, как и ранее,
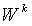 - начальный
капитал инвестора k, a
- начальный
капитал инвестора k, a 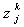 - доля
фирмы j,
выкупленная инвестором k в начальный момент времени.
Нетрудно убедиться, что капитал инвестора k в конце
периода оценивается формулой
- доля
фирмы j,
выкупленная инвестором k в начальный момент времени.
Нетрудно убедиться, что капитал инвестора k в конце
периода оценивается формулой
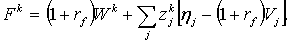 (25)
(25)
В этом выражении  определяет
доход от начального капитала,
определяет
доход от начального капитала, 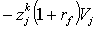 есть потери дохода из-за вложения
капитала в фирму j, наконец,
есть потери дохода из-за вложения
капитала в фирму j, наконец, 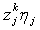 есть
выплаты фирмы j инвестору k.
есть
выплаты фирмы j инвестору k.
Предположим, что функция полезности 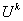 капитала
инвестора k является
квадратичной и определяется формулой (24). Тогда ожидаемая полезность конечного
капитала, заданного формулой (25), равна
капитала
инвестора k является
квадратичной и определяется формулой (24). Тогда ожидаемая полезность конечного
капитала, заданного формулой (25), равна
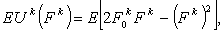 (26)
(26)
где Е обозначает математическое
ожидание выражения в квадратных скобках. В предположении, что на короткую
позицию нет ограничений, необходимое и достаточное условие для максимизации
ожидаемой полезности по переменным 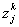 записывается в следующем виде:
записывается в следующем виде:
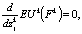
откуда после соответствующих
преобразований получаем, что
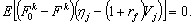 (27)
(27)
Воспользовавшись свойствами
математического ожидания и ковариации, из уравнения (25) нетрудно вывести
следующие соотношения:
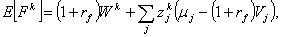 (28)
(28)
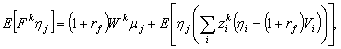 (29)
(29)
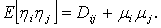 (30)
(30)
Раскрывая (27) и используя
(28)-(30), выпишем условия на 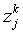 в следующем виде:
в следующем виде:
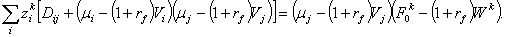 (31)
(31)
Отметим, что характеристики
инвесторов входят в правую часть множителем. Поэтому можно решить
соответствующую систему относительно вспомогательных переменных 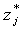 , умножив которые
затем на
, умножив которые
затем на 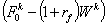 , мы получим
искомые переменные
, мы получим
искомые переменные 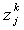 . Теорема об
инвестировании в два фонда, в сущности, основана на возможности представить
уравнение в такой форме. Окончательно, пусть
. Теорема об
инвестировании в два фонда, в сущности, основана на возможности представить
уравнение в такой форме. Окончательно, пусть 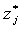 - решение следующей системы:
- решение следующей системы:

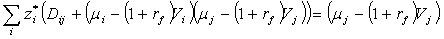 (32)
(32)
Тогда 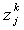 определяется уравнением
определяется уравнением
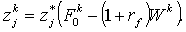
В равновесии должно выполняться
условие 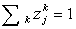 , т.е. сумма
долей любой из фирм по всем инвесторам должна равняться единице. Отсюда мы
имеем
, т.е. сумма
долей любой из фирм по всем инвесторам должна равняться единице. Отсюда мы
имеем
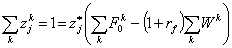 (33)
(33)
и, тем самым,
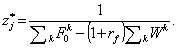 (34)
(34)
Из (33) и (34) следует
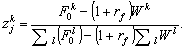 (35)
(35)
Из (35) видно, что 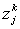 не зависит
от j, так что
доля любой фирмы для инвестора k определяется только
характеристиками инвестора. Эту долю обозначим через
не зависит
от j, так что
доля любой фирмы для инвестора k определяется только
характеристиками инвестора. Эту долю обозначим через 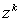 .
.
Используя данный результат,
становится относительно легко определить 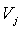 - рыночную стоимость фирмы j. Уравнение
спроса(31) можно теперь переписать в виде
- рыночную стоимость фирмы j. Уравнение
спроса(31) можно теперь переписать в виде
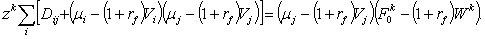
Поскольку 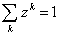 мы имеем
мы имеем
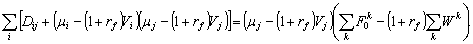 (36)
(36)
Наконец, используем тот факт, что 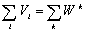 , т. е.
суммарная рыночная стоимость всех активов равна суммарному капиталу в
экономике. Подставляя в (36), получаем
, т. е.
суммарная рыночная стоимость всех активов равна суммарному капиталу в
экономике. Подставляя в (36), получаем
Раскрывая скобки, в итоге имеем
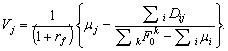 (37)
(37)
Уравнение (37) определяет рыночную
стоимость фирмы в целом. Уравнение утверждает, что стоимость фирмы j равна
текущей стоимости (по проценту безрискового актива) сконцентрированных с учетом
риска ожидаемых платежей. Поправка на риск зависит от среднего отношения
инвесторов к риску и от ковариаций платежей данной фирмы со всеми другими
фирмами в экономике (систематический риск).
Заключение
В нашей прежней экономике ценные бумаги не
пользовались популярностью, не считая принудительного насаждения облигаций
государственных займов, которые никто не называл и не считал ценными бумагами.
Получение процентов, дивидендов на ценные бумаги считалось нетрудовыми
доходами, исключение представляли выигрыши по облигациям и лотерейным билетам.
По мере перехода к рыночной экономике ситуация
стала существенным образом изменяться. В то же время рынку бумаг как части
более общего финансового рынка предстоит пройти еще длинный путь становления и
врастания в формирующуюся рыночную экономику.
Выпуск ценных бумаг - важный источник
привлечения средств для молодых предприятий, мобилизации дополнительного
капитала для уже существующих предприятий, а также пополнения государственного
и местного бюджета. Это своеобразный канал финансирования. Если тебе не достает
денег, ты выпускаешь ценные бумаги, продаешь их на рынке ценных бумаг и
обретаешь деньги.
Следует отметить, что введение различного вида
ценных бумаг в финансово-денежный оборот позволяет без увеличения общей денежной
массы повысить мобильность финансовых ресурсов, сосредоточить их на более
важных участках производства, обращение, потребление продукции, товаров и
услуг. Направление инвестирования, то есть вложения средств, определяется на
рынке спросом и предложением, возможностью получения для инвесторов большей
прибыли при равном риске вложений. Выпуск ценных бумаг чаще всего и
сосредоточен в тех областях и сферах, которые обещают принести большой доход.
Но прежде чем такой доход будет получен, предпринимателю приходится вложить в
дело первоначальный, стартовый капитал. Этот капитал и можно получить и
привлечь за счёт ценных бумаг.
Особое значение в нашей стране выпуск ценных
бумаг приобретает в условиях перевода государственных предприятий в
коллективную и частную собственность посредством приватизации. Основной формой,
главным способом приватизации является акционирование. Оно понимается двояким
образом.
С одной стороны, это возможность превращения
государственного предприятия в акционерное общество, то есть перехода от
государственной формы собственности к коллективно-частной, в рамках которой
собственниками предприятий становятся организации и лица, приобретающие акции
данных предприятий.
С другой стороны, если предприятие приходится
выкупать у нынешних собственников в лице уполномоченных государственных
органов, то необходимые для этого денежные средства могут быть получены путём
продажи акций приватизируемого предприятия.
Таким образом, приватизация государственных и
муниципальных предприятий способна дать толчок развитию рынка ценных бумаг.
Обладающие денежными ресурсами и покупающие
ценные бумаги выполняют полезную миссию. Согласно мудрому высказыванию М. Е.
Салтыкова -Щедрина, «разумный кредитор помогает должнику выйти из стеснённых
обязательств и в вознаграждение за свою разумность получает свой долг.
Неразумный кредитор сажает должника в острог или непрерывно сечёт его и в
вознаграждение не получает ничего».
Знание видов ценных бумаг, возможностей их
приобретения и продажи, правил обращения, выгод и опасностей их покупки сегодня
крайне необходимо не только хозяйственным руководителям и предпринимателям, но
членам трудовых коллективов просто человеку, желающему стать обладателем акции,
облигации, сертификата.
Довольно часто покупатель ценной бумаги,
приобретающий её тем или иным способом, просто не в состоянии оценить, какие
ценные бумаги целесообразно хватать, а какие нет. В особенности тяжело сделать
выбор российскому народу, который, не в обиду будет сказано, не ахти какой
грамотей в части рыночной, да и вообще любой экономики. Впрочем, в нынешней
экономической кутерьме и специалисту нелегко определить рациональный способ
действий. Рынок, как говорится, есть рынок, и риска на нём не избежать.
Список литературы
1.
Летчиков А.В. Лекции по финансовой математике. М.:Наука.
2008
.
Соловьев Е. Н. Фондовая биржа капиталистических стран. Киев: Слово,
.
148 с.
.
Сомов Е. Н., Киселева М. Б. Фондовая Биржа и ее роль в экономике. М.:
АО
Leon, 2004. 288 с.
.
Карташов А. Г. Как заработать деньги. М.: Наука, 2001. 107 с.
.
Фондовая Биржа/ Алехин Б.// Экономические науки. 1991. номер 8. с. 54-61.
.
Фондовая Биржа/ Мусатов В.// Экономические науки. 2001. номер 7. с. 55- 65.
.
Акция// Северное побережье.2009. 23. 09.