Задача максимизации прибыли от продаж
КУРСОВАЯ
РАБОТА
по
дисциплине: «Эконометрическое моделирование»
Задача
максимизации прибыли от продаж
Введение
В данной курсовой работе
раскрывается тема «Максимизации прибыли от продаж»: производится поиск
оптимальной цены продажи товаров трёх видов, закупленных у производителя по
некоторым ценам, при непрерывном распределении прибыли, представленным
нормальным законом, и при дискретном, - пуассоновским; проверяются гипотеза о
нормальности распределения прибыли с продаж и гипотеза о неравенстве её
дисперсий.
Целью работы является навык
нахождения оптимальной цены, дающей наибольшую прибыль при помощи программного
средства MATLAB.
Задача максимизации прибыли с
продаж
Регрессионный анализ решает
задачу максимизации текущей прибыли продавца, абстрагируясь от конкретных
механизмов ценообразования, которые, как известно, сложны и разнообразны в
условиях и совершенной конкуренции, и олигополии, и монополии. В дальнейшем
будем называть оптимальной ценой товара такую цену, которая приводит к максимуму
прибыли за выделенный период времени. Еще оговорим важное условие, что из-за
временного тренда цен в течение этого периода, изменение прибыли с продаж много
меньше возможного прироста прибыли в результате решения задачи максимизации.
Непрерывное распределение
прибыли
Задача 1
Найти оптимальную пену продажи
товаров трех видов, закупленных у производителя по ценам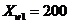 
руб., 
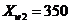и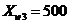 
руб. за 1
кг массы. Для проведения эксперимента использовать имитационную модель
profit3norm(D), где D - матрица дизайна эксперимента, генерирующую случайную
прибыль от продажи товаров. Цены за 1 кг могут изменяться в таких интервалах: 
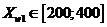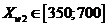руб.,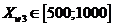 
руб., 
руб.
Прежде чем приступить к
регрессионным оценкам, покажем, каким образом имитационная модель profit3norm
позволяет проводить опыты, моделируя продажу товаров в обычном режиме.
Допустим, что за 1 кг первого товара
назначена из априорных соображений цена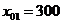 
руб., второго - 
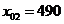руб. и
третьего - 
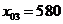руб.
Например, используя 4 точки продажи
товара в течение одного заданного периода времени пли 1 точку продажи в течение
четырех последовательных периодов получим следующие результаты.
Опыт 1=300;=490;=580;=[X01, X02,
X03];=profit3norm(D)
Массы продаж:= 17.4395 10.1606
18.2867
Прибыль:= 4629.38
Опыт 2=300;=490;=580;=[X01,
X02, X03];=profit3norm(D)
Массы продаж:
m = 17.7338 8.4880
16.9476
Прибыль:
Y = 4317.50
ОпытЗ=300;=490;=580;=[X01, X02,
X03];=profit3norm(D)
Массы продаж:= 17.9844
9.6691 17.7280
Прибыль:= 4570.35
Опыт 4=300;=490;=580;=[X01,
X02, X03];=profit3norm(D)
Массы продаж:= 18.1529 8.6035
18.3119
Прибыль:
Y = 4484.73
Так, получена средняя прибыль:mean=
(4629.38 + 4317.50 + 4570.35 + 4484.73 )/4mean =
.49
Для увеличения прибыли с продаж, т.
е. для поиска оптимальных цен товаров сформируем, схему продаж, основанную на
полном факторном эксперименте с числом опытов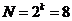
, где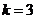 
- число факторов, т. е. число
товаров, вошедших в экспериментальную группу. Такая схема позволит построить
регрессионную модель продаж
Одним из практически важных
достоинств симметричного дизайна, которым обладает полный факторный
эксперимент, является то, что при его проведении не изменяется статистически
значимо средняя прибыль. Другими словами, продажи товаров в схеме полного
факторного эксперимента не снижают прибыли, получаемой в обычном режиме продаж.
Еще заметим, что в реальных условиях
проведение 8 опытов требует либо 8 точек продаж в течение 1 периода времени,
либо 4 точек продаж в течение двух, последовательных периодов времени и т. д. В
любом варианте необходимо провести 8 опытов.
Выберем в качестве основного уровня
матрицы дизайна уже известные нам значения цен 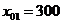руб., 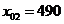руб. и 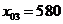руб. за 1 кг
зададим интервалы варьирования цен равными, к примеру, 10 % от значений
основных цен и примем уровень значимости статистических оценок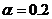 
. На этом
основании
) построим матрицу дизайна полного
факторного эксперимента,
) проведем продажи товаров в
соответствии с этой матрицей,
) получим для заданного уровня
значимости регрессионные оценки: оценки коэффициентов регрессии, оценки
доверительных интервалов коэффициентов регрессии и оценку р-величины
регрессионной модели.
Следующий скрипт-файл реализует
названные этапы решения задачи.all
disp('ПОЛНЫЙ ФАКТОРНЫЙ
ЭКСПЕРИМЕНТ’) %
format
bank=fracfact('a b с'); X=[ones(length(d),1) d];
%X=[X;X];=[300
490 580];=0.05*X0; %dX=[30 49 58];
%Xm=[248.00
420.00 670.00]; dX=[10 10 10]; X0=Xm;
%Xm=[249.5
419.5 667.5]; dX=[30 49 58]; X0=Xm;=length(X);=[X(:,1)*X0(:,1)+X(:,2)*dX(:,1)…(:,1)*X0(:,2)+X(:,3)*dX(:,2)…(:,1)*X0(:,3)+X(:,4)*dX(:,3)]=profit3norm(D)=0.2;
[b,bint,r,rint,stats]
= regress(Y,X,alpha);=[b bint]short=stats(3)
Получена
статистически значимая модель
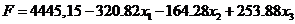
с оценками доверительных интервалов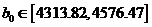 
, 
, 
, 
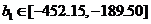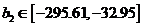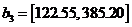на уровне
значимости 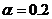. Эта модель
дает основание для использования градиентного метода.
Рассчитаем, например, 5 шагов
движения по градиенту, приняв параметр шага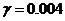 
disp('PACЧET ШАГОВ ДВИЖЕНИЯ ПО
ГРАДИЕНТУ’) % -------------
format bank=b(2:4)';
%=0.004;=6;j=1:ng(j,1:3)=X0+(j-1)*gamma*b.*dX;
Элементы матрицы G говорят о
том, что цена 1-го товара при движении по градиенту выйдет за границу его
закупочной цены на 6-м шаге. Поэтому при проведении опытов, обеспечивающих
движение по градиенту, ограничимся пятью шагами:
disp ('ДВИЖЕНИЕ ПО ГРАДИЕНТУ’)
% ----------=profit3norm(G(2:ng-1,:))
[[Ym,kYm]=max(Y);
Учитывая, что на основном
уровне выбранного дизайна получено значение прибыли 4445.15 руб., можно
предположить, что реализовано восхождение по градиенту. Далее надо убедиться,
что на третьем шаге восхождения было получено значение прибыли, которое
статистически значимо отличается от значения на основном уровне. С этой целью
начнем продавать товары по новым ценам:
disp('СРАВНЕНИЕ СРЕДНИХ’) %
N=4;=G(ones(1,N),:)=profit3norm(D0)('Средняя
прибыль на основном уровне матрицы дизайна:')mean=sum(Y0)/N=G([kYm kYm kYm
kYm],:)=profit3norm(D)('Средняя прибыль на 3-ем шаге движения по
градиенту:')=sum(Ymgrad)/N=[Y0 Ymgrad];('Оценка p-value различия
средних')short=anoval(gradmean)
Результаты сравнения средних,
представленные на рис. 1 и 2, говорят о статистически значимом их различии и
дают основание перейти к построению модели 2-го порядка с целью более точного
определения координат экстремальных продаж.
disp('ЦЕНТРАЛЬНЫЙ КОМПОЗИЦИОННЫЙ
ДИЗАЙН') %
format
bank=3;=ccdesign(k);=[ones(length(p),1),p,p(:,1).^2,p(:,2).^2,p(:,3).^2];=length(p)G=G(kYm+1,1:3)=0.1*X0G;
%xm=[249.5 419.5
667.50]bank=[ones(N,1)*X0G(:,1)+p(:,1)*dX2(:,1)…(N,1)*X0G(:,2)+p(:,2)*dX2(:,2)…(N,1)*X0G(:,3)+p(:,3)*dX2(:,3)]=profit3norm(D)
%alpha=0.2;
[b,bint,r,rint,stats] =
regress(Y,X,alpha);=[b bint]short=stats(3)
На основании полученной модели
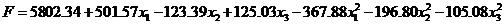
можно найти оценки координат
экстремума
format bank=[2*b(2) 0 0;0
2*b(3) 0; 0 0 2*b(4)],
В=[-b(5);-b(6);-b<7)]
хm=А^-1*B=X0G'+xm.*dX'=b(1)+sum(b(2:4).*xm(1:3))+sum(b(5:7).*xm(1:3).^2)
Графическая иллюстрация
результатов дана на рис. 3 и 4. На этих рисунках ромбом обозначены истинные
координаты экстремума, заданные в нашем случае имитационной моделью.
Рис. 3
Задача 2
Проверить гипотезу о
нормальности распределения прибыли с продаж, генерируемых имитационной моделью
profit3norm(D), где D - матрица дизайна эксперимента.
Для проведения опытов возьмем точку
факторного пространства с координатами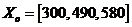 
.bank=[300 490
580];=200;=ones(N,1)*X0;=profit3norm(D);
%probplot(Y)(Y)
Результат исполнения этого
алгоритма, представленный на рис. 5, подтверждает гипотезу о нормальном
распределении прибыли с продаж
Задача 3
Проверить гипотезу о неравенстве
дисперсий прибыли с продаж, генерируемых имитационной моделью profit3norm(D),
где D - матрица дизайна эксперимента.
Проверим на уровне значимости 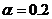гипотезу о
неравенстве дисперсий прибыли на основном уровне 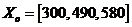полного факторного эксперимента и в
найденной точке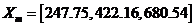 
экстремума
квадратичной модели.=10;
Х0=[300.00 490.00 580.00];=ones(N,1)*Х0;=profit3norm(D0);=[247.75
422.16 680.54];=ones(N,1)*XmCCD;=profit3norm(DmCCD);_YmCCD=[Y0 YmCCD]('Проверка
гипотезы о не равенстве дисперсий')=0.2;
[h,p,ci,stats] =
vartest2(Y0,YmCCD,alpha,'both')
Результаты тестовой статистики
говорят о том, что гипотеза о неравенстве дисперсий должна быть отклонена.
Дискретное распределение прибыли
прибыль распределение
дисперсный
Задача
Найти оптимальную цену продажи
товаров трех видов, закупленных у производителя по ценам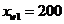 
руб., 
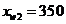и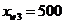 
руб. Для
проведения эксперимента использовать имитационную модель profit3(x1,x2,x3),
генерирующую случайную прибыль от продажи трех товаров, цены на которые могут
изменяться в следующих интервалах: 
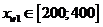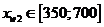руб.,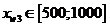 
руб., 
руб.
Сначала проверим, каким образом
имитационная модель profit3 позволяет проводить опыты, моделируя продажу
товаров в обычном режиме.
Допустим, на первый товар из
априорных соображений назначена цена х01= 300 руб., на второй - х02 = 490 руб.
и на третий - х03 = 580 руб. Например, используя 4 точки продажи товара в
течение одного заданного периода времени или 1 точку продажи в течение четырех
последовательных периодов получим следующие результаты.
Опыт
1=300;=490;=580;=[x01,x02,x03];=profit3{D)
Число продаж:= 19 8 22
Прибыль:= 4780.00
Опыт
2=300;=490;=580;=[x01,x02,x03];=profit3(D)
Число продаж:= 18 11 14
Прибыль:
Y = 4460.00
Опыт
3=300;=490;=580;=[x01,x02,x03];=profit3(D)
Число продаж:
n = 21 8 18
Прибыль:
Y= 4660.00
Опыт
4=300;=490;=580;=[x01,x02,x03];=profit3(D)
Число продаж:= 21 4 15
Прибыль:
Y = 3860.00
Средняя прибыльmean= (4780.00 +
4460.00 + 4660.00 + 3860.00)/4mean =
.00
Для увеличения прибыли с продаж, т.
е. для поиска оптимальных цен товаров вновь сформируем схему продаж, основанную
на полном факторном эксперименте. Выберем в качестве основного уровня значения
цен x01 =300 руб., х02 = 490 руб. и x03=580 руб., которые использовались в
обычной схеме продаж. Далее зададим интервалы варьирования цен равными 10% от
значений основных цен и примем уровень значимости статистических оценок .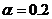
Простейшая стратегия поиска
экстремума
Для построения линейной модели
прибыли
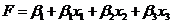
составим скрипт-файл дизайна полного
факторного эксперимента с определенными выше координатами основного уровня.
Сlearbank=fracfact('a
b с');=length(d);=[ones(N,1)d];=[300 490 580];=[30 49
58];=[ones(:,1)*x0(:,1)+x(:,2)*dx(:,1)…(:,1)*x0(:,2)+x(:,3)*dx(:,2)…(:,1)*x0(:,3)+x(:,4)*dx(:,3)]=profit3(D);_Y=[n,Y]=0.2;
[b,bint,r,rint,stats]
= regress(Y,X,alpha);=[b bint]short=stats(3)
Получена
статистически значимая модель
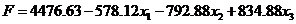
Которая
даёт основание для использования градиентного метода
Рассчитаем,
например, 10 шагов движения по градиенту, приняв параметр шага
.bank=[300
490 580];=[30 49 58];=[-578.12 -792.88
834.88];=0.001;n=1:10(n,1:3)=x0+(n-1)*gamma*b.*dx;
Элементы
матрицы G говорят о том, что цена одного товара при движении по градиенту
выйдет за границу его закупочной цены на 6-м шаге, а цена второго товара - на
4-м шаге. Поэтому при проведении опытов, обеспечивающих движение по градиенту,
ограничимся 3 шагами:
=profit3(G(2:4,:))
Учитывая,
что на основном уровне выбранного дизайна получено значение прибыли 4440.00
руб., можно предположить, что реализовано восхождение по градиенту. Далее надо
убедиться, что на 2-м шаге восхождения полученная величина прибыли 5465.16
статистически значимо отличается от величины прибыли на основном уровне. С этой
целью начнем продавать товары по новым цепам:
Опыт
1=265.31;
х02=412.3;
х03=676.85;=[x01,x02,x03];=profit3(D)
Число
продаж:= 32 37 15
Прибыль:=
.77
Опыт
2=265.31;
х02=412.3;
х0З=676.85;=[x01,x02,x03];=profit3(D)
Число
продаж:= 34 25 11
Прибыль:=
.39
Опыт
3=265.31;
х02=412.3;
х03=676.85;=[x01,x02,x03];=profit3(D)
Число
продаж:= 51 23 8
Прибыль:=
.51
Опыт
4=265.31;=412.3;=676.85;=[x01,x02,x03];=profit3(D)
Число
продаж:= 31 27 7
Y =
4944.66
Таким образом, в точке с
координатами х1=265.31 руб., х2=412.3 руб. и х3=676.85 руб. получена средняя
прибыльmean=(5723.39 +5723.39+6178.51+4944.66)/4mean=5642.49
которая на
(5642.49-4440.00)/4440.00*100=
.08 %
больше той, которую получил
продавец при обычной схеме назначения цен на товары.
Дадим оценку значимости
различия средних:, clc, close=4;('Опытные данные на основном уровне матрицы
дизайна:')= [4780.00;4460.00;4660.00:3860.00]('Среднее значение свойства на
основном уровне матрицы дизайна:')mean=sum(Y0)/N('Опытные данные на 2-ом шаге
движения по градиенту:’)= [5723.39;5723.39;6178.51;4944.66]('Среднее значение
свойства на 2-ом шаге движения по градиенту')mean=sum(Y2)/N=[Y0 Y2];('Оценка
p-value различия средних')short=anoval(gradmean)
На рис. 9.6 приведена таблица
ANOVA, которая, помимо оценки р-величины, содержит промежуточные оценки сумм
квадратов и величины F-статистики.
Таким образом, уменьшение цен
на первый товар с x01=300 руб. до x1=265.31 руб. и на второй товар с x02 =490
руб. до х2=412.3 руб. и увеличение цены на третий товар с х03=580 руб. до
х3=676.85 руб. привело к увеличению прибыли приблизительно на 27 %. Произошло
это за счет большего роста числа продаж менее дорогих 1-го и 2-го товаров по
сравнению с уменьшением числа продаж более дорогого 3-го товара.
Графическая иллюстрация результатов
исследования модели profit3 приведена на рис. 8 и 9. Точка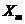 
на графиках
обозначает координаты экстремума имитационной модели дискретных продаж.
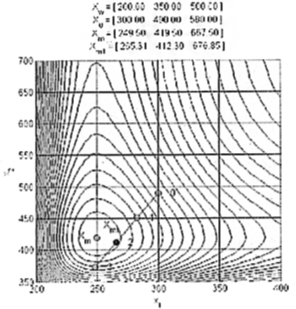
Рис. 8
Рассмотренный вариант простейшей
стратегии решения экстремальной задачи основывался на довольно хороших выборках
данных, что обеспечило быстрое ее решение, вряд ли требующее дальнейшего
анализа.
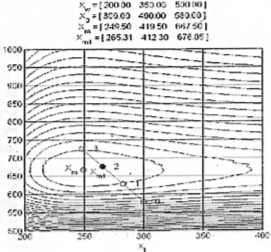
Рис. 9
Рассмотрим более реалистичный случай
с менее определенной выборкой данных, которая может существенно усложним,
стратегию решения экстремальной задачи.
Один из вариантов более реалистичной
стратегии
Вновь
обратимся к имитационной модели profit3 для проведения полного факторного
эксперимента при тех же значениях координат основного уровня и интервалов
варьирования переменных. Ясно, что в силу заложенной в модель profit3
стохастичности прибыли, регрессионный полином примет новый вид.bank=fracfact('a
b с');=length(d);=[ones(N,1)d];=[300 490 580];=[30 49
58];=[ones(:,1)*x0(:,1)+x(:,2)*dx(:,1)…(:,1)*x0(:,2)+x(:,3)*dx(:,2)…(:,1)*x0(:,3)+x(:,4)*dx(:,3)]=profit3(D);_Y=[n,Y]=0.2;
[b,bint,r,rint,stats]
= regress(Y,X,alpha);=[b bint]short=stats(3)
Итак,
оценка коэффициента линейной регрессии при второй переменной оказалась
статистически незначимой. Поэтому аппроксимационный полином принимает вид
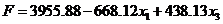
отличный
от вида полинома, полученного в предыдущем решении. Как следствие, движение по
градиенту приобретает качественно новые черты. Рассчитаем, например, 10 шагов
движения по градиенту, оставляя параметр шага .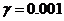
disp('PACЧET ШАГОВ ДВИЖЕНИЯ ПО
ГРАДИЕНТУ’) % -------------
format bank=[300 490 580];=[30
49 58];=[-668.12 0 438.13];=0.001;n=1:10(n,1:3)=X0+(n-1)*gamma*b.*dx;
Элементы матрицы G говорят о
том, что цена 1-го товара при движении по градиенту выйдет за границу его
закупочной цены на 5-м шаге. Поэтому при проведении опытов, обеспечивающих
движение по градиенту, следует ограничиться четырьмя шагами.
Процедура движения по
градиенту, в отличие от полного факторного эксперимента, несет в себе
потенциальную опасность потери некоторой части прибыли в случае неверного
определения направления наискорейшего возрастания функции прибыли. Для
уменьшения риска потерь следует двигаться по градиенту, последовательно ставя
повторные опыты в каждой намеченной-точке градиентного луча и каждый раз давая
оценку статистической значимости отличия средних на основном уровне и в новой
точке.
Ограничимся четырьмя повторными
опытами в каждой точке,
Шаг 1
% В рабочем пространстве MATLAB
должна быть матрица Gi=i:4,p(i)=profit3(G(2,:));Y=p(i),end,=4;('Опытные данные
на основном уровне матрицы дизайна:')=
[4780.00;4460.00;4660.00:3860.00]('Среднее значение свойства на основном уровне
матрицы дизайна:')mean=sum(Y0)/N('Опытные данные на 1-ом шаге движения по
градиенту:’)=p’('Среднее значение свойства на 1-ом шаге движения по
градиенту')mean=sum(Y1)/N=[Y0 Y1];('Оценка p-value различия
средних')short=anoval(gradmean)
Шаг 2all
% В рабочем пространстве MATLAB
должна быть матрица Gi=i:4,p(i)=profit3(G(3,:));Y=p(i),end,=4;('Опытные данные
на основном уровне матрицы дизайна:')= [4780.00;4460.00;4660.00:3860.00]('Среднее
значение свойства на основном уровне матрицы дизайна:')mean=sum(Y0)/N('Опытные
данные на 2-ом шаге движения по градиенту:’)=p’('Среднее значение свойства на
2-ом шаге движения по градиенту')mean=sum(Y2)/N=[Y0 Y2];('Оценка p-value различия
средних')short=anoval(gradmean)
Шаг 3all
% В рабочем пространстве MATLAB
должна быть матрица Gi=i:4,p(i)=profit3(G(4,:));Y=p(i),end,=4;('Опытные данные
на основном уровне матрицы дизайна:')= [4780.00;4460.00;4660.00:3860.00]('Среднее
значение свойства на основном уровне матрицы дизайна:')mean=sum(Y0)/N('Опытные
данные на 3-ем шаге движения по градиенту:’)=p’('Среднее значение свойства на
3-ем шаге движения по градиенту')mean=sum(Y3)/N=[Y0 Y3];('Оценка p-value различия
средних')short=anoval(gradmean)
Рис. 10-15 иллюстрируют
статистический анализ результатов шагов движения по градиенту. Из этого анализа
вытекает, что в точке факторного пространства с ценами x1=239.87 руб., х2=490.00
руб. и х3=656.23 руб. получена средняя прибыль, которая на
(5501.47-4440.00)/4440.00*100=
.9070 %
больше той, которую получал
продавец при обычной схеме назначения цен на товары.
По сравнению с выборкой,
обусловившей простейшую стратегию, рассмотренную в предыдущем разделе, новая
выборка привела к решению, которое оказалось более трудоемким и к тому же
привело к меньшему увеличению прибыли.
С целью большего увеличения
прибыли с продаж примем решение построить квадратичную аппросимацию области
экстремума с помощью полинома
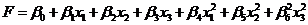
Для определения оценок коэффициентов
регрессии используем центральный композиционный дизайн.
Clear,('ЦЕНТРАЛЬНЫЙ
КОМПОЗИЦИОННЫЙ ДИЗАЙН') %
format
bank=3;=ccdesign(k);=[ones(length(p),1),p,p(:,1).^2,p(:,2).^2,p(:,3).^2];=length(p)=[20
80 100];
%xm=[249.5 419.5
667.50]bank=[ones(N,1)*x0(:,1)+p(:,1)*dx2(:,1)…(N,1)*x0(:,2)+p(:,2)*dx2(:,2)…(N,1)*x0(:,3)+p(:,3)*dx2(:,3)]=profit3norm(D)
%alpha=0.2;
[b,bint,r,rint,stats] =
regress(Y,X,alpha);=[b bint]short=stats(3)
Получена модель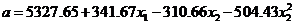 
, в которой
оценка коэффициента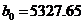 
подтверждает
с доверительным интервалом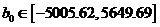 
при доверительной вероятности 
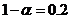предыдущую
оценку прибыли 5501.47 руб.
Коэффициент при 1-й переменной
оказался положительным. То есть при движении по градиенту область экстремума
вдоль 1-й переменной была пройдена, и необходимо уменьшить цену первого товара.
Сделать это можно либо новой реализацией градиентного восхождения, либо
повторной квадратичной аппроксимацией.
Вдоль второй переменной имеет место
максимум прибыли. Оценим координаты экстремума:bank=-310.66;b6=-504. 43 ;
хm=[0;-b3/b6/2; 0]=x0'+xm.*dx'=
.31
=
.87
.37
.23
Поправка оказалась небольшой.
Поэтому примем решение прервать процесс активного вмешательства в изменение цен
на заданную группу товаров и перейти к сбору статистической информации по
продаже этих товаров по ценам
х1 = 239.87 руб, х2 = 465.37 руб, х3
= 656.23 руб.,
найденным по результатам
квадратичной аппроксимации области экстремума прибыли. Реализуем это решение с
помощью уже использованного центрального композиционного дизайна, приняв за
основной уровень точку с координатами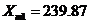 
руб., 
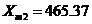и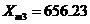 
руб.,clc=3;=ccdesign(k);=[ones(length(p),1),p,p(:,1).^2,р(:,2).^2,р(:,3).^2];=[X;X;X;X;X;X;X];=length(X)=[239.87
465.37 656.23];=[20 50 80];
%xm=[249.5 419.5 667.50]bank=[ones(N,1)*x0(:,1)+X(:,2)*dx(:,1)…(N,1)*x0(:,2)+X(:,3)*dx(:,2)…(N,1)*x0(:,3)+X(:,4)*dx(:,3)];=profit3(D);=0.2;
[b,bint,r,rint,stats] =
regress(Y,X,alpha);=[b bint]short=stats(3)bank=[2*b(2) 0 0;0 2*b(3) 0; 0 0
2*b(4)],=[-b(5);-b(6);-b(7)]=A^-l*B=x0'+xm.*dx'
Итак, текущее исследование говорит,
что средняя прибыль за выделенный период времени от реализации данной группы
товаров составляет величину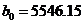 
руб. с доверительным интервалом 
.
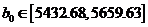Заметим лишь, что в реальных
условиях, в отличие от имитационных, отсутствует практическая возможность
получить линии уровней функции прибыли.
Задача 2
Дать иллюстрацию близости
распределения Пуассон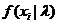а 
, которому
подчиняются дискретные величины хi прибыли с продаж, к нормальному
распределению при больших значениях параметра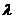 
.
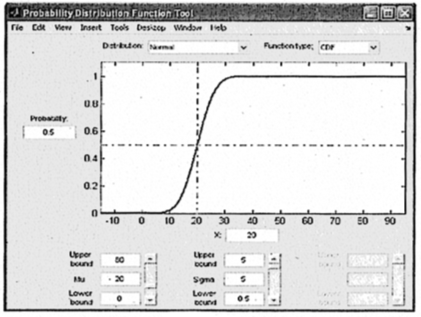
Рис. 17
Для быстрого решения задачи удобнее
обратиться к функции disttool, результаты исполнения которой показаны на рис.
18 и 19. Но при использовании высокоуровневого графического интерфейса не
всегда удается согласовать интервал значений переменной вдоль оси абсцисс, что
может породить некоторые сомнения в результатах сравнения распределений.
Поэтому обратимся к более надежному, но и более трудоемкому средству.
e-3:40;=20;=4.5;=normcdf(x,mu,sigma);=20;=poisscdf(x,lambda);(x,yl,'--',x,y2,'LineWidth',1.5),('Gauss','Poisson','Location','SouthEast'),set(gca,'GridLineStyle','-'),=12;('x','FontSize',Font),('F_N(\mu=20,\sigma=5),_P(\lambda=20)','FontSize',Font)(gca,'FontSize',Font)('Распределения
Гаусса и Пуассона',…
'FontName','Arial
Cyr','FontSize',Font)
Заключение
В рамках выполненной работы мы
смогли ознакомиться с одним из методов максимизации прибыли от продаж,
реализованном в программной среде MATLAB , основанном на регрессионном анализе
и уравнении регрессии, заключающемся в поиске оптимальной цены в зависимости от
спроса. Так же возникло понимание статистической природы спроса, так основой её
служат Гаусовское и Пуасоновское распределение.