Теория графов
Теория графов
Основные понятия и определения
·
Граф - пара множеств V и X - G = (V, X). V - множество вершин, X - множество ребер.
·
Петля - ребро вида (v, v).
·
Кратные рёбра - одинаковые пары в X.
·
Ориентированный граф (орграф D) - граф, для которого пары в Х упорядочены. Ребра в орграфе
называются дугами и обозначаются <u, v>.
·
Степенью вершины V графа G называется число d(v) рёбер графа, инцидентных вершине v. Если d(v) = 1, тогда v - висячая вершина, если d(v) = 0, тогда v - изолированная вершина.
·
Полустепенью исхода (захода) вершины v орграфа D называется d+(v) - число дуг, исходящих из v (δ - (v) - число дуг, заходящих в v).
·
Маршрутом для графа G (путём для орграфа D) называется последовательность v1x1v2x2v3…xkvk+1.
·
Цепь - незамкнутый маршрут (путь), в котором все рёбра (дуги) попарно
различны.
·
Простая цепь - цепь, в которой все вершины попарно различны.
·
Цикл (контур) - замкнутый маршрут (путь), в котором все рёбра (дуги)
попарно различны.
·
Простой цикл (контур) - цикл (контур), в котором все вершины попарно различны.
·
Длина пути - число рёбер (дуг) в маршруте (пути).
·
Путь в графе называется минимальным, если он состоит из
минимального количества рёбер.
Орграф D называется нагруженным, если на множестве дуг Х определена
весовая функция 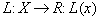 -
длина дуги хÎХ.
-
длина дуги хÎХ.
·
Путь называется минимальным в нагруженном графе или орграфе,
если он имеет минимальную длину пути.
·
Матрица смежности (графа, орграфа): А = [aij], V = {v1…, vn},
·
X = {x1…, xm}
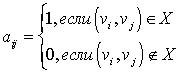 ·
·
·
Матрица инцидентности: B = [bij]
·
(орграфа D)
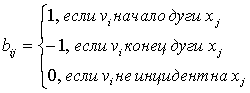 ·
·
·
(графа G)
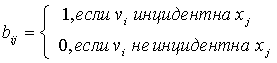 ·
·
·
Матрица достижимости T = [tij]
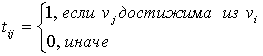 ·
·
·
Матрица связности S = [sij]
(орграфа D) 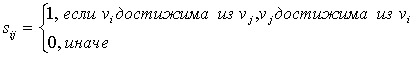
(графа G) 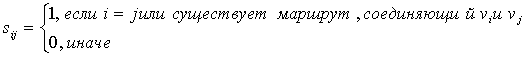
·
Дерево - связный граф без циклов
·
Остовное дерево графа (ОД) - любой связный подграф связного графа,
содержащий все вершины и являющийся деревом.
Минимальное остовное
дерево (МОД) - остовное дерево
нагруженного графа с минимальной суммой длин дуг, содержащихся в нём.
Цикломатическое число
связного графа G (число циклов в базисе
циклов графа) 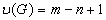 ,
где n - количество вершин, m
- количество ребер в графе.
,
где n - количество вершин, m
- количество ребер в графе.
Ориентированный граф
Назовем ребра графа:
1. Характеристика графа
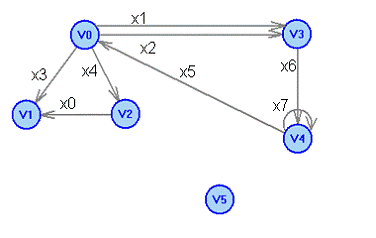
Ориентированный псевдограф D=(V, X).
V={V0, V1, V2, V3, V4, V5}; X={X0, X1, X2, X3, X4, X5, X6, X7}
X0=<V2, V1>, X1=<V0, V3>, X2=<V0, V3>, X3=<V0, V1>, X4=<V0, V2>, X5=<V4, V0>, X6=<V3, V4>, X7=<V4, V4>
. Специальные вершины и ребра
X7 - петля, X1, X2 - кратные ребра, V5 - висячая вершина
. Полустепени вершин
d+(V) - число дуг, заходящих в V
δ - (V) - число дуг, исходящих из V
δ+ (V0)=1 δ+ (V1)=2 δ+ (V2)=1 δ+ (V3)=2 δ+ (V4)=2 δ+ (V5)=0
δ¯(V0)=4 δ¯(V1)=0 δ¯(V2)=1 δ¯(V3)=1 δ¯(V4)=2 δ¯(V5)=0
. Матрицы смежности,
инцидентности, достижимости, связности
|
Смежности
|
V0
|
V1
|
V2
|
V3
|
V4
|
V5
|
|
V0
|
0
|
1
|
1
|
2
|
0
|
0
|
|
V1
|
0
|
0
|
0
|
0
|
0
|
0
|
|
V2
|
0
|
1
|
0
|
0
|
0
|
0
|
|
V3
|
0
|
0
|
0
|
0
|
1
|
0
|
|
V4
|
1
|
0
|
0
|
0
|
1
|
0
|
|
V5
|
0
|
0
|
0
|
0
|
0
|
0
|
|
Инцидентности
|
X0
|
X1
|
X2
|
X3
|
X4
|
X5
|
X6
|
X7
|
|
V0
|
0
|
-1
|
-1
|
-1
|
-1
|
1
|
0
|
0
|
|
V1
|
1
|
0
|
0
|
1
|
0
|
0
|
0
|
0
|
|
V2
|
-1
|
0
|
0
|
0
|
1
|
0
|
0
|
0
|
|
V3
|
0
|
1
|
1
|
0
|
0
|
0
|
-1
|
0
|
|
V4
|
0
|
0
|
0
|
0
|
0
|
-1
|
1
|
±1
|
|
V5
|
0
|
0
|
0
|
0
|
0
|
0
|
0
|
0
|
|
Достижимости
|
V0
|
V1
|
V2
|
V3
|
V4
|
V5
|
|
V0
|
1
|
1
|
1
|
1
|
0
|
0
|
|
V1
|
0
|
1
|
0
|
0
|
0
|
0
|
|
V2
|
0
|
1
|
1
|
0
|
0
|
0
|
|
V3
|
0
|
0
|
0
|
1
|
1
|
0
|
|
V4
|
1
|
0
|
0
|
0
|
1
|
0
|
|
V5
|
0
|
0
|
0
|
0
|
0
|
1
|
|
Связности
|
V0
|
V1
|
V2
|
V3
|
V4
|
V5
|
|
V0
|
1
|
0
|
0
|
0
|
0
|
0
|
|
V1
|
0
|
1
|
0
|
0
|
0
|
0
|
|
V2
|
0
|
0
|
1
|
0
|
0
|
|
|
V3
|
0
|
0
|
0
|
1
|
0
|
0
|
|
V4
|
0
|
0
|
0
|
0
|
1
|
0
|
|
V5
|
0
|
0
|
0
|
0
|
0
|
1
|
5. Цикл, цепь, простой цикл,
простая цепь
Простой цикл: V0 X1 V3 X6 V4 X5 V0 Цикл: V3 X6 V4 X7 V4 X5 V0 X2 V3
Простая цепь: V0 X4 V2 X0 V1 Цепь: V0 X1 V3 X6 V4 X5 V0 X4 V2 X0 V1
Неориентированный граф
. Начертить граф
. Характеристика графа
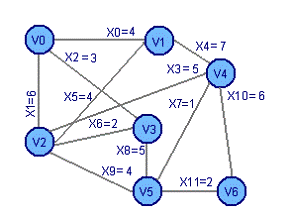
Неориентированный граф G=(V, X)
V={V0, V1, V2, V3, V4, V5, V6}
X={X0, X1, X2, X3, X4, X5, X6, X7, X8, X9, X10, X11}
X0={V0, V1}, X1={V0, V2}, X2={V0, V3}, X3={V2, V4}, X4={V1, V4}, X5={V1, V2}, X6={V2, V3}, X7={V4, V5}, X8={V3, V5}, X9={V2, V5}, X10={V4, V6}, X11={V5, V6}
. Специальные вершины и ребра
Нет
. Степени вершин
δ(V0)=3 δ(V1)=3 δ(V2)=5 δ(V3)=3 δ(V4)=4 δ(V5)=4 δ(V6)=2
.
Матрицы смежности, инцидентности, достижимости, связности
|
Смежности
|
V0
|
V1
|
V2
|
V3
|
V4
|
V5
|
V6
|
|
V0
|
0
|
1
|
1
|
1
|
0
|
0
|
0
|
|
V1
|
1
|
0
|
1
|
0
|
1
|
0
|
0
|
|
V2
|
1
|
1
|
0
|
1
|
1
|
1
|
0
|
|
V3
|
1
|
0
|
1
|
0
|
0
|
1
|
0
|
|
V4
|
0
|
1
|
1
|
0
|
0
|
1
|
1
|
|
V5
|
0
|
0
|
1
|
1
|
1
|
0
|
1
|
|
V6
|
0
|
0
|
0
|
0
|
1
|
1
|
0
|
|
Инцидентности
|
X0
|
X1
|
X2
|
X3
|
X4
|
X5
|
X6
|
X7
|
X8
|
X9
|
X10
|
|
V0
|
1
|
1
|
1
|
0
|
0
|
0
|
0
|
0
|
0
|
0
|
0
|
0
|
|
V1
|
1
|
0
|
0
|
0
|
1
|
1
|
0
|
0
|
0
|
0
|
0
|
0
|
|
V2
|
0
|
1
|
0
|
1
|
0
|
1
|
1
|
0
|
0
|
1
|
0
|
0
|
|
V3
|
0
|
0
|
1
|
0
|
0
|
0
|
1
|
0
|
1
|
0
|
0
|
0
|
|
V4
|
0
|
0
|
0
|
1
|
1
|
0
|
0
|
1
|
0
|
0
|
1
|
0
|
|
V5
|
0
|
0
|
0
|
0
|
0
|
0
|
0
|
1
|
1
|
1
|
0
|
1
|
|
V6
|
0
|
0
|
0
|
0
|
0
|
0
|
0
|
0
|
0
|
0
|
1
|
1
|
|
Достижимости
|
V0
|
V1
|
V2
|
V3
|
V4
|
V5
|
V6
|
|
V0
|
1
|
1
|
1
|
1
|
1
|
1
|
1
|
|
V1
|
1
|
1
|
1
|
1
|
1
|
1
|
1
|
|
V2
|
1
|
1
|
1
|
1
|
1
|
1
|
1
|
|
V3
|
1
|
1
|
1
|
1
|
1
|
1
|
1
|
|
V4
|
1
|
1
|
1
|
1
|
1
|
1
|
1
|
|
V5
|
1
|
1
|
1
|
1
|
1
|
1
|
1
|
|
V6
|
1
|
1
|
1
|
1
|
1
|
1
|
1
|
|
Связности
|
V0
|
V1
|
V2
|
V3
|
V4
|
V5
|
V6
|
|
V0
|
1
|
1
|
1
|
1
|
1
|
1
|
1
|
|
V1
|
1
|
1
|
1
|
1
|
1
|
1
|
1
|
|
V2
|
1
|
1
|
1
|
1
|
1
|
1
|
1
|
|
V3
|
1
|
1
|
1
|
1
|
1
|
1
|
1
|
|
V4
|
1
|
1
|
1
|
1
|
1
|
1
|
1
|
|
V5
|
1
|
1
|
1
|
1
|
1
|
1
|
1
|
|
V6
|
1
|
1
|
1
|
1
|
1
|
1
|
1
|
. Цикл, цепь, простой цикл,
простая цепь
Простой цикл: V0 X2 V3 X6 V2 X1 V0 Цикл: V0 X0 V1 X4 V4 X10 V6 X11 V5 X9 V2 X1 V0
Простая цепь: V4 X7 V5 X8 V3 Цепь: V4 X10 V6 X11 V5 X9 V2
. Числовые характеристики
графа
a) Максимальное удаление - r(V) = maxwd (V, W)
r(V0)=6, r(V1)=6,
r(V2)=6, r(V3)=6, r(V4)=6, r(V5)=6, r(V6)=6
б) Диаметр графа d(G)=maxv,wd (v, w)(G)=6
в) Радиус графа G
- r(G)=minv r(V)
R(G)=6
г) Центры графа-V|
R(G)=r(V)
центры графа - вершины V0,
V1, V2, V3, V4, V5, V6
. Остовное дерево и минимальное оставное дерево
Рассчитаем остовное дерево графа:
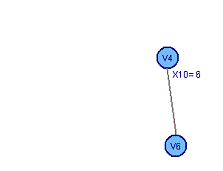

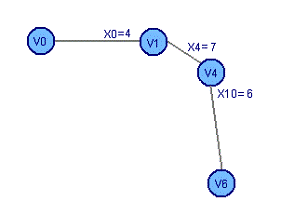
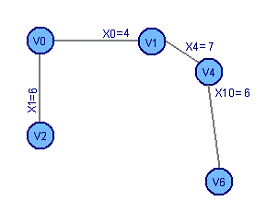
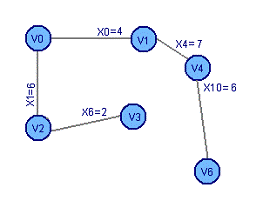
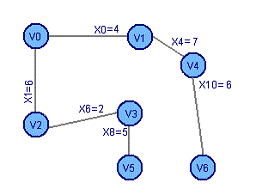
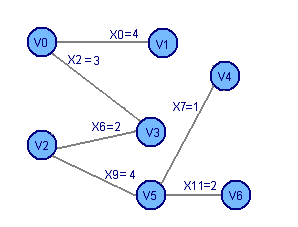
Рассчитаем минимальное остовное
дерево графа:
. Обход графа в глубину и в
ширину
Обход графа в глубину: V0®V1®V2®V3®V5®V4®V6
Обход графа в ширину. 1 ярус: V0; 2 ярус: V1, V2, V3; 3 ярус: V4, V5; 4 ярус: V6
. Базис циклов графа
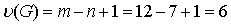
Чтобы найти базис циклов графа, к
остовному дереву будем добавлять по одному ребра, которые в остовное дерево не
вошли. При этом на каждом шаге будем получать один простой цикл.
граф
определенный матрица смежность
Добавим ребро X2 Добавим
ребро X3
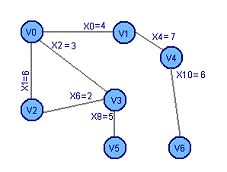
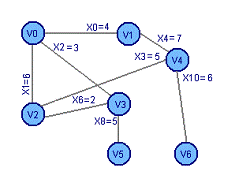
Получим цикл 1: V0 X1 V2 X6 V3 X2 V0 Получим цикл
2: V0 X1 V2 X3 V4 X4 V1 X0 V0
Добавим ребро X5 Добавим
ребро X7
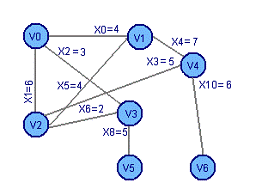
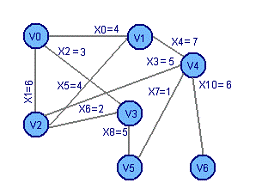
Получим цикл 3: V1 X5 V2 X1 V0 X0 V1 Получим цикл
4: V4 X7 V5 X8 V3 X6 V2 X3 V4
Добавим ребро X9 Добавим
ребро X11
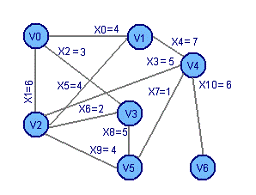
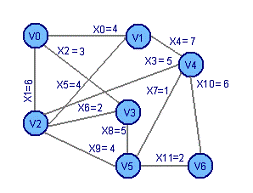
Получим цикл 5: V2 X6 V3 X8 V5 X9 V2 Получим цикл
6: V4 X7 V5 X11 V6 X10 V4