Симплекс-метод
Введение
Математическое программирование - это область математики,
разрабатывающая численные методы решения задач на экстремумах функций многих
переменных с ограничениями на область изменения этих переменных.
Задачи математического программирования возникли из
стремления к наиболее эффективному использованию имеющихся ресурсов. Такие
задачи могут встречаться в разных отраслях, таких как экономика, техника,
научные исследования. Например, в экономике часто возникали проблемы, связанные
с извлечение максимальной прибыли из производства. Такие задача при текущем
уровне развития экономики приобрели первостепенное значение. Сегодня нужно все
свои шаги в производстве рассчитывать очень основательно, так как состояние
экономики изменчиво. При этом нужно учитывать объем затрат на единицу
продукции, прибыль полученную с этой единицы и состояние рынка на момент
решения задачи. Среди множества возможных вариантов приходится отыскивать
наилучший, при ограничениях, налагаемых на ресурсы и затраты.
Для решения этих трудностей в экономическую науку активно
внедряется математическое программирование. Его применение существенно расширяет возможности
традиционного экономического анализа, что позволяет ставить и решать качественно новые экономические
проблемы. Одним
из таких методов, позволяющих решать поставленные задачи по максимуму прибыли
является симплекс - метод.
Симплекс - метод можно интерпретировать двумя способами:
) Экономически, в этом случае симплекс - метод позволяет
решать вопросы о наиболее эффективном распределении средств. Выбрав начальный
план действий и постепенно улучшая его достигается оптимальное решение. Каждому
переходу по симплекс-методу соответствует переход от одной программы действий к
другой, которая ближе к поставленной цели.
) Математически же симплекс-метод представляет собой
тождественные алгебраические преобразования, дающие возможность от одной
системы уравнений перейти к другой, эквивалентной ей системе. Достигнуть
оптимального решения можно не выходя за пределы первых четырех алгебраических операций.
1.
Теоретический раздел
.1
Постановка задачи
Используя симплекс-метод решить ЗЛП:
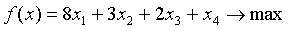
При ограничениях:
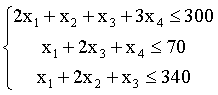
Описание
входной информации
Userform2 - форма для ввода целевой функции и ограничений
Описание
выходной информации
1) Лист «Каноническая таблица» - лист, на котором содержится
приведенная к каноническому виду таблица.
) Листы «Симплекс таблица № n» - лист, на котором
содержится n-ая
симплекс таблица.
) Лист «Оптимальный план» - лист, на котором содержится
оптимальный план.
) MsgBox - встроенная функция VBA, которая выводит сообщение о том, что
оптимальный план найден и значение функции.
1.2
Характеристика симплекс-метода
При решении задач линейного программирования наиболее
распространены 2 способа - графический и симплекс-метод.
Использование графического способа удобно только при решении
задач ЛП с двумя переменными. При большем числе переменных необходимо применение
алгебраического аппарата. Информация, которую можно получить с помощью
симплекс-метода, не ограничивается лишь оптимальными значениями переменных.
Симплекс-метод фактически позволяет дать экономическую интерпретацию
полученного решения и провести анализ модели.
Процесс решения задачи линейного программирования носит
итерационный характер: однотипные вычислительные процедуры в определенной
последовательности повторяются до тех пор, пока не будет получено оптимальное
решение. Процедуры, реализуемые в рамках симплекс-метода, требуют применения
вычислительных машин - мощного средства решения задач линейного
программирования.
Симплекс-метод - это характерный пример итерационных
вычислений, используемых при решении большинства оптимизационных задач.
При решении задачи ЛП симплекс-методом реализуется
упорядоченный процесс, при котором, начиная с некоторой исходной допустимой
угловой точки (обычно начало координат), осуществляются последовательные
переходы от одной допустимой экстремальной точки к другой до тех пор, пока не
будет найдена точка, соответствующая оптимальному решению.
Для нахождения оптимального решения необходимо от одной
угловой точки переходить к другой, то есть от исходного базисного решения к
другому, при этом значение функции должно расти, если задача на максимум и
убывать, если задача на минимум.
Выбор каждой последующей экстремальной (угловой) точки при
использовании симплекс-метода определяется следующими двумя правилами:
). Каждая последующая угловая точка должна быть смежной с
предыдущей. Этот переход осуществляется по границам (ребрам) пространства
решений
). Обратный переход к предшествующей экстремальной точке не
может производиться. Таким образом, отыскание оптимального решения начинается с
некоторой допустимой угловой точки, и все переходы осуществляются только к
смежным точкам, причем перед новым переходом каждая из полученных точек
проверяется на оптимальность.
1.3
Математическое описание алгоритма симплекс-метода
Математически алгоритм симплекс-метода можно представить в
несколько шагов:
Шаг 1. Построить и заполнить исходную симплекс-таблицу
(табл. 1).
Таблица 1. Исходная таблица
В столбце «базис» записываются базисные переменные. В столбце «С»
- записываются коэффициенты при базисных переменных в целевой функции. В
столбце «В» записываются свободные коэффициенты ограничений (все, что справа от
знака «=»). 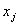 - это небазисные переменные.
- это небазисные переменные. 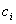 - коэффициенты переменных в целевой
функции.
- коэффициенты переменных в целевой
функции. 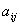 - коэффициенты при небазисных переменных
в ограничениях.
- коэффициенты при небазисных переменных
в ограничениях.
 - строка, в которой производятся вычисления.
- строка, в которой производятся вычисления.
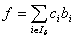 (1)
(1)
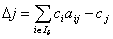 ;
; 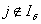 (2)
(2)
Шаг 2.
Проверить полученный базисный план по оптимальности.
Если:
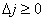 и среди базисных переменных нет искусственных, то план является
оптимальным, и задача разрешима;
и среди базисных переменных нет искусственных, то план является
оптимальным, и задача разрешима;
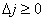 и среди базисных переменных есть искусственные, то задача
неразрешима;
и среди базисных переменных есть искусственные, то задача
неразрешима;
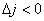 , то полученный опорный план не является оптимальным и необходимо
переходить к другому опорному плану.
, то полученный опорный план не является оптимальным и необходимо
переходить к другому опорному плану.
Если все 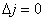 , то задача имеет бесконечное множество
решений.
, то задача имеет бесконечное множество
решений.
Шаг 3. Найти направляющий столбец и направляющую
строку.
Находим направляющий столбец и направляющую строку. Направляющий
столбец определяется следующим образом: 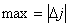 . Направляющая строка -
. Направляющая строка - 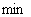 из отношений компонентов столбца
из отношений компонентов столбца 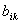 к положительным компонентам направляющего столбца
к положительным компонентам направляющего столбца 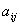 . На пересечении направляющего столбца и
направляющей строки находится разрешающий элемент
. На пересечении направляющего столбца и
направляющей строки находится разрешающий элемент 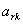 . Если окажется несколько одинаковых
наименьших значений, то выбирается любое из них. Если
. Если окажется несколько одинаковых
наименьших значений, то выбирается любое из них. Если 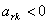 , то неразрешима.
, то неразрешима.
Шаг 4. Нахождение опорного плана.
Для определения нового опорного плана строится новая
симплекс-таблица, в которой 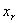 и
и 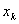 меняется местами вместе со своими
коэффициентами. Остальные переменные записываются без изменения со своими
коэффициентами.
меняется местами вместе со своими
коэффициентами. Остальные переменные записываются без изменения со своими
коэффициентами.
Элементы новой симплекс-таблицы рассчитываются по формулам:
элементы главной строки пересчитываются путём деления каждого элемента этой
строки на разрешающий, а главный элемент
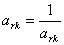
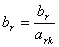 (3)
(3)
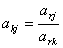
Элементы главного столбца рассчитываются путём деления каждого
элемента этого столбца на разрешающий со знаком «-»
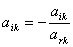 (4)
(4)
Все остальные элементы таблицы рассчитываются по правилу
четырёхугольника:
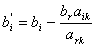
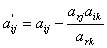 (5)
(5)
1.4
Описание операционной системы
Windows XP является следующей - после Windows
2000 и Windows Millennium - версией операционной системы Microsoft Windows. В
Windows XP осуществлена эффективная интеграция сильных сторон Windows 2000
(основанной на отраслевых стандартах системы безопасности, высокой надежности и
управляемости) с лучшими характеристиками систем Windows 98 и Windows Me,
такими как простой в применении интерфейс пользователя, возможности технологии
Plug and Play и новые принципы организации службы технической поддержки. Тем
самым сделан очередной шаг по пути сближения операционных систем семейства Windows.
В результате подобной интеграции была получена лучшая на сегодняшний день
операционная система.
2.
Экспериментальный раздел
.1
Решение задачи ручным способом
Используя симплекс-метод решить ЗЛП:
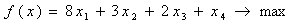
При ограничениях:
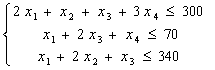
Результат вычислений:
Таблица 2. 1 симплекс-таблица
|
базис
|
|
|
8
|
3
|
2
|
|
С
|
В
|
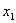 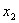 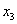 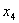
|
|
|
|
|
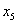 03002113 03002113
|
|
|
|
|
|
|
|
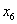 0701021 0701021
|
|
|
|
|
|
|
|
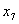 03401210 03401210
|
|
|
|
|
|
|
|
 0-8-3-2-1 0-8-3-2-1
|
|
|
|
|
|
Значение функции: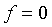
Таблица 3. 2 симплекс-таблица
|
базис
|
|
|
0
|
3
|
2
|
1
|
|
С
|
В
|
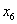 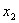 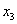 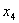
|
|
|
|
|
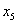 0160-21-31 0160-21-31
|
|
|
|
|
|
|
|
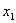 8701021 8701021
|
|
|
|
|
|
|
|
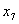 0270-12-1-1 0270-12-1-1
|
|
|
|
|
|
|
|
 5608-3147 5608-3147
|
|
|
|
|
|
Значение функции: 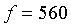
Таблица 4. 3 симплекс-таблица
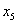 025-1,5
025-1,5
|
0,5-2,51,5
|
|
|
|
|
|
|
|
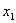 8701021 8701021
|
|
|
|
|
|
|
|
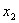 3135-0,50,50,50,5 3135-0,50,50,50,5
|
|
|
|
|
|
|
|
 9656,51,512,55,5 9656,51,512,55,5
|
|
|
|
|
|
Значение функции: 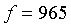 .
.
2.2
Схема алгоритма и описание схемы алгоритма программы
симплекс ограничение программирование алгоритм
Описание схемы алгоритма программы:
) Запуск программы
) Процедура ввода целевой функции и ограничений в форму Userform2 и запись из на лист
«Исходные данные»
) Процедура приведения исходных данных в канонический вид и
вывод и вывод таблицы на лист «Канонический вид»
) Нахождение Значений в симплекс таблице и вывод таблицы на
лист «Симплекс таблица №»
) Проверка является ли эта симплекс таблица последней, если
да то 6), если нет то переход к 4)
) Вывод сообщения о том что оптимальный план найден, значение
функции и на листе «Оптимальный план» вывод итоговой таблицы
) Выход из программы.
2.3
Описание процесса отладки программы
В VBA есть средства, которые позволяют либо исключить ошибки при
разработке, либо задать обработку ошибок при выполнении программ.
Отладка программ - это проверка и внесение исправлений в
программу при ее разработке. Отладка позволяет идентифицировать ошибки,
допущенные при программировании.
) Ошибки компиляции - возникают, когда компилятор не может
интерпретировать введенный текст. Некоторые ошибки компиляции обнаруживаются
при вводе, а другие - перед выполнением программы. Такие ошибки легко
определить и исправить, поскольку VBA выявляет их автоматически, а сами ошибки
очевидны.
) Ошибки выполнения - возникают при выполнении программы
после успешной компиляции. Их причиной обычно является отсутствие данных или
неправильная информация, введенная пользователем. Такие ошибки идентифицируются
VBA с указанием инструкции, при выполнении которой произошла ошибка. Для
исправления таких ошибок обычно приходится выводить значения переменных или
другие данные, которые влияют на успешное выполнение программы.
Логические ошибки трудно заметить и устранить. Они не
приводят к прекращению компиляции или выполнения, однако являются причиной
того, что программа не выдает желаемых результатов. Выявление таких ошибок
производят путем тщательной проверки с помощью средств отладки VBA.
2.4
Характеристика программы
Данная программа написана в среде программирования MS Office
(VBA 2003) и не требует значительных программных и аппаратных средств.
Описание минимальных требований к системе:
1) CPU Intel Pentiun III
2) 64 Mb оперативной памяти
3) Видеокарта 8Mb, поддерживающая разрешение
640х480
4) 288 Kb свободного места на HDD
5) OS Windows 98/NT/2000/Me/XP
6) Предустановленный пакет ПО MS Office
98/2000/XP
Размер Симплекс метод.xls: 91,0 КБ
Результат вычислений ручным способом:
Таблица 6. 1 симплекс-таблица
|
базис
|
|
|
8
|
3
|
2
|
1
|
|
С
|
В
|
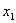 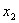 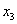 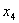
|
|
|
|
|
|
|
|
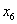 0701021 0701021
|
|
|
|
|
|
|
|
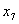 03401210 03401210
|
|
|
|
|
|
|
|
 0-8-3-2-1 0-8-3-2-1
|
|
|
|
|
|
Значение функции: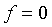
Таблица 7. 2
симплекс-таблица
|
базис
|
|
|
0
|
3
|
2
|
1
|
|
С
|
В
|
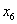 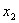 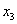 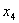
|
|
|
|
|
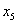 0160-21-31 0160-21-31
|
|
|
|
|
|
|
|
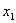 8701021 8701021
|
|
|
|
|
|
|
|
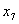 0270-12-1-1 0270-12-1-1
|
|
|
|
|
|
|
|
 5608-3147 5608-3147
|
|
|
|
|
|
Значение функции: 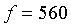
Таблица 8. 3
симплекс-таблица
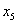 025-1,5
025-1,5
|
0,5-2,51,5
|
|
|
|
|
|
|
|
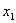 8701021 8701021
|
|
|
|
|
|
|
|
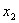 3135-0,50,50,50,5 3135-0,50,50,50,5
|
|
|
|
|
|
|
|
 9656,51,512,55,5 9656,51,512,55,5
|
|
|
|
|
|
Значение функции: 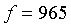
Анализ проделанной работы позволяет сказать, что при выполнении
расчетов на компьютере и в ручном варианте, получен один и тот же результат.
Список
литературы
1)
ГОСТ 19.105-78 ЕСПД. Общие требования к программным продуктам.
)
ГОСТ 19.106-77 ЕСПД. Требования к программным документам, выполненным печатным
способом.
)
ГОСТ 19.701-90 ЕСПД. Схемы алгоритмов, программ, данных и систем. Обозначения
условные и правила выполнения
)
И.Г. Семакин, E.
К. Хеннер Информационные системы и модели
)
А. Кофтин, А. Анри-Лабодер Методы и модели исследования операций
)
Электронный учебник по VBA (Excel). Курс лекций по VBA (www.mini-soft.ru)