Решение задачи повышения надежности резервирования
Решение задачи повышения
надежности резервирования
Введение
Данная дипломная работа посвящена решению задачи повышения
надежности резервирования компонентов стендовой информационно-управляющей
системы для проведения огневых испытаний жидкостных ракетных двигателей.
Актуальность данной тематики состоит в том, что не существует универсальных
формализованных методов, алгоритмов, программ, позволяющих автоматизировать
процесс управления надежностью для любой сложной технической системы на всех этапах
ее жизненного цикла. Основная сложность задачи обусловлена ее
многокритериальностью. Решение таких задач требует разработки специальных
алгоритмов и методов решения, которые не всегда удается получить. Поэтому
решение данной задачи было решено искать с помощью универсальных алгоритмов
эволюционного моделирования, которое заключается в замене моделирования
сложного объекта моделированием его эволюции. Эволюционные методы в отличие от
точных методов математического программирования позволяют находить решения,
близкие к оптимальным, за приемлемое время
Таким образом, целью данной работы является реализация
приложения, позволяющего с помощью алгоритмов эволюционного моделирования
получать оптимальные или близкие к оптимальным решения.
Для достижения поставленной цели были выполнены следующие
этапы:
. Изучение сути проблемы данной задачи;
. Изучение основы теории надежности;
. Изучение математической модели данной задачи;
. Разработка алгоритмов решения задачи;
. Программная реализация;
. Тестирование программы.
1. Суть проблемы повышения надежности
резервирования компонентов стендовой информационно-управляющей системы для
проведения огневых испытаний жидкостных ракетных двигателей
.1
Общие сведения о надежности аппаратных средств и методах резервирования
При проведении огневых испытаний жидкостных ракетных
двигателей (ЖРД) предъявляются особые требования к безотказности технических
средств автоматизированных систем управления технологическими процессами
(АСУТП). Одними из основных показателей безотказности технических средств АСУТП
являются среднее время наработки на отказ и вероятность безотказной работы.
Одним из самых радикальных способов повышения безотказности
(надежности) является резервирование. В промышленной автоматизации наибольшее
распространение получили следующие методы резервирования: резервирование
замещением «один из двух» (1оо2 - 1 out of 2) и метод мажоритарного
голосования «два из трех» (2оо3). Системы без резервирования классифицируются
как 1оо1.
1.2 Архитектура систем управления огневыми
испытаниями ЖРД
Системой управления называется комплекс устройств,
посредством которых осуществляется запуск, останов, изменение режимов работы и
контроль параметров двигателя. В основу системы управления положена релейная
автоматика. Основой релейной автоматики являются дискретные ключевые элементы,
обеспечивающие подачу и снятие команд управления и имеющие состояния:
«замкнут», «разомкнут». Ключевой элемент является одним из звеньев канала
(тракта) управления.
Высокие требования, предъявляемые к безотказности систем
управления испытаниями ЖРД относятся в первую очередь к надежности релейной
автоматики. Так как ключевой элемент имеет только два состояния, то и видов
отказов может только два: короткое замыкание (КЗ) и обрыв. Ключевой элемент
обычно представляет собой электромагнитное реле или полупроводниковый прибор
(транзистор).
На рис. 1 представлена структурная схема резервирования 1оо2
для ключевых элементов. Условные обозначения: КУ - команда дискретного
управления; ИП - источник питания; К1 - ключ; ОУ - объект управления.

Рис. 1. Резервирование ключевых элементов по схеме 1оо2
На рис. 1 а ключи объединены по схеме ИЛИ. Недостатком данной
схемы является то, что при возникновении отказа типа КЗ невозможно снять команду
с объекта управления. Схема представленная на рис. 1 б нечувствительна к
отказам типа КЗ из-за наличия блока переключения на резерв. Однако данной схеме
также присущи недостатки: блок переключения на резерв должен быть абсолютно
надежным (а он в общем случае также состоит из ключей), требуется достаточно
информативный сигнал диагностики для определения момента возникновения отказа,
имеется ограничение по времени переключения на резерв. Для некоторых
резервируемых элементов, такой блок переключения на резерв может просто
отсутствовать.
На рис. 2 а представлена классическая структурная схема
резервирования 2оо3 для ключевых элементов.

Рис. 2. Резервирование ключевых элементов по схеме 2оо3
Как видно из рис. 2 а при классическом резервировании 2оо3
требуется в 6 раз больше ключей, чем в схеме 1оо1. Этот недостаток можно
частично устранить, применив упрощенную схему рис. 2 б. В схеме на рис. 2 б
всего 4 ключа и один вентиль (В). Назначение вентиля (В) заключается в том, чтобы
разрешать подачу команды на ОУ только по направлению, указанному стрелкой.
Вентиль обеспечивает совместную работу ключей К1 и К3. В
качестве вентилей широкое применение нашли полупроводниковые диоды, надежность
которых как минимум на порядок выше надежности ключей, поэтому анализе
надежности всего ключевого элемента их можно вообще не учитывать. Тем не менее,
эта схема остается самой дорогостоящей (по сравнению с 1оо1 и 1оо2).
2. Основы теории надежности
2.1
Теория надежности как наука, понятие надежности и отказа
Теория надежности - наука, изучающая
закономерности отказов технических систем. Основными объектами ее изучения
являются:
· критерии надежности технических систем
различного назначения;
· методы анализа надежности в процессе
проектирования и эксплуатации технических систем;
· методы синтеза технических систем;
· пути обеспечения и повышения надежности
техники;
· научные методы эксплуатации техники,
обеспечивающие ее высокую надежность.
Надежность является важнейшим параметром любой технической
системы. Она во многом определяет такие характеристики системы, как качество,
эффективность, безопасность, живучесть, риск и др.
Надежностью называется свойство технического объекта
сохранять свои характеристики (параметры) в определенных пределах при данных
условиях эксплуатации. Из этого определения следует, что надежность - понятие
объективное, не зависимое от нашего сознания. В природе все, что имеет начало,
имеет и конец. В течение жизни объект расходует свои ресурсы и, наконец,
погибает. Так же происходит и с надежностью. Создается техническое средство с
определенным ресурсом. В процессе эксплуатации оно приносит человеку пользу за
счет потери этого ресурса. Оно отказывает (болеет), его ремонтируют (лечат).
Этот процесс длится до тех пор, пока эксплуатация технического средства
целесообразна. Этот процесс и все, что с ним связано (применительно к
техническим средствам), и изучает теория надежности.
Отказом называется событие, после возникновения которого
характеристики технического объекта (параметры) выходят за допустимые пределы.
Это понятие субъективно, т.к. допуск на параметры объекта устанавливает
пользователь. Отказ - фундаментальное понятие теории надежности. Критерий
отказа - отличительный признак или совокупность признаков, согласно которым устанавливается
факт возникновения отказа.
2.2
Терминология теории надежности
Надежность - один из самых важных параметров техники. Ее
показатели необходимы для оценки качества техники, ее эффективности,
безотказности, живучести, риска. Надежность зависит от многих внешних и
внутренних факторов и оценивается многими критериями и показателями. Все это
привело к появлению в теории надежности большого числа различных терминов и их
определений. Далее приводятся некоторые из них.
Элемент - объект (материальный, энергетический,
информационный), обладающий рядом свойств, внутреннее строение (содержание)
которого значения не имеет. В теории надежности под элементом понимают элемент,
узел, блок, имеющий показатель надежности, самостоятельно учитываемый при
расчете показателей надежности системы. Понятия элемента и системы
трансформируются в зависимости от решаемой задачи.
Система - совокупность связанных между собой элементов,
обладающая свойством (назначением, функцией), отличным от свойств отдельных ее
элементов. Практически любой объект с определенной точки зрения может
рассматриваться как система.
Структура системы - взаимосвязи и
взаиморасположение составных частей системы, ее устройство. Расчленение системы
на группы элементов может иметь материальную (вещественную), функциональную,
алгоритмическую и другую основу. В зависимости от связей между элементами
различают следующие виды структур: последовательные, параллельные, с обратной
связью, сетевые и иерархические.
Наработка - продолжительность или объем работы объекта,
измеряемые единицами времени, числом циклов нагрузки, километрами пробега и
т.п.
Наработка до отказа - наработка объекта от
начала его эксплуатации до возникновения первого отказа.
Средний срок службы - математическое
ожидание срока службы;
2.3
Критерии надежности невосстанавливаемых систем
Отказ элемента является событием случайным, а время ξ до его возникновения - случайной величиной. Основной
характеристикой надежности элемента является функция распределения
продолжительности его безотказной работы F (t) = Р (ξ< t), определенная при t > 0. На ее основе могут быть
получены следующие показатели надежности невосстанавливаемого элемента:
· P(t) - вероятность его безотказной работы
в течение времени t;
· Q(t) - вероятность отказа в течение
времени t;
· f(t) - плотность
распределения времени безотказной работы;
· λ(t) - интенсивность отказа
в момент времени t;
· T - среднее время
безотказной работы (средняя наработка до отказа);
Вероятностью безотказной работы называется вероятность
того, что технический объект не откажет в течение времени t или что время ξ работы до отказа технического объекта больше времени его
функционирования t:
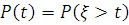
Вероятность безотказной работы является убывающей функцией во
времени, имеющей следующие свойства:
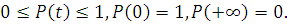
Вероятность отказа в течение времени t определяется следующим
образом:
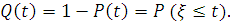
Плотность распределения времени безотказной работы - это плотность распределения случайной величины
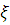
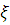 . Она наиболее полно характеризует надежности техники в данный
момент (точечная характеристика). По ней можно определить любой показатель
надежности невосстанавливаемой системы. В этом основное достоинство плотности
распределения времени безотказной работы.
. Она наиболее полно характеризует надежности техники в данный
момент (точечная характеристика). По ней можно определить любой показатель
надежности невосстанавливаемой системы. В этом основное достоинство плотности
распределения времени безотказной работы.
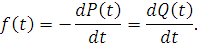
Интенсивностью отказов называется отношение плотности распределения к вероятности
безотказной работы объекта:
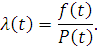
Интенсивность отказов 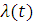
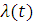 является основным показателем надежности элементов сложных
систем. Это объясняется следующими обстоятельствами: надежность многих
элементов можно оценить одним числом, т.к. интенсивность отказа элементов -
величина постоянная; по известной интенсивности
является основным показателем надежности элементов сложных
систем. Это объясняется следующими обстоятельствами: надежность многих
элементов можно оценить одним числом, т.к. интенсивность отказа элементов -
величина постоянная; по известной интенсивности 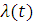
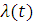 наиболее просто оценить остальные показатели надежности как
элементов, так и сложных систем.
наиболее просто оценить остальные показатели надежности как
элементов, так и сложных систем.
Средним временем безотказной работы называется математическое ожидание
времени безотказной работы технического объекта:
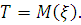
Как математическое ожидание случайной величины с плотностью 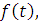
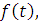 среднее время безотказной работы вычисляется по формуле:
среднее время безотказной работы вычисляется по формуле:
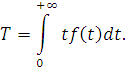
Среднее время безотказной работы является интегральным показателем
надежности. Его основное достоинство - высокая наглядность.
2.4
Экспоненциальное распределение времени до отказа
Одним из наиболее часто используемых в теории надежности
параметрических распределений случайной величины 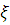
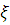 является экспоненциальное (или показательное)
распределение. Оно задается функцией
является экспоненциальное (или показательное)
распределение. Оно задается функцией
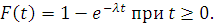
Экспоненциальным законом распределения можно аппроксимировать
время безотказной работы большого числа элементов. В первую очередь это
относится к элементам радиоэлектронной аппаратуры, а также к машинам,
эксплуатируемым в период после окончания приработки и до существенного
проявления постепенных отказов. Экспоненциальное распределение применяется в
областях, связанных с «временем жизни»: в медицине - продолжительность жизни
больных, в надежности - продолжительность безотказной работы устройства, в психологии
- время, затраченное на выполнение тестовых задач. Оно используется в задачах
массового обслуживания, в которых речь идет об интервалах времени между
телефонными звонками, или между моментами поступления техники в ремонтную
мастерскую, или между моментами обращения клиентов. Это распределение имеет
один параметр 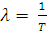
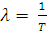 где
где 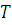
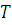 - средняя наработка элемента до отказа. Таким образом, параметр
- средняя наработка элемента до отказа. Таким образом, параметр 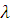
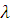 характеризует число отказов элемента в единицу времени и
называется интенсивностью отказов, он имеет размерность (время)-1,
например, час-1 или лет-1. Плотность экспоненциального
распределения задается как:
характеризует число отказов элемента в единицу времени и
называется интенсивностью отказов, он имеет размерность (время)-1,
например, час-1 или лет-1. Плотность экспоненциального
распределения задается как:
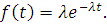
Функция надежности
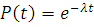
определяет вероятность безотказной работы за время 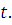
3. Математическая модель выбора вариантов
резервирования компонентов стендовой информационно-управляющей системы
Из главы 1 известно, что одними из основных показателей
безотказности технических средств АСУТП являются среднее время наработки на
отказ T
и вероятность безотказной работы P(t).
Для элементов установки вероятность безотказной работы можно
определить как:
надежность резервирование ракетный математический
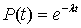
где l=const - интенсивность отказов.
При этом частота отказов по определению является плотностью
распределения времени до отказа 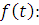
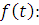
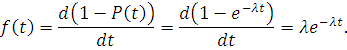
Среднее время наработки на отказ T определяется следующим образом:
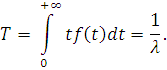
Также в главе 1 было сказано, что элементы установки могут быть
резервированы тремя способами: 1oo1, 1oo2 и 2oo3.
Обозначим как Ai -
событие, означающее безотказную работу i-го элемента системы, а отказ как 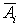 . При этом очевидно, что вероятность безотказной работы
нерезервированной системы будет определяться выражением
. При этом очевидно, что вероятность безотказной работы
нерезервированной системы будет определяться выражением
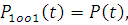
а среднее время наработки на отказ
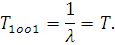
Рассмотрим резервированную систему, состоящую из двух элементов
(1оо2). События A1 и A2 означают безотказную работу этих элементов, следовательно событие
A, означающее безотказную работу всей
системы определяется как
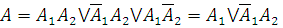
Учитывая, что элементы резервированной системы идентичны,
вероятности событий A1 и A2 равны, эти события независимы, то вероятность безотказной работы
системы 1оо2:
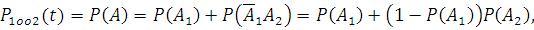
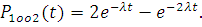
Тогда
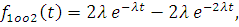
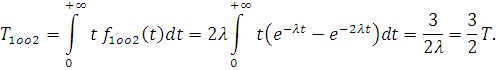
Аналогично для резервированной схемы 2оо3 можно получить:
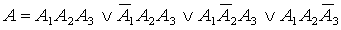
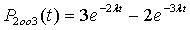
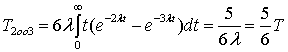
На рис. 3 показаны вероятности безотказной работы систем 1оо1,
1оо2 и 2оо3 при l=1 год-1.
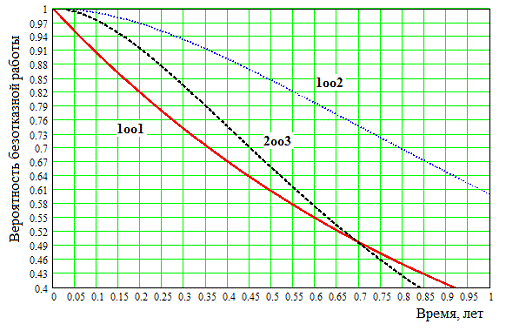
Рис. 3. Вероятность безотказной работы 1оо1, 1оо2 и 2оо3 при l=1 год-1
Приравняв P1oo1(t) к P2oo3(t), можно
узнать критическое время T2oo3кр=T×Ln(2)»0,7T, после которого вероятность безотказной
работы системы 2оо3 становится меньше, чем у системы 1оо1, а использование
резервирования становится неэффективным. Проанализировав P1oo1(t) и P1oo2(t), можно
сказать, что вероятность безотказной работы системы 1оо2 всегда больше, чем у
системы 1оо1, однако нельзя забывать про недостатки 1oo2, рассматриваемые в главе 1.
На основании вышесказанного составим оптимизационную модель выбора
вариантов резервирования компонентов стендовой информационно-управляющей
системы.
Каждому i-му компоненту может быть назначен один из трех вариантов
резервирования: 1 - элемент ставится без резервирования (1оо1), 2 -
резервирование замещением «один из двух» (1оо2), 3 - метод мажоритарного
голосования «два из трех» (2оо3). Пусть n - общее количество резервируемых компонентов.
Введем переменные:
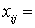 1, если j-му компоненту назначается i-й вариант резервирования;
1, если j-му компоненту назначается i-й вариант резервирования;
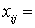 0, в противном случае;
0, в противном случае; 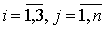 .
.
Важным ограничением является фиксированное среднее время
безотказной работы системы (наработка до отказа).
Было показано, что среднее время безотказной работы элемента,
резервируемого по схеме 1оо2, составляет 3/2 от среднего времени работы
нерезервируемого элемента, а среднее время безотказной работы элемента по схеме
2оо3 соответственно равно 5/6 от среднего времени работы 1oo1.
Исходя из того, что 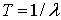 , наработку до отказа всей системы Tс можно представить
в виде
, наработку до отказа всей системы Tс можно представить
в виде 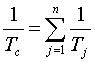 где Tj - наработка до отказа j-го элемента.
где Tj - наработка до отказа j-го элемента.
Тогда первое ограничение имеет вид:
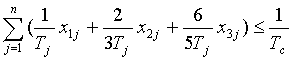 ,
,
где Tj - cреднее время наработки на отказ j-го элемента системы без
резервирования.
Поскольку каждому элементу назначается ровно один метод
резервирования, вторая группа ограничений задачи имеет вид:
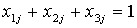 ,
, 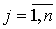 ,
,
В качестве критериев оптимизации могут рассматриваться общая
стоимость системы и величина вероятности безотказной работы всех ее
компонентов.
Стоимость элемента, резервируемого по схеме 1оо2 в два раза выше
стоимости элемента без резервирования, а стоимость элемента, резервируемого по
схеме 2оо3, как показано выше, в четыре раза выше стоимости нерезервируемого
элемента. Однако, схема 1оо2 не всегда реализуема, так как для нее необходим
абсолютно надежный блок переключения на резерв, который для некоторых
резервируемых элементов может отсутствовать. Если же такой блок присутствует,
его стоимость может увеличивать общую стоимость данного варианта
резервирования.
Поэтому первая целевая функция имеет вид:
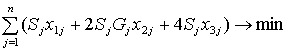
Здесь 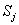 - стоимость j-го элемента резервирования, Gj ≥1 - коэффициент, увеличивающий стоимость схемы 1оо2 в
случае, если для данного резервируемого элемента существует надежный блок
переключения на резерв; и Gj=S в случае, если такой блок отсутствует (S - максимально
возможная суммарная стоимость резервируемых элементов, выполняет роль штрафного
коэффициента). Заметим, что если стоимости резервируемых элементов примерно
равны, то этот критерий можно интерпретировать как минимизацию общего
количества элементов системы (а, следовательно, и ее габариты).
- стоимость j-го элемента резервирования, Gj ≥1 - коэффициент, увеличивающий стоимость схемы 1оо2 в
случае, если для данного резервируемого элемента существует надежный блок
переключения на резерв; и Gj=S в случае, если такой блок отсутствует (S - максимально
возможная суммарная стоимость резервируемых элементов, выполняет роль штрафного
коэффициента). Заметим, что если стоимости резервируемых элементов примерно
равны, то этот критерий можно интерпретировать как минимизацию общего
количества элементов системы (а, следовательно, и ее габариты).
В качестве второго критерия оптимизации может рассматриваться
величина вероятности безотказной работы всех компонентов системы.
Пусть pj -
вероятность безотказной работы j-го элемента без резервирования. Тогда в схеме
1оо2 вероятность безотказной работы имеет вид 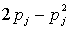 , а в схеме 2оо3 эта вероятность равна
, а в схеме 2оо3 эта вероятность равна 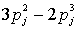 . Таким образом, вторая целевая функция
имеет вид:
. Таким образом, вторая целевая функция
имеет вид:
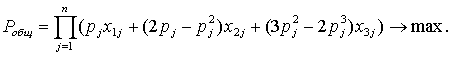
В итоге, модель выбора вариантов резервирования компонентов
стендовой информационно-управляющей системы принимает вид:
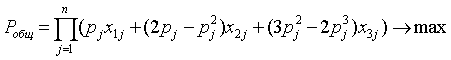
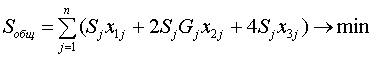
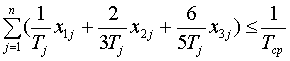
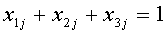 ,
, 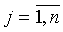 ,
,
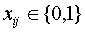 .
.
4.
Генетические алгоритмы
4.1
Общая схема генетического алгоритма
Задача формализуется таким образом, чтобы её решение могло
быть закодировано в виде вектора («генотипа») генов, где каждый ген может быть
битом, числом или неким другим объектом. В классических реализациях
генетического алгоритма (ГА) предполагается, что генотип имеет фиксированную
длину. Однако существуют вариации ГА, свободные от этого ограничения.
Некоторым, обычно случайным, образом создаётся множество
генотипов начальной популяции. Они оцениваются с использованием «функции
приспособленности», в результате чего с каждым генотипом ассоциируется
определённое значение («приспособленность»), которое определяет, насколько
хорошо фенотип им описываемый решает поставленную задачу.
Из полученного множества решений («поколения») с учётом
значения «приспособленности» выбираются решения (обычно лучшие особи имеют
большую вероятность быть выбранными), к которым применяются «генетические
операторы» (в большинстве случаев «скрещивание» и «мутация»), результатом чего
является получение новых решений. Для них также вычисляется значение
приспособленности, и затем производится отбор («селекция») лучших решений в
следующее поколение.
Этот набор действий повторяется итеративно, так моделируется
«эволюционный процесс», продолжающийся несколько жизненных циклов (поколений),
пока не будет выполнен критерий останова алгоритма. Таким критерием может быть:
· нахождение глобального, либо
субоптимального решения;
· исчерпание числа поколений, отпущенных на
эволюцию;
· исчерпание времени, отпущенного на
эволюцию.
Таким образом, можно выделить следующие этапы генетического
алгоритма:
Ø Создание начальной
популяции
начало цикла
Ø Отбор (селекция).
Ø Скрещивание (кроссовер).
Ø Формирование новой
популяции.
Ø Если условие останова не
выполняется, то начало цикла, иначе конец цикла.
4.2
Создание начальной популяции
Один из вариантов задания начальной популяции - взятие
случайных особей. Они могут быть очень плохими в смысле приспосабливаемости,
однако в результате алгоритма они будут эволюционировать, тем самым в итоге
давая хорошие показатели приспосабливаемости.
Другой вариант - взятие начальной популяции из
предположительной области оптимума, что может несколько ускорить работу
алгоритма.
Обозначим начальную популяцию через 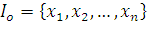
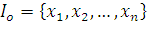 , где
, где 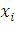
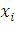 - i-ая особь (i=1,…, n), n - количество особей в популяции.
- i-ая особь (i=1,…, n), n - количество особей в популяции.
4.3
Отбор (селекция)
На каждой итерации с помощью вероятностного оператора отбора
выбираются два решения-родителя для их последующего скрещивания. Наиболее
распространенными среди операторов селекции являются операторы пропорциональной
и турнирной селекции.
Оператор пропорциональной селекции также известен как
«рулеточный» отбор. Принцип этого отбора состоит в следующем: особи
располагаются на колесе рулетки так, что размер сектора каждой особи
пропорционален ее приспособленности. Запуская рулетку, выбираем особей для
дальнейшего скрещивания. Математически, это выглядит так: если событие A = «i-ая особь
выбрана», f - функция приспособленности, P - вероятность наступления события, то P(A) = 
 .
.
Смысл оператора турнирной селекции состоит в следующем: из
популяции случайным образом выбирается определенное количество особей, среди
которых выбирается лучшая, которая затем будет участвовать в скрещивании.
Повторяется эта операция столько раз, сколько необходимо для формирования новой
популяции.
Очевидно, что в результате использования этих операторов в
следующем этапе скрещивания будут участвовать в основном наиболее
приспособленные особи.
4.4
Скрещивание (кроссовер)
На этом этапе особи, выбранные на этапе селекции, с заданной
вероятностью Pc подвергаются оператору скрещивания. Существует
много вариантов реализации скрещивания. Наиболее известные из них: одноточечный
кроссовер, двухточечный кроссовер и равномерный кроссовер.
При одноточечном кроссовере случайным образом выбирается
точка кроссовера - индекс вектора, которым представлена особь. Обозначим этот
индекс через k. Пусть в скрещивании принимают участие
две особи-родителя 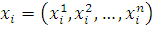
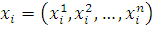 и
и 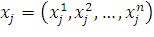
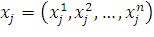 . Тогда в результате скрещивания будут получены особи-потомки
. Тогда в результате скрещивания будут получены особи-потомки
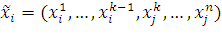
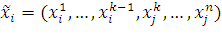 ,
, 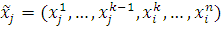
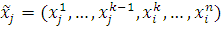 .
.
Схематично это выглядит так:
|
1
|
1
|
0
|
1
|
1
|
0
|
1
|
|
|
0
|
0
|
1
|
0
|
1
|
1
|
0
|
|
1
|
1
|
0
|
1
|
1
|
1
|
0
|
|
|
0
|
0
|
1
|
0
|
1
|
0
|
1
|
При двухточечном кроссовере действует тот же принцип,
что и при одноточечном кроссовере, только обмен частями векторов идет не от
точки k
до n, а от k1 до k2, где k1, k2 - точки двухточечного
кроссовера:
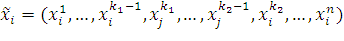
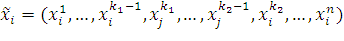 ,
,
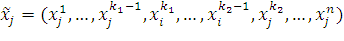
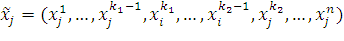 .
.
Схематично это представляется так:
|
1
|
1
|
0
|
1
|
1
|
0
|
1
|
|
|
0
|
0
|
1
|
0
|
1
|
1
|
0
|
|
1
|
1
|
1
|
0
|
1
|
0
|
1
|
|
|
0
|
0
|
0
|
1
|
1
|
0
|
В равномерном кроссовере каждый бит первого потомка
случайным образом наследуется от одного из родителей; второму потомку достается
бит другого родителя.
4.5 Мутация
После завершения этапа скрещивания полученные особи с
определенной вероятностью подвергаются мутации. Существуют различные варианты
мутации: одноточечная мутация, инверсия и транслокация.
При одноточечной мутации каждый бит с определенной
вероятностью подвержен изменению. Схематично это можно представить так:
|
1
|
0
|
1
|
0
|
0
|
1
|
0
|
|
↓
|
|
1
|
0
|
1
|
0
|
1
|
1
|
0
|
При инверсии выбираются два индекса k1 и k2 (k1 < k2), затем биты с индексами k1,…, k2-1 располагаются в обратном порядке, т.е. если была особь 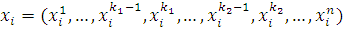
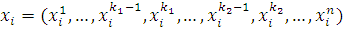 , то после мутации она имеет вид
, то после мутации она имеет вид 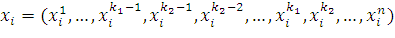
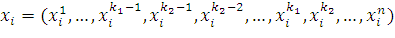 . Схематично это выглядит так:
. Схематично это выглядит так:
|
1
|
0
|
11
|
21
|
00
|
1
|
0
|
|
↓ ↓
|
|
1
|
0
|
00
|
-1
|
11
|
1
|
0
|
При транслокации происходит перенос части вектора в
другой сегмент этого же вектора:
|
1
|
1
|
1
|
0
|
0
|
1
|
1
|
|
↔
|
|
1
|
0
|
0
|
1
|
1
|
1
|
1
|
4.6 Формирование новой популяции.
Существуют различные подходы к формированию новой популяции:
можно в новую популяцию включать только особей-потомков, либо включать двух
лучших особей среди родителей и их потомков. Также существует подход, при котором
стараются сделать новую популяцию как можно разнообразнее. Еще один подход,
который называется принципом элитизма, заключается в том, чтобы в новую
популяцию всегда входили несколько лучших особей родителей, что не даст
потерять наиболее приспособленных индивидов.
5. Генетический алгоритм решения задачи выбора
вариантов резервирования компонентов стендовой информационно-управляющей
системы
1-й этап. Представление данных.
Хромосома, представляющая неизвестную матрицу X, задается с помощью строкового кодирования. Суть
кодирования заключается в следующем: экземпляр популяции - это строка длиною n (n - размерность
задачи), в которой на i-м месте стоит j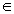 [1..3], если
[1..3], если 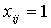 . Таким образом решение
. Таким образом решение 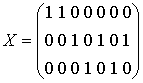 (фенотип) будет записано как «троичная»
строка: x=(1,1,2,3,2,3,2) (генотип).
(фенотип) будет записано как «троичная»
строка: x=(1,1,2,3,2,3,2) (генотип).
2-й этап. Генерация начальной популяции.
Первая популяция создаётся случайным образом из L различных «троичных» строк длиной n. Дополнительно (с целью улучшения генетического материала) в
первую популяцию можно ввести строки, представляющие собой приближенные решения
задач по обоим критериям в отдельности.
3-й этап. Оценка особей популяции по критерию
приспособленности.
1) Для каждого решения в популяции вычисляется вектор целей 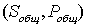 , по которому далее определяется скалярное
значение функции приспособленности.
, по которому далее определяется скалярное
значение функции приспособленности.
) Из текущей популяции выбирается множество недоминируемых внутри
этой популяции решений, они запоминаются и временно выбрасываются из
рассмотрения.
) Далее ищется множество недоминируемых вариантов в усеченном
множестве, и исключаются они. Эта процедура проделывается до тех пор, пока все
варианты не будут исключены из популяции.
) Теперь все строки ранжируются: принадлежащие последнему
исключённому множеству получают ранг 1, предпоследнему ранг 2. Строки, первыми
выброшенные из рассмотрения, получают самый высокий ранг. Внутри каждого
исключенного множества все варианты решения имеют одинаковый ранг.
) Далее, в отдельности для каждой группы строк одного ранга,
происходит назначение оценок приспособленности. Предположим, ранг k имеет m
строк. Тогда строка, сумма евклидовых расстояний от которой до остальных строк
данного ранга максимальна, получит оценку k+(m-1)/m.
Строка со второй по величине суммой расстояний получит оценку
k+(m-2)/m. Строка с минимальной суммой расстояний
до остальных особей данного ранга будет иметь оценку k.
Такой подход к оцениванию экземпляров популяции настраивает
алгоритм не только на поиск недоминируемых решений (любая недоминируемая строка
будет иметь оценку выше любой доминируемой), но и на поддержание разнообразия
популяции (удаленные точки получают более высокие оценки), что обеспечивает
лучшую аппроксимацию парето-оптимального множества.
4-й этап. Отбор(селекция).
В качестве процедуры селекции будем использовать стандартные
механизмы пропорционального или турнирного отбора, и чем выше у индивида оценка
приспособленности, тем вероятнее она попадет в родители следующего поколения.
Для создания новых особей-потомков может использоваться любая
стандартная мутация и любой из классических операторов скрещивания
(одноточечный, двухточечный, равномерный кроссовер), дополненные процедурой
исправления недопустимых решений. Недопустимыми решения могут оказаться только
за счет невыполнения ограничения 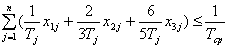 . Это можно
подкорректировать, исправив несколько координат в соответствующей строке
(например, случайным образом значение 3 исправить на 2 или 1, либо значение 1
исправить на 2). Такие исправления позволят уменьшить левую часть этого
ограничения. Они проводятся до тех пор, пока это ограничение не будет
выполнено.
. Это можно
подкорректировать, исправив несколько координат в соответствующей строке
(например, случайным образом значение 3 исправить на 2 или 1, либо значение 1
исправить на 2). Такие исправления позволят уменьшить левую часть этого
ограничения. Они проводятся до тех пор, пока это ограничение не будет
выполнено.
6-й этап. Критерий прекращения работы.
В качестве рекорда хранится множество недоминируемых за все
время заботы алгоритма вариантов. Как критерий остановки вычислений
используется следующая проверка: если за последние 100 поколений рекордное
множество не изменилось, то дальнейшая работа алгоритма прекращается.
6. Разработка приложения
6.1
Требования к приложению
Данное приложение должно позволять получать приблизительное
решение задачи выбора вариантов резервирования компонентов стендовой
информационно-управляющей системы с помощью генетических алгоритмов с
незначительными временными затратами
Данное приложение должно так же позволять получить точное
решение (множество всех оптимальных по Парето точек) данной задачи.
Данное приложение должно иметь простой в использовании русскоязычный
графический интерфейс, понятный пользователю, ознакомленному с сутью проблемы
резервирования компонентов стендовой информационно-управляющей системы и
математической моделью, описанной во главе 3.
Данное приложение должно адекватно реагировать на
некорректные данные и выводить соответствующие сообщения.
Данное приложение должно быть совместимо с операционными
системами Windows XP\Vista\7.
6.2
Особенности реализации
Для реализации данного приложения была выбрана программная
среда Embarcadero RAD Studio 2010. Язык программирования - Delphi. Выбор основан на том,
что данная среда имеет все необходимые визуальные компоненты, а язык
обеспечивает простую работу с динамическими массивами.
Программа состоит из двух модулей. Unit1 содержит обработчики
кнопок. Unit2 отвечает за реализацию генетического алгоритма.
При написании программы применялись как процедурный подход
(реализация генетических алгоритмов), так и подход ООП (визуальные компоненты).
В генетических алгоритмах использовались: случайное формирование
начальной популяции, турнирная селекция, одноточечный кроссовер, одноточечная
мутация.
6.3
Графический интерфейс
На рис. 4 представлен графический интерфейс приложения.
Рис. 4. Графический интерфейс
6.4
Тестирование приложения, определение оптимальных параметров
Путем многократного запуска программы и сравнения результатов
было установлено, что рекомендуемые параметры программы:
· Количество особей: 50 (увеличение не дает
улучшения результата, однако оказывает значительное влияние на скорость
выполнения алгоритма).
· Вероятность мутации: <0,1 (увеличение
данного значения ухудшает качество получаемого множества ответов, а также
замедляет алгоритм). На рис. 5 видно, как решения, получаемые при больших
значениях вероятности мутации, заметно отличаются от истинного оптимального
множества решений.
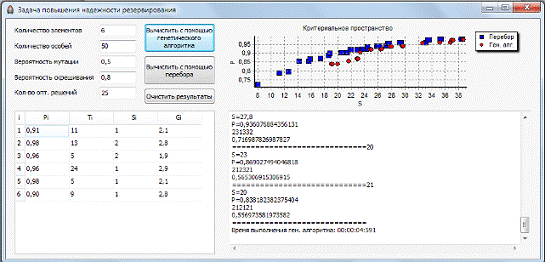
Рис. 5. Плохая аппроксимация оптимального множества решений
при большом значении вероятности мутации
· Вероятность скрещивания: <0,7 (изменения
в сторону увеличения и изменения не дают сильного эффекта, однако использование
критических значений, близких к 0 или 1 нежелательно).
· Количество оптимальных решений:
определяется пользователем. Чем больше данный параметр, тем разнообразнее множество
ответов.
Далее приведена сравнительная таблица времени работы
генетического алгоритма и перебора:
Таблица 1 - Время работы в зависимости от размерности задачи
|
Кол-во
элементов
|
Время перебора
|
Время работы
генетического алгоритма
|
|
100
|
|
00:00:10:288
|
|
19
|
|
00:00:02:496
|
|
18
|
|
00:00:01:956
|
|
17
|
|
00:00:01:766
|
|
16
|
|
00:00:01:756
|
|
15
|
|
00:00:01:683
|
|
14
|
|
00:00:01:432
|
|
13
|
|
00:00:01:233
|
|
12
|
00:01:04:409
|
00:00:01:204
|
|
11
|
00:00:46:573
|
00:00:01:054
|
|
10
|
00:00:06:226
|
00:00:00:543
|
|
9
|
00:00:00:943
|
00:00:00:466
|
|
8
|
00:00:00:255
|
00:00:00:474
|
|
7
|
00:00:00:33
|
00:00:00:471
|
|
6
|
00:00:00:05
|
00:00:00:492
|
Время перебора, начиная с 13 элементов, не было рассчитано,
т.к. оно требовало слишком больших временных затрат. Тем не менее, общая
динамика роста времени хорошо прослеживается. Далее для наглядности приведен
график зависимости времени выполнения алгоритмов от размерности задачи,
построенный по данной таблице.
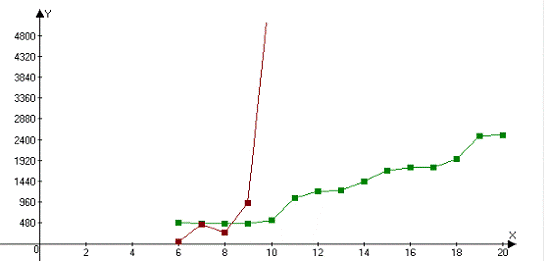
Приведем ниже несколько примеров работы программы с
рекомендуемыми параметрами.
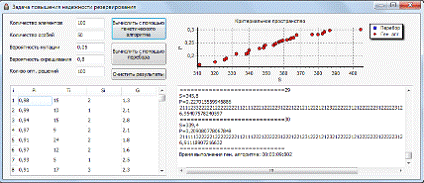
Рис. 6. Примеры работы программы с рекомендуемыми параметрами
Заключение
В ходе проделанной работы была изучена проблема повышения
надежности резервирования компонентов стендовой информационно-управляющей
системы для проведения огневых испытаний жидкостных ракетных двигателей и
разработано приложение, позволяющее быстро получать множество альтернативных
решений при выборе способа резервирования компонентов системы. При реализации
программы были использованы методы эволюционного моделирования, которые
являются достаточно универсальными, простыми, и в то же время довольно
неприхотливыми к условиям задачи. Для эффективности тестирования в программе
была также реализована возможность получения множества всех возможных решений с
помощью метода перебора. В ходе тщательного тестирования были выявлены
оптимальные параметры работы генетического алгоритма, а также оценена его
производительность: скорость работы алгоритма очень слабо зависит от
размерности задачи, что, бесспорно, является очень хорошим свойством. Также
стоит отметить, что множество решений, получаемое с помощью ГА, хорошо
покрывает множество всех возможных решений, получаемое с помощью перебора, что,
несомненно, является плюсом. Все это говорит о том, что генетические алгоритмы
являются хорошим средством решения различных оптимизационных задач.
Список источников
1. Половко
А.М., Гуров С.В. Основы теории надежности / СПб.: БХВ-Петербург, 2008.
2. Испытания
жидкостных ракетных двигателей. Учеб. пособие для авиац. специальностей вузов
под. ред. В.З. Левина - М.: Машиностроение, 1981.
. Львович
Я.Е., Каширина И.Л., Генетический алгоритм решения многокритериальной задачи
повышения надежности резервирования.
. Каширина
И.Л. Введение в эволюционное моделирование / Воронеж, 2007.
Приложение А
Листинг программы
unit Unit1;
interface, Messages, SysUtils, Variants, Classes,
Graphics, Controls, Forms,, StdCtrls, Grids, Unit2, TeEngine, ExtCtrls,
TeeProcs, Chart, Series,, Math;= 4;= 100;= class(TForm)_N: TEdit;_N: TLabel;:
TStringGrid;: TButton;: TMemo;: TButton;: TLabel;: TLabel;: TLabel;_L:
TEdit;_Pmut: TEdit;_Pcross: TEdit;: TLabel;_RecQuantity: TEdit;: TChart;:
TPointSeries;: TButton;: TPointSeries;FormCreate (Sender: TObject);Edit_NChange
(Sender: TObject);Button1Click (Sender: TObject);Button3Click (Sender:
TObject);FormResize (Sender: TObject);Button2Click (Sender: TObject);
{Private declarations}
{Public declarations};: TForm1;, time2:
TDateTime;
{$R *.dfm}InitInputData; i, j: integer;
// Проверка введенных данных на корректность и инициализация
try;:= StrToInt (Form1. Edit_RecQuantity.
Text);:= StrToInt (Form1. Edit_L. Text);:= StrToFloat (Form1. Edit_Pmut.
Text);:= StrToFloat (Form1. Edit_Pcross. Text);(Pmut < 0) or (Pmut > 1)
or (Pcros < 0) or (Pcros > 1) then;('Данные некорректны');;;i:= 1 to N do[i-1]:= StrToFloat (Form1.
StringGrid1. Cells [1, i]);[i-1]:= StrToFloat (Form1. StringGrid1. Cells [2,
i]);[i-1]:= StrToFloat (Form1. StringGrid1. Cells [3, i]);[i-1]:= StrToFloat
(Form1. StringGrid1. Cells [4, i]);(P [i-1]<0) or (P [i-1]>1) or (G
[i-1]<1) or (T [i-1]<=0) then;('Значения P, G или T введены некорректно');;;;;
ShowMessage ('Введены некорректные данные');;
end;;TForm1. Button1Click (Sender: TObject);i, j,
k: integer;: string;:= now;;;
// Создание начальной популяции:=
0;;;(Population);(TempPopulation);(TempPopulationCrossed);;(Population);(Population);
// ГА(Population, TempPopulation);(TempPopulation,
TempPopulationCrossed);(TempPopulationCrossed);(TempPopulationCrossed);(TempPopulationCrossed);(TempPopulationCrossed,
Population);(Population);(Population);(RefreshNum);RefreshNum =
MaxRefreshNum;:= now;
// Вывод результатовk:= 1 to RecQuantity doRec[k].S <> -9999999
then. Lines. Add ('============================='+IntToStr(k));. Lines. Add
('S='+FloatToStr (-Rec[k].S));. Lines. Add ('P='+FloatToStr (Rec[k].P));. AddXY
(-Rec[k].S, rec[k].P, '', clred);i:= 0 to Rec[k].Quantity-1 do:= «;j:= 0 to N-1
do:= str + IntTostr (Rec[k].Solutions[i] [j]);. Lines. Add(str);. Lines. Add
(FloatToStr(SumTxX (Rec[k].Solutions[i])));;. Lines. Add
('=============================');
// очистка памяти;;(Population);(TempPopulation);(TempPopulationCrossed);.
Lines. Add ('Время выполнения ген.
алгоритма: '+
FormatDateTime ('hh:mm:ss:zz',
time2-time1));;TForm1. Button2Click (Sender: TObject);
// перебор= 3; // кол-во вариантов резервирования
type= array of Tindivid;= array [1..3] of real;
// 1 - S, 2 - P, 3 - T= array of TKrArr;, j, k: longint;: longint; // 3^N_1:
real; // среднее время: TKrList; // массив S P T:
TSolutionArray; // массив x1 x2… xN
NotDominated: boolean; // флаг недоминируемости
// инициализация начальных переменных
time1:= now;;:= round (power(3, N)) - 1;(Kr, max
+ 1);(X, max + 1);_1:= 0;i:= 0 to N-1 do
Tavg_1:= Tavg_1 + 1/T[i];
// задание матрицы всех возможных значений Хj:= 0 to max do
// перебор на основе перевода чисел в троичную систему
// выделение памяти под xj(X[j], N);
// перевод числа в троичную систему
k:= j;
for i:= 0 to N-1 do[j] [N-i-1]:= (k - (k div
base) * base) + 1;:= k div base;;
// вычисление значения критериев
Kr[j] [1]:= - GetS (X[j]);
Kr[j] [2]:= GetP (X[j]);
Kr[j] [3]:= SumTxX (X[j]);;
// на этот момент мы имеем массив всех комбинаций
// и массив соответствующих значений критерия
// вывести недоминируемые точки
for j:= 0 to max do(Kr[j] [3]<=Tavg_1) then:=
true;i:= 0 to max doi <> j then(((Kr[i] [1]>Kr[j] [1]) and (Kr[i]
[2]>=Kr[j] [2])) or
((Kr[i] [1]>=Kr[j] [1]) and (Kr[i] [2]>Kr[j]
[2]))) and (Kr[i] [3]<=Tavg_1) then:= false;;;NotDominated then
// добавление на график. AddXY
(-Kr[j] [1], Kr[j] [2], '', clBlue);;:= now;;j:= 0 to max do[j]:= nil;:= nil;:=
nil;. Lines.
Add ('Время выполнения алгоритма перебора: '+
FormatDateTime ('hh:mm:ss:zz',
time2-time1));;TForm1. Button3Click (Sender: TObject);. Lines. Clear;. Clear;.
Clear;;TForm1. Edit_NChange (Sender: TObject);N_old: integer;, j:
integer;Edit_N. Text <> '' then_old:= N;:= StrToInt (Edit_N. Text);.
RowCount:= N+1;i:= N_old+1 to N doj:= 1 to COlCount do. Cells [j, i]:= «;.
Cells [0, i]:= IntToStr(i);;;;TForm1. FormCreate (Sender: TObject);i, j:
integer;:= StrToInt (Edit_N. Text);. RowCount:= N+1;. Cells [0,0]:= ' i';.
Cells [1,0]:= ' Pi';. Cells [2,0]:= ' Ti';. Cells [3,0]:= ' Si';. Cells [4,0]:=
' Gi';i:= 1 to N do. Cells [0, i]:= IntToStr(i);. ColWidths[0]:= 15;;TForm1.
FormResize (Sender: TObject);. Height:= Height - 205;. Height:= Height - 205;:=
937;;.Unit2;SysUtils;= array of 1..3;= array of real;= record: real;: real;= array
of TIndivid;= array of TFitness;= record: TIndividArray;: TFitnessArray;:
TRealArray;;= record: integer;: real;: real;= array of TEuc;= record: real;:
real;: TIndividArray;: integer;;= array of TRecElement;
//Individ: TIndivid;: TPopulation; // начальная популяция: TPopulation;
// временная популяция: TPopulation;
// временная популяция потомков
//NewPopulation: TPopulation;, T, S, G: TRealArray; // массивы входных
данных, L: integer; // длина хромосомы и кол-во особей соот-но: real; //
вероятность мутации: real; // вероятность скрещивания: real; // ср время:
TRecord; // рекордное множество: integer; // количество рекордных решений:
integer; // кол-во обновлений
procedure InitPopulation (var Pop: TPopulation);
// создание начальной популяции, состоящей из L особей длины
N
procedure ErasePopulation (var Pop: TPopulation);
// удаление популяцииRankPopulation (var Pop: TPopulation);
// ранжирование индивидов в
популяцииCountFitness
(var Pop: TPopulation);
// вычисление значений целевых функцийSelectPopulation
(var Pop: TPopulation; var tempPop: TPopulation);
// формирование временной популяции выбором из двух
procedure SelectPopulation2 (var Pop:
TPopulation; var tempPop: TPopulation);
// формирование временной популяции выбором из трех
procedure CrossPopulation (var TempPop:
TPopulation; var TempPopCr: TPopulation);
// скрещивание индивидов популяцииMutantPopulation (var TempPop: TPopulation);
// мутация популяцииFixPopulation (var TempPop: TPopulation);
// исправление популяцииInitTavg;
// вычисление T-среднего
function SumTxX (var Indiv: TIndivid): real;
// вычисление левой части ограничения по времениInitRecord;
// задание рекордного массива начальными числами
procedure AddToRecord (var TempPop: TPopulation);
// изменение рекордного множества при появлении новой
популяции
procedure CopyPopulation (var PopFrom:
TPopulation; var PopInto: TPopulation);
// копирование популяцийInitRec;
// инициализация рекордного множества
procedure EraseRec;
// инициализация входных массивовEraseInputArrays;
// удаление входных массивовGetS (var II:
TIndivid): real;
// определение стоимости по решению
function GetP (var II: TIndivid): real;
// определение вероятности по решениюGetS (var II:
TIndivid): real;j: integer;:= 0;j:= 0 to N-1 doII[j] of
: result:= result + S[j];
: result:= result + 2 * S[j] * G[j];
: result:= result + 4 * S[j];;;GetP (var II:
TIndivid): real;j: integer;:= 1;j:= 0 to N-1 doII[j] of
: result:= result * P[j];
: result:= result * (2*P[j] - P[j]*P[j]);
: result:= result * (3*P[j]*P[j] -
2*P[j]*P[j]*P[j]);;;CountFitness (var Pop: TPopulation);i, j: integer;i:= 0 to
L-1 do. Fitness[i].S:= - GetS (Pop. Individs[i]);. Fitness[i].P:= GetP (Pop.
Individs[i]);;;InitPopulation (var Pop: TPopulation);i, j: integer;
//randomize; // задаем длину(Pop. Individs, L);(Pop. Fitness, L);(Pop. Rank,
L);
// присваиваем случайные значения
for i:= 0 to L-1 do
begin(Pop. Individs[i], N);j:= 0 to N-1 do.
Individs[i] [j]:= random(3)+1;;
// исправляем популяцию(Pop);
// вычисляем значения целевых функций(Pop);
for i:= 0 to L-1 do // а нужно ли??. Rank[i]:=
0;;ErasePopulation (var Pop: TPopulation);i, j: integer;i:= 0 to L-1 do.
Individs[i]:= nil;. Individs:= nil;. Fitness:= nil;. Rank:= nil;;Sort (var Euc:
TEucArray; p, q: integer); {p, q - индексы начала и конца сортируемой части массива}i, j:
integer;, T: real;
Beginp<q then {массив из одного элемента тривиально
упорядочен}
begin:=Euc[p].distance;:=p-1;:=q+1;i<j
do:=i+1;Euc[i].distance>=r;:=j-1;Euc[j].distance<=r;i<j
then:=Euc[i].distance;[i].distance:=Euc[j].distance;[j].distance:=T;;;(Euc, p,
j);(Euc, j+1, q);;;IndivIsNotDominated (var Pop: TPopulation; index: integer;
str: string): boolean;k: integer;:= true;k:=0 to L-1 do(index <> k) and
(pos (' ' + IntToStr(k) + ' ', str)=0) then(Pop. Fitness[index].S<=Pop.
Fitness[k].S) and (Pop. Fitness[index].P <= Pop. Fitness[k].P) and
((Pop. Fitness[index].S<Pop. Fitness[k].S) or
(Pop. Fitness[index].P < Pop. Fitness[k].P)) then:= false;;RankPopulation
(var Pop: TPopulation);Scur, Stotal: string;: integer;: integer;: integer;:
integer;: TEucArray;: integer;: integer;: integer;i:= 0 to L-1 do.
Fitness[i].S:= - GetS (Pop. Individs[i]);. Fitness[i].P:= GetP (Pop.
Individs[i]);. Rank[i]:= 0;;:= ' ';:= 1;
repeat
// выбрать недоминируемые элементы и присвоить им ранг
NumsInStr:= 0;:= ' ';i:= 0 to L-1 dopos ('
'+IntToStr(i)+' ', Stotal)=0 thenIndivIsNotDominated (Pop, i, Stotal) then:=
Scur + IntToStr(i) + ' ';. Rank[i]:= r;(NumsInStr);
end;
//m:= length(Scur); // создаем массив текущего ранга!!!!!!!!!!!!!
m:= NumsInStr;(EucArr, m);:= 0;k:= 0 to L-1 dopos
(' '+inttostr(k)+' ', Scur)<>0 then[t].index:= k;(t);;k:= 0 to m-1 do // считаем расстрояния[k].distance:=
0;t:= 0 to m-1 do[k].distance:= EucArr[k].distance +(sqr(Pop. Fitness
[EucArr[k].index].S-Pop. Fitness [EucArr[t].index].S) +(Pop. Fitness
[EucArr[k].index].P-Pop. Fitness [EucArr[t].index].P));;(EucArr, 0, m-1); // сортируемk:= 0 to m-1
do. Rank [EucArr[k].index]:= r +(m-k-1)/m; // записываем ранки:= nil; // удаляем массив:= Stotal + Scur;(r);
(length(Scur)=1) or (r>L+2);
// после этого r - maxrank
// преобразовываем ранг
for i:= 0 to L-1 do. Rank[i]:= r + Pop. Rank[i] -
2 * trunc (Pop. Rank[i]) - 1;;SelectPopulation (var Pop: TPopulation; var
TempPop: TPopulation);i, j: integer;, t2: integer; // индексы выбранных особейi:= 0 to L-1
do:= random (L);:= random (L);Pop. Rank[t1] >= Pop. Rank[t2] thenj:= 0 to
N-1 do. Individs[i] [j]:= Pop. Individs[t1] [j];. Fitness[i].S:= pop.
Fitness[t1].S;. Fitness[i].P:= Pop. Fitness[t1].P;. Rank[i]:= Pop. Rank[t1]j:=
0 to N-1 do. Individs[i] [j]:= Pop. Individs[t2] [j];. Fitness[i].S:= pop.
Fitness[t2].S;. Fitness[i].P:= Pop. Fitness[t2].P;. Rank[i]:= Pop.
Rank[t2];;;SelectPopulation2 (var Pop: TPopulation; var tempPop:
TPopulation);i, j: integer;, t2, t3: integer; // индексы выбранных особейi:= 0 to L-1 do:= random (L);:= random (L);:= random
(L);(Pop. Rank[t1] >= Pop. Rank[t2]) and (Pop. Rank[t1] >= Pop. Rank[t3])
thenj:= 0 to N-1 do. Individs[i] [j]:= Pop. Individs[t1] [j];. Fitness[i].S:=
pop. Fitness[t1].S;. Fitness[i].P:= Pop. Fitness[t1].P;. Rank[i]:= Pop.
Rank[t1](Pop. Rank[t2] >= Pop. Rank[t1]) and (Pop. Rank[t2] >= Pop.
Rank[t3]) thenj:= 0 to N-1 do. Individs[i] [j]:= Pop. Individs[t2] [j];.
Fitness[i].S:= pop. Fitness[t2].S;. Fitness[i].P:= Pop. Fitness[t2].P;.
Rank[i]:= Pop. Rank[t2]j:= 0 to N-1 do. Individs[i] [j]:= Pop. Individs[t3]
[j];. Fitness[i].S:= pop. Fitness[t3].S;. Fitness[i].P:= Pop. Fitness[t3].P;.
Rank[i]:= Pop. Rank[t3];;CrossPopulation (var TempPop: TPopulation; var
TempPopCr: TPopulation);i, j: integer;, t2: integer;: integer; //crossover
point: 1..3;
{for i:= 0 to (L div 2) dorandom(101)/100 <=
Pcros then:= random (L);:= random (L);j:= CrPt to N-1 do:= TempPop.
Individs[t1] [j];. Individs[t1] [j]:= TempPop. Individs[t2] [j];. Individs[t2]
[j]:= temp;;;}i:= 0 to (L div 2) - 1 do:= random(L);:=
random(L);random(101)/100 <= Pcros then:= random (N);j:= 0 to CrPt-1 do.
Individs [2*i] [j]:=TempPop. Individs[t1] [j];. Individs [2*i+1] [j]:=TempPop.
Individs[t2] [j];;j:= CrPt to N-1 do. Individs [2*i] [j]:=TempPop. Individs[t2]
[j];. Individs [2*i+1] [j]:=TempPop. Individs[t1] [j];;j:= 0 to N-1 do.
Individs [2*i] [j]:=TempPop. Individs[t1] [j];. Individs [2*i+1] [j]:=TempPop.
Individs[t2] [j];;;L mod 2 <> 0 thenj:= 0 to N-1 do. Individs [L-1]
[j]:=TempPop. Individs[t1] [j];;MutantPopulation (var TempPop: TPopulation);i,
j: integer;: integer;
{for i:= 0 to L-1 doj:= 0 to N-1
dorandom(101)/100 <= Pmut then. Individs[i] [j]:= random(3) + 1;}i:= 1 to
L-1 dorandom(101)/100 <= Pmut thenj:= 1 to N-1 dorandom(101)/100 <= Pmut
then. Individs[i] [j]:= random(3) + 1;;SumTxX (var Indiv: TIndivid): real;:
integer;:= 0;j:= 0 to N-1 doIndiv[j] of
: result:= result + 1/T[j];
: result:= result + 2/3/T[j];
: result:= result + 6/5/T[j];;;FixPopulation (var
TempPop: TPopulation);i, index: integer;i:= 0 to L-1 doSumTxX (TempPop.
Individs[i]) > 1/Tavg do:= random (N);TempPop. Individs[i] [index] = 3 then
dec (TempPop. Individs[i] [index], random(2)+1)if TempPop. Individs[i] [index]
= 1 then inc (TempPop. Individs[i] [index]);;InitTavg;j: integer;: real;:=
0;j:= 0 to N-1 do:= temp + 1/T[j];:= 1/temp;;InitRecord;i: integer;i:= 1 to
RecQuantity do[i].S:= -9999999;[i].P:= -9999999;[i].Quantity:= 0;;;VectorIsHere
(var RecEl: TRecElement; var Indivs: TIndivid): boolean;i, j, k: integer;:
boolean;:= false; /// вектора нетi:= 0 to
RecEl. Quantity -1 do:= false;j:= 0 to N-1 doRecEl. Solutions[i] [j] <>
Indivs[j] then:= true;;;:= result or not raznitsa;result then
break;;;AddToRecord (var TempPop: TPopulation);i, j, k, q, g: integer;i:= 0 to
L-1 dok:= 1 to RecQuantity do:= 0;(TempPop. Rank[i] >=1) and (TempPop. Rank[i] < 2) then // в рекорд идут
недоминируемые решения
Begin // если вектор доминирует
if ((TempPop. Fitness[i].S >= Rec[k].S) and (TempPop.
Fitness[i].P > Rec[k].P))((TempPop. Fitness[i].S > Rec[k].S) and
(TempPop. Fitness[i].P >= Rec[k].P)) then[k].S:= TempPop.
Fitness[i].S;[k].P:= TempPop. Fitness[i].P;(rec[k].Solutions, 1);[k].Quantity:=
1; // остальные подтереть(rec[k].Solutions[0],
N);j:= 0 to N-1 do[k].Solutions[0] [j]:= TempPop. Individs[i] [j];:= 0;
// подтираниеg:= k+1 to RecQuantity
do((TempPop. Fitness[i].S >= Rec[g].S) and (TempPop. Fitness[i].P >
Rec[g].P))((TempPop. Fitness[g].S > Rec[k].S) and (TempPop. Fitness[i].P
>= Rec[g].P)) then[g].S:= -9999999;[g].P:= -9999999;[g].Quantity:= 0;;;
end// если вектор равен. то добавляем еще одно возможное
решение
if (TempPop. Fitness[i].S = Rec[k].S) and
(TempPop. Fitness[i].P = Rec[k].P) thennot VectorIsHere (Rec[k], TempPop.
Individs[i]) then(rec[k].Quantity);(rec[k].Solutions,
rec[k].Quantity);(rec[k].Solutions [rec[k].Quantity-1], N);j:= 0 to N-1
do[k].Solutions [rec[k].Quantity-1] [j]:= TempPop. Individs[i] [j];:= 0;;;if
(TempPop. Fitness[i].S <= Rec[k].S) and (TempPop. Fitness[i].P <=
Rec[k].P) then;;;CopyPopulation (var PopFrom: TPopulation; var PopInto:
TPopulation);i, j: integer;i:= 0 to L-1 do. Rank[i]:= PopFrom. Rank[i];.
Fitness[i].S:= PopFrom. Fitness[i].S;. Fitness[i].P:= PopFrom. Fitness[i].P;j:=
0 to N-1 do. Individs[i] [j]:= PopFrom. Individs[i] [j];;;;InitRec;(Rec,
RecQuantity + 1);;EraseRec;:= nil;;InitInputArrays;(P, N);(T, N);(S, N);(G,
N);;EraseInputArrays;:= nil;:= nil;:= nil;:= nil;;
END.