Преобразование Фурье и его некоторые приложения
Содержание
Введение
Интеграл
Фурье в комплексной форме. Формулировка теоремы о сходимости интеграла Фурье
для кусочно-гладких и абсолютно интегрируемых на числовой прямой функции
Преобразование
Фурье
Примеры
нахождения преобразования Фурье
Некоторые
свойства преобразования Фурье
Сверстка
и преобразование Фурье
Спектр
Некоторые
приложения
Литература
Введение
Преобразование Фурье вычисляется всякий раз,
когда мы слышим звук. Ухо автоматически выполняет вычисление, проделать которое
наш сознательный ум способен лишь после нескольких лет обучения математике. Наш
орган слуха строит преобразование, представляя звук как колебательное движение
частиц упругой среды, распространяющееся в виде волн в газообразной, жидкой или
твёрдых средах - в виде спектра последовательных значений громкости для тонов
различной высоты. Мозг превращает эту информацию в воспринимаемый звук.
Аналогичные операции можно производить с помощью
математических методов над звуковыми волнами или практически над любыми другими
колебательными процессами - от световых волн и океанских приливов до циклов
солнечной активности. Пользуясь этими математическими приёмами, можно
раскладывать функции, представляя колебательные процессы в виде набора
синусоидальных составляющих - волнообразных кривых, переходящих от максимума к
минимуму, затем опять к максимуму, подобно океанской волне.
Преобразование Фурье стало мощным инструментом,
применяемым в различных научных областях. В некоторых случаях его можно
использовать как средство решения сложных уравнений, описывающих динамические
процессы, которые возникают под воздействием электрической, тепловой или
световой энергии. В других случаях оно позволяет выделять регулярные
составляющие в сложном колебательном сигнале, благодаря чему можно правильно
интерпретировать экспериментальные наблюдения в астрономии, медицине и химии.
Первым человеком, поведавшим миру об этом
методе, был французский математик Жан Батист Жозеф Фурье, именем которого и
было названо преобразование. В 1789 году он вывел уравнение, описывающее
распространение тепла в твёрдом теле. К 1807 году Фурье изобрёл и метод решения
этого уравнения: преобразование Фурье.
Преобразование Фурье используется во многих
областях науки - в физике, теории чисел, комбинаторике, теории вероятностей,
статистике, акустике, океанологии, оптике, геометрии, и многих других.
Благодаря широкому применению метода Фурье и
сходных с ним аналитических методов мы и сегодня можем повторить с полным
основанием то, что лорд Кельвин сказал в 1867 году: "Теорема Фурье не
только является одним из самых изящных результатов современного анализа, но и
дает нам незаменимый инструмент в исследовании самых трудных вопросов
современной физики".
Интеграл Фурье в комплексной форме.
Формулировка теоремы о сходимости интеграла Фурье для кусочно-гладких и
абсолютно интегрируемых на числовой прямой функции
Интеграл Фурье в комплексной форме. Формулировка
теоремы о сходимости интеграла Фурье для кусочно-гладких и абсолютно
интегрируемых на числовой прямой функции
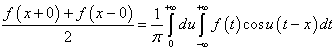 (1)
(1)
интегральная формула Фурье.
Вначале введем понятие главного значения
интеграла. Пусть функция 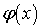 интегрируема на
любом отрезке числовой прямой.
интегрируема на
любом отрезке числовой прямой.
Определение 1.1. Если существует конечный предел
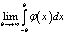 ,
,  ,(1.1)
,(1.1)
то этот предел называется главным значением
интеграла 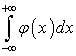 и обозначается:
v.p. (главное значение - по французки valeur principale)
и обозначается:
v.p. (главное значение - по французки valeur principale)
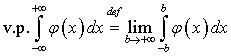 (1.2)
(1.2)
Замечание 1.1. Определение 3.1 есть частный
случай определения несобственного интеграла
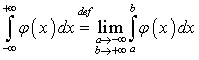 , (1.3)
, (1.3)
если 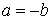 .
.
Если существует несобственный интеграл (1.3), то
и существует для этой функции и главное значение интеграла (1.2) и оно
совпадает с указанным несобственным интегралом. Обратное утверждение в общем
случае неверно, например:
 ,
,
но несобственный интеграл  расходится
(обосновать).
расходится
(обосновать).
Преобразуем интегральную формулу Фурье (1)
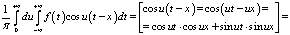
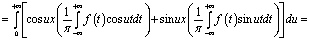
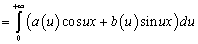 ,(1.4)
,(1.4)
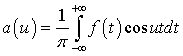 (1.5)
(1.5)
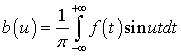 .(1.6)
.(1.6)
Замечание 1.2. В дальнейшем формулы будем
записывать, понимая несобственные интегралы в смысле главного значения
интеграла, не помечая это символами v.p. в отдельных случаях.
Если функция 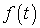 -
четная, то интегральная формула Фурье будет иметь вид правой части (1.4), где
-
четная, то интегральная формула Фурье будет иметь вид правой части (1.4), где 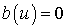 ;
если же функция
;
если же функция 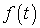 - нечетная, то в
правой части (1.4) будет
- нечетная, то в
правой части (1.4) будет 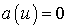 .
.
Дальше заметим, что
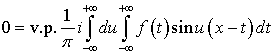 .(1.7)
.(1.7)
Сложив (1.7) с интегральной формулой Фурье (1),
получим интегральную формулу Фурье в комплексной форме
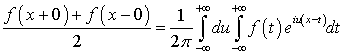 . (1.8)
. (1.8)
Преобразование Фурье
Запишем правую часть формулы (2.8) в виде
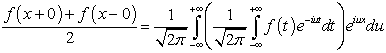 .(2.1)
.(2.1)
Положим:
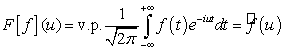 .(2.2)
.(2.2)
Определение 2.1. Функция 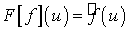 называется
преобразованием Фурье функции
называется
преобразованием Фурье функции 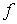 .
.
Замечание 2.1. Если функция 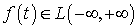 ,
то для нее преобразование Фурье определено и в смысле обычного определения
несобственного интеграла, так как
,
то для нее преобразование Фурье определено и в смысле обычного определения
несобственного интеграла, так как 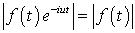 .
.
Формулу 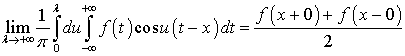
с учетом определения 2.1. можно записать
следующим образом
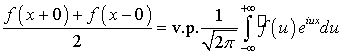 .(2.3)
.(2.3)
Эта формула называется формулой обращения, а
функцию
 .(2.4)
.(2.4)
называют обратным преобразованием Фурье функции 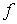 и
обозначают
и
обозначают 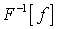 .
.
Замечание 2.2. Преобразование Фурье и обратное
преобразование Фурье определены на множестве функций, для которых
соответственно интегралы (2.2) и (2.3) существуют в смысле главного значения.
Примеры нахождения преобразования
Фурье
Пример 1.
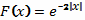
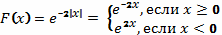
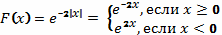 .
.
Тогда преобразование Фурье примет следующий вид:
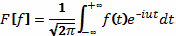
Ответ:
Пример 2.
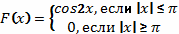

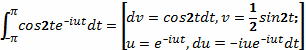
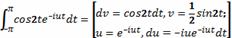 =
=


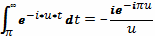
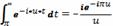
Пример 3.
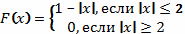
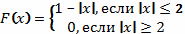
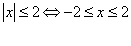
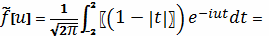
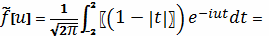
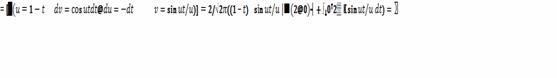
Некоторые свойства преобразования
Фурье
Теорема 1.1. (свойство линейности преобразования
и обратного преобразования Фурье)
Если 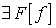 и
и
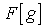 (
(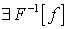
 и
и 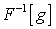 )
и взяты
)
и взяты  (
(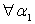 ,
,
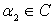 ),
то для функции
),
то для функции 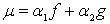
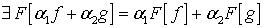 (
(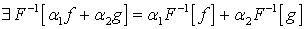 ).
).
Справедливость заключения теоремы следует из
свойства линейности для несобственного интеграла и формул (2.2) (2.4).
Пусть 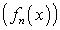 -
любая последовательность функций из пространства
-
любая последовательность функций из пространства  ,
то есть для любой функции
,
то есть для любой функции 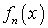 существует
существует 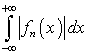 .
.
Определение 4.1. Последовательность 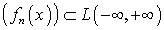 в
метрике пространства
в
метрике пространства  , если
, если 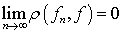 ,
где
,
где 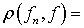
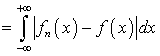 называется
расстояние между элементами
называется
расстояние между элементами 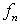 и
и 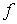 пространства
пространства
 .
.
Теорема 2.1. Если последовательность 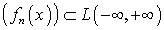 сходится
к функции
сходится
к функции 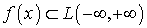 в метрике
указанного пространства, то соответствующая последовательность (
в метрике
указанного пространства, то соответствующая последовательность (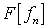 )
преобразований Фурье сходится к преобразованию Фурье
)
преобразований Фурье сходится к преобразованию Фурье 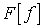 равномерно.
равномерно.
Воспользуемся следующим критерием равномерной
сходимости функциональной последовательности: последовательность (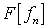 )
равномерно сходится к функции
)
равномерно сходится к функции 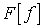 тогда и только
тогда, когда
тогда и только
тогда, когда 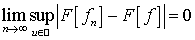 (
(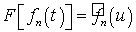 ,
,
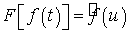 ).
).
Оценим сверху и снизу 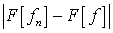 .
.
интеграл фурье теорема спектр
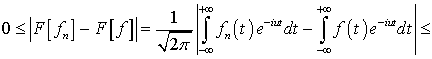
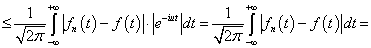
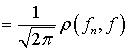 .(4.1)
.(4.1)
Для множества модулей 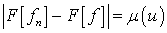 число
число
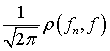 есть
верхняя граница по
есть
верхняя граница по 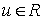 , а тогда для
наименьшей из верхних границ, то есть для
, а тогда для
наименьшей из верхних границ, то есть для 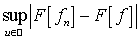 имеет
оценку
имеет
оценку
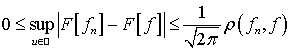 .(4.2)
.(4.2)
Далее воспользуемся аналогом теоремы о пределе
промежуточной функции.
Если 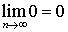 и
и
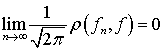 ,
то и
,
то и 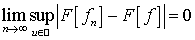 .
►
.
►
Теорема 2.2. (теорема Римана-Лебега) Если
функция 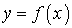 абсолютно
интегрируема на числовой прямой, то ее преобразование Фурье
абсолютно
интегрируема на числовой прямой, то ее преобразование Фурье 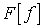 есть
непрерывная и ограниченная на числовой прямой функция, причем
есть
непрерывная и ограниченная на числовой прямой функция, причем 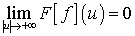 .
.
Вначале докажем ограниченность преобразования
Фурье на числовой прямой.
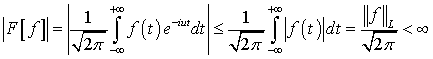 ,
,
где 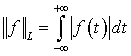 -
норма функции
-
норма функции 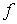 в пространстве
в пространстве  .
.
Дальше докажем остальные заключения теоремы.
Доказательство разобьем на 3 этапа.
Пусть 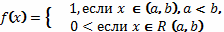
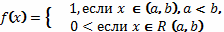
В этом случае функция 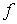 называется
характеристической функцией интервала
называется
характеристической функцией интервала 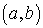 .
Очевидно, что
.
Очевидно, что 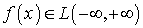 . Найдем
преобразование Фурье функции.
. Найдем
преобразование Фурье функции.
Очевидно, что преобразование Фурье есть
непрерывная функция на 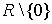 . Докажем, что
непрерывность будет и в точке
. Докажем, что
непрерывность будет и в точке 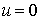 .
.
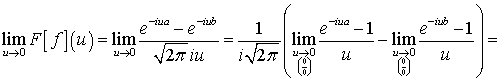
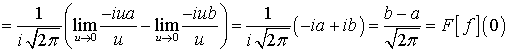 .
.
Утверждение доказано, то есть в рассматриваемом
случае преобразование Фурье есть непрерывная функция на всей числовой прямой 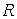 .
.
Покажем, что 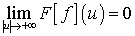 .
.
Вначале покажем, что функция 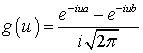 является
ограниченной даже на всей числовой прямой (нам же достаточно доказать ее
ограниченность в некоторой окрестности точки
является
ограниченной даже на всей числовой прямой (нам же достаточно доказать ее
ограниченность в некоторой окрестности точки 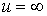 )
)
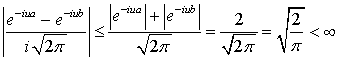 .
.
А тогда 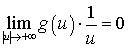 (имеем
произведение ограниченной функции на бесконечно малую при
(имеем
произведение ограниченной функции на бесконечно малую при 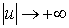 ).
Утверждение доказано.
).
Утверждение доказано.
Пусть отрезок 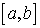 ,
,
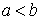 ,
есть объединение конечного числа частичных отрезков без общих внутренних точек,
то есть
,
есть объединение конечного числа частичных отрезков без общих внутренних точек,
то есть
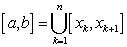
и таких, что
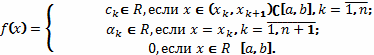
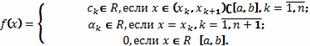 (4.3)
(4.3)
Функция (4.3) в рассматриваемом случае
называется ступенчатой функцией. Используя свойство линейности преобразования
Фурье и доказанные утверждения в пункте 1), показывается, что преобразование
Фурье функции (6.3) есть непрерывная функция на  ,
имеющая пределы, равные нулю при
,
имеющая пределы, равные нулю при  .
.
Пусть 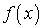 -
любая функция из класса
-
любая функция из класса  , то есть любая
суммируемая на числовой прямой функция. Можно доказать, что семейство
ступенчатых функций плотно в пространстве
, то есть любая
суммируемая на числовой прямой функция. Можно доказать, что семейство
ступенчатых функций плотно в пространстве  ,
то есть
,
то есть 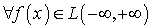 существует
последовательность
существует
последовательность 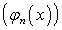 ступенчатых
функций, что
ступенчатых
функций, что
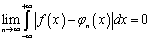 .(4.4)
.(4.4)
А тогда последовательность преобразований Фурье 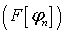 сходится
равномерно к преобразованию Фурье
сходится
равномерно к преобразованию Фурье 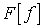 ,
причем члены последовательности
,
причем члены последовательности 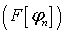 непрерывны на
непрерывны на 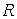 .
.
Покажем, что 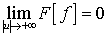 .
.
Из равномерной сходимости последовательности 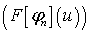 к
к
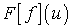 имеем,
что:
имеем,
что:
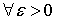
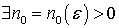
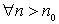
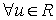
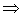
 .
.
Тогда
 ,
, 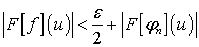 .
.
По указанному 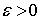
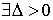
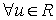
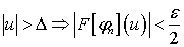 .
.
Окончательно получим:
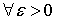
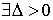
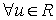
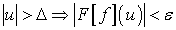 .
►
.
►
Сверстка и преобразования Фурье
Определение 5.1. Сверткой функций 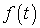 и
и
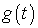 ,
абсолютно интегрируемых на числовой прямой
,
абсолютно интегрируемых на числовой прямой 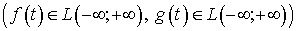 ,
называется функция
,
называется функция
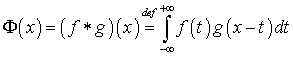 .(5.1)
.(5.1)
Теорема 5.1. Если 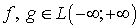 ,
то:
,
то:
свертка функций существует почти для любых 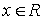 и
и
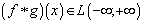 ;
;
для преобразования Фурье сверстки справедлива
формула
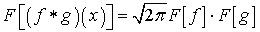 .(5.2)
.(5.2)
Вначале докажем, что 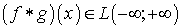 .
.
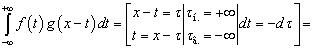
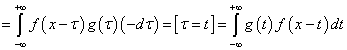 .
.
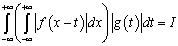 .
.
Во внутреннем интеграле при любом фиксированном 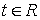 вводим
подстановку
вводим
подстановку
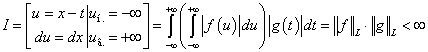 .
.
На основании следствия из теоремы Фубини ([1],
стр.318) из существования повторного интеграла 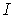 следует
существование второго повторного интеграла и соответствующего им двойного
интеграла, а также равенство этих интегралов.
следует
существование второго повторного интеграла и соответствующего им двойного
интеграла, а также равенство этих интегралов.
А тогда получим
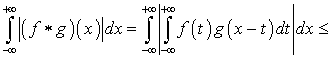
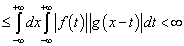 .(5.3)
.(5.3)
Правая часть оценки (5.3) есть один из указанных
выше повторных интегралов.
Из указанной оценки следует, что 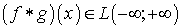 ,
что говорит о существовании почти для всех
,
что говорит о существовании почти для всех 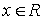 свертки
функций.
свертки
функций.
Если 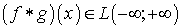 ,
то существует преобразование Фурье свертки. Тогда
,
то существует преобразование Фурье свертки. Тогда
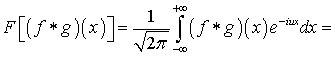
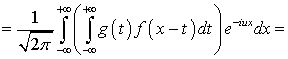
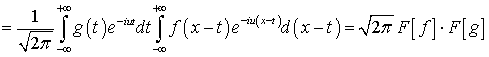 .
.
Изменение порядка интегрирования законно на
основании указанного выше следствия из теоремы Фубини (учесть еще, что 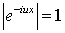 ).
).
Спектр
Спектральная теория является мощным и гибким
орудием исследования законов природы.
Если функция 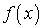 является
периодической с периодом
является
периодической с периодом 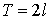 ,
, 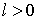 ,
а также кусочно-гладкой на любом отрезке числовой прямой, то формула
тригонометрического ряда Фурье в комплексной форме будет:
,
а также кусочно-гладкой на любом отрезке числовой прямой, то формула
тригонометрического ряда Фурье в комплексной форме будет:
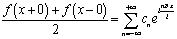 ,(6.1)
,(6.1)
где коэффициенты Фурье
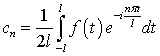 .(6.2)
.(6.2)
Числа 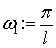 -
это основная частота, а совокупность комплексных чисел
-
это основная частота, а совокупность комплексных чисел 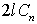 называется
спектром комплексных амплитуд функции
называется
спектром комплексных амплитуд функции 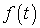 .
.
Аналогично в непериодическом случае
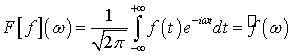 (6.2)
(6.2)
(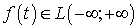 и
и 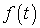 -
кусочно-гладкая на любом отрезке числовой прямой).
-
кусочно-гладкая на любом отрезке числовой прямой).
А тогда
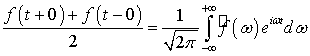 .(6.3)
.(6.3)
Формулу (11.3) будем понимать как бесконечную
«сумму» бесконечно малых гармоник
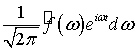 .(6.4)
.(6.4)
Комплексная амплитуда 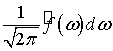 отдельного
колебания бесконечно мала. Частотный интервал между двумя соседними колебаниями
также бесконечно мал и равен
отдельного
колебания бесконечно мала. Частотный интервал между двумя соседними колебаниями
также бесконечно мал и равен 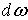 , то есть частоты
отдельных составляющих будут изменяться непрерывно (линии спектра будут
«плотно» заполнять чертеж). Получим так называемый сплошной спектр
, то есть частоты
отдельных составляющих будут изменяться непрерывно (линии спектра будут
«плотно» заполнять чертеж). Получим так называемый сплошной спектр 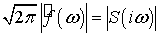 .
На некотором конечном промежутке
.
На некотором конечном промежутке 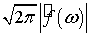 есть
огибающая дискретного ряда чисел
есть
огибающая дискретного ряда чисел 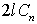 ,
соответствующего периодическому повторению заданных функций. Функция
,
соответствующего периодическому повторению заданных функций. Функция 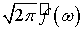 называется
спектральной плотностью функции
называется
спектральной плотностью функции 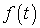 .
.
Задача 1.1. Пусть периодическая функция
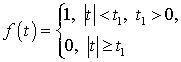
описывает короткий отрезок некоторого процесса
(импульс). Найти спектральную плотность этого импульса. Построить эскиз графика
спектральной плотности.
Находим преобразование Фурье функции 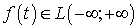
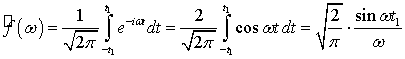 .
.
Тогда спектральная плотность будет
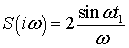 .
.
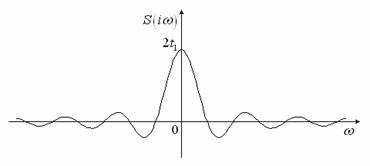
Рис. 1
Замечание 6.1. В приложениях есть задачи, в
которых необходимо находить спектральную плотность для данной непериодической
функции (смотри задачу 10.2). По спектральной плотности находят те промежутки
изменения 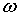 , которым
соответствуют относительно большие по модулю значения
, которым
соответствуют относительно большие по модулю значения  ,
то есть полосы частот, которым соответствуют гармонические функции, играющие
самую большую роль в представлении непериодической функции интегралом Фурье.
,
то есть полосы частот, которым соответствуют гармонические функции, играющие
самую большую роль в представлении непериодической функции интегралом Фурье.
Спектральный метод, связанный с интегралом
Фурье, применяется, например, при расчете нестационарных процессов в
электрических цепях (стационарный процесс - это такое состояние электрической
цепи, при котором величины этой цепи (ток, напряжение и т.д.) не зависят от
времени или являются гармоническими функциями времени).
Пусть линейная электрическая цепь включается под
напряжение 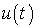 . Тогда ток и
напряжение могут быть представлены интегралом Фурье
. Тогда ток и
напряжение могут быть представлены интегралом Фурье
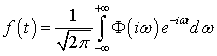 ,(6.5)
,(6.5)
где 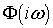 соответственно
есть или спектральная плотность тока
соответственно
есть или спектральная плотность тока 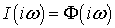 ,
или спектральная плотность напряжения
,
или спектральная плотность напряжения 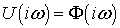 .
Если спектральная плотность полного сопротивления есть
.
Если спектральная плотность полного сопротивления есть 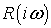 ,
то для указанных спектральных плотностей будет справедлив закон Ома
,
то для указанных спектральных плотностей будет справедлив закон Ома
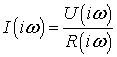 .(6.6)
.(6.6)
Пусть, например, надо найти ток 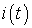 нестационарного
процесса. Поступаем при этом следующим образом:
нестационарного
процесса. Поступаем при этом следующим образом:
Определяем спектральную плотность напряжения по
заданному воздействию 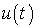
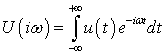 .(6.7)
.(6.7)
По схеме электрической цепи определяем плотность
ее полного сопротивления 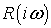 (полное
сопротивление цепи).
(полное
сопротивление цепи).
Спектральная плотность тока находится по формуле
(6.6).
Ток нестационарного режима находим по формуле
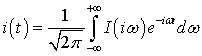 .(3)
.(3)
Конкретный пример. Дана электрическая цепь
(смотри рисунок 1). Необходимо определить ток 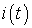 ,
если в момент времени
,
если в момент времени  рубильник
рубильник 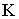 подключает
цепь к источнику постоянного напряжения
подключает
цепь к источнику постоянного напряжения 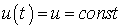 (
(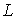 - индуктивность,
- индуктивность, 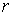 - сопротивление).
- сопротивление).
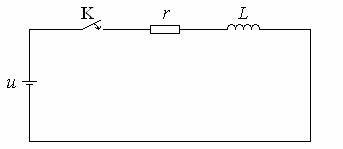
Рис. 2
Находим спектральную плотность напряжения (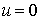 при
при 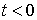 )
)
 .
.
Определяем полные сопротивления
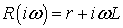 .
.
Находим спектральную плотность тока
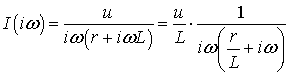 .(6.9)
.(6.9)
В правой части формулы (6.9) проведем следующие
преобразования:
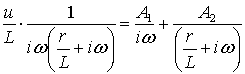 (6.10)
(6.10)
или (умножаем левую и правую части (6.10) на 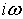 )
)
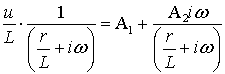 .(6.11)
.(6.11)
Если 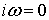 ,
то
,
то 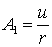 .
Далее умножим обе части (6.10) на
.
Далее умножим обе части (6.10) на 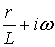 ,
получим:
,
получим:
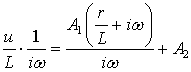 .(6.12)
.(6.12)
Если для (6.12) положить 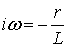 ,
то
,
то 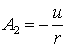 .
Тогда
.
Тогда
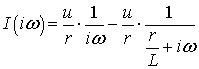 .(6.13)
.(6.13)
По формуле (6.8) находим ток нестационарного
режима, получим:
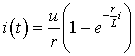 . (6.14)
. (6.14)
Замечание 6.2. Спектральную плотность 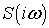 функции
функции
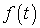 можно
находить по таблице интегральных преобразований Фурье или таблице интегральных
преобразований Лапласа, при этом надо учесть, что параметр
можно
находить по таблице интегральных преобразований Фурье или таблице интегральных
преобразований Лапласа, при этом надо учесть, что параметр 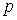 заменяется
на
заменяется
на 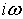 .
(Преобразование Лапласа
.
(Преобразование Лапласа 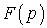 для функции
для функции 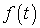 будет:
будет:
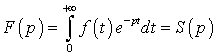 ).
).
Некоторые приложения
Задача 2.1. Найти температуру бесконечного
теплопроводящего стержня в любой момент времени 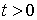 ,
если в начальный момент
,
если в начальный момент  его температура в
любой точке
его температура в
любой точке 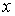 есть
есть 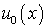 .
.
Имеем задачу Коши
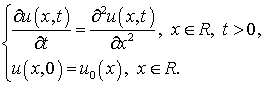 (7.1)
(7.1)
Дополнительно полагаем, что:
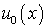 ,
, 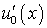 ,
,
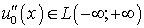 ;
;
Решение 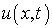 ищем
в классе функций:
ищем
в классе функций:
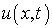 ,
, 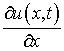 ,
,
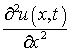 абсолютно
интегрируемы на числовой прямой по
абсолютно
интегрируемы на числовой прямой по 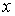 при
любых фиксированных
при
любых фиксированных  ,
,
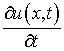 имеет в любом
конечном отрезке
имеет в любом
конечном отрезке 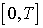 ,
, 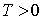 ,
интегрируемую мажоранту
,
интегрируемую мажоранту 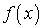
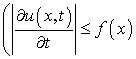 и
и
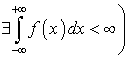 .
.
Подействуем оператором Фурье на правую часть
уравнения (7.1), используя формулу 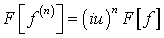 ,
то есть
,
то есть
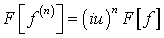 (вместо
(вместо 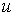 берем
берем
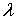 ).
).
Получим:
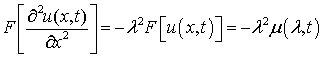 .(7.3)
.(7.3)
Интеграл
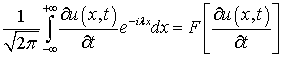 (7.4)
(7.4)
сходится равномерно относительно 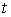 (учесть
пункт 3) из условия б) и признак Вейерштрасса равномерной сходимости
несобственных интегралов, зависящих от параметра). Тогда производная интеграла
по параметру
(учесть
пункт 3) из условия б) и признак Вейерштрасса равномерной сходимости
несобственных интегралов, зависящих от параметра). Тогда производная интеграла
по параметру 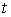 равна интегралу от
производной, то есть
равна интегралу от
производной, то есть
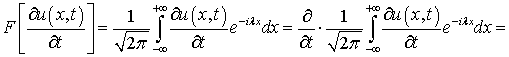
 .(7.5)
.(7.5)
Вывод. С помощью преобразования Фурье
дифференциальное уравнение (7.1) в частных производных переведено в
обыкновенное дифференциальное уравнение
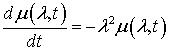 .(7.6)
.(7.6)
Для уравнения (7.6) имеем начальные условия:
при  будет
будет
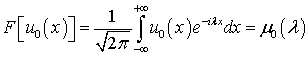 .(7.7)
.(7.7)
Решаем полученную задачу Коши
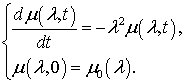 (7.8)
(7.8)
Решаем уравнение (7.8)
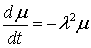 ,
, 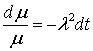 ,
,
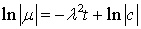 ,
,
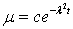 (7.10)
(7.10)
(тривиальное решение (7.8) есть 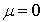 ).
).
Найдем частное решение, удовлетворяющее
начальным условиям (7.9)  , то
, то 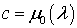 .
Тогда
.
Тогда
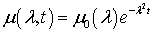 .(7.11)
.(7.11)
Дальше найдем такую функцию 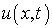 ,
что
,
что
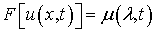 .(7.12)
.(7.12)
Равенство (7.11) имеет вид
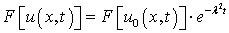 .(7.13)
.(7.13)
Найдем функцию  ,
преобразование Фурье которой есть
,
преобразование Фурье которой есть 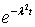 .
.
Используем формулу обращения преобразования
Фурье

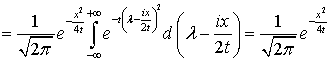 .
.
Равенство примет вид:
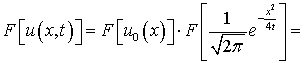

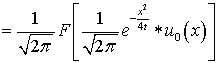 .(714)
.(714)
Применим к обеим частям равенства (10.14)
оператор обращения преобразования Фурье (показать, что 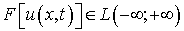 ,
также свертка (10.14) из
,
также свертка (10.14) из 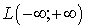 )
)
Получим:
 (7.15)
(7.15)
интеграл Пуассона для решения уравнения
теплопроводности стержня.
Задача 2.2. Многие физические приборы - это
операторы (преобразователи). На вход приборов подаются сигналы функции 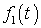 ,
,
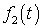 ,
… - они входят в область определения оператора. На выходе получаем
соответственно функции
,
… - они входят в область определения оператора. На выходе получаем
соответственно функции 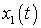 ,
, 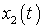 ,
…. Например, усилители можно рассматривать как операторы, преобразующие
напряжение переменного тока
,
…. Например, усилители можно рассматривать как операторы, преобразующие
напряжение переменного тока 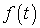 , подаваемого на
вход, в напряжение
, подаваемого на
вход, в напряжение 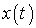 переменного тока,
получаемого на выходе. Преобразователь называется линейным, если он
удовлетворяет следующим условиям:
переменного тока,
получаемого на выходе. Преобразователь называется линейным, если он
удовлетворяет следующим условиям:
если 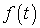 преобразуется
в
преобразуется
в 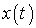 ,
то
,
то 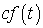 (
(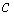 - любая действительная константа,
- любая действительная константа, 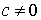 )
преобразуется в
)
преобразуется в 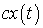 ;
;
если 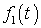 преобразуется
в
преобразуется
в 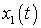 ,
а
,
а 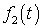 -
в
-
в 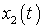 ,
то
,
то 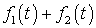 преобразуется
в
преобразуется
в 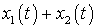 .
.
Если для преобразователя выполняются указанные выше
условия, то говорят, что для преобразователя выполняется принцип суперпозиции.
Дополнительно предполагаем, что функция  преобразуется
в функцию
преобразуется
в функцию 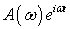 , то есть, что
установившееся гармоническое колебание с частотой
, то есть, что
установившееся гармоническое колебание с частотой 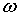 преобразуется
в установившееся гармоническое колебание с той же частотой
преобразуется
в установившееся гармоническое колебание с той же частотой 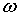 .
Причем,
.
Причем, 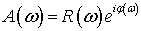 ,
где
,
где 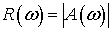 ,
,
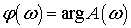 -
главное значение аргумента
-
главное значение аргумента 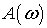 (
(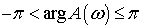 ).
).
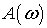 называется
спектральной характеристикой преобразователя, которая означает, что
гармонические колебания с различными частотами прибор преобразует по-разному.
Гармоническое колебание
называется
спектральной характеристикой преобразователя, которая означает, что
гармонические колебания с различными частотами прибор преобразует по-разному.
Гармоническое колебание  преобразуется в
гармоническое колебание
преобразуется в
гармоническое колебание
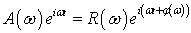 .(7.16)
.(7.16)
Модуль спектральной характеристики 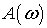 ,
то есть
,
то есть 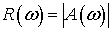 называется
частотной характеристикой преобразователя. Она показывает, во сколько раз
изменяется амплитуда гармонического колебания с данной частотой
называется
частотной характеристикой преобразователя. Она показывает, во сколько раз
изменяется амплитуда гармонического колебания с данной частотой 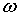 .
А
.
А 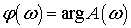 называется
фазовой характеристикой преобразователя. Она показывает изменение фазы. Имеем
прямую задачу.
называется
фазовой характеристикой преобразователя. Она показывает изменение фазы. Имеем
прямую задачу.
Дано: 1) физприбор - линейный преобразователь,
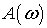 - его спектральная
характеристика;
- его спектральная
характеристика;
)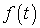 - функция на
выходе (абсолютно интегрируемая на числовой прямой и кусочно-гладкая на любом
отрезке числовой прямой).
- функция на
выходе (абсолютно интегрируемая на числовой прямой и кусочно-гладкая на любом
отрезке числовой прямой).
Найти: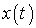 - преобразованную функцию на выходе.
- преобразованную функцию на выходе.
Находим преобразование Фурье функции 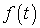 .
.
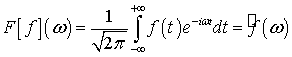 .(7.17)
.(7.17)
По формуле обращения преобразования Фурье
находим
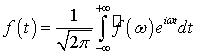 .(7.18)
.(7.18)
Интеграл правой части равенства (10.18) можно
рассматривать как «сумму» бесконечно большого числа бесконечно малых
гармонических колебаний
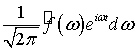 .(7.19)
.(7.19)
Преобразователем гармонические колебания (7.19)
преобразуются в гармонические колебания
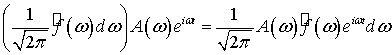 .(7.20)
.(7.20)
«Сумма» колебаний (7.19) преобразуется в «сумму»
колебаний (7.20). Тогда функция  , определяемая
соотношением (7.18), преобразуется в функцию
, определяемая
соотношением (7.18), преобразуется в функцию  ,
определяемую соотношением
,
определяемую соотношением
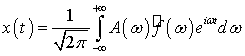 .(7.21)
.(7.21)
Задача решена.
Задача 2.3. (обратная для задачи 2.2)
Дано:1)физприбор - линейный преобразователь со
спектральной характеристикой 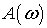 ;
;
)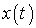 - преобразованная
функция, получаемая на выходе.
- преобразованная
функция, получаемая на выходе.
Найти:функцию 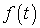 -
подаваемую на вход физприбора.
-
подаваемую на вход физприбора.
Из формулы (7.21) имеем: образ Фурье функции 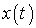 есть
есть
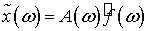 .(7.22)
.(7.22)
Тогда
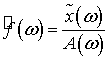 .(7.23)
.(7.23)
Применим к (7.23) формулу обращения
преобразования Фурье, получим:
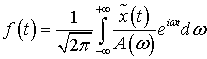 .(7.24)
.(7.24)
Задача решена.
Литература
2. Колмогоров
А.Н., С.В. Фомин. Элементы теории функций и функционального анализа. М.: Наука,
1981, 544 с.
. Scientific
American, Издание на русском языке, № 8 Август 1989 с. 48-56.