Декартовы координаты
Введение
координата декартовый
плоскость геометрия
Аналитическая геометрия изучает свойства
геометрических объектов при помощи аналитического метода, в основе которого
лежит так называемый метод координат, впервые систематически примененный
Декартом (французский математик и философ, 1596-1650).
Метод координат представляет собой глубокий и
мощный аппарат, позволяющий привлекать для исследования геометрических объектов
методы алгебры и математического анализа. Основные понятия геометрии (точки,
прямые линии, плоскости) относятся к числу начальных понятий. Вводятся
декартовы координаты точки на прямой, на плоскости и в пространстве. Из
школьного курса геометрии эти понятия известны, как известны и некоторые
сведения о векторах. Обобщим и дополним эти сведения. Векторная величина
характеризуется не только своим численным значением, но и направлением.
Физическими примерами векторных величин могут служить смещение материальной
точки, скорость и ускорение этой точки действующая на эту точку сила. В отличие
от векторных величин рассматриваются скалярные величины, каждая из которых
характеризуется только численным значением (площадь, объем, длина). Свойства
векторов и операции над ними позволяют получить уравнения прямой, плоскости и
изучить их взаимное положение.
Целью настоящей работы является исследование
кривых второго порядка. Задачи работы:
) изучение декартовых координат на прямой, на
плоскости, в пространстве;
) характеристика основных понятий векторов и
действий над ними;
) решение простейших задач методом координат;
) выявление геометрического смысла линейных
неравенств с двумя переменными;
) анализ видов кривых второго порядка.
Декартовы координаты на прямой, на
плоскости и в
пространстве
Прямую линию с указанным на ней направлением,
началом отчета и единицей масштаба назовем числовой осью. Каждому
действительному числу Х на числовой оси соответствует единственное число,
которое называется координатой данной точки.
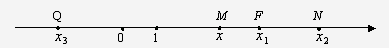
Здесь числа х2>х1>0,
х3<0.
х3, х1, х2, х -
координаты точек Q, F,
N, M
соответственно. Записывают:
Q (х3), F
(x1),
N(x2),
M (x).
Точки F
и N ограничивают
отрезок FN. Очевидно,
его длина | FN
| = х2- х1. Две взаимно
перпендикулярные оси на плоскости с общим началом и одинаковой единицей
масштаба образуют декартову прямоугольную систему координат на плоскости. Одна
из осей - ось абсцисс Ох, другая - ось ординат Оу.
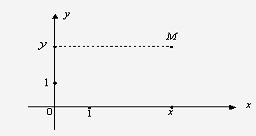
Рис.
Каждой точке плоскости соответствует
единственная пара чисел х, у.
x, у называют
координатами точки М и записывают М (х, у).
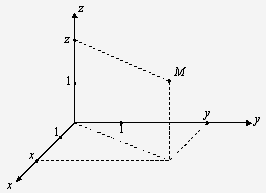
Рис.
В пространстве декартова прямоугольная система
координат представляет собой совокупность трех взаимно перпендикулярных осей с
общим началом и одинаковой единицей масштаба. Это ось абсцисс Ох, ось ординат
Оу и ось аппликат Оz. Каждая
точка пространства М имеет координаты х, у, z.
Записывают:
М (х, у, z).
Вектор. Основные понятия. Действия над
векторами
Вектором называется направленный отрезок
Будем обозначать вектор либо
символом 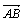 , где точки
А и В - начало и конец направленного отрезка, либо символом
, где точки
А и В - начало и конец направленного отрезка, либо символом  (малая
латинская буква с чертой).
(малая
латинская буква с чертой).
Для обозначения длины вектора будем
использовать символ модуля:
|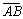 | - длина вектора
| - длина вектора 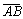 ,
,
| | - длина вектора
| - длина вектора  .
.
Вектор называется нулевым (или
нуль-вектором), если начало и конец его совпадают. Нулевой вектор не имеет
определенного направления, длина его равна числу 0. Записывают: |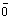 |
= 0.
|
= 0.
Векторы называются коллинеарными,
если они лежат на одной прямой или на параллельных прямых. Если векторы  и
и  коллинеарны,
то записывают:
коллинеарны,
то записывают: 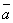 ||
|| .
.
Два вектора называются равными, если
они коллинеарны, имеют одинаковую длину и одинаковое направление. Записывают:  =
= .
.
Понятно, что вектор можно переносить
параллельно самому себе в любую точку пространства, т.е. изучаемые в геометрии
векторы являются свободными.
Векторы называются компланарными,
если они лежат в одной или в параллельных плоскостях.
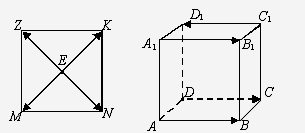
Рис.
Рассмотрим векторы, совпадающие с
ребрами куба.
Векторы 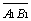 и
и 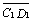
 коллинеарны, но не равны.
коллинеарны, но не равны.
Векторы 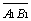 ,
, 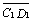 ,
, 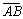 ,
, 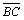 ,
компланарны, так как лежат в параллельных гранях.
,
компланарны, так как лежат в параллельных гранях.
Векторы 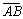 ,
, 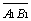 ,
, 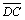 равны:
равны: 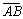 =
=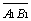 =
=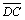 .
.
В квадрате MNKZ векторы 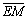 ,
, 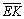 ,
, 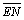 ,
,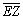 , имеют
одинаковые длины, но не равны. Если изменим направление у двух векторов, то
можно утверждать, что
, имеют
одинаковые длины, но не равны. Если изменим направление у двух векторов, то
можно утверждать, что  =
=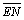 и
и  =
=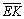 .
.
Рассмотрим векторы, совпадающие со
сторонами ромба ABCD.
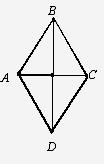
Рис.
Здесь 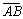 =
=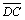 , но
, но 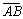 ¹
¹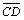 ,
, 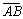 ¹
¹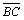 , хотя длины
векторов, совпадающих со сторонами ромба, равны:
, хотя длины
векторов, совпадающих со сторонами ромба, равны:
|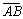 | = |
| = |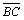 |
= |
|
= |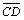 | = |
| = |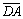 |.
|.
Линейными операциями над векторами
называют сложение векторов и умножение вектора на число.
Суммой  +
+ двух
векторов
двух
векторов  и
и  называется
вектор
называется
вектор 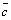 , идущий из
начала вектора
, идущий из
начала вектора  в конец
вектора
в конец
вектора  при
условии, что начало вектора
при
условии, что начало вектора  совпадает с концом вектора
совпадает с концом вектора  .
Записывают:
.
Записывают:
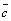 =
=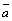 +
+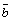 .
.

Рис. 1.Рис. 2.
Это правило называется
"правилом треугольника" (рис. 1). Для сложения двух векторов можно
использовать "правило параллелограмма" (рис. 2): если векторы  и
и  приложены к
общему началу и на них построен параллелограмм, то суммой
приложены к
общему началу и на них построен параллелограмм, то суммой  и
и  этих
векторов является вектор, совпадающий с диагональю параллелограмма, идущей из
общего начала векторов
этих
векторов является вектор, совпадающий с диагональю параллелограмма, идущей из
общего начала векторов  и
и  .
.
Сумму трех, четырех и большего числа
векторов можно построить по "правилу многоугольника": начало каждого
последующего вектора совмещают с концом предыдущего, а суммой всех векторов
является вектор, идущий из начала первого вектора в конец последнего.
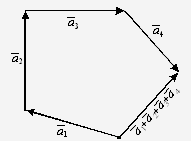
Рис. 3
На рис. 3 построена сумма четырех
векторов 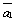 +
+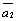 +
+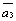 +
+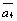 .
.
Три вектора в пространстве можно
складывать по "правилу параллелепипеда": если на трех векторах  ,
,  ,
,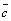 , как на
ребрах, построить параллелепипед, то его диагональ, выходящая из общего начала
данных векторов, и будет их суммой (рис. 4):
, как на
ребрах, построить параллелепипед, то его диагональ, выходящая из общего начала
данных векторов, и будет их суммой (рис. 4):
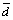 =
= +
+ +
+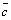 .
.

Рис. 4
Произведением 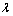 ×
× вектора
вектора  на число
на число 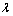 называется
вектор
называется
вектор  ,
коллинеарный вектору
,
коллинеарный вектору  , имеющий
длину, равную |
, имеющий
длину, равную |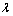 |×|
|×| |, одинаково с вектором
|, одинаково с вектором  направленный
в случае
направленный
в случае 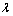 >0 и противоположно с ним
направленный в случае
>0 и противоположно с ним
направленный в случае 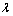 <0. Записывают:
<0. Записывают:
 =
=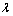 ×
× .
.
Когда 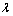 =0, для любого вектора
=0, для любого вектора  произведение
произведение
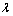 ×
× равно
нуль-вектору:
равно
нуль-вектору:
× =
=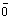 .
.
Когда 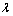 =1, 1×
=1, 1× =
= .
.
Когда 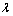 = -1, (-1)×
= -1, (-1)× =-
=- - вектор, противоположный вектору
- вектор, противоположный вектору  .
.
Итак, при умножении вектора на число
получаем вектор, коллинеарный данному. Поэтому, если известно, что 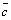 =
=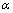 ×
× , где
, где 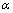 - число,
имеем два коллинеарных вектора
- число,
имеем два коллинеарных вектора 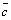 и
и . Иначе говоря, равенство
. Иначе говоря, равенство 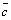 =
=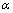 ×
× является
условием коллинеарности векторов
является
условием коллинеарности векторов 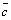 и
и .
.
Для примера рассмотрим векторы,
совпадающие со сторонами треугольника АВС: 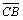 =
= ,
, 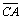 =
= .
.
Рис.
Требуется выразить через векторы  и
и 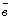 вектор
вектор 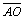 , где О -
точка пересечения медиан треугольника.
, где О -
точка пересечения медиан треугольника.
Известно, что точка О пересечения
медиан треугольника делит отрезок медианы в отношении 2:1, считая от вершины.
Поэтому 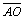 =2/3×
=2/3×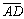 , где точка D - середина
стороны СВ.
, где точка D - середина
стороны СВ.
Но вектор 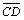 =1/2×
=1/2×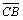 =1/2×
=1/2× ;
; 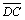 =-1/2×
=-1/2× .
.
В треугольнике САD вектор 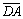 =
=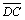 +
+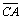 = -1/2×
= -1/2× +
+ .
.
Искомый вектор 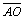 =-2/3(-1/2
=-2/3(-1/2 +
+ )= 1/3×
)= 1/3× -2/3×
-2/3× .
.
Итак, 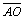 =1/3×
=1/3× -2/3×
-2/3× . Заметим, что разность векторов
. Заметим, что разность векторов  и
и  можно
рассматривать как сумму вектора
можно
рассматривать как сумму вектора  и вектора, противоположного вектору
и вектора, противоположного вектору
 :
:
 -
- =
= +(-1)×
+(-1)× =
= +(-
+(- ).
).
В нашем примере из треугольника САD можно
получить вектор 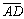 =
=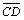 -
-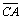 =1/2×
=1/2× -
- .
.
Если вектор  умножить на
число 1/|
умножить на
число 1/| |, получим так называемый
единичный вектор вектора
|, получим так называемый
единичный вектор вектора  (или орт
вектора
(или орт
вектора  ), который
обозначается
), который
обозначается  0. Итак, орт
вектора или единичный вектор вектора
0. Итак, орт
вектора или единичный вектор вектора 
 0=1/|
0=1/| |×
|× =
= /|
/| |; |
|; | 0|=1.
0|=1.
Принято единичные векторы на
координатных осях Ох, Оу, Оz обозначать 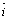 ,
, 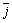 ,
, 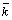 соответственно.
соответственно.
Линейные операции над векторами
обладают теми же свойствами, что и линейные операции над матрицами. Укажем
некоторые из них:
)  +
+ =
= +
+ - перестановочный закон сложения;
- перестановочный закон сложения;
)  +(
+( +
+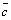 )=(
)=( +
+ )+
)+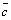 - сочетательный закон сложения;
- сочетательный закон сложения;
) 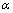 ×(
×(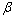 ×
× ) = (
) = (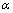 ×
×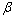 )×
)× - сочетательный закон умножения на
число;
- сочетательный закон умножения на
число;
) 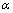 ×(
×( +
+ )=
)=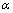 ×
× +
+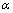 ×
× ;
;
) (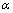 +
+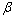 )×
)× =
=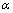 ×
× +
+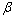 ×
× - распределительные законы.
- распределительные законы.
Рассмотрим координаты вектора, для
чего перенесем вектор  параллельно
самому себе так, чтобы его начало совпало с началом координат. Пусть конец
вектора - точка М.
параллельно
самому себе так, чтобы его начало совпало с началом координат. Пусть конец
вектора - точка М.
Координатами вектора назовем координаты его
конечной точки.
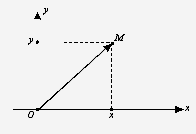
Рис. 5
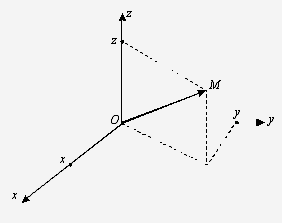
Рис. 6
Так как координатами точки на
плоскости являются два числа х и у, то на плоскости вектор  задается
двумя координатами.
задается
двумя координатами.
Записывают:  =(х, у)
(рис. 5).
=(х, у)
(рис. 5).
В пространстве вектор  задается
тремя координатами х, у и z.
задается
тремя координатами х, у и z.
Записывают:  =(х, у, z) (рис. 6).
=(х, у, z) (рис. 6).
Нетрудно показать, что при сложении векторов
складываются их соответствующие координаты, а при умножении вектора на число
все его координаты умножаются на это число.
Если даны координаты векторов  и
и 
 =(х1,
у1, z1),
=(х1,
у1, z1),  =(х2,
у2, z2) и
=(х2,
у2, z2) и
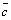 =
= +
+ ;
; 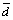 =
= -
- ;
; 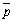 =
=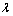 ×
× ,
,
то координаты векторов 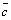 ,
, 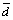 ,
, 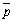 легко
находятся:
легко
находятся:
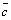 =(х1+х2; у1+у2;
z1+z2),
=(х1+х2; у1+у2;
z1+z2),
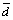 =(x1-x2; y1-y2; z1-z2),
=(x1-x2; y1-y2; z1-z2),
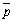 =(
=(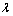 ×х1;
×х1; 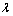 ×у1;
×у1; 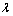 ×z1).
×z1).
На рис. 5 и рис. 6 видно, что длина
вектора равна корню квадратному из суммы квадратов его координат:
| |=|
|=|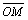 |=
|=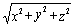 .
.
В плоском случае достаточно считать
третью координату z равной нулю.
Если вектор 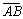 ограничен
двумя точками, координаты которых заданы: т. А (х1, у1, z1), т. В (х2,
у2, z2), то легко
найти координаты самого вектора
ограничен
двумя точками, координаты которых заданы: т. А (х1, у1, z1), т. В (х2,
у2, z2), то легко
найти координаты самого вектора 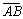 .
.
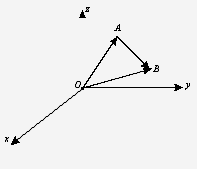
Рис. 7
На рис. 7 видно, что вектор 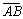 можно
получить как разность векторов
можно
получить как разность векторов 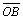 и
и 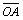 , где т. О - начало координат:
, где т. О - начало координат:
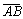 =
=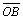 -
-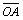 ,
,
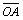 =(х1, у1, z1),
=(х1, у1, z1), 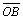 =(х2,
у2, z2).
=(х2,
у2, z2).
Тогда координаты вектора 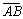 равны
разности соответствующих координат конца и начала вектора:
равны
разности соответствующих координат конца и начала вектора:
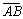 =(х2-х1; у2-у1;
z2-z1).
=(х2-х1; у2-у1;
z2-z1).
Расстояние между точками А и В
вычислим как длину вектора 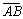 :
:
|АВ|=|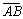 |=
|=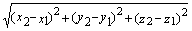 .
.
Углом между векторами  и
и  назовем
наименьший угол, на который надо повернуть один вектор до совпадения его с
другим.
назовем
наименьший угол, на который надо повернуть один вектор до совпадения его с
другим.

Рис.
Записывают (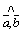 )=
)=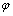 .
.
Покажем угол между вектором  и
координатной осью Ох, например. Обозначим этот угол через
и
координатной осью Ох, например. Обозначим этот угол через 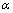 . Пусть
. Пусть  =
=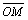 .
.
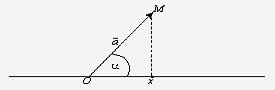
Рис.
Очевидно, что cos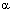 =
=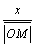 =
= .
.
Обозначим через 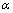 ,
, 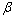 ,
, 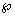 углы между
вектором
углы между
вектором  и
координатными осями Ох, Оу, Оz соответственно. Тогда
и
координатными осями Ох, Оу, Оz соответственно. Тогда
cos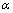 =
= , cos
, cos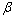 =
=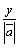 , cos
, cos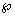 =
= .
.
Эти формулы определяют направляющие
косинусы вектора и полностью задают направление вектора в пространстве.
Направляющие косинусы вектора удовлетворяют условию:
cos2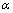 +cos2
+cos2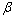 +cos2
+cos2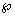 =1.
=1.
Это равенство легко получить,
учитывая, что длина вектора
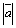 =
=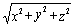 .
.
В школьном курсе рассматривается еще
одна операция над векторами - скалярное произведение векторов.
Скалярным произведением двух
векторов называется число, равное произведению длин этих векторов на косинус
угла между ними.
Обозначают скалярное произведение
векторов  и
и  символами
символами
 ×
× или (
или ( ,
, ).
).
Таким образом, по определению
 ×
× =
=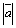 ×
×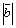 ×cos
×cos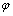 ,
,
где 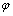 - угол между векторами
- угол между векторами  и
и 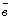 .
.
Скалярное произведение обладает
следующими свойствами:
. 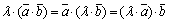
. ( +
+ )×
)×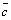 =
= ×
×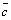 +
+ ×
×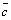
. Если векторы  и
и  взаимно
перпендикулярны, то их скалярное произведение равно нулю (и наоборот), т. е.
взаимно
перпендикулярны, то их скалярное произведение равно нулю (и наоборот), т. е.  ^
^
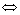
 ×
× =0.
=0.
Условие  ×
× =0 поэтому и
называют условием перпендикулярности векторов.
=0 поэтому и
называют условием перпендикулярности векторов.
.  ×
× =
=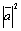 . Отсюда получают правило для
вычисления длины вектора:
. Отсюда получают правило для
вычисления длины вектора:
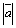 =
=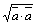
Если известны координаты векторов  и
и  , то легко
показать, что скалярное произведение равно сумме произведений одноименных
координат векторов, т. е. если
, то легко
показать, что скалярное произведение равно сумме произведений одноименных
координат векторов, т. е. если 
 =(х1, у1, z1) и
=(х1, у1, z1) и  =(х2,
у2, z2), то
=(х2,
у2, z2), то
 ×
× =х1×х2+у1×у2+z1×z2
=х1×х2+у1×у2+z1×z2
Условие перпендикулярности тогда
примет вид:
 ^
^
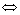 x1×x2+y1×y2+z1×z2=0
x1×x2+y1×y2+z1×z2=0
Пусть, например, даны векторы  = (2, -1,
2),
= (2, -1,
2),  = (1, 0, 4),
= (1, 0, 4),
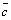 = (3, 4,
-1).
= (3, 4,
-1).
Найдем скалярные произведения
 ×
× = 2 × 1 + (-1) × 0 + 2 × 4 = 10,
= 2 × 1 + (-1) × 0 + 2 × 4 = 10,
 ×
×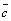 =2 × 3 + (-1) × 4 + 2 × (-1) = 0,
=2 × 3 + (-1) × 4 + 2 × (-1) = 0,
 ×
×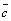 = 1 × 3 + 0 × 4 + 4 × (-1) = -1.
= 1 × 3 + 0 × 4 + 4 × (-1) = -1.
Мы обнаружили, что векторы  и
и 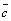 образуют
прямой угол.
образуют
прямой угол.
Используя определение скалярного
произведения, можно вычислить угол между векторами по формуле
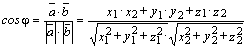 .
.
Простейшие задачи метода координат
При решении чисто геометрических задач
используются формулы и правила, позволяющие вычислить длину отрезка или
вектора, расстояние между точками, угол между векторами или осями, найти точку,
делящую данный отрезок.
Рассмотрим эти задачи.
. Расстояние между точками
А (х1, у1, z1)
и В(х2, y2,
z2):
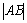 =
=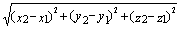 .
.
Эта же формула позволяет вычислить
длину вектора.
. Деление отрезка в данном отношении
Пусть в пространстве даны две точки
М1 и М2. Говорят, что точка М делит отрезок М1М2.
в отношении 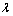 , если
, если 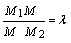
Точка М делит отрезок М1М2
в отношении 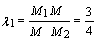 .
.
Точка N делит тот
же отрезок М1М2 в отношении 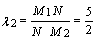 .
.
Видимо, при 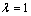 мы получим
середину отрезка.
мы получим
середину отрезка.
Если известны координаты начала М1
и конца М2 отрезка, то координаты точки М, делящей отрезок М1М2
в отношении 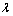 , находят по
формулам:
, находят по
формулам:
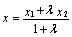 ,
, 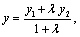
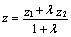 ,
,
где т. М1(х1,
у1, z1), т. М2(х2,
у2, z2), т. М(х,
у, z).
Координаты середины отрезка получают
при 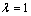 :
:
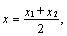
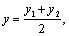
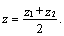
Например, если т. А(-2, 3, 4), т.
В(0, 1, -2), то координаты середины отрезка АВ получим из формул:
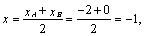

z=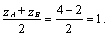
Итак, точка С(-1, 2, 1) является
серединой отрезка АВ.
. Угол между векторами вычисляется
по формуле
cos 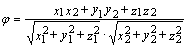 .
.
. Условие перпендикулярности двух
векторов: х1×х2+у1×у2+z1×z2=0.
. Условие коллинеарности двух
векторов: 
Если векторы коллинеарны, то их
соответствующие координаты пропорциональны.
Пример № 1.
Даны три вершины параллелограмма:
А(4;2), В(5;7), С(-3;4). Найти четвертую вершину D,
противолежащую вершине В.
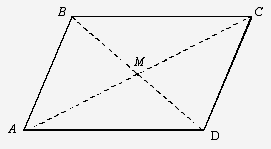
Рис.
Для решения этой задачи
воспользуемся свойством диагоналей параллелограмма: диагонали его, пересекаясь,
делятся точкой пересечения пополам.
Пусть точка М - точка пересечения
диагоналей параллелограмма АВСD.
Тогда точка М - середина отрезка АС;
координаты точки М найдем из формул:
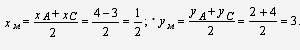
Итак, т. М(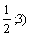 .
.
Но точка М является серединой и
отрезка ВD. Поэтому
верны равенства:
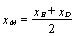 и
и 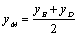 .
.
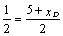 ;
; 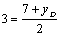 .
.
Из этих равенств находим координаты
вершины D(-4, -1).
Проверить правильность решения
можно, построив все вершины параллелограмма.
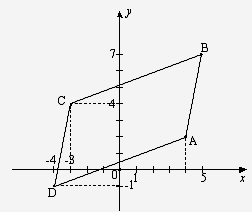
Рис.
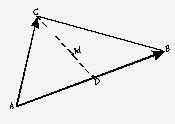
Рис.
Пример № 2.
Найти центр тяжести треугольника,
зная координаты его вершин: А(1;4), В(-5;0), С(-2;-1). Центр тяжести
треугольника лежит в точке пересечения медиан, которая делит отрезок любой
медианы в отношении 2:1, считая от вершины.
Точка М делит отрезок СD в отношении
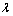 =2, а точка D - середина
стороны АВ.
=2, а точка D - середина
стороны АВ. 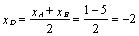 ;
; 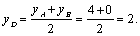
Середина стороны АВ - точка D(-2;2).
Координаты точки М найдем, рассматривая отрезок СD. 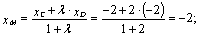
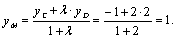
Итак, центр тяжести треугольника лежит в точке
М(-2,1).
Построим все точки и убедимся, что решение
верно.
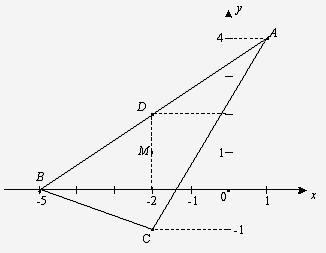
Пример № 3.
Проверить, что четырехугольник, вершины которого
находятся в точках А(5; 2; 6;), В(6; 4; 4), С(4; 3; 2) и D
(3; 1; 4), есть квадрат.
Квадратом является четырехугольник, у которого
стороны взаимно перпендикулярны и длины сторон равны.
Запишем координаты векторов, совпадающих со
сторонами:
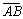 =(6-5; 4-2; 4-6)=(1; 2; -2)
=(6-5; 4-2; 4-6)=(1; 2; -2)
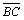 =(4-6; 3-4; 2-4)=(-2; -1; -2)
=(4-6; 3-4; 2-4)=(-2; -1; -2)
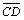 =(3-4; 1-3; 4-2)=(-1; -2; 2)
=(3-4; 1-3; 4-2)=(-1; -2; 2)
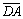 =(5-3; 2-1; 6-4)=(2; 1; 2)
=(5-3; 2-1; 6-4)=(2; 1; 2)
Проверим, выполняется ли условие
перпендикулярности для каждой пары смежных сторон-векторов.
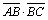 =1×(-2)+2×(-1)+(-2)×(-2)=-2-2+4=0,
что и доказывает, что
=1×(-2)+2×(-1)+(-2)×(-2)=-2-2+4=0,
что и доказывает, что 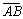 ^
^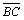 .
.
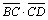 =(-2)×(-1)+(-1)×(-2)+(-2)×2=2+2-4=0,
т. е.
=(-2)×(-1)+(-1)×(-2)+(-2)×2=2+2-4=0,
т. е. 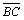 ^
^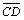 .
.
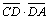 =(-1)×2+(-2)×1+2×2=0, т. е.
=(-1)×2+(-2)×1+2×2=0, т. е. 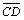 ^
^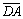 .
.
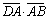 =2×1+1×2+2×(-2)=0, т. е.
=2×1+1×2+2×(-2)=0, т. е. 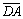 ^
^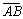 .
.
Мы установили, что стороны четырехугольника
взаимно перпендикулярны. Покажем, что и длины сторон его равны.
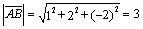 ,
,
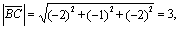
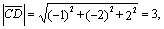
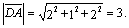
Итак, АВСD - квадрат.
Заметим, что построением эту задачу не проверить, так как точки заданы не на
плоскости, а в пространстве.
Уравнение линии. Прямая на плоскости
Одним из важнейших в аналитической
геометрии является вопрос об уравнении линии на плоскости.
Всякая линия есть множество точек
плоскости, координаты которых должны быть связаны некоторым условием. Это
условие записывается в виде уравнения.
Определение. Уравнение F(х, у)=0
называется уравнением линии, если этому уравнению удовлетворяют координаты х и
у любой точки, лежащей на линии, и не удовлетворяют координаты ни одной точки,
не лежащей на этой линии.
В этом случае говорят: уравнение F(х, у)=0
определяет эту линию.
Пример № 4.
Показать, что уравнение х2+у2=r2 определяет
окружность.
Окружностью называется множество
точек плоскости, расстояние каждой из которых до данной точки постоянно. Пусть
М(х, у) - любая точка плоскости. Расстояние этой точки от начала координат 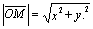
Тогда уравнению х2+у2=r2
удовлетворяют только те точки, для которых 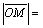 r, т. е. точки, лежащие на окружности
радиуса r с центром в
начале координат. Если же точка не лежит на окружности, то расстояние
r, т. е. точки, лежащие на окружности
радиуса r с центром в
начале координат. Если же точка не лежит на окружности, то расстояние 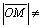 r.
r.
Итак, уравнению х2+у2=r2
удовлетворяют координаты любой точки окружности и не удовлетворяют координаты
никакой точки, не лежащей на окружности. Значит, уравнение х2+у2=r2 определяет
окружность при любом r>0.
Очевидно, уравнение (х-х0)2+(у-у0)2=r2 определяет
окружность с центром в точке С(х0, у0) радиуса r>0.
Например, уравнение х2+(у+1)2=1
определяет окружность радиуса r=1 с центром в точке С(0; -1).
Простейшей линией является прямая на плоскости.
Рассмотрим различные виды уравнения прямой.
1. Уравнение прямой, проходящей
через данную точку М0(х0,у0) перпендикулярно
данному вектору 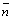 = (А; В).
= (А; В).
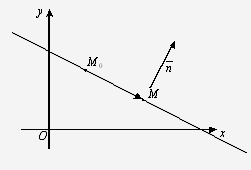
Рис.
Чтобы вывести уравнение прямой,
возьмем на ней любую точку М(х, у), которая может по прямой перемещаться.
В любом случае вектор 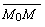 ,
ограниченный данной точкой М0(х0,у0) и
произвольной точкой М(х, у), всегда лежит на прямой и поэтому перпендикулярен
данному вектору
,
ограниченный данной точкой М0(х0,у0) и
произвольной точкой М(х, у), всегда лежит на прямой и поэтому перпендикулярен
данному вектору 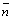 (А; В).
Найдем координаты вектора
(А; В).
Найдем координаты вектора 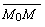 и запишем
условие перпендикулярности векторов
и запишем
условие перпендикулярности векторов 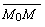 и
и 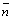 .
.
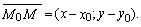
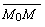 ^
^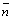 ÞА × (х - х0)
+ В × (у - у0)
= 0.
ÞА × (х - х0)
+ В × (у - у0)
= 0.
Полученному уравнению удовлетворяют координаты
любой точки прямой и не могут удовлетворять координаты точки, не лежащей на
прямой (тогда условие перпендикулярности не будет выполняться).
А × (х - хо)
+ В ×
(у - у0) = 0 (1)
- уравнение прямой, проходящей через
данную точку перпендикулярно данному вектору. Вектор 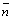 (А; В)
называют нормальным вектором.
(А; В)
называют нормальным вектором.
В уравнении (1) раскроем скобки:
А × х + В ×
у + (-А ×
х0 - В × уо) = 0
Обозначим число - А ×
х0 - В × у0 = С. Уравнение
прямой примет вид:
А × х + В ×
у + С = 0 (2)
Его называют общим уравнением
прямой, а коэффициенты при х и у задают нормальный вектор 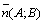 .
.
Заметим, что уравнение прямой -
уравнение первой степени с двумя переменными. Поэтому в аналитической геометрии
прямую линию называют линией первого порядка.
. Уравнение прямой, проходящей через
данную точку М0(х0, у0) параллельно данному
вектору 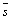 =(m; n).
=(m; n).
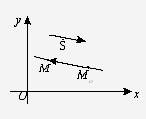
Рис.
Пусть М(х, у) - любая точка прямой.
Тогда векторы 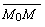 и
и 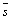 всегда
коллинеарны. Запишем условие коллинеарности векторов
всегда
коллинеарны. Запишем условие коллинеарности векторов 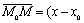 ; у-у0)
и
; у-у0)
и 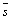 =(m; n):
=(m; n):
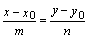 (3)
(3)
уравнение прямой, параллельной
вектору  =(m; n).
=(m; n).
3. Уравнение прямой, проходящей
через две данные точки М1(х1, у1) и М2(х2,
у2)
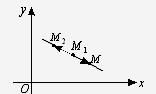
Рис.
Для любой точки М(х, у) прямой
векторы 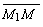 =(х - х1;
у - у1) и
=(х - х1;
у - у1) и 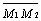 = (х2 -
х1; у2 -у1) всегда коллинеарны, а потому
= (х2 -
х1; у2 -у1) всегда коллинеарны, а потому
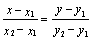 (4)
(4)
искомое уравнение.
. Уравнение прямой с угловым коэффициентом.
Выведем уравнение прямой, проходящей
через точку М0(х0, у0) под углом 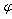 к оси
абсцисс Ох.
к оси
абсцисс Ох.
Угол 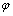 между прямой и осью Ох называют
углом наклона прямой, а угловым коэффициентом k прямой
называют тангенс угла
между прямой и осью Ох называют
углом наклона прямой, а угловым коэффициентом k прямой
называют тангенс угла 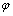 наклона
этой прямой, т. е. k =tg
наклона
этой прямой, т. е. k =tg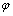 .
.
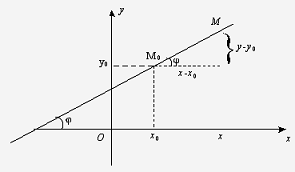
Рис.
Для любой точки М(х, у) прямой
отношение 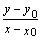 равно
равно 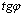 , поэтому
, поэтому 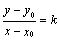 или у-у0=k×(х-х0).
или у-у0=k×(х-х0).
Получили уравнение прямой,
проходящей через данную точку М0(х0, у0) в
заданном направлении
у-у0 = k × (х-х0)
(5)
Здесь 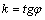 - угловой коэффициент прямой. Угол
наклона
- угловой коэффициент прямой. Угол
наклона 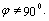
Если точка М0 - точка
пересечения прямой с осью ординат Оу, то ее координаты х0= 0, у0=
b. Уравнение
принимает вид: у-b=k×x, или
уравнение прямой с угловым
коэффициентом, b - начальная ордината прямой.
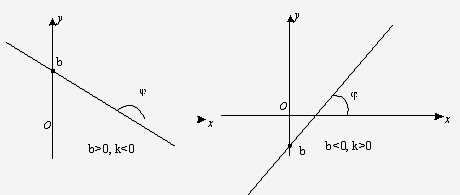
Рис.
. Угол между прямыми
Пусть даны две прямые своими общими уравнениями:
А1×х+В1×у+С1=0
и А2×х+В2×у+С2=0
Так как 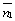 = (А1;
В1) и
= (А1;
В1) и 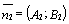 -
нормальные векторы данных прямых, то угол
-
нормальные векторы данных прямых, то угол 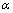 между прямыми равен углу между
нормальными векторами и
между прямыми равен углу между
нормальными векторами и 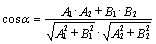 .
.
Если две прямые заданы уравнениями с
угловым коэффициентом:  и
и 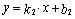 , то угол
, то угол 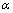 между ними
удобнее вычислять по формуле:
между ними
удобнее вычислять по формуле:
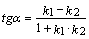
доказательство которой легко усматривается из
рисунка:
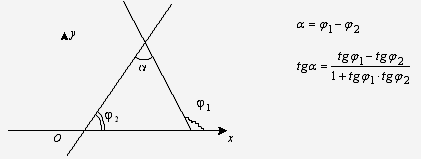
Рис.
Если прямые перпендикулярны, то 1 + k1 × k2 = 0 и 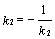 .
.
Если прямые параллельны, то
k1 = k2.
Пример № 5
Проверить, что четыре точки
А(-2;-2), В(-3;1), С(7;7) и D(3;1) служат вершинами трапеции, и
составить уравнение высоты, опущенной из вершины А.
В трапеции две стороны параллельны,
а две - нет. Составим уравнения каждой из четырех сторон по формуле (4).
Уравнение АВ: 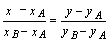
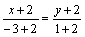 или у+2=-3(х+2).
или у+2=-3(х+2).
Уравнение ВС: 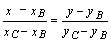 ,
,
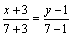 или у-1=
или у-1= .
.
Уравнение CD: 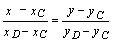
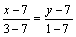 или у-7=
или у-7=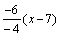 .
.
Уравнение DА: 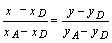 ,
,
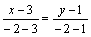 или у-1=
или у-1=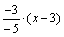 .
.
Сравним угловые коэффициенты
полученных прямых; они равны для прямых ВС и DA: 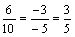 .
.
ВС и DA - основания
трапеции, АВ и СD - боковые стороны ее.
Высота трапеции перпендикулярна
основанию, и угловой коэффициент прямой, совпадающей с высотой, равен 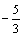 . Составим
уравнение прямой, проходящей через точку А(-2,-2) с угловым коэффициентом k=
. Составим
уравнение прямой, проходящей через точку А(-2,-2) с угловым коэффициентом k=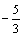 по формуле
(5):
по формуле
(5):
у+2=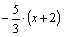 или 5х+3у+16=0.
или 5х+3у+16=0.
Построением убедимся в правильности
решения.
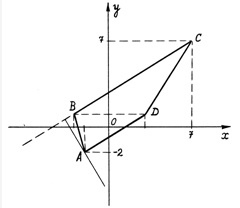
Рис.
Обзор кривых второго порядка
Прямая на плоскости является линией первого
порядка, так как определяется уравнением первой степени с двумя переменными.
Рассмотрим кривые второго порядка, то есть линии, определяемые в декартовых
координатах уравнениями второй степени. Установлено, что таких линий всего
четыре: окружность, эллипс, гипербола и парабола.
В п. 4 было получено уравнение окружности с
центром С(х0, у0) и радиусом r:
(х-х0)2 + (у-у0)2
= r2
(7)
Из этого уравнения можно получить так называемое
общее уравнение окружности: x2+y2+m×x+n×y+p=0.
Заметим, что коэффициенты при х2 и у2 в уравнении
окружности одинаковы. Если же в уравнении коэффициенты при х2 и у2
будут разными по величине, но одного знака, то такое уравнение будет определять
эллипс.
Простейшее (каноническое) уравнение эллипса
имеет вид:
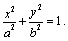 (8)
(8)
Чтобы построить такой эллипс,
отметим точки пересечения эллипса с осями координат: А1(a, 0), А2(-а,
0), В1(0, b), В2(0, -b), называемые
вершинами эллипса. Расстояние между вершинами |А1А2|=2а и |В1В2|=2b называют
осями, а числа а и b - полуосями эллипса (а>0, b>0). Из уравнения (8) эллипса
видно, что эллипс - фигура, симметричная относительно обеих осей и начала
координат. Для точного построения эллипса используем определение:
Эллипсом называется множество точек
плоскости, сумма расстояний от каждой из которых до двух данных точек F1 и F2, называемых
фокусами, есть величина постоянная.
Фокусы F1(c, 0) и F2(-c, 0)
построим, учитывая,
что 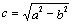 (при а>b).
(при а>b).
По определению сумма 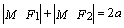 остается
постоянной для любой точки М(х, у) эллипса.
остается
постоянной для любой точки М(х, у) эллипса.
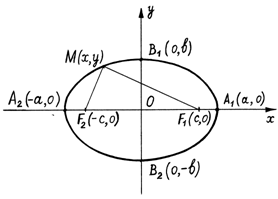
Рис.
Если центр симметрии эллипса
расположен в точке С(х0, у0) и оси симметрии параллельны
координатным осям, то уравнение эллипса:
 (9)
(9)
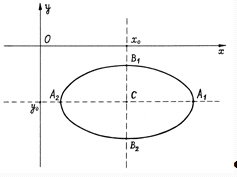
Рис.
В школьном курсе гипербола
рассматривается как график обратной пропорциональной зависимости 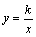 .
.
Рассмотрим более общий случай
гиперболы, начав с ее определения:
Гиперболой называется множество
точек плоскости, разность расстояний каждой из которых от двух данных точек
есть величина постоянная. Простейшее (каноническое) уравнение гиперболы имеет
вид:
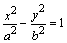 (10)
(10)
Как видно, коэффициенты при х2
и у2 имеют разные знаки.
Числа а и b (а>0 и b>0) называются полуосями
гиперболы.
Точки А1(а,0), А2(-а,0),
В1(0,b) и В2(0,-b) называют
вершинами гиперболы.
Построим прямоугольник со сторонами,
проходящими через вершины А1, А2, В1, В2
параллельно координатным осям. Диагонали этого прямоугольника называют
асимптотами гиперболы. Очевидно, уравнения асимптот
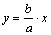 и
и 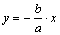
Через вершины А1(а, 0) и
А2(-а, 0) проведем теперь две симметричные относительно координатных
осей ветви гиперболы так, чтобы по мере удаления от центра симметрии - точки
О(0,0) - они приближались бы к асимптотам, но не пересекали бы их.
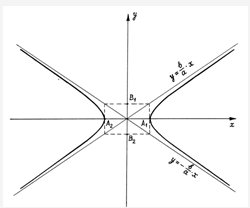
Рис.
Если же центр симметрии гиперболы
расположен в точке С(х0, у0) и оси симметрии параллельны
координатным осям, то уравнение гиперболы имеет вид:
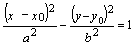 ,
,
Укажем, что гипербола является и
графиком дробно-линейной функции 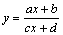 .
.
Параболу в школьном курсе
рассматривают как график квадратного трехчлена у=ах2+bх+с.
Выделяя из квадратного трехчлена
полный квадрат, это уравнение легко привести к виду
(х-х0)2=±2р×(у-у0)
(11)
Здесь точка С(х0, у0)
- вершина параболы, ось симметрии параллельна Оу. Коэффициент р(р>0)
называют параметром параболы. Знак плюс перед коэффициентом 2р соответствует
параболе, ветви которой направлены вверх, знак минус - вниз.
Рис.
Можно рассмотреть параболу с осью
симметрией, параллельной оси Ох. Ее уравнение имеет вид
(у-у0)2 = ±2р × (х-х0).
(12)
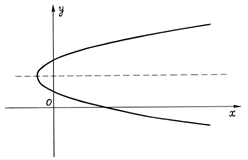
Рис.
Отметим, что уравнение параболы
содержит квадрат только одной переменной: либо х (формула 11), либо у (формула
12).
Дадим определение, которое часто
фигурирует как определение параболы. Параболой называется множество точек
плоскости, равноудаленных от данной прямой и от данной точки.
Заключение
В основу метода координат положены две идеи:
- введение переменной величины.
Переменная - величина, которая принимает
различные значения. Чаще всего обозначается буквами латинского алфавита: х, у, z
и т.д.
Аргумент функции - независимая переменная. Это
произвольный элемент из области определения. Обозначается обычно буквой х
латинского алфавита. Зависимость переменной у от переменной х называется
функцией, если каждому значению х соответствует единственное значение у. При
этом используют запись у = f
(х);
- использование прямолинейных (декартовых)
координат.
Возьмем две взаимно перпендикулярные
координатные прямые Ох и Оу с равными единичными отрезками. Точка пересечения
координатных прямых О называется началом координат, координатная прямая Ох -
осью абсцисс, а Оу - осью ординат. Т.о., мы задали систему координат.
Плоскость, на которой задана система координат, называется координатной
плоскостью.
Возьмем точку А координатной плоскости и
проведем через нее прямые l1
и l2,
параллельные координатным осям. Абсциссой точки А называется число, которое
соответствует точке пересечения прямой l1
и оси абсцисс. Ординатой точки А называется число, которое соответствует точке
пересечения прямой l2
и оси ординат. Упорядоченная пара (х; у) называется координатами точки А в
прямоугольной декартовой системе координат.
В заключение обзора кривых второго порядка
отметим, что эти линии часто встречаются в различных вопросах естествознания.
Например, движение материальной точки под воздействием центрального поля силы
тяжести происходит по одной из этих линий. Оптические свойства эллипса,
гиперболы и параболы широко используется в инженерном деле. В частности,
оптические свойства параболы используется при конструировании прожекторов,
антенн, телескопов. Такие термины, как «эллиптическая орбита», «эллипсоид
инерции», «параболическая траектория», «параболическое зеркало» и т.д.,
убеждают в широком применении кривых второго порядка.
Список использованной литературы
.Беклемишев
Д.В. Курс аналитической геометрии и линейной алгебры. - 2-е изд. - М., 2004.
.Беклемишева
Л.А. Сборник задач по аналитической геометрии и линейной алгебре / Л.А.
Беклемишева, А.Ю. Петрович, И.А. Чубаров. - 2-е изд. - М., 2007.
.Бугров
Я.С. Высшая математика. Задачник / Я.С. Бугров, С.М. Никольский. - 2-е изд. -
М., 2010.
.Бугров
Я.С. Элементы линейной алгебры и аналитической геометрии / Я.С. Бугров, С.М.
Никольский. - 2-е изд. - М., 2004.
.Высшая
математика для экономистов / Под ред. Н.Ш. Кремера. - 2-е изд. - М., 2008.
.Декарт
Р. Избранные произведения. М., 1950.
.Ильин
В.А. Линейная алгебра / В.А. Ильин, Э.Г. Позняк. - 2-е изд. - М., 2011.
.Кривич
М., Ольгин О. Мастерские науки. - 2-е изд. - М., 2004.
.Кузнецов
Б.Т. От Галилея до Эйнштейна. - 2-е изд. - М., 2006.
.Лятоер
Д.А. Декарт. М., 1975.
.Меркулов
И.П. Гипотетико-дедуктивная модель и развитие научного знания. - 2-е изд. - М.,
2010.