|
ni
|
6230840
|
3115420
|
1557710
|
778855
|
155771
|
22253
|
3179
|
289
|
17
|
|
pi
|
2
|
2
|
2
|
5
|
7
|
7
|
11
|
17
|
17
|
Таким образом, 6230840 = 23×5×72×11×172,
а -6230840 = -23×5×72×11×172.
Здесь и далее первые степени простых чисел не пишем.
Следствие (о взаимно простых
сомножителях степени). Если имеется разложение nk = m1×…×ms степени
целого числа n в произведение попарно взаимно
простых целых ненулевых сомножителей m1 , … , ms , то эти
сомножители, с точностью до знака, являются k-ми
степенями некоторых попарно взаимно простых чисел. Более точно:
mi = ei×uik
, где ei Î
{-1, 1}, ui Î N , НОД(ui
, uj) = 1 (1 £ i £
s, 1 £
j £
s), |n| = u1×…×us
, e1×…×es =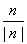 
.
Доказательство. Запишем mi = ei×|mi| , где ei = 1, если mi > 0 и ei = -1, если mi > 0 (1 £ i £ s), и
аналогично n = d×|n|. Тогда,
очевидно, получается равенство d k×|n|k = (e1×…×es)×|m1|×…×|ms|, откуда 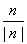= d = d k = e1×…×es , |n|k = = |m1|×…×|ms| . При этом
все модули являются натуральными числами, так что осталось доказать утверждение
для натуральных чисел.
Пусть n, m1 , … , ms Î N имеют
разложения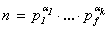 
, 
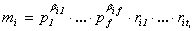(1 £ i £ s) в
произведения простых чисел, где выполнены неравенства p1 < … <
pf , а rij - простые
числа, не встречающиеся среди p1 , … , pf . Тогда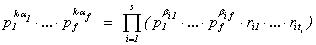 
.
Переставляя простые числа в правой части (собирая их в степени с одинаковыми
основаниями), получим в левой и правой частях равенства канонические
разложения, которые должны быть одинаковыми по основной теореме арифметики. Это
показывает, что в правой части должны отсутствовать сомножители rij (1 £ j £ ti , 1 £ i £ s), а
показатели степеней при простом числе pl в левой и
правой частях равны: k×al =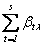 
(1 £ l £ f).
Таким образом,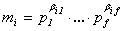 
, причём
ввиду попарной взаимной простоты чисел m1 , … , ms каждое
простое число pi (1 £ i £ f) участвует
лишь в одном из разложений чисел m1 , … , ms . Поэтому
,
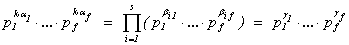где gl = b1l + … + bsl , но на
самом деле в этой сумме лишь одно ненулевое слагаемое. Значит, сравнивая
показатели степеней при pl в левой и
правой частях равенства, по основной теореме арифметики заключаем, что каждая
степень bij делится на k : bij = k×gij для
некоторого натурального или нулевого gij (1 £ i £ s, 1 £ j £ f).
Итак,
,
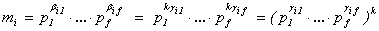т.е.
ui =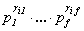 
(1 £ i £
s).
Эти числа попарно взаимно просты,
т.к. любой общий делитель двух из них ui , uj будет общим
делителем взаимно простых чисел mi , mj , а значит,
равен ± 1.
Следствие доказано.
Наконец, напомним простейшие
сведения из теории сравнений. Два целых числа a, b называются сравнимыми
по модулю m Î Z \ {0}, если a - b M m.
Примеры: 8 º 2 (mod 3), т.к. 8
- 2 = 3×2, -27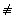 
12 (mod 5), т.к.
разность -27 - 12 = -39 не делится нацело на 5.
Упомянем некоторые важнейшие
свойства сравнений.
10.
Числа a и b сравнимы по модулю m тогда и только
тогда, когда они дают одинаковые остатки при делении на m.
20.
Условия a
M b
и a
º 0 (mod
b)
эквивалентны.
30.
Любое целое число a сравнимо само с собой по любому модулю m (рефлексивность
отношения сравнимости).
40.
Если a º b (mod m), то b º
a (mod m) (симметричность отношения сравнимости).
50.
Если a º b (mod m) и b º
с (mod m), то a º c (mod m)
(транзитивность отношения сравнимости).
60.
Если a º b (mod m), то для любого целого
числа c справедливо
a ±
c º b ±
c (mod m) , a×c º
b×c
(mod m).
70.
Если
a º b (mod m) и
c º d (mod m), то
a ± c º
b ± d (mod m).
80.
Если
a º b (mod m) и
c º d (mod m), то
a×c
º
b×d
(mod m).
90.
Если a º b (mod m), то для любого
натурального k верно сравнение ak º
bk (mod m).
100. Если целые
числа a, b, m делятся нацело на число d Î Z \ {0}, то a º b (mod m)
тогда и только тогда, когда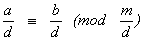 
.
110.
Если d×a
º
d×b
(mod
m)
и НОД(d
, m)
= 1, то a
º
b
(mod
m).
Сравнения
дают удобный язык для изучения делимости чисел. Связь сравнений с делимостью
выявлена в свойстве 20.
Примеры:
1.
Вычислить остаток числа a4
- 8×a3
+ 19 при делении на 23, если известно, что a
даёт
при делении на 23 остаток 5.
Если a º
5 (mod 23), то
a4 - 8×a3
+ 19 º (a2)2
- 8×a×a2
+ 19 º 22 - 8×5×2
+ 19 º
º - 40×2
+ (22 + 19) º
-(-6)×2 + 0 º
12 (mod
23),
т.е. искомым остатком будет 12.
2. Вычислить 18100
+ 20 (mod
25).
18100 + 20 º
(-7)100 - 5 º (72)50
- 5 º (-1)50 - 5 º
º 1 - 5 º
-4 º 21 (mod
25).
Таким образом, не вычисляя числа 18100
+ 20, можно сказать, что остаток этого числа при делении на 25 равен
21.
3. Найти
младшую цифру числа 2435 - 18 .
Нужно вычислить . Имеем
2435 - 18 º
435 - 8 º (42)17×4
- (-2) º 617×4
+ 2 º 6×4
+ 2 º 4 + 2 = 6 (mod
10).
Здесь использован тот факт, что младшая цифра
числа 6k
равна 6, т.е. 6k
º 6 (mod
10).
Таким образом, искомой младшей цифрой будет 6.
§
2. Диофантовы уравнения, пифагоровы тройки и Великая теорема Ферма
Диофантово уравнение
- это уравнение вида P(x1
, … , xn)
= 0,
где левая часть представляет собой многочлен от переменных x1
, … , xn
с целыми коэффициентами. Любой упорядоченный набор (u1
; … ; un)
целых чисел со свойством P(u1
, … , un)
= 0
называется (частным) решением диофантова уравнения P(x1
, … , xn)
= 0.
Решить диофантово уравнение - значит найти все его решения, или, как
говорят, общее решение этого уравнения. Часто диофантовыми называют
и уравнения вида P(x1
, … , xn)
= Q(x1
, … , xn),
где в левой и правой частях стоят многочлены от переменных x1
, … , xn
:
их всегда можно записать в виде диофантовых уравнений P(x1
, … , xn)
- Q(x1
, … , xn)
= 0.
Эти уравнения названы в честь Диофанта
Александрийского (жил около III
в. до РХ), о жизни которого почти ничего не известно. Через века до нас дошли
шесть книг из тринадцати его главного труда “Арифметика” и книга “О
многоугольных числах”. Выражаясь современным языком, он разрабатывал приёмы
нахождения рациональных решений алгебраических уравнений от нескольких
неизвестных.
Примеры: 1. 3×x - 8 = 0 - диофантово
уравнение первой степени от одной переменной x. Очевидно,
что оно не имеет решений, т.к. 8 не делится нацело на 3. В то же
время, это уравнение имеет корень x =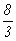 
, который не
является целым.
2. Диофантово уравнение 6×x = 24 имеет
единственное решение x = 4.
3. В курсе
алгебры и теории чисел рассматривают линейные диофантовы уравнения первой
степени от двух неизвестных x,
y, общий вид
которых таков: a×x
+ b×y
= c, где a,
b,
c
- заданные
целые числа. Известно, что такое диофантово уравнение имеет решение тогда и
только тогда, когда НОД(a,
b)
| c
- наибольший
общий делитель коэффициентов делит нацело правую часть. При выполнении этого
условия линейное диофантово уравнение от двух переменных имеет бесконечное
число решений.
Нахождение решений произвольных диофантовых
уравнений - непростая задача. Более того, в 70-х годах XX
в. было доказано, что она алгоритмически неразрешима, т.е. невозможно придумать
алгоритм (программу для ЭВМ), который для произвольного заданного диофантова
уравнения давал бы ответ на вопрос: “Есть у этого уравнения хотя бы одно
решение ?”.
Тем удивительнее, что для некоторых классов
диофантовых уравнений можно получить полное описание их решений. Классической
задачей такого рода, обсуждаемой в “Арифметике” Диофанта, является задача о
пифагоровых тройках, т.е. о нахождении всех решений диофантова уравнения x2
+ y2
= z2
,
представляющего собой соотношение Пифагора для прямоугольного треугольника.
Вначале найдём все его рациональные решения, а затем - и все целые решения.
1. Рациональные решения уравнения
Пифагора.
Во-первых, уравнение переписывается в виде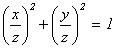 
, где отношения 
, 
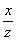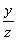рациональны,
если рациональными были x, y. Эти
отношения являются рациональными координатами точек на единичной окружности.
Точки с рациональными координатами на окружности назовём рациональными.
Если все рациональные точки M(u; v) окружности
уже описаны, то u2 + v2 = 1 и 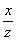= u, 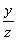= v, т.е. x = z×u, y = z×v , где z Î Q . Таким
образом, задача нахождения всех рациональных решений уравнения Пифагора свелась
к описанию всех рациональных точек окружности.
Изложим общий метод нахождения всех
рациональных точек окружности, применимый и для многих других кривых, заданных
полиномиальными уравнениями.
Выберем на кривой рациональную
точку, например точку S(0; -1) на
окружности (рис. 1). Если M(u; v) -
произвольная рациональная точка, то рациональным будет и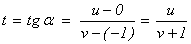 
.
Обратно, если t Î Q , то u = t×(v + 1) и u2 + v2 = 1, т.е. t2×(v + 1)2
+ v2 = 1 или (t2+1)×v2+2×t2×v+t2- 1= 0. Здесь
дискриминант D = 4×t4 - 4×(t4 - 1) = 4 и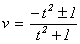 
. Если
взять знак минус, то получим v = -1, u = t×(v + 1) = 0, т.е. точку S(0; -1). Если же
брать плюс, то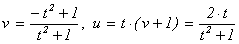 
Î Q .
Таким образом, доказано, что точка
на окружности рациональна тогда и только тогда, когда она либо совпадает с S(0; -1), либо
получается по формулам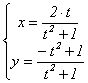 
при
некотором t Î Q .
Легко понять, что точка S(0; -1) не может
быть получена по приведённым формулам ни при каком рациональном t. Можно
видоизменить параметризацию, чтобы включить точку S в общие
решения. Для этого запишем число t Î Q в
несократимом виде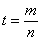 
, где m Î Z, nÎ N , НОД(m, n) = 1. Тогда
формулы перепишутся так: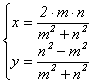 
. Они
определены при любых m, n Î Z и при n = 0 дают точку S(0;-1). Таким
образом, доказана следующая теорема:
Теорема (о рациональных точках на
окружности).
(1) Все рациональные точки M(x; y) единичной
окружности имеют координаты
,
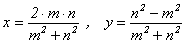при некоторых m, n Î Z , НОД(m, n) = 1.
(2) Все рациональные пифагоровы
тройки, т.е. рациональные решения уравнения x2 + y2 = z2 задаются
формулами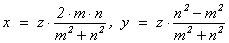 
, где m, n Î Z и НОД(m, n) = 1, z Î Q .
2. Целые решения уравнения Пифагора. Рассмотрим
диофантово уравнение x2 + y2 = z2 от трёх
неизвестных x, y, z. Оно,
конечно, имеет решения: например, (0; 0; 0), (0; 1; 1), (3; 4; 5) и
множество других. Решения, в которых одно из чисел равно нулю, называются
тривиальными. Ясно, что все тривиальные решения имеют вид: (0; y; ±y), (x; 0; ±x), где x, y Î Z . Поэтому
достаточно искать только нетривиальные решения.
Назовём решение (x; y; z) примитивным,
если любые два числа в нём взаимно просты, т.е. если НОД(x, y) = НОД(x, z) = НОД(y, z) = 1. Ясно, что
если есть некоторое решение (x; y; z) и D = НОД(x, y, z), то x = D×x1 , y = D×y1 , z = D×z1 при
некоторых целых x1 , y1 , z1 , причём
ввиду x2 + y2 = z2 получаем,
сокращая на D2, x12 + y12 = z12, т.е. тройка
(x1 ; y1 ; z1) тоже
является решением. Кроме того, это решение примитивно: если НОД(x, y) = d > 1, то x1 = d×x2 , y1=d×y2 , d2×(x22+y22)= z12 и число z1 делится на
любой простой делитель p числа d, вопреки
взаимной простоте чисел x1 , y1 , z1 .
Аналогично рассматриваются и другие случае НОД(x, z) > 1,
НОД(y, z) > 1.
Итак, доказано, что любое решение
уравнения Пифагора получается из примитивного умножением всех его компонент на
некоторое натуральное число D. Поэтому достаточно искать
лишь примитивные пифагоровы тройки. Поскольку каждая такая тройка состоит из
рациональных чисел, то можно применить описание рациональных пифагоровых троек.
Прежде всего, заметим, что из x2 + y2 = z2 следует, что
одно из чисел x, y чётно, а
другое нечётно. Действительно ввиду примитивности тройки x, y не могут
быть чётными одновременно. Если x, y оба нечётны,
то x2 + y2 чётно, т.е. z чётно и x2 + y2 делится на 4,
что ведёт к противоречию: если x=2×u+1, y = 2×v + 1 (u, v Î Z), то x2 + y2 = 4×(u2 + u + v2 + v) + 2 и не делится
на 4.
Поменяв, если нужно, x, y местами
(уравнение Пифагора симметрично по x, y), будем
считать, что x чётно, а y нечётно.
Согласно предыдущей теореме, каждая примитивная тройка (x; y; z) имеет вид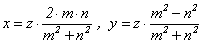 
при целых z, m, n, НОД(m, n) = 1. Значит, x×(m2 + n2) = z×2×m×n, причём
числа x и z взаимно
простые. По основному свойству взаимно простых чисел получаем m2 + n2 = z×t (t Î Z) и x×t =2×m×n, y =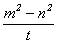 
, т.е. m2
- n2 = y×t . Отсюда 2×m2 = (z + y)×t, 2×n2
= (z - y)×t, т.е. t - общий
делитель чисел 2×m2 и 2×n2. Поэтому t делит НОД(2×m2, 2×n2)=2×НОД(m2,n2)=2.
Если t = ±2, то m2 + n2 = ±2×z M 2, т.е. взаимно
простые числа m, n оба
нечётны, и кроме того, ±2×x = 2×m×n, т.е. x= ±m×n - нечётно,
вопреки выбору x.
Значит, t = ±1, x = ±2×m×n, y = ±(m2 - n2), z = ±(m2 + n2), где целые
числа m, n взаимно
простые разной чётности (иначе y чётно), а
комбинации знаков могут быть любыми. Учитывая возможность поменять местами x, y, получаем ещё
возможность x = ±(m2 - n2), y = ±2×m×n, z = ±(m2 + n2). Любая
целочисленная тройка получается одновременным умножением компонент описанных
выше примитивных троек на произвольное целое число.
Легко проверить непосредственно, что
найденные тройки действительно являются пифагоровыми: так, для x = ±(m2 - n2), y = ±2×m×n, z = ±(m2 + n2) получаем
x2
+ y2 = (m2 - n2)2 + (2×m×n)2
= m4 - 2×m2×n2
+ n4 + 4×m2×n2
=
= m4 + +2×m2×n2 + n4 = (m2 + n2)2
= z2 .
доказательство теорема
ферма уравнение
Таким образом, доказана
Теорема (о пифагоровых тройках). Любая
пифагорова тройка имеет один из следующих видов:
,
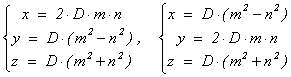где D, m, n - целые
числа, m и n взаимно
простые разной чётности.
Именно сочинение Диофанта
“Арифметика”, изданное в 1621 году в переводе Клода Гаспара де Баше де
Мазирьяка (1581-1630), в котором исследовались рациональные и целые решения
уравнения Пифагора, дало повод Пьеру Ферма записать на полях этого перевода
одно из самых достопримечательных замечаний в истории математики:
“Невозможно разложить куб на два
куба, или биквадрат на два биквадрата, или вообще степень, большую двух, на две
степени с тем же самым показателем; я нашел этому поистине чудесное
доказательство, однако поля слишком малы, чтобы оно здесь уместилось”. Таким
образом, большая или Великая теорема Ферма утверждает, что уравнение xn + yn = zn, ни при
каком натуральном n, большем
двух, неразрешимо в натуральных числах.
К сожалению, сам Ферма не оставил
своего чудесного доказательства, в его записках было обнаружено обоснование
лишь частного случая этой теоремы для n = 4. Долгие
годы все усилия по доказательству Великой теоремы Ферма были тщетны,
продвижения начали появляться лишь, начиная с XVIII в.: Л.
Эйлер доказал теорему Ферма для n = 3 (1770 г), А. Лежандр - при n = 5 (1825 г), и
Г. Ламе - для n = 7 (1839 г).
В 1908 году Пауль Вольфскель завещал
премию в 100 тысяч германских марок тому, кто первым представит доказательство.
В результате инфляции после первой мировой войны величина премии в настоящее
время ничтожна. К тому же как указывает Г. Эдвардс в своей книге о теореме
Ферма [5], премия была назначена лишь за доказательство предположения -
нахождение контрпримера не принесло бы ни пфеннига его открывателю !
После объявления о премии Великой
теоремой Ферма занялись не только профессионалы, но и широкая публика. Так как
в условие награждения входило требование, чтобы доказательство было
опубликовано, а научные издательства не желали принимать ложных доказательств,
то авторы печатали свои доказательства на собственный счет. Так во многих
странах, в том числе и в России, появилось много печатных неправильных
доказательств Великой теоремы Ферма.
Общим свойством этих “доказательств”
является то, что они ошибочны уже для наименьшего показателя в теореме Ферма, а
именно, для показателя n = 3. Авторы этих работ, преимущественно не
математики, оперировали только элементарными средствами. Между тем, известное
правильное доказательство, как будет ясно из дальнейшего, уже для показателя n = 3 является
неэлементарным.
Замечательные продвижения
принадлежат Э. Куммеру (1810-1893), который своими исследованиями по проблеме
Ферма оказал решающее влияние на развитие алгебраической теории чисел. В XX столетии
его методы были усовершенствованы и дополнены (1929 г. и позже) прежде всего
благодаря усилиям У. Вандивера, Г. Ламе и Э. Лемера. К 80-м годам XX в. с
использованием ЭВМ неразрешимость уравнения хn + yn = zn в
натуральных числах была установлена для всех n £ 2125000
(З.
Вагштафф, 1976 г.). Если принять во внимание, что число 2125000
записывается 37628-ю цифрами, то поиски контрпримера к Великой теореме
Ферма представлялись совершенно безнадежным занятием.
июня 1993 г. математик из Принстона
Эндрю Вайлс в докладе на конференции по теории чисел в Кембридже
(Великобритания) анонсировал решение проблемы Ю. Таниямы (о модулярности
эллиптических кривых с рациональными коэффициентами). Ранее уже было доказано
(в 1985 г. Г. Фрей выдвинул гипотезу, которую в 1986 г. доказал К. Рибет), что
из доказательства проблемы Таниямы следует утверждение Великой теоремы Ферма.
Однако, в начале декабря 1993 г., когда рукопись Э. Вайлса уже готова была
отправиться в печать, в его доказательстве были обнаружены пробелы. Автор
извинился и попросил два месяца для исправления. Только через год с небольшим
появилось полное доказательство гипотезы Таниямы, но уже двух авторов - Э.
Вайлса и его ученика Р. Тейлора [6, 7]. Новых пробелов в этих работах
специалистами пока не найдено.
Сама по себе Великая теорема Ферма
не имеет большого значения для математики. Однако она сыграла важную роль для
развития теории алгебраических чисел, теории идеалов, алгебраической геометрии
и математики в целом: попытки её доказательства приводили к открытию новых
методов, обогативших многие смежные области математики.
Закончим этот параграф следующими
элементарными замечаниями о Великой теореме Ферма.
Лемма (об уравнении xn + yn = zn). (1) Если
диофантово уравнение xn + yn = zn имеет
нетривиальные целочисленные решения, то оно имеет решение в попарно взаимно
простых целых числах.
(2) Великую теорему Ферма достаточно
доказать для простых нечётных показателей n = p и для n = 4.
Доказательство. (1) Если xn + yn = zn для x, y, z Î Z и НОД(x, y, z) = D, то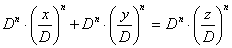 
, т.е. 
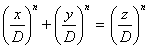, причём
целые числа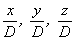 
взаимно
просты: НОД(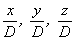) = 1. Поэтому
сразу можно считать, что НОД(x, y, z) = 1.
Если какие-то два из чисел x , y , z не взаимно
просты, то в их канонических разложениях участвует одно и то же простое число p. Пусть,
например, оно участвует в x и z, т.е. x M p, y M p. Тогда yn = zn - xn M p, а значит, y M p, вопреки НОД(x, y, z) = 1.
(2) Пусть
Великая теорема Ферма доказана для n = 4 и для
любого нечётного простого числа n = p. Рассмотрим
случай произвольного показателя n.
Если в каноническое разложение n входит
нечётное простое число p, т.е. n = p×m, то существование
нетривиального решения (x; y; z) диофантова
уравнения xn + yn = zn равносильно
тому, что (xm)p + (ym)p = (zm)p, т.е.
существованию нетривиального решения для теоремы Ферма с показателем p - противоречие.
Если же n не делится
ни на одно простое нечётное число, то 1 < n = 2k M 4, и
аналогичные рассуждения показывают, что n = 4×m и (xm)4
+ (ym)4
= (zm)4, вопреки
теореме Ферма для показателя 4.
Лемма доказана.
§
3. Метод бесконечного спуска и доказательство Великой теоремы Ферма для
показателя n
= 4
Метод бесконечного спуска.
Вот цитата из письма П. Ферма к Каркави от августа 1659 года: “Поскольку
обычные методы, которые изложены в книгах, недостаточны для доказательства
столь трудных предложений, я нашел совершенно особый путь для того, чтобы достичь
этого. Я назвал этот способ доказательства бесконечным (infinie) или
неопределенным (indefinie)
спуском; в начале я пользовался им только для доказательства отрицательных
предложений:
- что не существует числа, меньшего на
единицу кратного трёх, которое составлялось бы из квадрата и утроенного
квадрата;
- что не существует прямоугольного
треугольника в числах, площадь которого была бы квадратным числом.
Доказательство проводится путём приведения к
абсурду таким способом: если бы существовал какой-нибудь прямоугольный
треугольник в целых числах, который имел бы площадь, равную квадрату, то
существовал бы другой треугольник, меньший этого, который обладал бы тем же
свойством.
Если бы существовал второй, меньший первого,
который имел бы то же свойство, то существовал бы в силу подобного рассуждения
третий, меньший второго, который имел бы то же свойство, и, наконец, четвертый,
пятый, спускаясь до бесконечности.
Но если задано число, то не существует
бесконечности, по спуску меньших его (все время подразумеваются целые число).
Откуда заключают, что не существует никакого прямоугольного треугольника с
квадратной площадью”.
Этот метод бесконечного или
неопределенного спуска действительно сделался одним из наиболее мощных средств
диофантова анализа.
После П. Ферма его с успехом
применяли Л. Эйлер и Л. Лагранж, а в наши дни - Л. Дж. Морделл, А. Вейль и
другие. При этом метод был распространен на проблемы решения уравнения в
рациональных числах. Осуществить метод спуска в общем случае теоремы Ферма
мешает неединственность разложения целых чисел алгебраических колец в
произведение простых сомножителей из того же кольца.
Проиллюстрируем суть метода
бесконечного спуска простыми примерами.
Примеры: 1. Докажем,
что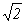 
-
иррациональное число.
Предположим противное, т.е.
что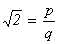 
, где p, q Î N. Тогда
имеем 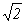×q = p, 2×q2 = p2, откуда
видно, что p чётно: p = 2×p1 (p1 Î Z). Поэтому q2 = 2×p12, и теперь q чётно: q = 2×q1 (q1 Î Z). Кроме того,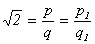 
. Таким
образом, начав с пары таких натуральных чисел (p; q), что
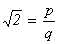, получили
новую пару натуральных чисел (p1 ; q1) , где p1 < p, q1 < q, с тем же
свойством. Точно так же по этой паре построим ещё одну пару (p2 ; q2), где p2 < p1 , q2 < q1 , и этот
процесс построения пар можно продолжать бесконечно. Однако убывающая цепочка
натуральных чисел p > p1 > p2 > … бесконечной
быть не может. Полученное противоречие доказывает, что предположение о
рациональности числа 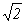было
неверно.
2.
Докажем, что диофантово уравнение x2 + y2 = 3×z2 имеет
только тривиальное решение x = y = z = 0.
Предположим, вопреки доказываемому,
что (x; y; z) -
нетривиальное решение. Тогда x и y делятся на 3.
Действительно, рассматривая уравнение по модулю 3, получим сравнение x2 + y2 º 0 (mod 3), которое
выполнено только при x º 0 º y (mod 3), в чём легко
убедиться, перебрав возможные значения x, y Î {0, 1, 2}:
|
x / y
|
0
|
1
|
2
|
|
0
|
02 + 02 º
0
|
02 + 12 º
1
|
02 + 22 º
1
|
|
1
|
12 + 02 º
1
|
12 + 12 º
2
|
12 + 22 º
2
|
|
2
|
22 + 02 º
1
|
22 + 12 º
2
|
22 + 22 º
2
|
Теперь x
= 3×x1
, y
= 3×y1
и 3×(x12
+ y12)
= z2
, значит, z
= 3×z1
. Поэтому x12
+ y12
= 3×z12.
Таким образом, начав с нетривиального решения (x;
y;
z),
получили новое нетривиальное решение (x1
; y1
; z1
), причём |x1|
< |x|
, |y1|
< |y|
, |z1|
< |z|
.
По этому решению можно построить новое нетривиальное решение (x2
; y2
; z2
), где |x2|
< |x1|
, |y2|
< |y1|
, |z2|
< |z1|
, и этот процесс можно продолжать бесконечно. Однако убывающая цепочка
натуральных чисел |x|
>
|x1|
> > |x2|
> … не может быть бесконечной. Полученное
противоречие показывает, что предположение о существовании нетривиального
решения рассматриваемого уравнения x2
+ y2
= 3×z2
было неверным.
Проблема Ферма для показателя n
= 4. Дадим короткое
доказательство, использующее классификацию пифагоровых троек.
Теорема (о диофантовом уравнении x4
+ y4
= z2).
Диофантово уравнение x4
+ y4
= z2
не имеет решений в натуральных числах. В частности, не имеет решений в
натуральных числах и уравнение x4
+ y4
= z4.
Доказательство.
Пусть (x;
y;
z)
-
натуральное решение, т.е. x,
y,
z
Î N.
Если
D = НОД(x,
y)
> 1, то для любого простого числа p,
входящего в каноническое разложение D
,
число p4
входит в разложение z2,
а
значит, p2
входит в разложение z.
Поэтому равенство x4
+ y4
= z2
можно последовательно сокращать на p4
,
не нарушая вида этого равенства. Таким образом, через несколько шагов придём к
аналогичному соотношению со взаимно простыми числами x,
y.
Если НОД(x,
y)
= 1,
то НОД(x,
z)
= 1 = НОД(y,
z).
Действительно, если, например, x
и z делятся на
некоторое простое число, то на это число делится и y4,
а значит, y вопреки условию НОД(x,
y)
= 1.
Таким образом, можно считать, что (x;
y;
z)
- примитивное решение уравнения, т.е. все числа x,
y,
z попарно
взаимно просты.
Если (x;
y;
z)
-примитивное решение диофантова уравнения x4
+ y4
= z2
в натуральных числах, то (x2;
y2;
z)
- примитивная пифагорова тройка. Следовательно, она имеет один из следующих
видов:
,
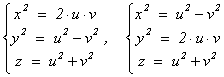где u, v - взаимно
простые целые числа разной чётности (§ 1).
Рассмотрим только первую
возможность, когда y нечётно, т.к. во втором случае всё
аналогично. Тогда y2 + v2 = u2, т.е. (y; v; u) - тоже
пифагорова тройка, причём примитивная, т.к. u, v взаимно
простые числа. Значит, можно считать, что y = s2 - t2, v = 2×s×t, u = s2 + t2 для
некоторых взаимно простых натуральных чисел s, t. Поэтому из x2 = 4×s×t×(s2 + t2) следует x = 2×x1 , где x12 = s×t×(s2 + t2), причём
числа s×t и s2 + t2 взаимно
просты: если простое число p - их общий делитель, то p | s или p | t и p | (s2 + t2), откуда по
свойствам делимости p - общий делитель взаимно
простых чисел s, t, что
невозможно. Следовательно, по следствию из основной теоремы арифметики получаем
s2 + t2 = b2, s×t = a2 , и далее s = m2 , t = n2 и m4 + n4 = b2.
Таким образом, по примитивному
решению (x; y; z) построено
новое примитивное решение (m; n; b), причём b < x12 < z, т.е.
реализован метод бесконечного спуска. Значит, диофантово уравнение x4 + y4 = z2 не имеет
нетривиальных решений, а значит, их не имеет и уравнение x4 + y4 = z4.
Теорема доказана.
§ 4. Сводка результатов: от Эйлера
до Куммера
Уже доказательство Великой теоремы Ферма для
показателя n
= 3
не элементарно. Впервые полученное Эйлером, оно в течение многих лет оставалось
идейным источником для дальнейших обобщений и модификаций.
1. Доказательство Великой теоремы
Ферма для показателя n
= 3. Пусть нашлись
такие x,
y,
z
Î
Z,
что z3
= x3
+ y3
= (x
+ y)×(x2
- x×y
+ y2)
.
Рассмотрим последовательно два случая.
I.
x
, y,
z
не делятся на 3.
Воспользуемся известным фактом: a3
º a
(mod
3),
в котором легко убедиться непосредственно, рассмотрев все возможности a
º
0, a
º
1, a
º
-1 (mod
3)
и проверив, что a3
º
0, a3
º
1, a3
º
-1 (mod
3)
соответственно. Поэтому z
º z3
= x3
+ y3
º x
+ y
(mod
3),
т.е. z
= x
+ y
+ 3×u
для
некоторого целого числа u.
Отсюда получаем x3
+ y3
= z3
= (x
+ y
+ 3×u)3
= (x
+ y)3
+ 9×(x
+ y)2×u
+ 27×(x
+ y)×u2
+ 27×u3
= x3
+ 3×x2×y
+ 3×x×y2
+ y3
+ 9×k
= x3
+ y3
+ 3×x×y×(x
+ y)
+ 9×k.
Значит, 3×x×y×(x
+ y)
+ 9×k
= 0,
т.е. x×y×(x
+ y)
= -3×k
и x×y×z
º x×y×(x
+ y)
º 0 (mod
3),
вопреки тому, что x,
y,
z
не
делятся на 3.
II.
x×y×z
M 3.
Без ограничения общности можно считать, что z
M
3 :
если, например, x
M
3,
то y3
+ (-z)3
= (-x)3,
т.е. x,
y,
z
можно
менять местами. Кроме того, ввиду попарной взаимной простоты чисел x,
y,
z
можно
считать, что x,
y
не
делятся на 3.
Из z3
= (x
+ y)×(x2
- x×y
+ y2)
= (x
+ y)×((x
+ y)2
- 3×x×y)
º (x
+ y)3
(mod
3)
следует, что x
+ y
M
3.
Пусть
z = 3×t,
x + y = 3×s.
Тогда
27×t3
= 3×s×(9×s2
- 3×x×(3×s
- x)), 3×t3
= s×(3×s2
- 3×s×x
+ x2).
При этом 3×s2 - 3×s×x + x2 
3 (иначе x M 3), так что s = 3×u и
получается равенство t3 = u×(x2 - 9×u×x + 27×u3). Ясно, что
числа u и x2 - 9×u×x + 27×u3 взаимно
простые: если p - их общий
простой делитель, то p | x2, т.е. p - общий
делитель 9×u = x + y и x2 , а значит,
p - общий
простой делитель x и y - противоречие.
Итак, произведение взаимно простых чисел u×(x2 - 9×u×x + 27×u3) является
кубом целого числа. По следствию из основной теоремы арифметики (§ 1 главы I), u = v3, x2 - 9×u×x + 27×u3 = n3 для
некоторых целых чисел v, n.
Здесь и проявилась гениальность
Эйлера: его идея состояла в том, чтобы разложить на множители величину x2 - 9×u×x + 27×u3, что не
удаётся сделать в обычных целых числах. Для этого можно рассмотреть квадратное
уравнение l2 - 9×l + 27 = 0, полученное
при l = 
и найти его
корни
l1 =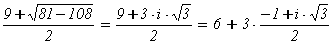 
= 3×(2 + w),
l2 =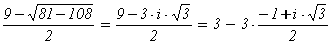 
= 3×(1 - w),
где w =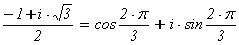 
.
Итак, l2 - 9×l + 27 = (l - l1)×(l - l2) и x2 - 9×u×x + 27×u3 = (x - 3×(2 + w)×u)×(x - 3×(1 - w)×u) = (x - 6×u - w×3×u)×(x - 3×u + w×3×u) = n3.
Таким образом, имеем разложение куба
в произведение двух множителей в числах K = {a + w×b Î C | a, b Î Z}. Сам Эйлер
сделал отсюда вывод о том, что множитель x - 3×(1 - w)×u является
кубом (k + w×m)3
,
где k, m Î Z , т.е.
x - 3×(1
- w)×u
= (k + w×m)3
Û
Û
x - 3×u
+ w×3×u
= k3 + w×3×k2×m
+ w2×3×k×m2
+ w3×m3.
Учитывая, что
w2 =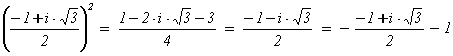 
= -w - 1 и w3 = w×w2 = w×(-w - 1) = -w2 - w = w + 1 - w = 1, получаем
x
- 3×u
+ w×3×u
= k3
+ w×3×k2×m
+ w2×3×k×m2
+ w3×m3
Û
Û
x - 3×u + w×3×u
= k3 + w×3×k2×m
- (w + 1)×3×k×m2
+ m3 Û
Û
x - 3×u + w×3×u
= (k3 - 3×k×m2
+ m3) + w×(3×k2×m
- 3×k×m2)
Û
Û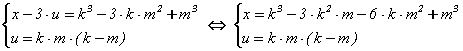 
.
Из взаимной простоты целых чисел u, x следует
взаимная простота целых чисел k, m, что вместе
с полученным ранее условием u = v3 даёт разложение
v3 = k×m×(k - m) куба целого
числа в произведение трёх попарно взаимно простых целых чисел. Поэтому k = p3, m = q3 и k - m = r3 для
некоторых p, q, r Î Z, т.е. p3 = r3 + q3 - равенство,
аналогичное исходному, причём модули чисел p, q, r меньше |v| < |v|3
= |u| =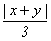 
< |z| = |x + y|×|x2 - x×y + y2|. Таким
образом, для завершения доказательства Великой теоремы Ферма при n = 3 можно
применить метод бесконечного спуска.
Теорема доказана.
2. Необходимые уточнения. Приведённое
рассуждение не вполне корректно. Так, например, в обосновании нуждается даже
вывод о том, что
x - 3×u + w×3×u = (k3 - 3×k×m2 + m3) + w×(3×k2×m - 3×k×m2) Û
.
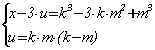Для этого нужно доказать, что из a + w×b = c + w×d, где a, b, c, d Î Z, следуют
равенства a = c и b = d. Это
сделать легко: если b ¹ d, то w =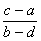 
Î Q , что
невозможно, ибо w
= 
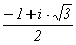Ï R .
Существенный пробел доказательства
состоит в выводе
(x - 3×(1 - w)×u)×(x - 3×(2 + w)×u) = n3 Þ x - 3×(1 - w)×u = (k + w×m)3.
Подобное утверждение для целых чисел
можно вывести на основании основной теоремы арифметики и только при условии
взаимной простоты сомножителей. Следовательно, для завершения доказательства
Эйлера нужно развить теорию делимости для чисел из множества K = {a + w×b Î C | a, b Î Z} и доказать
основную теорему арифметики. Это тем более необходимо, если учесть, что для
чисел вида a + i×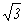
×b (a, b Î Z), очень
похожих на числа из K, однозначность разложения,
вообще говоря, не выполнена:
= 2×2 = (1 + i×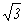)×(1 - i×).
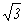Не имея возможности дать полное и
подробное обоснование однозначности разложения в произведение простых
множителей в K, наметим лишь канву рассуждений со
всеми необходимыми определениями и примерами, в которых видна идея общего
рассуждения.
а. множество K замкнуто
относительно сложения, вычитания, умножения и сопряжения:
= (p - q) - w×q
Î
K ,
(p + w×q)
± (r + w×s)
= (p ± r) + w×(q ± s) Î
K ,
(p + w×q)×(r
+ w×s)
= p×r
+ w×(q×r
+ p×s)
+ w2×q×s
=
= p×r
+ w×(q×r
+ p×s)
+ (-w
- 1)×q×s
= (p×r
- q×s)
+ w×(q×r
+ p×s
- q×s)Î
K .
Здесь использованы равенства:
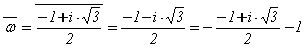= -1 - w,
w2 =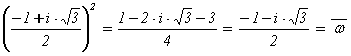 
= - 1 - w.
Подмножества в C , замкнутые
относительно сложения, вычитания и умножения, называются числовыми кольцами.
Значение их в том, что с их элементами можно производить вычисления почти как с
целыми числами.
Для удобства в дальнейшем при p, q Î Z будем, как
обычно, отождествлять числа p + q×w Î C и p + w×q Î K, а также p Î Z и p + w×0 Î K, q×w Î C и 0 + w×q Î K.
б) Пусть a , b Î K, a ¹ 0. Говорят,
что a делит b или b кратно a, если b = a×g для
некоторого g Î K .
Аналогично целым числам вводятся понятия общего делителя и общего
кратного нескольких элементов.
Элемент e Î K \ {0} называется обратимым,
если обратный элемент e -1 , который
существует в С, лежит в K . Например,
w×(w2) = w×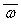
= 1, т.е. w - обратимый
элемент в K с обратным w2 = -1 + w×(-1) Î K.
Элементы a, b, … , g Î K называются взаимно
простыми, если любой их общий делитель обратим. Они называются попарно
взаимно простыми, если любые два из них взаимно простые.
Элемент π Î K называется простым,
если в любом разложении π = a×b (a , b Î K) один из множителей
a , b обратим,
т.е. разложение тривиально. Не всякое простое целое число будет простым
в K : 3 = (i×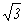)×(-i×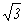) = = (1 + 2×w)×(-1 - 2×w), причём
элементы -1 - 2×w, 1 + 2×w не обратимы:
например, (1 + 2×w)-1 =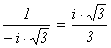 
Ï K, т.к. из
равенства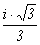 
= m + w×n = = m + 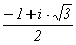×n получим
невозможное 2×i×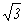 = 6×m - 3×n + i×3×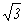×n.
Два элемента a, b Î K называются ассоциированными,
если a = e×b для
некоторого обратимого элемента e Î K. В этом
случае пишут a ~ b.
в) Для элемента a = p + w×q Î K определим норму
N(a) = (p + w×q)×(p + w2×q) = p2 +(w + w2)×p×q + q2 = p2 - p×q + q2 Î Z ,
которая на самом деле совпадает с
квадратом модуля комплексного числа a
: p + w2×q = p +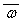 
×q = 
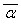. Таким
образом, N(a) = a×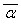 = |a|2
³ 0, и
справедливы следующие свойства квадрата модуля:
(N1) N(a) = 0 Û a = 0;
(N2) N(a)×N(b) = |a|2×|b|2
= |a×b|2
= N(a×b);
(N3) N(1) = 1.
г) Лемма (об обратимых элементах). Следующие
условия для элемента a
Î K
эквивалентны:
(1) элемент a Î K обратим;
(2) N(a) = 1;
(3) a Î {1, -1, w, -w, w2, -w2}.
д) Теорема (о делении с остатком). В числовом
кольце K выполняется
алгоритм деления с остатком относительно нормы, т.е. для любых a Î K, b Î K \ {0}
существуют такие g , d Î K , что a = b×g + d и N(d) < N(b).
Пример: Разделим a = 2 - w×5 на b = 3 + w×2 с остатком.
Вначале вычислим частное обычных
комплексных чисел
.
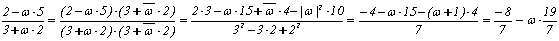Теперь найдём ближайшие целые числа
к дробям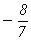 
и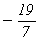 
: -1 и
-3 соответственно и образуем число g = -1 + w×(-3). Поэтому a = b×g + d , где
d = a - b×g = 2 - w×5 - (3 + w×2)×(-1 + w×(-3)) = 2 -
5×w + 3 + 11×w + 6×w2 = 5 + 6×w - 6×(w + 1) = -1 +
w×0, причём N(d) = N(-1 + w×0) = (-1)2
- (-1)×0 + 02
= 1 < 32 - 3×2 + 22 = 7 = N(b).
Таким образом, частное g = -1 + w×(-3), и остаток d = -1 + w×0.
е) Лемма (основное свойство простых
элементов).
Если π
- простой
в K элемент и π | a×b×…×g , где a , b, … , g Î K , то π делит один
из сомножителей a , b , … , g .
ж) Лемма (о простых числах). (1) Элемент
π
= x + w×y - простой в
K тогда и
только тогда, когда
либо π ~ p для
некоторого простого натурального числа p,
неразложимого в K,
либо N(π) = (x + w×y)×(x + 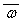×y) = p - простое
натуральное число. Все остальные элементы с нормой p имеют вид π×e или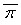 
×e для
обратимого элемента e
Î K .
Пример: Найдём все
простые элементы в K с нормой 13.
Если π = x + w×y - простой
элемент в K и N(π) = 13 = x2 - x×y + y2 = 13, то x2 - x×y + y2 - 13 = 0 - уравнение
для x, и D = y2 - 4×(y2 - 13) = 52
- 3×y2 ³ 0, т.е. 3×y2 £ 52, |y| £ 4 (x , y Î Z). При y = 1 находим x = -3, т.е. π = -3 + w.
Значит, остальные простые элементы с
нормой 13 имеют вид e×π или e×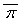
для
обратимых элементов e
Î {±1, ±w, ±w2}, т.е.
w×π = w×(-3 + w) = -w×3 - w - 1 = -1 - w×4, w×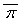 = w×(-4 - w) = 1 - w×3,
w2×π = w2×(-3 + w) = (w + 1)×3 + 1 = 4 + w×3 , w2×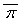 = w2×(-4 - w) = 3 + w×4.
В итоге получаем все элементы с
нормой 13:
±(3 - w), ±(4 + w), ±(1 + w×4), ±(1 - w×3), ±(4 + w×3), ±(3 + w×4).
з) Теорема (основная теорема
арифметики кольца K). (1)
Любой ненулевой элемент из K либо
обратим, либо является произведением некоторого обратимого и нескольких простых
элементов из K.
(2) Такое разложение единственно с
точностью до перестановки сомножителей и ассоциированности: если e×π1× … ×πs = d×r1× … ×rt , то s = t и после
перестановки сомножителей справедливы равенства πi = li×ri (1 £ i £ s), d = e×l1× … ×ls для
некоторых обратимых элементов l1 , … , ls Î K .
Пример: Найдём
каноническое разложение элемента a = 126 - w×68.
Ясно, что 126 - w×68 = 2×(63 - w×34), причём 2
- простой элемент в K: если 2 = a×b , то N(a)×N(b) = 4, т.е. N(a) = 2 = N(b), что
невозможно, т.к. квадратное уравнение x2 - y×x + y2 = 2 относительно
x не имеет
решений ввиду того, что его дискриминант D = 8 - 3×y2 не является
квадратом целого числа при y Î Z.
Разложим b = 63 - w×34. Вначале
разложим на множители число b×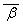
= = N(63 - w×34) = 632
+ 63×34 + 342
= 7267 = 132×43. Таким образом, в разложение
b могут
входить лишь простые элементы, участвующие в разложениях простых натуральных
чисел 13 и 43.
Число 13 уже было разложено
выше: 13 = (-3 + w)×(-4 - w). Если
разделить b на -4 - w, то
,
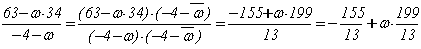т.е. деления нацело нет. Однако при
делении b на -3 + w имеем:
= -22 +w×3.
Таким образом, b = (-3 + w)×(-22 + w×3). Остаётся
разложить g = -22 + w×3 c нормой N(-22 + w×3) = N(b) / 13 = 13×43.
Снова поделим на простое число -3
+ w с нормой 13:
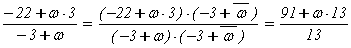= 7 + w.
Значит, g = (-3 + w)×(7 + w), где N(7 + w) = 43 - простое
натуральное число, так что 7 + w - простой элемент в K.
Итак, a = 126 - w×68 = 2×(-3 + w)2×(7 + w) - каноническое
разложение в K.
и) Следствие (о разложении степени). Если в K некоторая
степень разложена в произведение необратимых попарно взаимно простых
сомножителей: zn = u1× … ×uk , то каждый
сомножитель ui является (с
точностью до обратимого множителя) той же степенью подходящего элемента из K: ui = ei×tin , (1 £ i £ k), z = e×t1× … ×tk , en = e1× … ×ek .
Основываясь на этих результатах,
закончим обоснование гениальной догадки Эйлера.
В полученном разложении (x - 3×u + w×3×u)×(x - 6×u - w×3×u) = n3 сомножители x - 3×(1 - w)×u и x - 3×(2 + w)×u взаимно
просты. Действительно, любой их общий простой в K делитель π делит и
комбинации
(x - 3×(1
- w)×u)
- (x - 3×(2 + w)×u)
= 3×(2
+ w
- 1 + w)×u
= 3×(1
+ 2×w)×u,
(2 + w)×(x
- 3×(1
- w)×u)
- (1 - w)×(x
- 3×(2
+ w)×u)
= (1 + 2×w)×x.
Он не может делить u и x, т.к. иначе
u2 = N(u) M N(π) и x2 = N(x) M N(π), вопреки
взаимной простоте целых чисел u, x. Значит, π | (1 + 2×w) - простое в K с нормой 3,
и можно считать, что
π = 1 + 2×w = 1 - w + 3×w = 1 - w + (1 - w)×(1 - 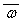)×w =
= (1 - w)×(1 + (1 - 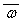)×w) = (1 - w)×w,
т.е. π | (1 - w). Из π | (x - 3×(1 - w)×u) получаем π | x , N(π) | N(x) или 3 | x2 - противоречие
с выбором x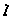 
3.
Итак, n3 = (x - 3×(1 - w)×u)×(x - 3×(2 + w)×u) - разложение
куба в произведение двух взаимно простых в K множителей.
Значит,
x - 3×(1 - w)×u = e×(k + w×m)3
= w e×(k + w×m)3
(e Î {0, 1, 2})
для некоторых целых k, m и обратимого
e Î {1, w, w2} . Здесь
учтено, что (-e×(k + w×m)3
= e×(-k - w×m)3). Более
подробно, правая часть равна:
e = 0: k3+3×w×k2×m+3×w2×k×m2+m3 = (k3-3×k×m2+m3)+3×w×k×m×(k-m);
e = 1:
w×((k3-3×k×m2+m3)+3×w×k×m×(k-m))
= -3×k×m×(k-m)+w×(k3-3×k2×m+m3);
e = 2:
w2×((k3-3×k×m2+m3)+3×w×k×m×(k-m))
= -k3+3×k2×m-m3-w×(k3-3×k×m2+m3).
Последние два случая невозможны, в чём легко
убедиться, рассматривая полученное равенство по модулю 3: при e
= 1
имеем x
- 3×u
= -3×k×m×(k-m),
т.е. x
M 3 - противоречие,
а при e
= 2 получаем
3×u
= -k3+3×k×m2-m3,
т.е. k3
+ m3
делится
на 3, так что из x
- 3×u
= -k3+3×k2×m-m3
снова x
M 3 - противоречие.
Итак, x
- 3×(1 - w)×u
= (k
+ w×m)3,
и доказательство Эйлера полностью обосновано (по модулю сформулированных выше
свойств кольца K).
Таким образом, для решения проблемы
Ферма о натуральных числах Эйлером были привлечены числа другой природы:
комплексные числа вида a + w×b, где a, b Î Z, w = 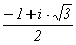. Здесь w - корень
уравнения x3 = 1, и можно
доказать, что каждое число a
= a + w×b
удовлетворяет некоторому кубическому уравнению с целыми коэффициентами: (a - a)3
= (w×b)3
= b3, т.е. a3 - 3×a2×a + 3×a×a2 - a3 - b3 = 0.
Любое комплексное число a Î С ,
удовлетворяющее уравнению с целыми коэффициентами, называется алгебраическим.
Таким образом, Эйлером был заложен фундамент теории алгебраических чисел,
бурное развитие которой продолжается до сих пор.
3. Метод Куммера. По лемме об
уравнении xn + yn = zn , Великую
теорему Ферма осталось доказать для любого нечётного простого числа p. Идея
Эйлера позволила (усилиями А. Лежандра и Г. Ламе) доказать Великую теорему
Ферма для n = 5, 7, 11 и
13, но общего доказательства на этом пути получить не удалось. Только Э.
Куммер в середине XIX в. сумел обобщить эту идею и
получить метод дающий доказательство для всех, так называемых, регулярных
простых показателей (см. [1]) (в частности, для всех показателей, меньших 100).
Куммер исходил из аналогичного
рассмотренному выше в доказательстве Эйлера разложения
xp
+ yp = (x + y)×(x + w×y)×
… ×(x
+ w
p-1×y),
где w p = 1 , w =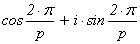 
. Таким
образом, можно рассмотреть числовое кольцо
Kp = {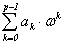
Î C | ak Î Z (0 £ k £ p - 1)}.
Если бы удалось доказать, что это
кольцо с однозначным разложением в произведение простых элементов, то Великая
теорема Ферма была бы доказана.
Проблема состоит в том, что
однозначность разложений в произведение простых элементов в кольце Kp выполняется
не всегда. Чтобы преодолеть эту преграду Куммер применил метод расширения
множества Kp до
полугруппы Д идеальных объектов, называемых ныне дивизорами, в которых
разложение на множители однозначно. В доказательстве Эйлера, ввиду основной
теоремы арифметики, справедливой в кольце K, достаточно
было взять Д = K \ {0}, но в общем
случае всё не так просто.
Такая конструкция расширения Kp Í Д была
обоснована им для регулярных простых чисел p, одна из
возможных характеризаций которых такова: нечётное простое число p регулярно
тогда и только тогда, когда для любого чётного k = 2, 4, … ,
p - 3 число 1k + 2k + … + (p - 1)k не делится
на p2.
Примеры: 1. p = 3 регулярно,
т.к. нет чисел k.
2. p = 5 регулярно,
т.к. для k = 2 имеем 12
+ 22 + 32 + 42 = 30 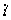52.
3. Среди простых чисел первой
сотни не регулярны только 37, 59, 67. Для них Куммер доказал Великую
теорему Ферма отдельно.
Хотя метод Куммера позволяет
доказать Великую теорему Ферма для широкого класса показателей, но до сих пор
не известно, является ли множество регулярных простых чисел бесконечным. С
появлением ЭВМ проверка регулярности стала возможной для очень больших чисел n
£ 2125000, так что
горизонт показателей, для которых Великая теорема Ферма доказана методом
Куммера, существенно расширился, но не стал беспредельным.
ГЛАВА
II.
ВЕЛИКАЯ ТЕОРЕМА ФЕРМА И a×b×c-ГИПОТЕЗА
§
1. Гипотеза Таниямы и доказательство Вайлса Великой теоремы Ферма
Удивительно, но, как это часто бывает в
математике, решение проблемы Ферма пришло совсем с другой стороны, нежели
ожидалось. Как уже отмечалось, Э. Вайлс и Р. Тейлор доказали гипотезу Таниямы,
относящуюся к теории эллиптических кривых, но из неё К. Рибет, основываясь на
гениальной догадке Г. Фрея, вывел Великую теорему Ферма.
К сожалению, объём работы не позволяет подробно
остановиться на исследованиях Вайлса-Тейлора. Поэтому лишь наметим путь,
ведущий к доказательству Проблемы Ферма.
1. Эллиптические кривые.
Эллиптической кривой называется кривая на плоскости, заданная
уравнением
y2 = x3 +
a×x2
+ b×x + c,
где
a, b, c Î
Q .
По аналогии с дискриминантом
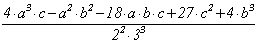
общего кубического уравнения x3 + a×x2 + b×x + c = 0 вводится дискриминант
D
эллиптической кривой y2 = x3 + a×x2 + b×x + c (a, b, c Î Q), равный по
определению D = -16×(4×a3×c - a2×b2 - 18×a×b×c + 27×c2 + 4×b3). Отличие в
числовом множителе от дискриминанта D здесь не принципиально, но удобно
тем, что при целых a и b
дискриминант тоже будет целым числом.
На рис. 2, 3 приведены некоторые
графики эллиптических кривых: неособые с ненулевым дискриминантом, и особые
- с нулевым.
Эллиптическая кривая y2 = x3 + a×x2 + b×x + c (a, b, c Î Z) называется полустабильной,
если сравнение x3 + a×x2 + b×x + c º 0 (mod p) не имеет
трёхкратных корней для любого простого p | (4×a3×c - a2×b2 - 18×a×b×c + 27×c2 + 4×b3).
Примеры: 1. Кривая y2 = x3 не
полустабильна: её дискриминант нулевой, т.к. a = b = c = 0, а правая
часть имеет трёхкратный корень x = 0 по любому
простому модулю.
2. Пусть A, B - взаимно
простые целые числа, С = A + B. Тогда
эллиптическая кривая y2 = x×(x - A)×(x - C)
полустабильна.
Действительно, уравнение кривой
имеет вид y2 = x3 - (A + C)×x2 + A×C×x, а
её дискриминант вычисляется так:
D = -16×(-
(A + C)2×(A×C)2
+ 4×(A×C)3)
= -16×(A×C)2×(A
- C)2 = -16×A2×B2×C2.
Поэтому, если p | A2×B2×C2, то p делит одно
из чисел A, B, C, причём два
из этих чисел не могут делиться на p ввиду
взаимной простоты A и B: например,
если A M p, C M p, то B = (C - A) M p -
противоречие. Таким образом, корни x º 0, x º A, xº C (mod p) правой части
уравнения кривой не могут все быть одинаковыми.
Определим для эллиптической кривой y2 = x3 + a×x2 + b×x + c понятие кондуктора,
ограничившись только важным для дальнейшего случаем, т.к. общее его определение
требует далеко выходящих за рамки данного изложения понятий. Грубо говоря, кондуктор
собирает в
одно произведение все простые числа, участвующие в каноническом разложении
дискриминанта эллиптической кривой. При этом степень ep , с которой
простое число p входит в кондуктор, равна 1,
если a2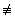 
3×b (mod p). Эта
степень ep равна 2,
если p > 3 и a2 º 3×b (mod p). В
случае, когда сравнение x3 + a×x2 + b×x + c º 0 (mod p) не имеет
решений, степень ep совпадает с
показателем, с которым p входит в
каноническое разложение дискриминанта D. Остальные
возможности p = 2, 3
для кривой с условием a2 º 3×b (mod p) исследуются
более сложно, но они не встретятся в дальнейшем, так что оставим их без
комментариев.
Примеры: 1. Для кривой
y2 = x3 - x + 1 имеем
D = -16×(4×a3×c-a2×b2-18×a×b×c+27×c2+4×b3)
= - 16×(27×12
+ 4×(-1)3)
= -24×23.
Таким образом, N = 2e×23d. Остаётся
вычислить степени e , d.
Поскольку многочлен x3 - x + 1 не имеет
корней по модулю 2, то e = 4. По модулю 23 имеем a2 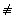3×b Û 02
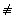3×(-1) (mod 23). Поэтому d = 1.
Итак, кондуктор эллиптической кривой y2
= x3
- x
+ 1 равен
N = 24×23.
2. Пусть A, B - взаимно
простые целые числа, С = A + B. Вычислим
кондуктор эллиптической кривой y2 = x×(x - A)×(x - C),
дискриминант которой вычислен ранее: D = -16×A2×B2×C2 .
Следовательно, в кондуктор N войдут
двойка, а также нечётные простые числа, делящие A2×B2×C2, т.е.
делящие одно из чисел A, B, C: N =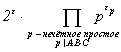 
. Вычислим
показатели, с которыми эти простые числа входят в кондуктор. При этом 2 |
A×B×C, т.к. в
равенстве A + B = C все три
числа не могут быть нечётными.
Ясно, что
x×(x
- A)×(x - C) = x3
- (A + C)×x2
+ A×C×x,
т.е.
a = A + C, b = A×C
и
a2 - 3×b
= A2 - A×C
+ C2 . Это
выражение не сравнимо с нулём по модулю p,
если p
| A
или
p | C
:
если A2
- A×C
+ C2
º
0 (mod
p),
то A
º
0 º C
(mod
p),
что противоречит взаимной простоте чисел A,
B,
C. Если же p
| B, то A
º C
(mod
p)
и A2
- A×C
+ C2
º
A2
º 0 (mod
p)
- противоречие.
Таким образом, a2 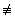3×b (mod p), т.е. ep = 1 для всех p | A×B×C.
Итак, кондуктор эллиптической кривой y2
= x×(x
- A)×(x
- C),
где C
= A
+ B, НОД(A,
B)
= 1,
является произведением всех простых чисел из канонического произведения
дискриминанта
D = 16×A2×B2×C2, т.е. N =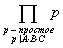 
.
. Модулярные формы и модулярные
эллиптические кривые. Пусть H
- верхняя
комплексная полуплоскость n
Î
N,
k
Î
Z.
Модулярной параболической формой веса k
и уровня n
называется
заданная и дифференцируемая на H
(аналитическая в H)
функция f
: H
® C
со
следующими свойствами:
,
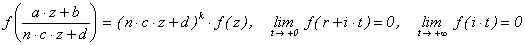где a, b, c, d - любые такие
целые числа, что a×d - b×c×n = 1, а r Î Q .
Нетрудно заметить, что для любого z Î H элемент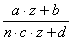 
при условии
a×d - b×c×n = 1 тоже
принадлежит H, так что данное определение
корректно. В самом деле,
,
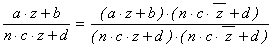где в знаменателе дроби стоит
положительное число |n×c×z + d|2 , а
числитель имеет мнимую часть, равную a×d×Im(z) - b×n×c×Im(z) = Im(z) > 0. Таким
образом, рассматриваемая дробь принадлежит H.
Множество всех модулярных
параболических форм веса k и уровня n обозначим
через Sk(n).
Примеры: 1. Нулевая
функция 0 : H ® C является,
очевидно, модулярной параболической формой веса k и уровня n.
2. Если
константа является модулярной параболической формой веса k
и
уровня n, то эта
константа равна нулю.
Действительно, если f(z) = c, то из
условия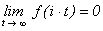 
получаем,
что
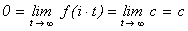, т.е. c = 0.
3. Если
k - нечётно,
то Sk(n)
= {0}.
В самом деле, ввиду (-1)×(-1) - 0×0 = 1, то из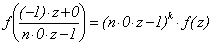 
получаем f(z) = -f(z), т.е. f(z) = 0.
В дальнейшем важную роль сыграют
модулярные параболические формы веса 2 и уровня n. Оказывается,
что множества S2(n) состоят
только из одной нулевой функции при n £ 10: S2(n) = {0} (0 £ n £ 10).
Любая модулярная параболическая
форма f Î Sk(n) удовлетворяет
условию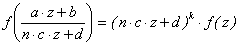 
при любых
целых a, b, c, d со
свойством a×d - b×c×n = 1. В
частности, при a = 1, d = 1, с = 0
получаем f(z + b) = f(z) при любом b Î Z. Это
показывает, что функция f однозначно
определяется своим заданием в полуполосе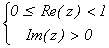 
, т.е. является периодической с
периодом T = 1 (рис. 4).
Например, f(-7+2×i) = = f((0 + 2×i) - 7) = f(0 + 2×i). Можно
доказать, что такую периодическую аналитическую функцию можно представить в
виде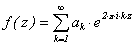 
, где для z = x + i×y величина ez = ex×(cos y + i×sin y) - обычная
экспонента в комплексной плоскости. Как известно, экспонента периодична
с периодом 2×π×i:
ez+2×π×i
= ex+i×(y+2×π)
= ex×(cos(y+2×π)
+ i×sin(y
+ 2×π))
= ex×(cos
y
+ i×sin
y)
= ez.
Поэтому функция q(z)
= e2×π×i×z
и
её любые степени q(z)k
= e2×π×i×k×z,
периодичны с периодом 1:
q(z + 1)k = e2×π×i×(z+1)×k
= e -2×π×y×k+2×π×i×(x+1)×k
= e -2×π×y×k+2×π×i×x×k+2×π×i×k
=
= e -2×π×y×k+2×π×i×x×k
= e (-2×π×y+2×π×i×x)×k
= e2×π×i×z×k
= q(z)k.
По сути дела, такое разложение функции f
по
степеням qk
(k
Î
N)
- это её разложение в ряд Фурье.
Модулярная параболическая форма f
Î S2(n)
называется
собственной (по аналогии с собственными числами линейных операторов: она
является собственной функцией для некоторого семейства операторов - всех
операторов Гекке), если все коэффициенты ak
в
ряде
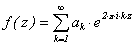
являются целыми числами,
удовлетворяющими условиям:
- a1
= 1;
am×k
= am×ak , если НОД(m,
k) = 1;
- 
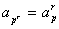для любого простого p | n;
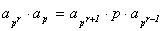для любого простого p 
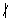n.
Наконец, эллиптическая кривая y2 = x3 + a×x2 + b×x + c с
кондуктором N называется модулярной,
если существует такая собственная модулярная параболическая форма 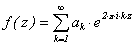Î S2(N), что ap = p - np для всех
простых чисел p, за исключением конечного их числа,
где np - это число
решений сравнения y2 º x3 + a×x2 + b×x + c (mod p).
3. Гипотеза Таниямы. На первый
взгляд, кажется невероятным существование хотя бы одной модулярной
эллиптической кривой, ибо вышеприведённые условия модулярности и собственности
формы слишком сложны, а числа np практически
не вычислимы. Однако обширный эмпирический материал и развитая математическая
сверхинтуиция позволили экстравагантному японскому математику Ютака Танияме
(1927-1958) в 1955 г. сформулировать следующую смелую гипотезу: всякая
эллиптическая кривая с рациональными коэффициентами модулярна.
В течение долгого времени эта
гипотеза не привлекала внимания математиков из-за своей неправдоподобности. Но
в 1970-е годы, благодаря работам Г. Шимуры и А. Вейля она стала
популярной, но не на много более понятной, чем раньше. Особенно усилилась её
популярность в математической среде после того как в 1985 г. немецкий математик
Г. Фрей предположил, а американец К. Рибет доказал, что из гипотезы Таниямы
следует Великая теорема Ферма.
Наконец, в 1993 г. математик и
Принстона Э. Вайлс объявил о доказательстве той части гипотезы Таниямы, которой
хватает для вывода Великой теоремы Ферма. В его рассуждениях были обнаружены
пробелы, которые удалось залатать спустя почти два года вместе со своим
учеником Р. Тейлором. С тех пор Великая теорема Ферма считается полностью
доказанной. Полная версия гипотезы Таниямы была доказана позже усилиями целой
группы специалистов, среди которых был и Р. Тейлор.
4. Вывод теоремы Ферма из гипотезы
Таниямы.
Пусть Великая теорема Ферма не верна, т.е. для какого-то простого числа s > 3 верно
равенство a s + b s = c s, т.е. A + B = C, где A = as , B = bs , C = cs , НОД(A, B) = 1.
Рассмотрим эллиптическую кривую
Фрея, в модулярности которой он усомнился первым, что и подтвердил
доказательством К. Рибет:
y2
= x×(x
- A)×(x
- C) = x3 - (A + C)×x2
+ A×C×x.
Эта кривая уже встречалась ранее:
она полустабильна, вычислен её дискриминант D = 16×A2×B2×C2 и кондуктор
.
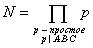Теорема (Рибета). Пусть g : y2 = x3 + a×x2 + b×x + c - модулярная
эллиптическая кривая с дискриминантом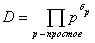 
, кондуктором 
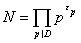и
собственной модулярной параболической формой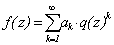 
Î S2(N) веса 2 и
уровня N. Тогда для
любого простого числа r и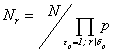 
существует
такая модулярная параболическая форма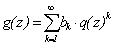 
Î S2(Nr) с целыми
коэффициентами, что при любом натуральном k верно (bk - ak) M r.
Если применить эту теорему к
рассматриваемой кривой Фрея, то
.
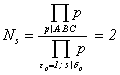Действительно, каждое нечётное
простое число p, участвующее в разложении
дискриминанта, встречается ровно один раз (либо в A, либо в B, либо в C ввиду
попарной взаимной простоты этих чисел) с показателем, делящимся на s, и поэтому
сократится в Ns . Число 2
участвует в дискриминанте в степени вида s×k + 4 < s×(k + 1) и не
делится на s > 3, так что 2
участвует в числителе, но не участвует в знаменателе, т.е. будет значением Ns .
По теореме Рибета найдётся форма
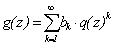Î S2(2)
со свойством: при любом
натуральном k верно (bk - ak) M s. Однако,
как отмечалось выше, S2(2) = {0}, поэтому bk = 0 (k Î N), а значит, ak M s при любом k Î N, вопреки
условию a1 = 1.
Великая теорема Ферма доказана.
Изложенное доказательство теоремы
Ферма снова подчёркивает всеединство математики. Для того чтобы понять
рассуждения Вайлса, нужно быть специалистом экстра класса не только в
современной (алгебраической) теории чисел, но понимать, как весьма тонкие
аналитические методы теории модулярных форм, так и причудливую геометрию
алгебраических кривых. Это не под силу ни узким специалистам в одной области
математики, ни широко, но не глубоко образованным дилетантам. Такая ситуация
обостряет проблемы математического образования: как нужно готовить студентов,
чтобы они были способны воспринимать новейшие методы науки ?
§ 2. a×b×c-гипотеза
и “Великая теорема Ферма” для многочленов
В последнее время наметился новый нетривиальный
подход к доказательству Великой теоремы Ферма. Так называемая a×b×c-гипотеза
для многочленов была доказана в 1983 г. Р. Мейсоном (Mason
R.C.
Diophantine
Equations
over Function
Fields // London
Math. Soc.
Lecture Note
Series, Vol.
96, Cambridge
University
Press, 1984).
Впоследствии обнаружилось, что полученный им результат в действительности уже
был открыт ранее В. Стотерсом (Stothers
W. Polynomial
identities
and hauptmoduln.
Quart. Math.
Oxford (2) 32 (1981), pp.
349-370), но математики, как это часто бывает, не обратили внимания на эту
работу.
a×b×c-Теорема
Мейсона-Стотерса.
Пусть a(t), b(t), c(t) Î C[t] - не
равные константе взаимно простые полиномы со свойством a(t) + b(t) = c(t). Тогда max(d(a) , d(b), d(c)) < r(a×b×c) - 1, где d(f) - степень
многочлена f(t), и для
заданного многочлена p(t) с
каноническим разложением p(t) =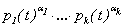 
символ r(p) обозначает
выражение p1(t)× … ×pk(t) и
называется радикальным многочленом для p(t).
Замечание: На самом
деле r(p) - это просто
количество различных корней многочлена p(t) в поле
комплексных чисел без учёта их кратностей. Действительно, все простые над С
имеют степень 1, так что полиномы p1(t), … , pk(t) в
каноническом разложении многочлена p(t) имеют
степень 1 и определяют один корень многочлена. Поэтому для многочлена p(t) = 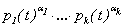верно r(p) = k - количество
различных корней многочлена.
Доказательство. Это
доказательство принадлежит ученику выпускного класса Н. Снайдеру, который нашёл
его после беседы с С. Ленгом, сформулировавшим для него теорему
Мейсона-Стотерса. Сейчас этот школьник уже окончил Гарвардский университет.
Лемма. Пусть f(t) -
многочлен положительной степени, f¢(t) - его
производная. Тогда d(f) = d(НОД(f , f ')) + r(f).
Доказательство. Во-первых,
сделаем замечание о корнях полинома f(t). Пусть a - корень f(t), т.е. такое
комплексное число, что f(a) = 0. Разложим f(t) по степеням
двучлена t - a, записав f(t) = fn×(t - a)n + … + fm×(t - a)m, где fn ¹ 0 ¹ fm , m ³ 1 - кратность
корня a . Тогда
можно вычислить производную f¢(t) = n×fn×(t - a)n-1 + … + m×fm×(t - a)m-1, т.е. m - 1 является
наибольшей степенью двучлена t - a , делящей f¢(t).
Пусть теперь a1 , … , ar - все
различные корни многочлена f(t) кратностей m1 , … , mr соответственно.
Тогда f(t) =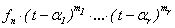 
. Сделанное
в предыдущем абзаце замечание и однозначность разложения на множители дают
разложение НОД(f , f¢ ) =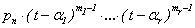 
для
некоторой ненулевой константы pn . Значит,
d(f) = m1
+ … + mr = (m1 - 1) + … + (mr - 1) + r = = d(НОД(f
, f¢))
+ r(f).
Лемма доказана.
Закончим доказательство теоремы
Мейсона-Стотерса. Прежде всего, три многочлена Da(t) = НОД(a , a¢), Db(t) = НОД(b , b¢), Dc(t) = НОД(c , c') попарно
взаимно просты. Действительно, любой делитель первых двух является общим
делителем a(t) и b(t), а значит,
тривиален. Точно так же общий делитель, например, первого и третьего из этих
многочленов будет общим делителем a(t) и c(t), и
делителем c(t) - a(t) = b(t), откуда
снова следует тривиальность этого общего делителя.
Далее, из условия a(t) + b(t) = c(t) получаем
аналогичное соотношение a(t)¢ + b(t)¢ = c(t)¢ для
производных. Значит,
a¢(t)×b(t)
- a(t)×b¢(t)
= a¢(t)×(a(t)
+ b(t)) - a(t)×(a¢(t)
+ b¢(t)) = a¢(t)×c(t)
- a(t)×c¢(t).
При этом Da
= НОД(a
, a¢)
и Db(t)
= НОД(b
, b¢)
делят
левую часть, а многочлен Dc(t)
= НОД(c
, c')
делит правую часть, а значит, и левую. Поскольку все эти три многочлена попарно
взаимно просты, то левая часть рассматриваемого равенства a¢(t)×b(t)
- a(t)×b¢(t)
делится
и на произведение этих трёх многочленов Da(t)×Db(t)×Dc(t).
Тогда
(Da×Db×Dc)
= d(Da) + d(Db) + d(Dc) £
d(a¢(t)×b(t)
- a(t)×b¢(t))
£
£ max{d(a¢(t)×b(t)),
d(a(t)×b¢(t))}
£
d(a) + d(b) - 1.
Прибавляя
d(c) к обеим
частям и переставляя слагаемые, получим
d(c) + d(Da ) + d(Db
) + d(Dc ) £ d(a) + d(b)
+ d(c) - 1,
т.е.
d(c) £ d(a) - d(Da ) + d(b) -
d(Db ) + d(c) - d(Dc ) - 1.
Согласно
лемме получаем d(c) £ r(a) + r(b) + r(c) - 1 = r(a×b×c) - 1 ввиду
взаимной простоты многочленов a(t), b(t), c(t).
Теорема
доказана.
Рассмотрим
некоторые следствия доказанной a×b×c - Теоремы для
многочленов, иллюстрирующие её скрытую силу.
Теорема
(“Великая теорема Ферма” для многочленов). Уравнение x(t)n + y(t)n = z(t)n с неизвестными
многочленами x(t), y(t) , z(t) Î C[t] , n ³ 3 допускает
только тривиальные решения: либо один из многочленов x(t), y(t), z(t) нулевой,
либо все эти многочлены являются константами.
Доказательство. Пусть x(t), y(t), z(t) - тройка
ненулевых многочленов со свойством x(t)n + y(t)n = z(t)n. Если хотя
бы один из этих многочленов не является константой, то можно выбрать такую
нетривиальную тройку с наименьшей суммой d(x) + d(y) + d(z).
Прежде
всего, можно считать эти многочлены попарно взаимно простыми. Действительно,
если, например, p(t) - неразложимый
многочлен положительной степени, делящий какие-то два из рассматриваемых
многочленов, то, очевидно, что он делит и n-ю степень
третьего многочлена, а значит, делит и сам третий многочлен. Значит, x(t) = p(t)×u(t), y(t) = p(t)×v(t), z(t) = p(t)×w(t), и сократив
равенство x(t)n + y(t)n = z(t)n на p(t)n получим,
что u(t)n + v(t)n = w(t)n, причём d(u) + d(v) + d(w) = d(x) - d(p) + d(y) - d(p) + d(z) - d(p) < d(x) + d(y) + d(z),
вопреки
предположению о минимальности последней суммы степеней.
Итак,
можно считать, что тройка x(t), y(t), z(t)
нетривиальна и состоит из попарно взаимно простых многочленов. Тогда взаимно
просты и многочлены a(t) = x(t)n, b(t) = y(t)n, причём a(t) + b(t) = c(t) = z(t)n. По a×b×c - теореме
max(d(a) , d(b), d(c)) £
r(a×b×c)
- 1 = r(a) + r(b) + r(c) - 1,
n×max(d(x),
d(y), d(z)) £ r(x) + r(y) + r(z) - 1 £
d(x) + d(y) + d(z) - 1.
В
частности, отсюда следует, что n×d(x) £ d(x) + d(y) + d(z) - 1, т.е.
(n - 1)×d(x) £ d(y) + d(z) - 1.
Аналогично,
(n - 1)×d(y) £ d(x) + d(z) - 1, (n - 1)×d(z) £ d(x) + d(y) - 1. Складывая
три полученных неравенства, приходим к оценкам
(n - 1)×(d(x) + d(y) + d(z)) £ 2×(d(x) + d(y) + d(z)) - 3,
(n - 3)×(d(x) + d(y) + d(z)) £ - 3,
что
невозможно при n ³ 3.
Теорема
доказана.
Замечание. Как и для
натуральных чисел, уравнение Ферма для многочленов при n = 2 имеет
бесконечно много решений, например, такие:
x(t) = 2×u(t)×v(t), y(t) = u(t)2
- v(t)2,
z(t) = u(t)2
+ v(t)2
при
любых u(t), v(t) Î C[t].
§ 3. abc-гипотеза для натуральных
чисел
Теоретико-числовая a×b×c-проблема
формулируется следующим образом: при любом e > 0
существует такая константа K(ε) > 0, что для
всех взаимно простых натуральных чисел a, b, c со свойством a + b = c, верно
неравенство c £ K(ε)·(r(a×b×c))1+e , где для
заданного натурального числа n с
каноническим разложением n =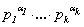 
символ r(n) обозначает
выражение p1× … ×pk и
называется радикалом числа n (при этом считаем,
что r(1) = 1).
Именно в таком довольно
неестественном виде эта гипотеза была сформулирована Массером и Остерле в 1986
г. Её значение состоит в том, что в случае её справедливости получаются изящные
и короткие доказательства известных трудных теорем теории чисел, в том числе и
доказательство Великой теоремы Ферма. Массер и Остерле не сразу сформулировали
эту гипотезу. Они работали над много более общей задачей, которая ни в коей
мере не элементарна, a×b×c-гипотеза
возникла из глубокого изучения алгебраической геометрии и теории модулярных
функций.
Примеры: r(24) = r(23×3) = 2×3 = 6, r(10) = r(2×5) = 2×5 = 10, r(2016) = = r(24×101) = 2×101 = 202.
Ясно, что для любого числа n Î N верны
неравенства r(n) £ n, r(nm) = = r(n) £ n = (nm)1 / m .
Любую тройку натуральных чисел (a; b; c) со
свойствами a + b = c, НОД(a, b) = 1 будем
называть a×b×c-тройкой. Нетрудно
понять, что условие НОД(a, b) = 1 взаимной
простоты чисел a, b равносильно
условию взаимной простоты любой пары чисел из a×b×c-тройки.
Например, НОД(a, c) = 1 : если D = НОД(a, c), то D | a, D | c и из
равенства a + b = c получаем,
что D | b , т.к. b = c - a, т.е. D - общий
делитель a и b, а значит, D = 1. Таким
образом, в определении a×b×c-тройки можно
ограничиться условием взаимной простоты НОД(a, b, c) = 1 всех трёх
чисел a, b, c в
совокупности.
Примеры: 1. 1 + 1 = 2. Здесь c = 2 < 1×r(a×b×c)1+e = 1×21+e, K(e) = 1.
2. 1
+ 2 = 3, c = 3 < 1×r(a×b×c)1+e
= 1×61+e, K(e)
= 1.
3. 1
+ 3 = 4. Здесь c = 4 < 1×r(a×b×c)1+e
= 1×61+e, K(e)
= 1.
4. 1
+ 8 = 9, c = 9 <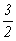 
×r(a×b×c)1+e
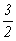= ×61+e, K(e)
= .
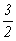5. 3
+ 125 = 128. Здесь c = 128 < 4×r(a×b×c)1+e
= 4×301+e, K(e)
= 4.
6. 5
+ 27 = 32, c = 32 < 1,1×r(a×b×c)1+e
= 1,1×301+e, K(e)
= 1,1.
7. 12
+ 13 = 25, c = 25 < 1×r(a×b×c)1+e
= 1×3901+e, K(e)
= 1.
a×b×c-Гипотеза для
натуральных чисел выглядит сложнее, чем для многочленов. Первое, что приходит в
голову, - упростить её формулировку: существует такая константа K > 0, что
для любой a×b×c-тройки
верно неравенство c < K×r(a×b×c). Однако,
как показали два студента Йельского университета Стейл Войтек Ястрзебовский и
Дэн Шпильман, такое предположение не верно:
Лемма. (1) Для
любого k Î N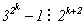 
.
(2) Для любого k Î N тройка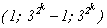 
является a×b×c-тройкой,
причём с =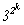 
> r(a×b×c) = 3×r(
).
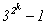(3) Не существует такой константы K > 0, что
для любого k Î N для a×b×c-тройки из
(1) верно c < K×r(a×b×c).
Доказательство. (1) Индукция
по k. База k = 1: 8 = 32
- 1 M 23.
Предположим, что 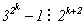для k = 1, … , m и докажем,
что это верно и при k = m + 1: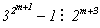 
.
Действительно, 
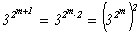, так что 
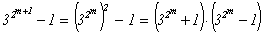. Первая
скобка чётна, т.е. делится на 2, а вторая скобка по предположению
индукции делится на 2 m+2.
Произведение же скобок делится на 2 m+3, что и
требовалось.
(2) То, что 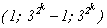- a×b×c-тройка, не
вызывает сомнений. Проверим неравенство из формулировки a×b×c-гипотезы.
Во- первых, r(a×b×c) = r(1×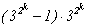
) = r(
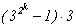). Во-вторых,
в каноническом разложении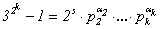 
, где s ³ k + 2, простые
числа в правой части не равны 3, т.к. иначе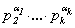, 3 | 
, 3 |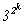 
и 3 | 1,
что невозможно. Наконец, r(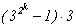) = 3×2×p2× … ×pk £ 
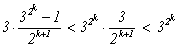. Таким
образом, с = 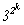> r(a×b×c).
(3) От
противного с учётом предыдущих вычислений:
,
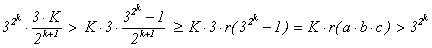т.е. K >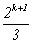 
, что
невозможно при k ® ¥ .
Лемма доказана.
Утверждение (2) леммы
показывает, что существует бесконечно много a×b×c-троек со
свойством c > r(a×b×c). Такие
тройки называются хитовыми. Расчёты на ЭВМ показывают, что хитовых троек
относительно мало: так, для c < 50000 есть только 276
хитовых троек. Приведём все хитовые тройки для c < 1000 (их всего 31):
|
№
|
тройка
|
№
|
тройка
|
|
1
|
1
+ 8 = 9 >
r(1×23×32)
= 6
|
2
|
1
+ 48 = 49
> r(1×3×24×72)
= 42
|
|
3
|
1
+ 63 = 64
> r(1×(32×7)×26)
= 42
|
4
|
1
+ 80 = 81
> r(1×(24×5)×34)
= 30
|
|
5
|
5
+ 27 = 32
> r(5×33×25)
= 30
|
6
|
32
+ 49 = 81
> r(25×72×34)
=
42
|
|
7
|
3
+ 125 = 128
> r(3×53×27)
= 30
|
8
|
4
+ 121 = 125
> r(22×112×53)
= 110
|
|
9
|
1
+ 224 = 225
> r(1×(25×7)×(32×52)
= 210
|
10
|
1
+ 242 = 243
> r(1×(2×112)×35)
= 66
|
|
11
|
1
+ 288 = 289
> r(1×(25×32)×172)
= 102
|
12
|
2
+ 243 = 245
> r(2×35×(5×72)
= 210
|
|
13
|
7
+ 243 = 250
> r(7×35×(2×53))
= 210
|
14
|
13
+ 243 = 256
> r(13×35×28)
= 78
|
|
15
|
81
+ 175 = 256
> r(34×(52×7)×28)
= 210
|
16
|
100
+ 243 = 343
> r((22×52)×35×73)
= 210
|
|
17
|
32
+ 343 = 375
> r(25×73×(3×53))
= 210
|
18
|
169
+ 343 = 512
> r(132×73×29)
= 182
|
|
19
|
1
+ 512 = 513
> r(1×29×(33×19)) = 114
|
20
|
5
+ 507 = 512
> r(5×(3×132)×29)
= 390
|
|
21
|
27
+ 512 = 539
> r(33×29×(72×11)) = 462
|
22
|
49
+ 576 = 625
> r(72×(26×32)×54)
= 210
|
|
23
|
81
+ 544 = 625
> r(34×(26×17)×54)
= 510
|
24
|
200
+ 529 = 729
> r((23×52)×232×36)
= 690
|
|
25
|
1
+ 624 = 625
> r(1×(24×3×13)×54)
= 390
|
26
|
1
+ 675 = 676
> r(1×(33×52)×(22×132))
= 390
|
|
27
|
104
+ 625 = 729
> r((23×13)×54×36)
= 390
|
28
|
343
+ 625 = 968
> r(73×54×(23×112))
= 770
|
|
29
|
1
+ 728 = 729
> r(1×(23×91)×36)
= 546
|
30
|
25
+ 704 = 729
> r(52×(26×11)×36)
= 330
|
|
31
|
1
+ 960 = 961 > r(1×(26×3×5)×312) = 930
|
|
|
Смысл хитовости понятен: только хитовые тройки
могут дать контрпример к a×b×c-гипотезе,
поэтому именно на них нужно сосредоточить особое внимание. Можно ввести меру
хитовости a×b×c-тройки
: для a×b×c-тройки
(a;
b;
c)
положим
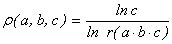
Ясно, что это равенство эквивалентно
следующим соотношениям:
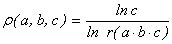Û
ln c = r×ln
r(a, b, c) Û
Û
c = er×ln
r(a, b, c) = (eln r(a,
b, c))r
Û
c = r(a, b, c)r(a,
b, c), r(a,
b, c) = log r(a, b, c) c
.
Оказывается, что все известные a×b×c-тройки
имеют ограниченную меру хитовости. Вот первые три тройки в хит-параде хитовых
троек:
. a
= 2, b
= 310×109,
c
= 235, r = 1,62991…
2. a
= 112, b
= 32×56×73,
c
= 221×23,
r = 1,62599…
3. a
= 19×1307, b
= 7×292×318,
c
= 28×322×54,
r = 1,62349…
Для примера приведём меры хитовости для всех
хитовых троек со значениями c
< 1000:
|
№
|
тройка
|
r
|
№
|
тройка
|
r
|
|
1
|
1
+ 8 = 9
|
1,22629…
|
2
|
1
+ 48 = 49
|
1,0412…
|
|
3
|
1
+ 63 = 64
|
1,11269…
|
4
|
1
+ 80 = 81
|
1,29203…
|
|
5
|
5
+ 27 = 32
|
1,01897…
|
6
|
32
+ 49 = 81
|
1,17571…
|
|
7
|
3
+ 125 = 128
|
1,42656…
|
8
|
4
+ 121 = 125
|
1,02719…
|
|
9
|
1
+ 224 = 225
|
1,01290…
|
10
|
1
+ 242 = 243
|
1,31110…
|
|
11
|
1
+ 288 = 289
|
1,22518…
|
12
|
2
+ 243 = 245
|
1,02882…
|
|
13
|
7
+ 243 = 250
|
1,03260…
|
14
|
13
+ 243 = 256
|
1,27279…
|
|
15
|
81
+ 175 = 256
|
1,03704…
|
16
|
100
+ 243 = 343
|
1,09175…
|
|
17
|
32
+ 343 = 375
|
1,10843…
|
18
|
169
+ 343 = 512
|
1,19875…
|
|
19
|
1
+ 512 = 513
|
1,31757…
|
20
|
5
+ 507 = 512
|
1,04562…
|
|
21
|
27
+ 512 = 539
|
1,02512…
|
22
|
49
+ 576 = 625
|
1,20396…
|
|
23
|
81
+ 544 = 625
|
1,03261…
|
24
|
1,00841…
|
|
25
|
1
+ 624 = 625
|
1,07904…
|
26
|
1
+ 675 = 676
|
1,09219…
|
|
27
|
104
+ 625 = 729
|
1,10484…
|
28
|
343
+ 625 = 968
|
1,03443…
|
|
29
|
1
+ 728 = 729
|
1,04586…
|
30
|
25
+ 704 = 729
|
1,13667…
|
|
31
|
1
+ 960 = 961
|
1,00479…
|
|
|
|
В связи с этим естественно возникают следующие
вопросы:
О верхней грани меры хитовости:
существует ли такое число g, что для всех a×b×c-троек
выполнено неравенство r(a,
b,
c)
£
g
?
О конечности числа a×b×c-троек
с высокой мерой хитовости: верно ли, что для
любого h > 1 существует лишь конечное число a×b×c-троек
со свойством r(a,
b,
c)
³
h,
и бесконечно много a×b×c-троек,
для которых выполнено 1 < r(a,
b,
c)
< h
?
Оба эти утверждения пока не доказаны, но и не
опровергнуты. Ясно, что из положительного ответа на второй вопрос следует
положительный ответ и на первый: если h
> 1 и лишь конечное число a×b×c-троек
имеют меры хитовости r1
, … , rk
больше
h, то можно взять g
= max{r1
, … , rk
} + 1. С другой стороны, положительный ответ на
второй вопрос эквивалентен справедливости a×b×c-гипотезы:
Теорема (об эквивалентных
формулировках a×b×c-гипотезы).
Следующие утверждения эквивалентны:
(1) a×b×c-гипотеза:
для любого e > 0 существует константа K(e)
> 0, для которой c
£
K(e)×r(a,
b,
c)1
+ e для любой a×b×c-тройки;
(2) для любого e
> 0 существует лишь конечное число хитовых a×b×c-троек
со свойством с > r(a,
b,
c)1
+ e ;
(3) для любого h > 1 существует
лишь конечное число a×b×c-троек
со свойством r(a,
b,
c)
³
h
.
Доказательство. (1) Þ (2) От
противного: пусть для некоторого e > 0 есть бесконечное множество хитовых a×b×c-троек {(ai ; bi ; ci )}i Î N со свойством
r(ai , bi , ci)1 + e < сi . По a×b×c-гипотезе для
числа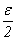 
найдётся
такая константа K =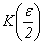 
, что ci £ K×r(ai , bi , ci)
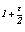, а значит,
будут верны неравенства r(ai , bi , ci)1 + e < ci £ K×r(ai , bi , ci) 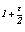, r(ai , bi , ci)
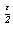< K, т.е.
ограничена последовательность {r(ai ; bi ; ci )}i Î N : r(ai , bi , ci) < K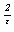 
. Поэтому
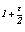ограничена последовательность {ci} i Î N : ci £ K×r(ai , bi , ci) < K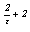 
, вопреки
бесконечности рассматриваемого множества хитовых троек.
(2) Þ (3) Пусть для
любого e > 0 существует
лишь конечное число хитовых a×b×c-троек со
свойством с > r(a, b, c)1 + e. Выбрав
число h > 1 и взяв e = h - 1, получим
набор хитовых троек (ai ; bi ; ci ) (1 £ i £ k),
удовлетворяющих неравенствам сi > r(ai , bi , ci)h . Если
тройка (a ; b ; c) имеет меру
хитовости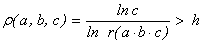 
, то c = r(a, b, c)r(a, b, c) > r(a, b, c)h, так что
любая такая тройка должна совпадать с одной из (ai ; bi ; ci ) (1 £ i £ k), что и
требовалось.
(3) Þ (1) Пусть для
любого h > 1 существует лишь конечное число a×b×c-троек со
свойством r(a, b, c) ³ h Û c = r(a, b, c)r(a, b, c) ³ r(a, b, c)h .
Зафиксировав произвольное e
> 0
и положив h = 1 + e, получим
лишь конечное число k = k(e) a×b×c-троек (ai ; bi ; ci ) (1 £ i £ k), удовлетворяющих
неравенствам сi ³ r(ai , bi , ci)h = r(ai , bi , ci)1 + e. Взяв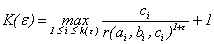 
, получим
сi < K(e)×r(ai , bi , ci)1 + e. Для
остальных хитовых a×b×c-троек
выполнены неравенства c £ r(a, b, c)1 + e < K(e)×r(a, b, c)1 + e. Таким
образом, из утверждения (3) следует a×b×c-гипотеза.
Теорема доказана.
Вера в правдоподобность a×b×c-гипотезы
укрепляется её справедливостью для многочленов и компьютерными расчётами. В
Интернете существует проект по проверке этой гипотезы (а также и некоторых
других) путём вычислений, распределённых по компьютерам многочисленных
пользователей. Справедливость a×b×c-гипотезы уже
проверена для всех натуральных чисел с несколькими десятками цифр. При этом не
только не найдено контрпримера, но и не превзойдёна максимальная мера хитовости
r = 1,62991… . Поэтому
не менее чем a×b×c-гипотеза
правдоподобно следующее предположение: для любой a×b×c-тройки
верно с < r(a, b, c)2, в котором
максимальная мера хитовости даже огрублена до двух. Это предположение будем в
дальнейшем называть (a×b×c)2
-гипотезой.
§ 4. Некоторые следствия abc-
и (abc)2- гипотез
. Великая теорема Ферма.
Диофантово уравнение xn
+ yn
= zn
не имеет натуральных решений x,
y,
z
Î
N
при n
> 2.
Доказательство.
От противного: пусть xn
+ yn
= zn
для
некоторых натуральных чисел x,
y,
z и n
> 2. По лемме об уравнении xn
+ yn
= zn
можно
считать, что НОД(x,
y)
= 1.
Тогда, числа xn
и
yn
тоже
взаимно просты, и обозначив a
= xn,
b
= yn
, c
= zn
получим a×b×c-тройку,
для которой, согласно (a×b×c)2-гипотезе,
выполняется цепочка неравенств:
zn = c < r(a×b×c)2
= r(xn×yn×zn)2
= r(x×y×z)2
£
(x×y×z)2
< (z3)2 = z6 .
Значит, n
< 6, что противоречит давно доказанным случаям
Великой теоремы Ферма для n
= 3, 4, 5.
Теорема доказана.
В этом доказательстве использована (a×b×c)2-гипотеза.
Если же пользоваться a×b×c-гипотезой,
то можно доказать справедливость Великой теоремы Ферма, начиная с некоторого
показателя n.
Действительно, согласно a×b×c-гипотезе
(см. теорему об её эквивалентных формулировках в прошлом параграфе) найдётся
такое h
> 1, что для любой a×b×c-тройки
верно неравенство c
< r(a,
b,
c)h.
Тогда, как и в приведённом выше доказательстве,
zn
= c
< r(a×b×c)h
= r(xn×yn×zn)h
= r(x×y×z)h
£
(x×y×z)h
< (z3)h
= z3×h
.
Значит, равенство xn
+ yn
= zn
может иметь место только при n
< 3×h,
что и утверждалось.
2. Уравнение Ферма-Каталана xk
+ ym
= zn
(2 £ k
£ m
£ n).
Это уравнение обобщает диофантово уравнение Ферма xn
+ yn
= zn
на
случай произвольных натуральных показателей.
При исследовании этого уравнения различают три
случая:
а)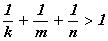 
, б) 
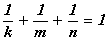, в)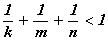 
.
Если в третьем случае неравенство
выполнено для многих значений k, m, n, то первые
два случая накладывают на эти значения серьёзные ограничения. Неравенство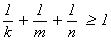 
, очевидно,
равносильно m×n + k×n + k×m ³ k×m×n, левая
часть которого не превосходит 3×m×n, что даёт
ограничение k £ 3, т.е. k = 2 или k = 3. Если k = 2, то 2×(m + n) ³ m×n Û (m - 2)×(n - 2) £ 4, т.е. либо m = 2, n ³ 2, либо m = 3, n £ 6. Если же k = 3, то 3×(m + n) ³ 2×m×n, и левая
часть не больше 6×n, а значит, m £ 3, т.е. m = 3 (m ³ k = 3) и n = 3.
Итак, случаи а), б)
имеют следующие описания:
а) 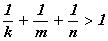Û (k; m; n) Î {(2; 2; n), (2; 3;
3), (2; 3; 4), (2; 3; 5)};
б) 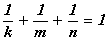Û (k; m; n) Î {(3; 3; 3),
(2; 4; 4), (2; 3; 6)}.
Оказывается, что в случае а)
каждое диофантово уравнение xk + ym = zn имеет
бесконечное число решений. Для того чтобы в этом убедиться, нужно для каждой из
выписанных троек степеней построить бесконечную серию решений. Например, для
уравнения x2 + y2 = z2×s+1 с нечётным n = 2×s + 1 можно взять x = a×(a2 + b2)s, y = b×(a2 + b2)s, z = a2 + b2 (a, b Î Z). Для
чётного значения n = 2×s решения
можно строить последовательно: если для уравнения x2 + y2 = zs уже
построена бесконечная серия (xp ; yp ; zp)p Î N решений, то
для уравнения x2 + y2 = z2×s можно взять
x = 2×xp×yp , y = xp2 - yp2, z = zp .
Для случая б) доказано, что
каждое диофантово уравнение xk + ym = zn имеет лишь
конечное число взаимно простых решений (НОД(x, y, z) = 1). Например,
уравнение x3 + y3 = z3 - это
уравнение Ферма и не имеет натуральных решений. Уравнение x2 + y4 = z4 аналогично
уравнению x4 + y4 = z2 ,
рассматривашемуся при доказательстве теоремы Ферма для показателя 4.
В случае в) из a×b×c-гипотезы
можно вывести следующую теорему (Nitaj, Abderrahmane La conjecture abc.
Enseign. Math., II. Ser. 42, No.1-2, 3-24 (1996).):
Теорема. Существует
лишь конечное число наборов (xk ; ym ; zn) со свойствами:
x, y, z Î N; НОД(x, y, z) = 1; xk + ym = zn ;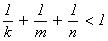 
; k, m, n ³ 2 .
Доказательство. Любой набор
(xk ; ym ; zn), очевидно,
определяет a×b×c-тройку с a = xk , b = ym , c = zn , причём
r(a×b×c) = r(xk×ym×zn) = r(x)×r(y)×r(z) £ x×y×z = (xk)1 / k×(ym)1 / m×(zn)1 / n =
= a1 /
k×b1
/ m×c1 / n < c1 / k×c1
/ m×c1 / n = c1 / h,
где h = .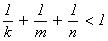
Поэтому c > r(a×b×c)h, т.е. любой
рассматриваемый набор определяет хитовую a×b×c-тройку с
мерой хитовости больше h. По a×b×c-гипотезе
таких троек лишь конечное число.
Теорема доказана.
В 1995 г. без использования a×b×c-гипотезы
была доказана следующая теорема Х. Дармона и А. Гранвилля (Darmon H., Granville A. On the equations zm = F(x,y) and A×xp + B×yq = C×zr. Bull. Lond. Math. Soc. 27, No.6, 513-543
(1995)):
Теорема. Для
любого набора (k ; m ; n), где 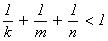; k, m, n ³ 2
диофантово уравнение xk + ym = zn имеет лишь
конечное число решений.
Ясно, что утверждение, выведенное
выше с использованием a×b×c-гипотезы,
значительно сильнее: оно утверждает глобальную конечность наборов, в отличие от
конечности числа решений каждого уравнения.
В частности, доказана и гипотеза
Каталана: диофантово уравнение Каталана 1 + ym = zn имеет лишь
конечное число решений. Ранее эта гипотеза была доказана без
использования a×b×c-техники
Преда Михайлеску (Preda Mihăilescu Primary cyclotomic units and
a proof of Catalan's conjecture, J. Reine Angew. Math. 572 (2004), 167-195).
Следует отметить, что на сегодняшний
день известны лишь следующие решения уравнения xk + ym = zn :
1k + 23
= 32, 132 + 73 = 29, 27
+ 173 = 712, 25 +72 = 34,
35 +114 = 1222,
7
+762713 = 210639282, 14143 + 22134592
= 657, 338 + 15490342 = 156133
8
+ 962223 = 300429072, 92623 + 153122832
= 1137.
. Гипотеза
Морделла (1922 г.). Пусть задан многочлен f(x,
y)
степени
n > 1 от
двух переменных x,
y с
комплексными коэффициентами. Тогда алгебраическое уравнение f(x,
y)
= 0
задаёт алгебраическую кривую, которую можно превратить (путём некоторой
компактификации) в риманово многообразие и рассмотреть род g
этого
многообразия. Долгое время оставалась недоказанной следующая гипотеза Морделла:
если g
³ 2, то на
рассматриваемой кривой с уравнением f(x,
y)
= 0
лишь конечное число рациональных точек, т.е. точек с рациональными
координатами (Mordell
L. J.
On the
rational
solutions
of the
indeterminate
equations
of the
third and
fourth degrees.
Cambr. Phil. Soc. Proc. 21, 179-192 (1922)).
Особо важен случай гладкой кривой :
кривая с уравнением f(x,
y)
= 0
называется гладкой, если система алгебраических уравнений
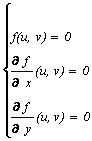
не имеет решений. Оказывается, что в
этом случае род кривой вычисляется просто: g =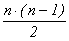 
. Таким
образом, проверка конечности числа рациональных точек превращается с помощью
гипотезы Морделла в чисто алгебраическое упражнение.
Примеры: 1.
Для кривой с уравнением xn + yn = 1, которая
тесно связана с уравнением Ферма xn + yn = zn, имеем f(x, y) = xn + yn - 1 и система
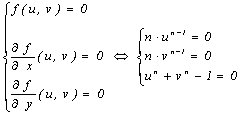
не имеет решений. Таким образом,
кривая гладкая, её род g = > 2 при n > 2, так что на
ней лежит лишь конечное число рациональных точек. Отсюда легко вывести, что
уравнение Ферма имеет конечное число взаимно простых нетривиальных решений.
2. Кривая с уравнением x2 + y2 = 1 гладкая, но
её род g = 1, так что на
ней лежит бесконечно много рациональных точек
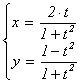(t Î R).
. Кривая с уравнением x + y = 2 гладкая, но
её род g = 0, на ней
лежит бесконечно много рациональных точек
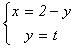(t Î R).
. Кривая с уравнением x + y = 0 не гладкая
(гладкости нет при x = 0 = y). На ней
бесконечно много рациональных точек.
Гипотеза Морделла была доказана Г.
Фалтингсом в 1984 г. ещё до появления a×b×c-гипотезы (Faltings G. Die Vermutungen von Tate und Mordell // Jahresber. Deutsch. Math.-Verein. 86 (1984),
no. 1, 1-13.). Это был революционный прорыв в изучении алгебраических кривых.
В 1991 г. Ноам Элкис доказал, что
гипотеза Морделла следует из a×b×c-гипотезы.
Более того, с её помощью можно получить эффективные оценки высоты рациональных
точек на алгебраических кривых (Elkies Noam D. abc implies Mordell. Int. Math. Res. Not. 1991, No.7, 99-109
(1991)).
4. Диофантово уравнение pv - pw = qx - qy имеет лишь
конечное число решений. Здесь p, q - различные
простые числа, v, x, w, y Î N. В 2003 г.
Флориан Люка (Luca) показал,
что из a×b×c-гипотезы
следует конечность числа наборов (p; q; v; w; x; y),
удовлетворяющих этому уравнению (Luca F. On the Diophantine equation
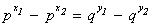// Indag.
Math., New Ser. 14, No. 2, 207-222 (2003)).
5. Теорема Туэ-Зигеля-Рота.
В 1955 г. Клаусом Ротом (Klaus Roth) была
доказана следующая теорема: для любого алгебраического числа a и n > 2
неравенство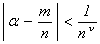 
имеет лишь
конечное число несократимых решений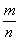 
. Эта теорема придала окончательную
форму исследованиям, начатым в своё время Дирихле, Туэ и Зигелем.
В 1994 г. Энрико Бомбьери доказал,
что эта мощная теорема является следствием a×b×c-гипотезы (Bombieri, E. Roth's theorem and the abc conjecture // preprint (1994), см.
также van Frankenhuysen M. The abc conjecture implies Roth's theorem and Mordell's conjecture // Math. Contemporanea, 76, 45-72
(1999)). Он получил и эффективную оценку: для любого алгебраического числа a существует
такая константа C = C(a), что
неравенство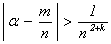 
выполнено
при k ³ C(a)×(ln n) -1 /
2× (ln (ln n)) -1.
6. Проблема Брокарда (Brocard): Какие
решения имеет диофантово уравнение n ! + 1 = m2 ? Его решения
называются парами Брауна (Brown). Очевидно, что решения есть: n = 4, m = 5; n = 5, m = 11; n = 7, m = 71. Есть ли
другие решения ?
С помощью a×b×c-гипотезы
удалось доказать, что это диофантово уравнение имеет лишь конечное число
решений, т.е. пар Брауна лишь конечное число (см. Nitaj, Abderrahmane
La conjecture abc. (The abc conjecture) // Enseign. Math., II. Ser. 42, No.1-2,
3-24 (1996), Overholt, Marius The diophantine equation n! + 1 = m2
// Bull. Lond. Math. Soc. 25, No.2, 104 (1993), Dabrowski, Andrzej On the
diophantine equation x! + A = y2 // Nieuw Arch. Wiskd., IV.
Ser. 14, No. 3, 321-324 (1996)).
7. Простые числа Вифериха
(Wieferich). Простое число p называется простым
числом Вифериха, если p2 делит 2p - 1 - 1. Эти числа,
как ни странно, возникали при доказательствах Великой теоремы Ферма, но их
очень мало: среди простых чисел меньших 4.000.000.000.000, всего два
числа Вифериха - 1093 и 3511. Отметим, что p | 2p - 1 - 1 для любого
нечётного p ввиду малой
теоремы Ферма.
В 1988 г. Джозефом Сильверманом (Silverman) было
доказано, что a×b×c-гипотеза
подтверждает наличие “малого” количества простых чисел Вифериха: для любого a Î N существует
бесконечно много простых чисел p со
свойством p2 не делит a p - 1 - 1 (Silverman, Joseph H. Wieferich's criterion and the abc-conjecture // J. Number Theory 30, No. 2, 226-237
(1988)).
8. Слабая гипотеза Маршалла
Холла: Для любого e > 0 существует такая константа С(e) > 0,
что если для натуральных x и y верно x3 ¹ y2 , то |x3 - y2|> C(e)×max(x3, y2)
(Nitaj, Abderrahmane La conjecture abc. (The
abc conjecture) // Enseign. Math., II. Ser. 42, No.1-2, 3-24 (1996), см.
также
Schmidt, Wolfgang M. Diophantine approximations and diophantine equations //
Lecture Notes in Mathematics. 1467. Berlin etc.: Springer-Verlag. viii, 217 p. (1991)).
9. Гипотеза Эрдёша (Erdös) о
последовательных степенных целых числах. Натуральное число называется степенным,
если любое простое число участвует в его каноническом разложении с показателем 2
или выше. Нетрудно понять, что любое степенное число представимо в виде A2×B3 для
некоторых натуральных A, B. Гипотеза
Эрдёша предполагает, что не существует трёх последовательных степенных чисел.
a·b·c-гипотеза
позволяет доказать более слабое утверждение: множество троек
последовательных степенных чисел конечно.
Можно доказать, что конечно и множество
степенных троек, являющихся последовательными членами арифметической прогрессии
и взаимно простыми с разностью этой прогрессии. Действительно, предположив,
что есть тройка n,
n + k,
n + 2×k
степенных
чисел, где НОД(n,
k)
= 1,
можно положить a
= k2,
b
= n·(n
+ 2×k)
= n2
+ 2×k×n
, причём
НОД(a,
b)
= НОД(k2
, n2
+ 2×k×n)
= НОД(k2
, n×(n
+ 2×k))
= 1,
т.к. НОД(n, k) = 1 = НОД(k , n + 2×k). Итак,
получена a·b·c-тройка вида:
a = k2, b = n·(n + 2×k) = n2 + 2×k×n, c = (n + k)2
= n2 + 2×k×n + k2. Тогда с
учётом того, что r(A2×B3) = r(A×B) £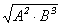 
, получим
,
.
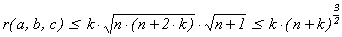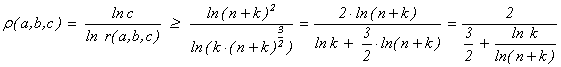При фиксированном k и стремлении
n к
бесконечности, отношение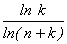 
стремится к
0. И тогда при больших n получим
хитовые a×b×c-тройки с
мерой хитовости r ³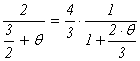 
> 1 при
любом сколь угодно малом q
> 0 .
Таких троек по a×b×c-гипотезе
лишь конечное число.
10. Свободные от квадратов значения
многочленов.
До сих пор не было известно ни одного неразложимого многочлена f(x) степени не
меньше 5 с целыми коэффициентами, у которого значения f(n) (n Î N) свободны от
квадратов (т.е. являются произведениями различных простых чисел) для бесконечно
многих n. Бровкин
Д., Филасета М., Гривс Г. и Скинзель А. (Browkin J., Filaseta M., Greaves G., Schinzel A.) доказали,
что a×b×c-гипотеза
позволяет утверждать, что этим свойством обладают многочлены деления круга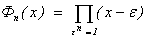 
и f(x) = 
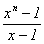= xn-1 + xn-2 + … +
x + 1 (см.
Browkin J., Filaseta M., Greaves G., Schinzel A. Squarefree values of polynomials
and the abc-conjecture // Greaves, G. R. H. (ed.) et al., Sieve methods,
exponential sums, and their applications in number theory. Proceedings of a
symposium, Cardiff, UK, July 17-21, 1995. Cambridge: Cambridge University
Press. Lond. Math. Soc. Lect. Note Ser. 237, 65-85 (1997)).
11. Гипотеза Чинзеля-Тиджемана
(Schinzel-Tijdeman). Эта гипотеза утверждает, что если
многочлен p(x) с
рациональными коэффициентами имеет по крайней мере 3 простых корня, то
диофантово уравнение p(x) = y2×z3 имеет лишь
конечное число нетривоальных решений (x; y; z). В
1999 г.
П.
Уолш
(Walsh) доказал,
что это следует из a×b×c-гипотезы
(Walsh P.G. On a conjecture of Schinzel and Tijdeman // Gyoery, Kalman (ed.) et
al., Number theory in progress. Proceedings of the international conference
organized by the Stefan Banach International Mathematical Center in honor of
the 60th birthday of Andrzej Schinzel, Zakopane, Poland, June 30-July 9, 1997.
Volume 1: Diophantine problems and polynomials. Berlin: de Gruyter. 577-582
(1999)).
12. Задача округления.
Пусть
x - положительное
вещественное число. Тогда для правильного округления числа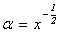 
в n-битовой
арифметике нужно вычислить 3×n + 1 старших
битов. В 2004 г. Э. Крут, Р. Ли и Х. Джунь доказали, что использовав a×b×c-гипотезу,
можно ограничиться 2×n старшими
битами (Croot E., Li R., Zhu H. The abc conjecture and correctly rounded reciprocal square roots // Theor. Comput. Sci. 315, No. 2-3,
405-417 (2004)).
ЗАКЛЮЧЕНИЕ
В результате выполнения дипломной
работы были достигнуты все поставленные во введении цели:
§ изучены основные понятия и результаты, связанные
с теорией диофантовых уравнений, теорией эллиптических кривых и a×b×c-гипотезой;
§ изучены метод бесконечного спуска и на его
основе доказательство теоремы Ферма для n
= 4;
§ изложены идеи доказательств Эйлера для n
= 3
и суть идей Куммера;
§ изложено вывод К. Рибета Великой теоремы Ферма
из гипотезы Таниямы;
§ изучены некоторые результаты об a×b×c-гипотезе
и вывод из неё Великой теоремы Ферма;
§ теоретические результаты проиллюстрированы
примерами;
§ результаты изложены, по возможности, полно,
подробно, доступно пониманию студентов математических факультетов вузов.
Дипломная работа имеет теоретическое значение. В
ней сделаны лишь первые шаги по осмыслению подходов к доказательству Великой
теоремы Ферма: хотя в работе нет новых, не известных специалистам
математических результатов, но она даёт по возможности связное и обоснованное
описание трудных, разнородных и разбросанных в литературе методов и идей.
Представленное изложение материала по силам студентам математических
факультетов вузов, а некоторые разделы работы - даже школьникам старших
классов. Поэтому дипломная работа может быть использована в качестве учебного
материала для изучения вопросов, связанных с представленными в ней темами, в
учебных курсах и спецкурсах для студентов физико-математических специальностей
вузов и на факультативных занятиях в школах.
Работа по изучению доказательства Великой
теоремы Ферма может быть продолжена в дальнейшем.
ЛИТЕРАТУРА
1. Боревич З.И., Шафаревич
И.Р. Теория чисел. - М.: Наука, 1972.
2. Бухштаб А.А. Теория чисел.
- СПб: Издательство “Лань”, 2008.
3. Дэвенпорт Г. Высшая
арифметика. - М., 1965.
4. Серпинский В. О решении
уравнений в целых числах. - M., 1961.
5. Эдвардс Г. Последняя
теорема Ферма. Генетическое введение в алгебраическую теорию чисел. - М.: Мир,
1980.
6. Wiles A. Modular
Elliptic Curves and Fermat’s Last Theorem // Annals of Math., 1995, Vol. 141,
P. 443-552.
7. Wiles A., Taylor R.
Ring theoretic properties of certain Hecke algebras // Annals of Math., 1995,
Vol. 141, P. 553-572.
8. Гипотеза АВС // Электронный
ресурс. - Режим доступа:://mindspring.narod.ru/math/ega/Lang/HypotABC.htm
9. Математическая энциклопедия
[Электронный ресурс] / ООО “РМГ Мультимедиа”. - Электрон. текстовые и граф.
дан. - М.: РМГ Мультимедиа, Большая Российская Энциклопедия, 2006. - (М: ООО
“РМГ Компании”, 2006). - 2 электронных опт. диска (CD-ROM).
- Систем. требования: Wn
98/Me/2000/XP,
Pentium 166, 64 Mb
RAM.
10. Следствия из гипотезы о
тройках АВС // Электронный ресурс. - Режим доступа: http://boinc.ru/doc/abc/abc_conjecture.ru/consequences.html