Экстремальные коды

Московский Институт Радиотехники, Электроники и Автоматики

(Технический университет)

Контрольная работа

по дисциплине

"Теория кодирования и информации"

на тему: "Экстремальные коды"

Выполнила: студентка гр. ВИ-1-07

Терёхина Юлия

Москва 2010

Содержание

Введение

Границы для параметров кодов

Заключение

Список используемой литературы

Введение

Целью моей работы, является рассмотрение так называемых "экстремальных кодов", то есть коды, границы параметров которых достигают равенства.

Границы для параметров кодов

Способность кода корректировать ошибки находится в прямой зависимости от величины кодового расстояния - хорошие корректирующие свойства обеспечиваются большим кодовым расстоянием и наоборот. Для построения кодов с большим кодовым расстоянием требуется вводить много проверочных символов, не передающих информацию от источника к адресату, а выполняющих вспомогательную роль. Наличие большого числа проверочных символов при фиксированной длине кодового слова уменьшает число информационных символов, а следовательно, и скорость передачи информации Таким образом, хорошие корректирующие свойства кода и высокая скорость передачи информации - требования противоречивые. Поэтому задача построения кодов с приемлемыми значениями d и R - задача оптимизации, не имеющая единственного решения. Параметры n,k,d, характеризующие код, не могут принимать произвольных значений. Нетрудно видеть, что:

среди кодов с одинаковыми параметрами n и k лучшим является код, который имеет больше кодовое расстояние d,

среди кодов с одинаковыми параметрами n и d лучшим является код, который имеет большее число информационных символов k,

среди кодов с одинаковыми параметрами k и d лучшим является код, который имеет меньшую длину n, а следовательно, и меньшее число проверочных символов.

Между рассмотренными параметрами n,k,d существуют определённые соотношения, задаваемые границами для кодового расстояния

или для скорости передачи информации. Различают верхние и нижние границы;

k - длина вектора, который кодируем

d - кодовое расстояние.

n - длина закодированного вектора.

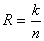 - скорость передачи информации кода.

) Если фиксированы n, k, то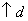

) Если фиксированы n, d, то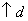

) Если фиксированы k, d, то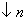

Теорема 1. (Верхняя граница Хемминга)

В теории кодирования <#"553017.files/image005.gif"> - оценка для d

Док-во: для 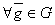 рассмотрим множество:

,

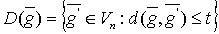
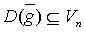
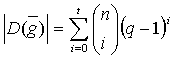
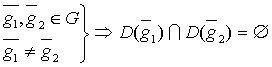
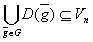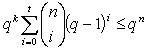
Следствие:

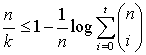 - верхняя граница для d и для R

Возможна такая ситуация:

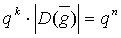
Равенство имеет место только для совершенных двоичных кодов.

Совершенный код обладает замечательным свойством: шары радиуса t с центрами в кодовых точках совершенного кода не пересекаются и одновременно заполняют всё пространство V_n.

Определение. Код, для которого справедливо:

,

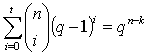называется совершенным (или плотноупакованным). Например, код кратных повторений, двоичный код Хемминга (7,4)

Двоичный код с повторениями при нечетной блоковой длине n исправляет вплоть до (n - 1) /2 ошибок. Для t = (n - 1) /2 и R = 1/n имеем

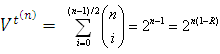
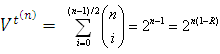
Таким образом, двоичный код с повторениями и нечетной блоковой длиной является совершенным, все другие совершенные коды должны иметь либо большую скорость передачи, либо малую блоковую длину. (*) описывает класс совершенных кодов с большой скоростью и малой корректирующей способностью (t = 1)

(*): В метрике Хемминга совершенный систематический код с исправлением одной ошибки и блоковой длиной n над алфавитом из q существует тогда и только тогда когда n =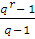

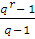
Совершенные коды

Коды плотноупакованные - коды, которые имеют число синдромов, точно равное их необходимому числу, позволяют исправить все однократные ошибки в любом информативном и проверочном символах и включают один нулевой синдром.

К совершенным кодам относятся, например, коды Хемминга <#"553017.files/image003.gif">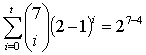 

получим верное равенство:

=2³ 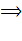 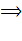код является экстремальным

 или  

Проверочная матрица любого кода Хэмминга всегда содержит минимум три линейно зависимых столбца, поэтому кодовое расстояние кода равно трем.

Если столбцы проверочной матрицы представляют упорядоченную запись десятичных чисел, т.е.1,2,3. в двоичной форме, то вычисленный синдром 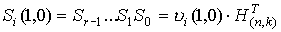 однозначно указывает на номер позиции искаженного символа.

Определение. Двоичный код с длиной блока n = 2^r-1, проверочной матрицей H_{r (}rxn), образованной всеми ненулевыми векторами из V_r (GF (2)), расположенными в порядке возрастания чисел, двоичные разложения которых совпадают с рассматриваемыми столбцами, называется двоичным кодом Хемминга.

Введённый (n = 2^r - 1, k = 2^r - 1 - r) - код будем обозначать Н_r.

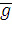
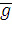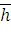
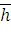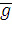
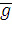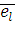
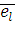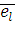
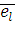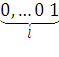
Рассмотрим процедуру декодирования для кодов Хемминга. Пусть произошла ошибка в i-м символе передаваемого кодового слова . Подсчитаем синдром полученного вектора:  =  + , где , = ( 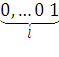0,…, 0)

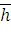
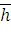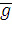
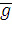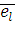
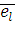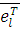
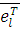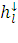
S () = Hh^-T = H ( + ) ^T = H= 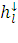(1)

Следовательно, если произошла одна ошибка, то синдром S (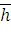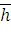) в двоичной записи указывает номер столбца, в котором произошла ошибка. Соотношение (1) задаёт изящный и очень простой способ декодирования. Из свойств кода исправлять одну ошибку следует, что кодовое расстояние d 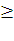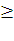3. Заметим, что вектор (1110,.,0) принадлежит Н_r, что проверяется умножением на проверочную матрицу.

Следовательно, d = 3.

Код Хэмминга используется в некоторых прикладных программах в области хранения данных; кроме того, метод Хемминга позволяет "на лету" исправлять однократные и обнаруживать двукратные ошибки.

При использовании совершенных кодов всегда возможна коррекция ошибок (не обязательно правильная). Помимо кодов Хэмминга, в настоящее время известно мало совершенных кодов.

Теорема 2. (Верхняя граница Плоткина)

Если существует q-ичный блоковый код с числом слов М и кодовым расстоянием d, то справедливо:

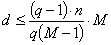
Пример: 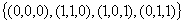, а также код кратных повторений.

Эквидистантные коды

Теорема. Каждое ненулевое кодовое слово циклического регистрового кода максимальной длины является циклическим сдвигом любого другого ненулевого кодового слова. Таким образом, в метрике Хэмминга все регистровые коды максимальной длины, являются эквидистантными.

Блочные эквидистантные коды с произвольным основанием q, в которых расстояние (Хэмминга) d строго достигает верхней границы, возможной при заданных q, числе кодовых слов M и длине кодового слова n. Такие коды именуются сокращенно EDm - кодами (q, M, n, d).

EDm - Коды интересны, в частности, по следующим причинам. Они составляют экстремальный класс q-ичных кодов. EDm - Коды можно использовать для построения других кодов с разными основаниями вплоть до q = 2.

Рассмотрим код с параметрами q, M, n, d. EDm - коды с d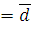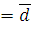_m и M= qt следующим образом:

Для достижения целочисленности 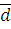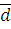_m:

так как 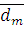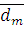= nM (q-l) / (M-l) q = nt (q - 1) / (qt - 1) (*),

то n = c (qt - 1) / (q - 1, t - 1), где с 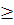 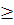1 - целое.

В EDm - кодах расстояние точно достигает (*), любой

из q символов повторяется в каждом столбце точно t раз, t 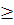 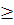1, и параметры имеют вид:

M = qt, n, d = nt (q - 1) / (qt - 1).

Из соотношений получаем, что параметры EDm - кодов всегда могут быть представлены в виде:

M = qt, n = c (qt - 1) / (q - 1, t - 1), d = ct (q - 1) / (q - 1, t - 1).

Тривиальным случаем является код с t = 1 с произвольным n и d = n.

Здесь каждое из q слов содержит n-кратное повторение одного из q символов.

Отметим, что имеются значения параметров t и q, для которых EDm-код при с = 1 не существует, но существует при некотором с > 1. Например,

при t = 3, q = 2 код с параметрами M = 6, n= 5, d = 3, соответствующий

значению с = 1, не существует.

Однако имеется EDm - код с с = 2 и параметрами M = 6, n = 10, d = 6

0 0 0 0 0 0 0 0 0

0 0 0 1 1 1 1 1 1

1 1 1 0 0 0 1 1 1

0 1 1 0 1 1 0 0 1

1 0 1 1 0 1 0 1 0

1 1 0 1 1 0 1 0 0

Подставим эти параметры в

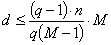
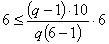
Получим верное равенство 6=6 код с таким параметрами является эквидистантным.

Тривиальным примером эквидистантного кода является код [n,1,n] _{Ω -} код с повторениями (или код констант).

Код с повторениями (или код констант)

Пусть Ω - произвольное конечное множество. Код K = { (a,…,a): a ∈Ω} есть [n,1,n] _{Ω -} код.

Пример. Пусть q = 2, n = 5. Рассмотрим код G, состоящий из двух

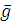
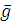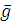
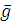кодовых слов ₀ = (00000),  ₁= (11111). Этот код предназначен для

кодирования двоичной информации. Он обладает большой

помехозащищенностью, но очень малой скоростью передачи

информации. На один информационный - полезный символ в кодовом

слове приходится 4 проверочных символа. Введённый код

называется кодом кратных повторений.

Пусть q = 2, n = 5.

=

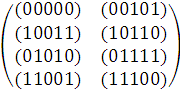
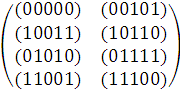
Очевидно, что код G - подпространство V₅ (GF (2)). Ненулевое слово минимального веса - (00101). Кодовое расстояние кода G равно 2.

Другим простым примером является код Σ₂= { (000), (110), (101), (011) }. Если отметить вершины единичного куба, соответствующие кодовым словам кода Σ_2, и соединить их, то построенная фигура будет представлять симплекс. Это и даёт основание назвать код Σ₂ симплексным. Другими примерами эквивидистантных кодов являются коды, построенные с использованием матриц Адамара, коды, составленные из последовательностей максимальной длины.

Эквидистантные двоичные коды из K слов с блоковой длиной K-1 могут быть построены на основе матрицы Адамара.

Матрицей Адамара называется ортогональная (K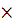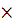K) - матрица, элементами которой являются числа +1 и - 1. Например:

H₂ =  =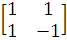

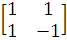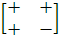
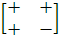
H₄ =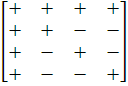

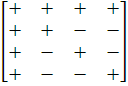
Без потери общности можно предположить, что все элементы первой строки и первого столбца матрицы Адамара равны +1. Отбрасывая первый столбец (K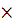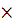K) - матрицы Адамара, получим K строк длины K-1, образующих двоичный эквидистантный код. Если K не есть степень числа 2, то получается нелинейный код.

Теорема 3. (Нижняя граница Варшамова - Гилберта).

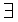 (n, k) - код (линейный) с минимальным кодовым расстоянием d, параметры которого удовлетворяют неравенству:

.

 -

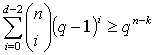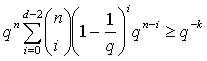вероятность получить не более (d-2) успехов в схеме Бернулли.

Граница Варшамова - Гильберта является границей существования и дает нижнюю оценку кодового расстояния для "наилучшего" кода.

Теорема 4. (Оценка Чернова для биномиальных коэффициентов).

Пусть 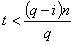, то справедливо:

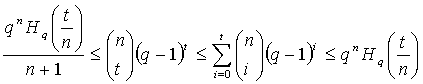
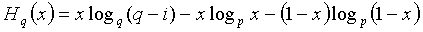
Из этих неравенств следует:

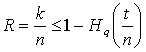) , d = 2t + 1

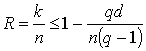)  - следует из гр. Плоткина в случае лин. кода

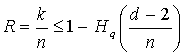)  - из гр. Варшамова-Гилберта

Заключение

Применение кодов

Первым кодом, исправляющим ошибки, который стал применяться в вычислительных машинах, был разработанный еще на заре теории кодирования в 1950 г. код Хэмминга. Этот код был разработан специально для применения в вычислительных машинах. Код Хэмминга стал применяться в вычислительных машинах не сразу, и это объясняется тем, что после появления кода Хэмминга постоянно совершенствовались сами запоминающие элементы; сначала использовались электронные лампы, далее появились параметроны, полупроводниковые элементы и наконец интегральные схемы. При этом надежность запоминающих элементов постоянно и быстро росла. Первой вычислительной машиной, в которой использовался код Хэмминга, была вычислительная машина IBM 7030, а в Японии - машина DIPS фирмы Japan Telephone and Telegraph Public. Однако если первая была построена спустя 10 лет после появления кода Хэмминга, то вторая - спустя 20 лет. До этого времени в вычислительных машинах использовался лишь простейший способ повышения надежности, а именно проверка на четность (или нечетность)

Код кратных повторений, который является эквидистантным кодом, предназначен для кодирования двоичной информации. Он обладает большой помехозащищенностью, но очень малой скоростью передачи информации.

В последние годы различные достаточно сложные коды, исправляющие большое число ошибок, начали применяться как в самих вычислительных машинах, так и в периферийном оборудовании, в частности в накопителях на магнитной ленте. По мере развития вычислительной техники коды, исправляющие ошибки, будут играть всё большую роль в повышении надежности вычислительных систем.

Технология применения кодов в современных условиях преследует цели защиты информации, сокращения трудозатрат и обеспечение быстроты ее обработки, экономии компьютерной памяти, формализованного описания данных на основе их систематизации и классификации.

экстремальный код равенство параметр

Список используемой литературы

1. А. А. Духин "Теория информации", Москва, Гелиос АРВ, 2007 г.

. Н.В. Семаков, В.А. Зиновьев "Эквидистантные q-ичные коды с  максимальным расстоянием и разрешимые уравновешенные блок-схемы" (1967 г.)