Расчет механической части воздушных линий электропередачи
Введение
Энергетика России с момента принятия плана
ГОЭЛРО в 1920г. Строилась как единое целое на плановой основе. Заложенные в
Плане ГОЭЛРО энергетических мощностей, централизация управления были ведущими
на все последующие семь десятилетий развития энергетики. Созданная в результате
этого Единая энергосистема и сейчас успешно обслуживает народное хозяйство
страны.
Линии электропередач составляют основу
энергосистемы. Они состоят из воздушных линий (ВЛ) основной и распределительной
сети. ВЛ основной сети обеспечивают связь между крупными электростанциями и
передачу мощности от них в районы потребления электроэнергии. ВЛ
распределительной сети обеспечивают передачу электроэнергии от подстанций (ПС)
основной сети и электростанций к потребителям энергии.
При проектировании основной электрической сети
энергосистем рекомендуется:
намечать линии электропередачи через крупные
узлы нагрузки, избегать прямых связей между электростанциями;
производить выбор схемы присоединения
электростанции и ПС к основной сети с учетом надежности питания узла
электрической сети и необходимости обеспечения транзита мощности по ВЛ;
сооружать между двумя узлами сети по одной
трассе, как правило, не более двух линий электропередачи одного напряжения. При
необходимости дополнительного усиления сети следует рассматривать
целесообразность сооружения ВЛ по другим направлениям или выполнение
электропередачи на более высоком напряжении.
Проектирование распределительной сети
энергосистем осуществляется с учетом следующего:
в районах с малым охватом территории сетями при
близких значениях технико-экономических показателей вариантов развития сети
рекомендуется отдавать предпочтение сооружению ВЛ по новым трассам;
в крупных городах и промышленных районах с
большой концентрированной нагрузкой по одной трассе может предусматриваться
строительство двух и более ВЛ;
при прохождении ВЛ по территории городов,
промышленных районов, на подходах к электростанциям ПС, в стесненных условиях,
лесных массивах и т. д. ВЛ рекомендуется выполнять на двухцепных опорах. При
этом подвеска одной цепи рекомендуется в случае, когда необходимость ввода
второй цепи возникает на время более трех лет после ввода первой, а также когда
отключение первой цепи на время проведения работ по подвеске второй допустимо
по условиям электроснабжения. Допускается подвеска на одних опорах ВЛ разных
классов напряжений;
при питании ПС с потребителями первой категории
применение двух одноцепных ВЛ вместо одной двухцепной допускается при наличии
обоснований.
При развитии распределительных сетей отдельных
номинальных напряжений необходимо учитывать следующие рекомендации.
При напряжении сети 220-330 кВ:
использовать в сети одно- и двухцепные ВЛ
220-330 кВ;
при питании ПС по одноцепной ВЛ с двухсторонним
питанием общее число промежуточных ПС не должно превышать трех, а длина такой
ВЛ, как правило, не должно быть больше 250 км;
присоединять к двухцепной ВЛ 220 кВ с
двухсторонним питанием до пяти промежуточных ПС. При этом присоединение ПС
рекомендуется принимать по схеме «мостик» или блочной схеме (от одной или двух
ВЛ 220 кВ);
проектировать цепь 220-330 кВ внешнего
электроснабжения крупных и крупнейших городов с использованием принципа
кольцевой конфигурации. В системе электроснабжения таких городов рекомендуется
предусматривать сооружение не менее двух ПС 220-330 к В, через которые
осуществляется связь с сетью энергосистемы, а питающие ВЛ рекомендуется
прокладывать по разным трассам. При присоединении сети крупных и крупнейших
городов к энергосистеме рекомендуется обеспечивать минимальные транзитные
перетоки мощности через городскую сеть. Общее количество и пропускная
способность линий, связывающих сети таких городов с энергосистемой,
рекомендуется выбирать с учетом обеспечения питания городских потребителей без
ограничения двухцепной питающей ВЛ 220 кВ;
выполнять, как правило, ПС 220-330 кВ
двухтрансформаторными.
В данном дипломном проекте рассмотрено
проектирование новой воздушной линии 220 кВ, которая должна обеспечить покрытие
возрастающей нагрузки на севере Томской области, а также увеличить надежность и
экономичность сети.
1. Основы расчета и проектирования механической
части воздушных линий электропередачи
1.1 Исходные положения и задачи расчета
Проектирование конкретной линии электропередачи
ведется на основании разработанной схемы развития электрической системы. В
задании на проектирование указываются пункты начала и конца линии, номинальное
напряжение, число цепей, марка проводов, материал опор. На основании
предварительных изысканий трассы для рабочего проектирования линии
устанавливаются также расчетные климатические условия: толщина стенки гололеда,
максимальная скорость ветра, высшая, низшая и среднегодовая температуры.
Воздушные линии сооружаются преимущественно на
унифицированных опорах, при этом нет необходимости для каждой проектируемой
линии разрабатывать конструкцию опор. Поэтому при проектировании должны
решаться следующие вопросы: рациональный выбор и применение унифицированных
опор, прочностной расчет проводов и тросов в нормальных и аварийных режимах,
расстановка опор по профилю трассы линии.
В механический расчет воздушных линий
электропередачи входят:
· Расчет опор и их фундаментов;
· Расчет проводов и грозозащитных
тросов.
Задача механического расчета проводов и тросов
состоит в обеспечении прочности и габаритов для следующих условий:
) нормального режима работы ВЛ, под которым
понимается состояние ВЛ при необорванных проводах и тросах;
) аварийного режима работы, который
характеризуется оборванными одним или несколькими проводами или тросами. При
этом проверяются тяжение и стрелы провеса в пролетах, смежных с аварийным;
) монтажного режима, характеризующегося
состоянием в условиях монтажа опор, проводов и тросов;
) режим работы ВЛ, связанных с возможными
приближениями проводов к элементам опор и сооружения по рабочему напряжению,
возможными внутренними и атмосферными перенапряжениями.
Расчет производится в следующей
последовательности:
1. Выбор материалов и конструкций проводов,
тросов и поддерживающих зажимов.
2. Выбор схемы размещения проводов и тросов
на опорах.
. Выбор материалов опор и основного типа
опор для ВЛ.
. Выбор расчетного пролета линии.
. Определение напряжений в материале и
стрел провеса проводов и тросов в нормальном режиме работы (систематический
расчет), в том числе для наихудших условий.
. Определение тяжений по проводам и
тросам при обрыве части из них.
. Расчет переходов через инженерные
сооружения в нормальном и аварийном режимах.
. Расчет габаритов провода до элементов
опоры, зданий и сооружений под воздействием ветра.
. Расчет габаритов между проводами и тросами
по условиям грозозащиты.
. Расстановка опор по трассе ВЛ.
. Расчет монтажных стрел провеса
(монтажных кривых).
В соответствии с ПУЭ [3], механический расчет
проводов и тросов производится по методу допустимых напряжений. В его основу
положены нормируемые допустимые напряжения в материале провода при различных
условиях с учетом возможных деформаций провода (троса) при его растяжении.
На воздушных линиях могут встретиться пролеты
различной длины, что обусловлено рельефом местности, наличием различных преград
и пересекаемых инженерных сооружений и пр. Поэтому по известным исходным данным
применительно ко всем необходимым расчетным режимам работы линии заранее
выполняют расчет провода заданной марки для всего диапазона длин пролетов,
которые могут получиться на данной линии, называемый систематическим расчетом.
Он дает информацию о механическом напряжении в проводе и стрелах провеса при
решении различных задач, возникающих в процессе проектирования механической
части линии.
Систематический расчет проводов выполняют в
такой последовательности:
. Определяют удельные нагрузки, действующие на
провода.
. Вычисляют критические значения длины пролета.
. Находят напряжение в проводе при различных
расчетных режимах (расчетных сочетаний климатических условий).
. Определяют стрелы провеса провода для
выбранных расчетных режимов.
. По результатам расчетов составляют сводные
таблицы и кривые в виде зависимостей напряжения в проводе и стрелы провеса от
длины пролета.
Воздушные линии оказывают определенное влияние
на окружающую среду: занимают часть земельной площади, при высоких напряжениях
создают заметную напряженность электрического поля, генерируют радиопомехи и
акустические шумы. При выборе вариантов трассы следует стремиться уменьшить
отрицательное воздействие воздушных линий на окружающую среду и выполнять
требования их гармоничного слияния с окружающим ландшафтом. При этом с целью
снижения стоимости сооружения и эксплуатации линии проектировщик стремится,
чтобы трасса была как можно короче, максимально приближалась к дорогам и
существующим линиям. Необходимо избегать мест с болотами и широкими поймами
рек, оползнями, районов с грязной атмосферой. При прохождении линии по
культурным землям трасса должна выбираться так, чтобы сельскому хозяйству
наносился минимальный ущерб. В лесных массивах трассы линий прокладываются
вдоль имеющихся просек. Направление трассы выбирают таким, чтобы по возможности
избегать ее сближения с линиями слабого тока. Кроме того, следует стремиться к
минимальной реконструкции пресечений с другими линиями электропередачи.
В предварительных изысканиях для выбранной
трассы получают сведения о высшей, низшей и среднегодовой температурах,
направлении и максимальной скорости ветра, максимальной толщине стенки
гололеда, интенсивности гроз.
Вариант трассы линии согласовывается с рядом
организаций: управлениями энергосистем, связи, железных и шоссейных дорог,
отделами архитектуры и др. После окончательного принятия варианта трассы
выполняются технические изыскания: вешение линии, пикетаж, нивелирование, составление
абриса и определение характера грунтов. Вешение линии - это обозначение оси
линии непосредственно на местности с помощью специальных вех. После этого
приступают к ее промеру, для чего через каждые 100 м забивают пикеты. Каждый
пикет имеет номер и отметку превышения его местоположения относительно какой-то
зафиксированной отметки, полученной посредством нивелирования. По этим высотным
отметкам вычерчивают профиль трассы. Одновременно с выполнением пикетажа
составляют абрис трассы, т.е. зарисовывается ситуация местности на расстоянии
25 м по обе стороны трассы. На абрисе указываются углы поворота линии, их
направление.
В результате технических изысканий получают план
и продольный профиль трассы линии. В практике проектирования горизонтальный
масштаб обычно принимают 1:5000, а вертикальный - 1:500. Продольный профиль
используют после проведения соответствующих расчетов проводов и тросов для
проектной расстановки опор по трассе линии.
Рассмотрим кратко отдельные этапы расчета и
проектирования. Заметим, что все рассуждения справедливы как для проводов, так
и для тросов.
.2 Климатические условия и их нормирование
Функционирование воздушной линии электропередачи
происходит в условиях воздействия на них окружающей температуры, ветра,
гололеда, образующегося на проводах и тросах, грозовых явлений.
Величина температуры воздуха оказывает прямое
влияние на степень натяжения и провисания проводов и тросов. При этом
наибольшее значение имеют высшая, низшая и среднегодовая температуры. Кроме
того, на работу ВЛ влияет температура, при которой происходит процесс
образования гололеда. Ветер оказывает давление на провода, тросы и опоры.
Возникающая поперечная нагрузка на провода и тросы увеличивает их натяжение.
Обычно максимальная скорость ветра не совпадает
во времени ни с низшей температурой, ни с процессами образования гололеда. Это
обстоятельство учитывается при выборе расчетных сочетаний климатических
условий.
При проектировании конкретной ВЛ выбор расчетных
климатических условий производится в соответствии с картами климатического
районирования [3], которые предполагают разделение всей территории СНГ на семь
районов по ветру (от І до VІІ) и пять районов по гололеду (от І до ІV и
особого). Каждый район по ветру характеризуется скоростным напором ветра
(скорость ветра) на высоте 10 м от земли, а по гололеду - толщиной стенки
гололеда в зависимости от срока их повторяемости. Скоростной напор ветра q
(Па) связан со скоростью ветра V
(м/с) соотношением:
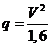(1.1)
Повторяемость максимальной скорости
ветра и наибольшей толщины гололеда принимают в зависимости от важности ВЛ,
которая в данном случае характеризуется номинальным напряжением, т.е. при более
высоком напряжении учитываются менее вероятные значения скорости ветра и толщины
гололеда. В соответствии с [3], максимальные нормативные скорость ветра и
толщину гололедно-изморозевых отложений определяют исходя из их повторяемости:
для ВЛ 500кВ и выше - 1 раз в 15 лет, для ВЛ 6-330 кВ - 1 раз в 10 лет, для ВЛ
3 кВ и ниже - 1 раз в 5 лет.
Таким образом, зная район сооружения
ВЛ, принимают районы по ветру и гололеду с соответствующими скоростью ветра и
толщиной гололеда.
Расчеты и проектирование ВЛ ведут по расчетным
сочетаниям климатических условий, которые составлены на основе наиболее
вероятного одновременного появления определенной скорости ветра, гололеда и
определенной температуры. В ПУЭ [3] сочетания климатических условий задаются
для расчетов нормального, аварийного, монтажного режимов, а также для расчетов
приближений токоведущих частей к элементам опор ВЛ и сооружений.
.3 Определение удельных нагрузок на провода и
тросы
Провода и тросы воздушных линий испытывают
действие нагрузок - вертикальных (вес провода и гололеда) и горизонтальных
(давление ветра). В результате этого возникают растягивающие напряжения.
При расчетах удобно пользоваться удельными
(приведенными) нагрузками, которые относятся к 1 м длины линии и 1 мм2 сечения
провода (троса). Удельные нагрузки рассчитывают исходя из условия, что нагрузка
по длине провода в пролете распределяется равномерно и порывы ветра
отсутствуют.
При проектировании следует учитывать, что линия
имеет большую длину, то ее отдельные участки могут оказаться в неодинаковых
климатических условиях. Такое положение наиболее часто возникает при
прохождении трассы по горам, мимо широких рек и больших водоемов. Для разных
частей такой линии расчетные климатические условия могут приниматься
различными.
.4 Основные уравнения, характеризующие состояние
провода в пролете
Пусть на провод действует только вертикальная
равномерно распределенная по длине нагрузка, например нагрузка от собственного
веса провода. Под действием нагрузки провод провиснет, подобно гибкой нити (рисунок
1.1). Идеальная гибкая нить, не обладающая жесткостью на изгиб, при такой
загрузке принимает очертание цепной линии. Кривая провисания провода за счет
наличия некоторой жесткости лишь приближается по форме к цепной линии. При этом
напряжение в проводе будет обусловлено не только растяжением, но и отчасти
изгибом. Однако напряжение в проводе из-за изгиба обычно не превышает 0.01
напряжения от растяжения. Поэтому можно считать, что напряжение в проводе
возникает только за счет растягивающего усилия, направленного в каждой точке по
касательной к кривой провисания. Оно определяется по формуле
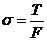(1.2)
Где Т - тяжение по проводу сечением F.
Для одного пролета линии уравнение
провисания провода в виде цепной линии можно представить:
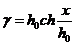(1.3)
Где h0 -
расстояние низшей точки провода до оси х.
Если полагать, что в точке А провод
закреплен жестко, то для обеспечения состояния равновесия в точке В необходимо
приложить соответствующую нагрузку. Сделаем это путем подвески провода через
блок. При идеальном блоке нагрузка за ним должна быть равна тяжению по проводу:
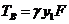(1.4)
где γ - удельная
нагрузка на провод.
По аналогии можно записать выражение
для тяжения в низшей точке провода:
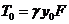(1.5)
Разность тяжений в точках В и О:
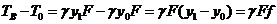
где f - стрела
провеса провода в пролете.
С учетом формулы (1.2) можно
записать:
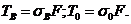
Тогда
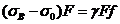
Отсюда
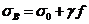(1.6)
где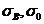 
- напряжение в материале провода в
точке В и низшей точке О.
Из выражения (1.6) следует, что в
низшей точке провода напряжение - наименьшее, а в точках закрепления провода -
наибольшее. Однако в пролетах до 300..400 м это различие в напряжениях мало (не
более 0,3%), и им пренебрегают, используя выражение в низшей точке σ0.
Из формулы (1.5) можно найти:
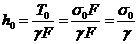(1.7)
Разложим в ряд функцию (1.3):
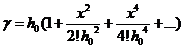
Подставим значение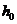 
из (1.7) и
определим функцию в точке В:
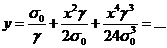(1.8)
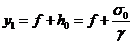(1.9)
Приравнивая выражения (1.8), (1.9) и
читая, что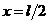 
, получим:
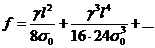(1.10)
где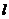 
- длина пролета линии.
Анализ показывает, что для длин
пролетов, которые встречаются на ВЛ, определение стрелы провеса можно
производить, используя только первый член выражения (1.10):
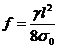(1.11)
Длина дуги АВ цепной линии,
характеризующая длину провода в пролете, описывается выражением:
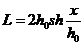(1.12)
Разложим функцию (1.12) в ряд и
получим:
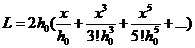
Пр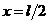и и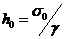 
(1.7) получим:
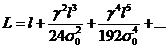
Для пролетов, встречающихся на
практике, достаточно брать только первые два члена ряда. Тогда:
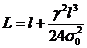(1.13)
С учетом формулы (1.11) длину
провода в пролете можно выразить через стрелу провеса:
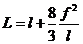(1.14)
Заметим, что длина провода в пролете
лишь на (0,1.. .0,3)% больше длины пролета. Так, при длине пролета l = 300 м и
стреле провеса f = 8 м по формуле (1.14) получим:
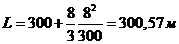
При изменении атмосферных условий
(температуры и нагрузки на провода) изменяются тяжение по проводу и его стрела
провеса. Установим математическую зависимость между этими величинами.
Пусть провод в каком-то состоянии
при температуре воздуха tm и нагрузке γm имеет
напряжение σm и длину lm. Для этого
состояния длина провода в пролете по формуле (1.14):
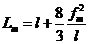
Для других условий (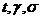
) будем
иметь:
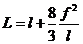
Изменение длины провода можно учесть
в виде:
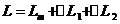(1.15)
Приращение длины, вызванное
соответственно изменением температуры и напряжения:
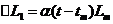
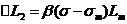
где α - температурный
коэффициент линейного расширения; β - коэффициент упругого
удлинения (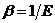
; Е - модуль
упругости).
Приравнивая выражения (1.15), (1.16)
и заменяя по формуле (1.11):
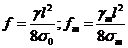
получим
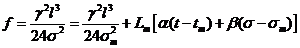(1.16)
Ввиду малого отличия длины провода в
пролете от длины пролета допустим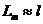 
. Тогда из выражения (1.16) получим:
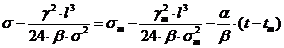(1.17)
Выражение (1.17) называется
уравнением состояния провода в пролете. Оно позволяет при известных данных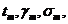 
найти
напряжение σ
в
проводе для других условий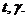 
В качестве известного обычно
выступает один режим, соответствующий какому-то расчетному сочетанию
климатических условий (таблица 1.1).
Кубическое уравнение (1.17) можно
представить в виде:
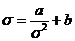(1.18)
Где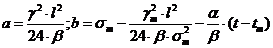 
Решение уравнения (1.18) с
погрешностью не более 5% дает формула
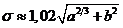(1.19)
Для каждой марки провода существует
предел прочности, превышение которого вызывает необратимые изменения его
механических свойств. У проводов и тросов воздушных линий должен быть определенный
запас механической прочности. При выборе его величины следует считаться с
возможными погрешностями исходных данных (температуры и нагрузок), другими
допущениями. Поэтому приходится принимать значительный запас прочности.
Действующие ПУЭ [3] задают запас
прочности в виде допустимых напряжений в проводах в процентах от предела
прочности провода σ
для
следующих условий:
а) наибольшей внешней нагрузки;
б) низшей температуры при отсутствии
внешних нагрузок;
в) среднегодовой температуры при
отсутствии внешних нагрузок.
Монометаллические провода, в которых
все проволоки выполнены из одного метала (например, алюминия), при механическом
растяжении или изменении температуры испытывают по всему сечению одинаковое
изменение напряжения. Поэтому допустимые напряжения при низшей температуре и
наибольшей нагрузке могут приниматься одинаковыми. В сталеалюминевых проводах
алюминиевые и стальные проволоки имеют различные коэффициенты температурного
расширения и модули упругости. Поскольку алюминиевые и стальные проволоки не
могут перемещаться относительно друг друга, при изменении температуры и
нагрузки в них получится различное изменение напряжения. В связи с этим
нормируемые допустимые напряжения для сталеалюминевых проводов следовало бы
принимать различными в режимах низших температур и наибольших нагрузок. Однако
на практике такими особенностями сталеалюминевых проводов пренебрегают и
допустимые напряжения при низшей температуре и наибольшей нагрузке принимают
одинаковыми (таблица 2.5.7, [3]).
Ограничения напряжений при
наибольшей нагрузке σг и низшей
температуре σ_
необходимы
для проверки провода на статическое растяжение при наиболее тяжелых режимах.
Эти ограничения могут оказаться недостаточными при возникновении из-за вибрации
проводов динамических нагрузках, которые приводят к уменьшению прочности
провода в местах его закрепления. Поэтому при расчете проводов необходимо
вводить также ограничение по среднеэксплуатационному напряжению σэ. Заметим,
что в результате ограничения напряжения уменьшается, хотя полностью не
исключается вредное влияние вибрации. Поэтому должны также проводиться расчеты
для проверки необходимости установки дополнительных средств защиты от вибрации.
При расчете в качестве исходного
(начального) можно принимать любое состояние проводов, характеризующееся любой
нагрузкой и температурой. Однако после монтажа проводов напряжения в них не
должны превышать соответствующих допустимых напряжений для режимов максимальной
нагрузки, низшей и среднегодовой температур. Чтобы выполнить это условие,
целесообразно при расчете за исходное принять одно из состояний, в котором
напряжение может быть равным допустимому. При этом достаточно правильно выбрать
один из трех ограничивающих режимов.
Влияние температуры проявляется в
большей или меньшей степени в зависимости от длины пролета. При малых пролетах
на напряжение в проводе значительное влияние оказывает температура, при больших
- нагрузка.
Поясним сказанное более подробно,
для чего рассмотрим зависимость изменения напряжения в проводе для режима
среднегодовой температуры от длины пролета и исходного расчетного режима
(рисунок 1.2). Кривые σэ(-) и σэ(г)
характеризуют напряжение в проводе при среднегодовой температуре для случаев,
когда в качестве исходного принят режим соответственно низшей температуры и
наибольшей нагрузки. Там же нанесены линии, соответствующие допустимым
напряжениям в различных режимах σэ, σг, σ_.
В точке О1, соответствующей первому
критическому пролету l1k напряжения
одновременно равны допустимым в режимах среднегодовой температуры и низшей температуры,
в точке О2 при втором критическом пролете l2k - в режимах
низшей температуры и нагрузки, в точке О3 при третьем критическом пролете - в
режимах среднегодовой температуры и наибольшей нагрузки.
Наиболее часто имеют место следующие
соотношения длин критических пролетов: l1k < l2k < l3k и l1k > l2k > l3k.
Если для первого случая расчетный
пролет линии лежит в пределах 0 < l < l1k, то за
исходный следует принимать режим низшей температуры. В противном случае, если
за исходный взять, например, режим наибольшей нагрузки, то при длине пролета l' напряжение
при среднегодовой температуре превысит допустимое (точка А на рисунок 1.2, а).
При l1k < l < l3k за исходный
должен быть взят режим среднегодовой температуры, так как при других исходных
режимах и длине пролета l'' напряжение в этом режиме может
превысить допустимое (точка В). Соответственно при l > l3k в качестве
исходного принимается режим наибольших нагрузок.
При втором соотношении длин
критических пролетов в случае l < l2k исходным
должен служить режим низшей температуры, а при l > l2k - режим
наибольшей нагрузки.
Дадим более четкие определения
критических пролетов.
Первый критический пролет - это
пролет такой длины, при которой напряжение в проводе в режиме среднегодовой
температуры равно допустимому при среднегодовой температуре σэ, а в
режиме низшей температуры - допустимому напряжению при низшей температуре σ_.
Второй критический пролет - это
пролет, при котором напряжение в проводе при наибольшей нагрузке равно
допустимому напряжению при наибольшей нагрузке σг, а в
режиме низшей температуры - допустимому напряжению при низшей температуре σ_.
Третий критические пролет - это
пролет, при котором напряжение в проводе при среднегодовой температуре
достигает допустимого при среднегодовой температуре σэ, а в
режиме максимальной нагрузки равно допустимому при максимальной нагрузке σг.
Формулы для определения критических
пролетов могут быть получены из уравнения состояния провода (1.17).
Для получения формулы какого-либо
критического пролета нужно в уравнение состояния провода вместо значений γm, σm, tm подставить
значения для одного из ограничивающих режимов, вместо значений γ, σ, t - другого,
а длину пролета считать неизвестным значением.
Например, для нахождения первого
критического пролета вместо γm, σm, tm следует
подставить γ1, σэ, tэ (для
режима среднегодовой температуры), а вместо γ, σ, t - γ1, σ-, t-.
Формулы для определения критических
пролетов при σг = σ- = σmax имеют вид
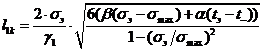(1.20)
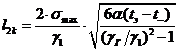(1.21)
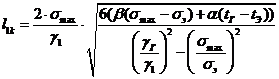(1.22)
где tг, t-, tэ -
соответственно температура в режиме максимальной нагрузки, низшей и
среднегодовой температур;
γ - удельная нагрузка в режиме
максимальной нагрузки.
Возможен еще один случай, когда
кривые σэ(-) и σэ(г)
пересекаются на прямой σэ. При этом
все критические пролеты равны l1k = l2k = l3k.
Тогда из формул (1.20)…(1.22) видно,
что при заданных низшей и среднегодовой температурах для конкретного сечения
провода (данной удельной нагрузки γ1) длины критических пролетов
будут зависеть только от величины максимальной нагрузки γг . Эта
величина, при которой напряжения при всех исходных расчетных условиях
одинаковы, называется критической нагрузкой γк. Отношение критической
нагрузки к удельной нагрузке от собственного веса провода называется уровнем
критической нагрузки
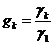(1.23)
.6 Систематический расчет проводов и
тросов
Цель систематического расчета
заключается в построении зависимостей изменения напряжения в проводе от длины
пролета 
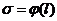и стрелы
провеса от длины пролета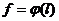 
. Эти
зависимости находят для определенных расчетных сочетаний климатических условий.
Поясним назначение каждого из них.
Расчетные режимы 1..6 необходимы для
проверки работы линии в нормальных условиях (при необорванных проводах и
тросах), режим 13 применяют для проверки линии по условиям монтажа (при
грозовых и внутренних перенапряжениях) и 9 (для обеспечения безопасного подъема
на опору под напряжением).
Сочетания климатических условий,
соответствующие расчетным режимам 1 и 4, необходимы для нахождения максимальной
вертикальной стрелы провеса, которая может возникнуть при высшей температуре
либо когда провода и тросы нагружены гололедом. Режим 2 используется для
проверки проводов по допустимому напряжению в условиях низшей температуры, а
также для определения минимальной стрелы провеса, которая нужна для вычисления
габаритов при пересечении с инженерными сооружениями и других целей. По
расчетному режиму 3 контролируют напряжение в средних эксплуатационных
условиях, чтобы оно не превышало допустимого при среднегодовой температуре.
Режимы 5 или 6 позволяют определить максимальную внешнюю нагрузку на провода. По
выбранному режиму производится проверка на допустимое напряжение при
максимальных нагрузках. Режимы 5,6 используют также для нахождения косых
(наклонных) стрел провеса проводов и тросов (при воздействии ветра).
Зависимост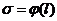и и 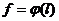для каждого
расчетного сочетания климатических условий строятся по 8..10 точкам. Значения
наибольшего и наименьшего пролетов принимаются в зависимости от высоты
принятого типа опор, заданных климатических условий (гололеда и ветра), марки
провода должны охватывать все длины пролетов, которые могут встретиться на
проектируемой линии (для линий 35-220кВ они находятся в пределах 70..400 м).
Промежуточные значения пролетов принимаются через 30..50 м. В число промежуточных
точек следует включать длины критических пролетов. Исходные расчетные условия
выбираются в зависимости от соотношения критических пролетов (таблица 1.2).
Например, при соотношении
критических пролетов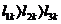 
для точек,
соответствующих пролетам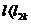 
, за
исходный принимают режим низших температур 2, а для пролетов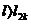 
- режим
максимальных нагрузок 5 или 6.
Напряжение в проводе определяется из
уравнения состояния провода (1.17). Для этого вместо значений с индексом m подставляют
значения для соответствующего исходного режима, а вместо γ и t - значения
режима, для которого необходимо найти напряжение в проводе. Стрела провеса
вычисляется по формуле (1.11).
Результаты расчетов сводят в таблицы
и по ним вычерчивают соответствующие графики.
1.7 Расчет грозозащитного троса
Для расчета грозозащитного троса
используются методы и приемы расчета проводов. Кроме того, расположение троса
на опоре должно быть таким, чтобы гарантировать защиту проводов от ударов
молнии, т.е. необходимо иметь соответствующий угол защиты проводов. Угол защиты
проводов учитывается при конструировании опор.
Наименьшие допустимые расстояния
между тросом и проводом в середине пролета без учета отклонения их ветром
выбираются в соответствии с ПУЭ [3].
Допустимые расстояния должны
соблюдаться для условий грозового режима, когда провода и тросы нагружены
только собственным весом, ветер отсутствует и температура воздуха равна +15°C.
Стрела провеса троса в этих условиях должна быть не больше, чем рассчитанная по
формуле:
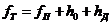(1.24)
где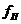 
- стрела провеса провода в середине
пролета (рисунок 1.4);
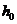- расстояние по вертикали между
точками подвеса провода и троса, оно известно из конструкции опоры;
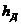- допустимое расстояние между
тросом и проводом.
Определим, каким должно быть
напряжение в тросе, чтобы соблюдалась эта стрела провеса. Связь между стрелами
провеса и напряжениями в тросах и проводах имеет вид:
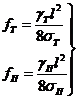(1.25)
где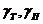 
- удельные нагрузки соответственно
на трос и провод от собственного веса;
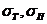- механические напряжения в тросе и
проводе в условиях грозового режима;
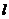- длина пролета.
Подставив выражения (1.25) в (1.24)
и решив уравнение относительно σт, получим:
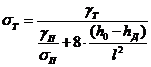(1.26)
Допустимое расстояние между тросом и
проводом соблюдается, если напряжение в тросе при грозовом режиме не меньше
подсчитанного по формуле (1.26).
Таким образом, можно установить
следующий порядок расчета троса:
. По уравнению состояния провода
(1.17) определяют напряжение в проводе σп для условий грозового
режима.
. По формуле (1.26) определяют
граничное напряжение в тросе, при котором еще соблюдается допустимое расстояние
между тросом и проводом в середине пролета.
. В качестве исходного состояния
принимают грозовой режим с полученным напряжением в тросе и по уравнению
состояния провода находят напряжение в тросе для режимов максимальной нагрузки,
низшей и среднегодовой температуре.
. Сравнивают полученные напряжения в
этих трех режимах с допустимыми при максимальной нагрузке, низшей и
среднегодовой температуре.
Если напряжения не превышают
допустимые, можно сделать вывод о пригодности выбранного троса для условий
проектируемой линии в нормальных режимах работы. В противном случае
удовлетворительного решения можно добиться, приняв другое сечение троса,
увеличив высоту тросостойки и др.
При ровном профиле трассы в формулу
(1.26) подставляют длину расчетного (габаритного) пролета линии. Если же
очевидно, что после расстановки опор по профилю трассы в анкерном участке
пролеты будут различной длины, то для обеспечения допустимых расстояний между
тросом и проводом во всех пролетах в формулу подставляют значение
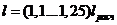
Результаты расчета напряжения в
тросе при среднегодовой температуре используются для решения вопроса о
необходимости его защиты от вибрации. Трос должен быть также проверен по
условию аварийного режима линии.
.8 Критическая температура
Как следует из формулы (1.11),
стрела провеса при неизменной длине пролета зависит от величины нагрузки γ и напряжения
σ,
которое,
в свою очередь, зависит от нагрузки и температуры. Таким образом, на стрелу
провеса влияет нагрузка и температура. В зависимости от отношения γ/ σ стрела
провеса может получиться больше тогда, когда на провод действует дополнительная
нагрузка (гололед, ветер) при относительно низкой температуре либо когда провод
находится только под действием своего веса при более высокой температуре.
Очевидно, существует и такая температура, при которой провод под действием
только своего веса будет иметь такую же стрелу провеса, как в режиме
дополнительной нагрузки. Эта температура называется критической. Выведем
формулу для ее определения.
Пусть провод находится под действием
дополнительной нагрузки γг (гололед,
ветер) при температуре tг и имеет стрелу провеса fг при
напряжении σг . При
критической температуре t нагрузка от собственного веса равна
γ1
и
стрела провеса fк.
Тогда из условия fг = fк по формуле
(1.11) можно записать:
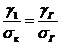
Отсюда напряжение при критической
температуре:
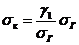(1.27)
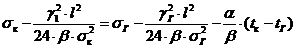
Отсюда
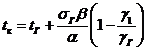(1.28)
.9 Расстановка опор по профилю
трассы
Расстановка опор - наиболее
ответственный этап в проектировании линии. После ее выполнения окончательно
определяются число и тип опор, количество изоляторов, линейной арматуры и др.
Одна из главных задач при
расстановке опор по профилю трассы - проверка расстояний от проводов до земли и
до пересекаемых инженерных сооружений. Габариты должны проверяться в следующих
режимах:
а) в нормальном режиме линии (при
необорванных проводах и тросах) по максимальной стреле провеса, получаемой из
сопоставления стрел провеса в режиме высшей температуры и в режиме гололеда без
ветра;
б) при аварийном состоянии линии
(обрыв провода в соседнем пролете) в режиме среднегодовой температуры.
Если пересекаются две воздушные
линии, то должны проверяться расстояния по вертикали между ближайшими проводами
и тросами в грозовых условиях (температура воздуха +15 °C, ветер и гололед
отсутствуют). Основные габариты линий приведены в ПУЭ [3].
На заданном профиле трассы
расстановка опор производится с помощью специальных шаблонов (рисунок 1.5),
построенные в виде парабол для режима, при котором возникает максимальная
стрела провеса (при высшей температуре или гололеде без ветра). Режим
максимальной стрелы провеса находится из систематического расчета для
габаритного пролета.
Под ним понимается пролет, длина
которого определяется нормативным габаритом до земли от низшей точки провода
при установке опор на ровной местности. Режим максимальной стрелы провеса может
быть также определен вычислением критической температуры, при которой стрела
провеса провода при отсутствии гололеда и ветра достигает такого же значения,
как при гололеде без ветра.
Если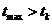 
, то наибольшая стрела провеса будет
возникать при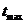 
, а в случае
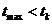- при
гололеде без ветра.
Кривая 1 шаблона строится на основе
формулы стрелы провеса (1.12).
Подставив в нее l=2x , получим:
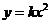(1.29)
где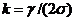 
Удельная нагрузка γ и напряжение
провода σ
принимаются
для режима, соответствующего максимальной стреле провеса. Напряжение находится
по результатам систематического расчета проводов для длины пролета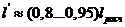 
, т.е.
несколько меньшей, чем расчетная длина пролета. Из опыта проектирования
установлено, что средний пролет после расстановки опор примерно на 10% меньше,
чем расчетный, за счет наличия ограничений по трассе (дороги, реки, углы и
т.п.). Задавая различные значения х , по формуле (1.29) находят соответствующие
значения у.
Кривую 2, называемую габаритной,
строят параллельно первой, отложив от нее по вертикали расстояние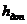 
, равное
допустимому габариту от провода до земли. Аналогично строят кривую 3,
называемую земляной. Расстояние по вертикали от кривой 2 до кривой 3 принимают
равным максимальной стреле провеса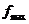 
.
Шаблон выполняют в тех же масштабах,
что и продольный профиль трассы.
До расстановки опор всю трассу
разбивают на участки, ограниченные анкерными опорами. Расстановка промежуточных
опор производится на каждом анкерном участке независимо от других анкерных
участков.
Шаблон накладывается на профиль
трассы так, чтобы кривая 3 пересекала профиль в месте установки первой анкерной
опоры, а кривая 2 касалась его. При этом ось у должна находиться в вертикальном
положении. Тогда другая точка пересечения кривой 3 с профилем будет
соответствовать месту установки первой промежуточной опоры. При таком положении
шаблона во всех точках пролета габарит до земли будет не меньше допустимого.
Затем шаблон продвигают и аналогичным образом находят положение следующей
опоры. Длина последнего пролета в конце анкерного участка может оказаться
малой. В этом случае ее следует увеличить, уменьшая соответственно ряд длин
соседних пролетов и стремясь сделать их примерно одинаковыми. С помощью шаблона
следует произвести дополнительную проверку и убедиться, что при перемещении
опор габариты остаются не меньше допустимых. При массовых расчетах расстановку
опор производят с применением ЭВМ. После расстановки опор определяют значение
приведенного пролета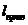 
.
Его физический смысл заключается в
том, что после монтажа провода в анкерном пролете с помощью подвесных
изоляторов по всему анкерному участку произойдет выравнивание напряжения
провода, которое будет соответствовать какому-то условному пролету. В
дальнейших расчетах напряжение провода в анкерном участке определяют по
приведенному пролету.
Приведенный пролет вычисляют как
квадратный корень из суммы кубов пролетов, которые входят в анкерный пролет
(между двумя соседними анкерными опорами), деленной на длину анкерного участка
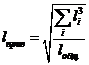(1.30)
Приведенный пролет для разных
анкерных участков в общем случае различен.
Если приведенный пролет оказался
близким к расчетному l' , которому был построен шаблон, то
расстановку опор можно считать удовлетворительной.
Пр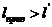и 
или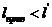 
следует найти по результатам
систематического расчета напряжение провода, соответствующего 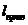, и сравнить
его с напряжением, которое принималось при построении шаблона. При существенном
различии этих напряжений нужно построить шаблон для нового напряжения и
произвести перерастановку опор. Необходимость этого вызывается тем, что при
меньшем полученном напряжении будут возникать большие стрелы провеса, при
которых может возникнуть нарушение значений габаритов до земли.
Если же напряжение окажется выше
расчетного, для которого строился шаблон, то будут создаваться излишние запасы
в габаритах, что приведет к перерасходу опор.
На участках трассы с сильно
пересеченным профилем необходима проверка опор на вырывание, которое может
наблюдаться в случае, когда отметка расположения опоры находится значительно
ниже отметок двух соседних опор. Проверка на вырывание производится с помощью
шаблона, представляющего кривую провисания провода при минимальной стреле
провеса. Шаблон рассчитывается по формуле (1.29), куда подставляются удельная
нагрузка от собственного веса провода и напряжение в режиме низшей температуры.
Тогда Шаблон, соответствующий
минимальной стреле провеса накладывают на профиль так, чтобы кривая проходила
через вершины опор 1 и 3. Если при этом кривая шаблона окажется выше точки а,
то опора 2 будет испытывать силу, действующую вертикально вверх. Для ее
устранения могут быть осуществлены следующие мероприятия: перестановка опоры 2
на более высокую отметку, ликвидация опоры 2, применение повышенной опоры 2,
установка анкерной опоры 2 вместо промежуточной, подвеска компенсирующих
грузов.
При расстановке опор на профиле
трассы все они должны быть проверены на нагрузки, которые будут возникать в
реальных условиях. Вертикальные нагрузки, действующие на опору, определяются
собственным весом проводов и гололеда, а горизонтальные - действием ветра на
провода линии. Проверку производят путем вычисления для каждой опоры весового и
ветрового пролетов и сравнения их с соответствующими расчетными.
Весовой пролет соответствует
вертикальной нагрузке на опору и определяется суммой двух смежных эквивалентных
полупролетов, прилегающих к данной опоре.
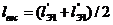(1.31)
Эквивалентный пролет - это условный
пролет с подвеской провода на одинаковых высотах, вычисляемый по формулам:
а) первый (большой) эквивалентный
пролет
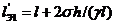(1.32)
б) второй (малый) эквивалентный
пролет
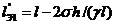(1.33)
где l -
действительная длина пролета;
h - разность
между высотами точек подвеса провода.
Так, для опоры 2 (рисунок 1.8):
, 
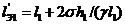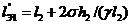
Где γ - удельная
нагрузка от собственного веса провода и гололеда;
σ - напряжение провода в
режиме гололеда без ветра, взятое для приведенного пролета данного анкерного
участка;
l1 и l2 - длины
пролетов, которые берутся с профиля трассы.
Смежными эквивалентными пролетами
для данной опоры не всегда будут один большой и один малый. Возможны случаи,
когда к опоре прилегают два больших или два малых эквивалентных пролета. В этих
случаях формула (1.31) принимает вид
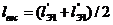или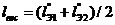 
(1.34)
Очевидно, что при подвеске провода
на одинаковой высоте h=0 и весовой пролет равен полусумме
действительных пролетов.
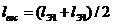(1.35)
На опору действует вертикальная
нагрузка, не выше расчетной, если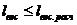 
. Расчетный пролет обычно известен
из технических данных унифицированных опор.
Проверку горизонтальной нагрузки от
действия ветра производят путем вычисления ветрового пролета и сравнения его с
расчетным. В инженерных расчетах с достаточной точностью ветровой пролет можно
вычислить как полусумму смежных пролетов:
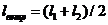(1.36)
Для каждой опоры должно соблюдаться
условие 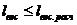. Расчетный
ветровой пролет указывается в паспортных данных унифицированных опор. Если
весовой или ветровой пролет для какой-либо опоры оказался выше расчетного, то
должна быть произведена соответствующая перерастановка опор на профиле трассы.
В населенной местности габариты до
земли должны соблюдаться не только в нормальном, но и в аварийном режимах
линии. Проверка аварийного режима производится при среднегодовой температуре и
отсутствии гололеда и ветра.
Габарит до земли определяется на
основании вычисления стрелы провеса:
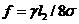
где γ - удельная
нагрузка от собственного веса провода;
l -длина
пролета (при неодинаковой высоте точек подвеса провода в формулу подставляется
соответствующая длина эквивалентного пролета);
σ - напряжение провода,
найденное по результатам расчета аварийного режима.
.10 Расчет переходов через
инженерные сооружения
Под переходами через инженерные
сооружения понимают пересечения проектируемой линии с железнодорожными и
шоссейными дорогами, линиями электропередач, линиями связи и сигнализации. Цель
расчета заключается в определении расстояний от проводов линии до пересекаемого
сооружения и сравнения их с допустимыми. Действительное расстояние от нижнего
провода до инженерного сооружения.
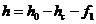. (1.37)
где h0 - высотная
отметка точки подвеса нижнего провода на профиле трассы, определяемая отметкой
в месте установки опоры и размерами отдельных элементов опоры;
hс - высотная
отметка верхней части инженерного сооружения на профиле трассы;
f1 - стрела
провеса провода в месте пересечения, отстоящего на расстояние ln от опоры с
большей отметкой точки подвеса провода.
Стрела провеса провода в нормальном
режиме:
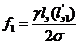. (1.38)
где γ - удельная
нагрузка провода, соответствующая режиму наибольшей стрелы провеса (режимы
температуры или гололеда при отсутствии ветра);
σ - напряжение провода в
режиме наибольшей стрелы провеса, находится для приведенного пролета данного
анкерного участка;
длина первого (большого)
эквивалентного пролета.
Если один пролет пересекается с
несколькими инженерными сооружениями, то проверка габаритов должна
производиться каждого из них.
При выбранной высоте опор проектируемой
линии расстояние до пересекаемых сооружений могут оказаться меньше допустимых.
В этом случае должны быть разработаны соответствующие мероприятия. Прежде всего
следует попытаться увеличить габариты путем перемещения опоры проектируемой
линии ближе к месту пересечения и за счет этого уменьшить стрелу провеса над
инженерным сооружением. В ряде случаев допускается переустройство пересекаемых
линий электропередачи и линий связи путем понижения их опор или перекладки в
подземные кабели. Может оказаться целесообразным применение повышенных опор на
проектируемой линии в месте пересечения.
.11 Расчет монтажных стрел провеса
Поскольку монтаж провода может
выполняться в широком диапазоне температур окружающего воздуха, важно правильно
выбрать соответствующие стрелы провеса в реальных условиях.
Расчет монтажных стрел провеса
выполняют в следующем порядке:
1) определяют приведенные пролеты lпр
для всех анкерных участков;
2) устанавливают соотношение между
пролетами приведенным и критическим, по которому принимают один из трех
исходных режимов, ограничивающих допустимые напряжения провода;
) находят напряжение провода для данного
приведенного пролета анкерного участка при различных температурах, используя
уравнение состояния провода (1.17). Для этого в правую часть уравнения
подставляют параметры принятого режима, ограничивающего допустимое напряжение
провода, а в левую - удельную нагрузку от собственного веса провода (так как
монтаж проводов ведется при отсутствии гололеда и сильного ветра). Значения
температур задаются от +30 до -30°C через каждые 10°C;
) намечают пролеты, для которых надо
рассчитать монтажные стрелы провеса;
5) определяют для каждого из
них стрелы провеса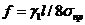 
. Здесь l - длина
пролета; σпр -
напряжение провода в приведенном пролете, полученное из уравнения состояния
провода в приведенном пролете;
) определяют тяжение провода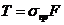 
Результаты расчетов сводят в
монтажные таблицы, по которым строят монтажные кривые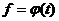 
и 
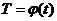(рисунок
1.10). Зависимость 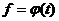получают
линейно. Поэтому при расчете монтажных кривых достаточно вычислить стрелы
провеса для двух температур и по ним построить зависимость для всего диапазона
температур.
.12 Алгоритм расчета механической
части воздушных линий электропередачи
Расчет ведется по методу допустимых
напряжений.
.12.1 Определение удельных нагрузок
. Удельная нагрузка от собственного
веса провода, Н/(м·мм2)
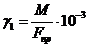
Где М - расчетный вес провода,
кг/км;
Fпр - площадь
поперечного сечения провода, мм2;
-3 - для получения единичной
нагрузки от собственного веса в килограммах на один метр следует разделить на
1000 вес, указанный в стандарте.
. Удельная нагрузка от массы
гололедных отложений, Н/( м·мм2):
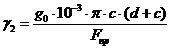
g - ускорение
свободного падения, принимается равным 9,8 м/с2;
Fпр - площадь
поперечного сечения провода, мм2;
с - толщина стенки гололеда,
d - диаметр
провода.
. Суммарная вертикальная удельная
нагрузка от собственной массы провода и массы гололеда, Н/( м·мм2):
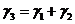
. Удельная горизонтальная нагрузка
от давления ветра на провод, свободный от гололеда, Н/м:
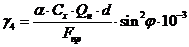
где α - коэффициент,
учитывающий неравномерность ветрового давления по пролету ВЛ (берется из
[2.5.52] в зависимости от ветрового давления W).
Сх - коэффициент лобового
сопротивления, принимаемый равным: 1,1 для проводов и тросов, свободных от
гололеда, диаметром 20 мм и более; 1,2 - для всех проводов и тросов, покрытых
гололедом, и для всех проводов и тросов, свободных от гололеда, диаметром менее
20 мм;
d - диаметр
провода, мм;
Fпр - площадь
поперечного сечения провода, мм2;
φ - угол между направлением ветра
и осью ВЛ, принимается равным 90°;
. Удельная горизонтальная нагрузка
от давления ветра на провод, покрытый гололедом, Н:
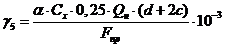
где α - коэффициент,
учитывающий неравномерность ветрового давления по пролету ВЛ (берется из
[2.5.52] в зависимости от ветрового давления W);
Сх - коэффициент лобового
сопротивления, принимаемый равным: 1,1 - для проводов и тросов, свободных от
гололеда, диаметром 20 мм и более; 1,2 - для всех проводов и тросов, покрытых
гололедом, и для всех проводов и тросов, свободных от гололеда, диаметром менее
20 мм;
d - диаметр
провода, мм;
Fпр - площадь
поперечного сечения провода, мм2;
φ - угол между направлением ветра
и осью ВЛ, принимается равным 90°;
. Результирующая удельная нагрузка
от массы провода, массы гололеда и давления ветра, Н/( м·мм2):
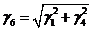
. Результирующая удельная нагрузка
от массы провода, массы гололеда и давления ветра, Н/( м·мм2):
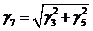
Выбираем наибольшее из γ6 и γ7.
1.12.2 Определение расчетных условий
Сталеалюминевый провод состоит из
двух сплошных частей: внутренней - в виде стального круглого цилиндра и внешней
- в виде алюминиевого слоя, т.е. в работе участвуют два разных металла, имеющие
различные физико-механические свойства и по-разному воспринимающие действия
внешних сил и изменение температуры по сравнению с той, при которой был
изготовлен. Поэтому для определения коэффициента линейного удлинения
(расширения) α
и
модуля упругости - Е комбинированных проводов необходимо предварительно
определить соотношение «m» сечений алюминия и стали по
формуле:
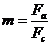
где Fа - сечение
алюминия, мм2;
Fст - сечение
стального сердечника, мм2.
Расчет критических пролетов:
Первый критический пролет, м
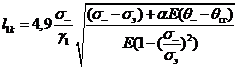
где σ(-) - напряжение в
проводе при низшей температуре, Н/мм2;
γ1 - удельная нагрузка от
собственного веса провода, Н/( м·мм2);
α - температурный коэффициент
линейного удлинения провода, град-1;
Е - модуль упругости, Н/мм2;
ΘСГ - среднегодовая
температура;
Θ(-) - низшая
температура;
. Второй критический пролет, м
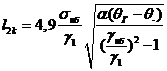
где σГ -
напряжение в проводе при действии γНБ, Н/мм2;
γ1 - удельная нагрузка от собственного
веса провода, Н/( м·мм2);
γНБ - наибольшая нагрузка на
провод, Н/( м·мм2);
α - температурный коэффициент
линейного удлинения провода, град-1;
ΘГ - температура при гололеде;
Θ(-) - низшая
температура.
. Третий критический пролет, м
σНБ - напряжение в проводе при
действии γНБ , Н/мм2;
γ1 - удельная нагрузка от
собственного веса провода, Н/( м·мм2);
γНБ - наибольшая нагрузка на
провод, Н/( м·мм2);
α - температурный коэффициент
линейного удлинения провода, град-1;
Е - модуль упругости, Н/мм2;
ΘСГ - среднегодовая
температура;
ΘГ - температура при гололеде.
В зависимости от соотношения
критических пролетов между собой, а также соотношения расчетных и критических
пролетов выбираем исходные расчетные условия (таблица 1.2).
Запишем уравнение состояния провода:
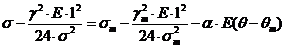
где σm, γm, Θm -
напряжение в проводе, удельная нагрузка и температура, выбранные в качестве
исходных условий;
σ, γ, Θ - напряжение
в проводе, удельная нагрузка и температура рассчитываемого режима;
α - температурный коэффициент
линейного удлинения провода, град-1;
Е - модуль упругости, Н/мм2;
l - длина
приведенного пролета, м.
Для решения получаемого кубического
уравнения вычисляем коэффициенты:
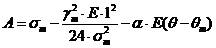
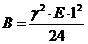
Тогда уравнение примет вид:
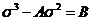
Для решения этого уравнения можно
воспользоваться программой MS Excel.
Стрела провеса:
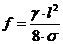
где l - длина
приведенного пролета, м;
σ, γ - напряжение в
проводе и удельная нагрузка рассчитываемого режима.
линия электропередача трос провод
1.12.3 Расчет критической температуры и
выявление климатических условий, соответствующих наибольшему провисанию провода
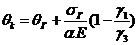, °C
где ΘГ -
температура при гололеде;
σГ - напряжение в проводе при
гололеде, Н/мм2;
α - температурный коэффициент
линейного удлинения провода, град-1;
Е - модуль упругости, Н/мм2;
γ1 - удельная нагрузка от
собственного веса провода, Н/( м·мм2);
γ3 - суммарная вертикальная
удельная нагрузка от собственной массы провода и массы гололеда, Н/( м·мм2);
Если Θ+ > Θк, то
наибольшая стрела провеса провода будет при наивысшей температуре, иначе
наибольшая стрела провеса провода будет при гололеде.
Найдем габаритный пролет, использую
уравнение состояния провода:
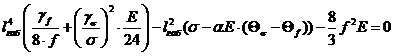
где γf - удельная
механическая нагрузка, при которой имеет место наибольшее провисание провода,
Н/( м·мм2);
f - стрела
провеса провода, м;
γσ - наибольшая
удельная механическая нагрузка, выбранная как исходная для климатических
условий, Н/( м·мм2);
σ - напряжение в проводе,
выбранное как исходное для климатических условий, Н/мм2;
σσ - температура,
выбранная как исходная для климатических условий, °C.
Введем коэффициенты А, В, С:
;
.
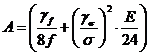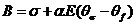
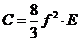Получим биквадратное уравнение
относительно длины габаритного пролета:
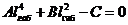, тогда
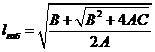
Построение расстановочного шаблона
Уравнение первой кривой:
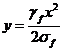
где γf - удельная
механическая нагрузка, при которой имеет место наибольшее провисание провода,
Н/( м·мм2);
σf -
напряжение в проводе, выбранное как исходное для климатических условий, Н/мм2;
Вторая (габаритная) кривая сдвинута
по вертикали вниз от первой кривой на расстояние, равное требуемому габариту Г
с запасом габарита на 0,3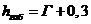м.
, м
Третья (земляная) кривая сдвинута
относительно первой на расстояние:
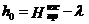, м
где 
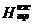- высота опоры от нижней траверсы до
земли, м;
λ - высота гирлянды изоляторов,
м.
Для построения расстановочного
шаблона принимаем масштаб: по горизонтали - 1:5000, по вертикали - 1:500.
Шаблон строится на отдельном листе.
.12.3 Расчет напряжения в тросе
Определяем по уравнению состояния
провода напряжение в проводе для условий грозового режима (температура равна
+15, гололед и ветер отсутствуют).
Определение удельных нагрузок для
троса осуществляется также и для провода.
Минимальное допустимое расстояние
между тросом и проводом в середине пролета согласно (3.31), [2]:
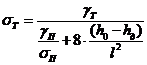
где γт - удельная
нагрузка в тросе для условий грозового режима, Н/( м·мм2);
σп, γп -
напряжение и удельная нагрузка в проводе для условий грозового режима;
h0 -
расстояние по вертикали между точками подвеса троса и провода, м;
l - длина
приведенного пролета, м.
В качестве исходного состояния
принимают грозовой режим с полученным напряжением в тросе и по уравнению
состояния провода находят напряжение в тросе для режимов максимальной нагрузки,
низшей и среднегодовой температурю
Сравниваем полученные напряжения в
этих трех режимах с допустимыми при максимальной нагрузке, низшей и
среднегодовой температурах.