Расчет и проектирование воздушных линий электропередач
Содержание
Введение. 3
1 Исходные данные. 4
2 Определение
физико-механических характеристик провода и троса. 5
3 Выбор унифицированной
опоры.. 7
4 Расчет проводов и троса
на механическую прочность. 9
4.1 Определение толщина
стенки гололеда и величины скоростного напора ветра 9
4.2 Определение удельных
нагрузок на провод и трос. 11
4.3 Расчет критических
пролетов. 13
4.4 Расчет напряжений в
проводе. 15
4.5 Определение стрелы
провеса проводов и троса. 17
4.6 Определение напряжений
в тросе. 18
5 Выбор изоляторов и
линейной арматуры.. 21
6 Расстановка опор по
профилю трассы.. 28
6.1 Построение шаблона. 28
6.2 Проверка опор на
прочность. 31
7 Расчет монтажных стрел
провеса провода и троса. 34
Заключение. 40
Список литературы.. 41
Введение
Проектирование механической части воздушных линий
электропередачи является важной частью проектирования электроснабжения. От правильного
выбора элементов ЛЭП зависит долговременная и безопасная эксплуатация линий, и,
соответственно, надежное и качественное электроснабжение потребителей.
В данном курсовом проекте рассмотрены основные этапы
проектирования механической части воздушных ЛЭП: выбор промежуточных опор,
механический расчет проводов и грозозащитного троса, выбор линейной арматуры,
произведены расстановка опор по профилю трассы и расчет монтажных стрел
провеса.
1 Исходные данные
Тип ЛЭП: двухцепная воздушная линия напряжением 110 кВ,
проходящая в ненаселенной местности.
Климатические условия:
район по ветру – II;
район по гололеду – IV;
температура:
высшая tmax=40°С;
низшая tmin= -10°С;
среднегодовая tср=5°С.
Тип опор: унифицированные железобетонные.
Марки провода: АС-150.
Марка грозозащитного троса: ТК-50.
Материал изоляторов: фарфор
Степень загрязненности атмосферы I.
2 Определение физико-механических характеристик провода и
троса
Физико-механические характеристики провода и троса приведены
в таблицах 2.1 и 2.2.
Таблица 2.1 - Физико-механических характеристики провода
АС-150/24
|
Сечение, мм2:
алюминиевой части
стальной части
суммарное F
|
149
24,2
173,2
|
|
Диаметр провода d, мм
|
17,1
|
|
Количество и диаметр проволок, шт×мм:
алюминиевых
стальных
|
26×2,7
7×2,1
|
|
Количество повивов, шт.
алюминиевой части
стальной части
|
2
1
|
|
Вес провода Gп, даН/км
|
600
|
|
Модуль упругости Е, даН/мм2
|
8,25·103
|
|
Температурный коэффициент линейного
удлинения α, град-1
|
19,2·10-6
|
|
Предел прочности, даН/мм2
|
29
|
|
Удельная нагрузка от собственного
веса γ1, даН/(м×мм2)
|
3,46·10-3
|
|
Допустимое напряжение, даН/мм2
при среднегодовой температуре σt.ср
при низшей температуре σt min
при наибольшей нагрузке σγ
max
|
8,7
13,0
13,0
|
Таблица 2.2 - Физико-механических характеристики троса
ТК-50
|
Сечение, мм2:
номинальное
фактическое Fт
|
50
48,6
|
|
Диаметр троса dт, мм
|
9,1
|
|
Количество и диаметр проволок, шт×мм
|
19×1,8
|
|
Количество повивов, шт.
|
2
|
|
Вес троса Gт, даН/км
|
417
|
|
Модуль упругости Ет, даН/мм2
|
20·103
|
|
Температурный коэффициент линейного
удлинения αт, град-1
|
12·10-6
|
|
Предел прочности, даН/мм2
|
120
|
|
Удельная нагрузка от собственного
веса γт1, даН/(м×мм2)
|
8·10-3
|
|
Допустимое напряжение, даН/мм2
при среднегодовой температуре σтt.ср
при низшей температуре σтt.min
при наибольшей нагрузке σтγ.max
|
42
60
60
|
3 Выбор унифицированной опоры
По исходным данным выбирается тип унифицированной
промежуточной опоры ПБ110-8. Основные размеры опоры показаны на рисунке 3.1,
технические характеристики опоры приведены в таблице 3.1.
H=26,0м; h1=3,0м; h2=13,5м; h3=4,0м;
a1=2,0м; a2=3,5м; a3=2,0м; b=3,3м
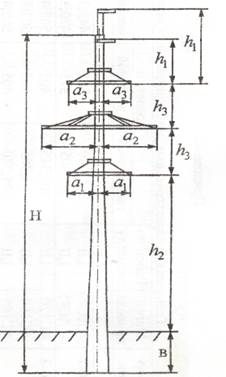
Рисунок 3.1 – Унифицированная железобетонная опора
ПБ110-8
Таблица 3.1 – Технические характеристики опоры ПБ110-8
|
Марка провода
|
Район по гололеду
|
Пролет, м
|
Масса, т
|
|
габаритный
|
ветровой
|
весовой
|
|
АС-150
|
III,IV
|
225
|
250
|
280
|
7,5
|
Расчетный пролет, м,
lр=α·lгаб,
где α=0,9 для ненаселенной местности;
lр=0,9·225=202,5.
4 Расчет проводов и троса на
механическую прочность
4.1 Определение толщина стенки
гололеда и величины скоростного напора ветра
Средняя высота подвеса проводов на опоре, м,
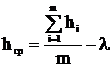 ,
(4.1)
,
(4.1)
где hi – расстояние от земли до j-ой траверсы опоры, м;
m – количество проводов на опоре;
λ – длина гирлянды изоляторов, м.
Для предварительных расчетов длина гирлянды изоляторов
принимается для ВЛ 110 кВ 1,3 м.
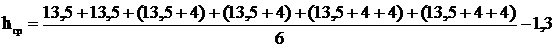 =16,2.
=16,2.
Средняя высота подвеса троса на опоре, м,
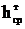 =h2+2·h3+h1,
(4.2)
=h2+2·h3+h1,
(4.2)
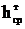 =13,5+2·4+3=24,5.
=13,5+2·4+3=24,5.
Допустимая стрела провеса провода, м,
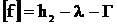 ,
(4.3)
,
(4.3)
где h2 – расстояние от земли до нижней траверсы, м;
Г – габаритный размер, м;
 =6,2.
=6,2.
Допустимая стрела провеса троса, м,
[fт]= 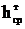 -(Г+2·h3+z), (4.4)
-(Г+2·h3+z), (4.4)
где z – наименьшее допустимое расстояние по вертикали
между проводом и тросом в середине пролета, м, для lр=202,5 м z=4;
[fт]=24,5-(6+2·4+4)=6,5.
Высота приведенного центра тяжести провода и троса, м,
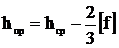 ,
(4.5)
,
(4.5)
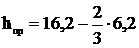 =12;
=12;
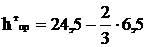 =20,2
=20,2
Толщина стенки гололеда для провода и троса, мм,
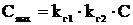 ,
(4.6)
,
(4.6)
где С – нормативное значение стенки гололеда, мм, (для
2-го района по гололеду С=10 мм);
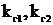 -
поправочные коэффициенты на высоту и диаметр провода или троса
-
поправочные коэффициенты на высоту и диаметр провода или троса
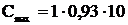 =9,3;
=9,3;
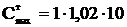 =10,2.
=10,2.
Скоростной напор ветра на провод и трос, даН/м2,
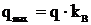 ,
(4.7)
,
(4.7)
где q – нормативный скоростной напор ветра, даН/м2;
kВ – поправочный коэффициент;
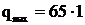 =65;
=65;
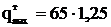 =81,25.
=81,25.
4.2 Определение удельных нагрузок
на провод и трос
Удельная нагрузка от собственного веса, даН/(м∙мм2),
берется из таблиц 2.1 и 2.2:
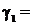 3,46·10-3;
3,46·10-3;
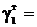 8·10-3.
8·10-3.
Удельная нагрузка от веса гололеда, даН/(м∙мм2),
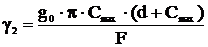 ,
(4.8)
,
(4.8)
где d – диаметр провода или троса, мм;
F – фактическое сечение провода или троса, мм2;
g0=0,9·10-3 даН/(м∙мм2) – плотность гололедных
отложений;
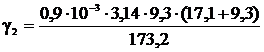 =4·10-3;
=4·10-3;
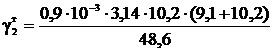 =11,4·10-3.
=11,4·10-3.
Удельная нагрузка от веса гололеда и собственного веса
провода (троса), даН/(м∙мм2),
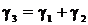 ,
(4.9)
,
(4.9)
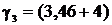 ·10-3=7,46·10-3;
·10-3=7,46·10-3;
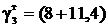 ·10-3=19,4·10-3.
·10-3=19,4·10-3.
Удельная нагрузка от давления ветра при отсутствии
гололеда, даН/(м∙мм2),
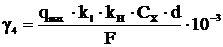 ,
(4.10)
,
(4.10)
где kl – коэффициент, учитывающий влияние длины пролета
на ветровую нагрузку;
kH – коэффициент, учитывающий неравномерность скоростного
напора ветра по пролету;
СХ – коэффициент лобового сопротивления, равный 1,1 – для
проводов диаметром 20 мм и более, свободных от гололеда; 1,2 – для всех
проводов, покрытых гололедом, и для проводов диаметром меньше 20 мм, свободных
от гололеда;
 =5,7·10-3;
=5,7·10-3;
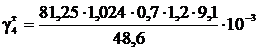 =13,1·10-3.
=13,1·10-3.
Удельная нагрузка от давления ветра на провод и трос при
наличии гололеда, даН/(м∙мм2),
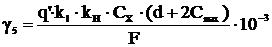 ,
(4.11)
,
(4.11)
где q′=0,25∙qmax для районов с толщиной
стенки гололеда до 15 мм;
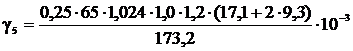 =4,1·10-3;
=4,1·10-3;
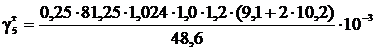 =15,1·10-3.
=15,1·10-3.
Удельная нагрузка от давления ветра и веса провода
(троса) без гололеда, даН/(м∙мм2),
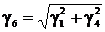 ,
(4.12)
,
(4.12)
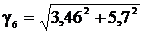 ·10-3=6,7·10-3;
·10-3=6,7·10-3;
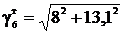 ·10-3=15,3·10-3.
·10-3=15,3·10-3.
Удельная нагрузка на провод от давления ветра и веса
провода, покрытого гололедом, даН/(м∙мм2),
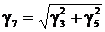 (4.13)
(4.13)
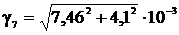 =8,5·10-3;
=8,5·10-3;
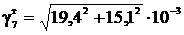 =24,6·10-3.
=24,6·10-3.
4.3 Расчет критических пролетов
Первый критический пролет, м,
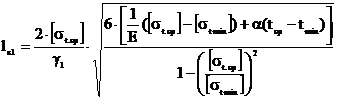 ,
(4.14)
,
(4.14)
где Е – модуль упругости, даН/мм2;
α – температурный коэффициент линейного удлинения
материала провода, град-1;
lk1=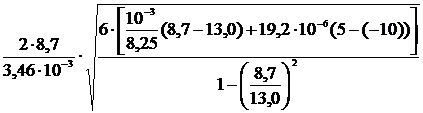 .
.
Выражение под корнем меньше нуля. Первый критический
пролет – мнимый.
Второй критический пролет, м,
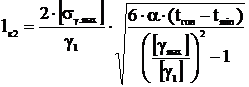 ,
(4.15)
,
(4.15)
где tгол – температура гололеда, равная -5ºС;
γmax=γ7;
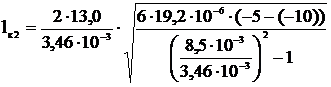 =80,4.
=80,4.
Третий критический пролет, м,
 ,
(4.16)
,
(4.16)
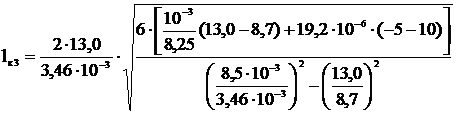 =144,2.
=144,2.
В результате получается следующее соотношение критических
пролетов и расчетного пролета: lк1 – мнимый, lр=202,5 м>lк3=144,2 м.
На основании полученных соотношений определяется исходный
режим. Это режим максимальной нагрузки с параметрами: σ=[σγ.max]=13,0
даН/мм2, γ=γmax=8,5·10-3 даН/(м·мм2), t=tгол=-5°С.
4.4 Расчет напряжений в проводе
По уравнению состояния провода рассчитываются напряжения в
проводе для режимов среднегодовой температуры – σtср, режима низшей
температуры – σtmin и наибольшей нагрузки – σγmax.
Расчет напряжения в проводе для режима низшей
температуры. В уравнение состояния провода подставляются все известные
параметры.
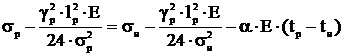 ,
(4.17)
,
(4.17)
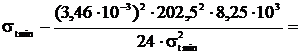
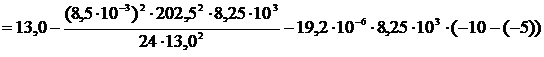 .
.
Полученное уравнение приводится к виду:
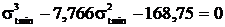
Решение полученного уравнения выполняется итерационным
методом касательных. В качестве нулевого приближения принимается значение σ0=10
даН/мм2.
Производная полученной функции y= :
:
y’=3·σ2tmin-2·7,766·σtmin
Определяется поправка на первой итерации:
Δ1=y(σ0)/y’(σ0),
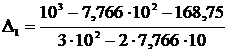 =0,378.
=0,378.
Новое значение напряжения:
σ1=σ0-Δ1,
σ1=10-0,377=9,623.
Проверка итерационного процесса. Для этого задается
точность расчета ε=0,01 даН/мм2.
0,377>0,01,
следовательно расчет нужно продолжить, приняв в качестве
нового приближения σ=9,623.
Поправка на второй итерации:
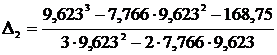 =0,025.
=0,025.
Новое значение напряжения:
σ2=9,623-0,025=9,598.
Выполняется проверка:
0,025>0,01.
Поправка на третьей итерации:
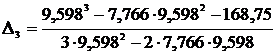 =0,00013.
=0,00013.
Проверка:
0,00013<0,01,
следовательно за искомое выражение σtmin принимаем σ3:
σtmin=9,598 даН/мм2.
Расчеты напряжений в проводе для режимов среднегодовой
температуры и наибольшей нагрузки выполняются с помощью программы «MERA2». В
результате получены следующие значения:
σtср=7,987 даН/мм2;
σγmax=12,517 даН/мм2.
Выполняется проверка условий механической прочности:
σtср≤[σtср], 7,987<8,7;
σtmin≤[σtmin], 9,598<13,0;
σγmax≤[σγmax], 12,517<13,0.
Условия выполняются, значит механическая прочность
проводов будет достаточной для условий проектируемой линии.
По уравнению состояния провода выполняются расчеты
напряжений для режимов гололеда без ветра –σгол, высшей температуры – σtmax,
грозового режима – σгр. Результаты расчетов следующие:
σtmax=5,475 даН/мм2;
σгол=12,277 даН/мм2;
σгр=7,129 даН/мм2.
4.5 Определение стрелы провеса
проводов и троса
Определяются стрелы провеса проводов в режиме гололеда
без ветра, высшей температуры и грозовом режиме, м,
 ,
(4.18)
,
(4.18)
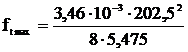 =3,24;
=3,24;
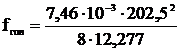 =3,11;
=3,11;
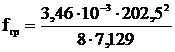 =2,49.
=2,49.
Проверка соблюдения требуемых расстояний от низшей точки
провисания провода до земли по условию:
f≤[f]=6,2;
ftmax=3,24<6,2;
fгол=3,11<6,2.
Условия выполняются, значит расстояние от провода до
земли будет не менее габаритного размера.
Стрела провеса грозозащитного троса в грозовом режиме, м,
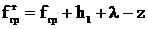 ,
(4.19)
,
(4.19)
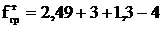 =2,79.
=2,79.
4.6 Определение напряжений в
тросе
Напряжение в тросе в грозовом режиме, даН/мм2,
 ,
(4.20)
,
(4.20)
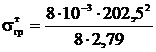 =14,7.
=14,7.
В качестве исходного принимается грозовой режим с
параметрами: σтгр, γт1, t=15°C. По уравнению состояния провода
определяются напряжения в тросе для режимов максимальной нагрузки, низшей и
среднегодовой температуры.
Расчет напряжения в тросе для режима среднегодовой
температуры. В уравнение состояния провода подставляются все известные
параметры.
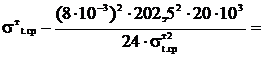
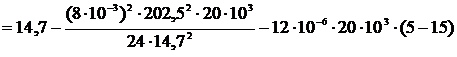 .
.
Полученное уравнение приводится к виду:
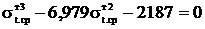 .
.
В качестве нулевого приближения принимается значение σ0=16
даН/мм2.
Производная полученной функции
y=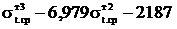 :
:
y’=3·σт2tср-2·6,979·σтtср
Определяется поправка на первой итерации:
Δ1=y(σ0)/y’(σ0),
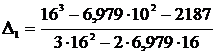 =0,225.
=0,225.
Новое значение напряжения:
σ1=σ0-Δ1,
σ1=16-0,225=15,775.
Проверка итерационного процесса, ε=0,01 даН/мм2.
0,225>0,01,
следовательно расчет нужно продолжить, приняв в качестве
нового приближения σ=15,775
Поправка на второй итерации:
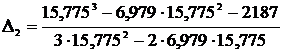 =0,003.
=0,003.
Проверка:
0,003<0,01,
следовательно за искомое выражение σтtср принимаем σ1:
σтtср=15,775 даН/мм2.
В результате расчетов остальных режимов получены
следующие значения:
σтγmax=31,476 даН/мм2;
σтtmin=17,606 даН/мм2.
Проверка условий механической прочности троса:
σтγmax=31,476 даН/мм2≤ [σтγmax]=60
даН/мм2;
σтtmin=17,606 даН/мм2≤ [σтtmin]=60
даН/мм2;
σтtср=15,775 даН/мм2≤ [σтtср]=42 даН/мм2.
Условия выполняются, значит выбранный провод пригоден для
условий проектируемой линии.
5 Выбор изоляторов и линейной
арматуры
Тип изолятора выбирается по механической нагрузке с
учетом коэффициента запаса прочности, который представляет собой отношение
разрушающей электромеханической нагрузки к нормативной нагрузке на изолятор.
Согласно ПУЭ, коэффициенты запаса прочности в режиме наибольшей нагрузки должны
быть не менее 2,7, а в режиме среднегодовой температуры – не менее 5,0.
В нормальных режимах поддерживающая гирлянда изоляторов
воспринимает осевую нагрузку, состоящую из веса провода, гололеда и веса самой
гирлянды.
Нагрузка для изоляторов поддерживающих гирлянд, даН,
2,7·(Gг+Gи)≤ Gэм,
5,0·(Gп+Gи)≤Gэм, (5.1)
где Gг – нагрузка на изолятор от веса провода, покрытого
гололедом, даН,
Gг=γ7·F·lвес, (5.2)
где lвес=280 м – длина весового пролета;
F – общее фактическое сечение провода, мм2;
Gи – нагрузка на изолятор от веса гирлянды, даН,
предварительно Gи=50 даН;
Gп – нагрузка на изолятор от веса провода, даН,
Gп=γ1·F·lвес, (5.3)
Тогда
2,7·( γ7·F·lвес+
Gи)=2,7·(8,5·10-3·173,2·280+50)=1248;
5,0·( γ1·F·lвес+
Gи)=5,0·(3,46·10-3·173,2·280+50)=1089.
Выбирается изолятор с такой разрушающей
электромеханической нагрузкой, чтобы выполнялись условия (5.1). Выбирается
изолятор ПФ70-В с разрушающей электромеханической нагрузкой 7500 даН:
1248<7500;
1089<7500,
т.е. условия выполняются.
Определяется число изоляторов в поддерживающей гирлянде,
n≥ , (5.4)
, (5.4)
где λэф – нормированная удельная эффективная длина
пути утечки. Для степени загрязненности атмосферы I λэф=13 мм/кВ;
Uнаиб=1,15·Uном;
lэф – эффективная длина пути утечки, мм,
lэф=lут/k, (5.5)
где lут =355 мм для выбранного изолятора;
k – поправочный коэффициент,
k=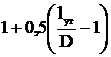 ,
(5.6)
,
(5.6)
где D – диаметр тарелки изолятора, D=270 мм;
k=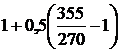 =1,157;
=1,157;
lэф=355/1,157=306,8;
n≥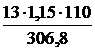 =5,4.
=5,4.
Полученное значение округляется до шести и увеличивается
на один. В итоге число изоляторов в поддерживающей гирлянде равно семи.
При выборе изоляторов натяжных гирлянд в условия (5.1)
добавляется величина тяжения провода.
Нагрузка на изолятор натяжной гирлянды, даН,
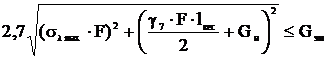
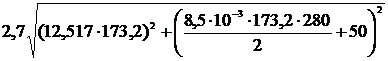 =5894,
=5894,
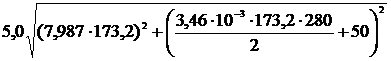 =6949.
=6949.
Выбирается изолятор ПФ70-В с разрушающей
электромеханической нагрузкой 7500 даН:
5894<7500;
6949<7500,
т.е. условия выполняются.
Число изоляторов в натяжной гирлянде принимается на один
больше, чем в поддерживающей, т.е. восемь штук. Выбор арматуры аналогичен
выбору изоляторов. Коэффициент запаса прочности для условий гололеда должен
быть не менее 2,5. Нагрузка на арматуру поддерживающей гирлянды, даН,
2,5·(Gг+Gи)≤ Gр, (5.8)
2,5·(8,5·10-3·173,2·280+50)=1156.
Выбирается узел крепления гирлянды к траверсе опоры
КГП-7-1, серьгу СР-7-16, ушко У1-7-16 с разрушающей минимальной нагрузкой 70
кН; глухой поддерживающий зажим ПГН-3-5 с минимальной разрушающей нагрузкой 25
кН.
Нагрузка на арматуру натяжной гирлянды, даН,
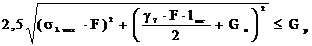 ,
(5.9)
,
(5.9)
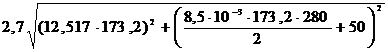 =5457.
=5457.
Для натяжной гирлянды выбирается та же арматура что и для
поддерживающей. Для натяжной гирлянды выбираем болтовой зажим.
Изолятор и линейная арматура изображены на рисунках
5.1-5.5.
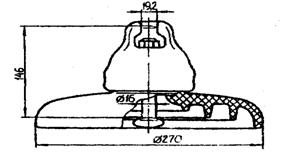
Рисунок 5.1 – Изолятор ПФ70-В
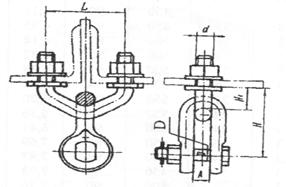
Рисунок 5.2 – Узел крепления КГП-7-1
D=16 мм; А=17 мм; d=16 мм; L=80 мм; Н1=32 мм; Н=82 мм
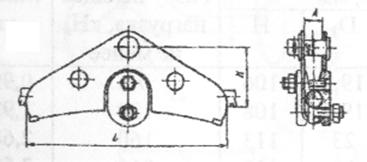
Рисунок 5.3 – Зажим поддерживающий ПГН-3-5
L=220 мм; А=20 мм; Н=66 мм
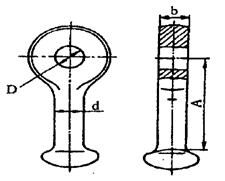
Рисунок 5.4 – Серьга СР-7-16
D=17 мм; d=16 мм; А=65 мм; b=16 мм
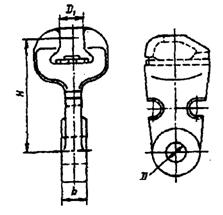
Рисунок 5.5 – Ушко У1-7-16
D=17 мм;D1=19,2 мм; b=16 мм; Н=104 мм
Фактический вес поддерживающей гирлянды, даН,
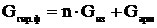 ,
(5.10)
,
(5.10)
где Gиз – вес одного изолятора, даН;
Gарм – суммарный вес элементов арматуры, даН;
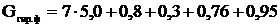 =37,81.
=37,81.
Фактическая длина поддерживающей гирлянды, м,
 ,
(5.11)
,
(5.11)
где Низ – высота одного изолятора, м;
Нарм – суммарная высота элементов арматуры, м;
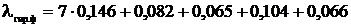 =1,339.
=1,339.
Получили λгир.ф =1,339 больше, чем принятое в
расчетах λ=1,3.
Проверка соблюдения габарита.
Пересчитанная допустимая стрела провеса, м,
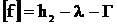 ,
,
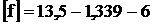 =6,161.
=6,161.
Проверка соблюдения требуемых расстояний от низшей точки
провисания провода до земли по условию:
f≤[f]=6,161,
ftmax=3,24<6,161.
Условие соблюдается, т.е. такая длина гирлянды допустима.
Защита от вибрации осуществляется с помощью гасителей
вибрации, представляющих собой два груза, закрепленных на стальном тросике
(рисунок 5.6).
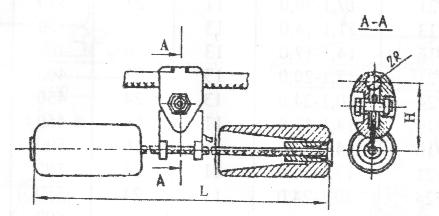
Рисунок 5.6 – Гаситель вибрации ГПГ-1,6-11-400/21
d=11 мм; 2R=21 мм; L=400 мм; H=78 мм
Выбор гасителя вибрации осуществляется с учетом марки и
сечения провода. Выбирается гаситель вибрации ГПГ-1,6-11-400/21. Для
грозозащитного троса гаситель вибрации не требуется, так как σтtср<18,0
даН/мм2.
Расстояние от зажима до места крепления виброгасителя,
мм,
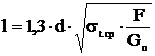 ,
(5.12)
,
(5.12)
где d – диаметр провода, мм;
Gп – вес одного метра провода, даН;
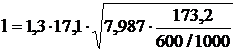 =1067,4
мм≈1,07 м.
=1067,4
мм≈1,07 м.
6 Расстановка опор по профилю
трассы
6.1 Построение шаблона
На заданном профиле трассы расстановка опор производится
с помощью специальных шаблонов. Шаблон представляет собой три кривые провисания
провода, сдвинутые относительно друг друга, построенные в виде парабол для
режима, при котором возникает наибольшая стрела провеса. В п. 4.5 была
определена максимальная стрела провеса, которая соответствует режиму
максимальной температуры, fmax=3,24 м.
Кривая 1 – кривая провисания нижнего провода – строится
на основе формулы стрелы провеса:
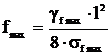 ,
(6.1)
,
(6.1)
где γfmax, σfmax – удельная нагрузка и
напряжение в проводе в режиме, отвечающем наибольшей стреле провеса. Данная
формула представляется в виде уравнения:
y=a·x2, (6.2)
где
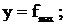
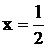 ; a=
; a=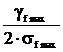 .
.
Для режима максимальной температуры уравнение примет вид:
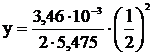 ,
,
Для построения кривой 1 в 1-ом квадранте выполняется
несколько расчетов, представленных в виде таблицы 6.1.
Таблица 6.1 – Построение кривой 1
|
l
|
0
|
50
|
100
|
150
|
202,5
|
|
x
|
0
|
25
|
50
|
75
|
101,
|
|
y
|
0
|
0,27
|
0,79
|
1,78
|
3,24
|
Кривая 2, называемая габаритной, сдвинута о вертикали
вниз от кривой 1 на расстояние требуемого габарита от земли Г=6 м. Кривая 3 –
земляная – сдвинута от кривой 1 вниз на расстояние h2-λгир.ф=13,5-1,339=12,161
м (рисунок 6.1).
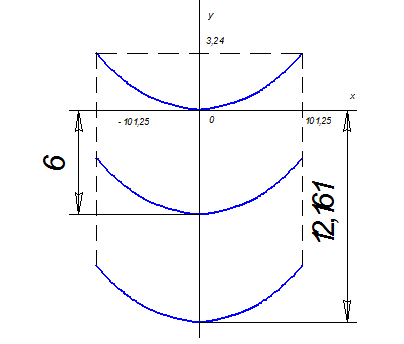
Рисунок 6.1 – Построение шаблона
Шаблон накладывают на профиль трассы так, чтобы кривая 3
пересекала профиль в месте установки первой анкерной опоры, а кривая 2 касалась
его, при этом ось у должна быть строго вертикальной. Тогда другая точка
пересечения кривой 3 с профилем будет соответствовать месту установки первой
промежуточной опоры. При таком положении шаблона во всех точках пролета габарит
будет не меньше допустимого. Аналогично находится место установки второй
промежуточной опоры и т.д.
После монтажа анкерного участка в проводах происходит
выравнивание напряжения, которое соответствует какому-то условному пролету.
Этот пролет называется условным, и его длина, м, определяется из выражения:
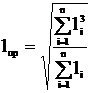 ,
(6.3)
,
(6.3)
где li – фактическая длина i-го пролета в анкерном
участке, м;
n – количество пролетов в анкерном участке;
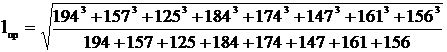 =166.
=166.
В результате расчетов получили что lпр отличается от lр
на
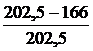 ∙100%=18%,
∙100%=18%,
что больше допустимых 5%. В таком случае заново
проводится механический расчет, построение шаблона и расстановка опор на
трассе. Для данного курсового проекта допускается изменить расстановку опор без
проведения повторного механического расчета.
Построение нового шаблона.
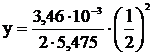 ,
,
Для построения кривой 1 в 1-ом квадранте выполняется
несколько расчетов.
Таблица 6.2 – Построение кривой 1
|
l
|
0
|
50
|
100
|
166
|
|
x
|
0
|
25
|
50
|
83
|
|
y
|
0
|
0,27
|
0,79
|
2,18
|
Новая расстановка опор показана на рисунке 6.3.
Приведенный пролет, м,
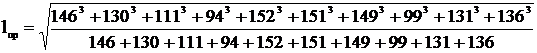 =132
=132
Проверка:
 ∙100%=20%.
∙100%=20%.
В результате повторного расчета разница между приведенным
и расчетным пролетом снова велика. Расчет повторяется до тех пор пока разница
между значениями пролетов будет не более 5%.
6.2 Проверка опор на прочность
При расстановке опор по профилю трассы все они должны
быть проверены на прочность в реальных условиях. Проверка выполняется
сопоставлением вычисленных для каждой опоры весового и ветрового пролетов со
значениями этих пролетов, указанных в технических характеристиках опоры.
Весовой пролет, м,
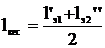 ,
(6.4)
,
(6.4)
где эквивалентные пролеты вычисляются по формулам:
-первый (большой) эквивалентный пролет, м,
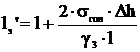 ,
(6.5)
,
(6.5)
-второй (малый) эквивалентный пролет, м,
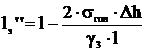 ,
(6.6),
,
(6.6),
где l – действительная длина пролета, м;
Δh – разность между высотами точек подвеса провода,
м;
Смежными эквивалентными пролетами, прилегающими к опоре,
могут быть и два больших или два малых эквивалентных пролета. Тогда выражение
(6.4) будет иметь вид:
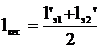 ;
;
или
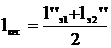 .
.
Ветровой пролет, м,
 .
(6.7)
.
(6.7)
Расчет для второй опоры.
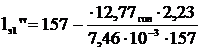 =108,4;
=108,4;
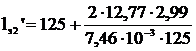 =206,9;
=206,9;
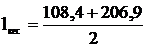 =157,6;
=157,6;
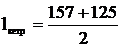 =141,0.
=141,0.
Для остальных опор расчет сводится в таблицу 6.2.
Таблица 6.2 – Проверка опор на прочность
|
№ опоры i
|
l'эi-1, м
|
l”эi-1, м
|
l’эi, м
|
l”эi, м
|
Δhi-1, м
|
Δhi, м
|
lвес, м
|
lветр, м
|
|
1
2
3
4
5
6
7
|
-
-
-
-
204,3
-
-
|
184,3
108,4
43,1
168,0
-
104,6
148,7
|
205,6
206,9
200,0
-
189,4
173,3
165,0
|
-
-
-
143,7
-
-
-
|
0,55
2,23
2,99
0,86
1,54
1,82
0,58
|
2,23
2,99
0,86
1,54
1,82
0,58
0,41
|
194,9
157,6
121,5
155,8
196,8
138,9
156,8
|
175,5
141,0
154,5
179,0
160,5
154,0
158,5
|
Таким образом, для каждой опоры выполняются условия
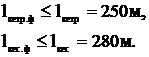
7 Расчет монтажных стрел провеса
провода и троса
Определяется исходный режим из соотношений трех
критических пролетов и приведенного пролета: lк1 – мнимый, lпр=166 м>lк3=144,2
м.
На основании полученных соотношений определяется исходный
режим. Это режим максимальной нагрузки с параметрами: σи=[σγ.max]=13,0
даН/мм2, γи=γmax=8,5·10-3 даН/(м·мм2), tи=tгол=-5°С.
Расчет напряжения при монтаже осуществляется с помощью
уравнения
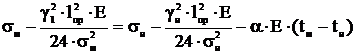 .
(7.1)
.
(7.1)
Стрела провеса провода в интересующем пролете lф, м,
определяется из выражения
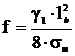 ,
(7.2).
,
(7.2).
Тяжение провода, даН, рассчитывается по формуле
 ,
(7.3)
,
(7.3)
С помощью уравнения состояния рассчитывается напряжение в
проводе при температуре монтажа tmax=40°C и tmin=-10°C.
при tmax=40°C:

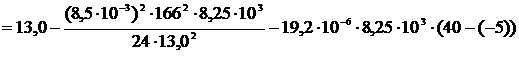 .
.
Полученное уравнение приводится к виду:
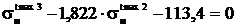 .
.
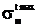 =5,53
даН/мм2.
=5,53
даН/мм2.
Тяжение в проводе, даН,
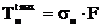 ,
,
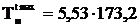 =957,8.
=957,8.
при tmin=-10°C:
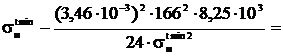
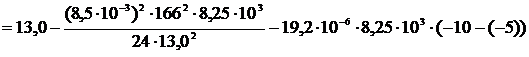 .
.
Полученное уравнение приводится к виду:
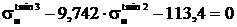 .
.
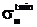 =10,74
даН/мм2.
=10,74
даН/мм2.
Тяжение в проводе, даН,
 =1860,2
даН.
=1860,2
даН.
Для наибольшего пролета lmax=194 м и наименьшего пролета
lmin=125 м по формуле (7.2) рассчитываются стрелы провеса при максимальной и
минимальной температурах, м,
lmax=194 м
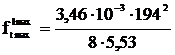 =2,94;
=2,94;
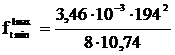 =1,52;
=1,52;
lmin=125 м
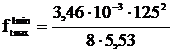 =1,22;
=1,22;
 =0,63.
=0,63.
Расчет при других температурах выполняется аналогично,
результаты заносятся в таблицу 7.1.
Стрела провеса провода в габаритном пролете при
температуре 15°С, м,
 ,
(7.4)
,
(7.4)
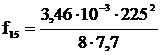 =2,84.
=2,84.
Исходные данные для троса: σтгр=14,7 даН/мм2, γт1=8·10-3
даН/(м·мм2), t=15°C.
Стрела провеса троса в габаритном пролете в режиме грозы
исходя из требуемого расстояния z для габаритного пролета, м,
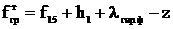 ,
(7.5)
,
(7.5)
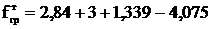 =3,104.
=3,104.
Определяется величина напряжения в тросе по известной
величине fтгр, даН/мм2,
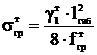 ,
(7.6)
,
(7.6)
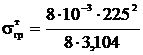 =16,3.
=16,3.
Определяются напряжения в тросе при температуре монтажа
из уравнения состояния, принимая в качестве исходного грозовой режим.

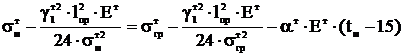 , (7.7)
, (7.7)
Для наибольшего пролета lmax=194 м и наименьшего пролета
lmin=125 м рассчитываются стрелы провеса троса, м,
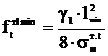 ,
(7.8)
,
(7.8)
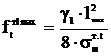 ,
(7.9)
,
(7.9)
Тяжение в тросе, даН,
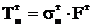 ,
(7.10)
,
(7.10)
Расчет для температуры -10°С.
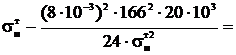
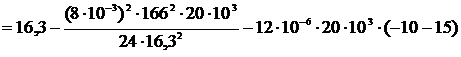
Полученное уравнение приводится к виду:
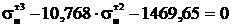 .
.
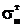 =20,33
даН/мм2.
=20,33
даН/мм2.
Тяжение в тросе, даН,
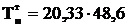 =988
даН.
=988
даН.
Стрела провеса при lmax=194 м, м,
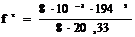 =1,85.
=1,85.
Стрела провеса при lmin=125 м, м,
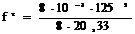 =0,77.
=0,77.
Расчет при других температурах выполняется аналогично,
результаты заносятся в таблицу 7.2.
Таблица 7.1 – Монтажная таблица провода
|
Температура, °С
|
Напряжение, даН/мм2
|
Тяжение, даН
|
Стрела провеса в пролете длиной, м
|
|
l=194
|
l=125
|
|
-10
0
10
15
20
30
40
|
10,74
9,42
8,24
7,70
7,19
6,28
5,53
|
1860,2
1631,5
1427,2
1333,6
1245,3
1087,7
957,8
|
1,52
1,73
1,97
2,11
2,26
2,59
2,94
|
0,63
0,72
0,82
0,88
0,94
1,08
1,22
|
Таблица 7.2 – Монтажная таблица троса
|
Температура, °С
|
Напряжение, даН/мм2
|
Тяжение, даН
|
Стрела провеса в пролете длиной, м
|
|
194 м
|
125 м
|
|
-10
0
10
20
30
40
|
20,33
18,61
17,03
15,60
14,33
|
988,0
904,4
827,7
758,2
696,4
641,5
|
1,85
2,02
2,21
2,41
2,63
2,85
|
0,77
0,84
0,92
1,00
1,09
1,18
|
Монтажные графики для провода и троса изображены на
рисунках 7.1 и 7.2.
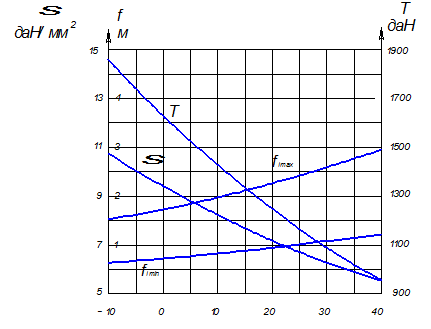
Рисунок 7.1 – Монтажные графики для провода
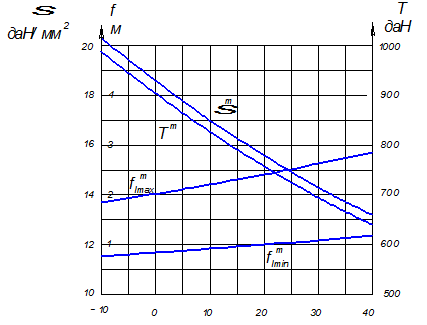
Рисунок 7.2 – Монтажные графики для троса
Заключение
В данном курсовом проекте были рассмотрены основные этапы
проектирования механической части воздушных ЛЭП: выполнены выбор промежуточных
опор, механический расчет проводов и грозозащитного троса, выбор линейной
арматуры, произведены расстановка опор по профилю трассы и расчет монтажных
стрел провеса.
В ходе выполнения данного курсового проекта получены
навыки пользования справочными материалами и нормативными документами, а также
навыки выполнения самостоятельных инженерных расчетов с привлечением
прикладного программного обеспечения персональных компьютеров.
Список литературы
1. Правила
устройства электроустановок. – СПб.: Издательство ДЕАН, 2001. – 928 с.
2. Проектирование
механической части воздушных ЛЭП. Учебное пособие по курсовому и дипломному
проектированию. – Киров, 2004.-99 с.