Определение производственного плана предприятия при наличии различных критериев

Определение производственного плана предприятия при наличии различных критериев

Введение

Математическое программирование представляет собой математическую дисциплину, занимающуюся изучением экстремальных задач и разработкой методов решений.

Экономико-математические модели (ЭММ) - модели экономических процессов, при описании которых используются математические средства.

В рамках курсовой работы необходимо рассмотреть задачу оптимизации ресурсов при планировании производства. Для этого в работе должно быть проведено:

Построить ЭММ однокритериальных и многокритериальных задач

Решить однокритериальную задачу, выполнить послеоптимизационный анализ, получить целочисленное решение методом Гомори и ветвей и границ.

Решить две однокритериальные задачи с параметром в целевой функции и в правой части ограничений.

Решить многокритериальные задачи (МКЗ) заданными методами.

Анализ решения МКЗ с указанием и обоснованием приоритетов, расчет рентабельности.

Целью работы является определение производственного плана предприятия с помощью различных математических методов и получение навыков пользование программой WinQSB.

Постановка задачи

Промышленное предприятие может изготавливать три вида изделий А, В и С, используя при этом три основных, т.е. определяющих программу выпуска вида ресурсов R1, R2, R3. Нормы расхода ресурсов на единицу изделий каждого вида, запасы ресурсов на месяц, себестоимость изготовления единицы изделия и их цены приведены в таблице 1. По требованиям технологии ресурс R3 должен быть полностью израсходован в течении месяца. Необходимо сформировать план выпуск изделий на месяц, применяя следующие критерии:

Максимум выручки от реализации произведенной продукции.

Минимум себестоимости изготовления изделий.

Максимум получаемой прибыли.

Задача решается для двух критериев: себестоимость и прибыль.

Исходные данные: Вариант А6: x=2, y=1, z=6.

Таблица 1

Теоретические основы решения задач

Математическая постановка оптимизационной задачи.

Общей задачей линейного программирования называется задача, которая состоит в определении максимального (минимального) значения функции при условиях - ограничениях (матричная форма записи задачи линейного программирования):

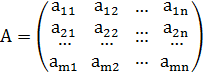
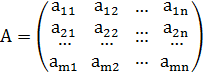 - технологическая матрица коэффициентов.

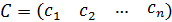
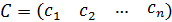 - вектор удельной прибыли от реализации продукции.

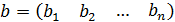
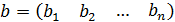 - вектор запасов ресурсов.

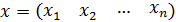
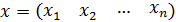 - вектор переменных.

Используя данные обозначения, получим искомый план производства продукции:

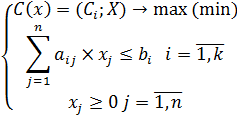
Где ci, aij, bi - заданные постоянные величины.

Каноническая форма записи задачи линейной оптимизации (ЗЛО) имеет особенность, принципиально отличающую ее от других форм записи. А именно, если в стандартной форме соотношении между количеством переменных n и не прямых ограничений m произвольное, то в канонической ЗЛО всегда число уравнений строго меньше числа переменных, т.е. m<n.

Сведение стандартной формы записи ЗЛО к канонической производится путем введение дополнительных переменных  :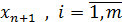

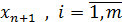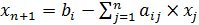
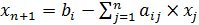
Таким образом, ограничения - неравенства преобразуются в ограничения равенства. Матрица коэффициентов новой системы ограничений имеет вид:

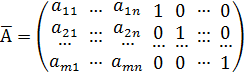
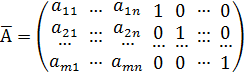
Итак, введение дополнительных переменных в стандартную форму ЗЛО (1) преобразовывает ее в ЗЛО (2):

Основные определения линейной оптимизации (ЛО).

Определение 1. Множество векторов

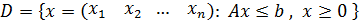
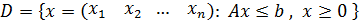
называется множеством допустимых решений задачи или допустимым множеством.

Определение 2. Вектор 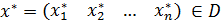 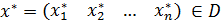(из множества допустимых планов) называется оптимальном планом задачи, или задачи, если для любого вектора х из допустимого множества выполняется неравенство С(х) ≤ С(х*).

Определение 3. Пусть 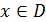 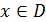- допустимый план ЗЛО. Носителем плана х называется множеством индексов .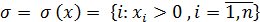

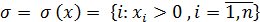Определение 4. Пусть 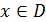 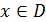- допустимый план ЗЛО и σ - его носитель. Если векторы Аi, 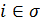 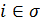линейно независимые, то план Х называется базисным допустимым планом (БДП) или базисным допустимым решением (БДР).

Симплекс - метод.

Основные этапы симплекс - метода, при этом ЗЛО должна быть в приведенной форме:

Построение начального БДП х0.

Проверка плана х0 на оптимальность. Вычисление двойственных оценок.

Если все Δj ≥ 0, 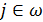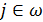, тогда БДП х0 - оптимальный.

Если условие оптимальности не выполнено, т.е. существует Δs<0, то реализуется процедура поиска нового БДП х1, которая заключается в определении вектора Ak, вводимого в базис, и вектора Ar, выводимого из базиса. При этом значение целевой функции на новом плане будет не меньше, чем на плане х0, т.е. С (х0) ≤ С (х1). В процессе поиска нового БДП может быть сделан вывод, что в ЗЛО существует оптимальный план.

Если БДП х1 существует, то происходит возврат к п. 2, а именно вычислению двойственных оценок, но уже для плана х1 и т.д., пока не будет найден оптимальный план, или не будет установлено, что такого плана нет.

Методы решения задач параметрической оптимизации

Параметрическая оптимизация - это метод определения того, как меняется решение задачи с изменением или вектора коэффициентов целевой функции, или вектора ограничений, или того и другого вместе.

Параметры μ и λ могут изменяться в интервале (-∞, ∞), однако из содержательной постановки задачи обычно следует их принадлежность более узкому интервалу.

Методы решения многокритериальных задач (МКЗ).

Многокритериальная задача линейной оптимизации (МКЗ ЛО) записывается в следующем виде:

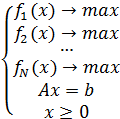
Здесь 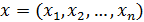 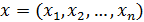- вектор переменных.

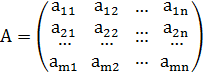
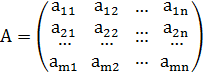 - матрица системы ограничений.

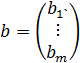
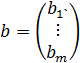 - вектор правых частей ограничений

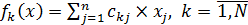
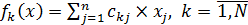 - k-й критерий (целевая функция).

План 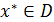 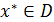называется эффективным (или Парето - оптимальным, или оптимальным по Парето) если не существует другого плана 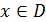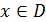, который не хуже, чем х*, по всем критерием и лучше, чем х* по некоторому критерию fk, другими словами, не существует 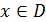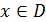, такого что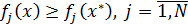 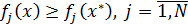 , и хотя бы для одного k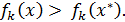

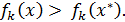
Метод сверстки критериев. Суть метода - сведение имеющего множества критериев к одному скалярному критерию, отражающую комбинированную (общую) цель системы критериев.

Каждому из критериев 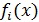 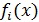приписываются весовые коэффициенты ai , причем на эти коэффициенты накладывается требование:

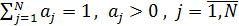
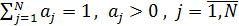
Сверстка критериев представляет собой функцию следующего вида:

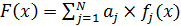
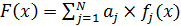
Однако критерии могут иметь различную физическую природу и, следовательно, выражаться в различных единицах измерения. Для этого предварительно целевые функции нормируют, переходя к новым функциям вида:

 ,

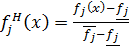
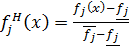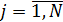
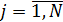
Где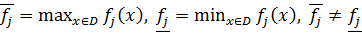

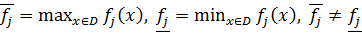
В результате таких действий решении задачи выглядит так:

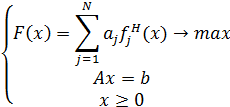
Замечание 1. Если все критерии однородны, т.е. выражены в одинаковых единицах измерения, то можно не нормировать целевые функции, а в задачи применять свертку.

Замечание 2. Решение задачи, получаемое с помощью любого свертывания критериев (при любых 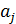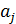, удовлетворяющих условию), является эффективным планом.

Замечание 3. Весовые коэффициенты 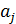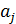, лицо принимающее решение (ЛРП) может изменять по своему усмотрению с целью получения наиболее приемлемого плана.

Метод главного критерия. Суть метода - из множества имеющихся критериев выбирается наиболее важный для ЛРП, а остальные критерии записываются в виде дополнительных ограничений.

Предположим, что 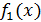 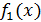- главный (наиболее важный для ЛРП) критерий. Пусть 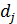 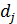- нижняя граница j-го критерия, устанавливаемая ЛРП. При этом .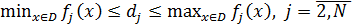

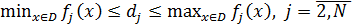Тогда решение будет:

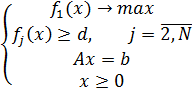
Модифицированный метод идеальной точки. Суть метода - найти допустимое решение 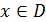 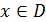такое, что точка достижимого множества 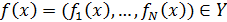 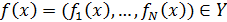оказывается ближайшей к идеальной точке .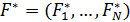

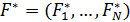Чтобы нелинейный критерий привести к линейному виду, введем новую переменную 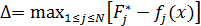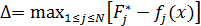. Таким образом, в данном методе решение МКЗ ЛО определяется в результате нахождения оптимального плана следующей задачи ЛО:

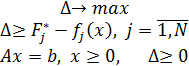
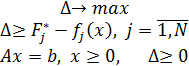
Идеальная точка - это некоторая точка, которая существует, и мы не можем улучшить одно значение, не ухудшая при этом другое.

Метод последовательных уступок (или пороговых значений). Суть метода - все критерии ранжируются по степени важности для ЛРП. Далее последовательно решаются однокритериальные задачи в установленном порядке с добавлением в каждую последующую задачу дополнительного ограничения на предыдущий критерий.

Пусть 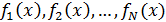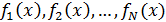. Сначала решает задача ЛО:

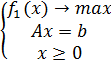
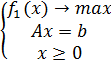
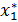
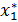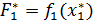
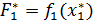В результате решения задачи определяется финальный план  и вычисляется значения целевой функции на этом плане . Затем вычисляются и анализируются значения остальных критериев на этом плане 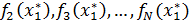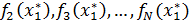. ЛРП анализирует значение первого критерия 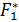 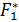и назначают максимальную уступку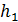 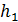такую, что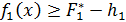 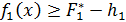. Далее решается следующая задача:

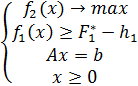
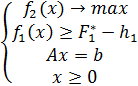
Для оптимального плана задачи 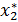 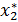анализируется значение критериев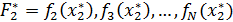 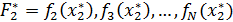. Если значение устраивает ЛРП, то план 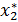 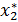принимается за лучшее решение. В противном случае вводится следующая уступка 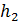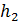, по второму критерию и решается задача, и так далее пока решение не будет удовлетворять ЛРП.

Экономико-математическая модель.

Переменные:

х1 - количество изделий вида А, шт.

х2 - количество изделий вида В, шт.

х3 - количество изделий вида С, шт.

Целевая функция:

Минимум себестоимости изготовления изделий, тыс. рублей

L(х) = 10х1 + 17х2 + 18х3 → min

Максимум получения прибыли, тыс. рублей

C(х) = 4х1 + 2х2 + 4х3 → max

Максимум получаемой выручки, тыс. рублей

M(х) = 14х1 + 19х2 + 22х3 → max

Ограничения:

По ресурсу R1 2х1 + х2 + 3х3 ≤ 27

По ресурсу R2 2х1 + х2 + 4х3 ≤ 35

По ресурсу R3 3х1 + 2х2 + 6х3 = 44

Не отрицательность переменных х1, х2, х3 ≥ 0

Целочисленности х1, х2, х3 - целые

Канонический вид.

L(х) = - 10х1 - 17х2 - 18х3 → max(х) = 4х1 + 2х2 + 4х3 → max(х) = 14х1 + 19х2 + 22х3 → max

х1 + х2 + 3х3 + х4 = 27

х1 + х2 + 4х3 х5 = 35

х1 + 2х2 + 6х3 = 44

х1, х2, х3 х4 х5 ≥ 0

х1, х2, х3 - целые

Решение однокритериальной задачи симплекс - методом. Послеоптимизационный анализ. Целочисленное решение.

Задание: решить однокритериальную задачу ЛП с целевой функцией «выручка» симплекс-методом. Выполнить послеоптимизационный анализ. Целочисленное решение получить методом Гомори и методом ветвей и границ.

С(х) = 14Х1 + 19Х2 + 22Х3 à max - выручка

Ограничения по запасам:

Х1+Х2+3Х3 <= 27

X1+3X2+4X3 <= 35

X1+2X2+4X3 = 44

Х1,Х2,Х3 >= 0

Решаем задачу при условии максимизации выручки симплекс методом

Приводим к каноническому виду:

С(х) = 14Х1 + 19Х2 + 22Х3 à max

Ограничения по запасам:

Х1+Х2+3Х3 + Х4 = 27

X1+3X2+4X3 + Х5 = 35

X1+2X2+4X3 = 44

Х1, Х2, Х3, Х4, Х5 >= 0

Вводим искусственный базис.

Х1+Х2+3Х3 + Х4 = 27

X1+3X2+4X3 + Х5 = 35

X1+2X2+4X3 + Х6 = 44

Х1, Х2, Х3, Х4, Х5, Х6 >= 0

Вводим новую целевую функцию(с искусственным базисом).

С(х) = -Х6 à max

Ответ: С(х) = 418; Х*=(0; 22; 0)

У задачи сразу нашлось целочисленное решение, поэтому применение метода Гомори и метода Ветвей и границ(которые нужны для получения целочисленного решения), к сожалению, не требуется.

Отчет по устойчивости

Для того, чтобы получить максимальную выручку от реализации произведенной продукции, равную 418 тыс. руб., нужно изготавливать 0 шт. изделия А, 22 шт. изделия В и 0 шт. изделия С.

Допустимое увеличение, допустимое уменьшение таблицы «изменяемые ячейки» - показывает границы изменений коэффициентов целевой функции, при которых сохраняется набор переменных, входящих в оптимальное решение. Например, если стоимость изделия А увеличится(из-за каких-либо изменений на рынке) на 14,5 и более единиц, то изменится набор переменных, входящих в оптимальное решение. Уменьшаться цена этого изделия может до нуля, без изменения структуры плана. Цена изделия В может уменьшаться на 9,6667 ед. и неограниченно увеличиваться без изменения структуры плана. Цена на продукт С может изменяться в диапазоне от 0 до 35 без изменения структуры плана.

Результирующее значение таблицы ограничений - значение левой части ограничения при оптимальном плане. Т.е. сколько фактически использовано ресурса. Например, ресурса R1 - 22 ед., ресурса R2 - 22, а ресурса R3 - 44.

Теневая цена - изменение целевой функции при изменении ресурса на 1 единицу. Теневая цена недефицитного ресурса будет равна 0. Например, изменения количества ресурса R1 или ресурса R2 не повлияет на значение целевой функции (= 0), а увеличение запаса ресурса R3 приведет к увеличению выручки на 9,5 единиц. Допустимое увеличение, допустимое уменьшение таблицы ограничений - показывает, насколько можно изменить правую часть ограничения до того момента пока это будет влиять на структуру целевой функции. Например, увеличение ресурсов R1 и R2 никак не повлияет на целевую функцию. Уменьшение же ресурса R1 более чем на 5 единиц или ресурса R2 более чем на 13 единиц приведет к изменению структуры плана. Ресурс R3 может изменяться в диапазоне от 10 до 44 единиц без изменения структуры плана.

Решение однокритериальных задач с параметром в целевой функции и в ограничениях

Решить две однокритериальные задачи при следующих условиях.

Параметр в целевой функции

Данный этап выполняется с помощью программы. Изначально я ввожу свои ограничения и коэффициенты целевой функции, затем получаю необходимые мне таблицы.   

Таблица№1

Ввод данных

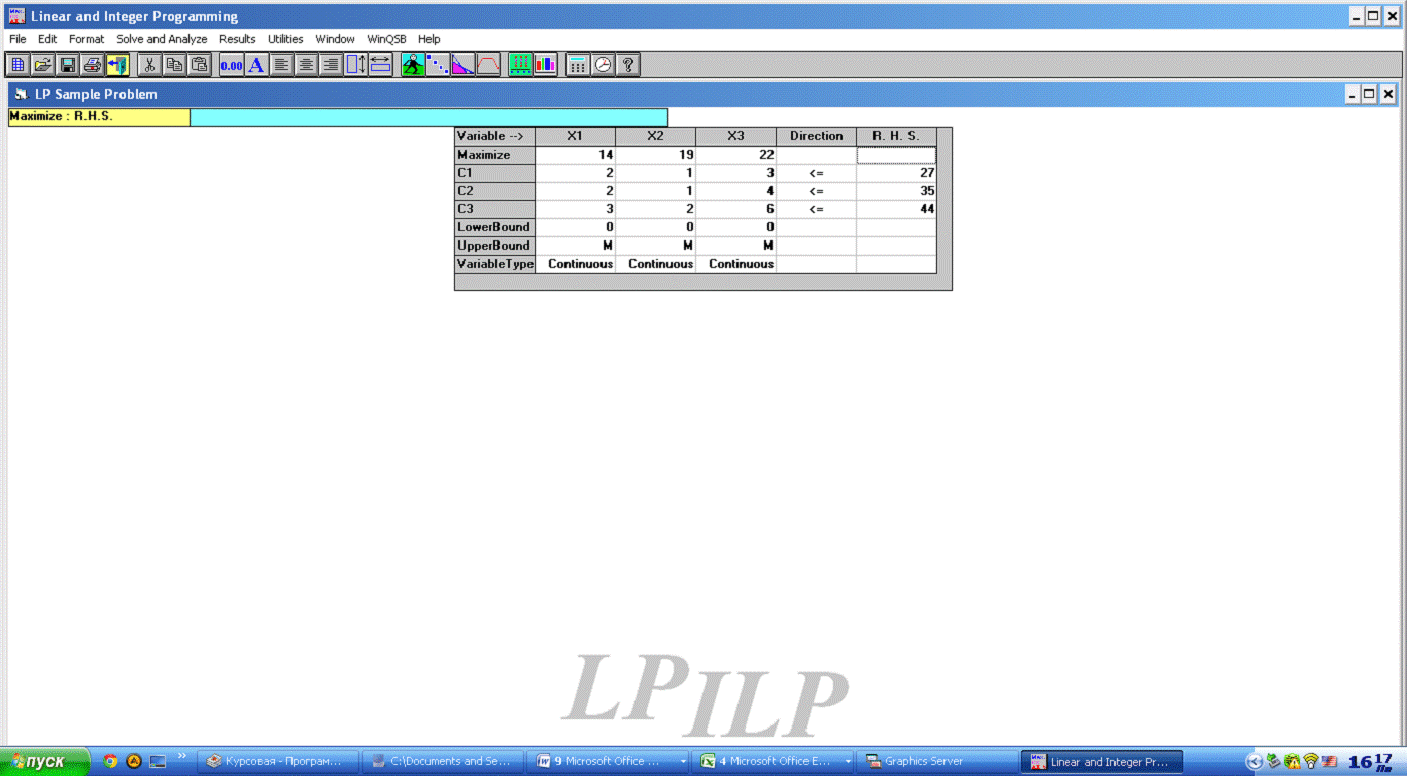
Таблица№2

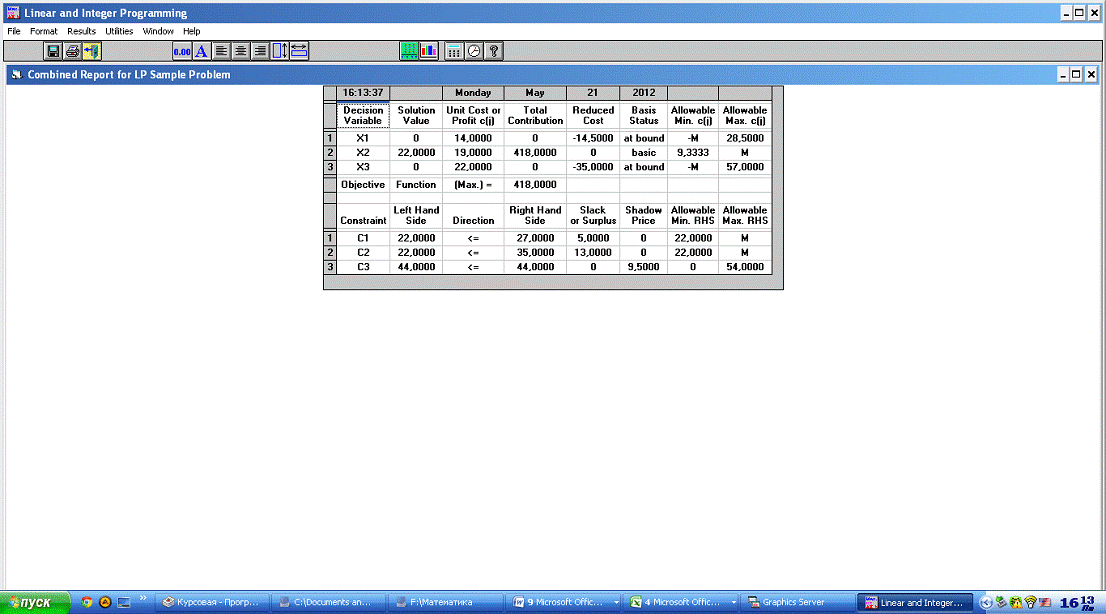
Таблица№3

Интервалы

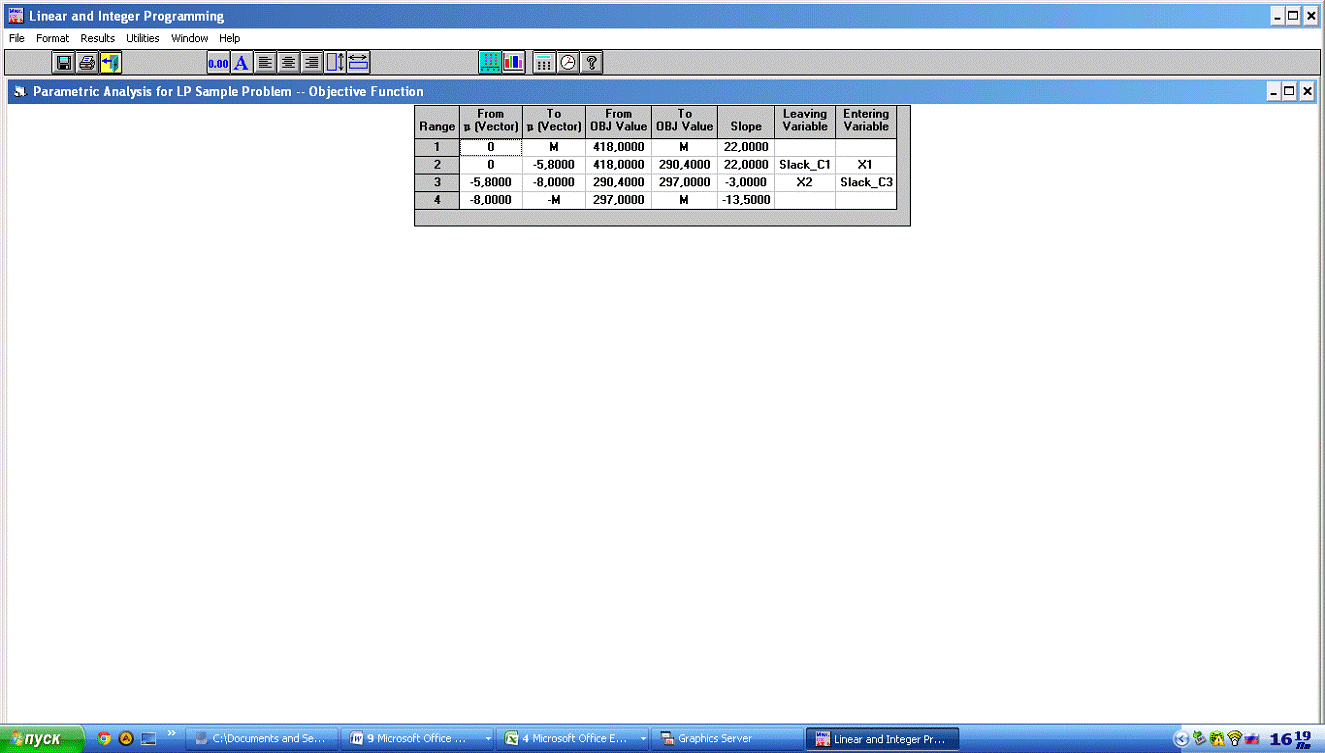
С этой таблицей я и буду работать, в ней мне необходимо пересчитать значения. Моя целевая функция имеет вид C(X) = 14X1+19X2+22X3 стремится к max. Добавив параметр, я получаю:

(14-Л)X1+(19+Л)X2+(22+2Л)X3, (Л - параметр лямбда).

Л максимальное = 14

Л минимальное = -11

Произвожу пересчет верхней и нижней границ моего интервала, подставив, вместо Х1, Х2, Х3 - 0, 22, 0, соответственно, поскольку X*(0,22,0). В итоге я получаю, что М=726, а -М=176.

Вывод: Если цена на первый товар колеблется в интервале [0;14], то вторая цена - [19;33], третья - [22;50], то целевая функция изменяется в этом же интервале. При изменении цен (первая уменьшится на единицу, вторая увеличится на единицу, а третья увеличится на 2 единицы), целевая функция увеличится на 22.

График

Таблица№4

Данные для графика

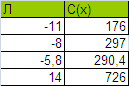
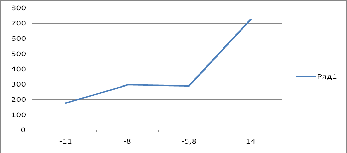
Параметр в правой части ограничений

Задание: предприятие может использовать не более чем 3(x+y+z)+2ℷ единицы ресурса R1 и не более чем 4x+3y+4z-ℷ единицы ресурса R2, где ℷ - некоторый параметр. Для каждого возможного значения ℷ определить план производства изделий, при котором выручка от реализации является максимальной.

С(х) = 14Х1 + 19Х2 + 22Х3 à max

х1 + х2 + 3х3 ≤ 27+2t

х1 + 3х2 + 4х3 ≤ 35-t

х1, х2, х3 ≥ 0

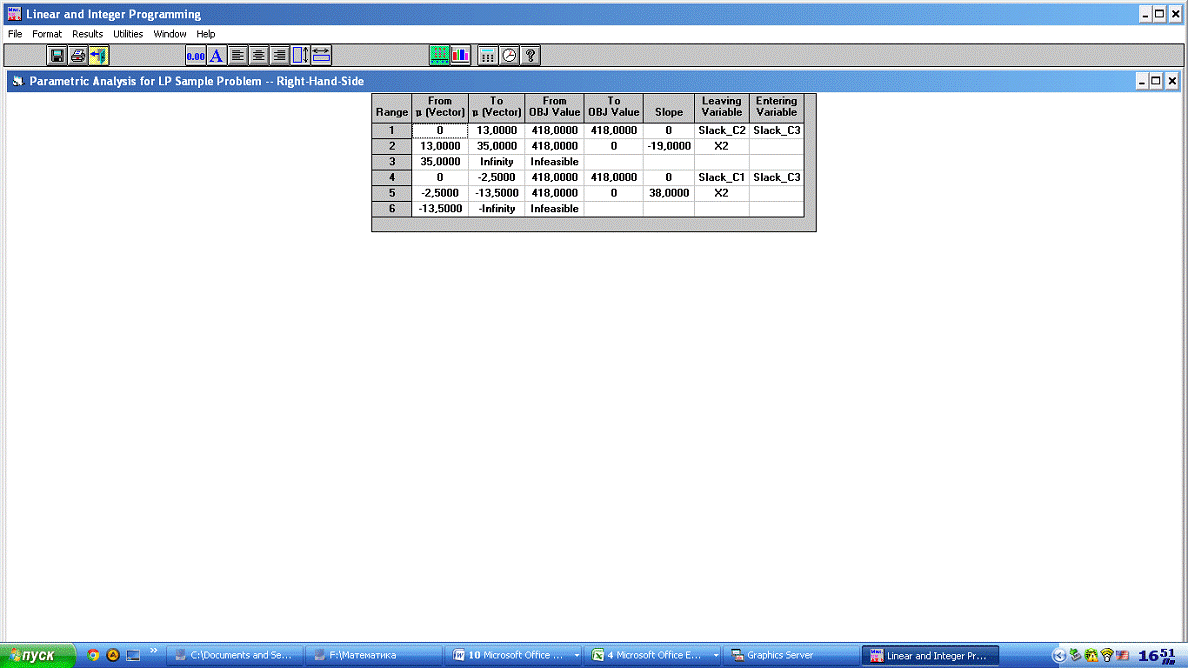
Выводы

В случае, если μ будет находиться в интервале -∞ ≤ μ ≤ -13,5, то задача не будет иметь решения.

Если μ будет находиться в интервале -13,5 ≤ μ ≤ -2,5, то выручка будет изменяться от 418 тыс. руб. до 0 тыс. руб., при этом запас ресурса R1 будет изменяться от 0 кг до 22 кг, а запас ресурса R2 будет изменяться от 37,5 кг до 48,5 кг.

Если μ будет находиться в интервале -2,5 ≤ μ ≤ 0, то выручка будет 418 тыс. руб., при этом запас ресурса R1 будет изменяться от 22 кг до 27 кг, а запас ресурса R2 будет изменяться от 37,5 кг до 35 кг

Если μ будет находиться в интервале 0 ≤ μ ≤ 13, то выручка будет 418 тыс. руб., при этом запас ресурса R1 будет изменяться от 27 кг до 53 кг, а запас ресурса R2 будет изменяться от 35 кг до 22 кг.

Если μ будет находиться в интервале 13 ≤ μ ≤ 35, то выручка будет изменяться от 418 тыс. руб. до 0 тыс. руб., при этом запас ресурса R1 будет изменяться от 53 кг до 97 кг, а запас ресурса R2 будет изменяться от 22 кг до 0 кг.

В случае если μ будет находиться в интервале 35 ≤ μ ≤ ∞, то задача не будет иметь решения.

Решение многокритериальной задачи

Задание 6.1. Решение многокритериальной задачи методом свертки критериев

Решение многокритериальной задачи осуществлялось относительно следующих целевых функций:

Выручка (тыс. руб.):

f1(x) = 14x1+19x2+22x3

Себестоимость (тыс. руб.):

f2(x) = 10x1 + 17x2 + 18x3 → min

Ограничения:

2х1 + х2 + 3х3 ≤ 27

х1 + х2 + 4х3 ≤ 35

х1 + 2х2 + 6х3 = 44

х1, х2, х3 ≥ 0

Нормирование функций не требуется, т.к. они имеют одинаковые единицы измерения тыс. руб.

Вводим новую функцию:

F(x) = (14x1+19x2+22x3)*a2 - (10x1 + 17x2 + 18x3 )*a1

С помощью Поиска решения получаем таблицу значений переменных и функций:

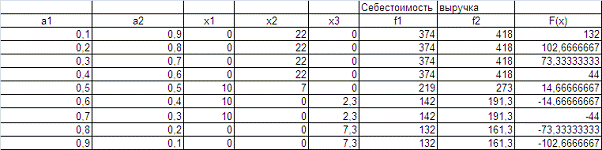
Задание 6.2. Решение многокритериальной задачи методом главного критерия

Решение многокритериальной задачи осуществлялось относительно следующих целевых функций:

Главный критерий - выручка (тыс. руб.):

f1(x) = 14x1 + 19x2 + 22x3 → max

Cебестоимость (тыс. руб.):

f2(x) = 10x1 + 17x2 + 18x3 → min

Критерий себестоимости был использован при решении задачи в качестве ограничения. Для этого с помощью надстройки MS Excel «Поиск решения» были определены максимальное и минимальное значение функции себестоимости:

f2(x)max = 374(x)min = 132

Полученные значения позволяют определить правую часть ограничения, полученного при использовании функции себестоимости: d1 = 200.

При этом условие задачи выглядит следующим образом:

f1(x) = 14x1 + 19x2 + 22x3 → max

x1 + x2 + 3x3 ≤ 27

x1 + x2 + 4x3 ≤ 35

x1 + 2x2 + 6x3 = 44

x1 + 17x2 + 18x3 ≤ 200, x2, x3 ≥ 0

При решении данной задачи с помощью надстройки MS Excel «Поиск решения» был получен оптимальный план указанной задачи: Х1* = (10; 5,27; 0,58),

f1 (Х1*) = 252,8, f2 (Х1*) = 200.

Возьмем d2 = 270, в этом случае условие задачи выглядит следующим образом:

f1(x) = 14x1 + 19x2 + 22x3 → max

x1 + x2 + 3x3 ≤ 27

x1 + x2 + 4x3 ≤ 35

x1 + 2x2 + 6x3 = 44

x1 + 17x2 + 18x3 ≤ 101, x2, x3 ≥ 0

При решении данной задачи с помощью надстройки MS Excel «Поиск решения» был получен оптимальный план указанной задачи: Х2* = (6,7; 11,9; 0),

f1 (Х2*) =320,7, f2 (Х2*) = 270.

Возьмем d3 = 370, в этом случае условие задачи выглядит следующим образом:

f1(x) = 14x1 + 19x2 + 22x3 → max

x1 + x2 + 3x3 ≤ 27

x1 + x2 + 4x3 ≤ 35

x1 + 2x2 + 6x3 = 44

x1 + 17x2 + 18x3 ≤ 101, x2, x3 ≥ 0

При решении данной задачи с помощью надстройки MS Excel «Поиск решения» был получен оптимальный план указанной задачи: Х3* = (0,26;21,6; 0),

f1 (Х3*) =414,26, f2 (Х3*) = 370.

Вывод: при увеличении предельной величины d функции f2 (х), т.е. себестоимости, значение функции f1(х), т.е. выручки, также увеличивается. При этом для получения максимальной выручки необходимо уменьшать объем производства изделия вида А, и увеличивать объем производства изделия вида В, изделие С при этом лучше вообще не производить.

Задание 6.3. Решение многокритериальной задачи методом последовательных уступок

параметрическая оптимизация критерий

Решение многокритериальной задачи осуществлялось относительно следующей целевой функции:

Выручка (тыс. руб.):

f1(x) = 14x1 + 19x2 + 22x3 → max

x1 + x2 + 3x3 ≤ 27

x1 + x2 + 4x3 ≤ 35

x1 + 2x2 + 6x3 = 44, x2, x3 ≥ 0

С помощью надстройки MS Excel «Поиск решения» был получен оптимальный план указанной задачи: Х1* = (0; 22; 0), f1(Х1*) = 418.

После этого была решена однокритериальная задача на функцию себестоимости с добавлением дополнительного ограничения на предшествующий критерий - функцию выручки f1(x):ебестоимость (тыс. руб.):

f2(x) = 10x1 + 17x2 + 18x3 → min

x1 + x2 + 3x3 ≤ 27

x1 + x2 + 4x3 ≤ 35

x1 + 2x2 + 6x3 = 44

x1 + 19x2 + 22x3 ≥ 14∙0+19∙22+22∙0, x2, x3 ≥ 0

При решении данной задачи с помощью надстройки MS Excel «Поиск решения» был получен оптимальный план указанной задачи: Х1* = (0; 22; 0),

f2(Х1*) = 374.

Вычтем из последнего ограничения допустимую величину h, ухудшая значение первого критерия, т.е. выручки.

Пусть h1 = 68 (максимум выручки составит 350 тыс. руб.), тогда:

f2(x) = 10x1 + 17x2 + 18x3 → min

x1 + x2 + 3x3 ≤ 27

x1 + x2 + 4x3 ≤ 35

x1 + 2x2 + 4x3 = 44

x1 + 19x2 + 22x3 ≥ 350, x2, x3 ≥ 0

При решении данной задачи с помощью надстройки MS Excel «Поиск решения» был получен оптимальный план указанной задачи: Х1* = (4,69; 14,97; 0),

f2(Х1*) = 301,31.

При полученном оптимальном плане значение критерия себестоимости уменьшилось, также уменьшилось и значение критерия выручки.

Пусть h2 = 88 (максимум выручки составит 330 тыс. руб.), тогда:

f2(x) = 10x1 + 17x2 + 18x3 → min

x1 + x2 + 3x3 ≤ 27

x1 + x2 + 4x3 ≤ 35

x1 + 2x2 + 4x3 = 44

x1 + 19x2 + 22x3 ≥ 330, x2, x3 ≥ 0

При решении данной задачи с помощью надстройки MS Excel «Поиск решения» был получен оптимальный план указанной задачи: Х3* = (6,07; 12,9; 0),

f2(Х3*) = 279,9.

Пусть h3 = 108 (максимум выручки составит 310 тыс. руб.), тогда:

f2(x) = 6x1 + 10x2 + 12x3 → min

x1 + x2 + 3x3 ≤ 24

x1 + 2x2 + 4x3 ≤ 30

x1 + 2x2 + 4x3 = 34

x1 + 13x2 + 14x3 ≥ 120, x2, x3 ≥ 0

При решении данной задачи с помощью надстройки MS Excel «Поиск решения» был получен оптимальный план указанной задачи: Х4* = (6,9; 11,6; 0),

f2(Х4*) = 267,1.

Вывод: при увеличении уступки для критерия выручки, значение критерия себестоимости уменьшается. При увеличении уступки объем выпуска изделий вида А увеличивается, а изделий вида В - снижается, изделия вида С не производятся.

Задание 6.4. Решение многокритериальной задачи модифицированным методом идеальной точки

Решение многокритериальной задачи осуществлялось относительно следующих критериев:

Выручка (тыс. руб.):

f1(x) = 14x1 + 19x2 + 22x3 → max

ебестоимость (тыс. руб.):

f2(x) = 10x1 + 17x2 + 18x3 → min

С помощью надстройки MS Excel «Поиск решения» были определены оптимальные значения указанных функций:

F1* = 418* = 132

С(х) = x4 → min

x1 + x2 + 3x3 ≤ 27

x1 + x2 + 4x3 ≤ 35

x1 + 2x2 + 6x3 = 44

+14x1 + 19x2 + 22x3 ≤ x4

- 10x1 - 17x2 - 18x3 ≤ x4, x2, x3, x4 ≥ 0

x1 + x2 + 3x3 ≤ 24

x1 + x2 + 4x3 ≤ 30

x1 + 2x2 + 6x3 = 34

x1 + 19x2 + 22x3 - x4 ≤ -418

x1 - 17x2 - 18x3 - x4 ≤ -132, x2, x3, x4 ≥ 0

При решении данной задачи с помощью надстройки MS Excel «Поиск решения» был получен следующий оптимальный план, при котором значение каждого критерия не может быть улучшено без ухудшения значения другого критерия: Х* = (0; 0; 7,33; 579,33), при этом f1(Х*) = 161,33, f2(Х*) = 132.

Задание 7.

Сведение результатов МКЗ в таблицу

Выводы по работе

В результате проделанной работы были использованы различные методы решения задач по оптимизации ресурсов при планировании производства. Так же при решении данной задачи были получены навыки в использовании программой WinQSB. На основе полученных данных был проведен анализ и выбран наиболее оптимальный план для решения данной задачи.

Для производства трех видов изделий А, В и С, используя при этом три основных вида ресурсов R1, R2 и R3 наилучший вариант для предприятия это производить продукцию А в размере 10 шт, продукцию В в размере 7 шт,а С - 0 шт., при этом себестоимость изделий будет составлять 219 тыс. рублей, прибыль - 54 тыс. рублей, а выручка - 273 тыс. рублей.

Список использованной литературы:

1. Кузменков В.А. Математические методы и модели исследования операций. Параметрическая, многокритериальная и целочисленное оптимизация: учеб. Пособие / В.А. Кузменков, В.Н. Юрьев. - 2-е изд., перераб. И доп. - СПб.: Изд-во Политехн. Ун-та, 2011. - 120 с.