Линейные системы передачи сигнала при несинусоидальных воздействиях
Министерство образования Российской
Федерации
Пензенский филиал Российского
государственного университета ИТП
Кафедра «Информационных систем»
Индивидуальная работа
По дисциплине: «Правила оформления
документации»
Выполнил: ст. гр. 10и1
Тарасов С.Г.
Проверил: Долотин А.И.
Пенза 2011 г
Содержание
Лист задания
Задание №1
Задание №2
Задание №3
Выводы
Список
использованных источников
Приложение А
Лист задания
Вариант 12-7-4г-12
Задание 1. Разложить периодическую несинусоидальную функцию (рисунок 1) в
ряд Фурье. Построить спектры амплитуд и фаз входного сигнала. Вычислить
коэффициент искажения формы сигнала
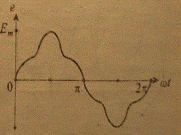
Рисунок 1 - Периодическая несинусоидальная функция
Параметры функции:
Еm=24В (максимальное значение ЭДС
входного сигнала);
Е0= -5В (значение дополнительной постоянной ЭДС);
w1=18000
рад/с (угловая частота несинусоидального сигнала);
Задание 2. Определить характеристические параметры
четырехполюсника (рисунок 2) на основной частоте сигнала w1. Построить амплитудно-частотные характеристики (АЧХ)
и фазо-частотные характеристики (ФЧХ) нагруженного четырехполюсника
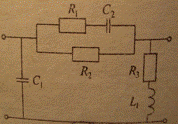
Рисунок 2 - Четырехполюсник
Параметры элементов четырехполюсника:
R1
= 50 Ом; ХС1(1)
= 210 Ом;
R2 = 140 Ом; ХС2(1) = 150 Ом; 
R3 = 60 Ом; ХL1(1)
= 20 Ом.
Задание
3. Определить коэффициент усиления КУ(w) из
условия наименьшего ослабления основной гармоники (w1).
Задание 1
Разложить несинусоидальную периодическую функцию (рисунок 1) в ряд Фурье,
построить спектры амплитуд и фаз входного сигнала и вычислить коэффициент
искажения.
Период функции T=2p.
Основные параметры входного сигнала:
Максимальное значение ЭДС входного сигнала Em = 24В
Дополнительная постоянная ЭДС E0 = -5В
Основная угловая частота несинусоидального сигнала w1 =18000 рад/с
Чтобы разложить функцию в ряд Фурье (формула (1)) функцию ƒ(ωt):
∞
ƒ(ωt)=A0+∑(ancos(nω1t)+bnsin(nω1t)), (1)=1
где ω - угловая частота, рад/с;
t -
время, с;
A0 - постоянная составляющая ряда;
n -
номер гармоники;
an - амплитуда косинусоидального члена;
bn - амплитуда синусоидального члена ряда.
Постоянная составляющая, которая рассчитывается по формуле (2)
представляет собой среднее значение функции ƒ(wt) за период:
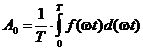
Коэффициенты
an и bn ряда
Фурье определяются по формулам (3), (4):


где n - номер гармоники. Ограничимся
четырьмя гармониками.
Процесс разложения облегчается, если несинусоидальная функция ƒ(ωt) обладает каким-либо видом
симметрии:
- функция ƒ(ωt) симметрична относительно координат
оси ординат, то есть
ƒ(ωt) = ƒ(-ωt);
функция ƒ(ωt) симметрична относительно начала оси
координат, то есть
ƒ(ωt) = ƒ(-ωt);
функция ƒ(ωt) симметрична относительно оси
абсцисс при совмещении двух полупериодов, то есть
ƒ(ωt) = -ƒ(ωt+π);
функция ƒ(ωt) симметрична относительно оси
ординат и оси абсцисс при совмещении двух полупериодов, то есть
ƒ(ωt) = ƒ(-ωt) = -ƒ(ωt+π);
функция ƒ(ωt) симметрична относительно начала
координат и оси абсцисс при совмещении двух полупериодов, то есть
ƒ(ωt) = -ƒ(-ωt) = -ƒ(ωt+π);
Данная функция обладает двумя видами симметрии:
функция ƒ(ωt) симметрична относительно начала оси
координат, то есть
(ωt) = ƒ(-ωt);
Тогда A0=an=b2n=0, а b2n+1 можно определить за четверть периода
по формуле (5):

Так как график функции ƒ(ωt) имеет сложную форму, то для
разложения в ряд Фурье используем графоаналитический метод: функция ƒ(ωt) разбивается на k равных интервалов и определяются
значения функции в точках разбиения. Тогда коэффициент bn найдём по формуле (6):

где k-число заданных точек за период,
возьмём 24 точки;
p - номер точки разбиения;
ƒp(ωt)-значение функции ƒ(ωt) в точке разбиения;
Δx=2π/k-интервал между точками разбиения, Δx=15°.
Данные по разбиению функции ƒ(ωt) представлены в таблице 1
Таблица 1
Данные по разбиению функции ƒ(ωt)
|
p
|
1
|
2
|
3
|
4
|
5
|
6
|
7
|
8
|
9
|
10
|
11
|
12
|
|
ƒp(ωt)
|
5
|
9
|
11
|
14
|
18
|
19
|
18
|
14
|
11
|
9
|
5
|
0
|
Вычислим коэффициент bn на первой гармонике (n=1):
b1=4/24∙[5sin(1∙1∙15)+9sin(1∙2∙15)+11sin(3∙15)+14sin(1∙4∙15)+18sin(5∙15)+
sin(6∙5)+
+18sin(1∙7∙15)+14sin(1∙8∙15)+11sin(1∙9∙15)+9sin(1∙10∙15)+5sin(11∙5)=4/24∙
(1,29+4,5++7,78+12,12+17,39+19+17,39+ +12,12+7,78+4,5+1,29)=17,53
Расчёт коэффициента bn по остальным гармоникам выполнен аналогичным способом, результаты
представлены в таблице 2
Таблица 2
Результат расчёта коэффициента bn
Амплитуда n-ой
синусоидальной гармоники определяется по формуле (7):
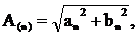 (7)
(7)
где
А(n) -
амплитуда n-ой синусоидальной гармоники.
Начальные
фазы для каждой гармоники определяются по формуле (8)
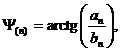 (8)
(8)
где
Y - начальная фаза для гармоники.
Вычислим
амплитуду и начальную фазу на первой гармонике:

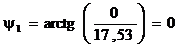
Расчёт
амплитуд и начальных фаз по остальным гармоникам выполнен аналогичным способом,
результаты представлены в таблице 3
Таблица 3
Расчёт амплитуд и начальных фаз
|
n
|
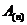 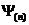
|
|
|
1
|
17,53
|
0
|
|
3
|
0,63
|
0
|
Запишем функцию f(wt):
f(wt)=17,53sin(wt)+0,63sin(3wt)+1,2sin(5wt)+0,057sin(7wt)
Построим график функции f(wt), который является входным сигналом
четырехполюсника (рисунок 4).
График чуть отличается от исходного в задании из-за погрешности
восстановления сигнала, происходит это за счет искажения гармоник.
Для визуального анализа вклада каждой гармоники в формирования исходной
функции построим дискретные спектры амплитуд (рисунок 5) и фаз (рисунок 6).
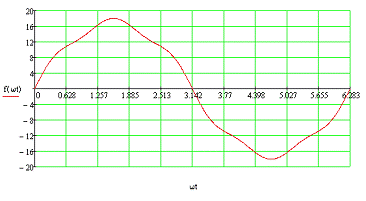
Рисунок 4 - График функции f(wt), который является входным сигналом
четырехполюсника
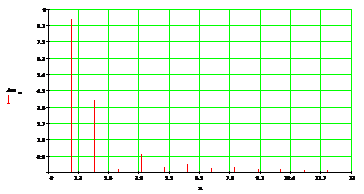
Рисунок
5 - Дискретные спектры амплитуд
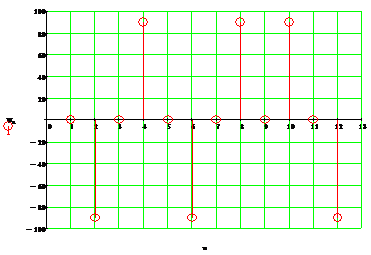
Рисунок 6 - Дискретные спектры фаз
Вычислим коэффициент искажения формы сигнала генератора Ки по
формуле (9):
Ки = A(1)/A, (9)
где Ки - коэффициент искажения формы сигнала генератора,
A(1)
- действующее значение
основной гармоники;
A -
действующее значение всех гармоник.
Рассчитаем коэффициент искажения:
A(1)= 17,53
A=A0+∑1/2∙A2m(n)=17,58
Ки=17,53/2∙17,58 =0,7
Задание 2
Задание 2: Определить характеристические параметры
четырехполюсника (рисунок 2) на основной частоте сигнала w1. Построить амплитудно-частотные характеристики (АЧХ)
и фазо-частотные характеристики (ФЧХ) нагруженного четырехполюсника.
Комплексные сопротивления четырёхполюсника (рисунок 7) для n-ой гармоники, которые рассчитываются
по формулам (9), (10), (11):
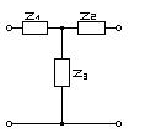
Рисунок 7 - Комплексные сопротивления четырёхполюсника
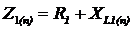 (9)
(9)
где
Z(n) - комплексное сопротивление;
R - реактивное
сопротивление резистора;
XL -
реактивное сопротивление катушки.
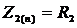 (10)
(10)
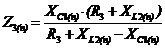 (11)
(11)
где
XС -
реактивное сопротивление конденсатора.
Вычислим
комплексные сопротивления четырёхполюсника на первой гармонике (n=1):
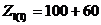
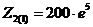
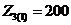
Расчет
комплексных сопротивлений по остальным гармоникам выполнен аналогичным
способом, результаты представлены в таблице 1 приложения А.
При
исследовании передачи энергии в электрических цепях чаще всего используют 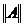 форму, которая определяется по формуле (12), где
входные величины U1 (входное
напряжение) и I1 (входной
ток) выражаются через выходные величины U2 (выходное напряжение), I2 (выходной ток) и A - параметры:
форму, которая определяется по формуле (12), где
входные величины U1 (входное
напряжение) и I1 (входной
ток) выражаются через выходные величины U2 (выходное напряжение), I2 (выходной ток) и A - параметры:
U1=A11U2+A12I2,1=A21U2+A22I2;
(12)
где
A11=U1/U2 при I2=0 - величина, обратная коэффициенту передачи по
напряжению в режиме холостого хода по выходу; A12=U1/I2 при U2=0 -
передаточное сопротивление четырёхполюсника в режиме короткого замыкания по
выходу; A21=I1/U2 при I2=0 - передаточная проводимость в режиме холостого хода
по выходу; A22=I1/I2 при U2=0 - величина, обратная коэффициенту передачи по току
в режиме короткого замыкания по выходу.
Найдём
параметры A11, A12, A21, A22 для Т - образного четырёхполюсника.
Выведем
параметры A11, A21, которые определяются в режиме холостого хода по
выходу (I2=0). По
закону Ома (формула 13) ток равен:
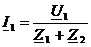 (13)
(13)
Найдём
напряжение U2 по
формуле (14):
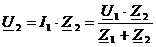 (14)
(14)
Выведем
параметр A11 по
формуле (15):
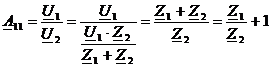 (15)
(15)
Выведем
параметр A21 по
формуле (16):
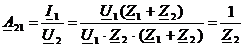 (16)
(16)
Выведем
параметры A12, A22, которые определяются в режиме короткого замыкания по
выходу (U2=0).
По
первому закону Кирхгофа (формула (17)) определим ток I1:
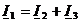 (17)
(17)
Далее
найдём ток I2 и I3 по формулам (18), (19):
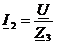 (18)
(18)
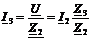 (19)
(19)
Тогда
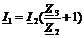 ,
,
по
закону Ома (формула (20)):
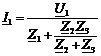 (20)
(20)
Выведем
параметр A12 по
формуле (21):
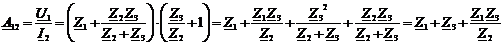 (21)
(21)
Выведем
параметр A22 по
формуле (22):
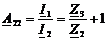 (22)
(22)
Вычислим
параметры A11, A12, A21, A22 на первой гармонике:
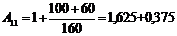
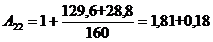
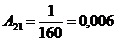
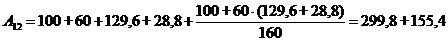
Расчёт
A параметров по остальным гармоникам выполнен
аналогичным образом, и результаты представлены в таблице 3
Таблица 3
Расчёт A параметров по гармоникам
|
ω/ω1
|
A11
|
A12
|
A21
|
A22
|
|
1
|
2
|
3
|
4
|
5
|
|
1
|
1,625+0,375
|
299,8+155,4
|
0,006
|
1,81+0,18
|
|
2
|
1,625+0,75
|
514,926+238,456
|
0,006
|
2,489-0,232
|
|
3
|
1,625+1,5
|
331,577+70,385
|
0,006
|
1,156-0,796
|
|
4
|
1,625+1,125
|
478,529+0,882
|
0,006
|
1,662-1,147
|
|
5
|
1,625+1,875
|
284,344+167,695
|
0,006
|
1,052-0,569
|
|
6
|
1,625+2,25
|
265,15+253,05
|
0,006
|
1,022-0,442
|
|
7
|
1,625+2,625
|
255,493+330,327
|
0,006
|
1,011-0,363
|
|
8
|
1,625+3
|
249,916+402,739
|
0,006
|
1,006-0,309
|
|
9
|
1,625+3,75
|
246,385+472,077
|
0,006
|
1,004-0,269
|
|
10
|
1,625+3,75
|
243,996+539,361
|
0,006
|
1,002-0,239
|
|
11
|
1,625+4,125
|
242,3+605,207
|
0,006
|
1,002-0,215
|
|
12
|
1,625+4,5
|
241,05+670,007
|
0,006
|
1,001-0,195
|
Определим характеристические параметры четырёхполюсника Z1С, Z2C - характеристические сопротивления и g - собственную постоянную передачи.Z1С - это входное сопротивление
четырёхполюсника при нагрузке на выходе Z2C, а Z2С - это выходное сопротивление четырёхполюсника
при нагрузке на входе Z1С. Собственная постоянная передачи g - это параметр, позволяющий оценить
передачу входного сигнала четырёхполюсником при согласованной нагрузке.
Определим характеристические сопротивления Z1C и Z2С на основной частоте сигнала w1 по формулам (23), (24):
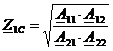 (23)
(23)
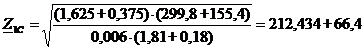
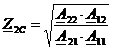 (24)
(24)
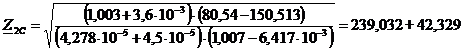
Рассчитаем
собственную постоянную передачи на основной частоте w1 по
формуле (25):
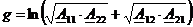 (25)
(25)
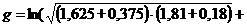
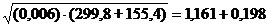
В
общем случае g определяется по формуле (26):
g=a+b,
(26)
где
a=1,034 Нп - собственная постоянная ослабления
(характеризует затухание входного сигнала);
b=-0,344 рад -
собственная постоянная фазы (характеризует сдвиг фазы входного сигнала).
Расчёт
собственной постоянной передачи g по остальным гармоникам выполнен аналогичным образом,
и результаты представлены в таблице 4
несинусоидальный амплитуда сигнал гармоника
Таблица 4
Расчёт собственной постоянной передачи g по гармоникам
|
ω/ω1
|
g
|
|
1
|
1,161+0,198
|
|
2
|
1,386+0,192
|
|
3
|
1,316+0,007
|
|
4
|
1,168+0,086
|
|
5
|
1,149+0,22
|
|
6
|
1,184+0,321
|
|
7
|
1,223+0,392
|
|
8
|
1,284+0,445
|
|
9
|
1,33+0,485
|
|
10
|
1,379+0,517
|
|
11
|
1,422+0,542
|
|
12
|
1,462+0,563
|
Наиболее часто для оценки передачи сигнала четырехполюсником используются
передаточные функции. Передаточная функция (или коэффициент передачи) - это
отношение комплексной выходной величины (U2 или I2) к
комплексной входной величине (U1 или I1).
Модули этих комплексных отношений представляют собой АЧХ
четырехполюсника, а их аргументы - ФЧХ.
Одной
из передаточных функций четырехполюсника является коэффициент передачи по
напряжению 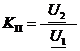 , который может быть выражен через А-параметры по
формуле (27):
, который может быть выражен через А-параметры по
формуле (27):
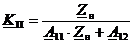 , (27)
, (27)
где
Zн -
сопротивление нагрузки четырёхполюсника.
В общем случае по формуле (28)
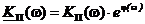 , (28)
, (28)
где KП(w) - модуль KП(w) (АЧХ);
j(w) - аргумент KП(w)
(ФЧХ).
Определим коэффициент передачи по напряжению четырёхполюсника на первой
гармонике KП(w1):
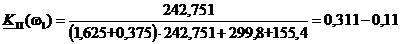
Определим
модуль коэффициента передачи по напряжению:
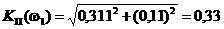
Определим
аргумент коэффициента передачи по напряжению четырехполюсника j(w):
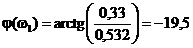 °
°
Расчёт модуля коэффициента передачи по напряжению KП и аргумента коэффициента передачи по напряжению по
остальным гармоникам выполнен аналогичным образом, и результаты представлены в
таблице 5.
Таблица 5
Расчёт модуля коэффициента передачи по напряжению KП
|
ω/ω1
|
KП
|
j, град.
|
|
1
|
0,33
|
-19,542
|
|
2
|
0,242
|
|
3
|
0,265
|
-17,424
|
|
4
|
0,287
|
-30,899
|
|
5
|
0,263
|
-42,538
|
|
6
|
0,234
|
-50,467
|
|
7
|
0,208
|
-56,108
|
|
8
|
0,186
|
-60,328
|
|
9
|
0,168
|
-63,606
|
|
10
|
0,153
|
-66,23
|
|
11
|
0,14
|
-68,379
|
|
12
|
0,13
|
-70,171
|
Теперь построим АЧХ (рисунок 8) и ФЧХ (рисунок 9) четырёхполюсника:
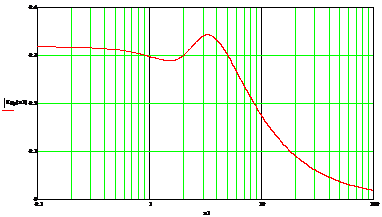
Рисунок 8 - АЧХ четырехполюсника
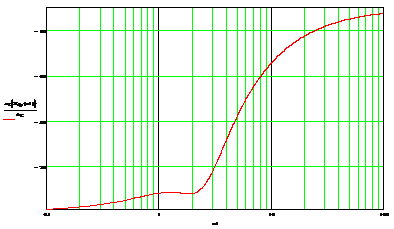
Рисунок 9 - ФЧХ четырехполюсника
Определим
коэффициент передачи сигнала по напряжению KГ от источника с ЭДС Ег и внутренним
сопротивлением Zг=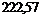 Ом к четырехполюснику на первой гармонике по формуле
(29):
Ом к четырехполюснику на первой гармонике по формуле
(29):
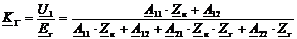 (29)
(29)
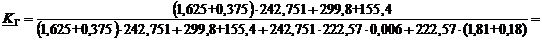
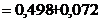
Расчёт коэффициента передачи сигнала по напряжению по остальным
гармоникам рассчитывается аналогично и результаты представлены в таблице 6.
Таблица 6
Расчёт коэффициента передачи сигнала по напряжению по гармоникам
|
w/w1
|
KГ
|
j, град
|
|
1
|
2
|
3
|
|
1
|
0,504
|
8,25
|
|
2
|
0,545
|
13,239
|
|
3
|
0,579
|
16,747
|
|
4
|
0,629
|
19,876
|
|
5
|
0,685
|
20,899
|
|
6
|
0,734
|
20,693
|
|
7
|
0,776
|
19,935
|
|
8
|
0,81
|
18,955
|
|
9
|
0,838
|
17,912
|
|
10
|
0,861
|
16,885
|
|
11
|
0,879
|
15,91
|
|
12
|
0,895
|
15,002
|
Определить коэффициент усиления Kу из условия
наименьшего ослабления основной гармоники (w1)
по формуле (30):
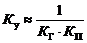 , (30)
, (30)
где КГ и КП - модули коэффициентов передачи по
напряжению генератора и четырехполюсника соответственно.
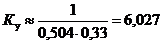
Входное
сопротивление усилителя Rу
равняется модулю характеристического сопротивления четырехполюсника 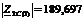 Ом на основной частоте входного сигнала. Выходное
сопротивление усилителя, в нашем случае равно нулю.
Ом на основной частоте входного сигнала. Выходное
сопротивление усилителя, в нашем случае равно нулю.
Определим
напряжение UmП(1) по
формуле (31), которое подаётся на вход четырехполюсника с генератора на
основной частоте сигнала:
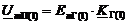 (31)
(31)
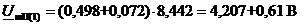
Значения
напряжения на всех гармониках рассчитываются аналогично,
Таблица 7
Значения напряжения на гармониках
|
ω/ω1
|
UmП, В
|
j, град
|
|
1
|
4,251
|
8,25
|
|
2
|
2,18
|
-76,761
|
|
3
|
0,118
|
-163,253
|
|
4
|
0,629
|
-70,124
|
|
5
|
0,183
|
-159,101
|
|
6
|
0,326
|
-69,307
|
|
7
|
0,17
|
-160,065
|
|
8
|
0,202
|
-71,045
|
|
9
|
0,151
|
-162,088
|
|
10
|
0,138
|
-73,115
|
|
11
|
0,133
|
-164,09
|
|
12
|
0,099
|
-74,998
|
Определим напряжение на входе усилителя UmУ по формуле (32) при нагрузке Z2C четырехполюсника на основной гармонике:
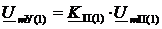 (32)
(32)
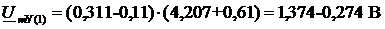
Расчёт напряжения на входе усилителя по остальным гармоникам производится
аналогичным образом, и результаты представлены в таблице 8.
Таблица 8
Расчёт напряжения на входе усилителя по гармоникам
|
ω/ω1
|
UmУ, В
|
j, град
|
|
1
|
2
|
3
|
|
1
|
1,401
|
-11,292
|
|
2
|
0,528
|
-101,578
|
|
3
|
0,031
|
179,323
|
|
4
|
0,18
|
-101,023
|
|
5
|
0,048
|
158,361
|
|
6
|
0,076
|
-119,774
|
|
7
|
0,035
|
143,827
|
|
8
|
0,038
|
-131,372
|
|
9
|
0,025
|
134,306
|
|
10
|
0,021
|
-139,345
|
|
11
|
0,019
|
127,531
|
|
12
|
0.013
|
-145.169
|
Вычислим напряжение на выходе усилителя, то есть напряжение на входе
фильтра (UmФ) на основной гармонике по формуле (33):
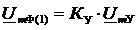 (33)
(33)
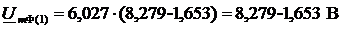
Расчёт напряжения на входе фильтра по остальным гармоникам производится
аналогичным образом, и результаты представлены в таблице 9:
Таблица 9
Расчёт напряжения на входе фильтра по гармоникам
|
ω/ω1
|
UmФ, В
|
j, град
|
|
1
|
2
|
3
|
|
1
|
8,442
|
-11,292
|
|
2
|
3,183
|
-101,578
|
|
3
|
0,189
|
179,323
|
|
4
|
1,087
|
-101,023
|
|
5
|
0,291
|
158,361
|
|
6
|
0,461
|
-119,774
|
|
7
|
0,210
|
143,827
|
|
8
|
0,228
|
-131,372
|
|
9
|
0,153
|
134,306
|
|
10
|
0,127
|
-139,345
|
|
11
|
0,112
|
127,531
|
|
12
|
0,078
|
-145,169
|
Построим на одном графике (рисунок 10) два сигнала: 1) Входной сигнал
(пунктирный); 2) Сигнал на входе фильтра (сплошной).
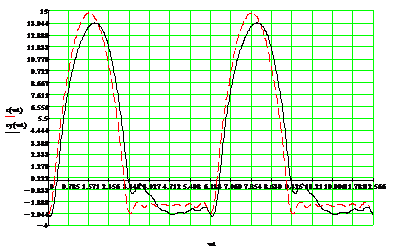
Рисунок
10 - Входной сигнал и сигнал на входе фильтра
Построим спектры амплитуд и фаз на входе фильтра.
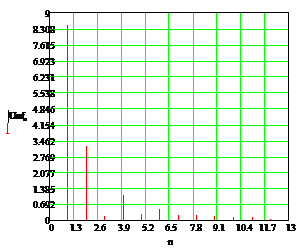
Рисунок
11 - Спектры амплитуд
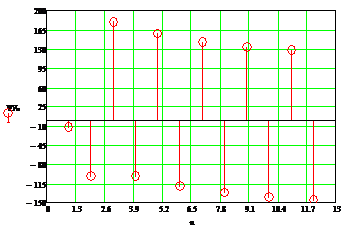
Рисунок
12 - Спектры фаз
Вычислим
коэффициент искажения формы сигнала фильтра (на выходе усилителя) КиФ по
формуле (34):
Киф
= Uмф(1)/ Uмф
(34)
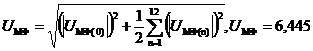
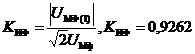
Выводы
.
Из получившегося ряда Фурье и спектра амплитуд видно, что основной вклад в
формирование сигнала вкладывает первая гармоника. Далее с увеличением частоты
максимальные амплитуды напряжений уменьшаются и на более старших гармониках
сравнимы с нулем.
.
По виду получившихся АЧХ и ФЧХ четырехполюсника можно сказать, что коэффициент
передачи по напряжению Кп ниже третьей гармоники сильно уменьшается,
идет достаточно заметный провал. Наибольший модуль коэффициента передачи
четырехполюсника наблюдается на частоте 2w1, наименьший на частоте 12w1.
.
Некоторые амплитудные искажения и некоторый сдвиг по фазе сигнала на выходе
усилителя по отношению к входному сигналу обусловлен наличием реактивной
составляющей сопротивления четырехполюсника. А также это объясняется тем, что
согласование работы четырехполюсника и фильтра возможно только на определенной
частоте. В качестве этой частоты была взята частота первой гармоники входного
воздействия. На частотах остальных гармоник режим работы, как четырехполюсника,
так и фильтра не является согласованным. Также в качестве характеристических
сопротивлений были взяты только их модули. Все перечисленные факторы повлияли
на форму сигнала. Наибольший вклад в формирование сигнала на выходе усилителя
вносит 1-я гармоника.
Список
использованных источников
1. Методические
указания по расчету «Линейной системы передачи сигнала при несинусоидальных
воздействиях» Пенза 1998 г.
2. Атабеков
Г.И. «Основы теории цепей» учебник для ВУЗов М.: Энергия, 1978 г.
. Ландау
Л.Д. «Теоретическая физика»: Физматлит, 2006 г.
. Ельяшевич
М.А. «Атомная и молекулярная спектроскопия»: Либроком, 2009 г.
. Громов
С.В. «Теория относительности»: Просвещение, 2006г.
. Лебедев
А.И. «Физика полупроводниковых приборов»: Физмалит, 2008 г.
. Козлов
С.А. «Основы фемтосекундной оптики»: Физмалит, 2009 г.
. С.А.
Сметана «Новый взгляд на природу сил взаимодействия»: КомКнига, 2007 г.
Приложение А
Таблица результатов расчета
Таблица А.1
Расчет комплексных сопротивлений по гармоникам
|
ω/ω1
|
Z1
|
Z2
|
Z3
|
|
1
|
2
|
3
|
4
|
|
1
|
2
|
3
|
4
|
|
1
|
100+60
|
160
|
129,6+28,8
|
|
2
|
100+120
|
160
|
238,235-37,059
|
|
3
|
100+180
|
160
|
105,882-183,529
|
|
4
|
100+240
|
160
|
24,923-127,385
|
|
5
|
100+300
|
160
|
8,363-91,069
|
|
6
|
100+360
|
160
|
3,6-70,8
|
|
7
|
100+420
|
160
|
1,814-58,113
|
|
8
|
100+480
|
160
|
1,016-49,422
|
|
9
|
100+540
|
160
|
0,615-43,077
|
|
10
|
100+600
|
160
|
0,395-38,228
|
|
11
|
100+660
|
160
|
0,265-34,392
|
|
12
|
100+720
|
160
|
0,185-3,278
|