Исследование вольтамперных характеристик диодов
Содержание
Исследование вольтамперных
характеристик диодов
Диод Simscape:
Снятие характеристик при
Uпр=0,6 В; R=0,3 Ом; ρ=1*10-8 1/Ом
Снятие характеристик при
Uпр=0,2 В; R=0,1 Ом; ρ=1*10-7 1/Ом
Снятие характеристик при
Uпр=0,4 В; R=0,5Ом; ρ=1*10-91/Ом
Диод SimElectronics
Снятие характеристик при
Uпр=0,6 В; R=0,3 Ом; ρ=1*10-8 1/Ом
Снятие характеристик при
Uпр=0,3 В; R=0,3 Ом; ρ=1*10-8 1/Ом
Снятие характеристик при
Uпр=0,2 В; R=1 Ом; ρ=1*10-8 1/Ом
Снятие характеристик при
Uпр=0,2 В; R=0,3 Ом; ρ=1*10-8 1/Ом
Вывод
Аппроксимация графиков
вольтамперных характеристик диодов
Исходный график
Функции первой степени
Исходный код программы
Полученные данные
Функция второй степени
Исходный код программы
Полученные данные
Функция третьей степени
Исходный код программы
Полученные данные
Функция экспоненты
Исходный код программы
Полученные данные
Вывод
Исследование вольтамперных
характеристик диодов
Построить схемы с диодом из
библиотеки SimElectronics и электрическим диодом из библиотеки Simscape.
Снять ВАХ, построить графики зависимости тока от напряжения.
Диод Simscape:
Описание:
Элемент библиотеки Simulink Simscape “Диодный блок” моделирует
кусочно-линейный диод. Если напряжение через диод идёт большее, чем указанное в
параметре Forward, то диод ведёт себя как линейный резистор с низкой
проводимостью, определяемой параметром On, так же включая ряд иных источников
напряжения. Если же напряжение через диод идёт меньшее, чем указанное в
параметре Forward, то диод ведёт себя как линейный резистор с низкой
проводимостью, определяемой параметром Off.
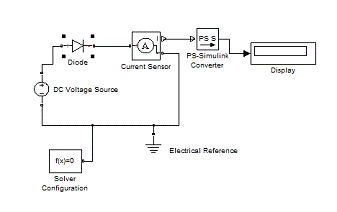
Снятие характеристик при Uпр=0,6 В; R=0,3 Ом; ρ=1*10-8
1/Ом
Таблица 1. U>0
|
№
|
U, В
|
I, А
|
|
№
|
U, В
|
I, А
|
|
1
|
0
|
0
|
|
14
|
4,5
|
13
|
|
2
|
0,3
|
3*10-9
|
|
15
|
5
|
14,67
|
|
3
|
0,6
|
6*10-9
|
|
16
|
5,5
|
16,33
|
|
4
|
0,9
|
1
|
|
17
|
6
|
18
|
|
5
|
1,2
|
2
|
|
18
|
6,5
|
19,67
|
|
6
|
1,5
|
3
|
|
19
|
7
|
21,33
|
|
7
|
1,8
|
4
|
|
20
|
7,5
|
23
|
|
8
|
2,1
|
5
|
|
21
|
8
|
24,67
|
|
9
|
2,4
|
6
|
|
22
|
8,5
|
26,33
|
|
10
|
2,7
|
7
|
|
23
|
9
|
28
|
|
11
|
3
|
8
|
|
24
|
9,5
|
29,67
|
|
12
|
3,5
|
9,667
|
|
25
|
10
|
31,33
|
|
13
|
4
|
11,33
|
|
|
|
|
|
|
|
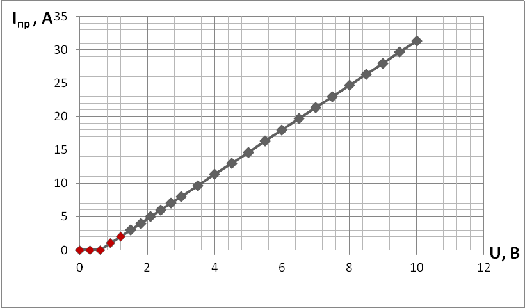
Рис.2. График зависимости U
от I при U>0
|
Таблица 2. U<0
|
№
|
U, В
|
I, нА
|
|
№
|
U, В
|
I, нА
|
|
1
|
0
|
0
|
|
22
|
-0,42
|
-4,2
|
|
2
|
-0,02
|
-0,2
|
|
23
|
-0,44
|
-4,4
|
|
3
|
-0,04
|
-0,4
|
|
24
|
-0,46
|
-4,6
|
|
4
|
-0,06
|
-0,6
|
|
25
|
-0,48
|
-4,8
|
|
5
|
-0,08
|
-0,8
|
|
26
|
-0,5
|
-5
|
|
6
|
-0,1
|
-1
|
|
27
|
-0,6
|
-6
|
|
7
|
-0,12
|
-1,2
|
|
28
|
-0,7
|
-7
|
|
8
|
-0,14
|
-1,4
|
|
29
|
-0,8
|
-8
|
|
9
|
-0,16
|
-1,6
|
|
30
|
-0,9
|
-9
|
|
10
|
-0,18
|
-1,8
|
|
31
|
-1
|
-10
|
|
11
|
-0,2
|
-2
|
|
32
|
-1,1
|
-11
|
|
12
|
-0,22
|
-2,2
|
|
33
|
-1,2
|
-12
|
|
13
|
-0,24
|
-2,4
|
|
34
|
-1,3
|
-13
|
|
14
|
-0,26
|
-2,6
|
|
35
|
-1,4
|
-14
|
|
15
|
-0,28
|
-2,8
|
|
36
|
-1,5
|
-15
|
|
16
|
-0,3
|
-3
|
|
37
|
-1,6
|
-16
|
|
17
|
-0,32
|
-3,2
|
|
38
|
-1,7
|
-17
|
|
18
|
-0,34
|
-3,4
|
|
39
|
-1,8
|
-18
|
|
19
|
-0,36
|
-3,6
|
|
40
|
-1,9
|
-19
|
|
20
|
-0,38
|
-3,8
|
|
41
|
-2
|
-20
|
|
21
|
-0,4
|
-4
|
|
|
|
|
|
|
|
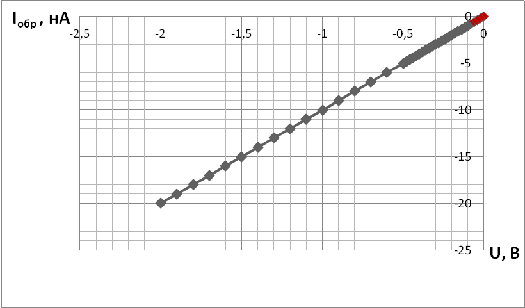
Рис.3. График зависимости U
от I при U<0
|
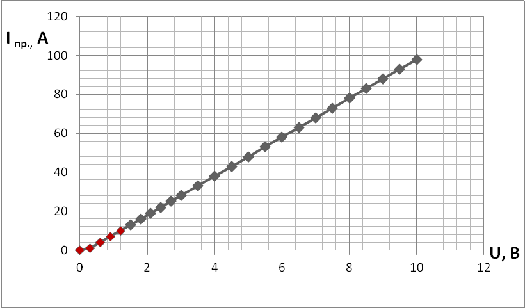
Снятие характеристик при Uпр=0,2 В; R=0,1 Ом; ρ=1*10-7
1/Ом
Таблица 3. U>0
|
№
|
U, В
|
I, А
|
|
№
|
U, В
|
I, А
|
|
1
|
0
|
0
|
|
14
|
4,5
|
43
|
|
2
|
0,3
|
1
|
|
15
|
5
|
48
|
|
3
|
0,6
|
4
|
|
16
|
5,5
|
53
|
|
4
|
0,9
|
7
|
|
17
|
6
|
58
|
|
5
|
1,2
|
10
|
|
18
|
6,5
|
63
|
|
6
|
1,5
|
13
|
|
19
|
7
|
68
|
|
7
|
1,8
|
16
|
|
20
|
7,5
|
73
|
|
8
|
2,1
|
19
|
|
21
|
8
|
78
|
|
9
|
2,4
|
22
|
|
22
|
8,5
|
83
|
|
10
|
2,7
|
25
|
|
23
|
9
|
88
|
|
11
|
3
|
28
|
|
24
|
9,5
|
93
|
|
12
|
3,5
|
33
|
|
25
|
10
|
98
|
|
13
|
4
|
38
|
|
|
|
|
|
|
|
Рис.4. График зависимости U
от I при U>0
|
Таблица 4. U<0
|
№
|
U, В
|
I, нА
|
|
№
|
U, В
|
I, нА
|
|
1
|
0
|
0
|
|
22
|
-0,42
|
-42
|
|
2
|
-0,02
|
-2
|
|
23
|
-44
|
|
3
|
-0,04
|
-4
|
|
24
|
-0,46
|
-46
|
|
4
|
-0,06
|
-6
|
|
25
|
-0,48
|
-48
|
|
5
|
-0,08
|
-8
|
|
26
|
-0,5
|
-50
|
|
6
|
-0,1
|
-10
|
|
27
|
-0,6
|
-60
|
|
7
|
-0,12
|
-12
|
|
28
|
-0,7
|
-70
|
|
8
|
-0,14
|
-14
|
|
29
|
-0,8
|
-80
|
|
9
|
-0,16
|
-16
|
|
30
|
-0,9
|
-90
|
|
10
|
-0,18
|
-18
|
|
31
|
-1
|
-100
|
|
11
|
-0,2
|
-20
|
|
32
|
-1,1
|
-110
|
|
12
|
-0,22
|
-22
|
|
33
|
-1,2
|
-120
|
|
13
|
-0,24
|
-24
|
|
34
|
-1,3
|
-130
|
|
14
|
-0,26
|
-26
|
|
35
|
-1,4
|
-140
|
|
15
|
-0,28
|
-28
|
|
36
|
-1,5
|
-150
|
|
16
|
-0,3
|
-30
|
|
37
|
-1,6
|
-160
|
|
17
|
-0,32
|
-32
|
|
38
|
-1,7
|
-170
|
|
18
|
-0,34
|
-34
|
|
39
|
-1,8
|
-180
|
|
19
|
-0,36
|
-36
|
|
40
|
-1,9
|
-190
|
|
20
|
-0,38
|
-38
|
|
41
|
-2
|
-200
|
|
21
|
-0,4
|
-40
|
|
|
|
|
|
|
|
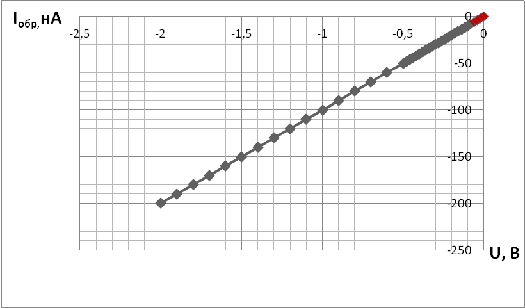
Рис.5. График зависимости U
от I при U<0
|
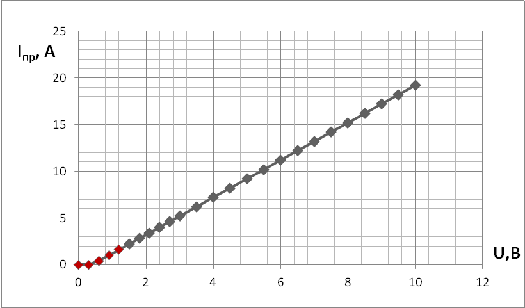
Снятие характеристик при Uпр=0,4 В; R=0,5Ом; ρ=1*10-91/Ом
Таблица 5. U>0
|
№
|
U, В
|
I, А
|
|
№
|
U, В
|
I, А
|
|
1
|
0
|
0
|
|
14
|
4,5
|
8,2
|
|
2
|
0,3
|
3*10-10
|
|
15
|
5
|
9,2
|
|
3
|
0,6
|
0,4
|
|
16
|
5,5
|
10,2
|
|
4
|
0,9
|
1
|
|
17
|
6
|
11,2
|
|
5
|
1,2
|
1,6
|
|
18
|
6,5
|
12,2
|
|
6
|
1,5
|
2,2
|
|
19
|
7
|
13,2
|
|
7
|
1,8
|
2,8
|
|
20
|
7,5
|
14,2
|
|
8
|
2,1
|
3,4
|
|
21
|
8
|
15,2
|
|
9
|
2,4
|
4
|
|
22
|
8,5
|
16,2
|
|
10
|
2,7
|
4,6
|
|
23
|
9
|
17,2
|
|
11
|
3
|
5,2
|
|
24
|
9,5
|
18,2
|
|
12
|
3,5
|
6,2
|
|
25
|
10
|
19,2
|
|
13
|
4
|
7,2
|
|
|
|
|
|
|
|
Рис.6. График зависимости U
от I при U>0
|
Таблица 6. U<0
|
№
|
U, В
|
I, нА
|
|
№
|
U, В
|
I, нА
|
|
1
|
0
|
0
|
|
22
|
-0,42
|
-0,42
|
|
2
|
-0,02
|
-0,02
|
|
23
|
-0,44
|
-0,44
|
|
3
|
-0,04
|
-0,04
|
|
24
|
-0,46
|
-0,46
|
|
4
|
-0,06
|
-0,06
|
|
25
|
-0,48
|
-0,48
|
|
5
|
-0,08
|
-0,08
|
|
26
|
-0,5
|
-0,5
|
|
6
|
-0,1
|
-0,1
|
|
27
|
-0,6
|
-0,6
|
|
7
|
-0,12
|
-0,12
|
|
28
|
-0,7
|
-0,7
|
|
8
|
-0,14
|
-0,14
|
|
29
|
-0,8
|
-0,8
|
|
9
|
-0,16
|
-0,16
|
|
30
|
-0,9
|
-0,9
|
|
10
|
-0,18
|
-0,18
|
|
31
|
-1
|
-1
|
|
11
|
-0,2
|
-0,2
|
|
32
|
-1,1
|
-1,1
|
|
12
|
-0,22
|
-0,22
|
|
33
|
-1,2
|
-1,2
|
|
13
|
-0,24
|
-0,24
|
|
34
|
-1,3
|
-1,3
|
|
14
|
-0,26
|
-0,26
|
|
35
|
-1,4
|
-1,4
|
|
15
|
-0,28
|
-0,28
|
|
36
|
-1,5
|
-1,5
|
|
16
|
-0,3
|
-0,3
|
|
37
|
-1,6
|
-1,6
|
|
17
|
-0,32
|
-0,32
|
|
38
|
-1,7
|
-1,7
|
|
18
|
-0,34
|
-0,34
|
|
39
|
-1,8
|
-1,8
|
|
19
|
-0,36
|
-0,36
|
|
40
|
-1,9
|
-1,9
|
|
20
|
-0,38
|
-0,38
|
|
41
|
-2
|
-2
|
|
21
|
-0,4
|
-0,4
|
|
|
|
|
|
|
|
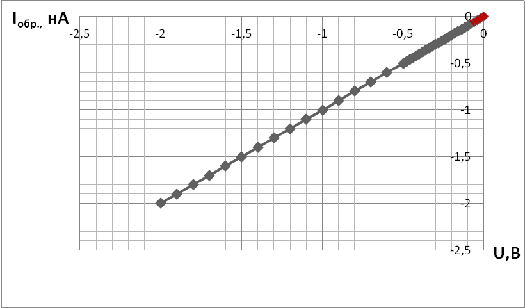
Рис.7. График зависимости U
от I при U<0
|
Диод SimElectronics
Описание:
Диодный блок представляет собой один из следующих типов диодов:
· Кусочно-линейный
Моделирует кусочно-линейный диод, такой же, как и в Simscape Diode block,
но с добавлением фиксированной емкости перехода. Если напряжение на диоде
превышает значение, указанное в параметре Forward, то диод ведет себя как линейный резистор с
сопротивлением, указанным в параметре "On". В противном случае диод
ведет себя как линейный резистор с небольшой проводимостью, указанной в параметре
"Off". Нулевое напряжение на диоде приводит к отсутствию тока.
· Кусочно-линейный
Зенера
Кусочно-линейная модель Зенера ведет себя как кусочно-линейная модель
диода для напряжения выше Vz,
где Vz является значением обратного
напряжения пробоя Vz. При напряжении
менее Vz, диод ведет себя как линейный
резистор с низким сопротивлением Зенера, указанного в параметре Rz сопротивления Зенера. Эта модель
диода также включает в себя фиксированную емкость перехода.
· Экспоненциальный
Экспоненциальная диодная модель обеспечивает следующие отношения между
диодным током I и диодным напряжением V:
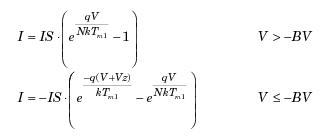
где:- элементарный заряд электрона (1.602176e-19 Кл).- Постоянная
Больцмана (1.3806503e-23 J/K).- значение напряжения пробоя.- коэффициент
эмиссии.- поток насыщенности.- температура, при которой диодные параметры
должны быть заданы, как определено значением параметра измерения температуры.
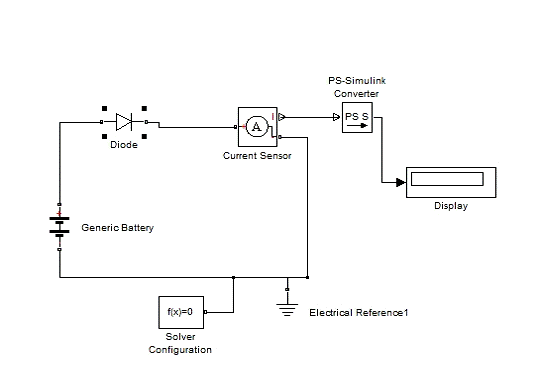
Рис.8. Схема с диодом
Снятие характеристик при Uпр=0,6 В; R=0,3 Ом; ρ=1*10-8
1/Ом
Таблица 7. U>0
|
№
|
U, В
|
I, А
|
|
№
|
U, В
|
|
1
|
0
|
0
|
|
13
|
5
|
1,913
|
|
2
|
1
|
0,174
|
|
14
|
5,5
|
2,13
|
|
3
|
1,2
|
0,2609
|
|
15
|
6
|
2,348
|
|
4
|
1,5
|
0,3913
|
|
16
|
6,5
|
2,565
|
|
5
|
1,8
|
0,5218
|
|
17
|
7
|
2,783
|
|
6
|
2,1
|
0,6522
|
|
18
|
7,5
|
3
|
|
7
|
2,4
|
0,7827
|
|
19
|
8
|
3,218
|
|
8
|
2,7
|
0,9132
|
|
20
|
8,5
|
3,435
|
|
9
|
3
|
1,044
|
|
21
|
9
|
3,652
|
|
10
|
3,5
|
1,261
|
|
22
|
9,5
|
3,87
|
|
11
|
4
|
1,478
|
|
23
|
10
|
4,088
|
|
12
|
4,5
|
1,696
|
|
|
|
|
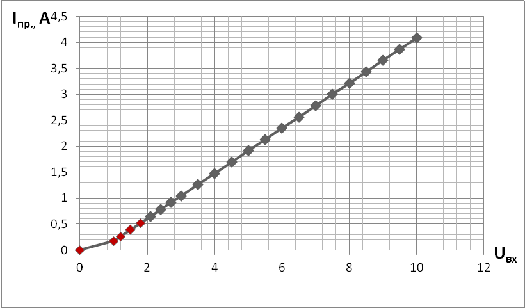
Рис.9. График зависимости U от I при U>0
Снятие характеристик при Uпр=0,3 В; R=0,3 Ом; ρ=1*10-8
1/Ом
Таблица 8. U>0
|
№
|
U, В
|
I, А
|
|
№
|
U, В
|
I, А
|
|
1
|
0
|
0
|
|
13
|
4,5
|
1,826
|
|
2
|
0,6
|
0,1305
|
|
14
|
5
|
2,044
|
|
3
|
0,9
|
0,2609
|
|
15
|
5,5
|
2,261
|
|
4
|
1,2
|
0,3913
|
|
16
|
6
|
2,479
|
|
5
|
1,5
|
0,5218
|
|
17
|
6,5
|
2,696
|
|
6
|
1,8
|
0,6522
|
|
18
|
7
|
2,913
|
|
7
|
2,1
|
0,7827
|
|
19
|
7,5
|
3,131
|
|
8
|
2,4
|
0,9132
|
|
20
|
8
|
3,348
|
|
9
|
2,7
|
1,044
|
|
21
|
8,5
|
3,565
|
|
10
|
3
|
1,174
|
|
22
|
9
|
3,783
|
|
11
|
3,5
|
1,391
|
|
23
|
9,5
|
4
|
|
12
|
4
|
1,609
|
|
24
|
10
|
4,217
|
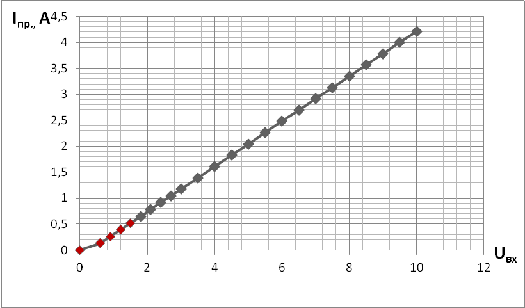
Рис. 10. График зависимости U от I при U>0
Снятие характеристик при
Uпр=0,2 В; R=1 Ом; ρ=1*10-8 1/Ом
Таблица 9. U>0
|
№
|
U, В
|
I, А
|
|
№
|
U, В
|
I, А
|
|
1
|
0
|
0
|
|
14
|
4,5
|
1,434
|
|
2
|
0,3
|
0,03336
|
|
15
|
5
|
1,601
|
|
3
|
0,6
|
0,1334
|
|
16
|
5,5
|
1,767
|
|
4
|
0,9
|
0,2335
|
|
17
|
6
|
1,934
|
|
5
|
1,2
|
0,3335
|
|
18
|
6,5
|
2,1
|
|
6
|
1,5
|
0,4334
|
|
19
|
7
|
2,267
|
|
7
|
1,8
|
0,5334
|
|
20
|
7,5
|
2,434
|
|
8
|
2,1
|
0,6334
|
|
21
|
8
|
2,6
|
|
9
|
2,4
|
0,7334
|
|
22
|
8,5
|
2,767
|
|
10
|
2,7
|
0,8334
|
|
23
|
9
|
2,934
|
|
11
|
3
|
0,9336
|
|
24
|
9,5
|
3,102
|
|
12
|
3,5
|
1,1
|
|
25
|
10
|
3,268
|
|
13
|
4
|
1,267
|
|
|
|
|
|
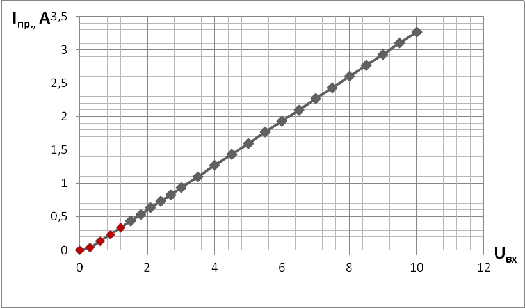
|
|
Рис.11. График зависимости U
от I при U>0
|
Снятие характеристик при Uпр=0,2 В; R=0,3 Ом; ρ=1*10-8 1/Ом
Таблица 10. U>0
|
№
|
U, В
|
I, А
|
|
№
|
U, В
|
I, А
|
|
1
|
0
|
0
|
|
14
|
4,5
|
1,87
|
|
2
|
0,3
|
0,04349
|
|
15
|
5
|
2,087
|
|
3
|
0,6
|
0,1739
|
|
16
|
5,5
|
2,304
|
|
4
|
0,9
|
0,3044
|
|
17
|
6
|
2,522
|
|
5
|
1,2
|
0,4348
|
|
18
|
6,5
|
2,739
|
|
6
|
1,5
|
0,5653
|
|
19
|
7
|
2,957
|
|
7
|
1,8
|
0,6957
|
|
20
|
7,5
|
3,174
|
|
8
|
2,1
|
0,8261
|
|
21
|
8
|
3,391
|
|
9
|
2,4
|
0,9566
|
|
22
|
8,5
|
3,609
|
|
10
|
2,7
|
1,087
|
|
23
|
9
|
3,826
|
|
11
|
3
|
1,217
|
|
24
|
9,5
|
4,044
|
|
12
|
3,5
|
1,435
|
|
25
|
10
|
4,261
|
|
13
|
4
|
1,652
|
|
|
|
|

Рис.12. График зависимости U от I при U>0
Вывод
В проделанной работе мы исследовали два диода из библиотек Simscape и SimElectronics. Обе модели оказались ограничены,
так как предусмотрено ограничение по сопротивлению, однако в исследуемых
пределах модели диодов работали хорошо. В итоге мы исследовали 7 цепей,
построили их вольтамперные характеристики.
библиотека simelectronics диод вольтамперный
Аппроксимация графиков вольтамперных характеристик диодов
Даны вольтамперные характеристики реальных диодов при 2х разных
температурах. Необходимо аппроксимировать эти функции различными методами. При
выполнении работы я использовал различные методы аппроксимации: с помощью
функций линейной, квадратичной, кубической и экспоненциальной зависимостей.
Функции и области их значений определялись с помощью подстановки различных
значений.
Исходный график
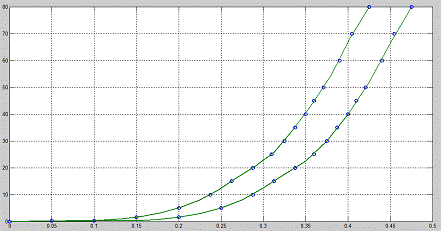
Рис.1. Исходный график ВАХ исследуемого диода
Функции первой степени
Исходный код программы
% рисуем первый график
x_1 = [0 .05 .15 .2 .2375 .2625 .2875 .31 .325 .3375 .35 .36 .371 .39
.405 .425];_1 = [0 .15 1.5 5 10 15 20 25 30 35 40 45 50 60 70 80];
cs_1 = spline(x_1, [0 y_1 0]);_1 = linspace(0, .425, 20);(x_1,
y_1, 'o', xx_1, ppval(cs_1, xx_1), '-', 'LineWidth', 2);
hold on;
% рисуем второй график
x_2 = [0 .1 .2 .25 .2875 .3125 .3375 .36 .375 .3875 .4 .41 .421 .44 .455
.475];
y_2 = [0 .15 1.5 5 10 15 20 25 30 35 40 45 50 60 70 80];_2 =
spline(x_2, [0 y_2 0]);_2 = linspace(0, .475, 20);(x_2, y_2, 'o', xx_2,
ppval(cs_2, xx_2), '-', 'LineWidth', 2);
% апроксимируем первый график
x11 = [0 0.17];= x11 * 6;
plot (x11, y11, 'm', 'LineWidth', 2);
= [0.15 0.24];= (x12 * 100) - 15;(x12, y12, 'g', 'LineWidth',
2)
= [0.22 0.31];= (x13 * 200) - 38;(x13, y13, 'r', 'LineWidth',
2);
= [0.29 0.36];= (x14 * 330) - 77;(x14, y14, 'k', 'LineWidth',
2);
x15 = [0.34 0.43];= (x15 * 545) - 152;(x15, y15, 'b',
'LineWidth', 2);
% апроксимируем второй график
x21 = [0 0.22];= x21 * 4;
plot (x21, y21, 'm', 'LineWidth', 2);
= [0.2 0.29];= (x22 * 100) - 20;(x22, y22, 'g', 'LineWidth',
2);
= [0.265 0.365];= (x23 * 200) - 47.5;(x23, y23, 'r',
'LineWidth', 2);
= [0.345 0.41];= (x24 * 330) - 94;(x24, y24, 'k',
'LineWidth', 2);
= [0.39 0.475];= (x25 * 545) - 180;(x25, y25, 'b',
'LineWidth', 2);
Полученные данные
Рис.2. Аппроксимация графиков функциями линейной зависимости
Первый график:
Y1 = X1 * 6; X1 Є [0 0.16)
Y2 = X2 * 100 - 15; X2
Є [0.16 0.24)3
= X3 * 200 - 38; X3 Є [0.22 0.31)4 = X4
* 330 - 77; X4 Є [0.29 0.36)5 = X5 * 545 - 152; X5 Є [0.34 0.43]
Второй график:
Y1 = X1 * 10 - 1.2; X1
Є [0 0.21)2
= X2 * 100 - 20; X2 Є [0.21 0.275) 3 =
X3 * 200 - 47.5; X3 Є [0.275 0.355)4 = X4 * 330 - 94; X4 Є [0.355 0.4)
Y5 = X5 * 545 - 180; X5 Є [0.4 0.475]
Функция второй степени
Исходный код программы
% рисуем первый график
x_1 = [0 .05 .15 .2 .2375 .2625 .2875 .31 .325 .3375 .35 .36
.371 .39 .405 .425];_1 = [0 .15 1.5 5 10 15 20 25 30 35 40 45 50 60 70 80];_1 =
spline(x_1, [0 y_1 0]);_1 = linspace(0, .425, 20);(x_1, y_1, 'o', xx_1,
ppval(cs_1, xx_1), '-', 'LineWidth', 2);on;on;
% рисуем второй
график
x_2 = [0 .1 .2 .25 .2875 .3125 .3375 .36 .375 .3875 .4 .41
.421 .44 .455 .475];_2 = [0 .15 1.5 5 10 15 20 25 30 35 40 45 50 60 70 80];_2 =
spline(x_2, [0 y_2 0]);_2 = linspace(0, .475, 20);(x_2, y_2, 'o', xx_2,
ppval(cs_2, xx_2), '-', 'LineWidth', 2);
% апроксимируем первый график
x1 = 0 : 0.0001 : 0.425;= ((x1.^2) * 640) - (x1 * 100) - 1;
plot(x1, y1, 'b', 'LineWidth', 2);
% апроксимируем второй график
x2 = 0 : 0.0001 : 0.475;= ((x2.^2) * 460) - (x2 * 50) - 12;
plot(x2, y2, 'r', 'LineWidth', 2);
Полученные данные
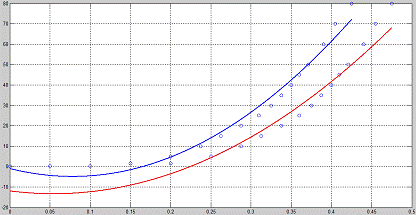
Рис.3. Аппроксимация графиков функцией квадратичной зависимости
Первый график:
Y1 = (640 * X12)
- (100 * X1) - 1; X1 Є [0.19 0.4)
Второй график:
Y2 = (460 * X22)
- (50 * X2) - 12; X2 Є [0.235 0.44)
Функция третьей степени
Исходный код программы
% рисуем первый график
x_1 = [0 .05 .15 .2 .2375 .2625 .2875 .31 .325 .3375 .35 .36 .371 .39
.405 .425];_1 = [0 .15 1.5 5 10 15 20 25 30 35 40 45 50 60 70 80];
cs_1 = spline(x_1, [0 y_1 0]);_1 = linspace(0, .425,
20);(x_1, y_1, 'o', xx_1, ppval(cs_1, xx_1), '-', 'LineWidth', 2);on; on;
% рисуем второй
график
x_2 = [0 .1 .2 .25 .2875 .3125 .3375 .36 .375 .3875 .4 .41
.421 .44 .455 .475];_2 = [0 .15 1.5 5 10 15 20 25 30 35 40 45 50 60 70 80];_2 =
spline(x_2, [0 y_2 0]);_2 = linspace(0, .475, 20);(x_2, y_2, 'o', xx_2,
ppval(cs_2, xx_2), '-', 'LineWidth', 2);
% апроксимируем первый график
x1 = 0 : 0.0001 : 0.425;= ((x1.^3) * 1465) - ((x1.^2) * 180);
plot(x1, y1, 'b', 'LineWidth', 2);
% апроксимируем второй график
x2 = 0 : 0.0001 : 0.475;= ((x2.^3) * 1307) - ((x2.^2) * 280) + 2;
plot(x2, y2, 'r', 'LineWidth', 2);
Полученные данные
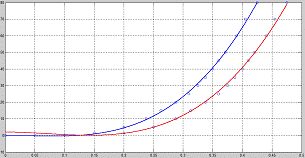
Рис.4. Аппроксимация графиков функцией кубической зависимости
Первый график:
Y1 = (1465 * X13)
- (180 * X12); х1 Є [0 0.425)
Второй графкик:
Y2 = (1307 * X23)
- (280 * X22) + 2; х2 Є [0.12 0.475)
Функция экспоненты
Исходный код программы
% рисуем первый график
x_1 = [0 .05 .15 .2 .2375 .2625 .2875 .31 .325 .3375 .35 .36
.371 .39 .405 .425];_1 = [0 .15 1.5 5 10 15 20 25 30 35 40 45 50 60 70 80];_1 =
spline(x_1, [0 y_1 0]);_1 = linspace(0, .425, 20);(x_1, y_1, 'o', xx_1,
ppval(cs_1, xx_1), '-', 'LineWidth', 2);on;on;
% рисуем второй
график
x_2 = [0 .1 .2 .25 .2875 .3125 .3375 .36 .375 .3875 .4 .41
.421 .44 .455 .475];_2 = [0 .15 1.5 5 10 15 20 25 30 35 40 45 50 60 70 80];_2 =
spline(x_2, [0 y_2 0]);_2 = linspace(0, .475, 20);(x_2, y_2, 'o', xx_2,
ppval(cs_2, xx_2), '-', 'LineWidth', 2);
% апроксимируем первый график
x1 = 0 : 0.0001 : 0.425;= exp(((x1 * 10649 / 1000) + 0) / 1) - 2.4;
plot(x1, y1, 'b', 'LineWidth', 2);
% апроксимируем второй график
x2 = 0 : 0.0001 : 0.475;= exp(((x2 * 9.45) + 0) / 1) - 4.8;
plot(x2, y2, 'r', 'LineWidth', 2);
Полученные данные
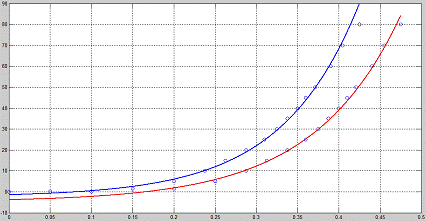
Рис.5. Аппроксимация графиков функциями линейной зависимости
Первый график:
Y1 = exp(10.649 * X1) - 2.4; X1 Є [0.05 0.4]
Второй график:
Y2 = exp(9.45 * X2) - 4.8; X2 Є [0.15 0.4625]
Вывод
Работа показала, что наилучшей функцией для аппроксимации данных графиков
является функция третьей степени. Чуть хуже повторяют график функции линейной
зависимости. При большем количестве линий удалось бы довольно точно повторить
график. Экспоненциальная зависимость так же неплохо подходит для аппроксимации
данных графиков. Дальше всего от оригинала оказалась функция квадратичной
зависимости.