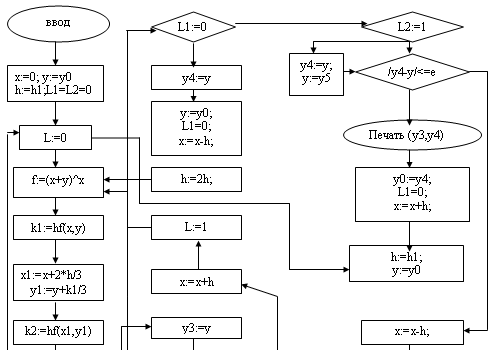
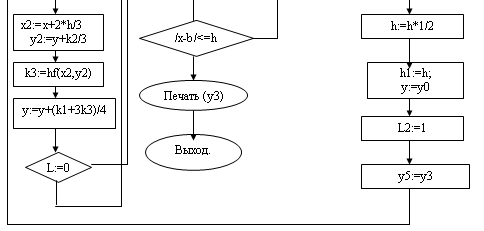
Использование методов численного интегрирования с использованием программного обеспечения
Введение
Курс численных методов является важной частью
математической подготовки студентов педагогических специальностей и
направлений. Его значение в настоящее время определяется не только
увеличивающимися возможностями применения методов вычислительной математики в
вузовском учебном процессе, но и проникновением численных алгоритмов
приближенного решения задач в среднее образование, т.е. в сферу деятельности
учителя.
Виду того, что разумное применение и
квалифицированное преподавание методов приближенного численного анализа
затруднительны без основательной подготовки, будущему учителю математики,
физики или информатики следует глубоко вникать в суть изучаемых методов
приближений и оценок погрешностей, знать их обоснование и соответствующий
математический инструментарий.
В курсе математического анализа доказывается,
что когда функция f непрерывна на [a,b], для нее существует первообразная
F(F’(x)= f(x) для всех x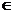 [a,b]), причем
[a,b]), причем 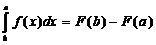 .(1)
Формула (1), называемая формулой Ньютона - Лейбница, представляет собой точный
метод вычисления определенного интеграла. Однако в реальности использовать ее
удается не всегда. Таким образом, выбранная тема исследования является
актуальной.
.(1)
Формула (1), называемая формулой Ньютона - Лейбница, представляет собой точный
метод вычисления определенного интеграла. Однако в реальности использовать ее
удается не всегда. Таким образом, выбранная тема исследования является
актуальной.
Цель курсовой работы: использование на практике
методов численного интегрирования с использованием программного обеспечения.
Задачами исследования является:
Изучение теоретического материала по теме
«Численное дифференцирование».
Изучение различных методов интегрирования.
Практическое применение приближенного вычисления
определенного интеграла с использованием программного обеспечения.
Предметом исследования - дисциплина «Численные
методы»
Объект - «Численное интегрирование. Приближенное
вычисление определенного интеграла с использованием формул прямоугольников,
трапеций, формула Симпсона».
В приложениях математики одной из наиболее часто
встречающихся задач является вычисление определенного интеграла. Существуют
точные методы вычисления определенного интеграла.
1. Численное интегрирование
.1 Формулы интегрирования
.1.1 Формулы прямоугольников
Вывод формул
Интегрируемость функции f на отрезке [а; b]
означает, что если этот отрезок разбивать точками а = х0 < х1 < ... <
хn = b на n частей (п € N), выбирать числа t1 € [хi-1 ; xi] и составлять
интегральные суммы
= 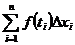
(∆xi = xi - xi-1),
то будет существовать конечный предел этих сумм
при h→0 (h= max ∆xi - шаг разбиения), не зависящий ни от способа
разбиения отрезка на части, ни от выбора точек ti, из этих частей. Этот предел
и есть определенный интеграл
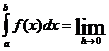 Sn
[1,c.108] (1)
Sn
[1,c.108] (1)
Поскольку способ разбиения отрезка может быть
любым, в дальнейшем будем разбивать [а; b] на равные части. В этом случае
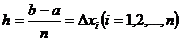
а условие h→0 равносильно условию п →
∞. Следовательно, при достаточно больших п можно положить:
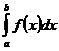
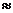
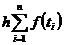
Конкретизируем правило выбора ti. Если взять их
равными левыми концам отрезков [xi-1; ix], yi-1 = f(xi-1)то получим
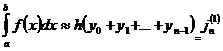 [1,c.109](2)
[1,c.109](2)
Приняв t1 =xi - правые концы отрезков [xi-1;
xi], yi-1 = f(xi), будем иметь
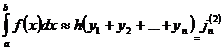 [1,c.109](3)
[1,c.109](3)
Квадратурная формула (2) называется формулой
прямоугольников c левыми ординатами, а формула (3) - формулой прямоугольников с
правыми ординатами. Взяв в качестве ti середины частичных отрезков, получим
формулу прямоугольников с центральными ординатами.
Эти названия объясняются геометрическим смыслом
формул. Как известно, определенный интеграл от неотрицательной интегрируемой
функции на f отрезке [а; b] равен площади соответствующей криволинейной
трапеции. Если криволинейную трапецию заменить ступенчатой фигурой D,
составленной из прямоугольников с основаниями [xi-1; xi] и с высотами, равными
ординатам точек (xi-1; yi-1 ) графика у = f(x) (i= 1, 2,..., п), то формула (2)
выражает замену площади криволинейной трапеции на площадь фигуры D. На рисунке
1 взято п = 2, фигура D с «левыми» ординатами заштрихована.
Аналогичный смысл имеет и формула (3).
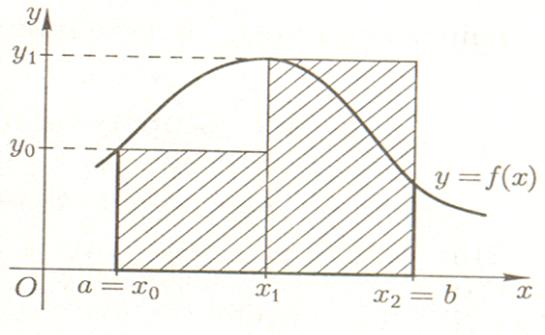
Рис.1. Ступенчатая фигура
.1.2 Формула трапеций
Вывод формулы
Разобьем отрезок [а; b] точками а = х0 < х1
< ... < хn = b на n равных частей одинаковой длины 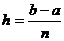 и
найдем yi = f(xi)(i= 0,1, …, n). На каждом из отрезков [xi-1; xi] функцию f
заменим по формуле линейного интерполирования
и
найдем yi = f(xi)(i= 0,1, …, n). На каждом из отрезков [xi-1; xi] функцию f
заменим по формуле линейного интерполирования
На отрезке [x0; x1]
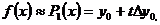
где 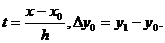
Тогда 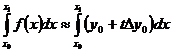
Найдем правый интеграл переходом к переменной t:
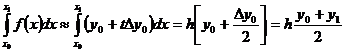 [5,c.15](4)
[5,c.15](4)
На остальных отрезках аналогичные выкладки дают
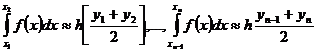 [5,c.15](5)
[5,c.15](5)
Складываем почленно приближенные равенства (4),
(5) и в силу аддитивности интеграла получим формулу трапеций:
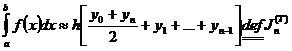 [5,c.15](6)
[5,c.15](6)
На рисунке 2 показан геометрический смысл этой
формулы при п = 2. Линейная интерполяция приводит к замене графика функции f
ломаной, соединяющей точки (х0, у0), (х1, y1),..., (хn, уn) этого графика.
Затем вместо криволинейной трапеции рассматривают фигуру D, составленную из
прямолинейных трапеций с основаниями y1 и yi+1 и высотой h. Правые части
соотношений (4) и (5) равны площадям этих прямолинейных трапеций, а (6)
означает замену площади криволинейной трапеции площадью фигуры D.
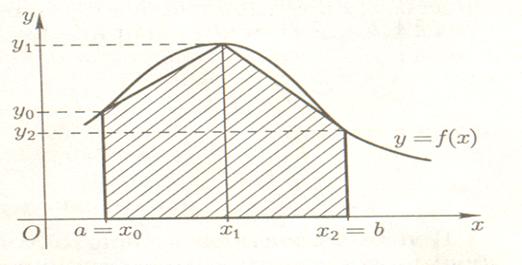
Рис.2. Криволинейная трапеция
.1.3 Формула Симпсона
От квадратурной формулы следует ожидать большей
точности, если для приближения подынтегральной функции / на частичных отрезках
использовать квадратичное интерполирование.
Снова разобьем отрезок [а; b] на п равных частей
точками a = x0 < x1 < … < xn = b с общей длиной 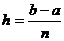 и
обозначим yi = f(xi ) (I = 0, …, n), но теперь возьмем четное число п. Тогда
можно рассматривать «сдвоенные» отрезки [х0 ; х2 ], [х2 ; х4 ], … , [хn-2 ; хn
] с тремя известными узлами и на них функцию f заменять интерполяционными
многочленами Ньютона второй степени (на каждом отрезке свой многочлен).
и
обозначим yi = f(xi ) (I = 0, …, n), но теперь возьмем четное число п. Тогда
можно рассматривать «сдвоенные» отрезки [х0 ; х2 ], [х2 ; х4 ], … , [хn-2 ; хn
] с тремя известными узлами и на них функцию f заменять интерполяционными
многочленами Ньютона второй степени (на каждом отрезке свой многочлен).
Для x 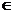 [х0
; х2 ] имеем
[х0
; х2 ] имеем
(x) 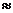 y0
+ t
y0
+ t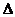 y0
+
y0
+ 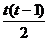
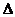 2 y0, где t=
2 y0, где t=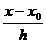 .
[3,c.225](7)
.
[3,c.225](7)
Вычислим интеграл от правой части на отрезке [х0
; х2 ] с заменой переменной
= х0 + ht:
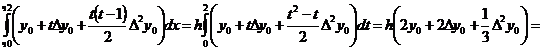
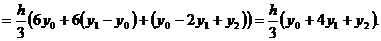
Следовательно,
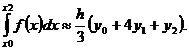 [3c.225](8)
[3c.225](8)
Аналогично на остальных отрезках:
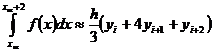 (i
=2, 4, …, n - 2) [3,c.227](9)
(i
=2, 4, …, n - 2) [3,c.227](9)
Результатом суммирования всех полученных
приближенных равенств и будет формула Симпсона:
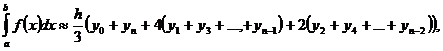 [3,c.227](10)
[3,c.227](10)
правую часть, которой обозначим Jn(C)
Формула Симпсона выглядит более громоздкой по
сравнению с формулами прямоугольников и трапеций, но она значительно точнее их
и может привести к требуемому результату при меньших п.
Теорема 1. Если производная четвертого порядка
f(4) подынтегральной функции непрерывна на [а; b], то
(C)= 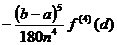 (d
(d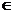 [а;
b]), [3,c.228](11)
[а;
b]), [3,c.228](11)
и поэтому,
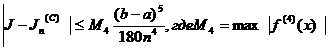 [3,c.228](12)
[3,c.228](12)
Как видно по оценке Vn M4 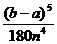 ,
точность формулы Симпсона на два порядка выше точности формулы трапеций и
формулы прямоугольников с центральными ординатами. Она является одной из самых
употребительных в практике вычисления определенных интегралов.
,
точность формулы Симпсона на два порядка выше точности формулы трапеций и
формулы прямоугольников с центральными ординатами. Она является одной из самых
употребительных в практике вычисления определенных интегралов.
2. Оценка погрешностей интегрирования
.1 Оценка погрешностей
.2.1 Оценка погрешностей по формулам
треугольников
Здесь и далее нам понадобятся следующие теоремы.
Теорема 2. (вторая теорема Больцано- Коши).
Пусть функция f непрерывна на отрезке [а; b], а числа m и М - ее наименьшее и
наибольшее значения на [а; b]. Тогда для любого числа С, заключенного между т и
М, найдется точка с 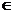 [a; b] такая, что
f(с) = С.
[a; b] такая, что
f(с) = С.
Теорема 3. (аддитивность интеграла) Если a = x0 ≤
x1 ≤ x2 ≤ … ≤ xn = b, то
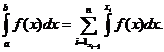
Теорема 4. (обобщенная теорема о среднем
значении интеграла). Пусть:
) функция f непрерывна на отрезке [а; b], а
функция g интегрируема на этом отрезке;
) функция g не меняет знак на всем отрезке [а;
b]. Тогда существует точка с 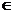 [а; b] такая, что
[а; b] такая, что
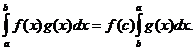
Погрешности формул (2) и (3) оцениваются
одинаково, поэтому далее правые части этих формул Jn (i) и их остаточные члены
Rn (i) (i = 1, 2) для простоты будем записывать без верхних индексов.
Теорема 5. Если подынтегральная функция f имеет
на [а; b] непрерывную производную f ' то оценка погрешностей формул (2) и (3)
дается неравенством
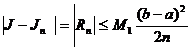 [15,c.107](13)
[15,c.107](13)
Где М1 = max 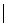 f
' (x)
f
' (x)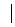
На практике за М1 обычно принимают число,
удовлетворяющее неравенству 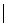 f'(x)
f'(x)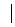 ≤
М1 для всех x
≤
М1 для всех x 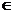 [a; b].
[a; b].
О Доказательство проведем для формулы (2). Пусть
отрезок [а; b] разбит на п равных частей [х0 ; х1 ], … , [хn-1 ; хn ]
одинаковой длины
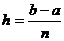
Возьмем любой отрезок [хi-1 ; хi ](I = 1,2, … ,
n). Для всякого х из него найдется зависящее от x число сi*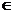 [хi-1
; х]такое, что f(x)= f(хi-1 )+ f '(сi*)(x- хi-1 ) (теорема Лагранжа). Тогда
[хi-1
; х]такое, что f(x)= f(хi-1 )+ f '(сi*)(x- хi-1 ) (теорема Лагранжа). Тогда
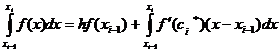
Функция f ' непрерывна, а функция g: g(x) =x
-xi-1 интегрируема и неотрицательна на [хi-1 ; хi ]. Следовательно, к
интегралу в правой части полученного соотношения можно применить теорему 4 с
некоторым числом сi 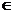 [хi-1 ; хi]:
[хi-1 ; хi]:
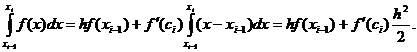
Сложив левые и правые части при i = 1,2, ..., п
и воспользовавшись теоремой 3, получим
= h(y0 +…+yn-1 )+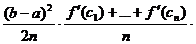
Первое слагаемое справа есть Jn , тогда второе -
Rn. Число
= 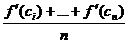
представляет собой среднее арифметическое
значений функции f ' находящееся между ее наименьшим и наибольшим значениями на
[а; b], и потому равно f'(с) для некоторого с 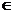 [a;
b] (теорема 2). Следовательно,
[a;
b] (теорема 2). Следовательно,
Rn =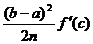 (c
(c 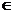 [a;b])
[15,c.107](14)
[a;b])
[15,c.107](14)
Для получения оценки (13) осталось учесть
определение Мi •
Таким образом, погрешность первого из
приближенных равенств J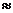 Jn
Jn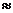
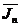 , порождаемая
формулами (2) и (3), оценивается числом
, порождаемая
формулами (2) и (3), оценивается числом 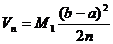 .
Общее правило
.
Общее правило 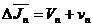 (где Vn vn -
являются абсолютными погрешностями) вычисления абсолютной 2п погрешности
приближенных интегралов примет вид
(где Vn vn -
являются абсолютными погрешностями) вычисления абсолютной 2п погрешности
приближенных интегралов примет вид
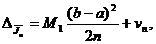
Где vn - оценка точности вычисления значения Jn.
Как видно из выражения для Vn, оценка
погрешностей формул (2) и (3) зависит от подынтегральной функции, от величины
отрезка интегрирования и количества п частей его разбиения. Поскольку для
каждого конкретного интеграла числа М1 и (b - а)2 постоянны, можно сказать, что
погрешность обратно пропорциональна п.
.2.2 Оценка погрешностей по формуле трапеции
Теорема 6. Если вторая производная функции f
непрерывна на [а; b], для квадратурной формулы (6) имеет место неравенство
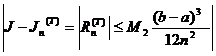 [17,c.55](15)
[17,c.55](15)
где М2 = 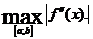
Пусть [xi-1 ; xi ] - произвольный отрезок из
разбиения [а; b] на п равных частей с шагом 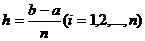 Пользуясь
формулой остаточного члена для интерполяционного многочлена первой степени,
построенного на узлах xi-1 ; xi получим
Пользуясь
формулой остаточного члена для интерполяционного многочлена первой степени,
построенного на узлах xi-1 ; xi получим
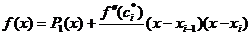 [17,c.55]
(16)
[17,c.55]
(16)
Где 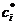 -
зависящее от x число между xi-1 ; xi . Проинтегрируем левую и правую части (8)
на отрезке [xi-1 ; xi ]. При этом учтем следующее: во-первых, интеграл от P1
(x) равен
-
зависящее от x число между xi-1 ; xi . Проинтегрируем левую и правую части (8)
на отрезке [xi-1 ; xi ]. При этом учтем следующее: во-первых, интеграл от P1
(x) равен 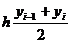 (соотношения (4) и
(5)); во-вторых, к интегралу от второго слагаемого правой части можно применить
обобщенную теорему о среднем ( f " непрерывна, а выражение
(соотношения (4) и
(5)); во-вторых, к интегралу от второго слагаемого правой части можно применить
обобщенную теорему о среднем ( f " непрерывна, а выражение 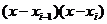 не
меняет знак); в-третьих,
не
меняет знак); в-третьих,
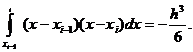
Следовательно,
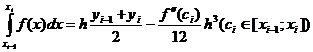
Просуммировав, левые и правые части полученных
равенств при i=1,2, …, n, по аналогии с окончанием доказательства теоремы 5
сначала получим
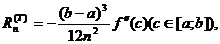
а затем, с учетом определения М2, и требуемую
оценку (15). •
Итак, формула трапеций порождает погрешности,
оцениваемые числом 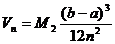 . Ее точность
практически такая же, как и у формулы прямоугольников с центральными
ординатами.
. Ее точность
практически такая же, как и у формулы прямоугольников с центральными
ординатами.
Вычислив значение 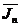 выражения
выражения
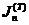 с
точностью до vn, находим оценку его полной погрешности относительно J:
с
точностью до vn, находим оценку его полной погрешности относительно J:
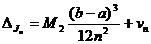 .
[17,c.55] (17)
.
[17,c.55] (17)
2.2 Учет погрешностей квадратурных формул
методом двойного
пересчета
Выше были получены формулы строгой оценки
погрешностей квадратурных формул. Все они пригодны лишь в случае аналитически заданной
подынтегральной функции и требуют нахождения максимума модуля производных, что
подчас представляет собой далеко не простую задачу.
Существует не связанный с вычислением
производных способ ориентировочной оценки погрешностей, применимый и для интегралов
от табличных функций. Это так называемый метод двойного пересчета или метод
Руте.
Рассмотрим его сначала для формул
прямоугольников (2) и (3).
Выбираем некоторое натуральное число п и
проводим вычисления по одной из этих формул дважды: при разбиениях отрезка на n
и на 2п частей (с шагом 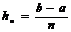
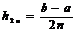 соответственно).
Обозначим полученные результаты через
соответственно).
Обозначим полученные результаты через 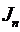
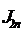 .
Ясно, что лучшим приближением будет
.
Ясно, что лучшим приближением будет 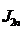 ,
которое и считаем в дальнейшем приближенным значением интеграла.
,
которое и считаем в дальнейшем приближенным значением интеграла.
Для остаточного члена 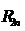 ,
равного погрешности числа
,
равного погрешности числа 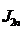 , справедливо
равенство (14) с некоторым числом
, справедливо
равенство (14) с некоторым числом 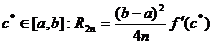 Пусть
значения производной f 'мало изменяются на отрезке [а; b]. Тогда
Пусть
значения производной f 'мало изменяются на отрезке [а; b]. Тогда
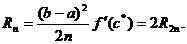 [19,c.68] (18)
[19,c.68] (18)
С учетом (18) и очевидных равенств
= Jn + Rn = J2n + R2n ,
получим сначала
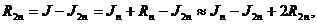
а затем,
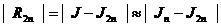 |
[19,c.68](19)
|
[19,c.68](19)
Таким образом, соотношение (19) дает приблизительную
оценку погрешности числа 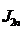 , полученного по
формуле прямоугольников с левыми (или правыми) ординатами.
, полученного по
формуле прямоугольников с левыми (или правыми) ординатами.
Аналогичные оценки имеют место в случае других
квадратурных формул. Для формулы трапеций и формулы прямоугольников с
центральными ординатами
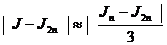 [19,c.69](20)
[19,c.69](20)
для формулы Симпсона,
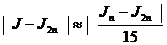 [19,c.70](21)
[19,c.70](21)
Они тем точнее, чем менее значительно изменяются
на [а; b] вторая и соответственно четвертая производные подынтегральной
функции.
Хотя соотношения (19) - (21) требуют двойного
счета по квадратурным формулам, они практически удобны, особенно при
компьютерных вычислениях.
3. Практическое решение приближенного вычисления
определенного
интеграла
Формулы численного интегрирования
Задание.
1) Вычислить интеграл но формуле трапеций с
тремя десятичными
знаками
2) Вычислить интеграл по формуле Симпсона при
n=8; оценить погрешность результата, составив таблицу конечных разностей.
Образец решения
1)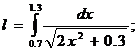
2)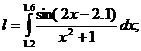
) Для достижения заданной степени точности
необходим определить значение п так, чтобы
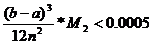
Здесь a=0.7; b= 1.3;M2 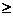
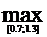
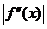 где
где
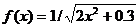
Находим
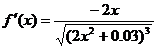 ,
, 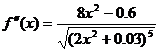 ;
;
Положим M2 = 7, тогда неравенство примет вид
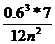 <0.0005,
откуда n2 >252, т.е. n >16; возьмем п = 20. Вычисление интеграла
производим по формуле;
<0.0005,
откуда n2 >252, т.е. n >16; возьмем п = 20. Вычисление интеграла
производим по формуле;
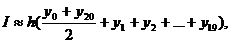
Где
h=(b-a)/h=0.6/20=0.003,
yi =y(xi)= 1/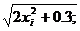
xi =0.7+
in(i=0,1,2….,20)
Все расчеты приведены в таблице 1
Таблица 1. Параметры для вычисления интеграла по
формуле трапеций
|
i
|
xi
|
xi2
|
2xi2+0.3
|
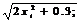
|
y0
;y20
|
y1
,y2 , …, y18 ,y19
|
|
0
|
0.7
|
0.49
|
1.28
|
1.1314
|
0.88386
|
|
|
1
|
0.73
|
0.5329
|
1.3658
|
1.1686
|
|
0.85572
|
|
2
|
0.76
|
0.5776
|
1.4552
|
1.2063
|
|
0.82898
|
|
3
|
0.79
|
0.6241
|
1.5482
|
1.2443
|
|
0.80366
|
|
4
|
0.82
|
0.6724
|
1.6448
|
1.2825
|
|
0.77973
|
|
5
|
0.85
|
0.7225
|
1.7450
|
1.3210
|
|
0.75700
|
|
6
|
0.88
|
0.7744
|
1.8488
|
1.3597
|
|
0.73546
|
|
7
|
0.91
|
0.8281
|
1.9562
|
1.3986
|
|
0.71501
|
|
8
|
0.94
|
0.8836
|
2.0672
|
1.4378
|
|
0.69551
|
|
9
|
0.97
|
0.9409
|
2.1818
|
1.4771
|
|
0.67700
|
|
10
|
1.00
|
1.0000
|
2.3000
|
1.5166
|
|
0.65937
|
|
11
|
1.03
|
1.0609
|
2.4218
|
1.5562
|
|
0.64259
|
|
12
|
106
|
1.1236
|
2.5472
|
1.5960
|
|
0.62657
|
|
13
|
1.09
|
1.1881
|
2.6762
|
1.6356
|
|
0.61140
|
|
14
|
1.12
|
1.2544
|
2.8088
|
1.6759
|
|
0.59669
|
|
15
|
1.15
|
1.3225
|
2.9450
|
1.7161
|
|
0.58272
|
|
16
|
1.18
|
1.3924
|
3.0848
|
1.7564
|
|
0.56935
|
|
17
|
1.21
|
1.4641
|
3.2282
|
1.7967
|
|
0.55653
|
|
18
|
1.24
|
1.5376
|
3.3752
|
1.8372
|
|
0.54431
|
|
19
|
1.27
|
1.6129
|
3.5258
|
1.8777
|
|
0.53253
|
|
20
|
1.30
|
1.6900
|
3.6800
|
1.9187
|
0.52129
|
|
|
21
|
|
|
|
|
1.40515
|
12.77022
|
Формулы для вычисления параметров смотри
приложение 1
Таким образом,
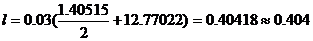
Ответ: l= 0.404
) Согласно условию n=8, поэтому h=(b-a)/n=(1.6 -
1.2)/8=0.05 Вычислительная формула имеет вид
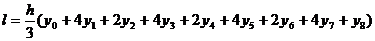 ,
,
Где 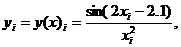
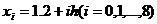
Вычисление значений функции, а также сложение
значений функции, имеющих одинаковые коэффициенты в формуле, производим в
таблице 2
Таблица 2. Параметры для вычисления интеграла по
формуле Симпсона
|
i
|
xi
|
2xi-2,1
|
Sin(2xi-2,1)
|
xi2+1
|
y0
;y8
|
y1,y3,y5,y7
|
Y2,y4,y6
|
|
0
|
1.20
|
0.30
|
0.29552
|
2.44
|
0.1211
|
|
|
|
1
|
1.25
|
0.40
|
0.38942
|
2.5625
|
|
0.1520
|
|
|
2
|
1.30
|
0.50
|
0.4794
|
2.69
|
|
|
0.1782
|
|
3
|
1.35
|
0.60
|
0.5646
|
2.8225
|
|
0.2000
|
|
|
4
|
1.40
|
0.70
|
0.6442
|
2.96
|
|
|
0.2176
|
|
5
|
1.45
|
0.7174
|
3.1024
|
|
0.2312
|
|
|
6
|
1.50
|
0.90
|
0.7833
|
3.25
|
|
|
0.2410
|
|
7
|
1.55
|
1.00
|
0.8415
|
3.4025
|
|
0.2473
|
|
|
8
|
1.60
|
1.10
|
0.8912
|
3.56
|
0.2503
|
|
|
|
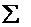
|
|
|
|
|
0.3713
|
0.8305
|
0.6368
|
Формулы для вычисления параметров смотри
приложение 2
Следовательно,
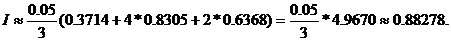
Для оценки точности полученного результата
составим таблицу конечных разностей функций до разностей четвертого порядка
(таблица 3)
Таблица 3. Параметры для вычисления таблицы
конечных разностей
|
i
|
yi
|
∆
yi
|
∆2
yi
|
∆3yi
|
∆4
yi
|
|
0
|
0.1211
|
0.0309
|
-0.0047
|
0.0003
|
-0.0001
|
|
1
|
0.1520
|
0.0262
|
-0.0044
|
0.0002
|
0.0000
|
|
2
|
0.1782
|
0.0218
|
-0.0042
|
0.0002
|
0.0000
|
|
3
|
0.2000
|
0.0176
|
-0.0040
|
0.0002
|
0.0001
|
|
4
|
0.2176
|
0.0136
|
-0.0038
|
0.0003
|
-0.0001
|
|
5
|
0.2312
|
0.0098
|
-0.0035
|
0.0002
|
|
|
6
|
0.2410
|
0.0063
|
-0.0033
|
|
|
|
7
|
0.2473
|
0.0030
|
|
|
|
|
8
|
0.2503
|
|
|
|
|
Формулы для вычисления параметров смотри
приложение 3
Так как mах | ∆4 yi | = 0,0001, то
остаточный член формулы
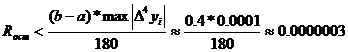
Вычисления проводились с четырьмя значащими
цифрами, а потому величина остаточного члена на погрешность не влияет.
Погрешность вычислений можно оценить из
соотношения

Значит, полученные четыре десятичных знака
верны.
Ответ: = 0,0828
Заключение
Вычисление определенного интеграла приближенными
методами сводится к вычислениям их аналитическими методами и численными
методами
Численные методы позволяют обходиться без
аналитических построений. Приближение к интегралу отыскивается по числовому
выражению на основе значений подынтегральной функции в конечном множестве точек
из отрезка интегрирования. Такой способ вычислений часто называется
механической квадратурой, соответствующие приближенные формулы называют
формулами численного интегрирования или квадратурными формулами, а используемые
при этом аргументы функции - узлами квадратуры.
В работе были рассмотрены приближенные методы
вычисления определенных интегралов с помощью формул треугольников, трапеции и
формулы Симпсона.
На основании исследования можно сделать
следующий вывод: когда вся информация о функции f сосредоточена в таблице, сама
постановка задачи интегрирования предполагает использование приближенных
методов. Действительно, тогда точный интеграл от f заведомо не может быть
найден, а понятие определенного интеграла от таблицы лишено смысла. В то же
время на основе таблицы методами, описанными выше, можно отыскать простое
аналитическое приближение к функции и вычислить приближенное значение интеграла
по одной из рассмотренных нами формул.
численный анализ интегрирование
погрешность
Список литературы
1.
Бахвалов, Н.С. Численные методы : учеб. для вузов / Н.С. Бахвалов. - М.: Наука,
2002. - 621с.
.
Березин, И.С. Методы вычислений / И.С. Березин, Н.П. Жидков, - М.: Наука,
2001.- 325с.
.
Бохан, К.А. Курс математического анализa / К.А. Бохан, И.А.Егорова, К.В.
Лащенов. Т.1.- М. : Просвещение, 2001. - 315с.
.
Бохан, К.А. Курс математического анализa / К.А. Бохан, И.А.Егорова, К.В.
Лащенов. Т.2.- М. : Просвещение, 2002. - 305
.
Вычислительная математика : учеб. пособие / Н.И. Данилина, Н.С. Дубровская,
О.П. Кваша, Г.Л. Смирнов. - М. : Высшая школа, 2002. - 727с.
.
Демидович, Б.Л. Основы вычислительной математики / Б.Л. Демидович, И.А. Марон,-
М. : Наука, 2002. - 412с.
.
Демидович, Б.Л. Численные методы анализа / Б.Л. Демидович, И.А. Марон, З.З.
Шувалова . - М. : Наука, 2002. - 424с.
.
3аварыкин, В.М. Численные методы / В.М. 3аварыкин, В.Г.Житомирский, М.Л. Лапчик
. - М. : Просвещение, 2005. - 558с.
.
Ильин, В.А. Математический анализ / В.А. Ильин, Е.А. Садовничий, Б.Х. Сендов. -
М. : Изд-во МГУ, 2002.- 217с.
.
Калиткин, Н.Н. Численные методы: учеб. для вузов / Н.Н. Калиткин. - М. : Наука,
2004.- 405с.
.
Коллатц, Л. Численные методы решения дифференциальных уравнений: учеб. для
вузов / Л. Коллатц. - М. : Иностранная литература, 2002. -185с.
.
Колмогоров, А.Н. Элементы теории функций и функционального анализа / А.Н.
Колмогоров, С.В. Фомин. - М. : Наука, 2001. - 420с.
.
Копченова, Н.В. Вычислительная математика в примерах и задачах / Н.В.
Копченова, И.А. Марон. - М. : Наука, 2001.- 210с.
.
Курош, А.Г. Курс высшей алгебры: учеб. для вузов / А.Г. Курош. - М. : Наука,
2002. - 325с.
.
Пулькин, С.П. Вычислительная математика / С.П. Пулькин, Л.Н. Никольская, А.С.
Дьячков. - М. : Просвещение, 2004. - 292с.
.
Матвеев, Н.М. Дифференциальные уравнения : учеб. для вузов / Н.М. Матвеев. -
М.: Просвещение,2004.- 445с.
.
Матвеев, Н.М. Методы интегрирования обыкновенных дифференциальных уравнений :
учеб. для вузов / Н.М. Матвеев.- М.: Высшая школа, 2002. - 365с.
.
Мысовскux, И.П. Лекции по методам вычислений : учеб. для вузов / И.П.
Мысовских.- М. : Физматгиз,2001. - 235с.
.
Самарский, А.А. Численные методы / А.А. Самарский, А.В. Гулин. - М. : Наука,
2003.- 235с.
.
Турчак, Л.И. Основы численных методов: учеб. для вузов / Л.И. Турчак. - М. :
Наука, 2005.- 356с.
Приложения
Приложение 1
Решим задачу с помощью электронной таблицы
EXCEL.
В диапазон А1:В20 введем исходные данные: в
ячейки В1: В20 значения Хi
) В С1=> В1^2;
Cкопируем полученную формулу в буфер;
Аналогично введем формулы в диапазон ячеек
С2:С20;
) В D1=>2*B1^2+0.3
Cкопируем полученную формулу в буфер;
Аналогично введем формулы в диапазон ячеек
D2:D20;
) В E1=> ABS(2* B1^2+0.3)
Cкопируем полученную формулу в буфер;
Аналогично введем формулы в диапазон ячеек
E2:E20;
) В F1=>1/(ABS(2* B1^2+0.3));
копируем полученную формулу в буфер;
Аналогично введем формулы в диапазон ячеек F20;
) В G2=> ABS(2* B1^2+0.3)
Cкопируем полученную формулу в буфер;
Аналогично введем формулы в диапазон ячеек
G3:G19;
) B F21=>F1+F20;
) B G21=>CУММ(G2:G19);
Получим таблицу 1.
Таблица 1. Параметры для вычисления интеграла по
формуле трапеций
|
A
|
B
|
C
|
D
|
E
|
F
|
G
|
|
i
|
xi
|
xi2
|
2xi2+0.3
|
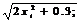
|
y0
;y20
|
y1
,y2 , …, y18 ,y19
|
|
0
|
0.7
|
0.49
|
1.28
|
1.1314
|
0.88386
|
|
|
1
|
0.73
|
0.5329
|
1.3658
|
1.1686
|
|
0.85572
|
|
2
|
0.76
|
0.5776
|
1.4552
|
1.2063
|
|
0.82898
|
|
3
|
0.79
|
0.6241
|
1.5482
|
1.2443
|
|
0.80366
|
|
4
|
0.82
|
0.6724
|
1.6448
|
1.2825
|
|
0.77973
|
|
5
|
0.85
|
0.7225
|
1.7450
|
1.3210
|
|
0.75700
|
|
6
|
0.88
|
0.7744
|
1.8488
|
1.3597
|
|
0.73546
|
|
7
|
0.91
|
0.8281
|
1.9562
|
1.3986
|
|
0.71501
|
|
8
|
0.94
|
0.8836
|
2.0672
|
1.4378
|
|
0.69551
|
|
9
|
0.97
|
0.9409
|
2.1818
|
1.4771
|
|
0.67700
|
|
10
|
1.00
|
1.0000
|
2.3000
|
1.5166
|
|
0.65937
|
|
11
|
1.03
|
1.0609
|
2.4218
|
1.5562
|
|
0.64259
|
|
12
|
106
|
1.1236
|
2.5472
|
1.5960
|
|
0.62657
|
|
13
|
1.09
|
1.1881
|
2.6762
|
1.6356
|
|
0.61140
|
|
14
|
1.12
|
1.2544
|
2.8088
|
1.6759
|
|
0.59669
|
|
15
|
1.15
|
1.3225
|
2.9450
|
1.7161
|
|
0.58272
|
|
16
|
1.18
|
1.3924
|
3.0848
|
1.7564
|
|
0.56935
|
|
17
|
1.21
|
1.4641
|
3.2282
|
1.7967
|
|
0.55653
|
|
18
|
1.24
|
1.5376
|
3.3752
|
1.8372
|
|
0.54431
|
|
19
|
1.27
|
1.6129
|
3.5258
|
1.8777
|
|
0.53253
|
|
20
|
1.30
|
1.6900
|
3.6800
|
1.9187
|
0.52129
|
|
|
21
|
|
|
|
|
1.40515
|
12.77022
|
Приложение 2
В диапазон A1:B9 введем исходные данные: в
ячейки B1:B9 значения Хi
) В С1=> 2*В1-2.1;
Cкопируем полученную формулу в буфер;
Аналогично введем формулы в диапазон ячеек
С2:С9;
) В D1=> Sin (2*В1-2.1);
Cкопируем полученную формулу в буфер;
Аналогично введем формулы в диапазон ячеек
D2:D9;
) В E1=> В1^2+1;
Cкопируем полученную формулу в буфер;
Аналогично введем формулы в диапазон ячеек
E2:E9;
) В F1=> Sin (2*В1-2.1)/В1^2;
) В F9=> Sin (2*В9-2.1)/В9^2;
) B F10=> Сумм(F1:F9);
) В G2=> Sin (2*В2-2.1)/В2^2;
) В G4=> Sin (2*В4-2.1)/В4^2;
) В G6=> Sin (2*В6-2.1)/В6^2;
) В G8=> Sin (2*В8-2.1)/В8^2;
) B G9=> сумм(G2:G8);
) B I3=> Sin (2*В3-2.1)/В3^2;
) B I5=> Sin (2*В5-2.1)/В5^2;
14) B I7=> Sin (2*В7-2.1)/В7^2;
) B I10=> сумм(I
3:I 7);
Получим таблицу 2
Таблица 2. Параметры для вычисления интеграла по
формуле Симпсона
|
A
|
B
|
C
|
D
|
E
|
F
|
G
|
I
|
|
i
|
xi
|
2xi-2,1
|
Sin(2xi-2,1)
|
xi2+1
|
y0
;y8
|
y1,y3,y5,y7
|
Y2,y4,y6
|
|
0
|
1.20
|
0.30
|
0.29552
|
2.44
|
0.1211
|
|
|
|
1
|
1.25
|
0.40
|
0.38942
|
2.5625
|
|
0.1520
|
|
|
2
|
1.30
|
0.50
|
0.4794
|
2.69
|
|
|
0.1782
|
|
3
|
1.35
|
0.60
|
0.5646
|
2.8225
|
|
0.2000
|
|
|
4
|
1.40
|
0.70
|
0.6442
|
|
|
0.2176
|
|
5
|
1.45
|
0.80
|
0.7174
|
3.1024
|
|
0.2312
|
|
|
6
|
1.50
|
0.90
|
0.7833
|
3.25
|
|
|
0.2410
|
|
7
|
1.55
|
1.00
|
0.8415
|
3.4025
|
|
0.2473
|
|
|
8
|
1.60
|
1.10
|
0.8912
|
3.56
|
0.2503
|
|
|
|
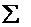
|
|
|
|
|
0.3713
|
0.8305
|
0.6368
|
Приложение 3
В диапазон А1:В9 введем исходные данные.
) С1=> B2-B1;
) С2=> B3-B2;
) С3=> B4-B3;
) С4=> B5-B4;
) С5=> B6-B5;
) С6=> B7-B6;
) С7=> B8-B7;
) С8=> B9-B8;
) D1=> C2-C1;
)D2=> C3-C2;
)D3=> C4-C3;
)D4=> C5-C4;
13)D5=> C6-C5;
)D6=> C7-C6;
)D7=> C8-C7;
) E1=>D2-D1;
) E2=>D3-D2;
) E3=>D4-D3;
) E4=>D5-D4;
) E5=>D6-D5;
) E6=>D7-D6;
22) G1=>E2-E1;
) G2=>E3-E2;
) G3=>E4-E3;
25) G4=>E5-E4;
) G5=>E6-E5;
Получим таблицу 3
Таблица 3. Параметры для вычисления таблицы
конечных разностей
|
A
|
B
|
C
|
D
|
E
|
G
|
|
i
|
yi
|
∆
yi
|
∆2
yi
|
∆3yi
|
∆4
yi
|
|
0
|
0.1211
|
0.0309
|
-0.0047
|
0.0003
|
-0.0001
|
|
1
|
0.1520
|
0.0262
|
-0.0044
|
0.0002
|
0.0000
|
|
2
|
0.1782
|
0.0218
|
-0.0042
|
0.0002
|
0.0000
|
|
3
|
0.2000
|
0.0176
|
-0.0040
|
0.0002
|
0.0001
|
|
4
|
0.2176
|
0.0136
|
-0.0038
|
0.0003
|
-0.0001
|
|
5
|
0.2312
|
0.0098
|
-0.0035
|
0.0002
|
|
|
6
|
0.2410
|
0.0063
|
-0.0033
|
|
|
|
7
|
0.2473
|
0.0030
|
|
|
|
|
8
|
0.2503
|
|
|
|
|
Приложение 4