Связность графов
Министерство образования и науки
Российской Федерации
Федеральное государственное бюджетное
образовательное учреждение высшего профессионального образования
Тюменский государственный
нефтегазовый университет»
Филиал: Тобольский индустриальный
институт»
Кафедра математики и информатики
КУРСОВАЯ РАБОТА
по дисциплине «Дискретная математика»
на тему «Связность графов»
Выполнил студент группы ИВТ(б)-10
Гарюткин А.Е.
Руководитель курсового проекта:
Татьяненко С.А
Тобольск, 2011г.
Содержание
Введение
Глава 1.
Понятие графа
§1.
Определения
§2. Примеры
графов
§3. Связность
графов
Глава 2. Цепи
и Циклы
§4. Новые
определения
§5. Эйлеровы
графы
§6.
Гамильтоновы графы
§7. Бесконечные
графы
Глава 3.
ДЕРЕВЬЯ
§8. Элементарные
свойства деревьев
Практическая
часть
Заключение
Введение
Родоначальником теории графов принято считать математика Леонарда Эйлера
(1707-1783). Историю возникновения этой теории можно проследить по переписке
великого ученого. Вот перевод латинского текста, который взят из письма Эйлера
к итальянскому математику и инженеру Маринони, отправленного из Петербурга 13
марта 1736 года.
"Некогда мне была предложена задача об острове, расположенном в
городе Кенигсберге и окруженном рекой, через которую перекинуто семь мостов.
Спрашивается, может ли кто-нибудь непрерывно обойти их, проходя только однажды
через каждый мост. И тут же мне было сообщено, что никто еще до сих пор не мог
это проделать, но никто и не доказал, что это невозможно. Вопрос этот, хотя и
банальный, показался мне, однако, достойным внимания тем, что для его решения
недостаточны ни геометрия, ни алгебра, ни комбинаторное искусство. После долгих
размышлений я нашел легкое правило, основанное на вполне убедительном
доказательстве, с помощью которого можно во всех задачах такого рода тотчас же
определить, может ли быть совершен такой обход через какое угодно число и как
угодно расположенных мостов или не может”. Множество самых разнообразных задач
естественно формулируется в терминах графов. Так, например, могут быть
сформулированы задачи составления расписаний в исследовании операций, анализа
сетей в электротехнике, установления структуры молекул в органической химии,
сегментации программ в программировании, анализа цепей Маркова в теории
вероятностей. В задачах, возникающих в реальной жизни, соответствующие графы
часто оказываются так велики, что их анализ неосуществим без ЭВМ. Таким
образом, решение прикладных задач с использованием теории графов возможно в той
мере, в какой возможна обработка больших графов на ЭВМ, и поэтому эффективные
алгоритмы решения задач теории графов имеют большое практическое значение.
Глава 1. Понятие графа
§1. Определения
Дадим сначала определение простого графа G. Пара (V(G), Е(G)) называется простым графом, если V(G) - непустое конечное множество элементов, называемых вершинами
(или узлами, или точками), а Е(G) - конечное множество неупорядоченных пар различных
элементов из V(G), называемых ребрами (или линиями). Иногда V(G) называют множеством вершин, а Е(G) - множеством ребер графа G. Например, на Рис. 1 изображен
простой граф G, у которого множеством вершин V(G) является множество {u, v, w, z}, а множество ребер Е(G) состоит из пар {u, v}, {v, w}, {u, w} и {w, z}. Говорят, что ребро {v, w} соединяет вершины v и w. Отметим, что так как Е(G) является множеством, а не
семейством, то в простом графе данную пару вершин может соединять не более чем
одно ребро.
Оказывается, многие результаты, полученные для простых графов, без труда
можно перенести на более общие объекты, в которых две вершины могут быть соединены
более чем одним ребром. Кроме того, часто бывает удобно снять ограничение,
состоящее в том, что ребро должно соединять две различные вершины, и допустить
существование петель, т. е. ребер, соединяющих вершину с ней самой.
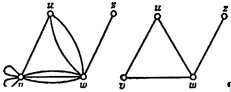
Рис. 1. Рис. 2
Получающийся при этом объект, в котором могут быть петли и кратные ребра,
называется общим графом, или просто графом (Рис. 2). Подчеркнем
тот факт, что каждый простой граф является графом, но не каждый граф является
простым графом.
Более точно, графом G
называется пара (V(G), Е(G)), где V(G) - непустое конечное множество
элементов, называемых вершинами, а Е(G) - конечное семейство неупорядоченных пар элементов из V(G) (не обязательно различных), называемых ребрами.
Заметим, что употребление слова «семейство» говорит о том, что допускаются
кратные ребра. Будем называть V(G) множеством вершин, а Е(G) - семейством ребер графа G; на Рис. 2 V(G) - это множество
{u, v, w, z}, а Е(G) - это семейство, состоящее из ребер {u, v}, {v, v), {v, v), {v, w}, {v, w}, (v, w}, {u, w}, {u, w} и {w, z}. О каждом ребре вида {v, w} говорят, что
оно соединяет вершины v и w;
значит, каждая петля {v, v} соединяет вершину v саму с собой. Предметом
изучения в теории графов являются также ориентированные графы (называемые
иногда орграфами или сетями; однако мы будем употреблять слово «сеть» в
несколько ином смысле). Орграфом D называется пара (V(D), A (D)), где V(D) - непустое конечное множество элементов, называемых вершинами,
а А (D) - конечное семейство упорядоченных
пар элементов из V(D), называемых дугами (или ориентированными
ребрами). Дуга, у которой вершина v является первым элементом, а вершина w - вторым, называется дугой из
v в w и обозначается (v, w). Заметим, что дуги (v, w) и (w, v)
различны. На Рис. 3 изображен орграф, дугами которого являются (u, v), (v, v), (v, w), (v, w), (w, v), (w, u) и (w, z); порядок вершин на дуге указан стрелкой.
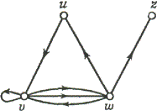
Рис 3
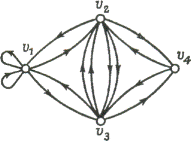
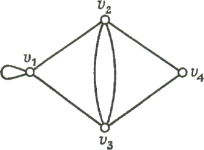
Рис. 4
Графы и орграфы - существенно различные объекты, в определенных случаях
графы можно рассматривать как орграфы, в которых каждому ребру соответствуют
две противоположно ориентированные дуги (Рис. 4).
Замечание по поводу терминологии. Язык теории графов, бесспорно, еще не
стал стандартным - каждый автор вводит свою собственную терминологию. Я
пользуюсь в основном терминологией Басакера и Саати . Некоторые специалисты по
теории графов называют графом то, что мы назвали простым графом. Во многих
случаях, и особенно в приложениях, под графом понимается орграф. Еще хуже,
иногда графом называют объект, который получается, если снять условие
конечности множества вершин или семейства ребер. (Если оба они бесконечны,
будем называть соответствующий объект бесконечным графом; изучение
бесконечных графов мы отложим до §8.) Следует подчеркнуть, что любое из
перечисленных определений графа вполне допустимо, если только пользоваться им
последовательно.
Прежде чем привести примеры некоторых важных типов графов (§3), удобно
дать еще несколько простых определений.
Две вершины v и w
графа G называются смежными, если
существует соединяющее их ребро (т. е. ребро вида {v, w}); при этом
вершины v и w называются инцидентными этому
ребру (а ребро - инцидентным этим вершинам). Аналогично, два различных
ребра графа G называются смежными, если они имеют
по крайней мере одну общую вершину. Степенью (или валентностью)
вершины v графа G
называется число ребер, инцидентных v; степень вершины v обозначается через ρ(v). При вычислении степени вершины v
будем учитывать петлю в v два раза, а не один (если только явно не сказано
иное). Вершина степени 0 называется изолированной вершиной, вершина
степени 1 называется висячей (или концевой) вершиной. Так, граф,
изображенный на Рис. 2, имеет одну висячую вершину, одну вершину степени 3,
одну - степени 6 и одну - степени 8.
Легко видеть, что если сложить степени всех вершин графа, то получится
четное число - равное удвоенному числу ребер, так как каждое ребро участвует в
этой сумме ровно два раза. Этот результат, известный еще двести лет назад
Эйлеру, часто называют леммой о рукопожатиях. Из нее следует, что если
несколько человек обменялись рукопожатиями, то общее число пожатых рук
обязательно четно, ибо в каждом рукопожатии участвуют две руки (при этом каждая
рука считается столько раз, сколько она участвовала в рукопожатиях). Из леммы о
рукопожатиях сразу следует, что в любом графе число вершин нечетной степени
должно быть четным.
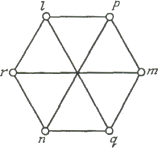
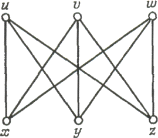
Рис. 5
Два графа G1 и G2 называются изоморфными, если существует взаимно
однозначное соответствие между множествами их вершин, обладающее тем свойством,
что число ребер, соединяющих любые две вершины в G1, равно числу ребер, соединяющих соответствующие вершины в G2. Так, два графа, изображенные на Рис. 5, изоморфны
при соответствии u↔l, v↔m, w↔n, x↔p, y↔q.
Заметим, что эти графы имеют по шесть вершин - другие точки пересечения ребер
вершинами не являются.
Подграфом графа G называется граф, все вершины
которого принадлежат V(G), а все ребра принадлежат Е(G). Так, граф на Рис. 1 является
подграфом графа, изображенного на Рис. 4, но не является подграфом ни одного из
графов, приведенных на Рис. 5 (так как последние не содержат «треугольников»).
Наконец, матрицей смежности графа G с множеством вершин {v1, ..., vn} (соответствующей данной нумерации
вершин) называется матрица А = (аij) размера n xn, в
которой элемент аij равен
числу ребер в G, соединяющих vi и vj. Например, на Рис. 6 дана матрица смежности графа,
изображенного на Рис. 4. Можно получить несколько различных матриц смежности
данного графа, меняя обозначения его вершин; это приведет к изменению порядка
строк и столбцов матрицы A. Но
в результате всегда получится симметричная матрица из неотрицательных целых
чисел, обладающая тем свойством, что сумма чисел в любой строке или столбце
равна степени соответствующей вершины (здесь каждая петля учитывается в степени
вершины один раз).
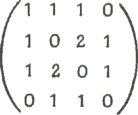
Рис. 6
Обратно, по любой заданной симметричной матрице из неотрицательных целых
чисел легко построить граф (единственный с точностью до изоморфизма), имеющий
данную матрицу своей матрицей смежности. Отсюда следует, что теорию графов
можно свести к изучению матриц особого типа.
§2. Примеры графов
В этом параграфе я расскажу об исследованиях некоторых важных типов
графов.
Вполне несвязные графы. Граф, у которого множество ребер пусто, называется вполне
несвязным (или пустым) графом. Будем обозначать вполне несвязный
граф с n вершинами через Nn; N4 показан на Рис. 1. Заметим, что у вполне несвязного графа
все вершины изолированы. Вполне несвязные графы не представляют особого
интереса.
Полные графы. Простой граф, в котором любые две вершины смежны,
называется полным графом. Полный граф с n вершинами оО, обычно обозначается через Кn. Графы K4 и K5 изображены на Рис. 2 и 3.3. Убедимся
в том, что Кn имеет ровно n(n - 1)/2 ребер.
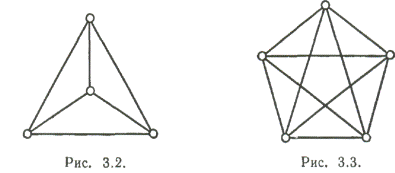
Рис. 1. оо
Регулярные графы
Граф, у которого все вершины имеют одну и ту же степень, называется
регулярным графом. Если степень каждой вершины равна r, то граф называется регулярным степени r. Регулярные графы степени 3,
называемые также кубическими (или трехвалентными) графами (см., например, Рис.
5, 3,2 и 3.4), представляют особый интерес в связи с задачей раскраски. Другим
известным примером кубического графа является так называемый граф Петерсена,
показанный на Рис. 5. Отметим, что каждый вполне несвязный граф является
регулярным степени 0, а каждый полный граф Кn - регулярным степени n-1.
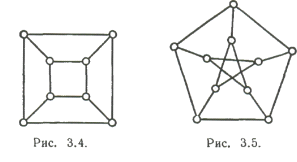
Платоновы графы. Среди регулярных графов особенно интересны так
называемые платоновы графы - графы, образованные вершинами и ребрами пяти
правильных многогранников - платоновых тел: тетраэдра, куба, октаэдра,
додекаэдра и икосаэдра. Граф К4 соответствует тетраэдру (Рис. 2);
графы, соответствующие кубу и октаэдру, показаны на Рис. 4 и 3.6; граф,
соответствующий додекаэдру, изображен на Рис. 4
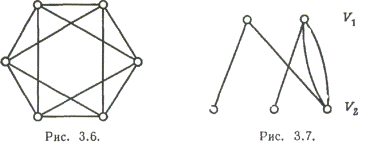
Двудольные графы. Допустим, что множество вершин графа можно разбить на
два непересекающихся подмножества V1 и V2 так, что каждое ребро в G соединяет какую-нибудь вершину из V1 c какой-либо из V2 (Рис. 7); тогда G называется двудольным графом. Такие графы иногда обозначают G(V1,V2), если хотят выделить два указанных
подмножества.
Двудольный граф можно определить и по-другому - в терминах раскраски его
вершин двумя цветами, скажем красным и синим. При этом граф называется
двудольным, если каждую его вершину можно окрасить красным или синим цветом
так, чтобы любое ребро имело один конец красный, а другой - синий.
Следует подчеркнуть, что в двудольном графе совсем не обязательно каждая
вершина из V1 соединена с каждой вершиной из V2; если же это так и если при этом граф G простой, то он называется полным
двудольным графом и обычно обозначается Km,n, где m и n - число вершин соответственно в V1 и V2. Например, на Рис. 8 изображен граф
К4,3 а на Рис. 5 - два варианта графа Kз,з. Заметим, что граф Km,n имеет ровно m+ n вершин и mn ребер. Полный двудольный граф вида K1,n называется звездным графом; на Рис. 9 изображен
звездный граф K1,5.
Связные графы. Все рассмотренные графы, состояли «из одного
куска». Исключениями были вполне несвязные графы Nn (n ≥ 2) и
объединения графов, состоящие из «не соединенных друг с другом частей».
Формализуем это различие, называя граф связным, если его нельзя
представить в виде объединения двух графов, и несвязным в противном
случае.
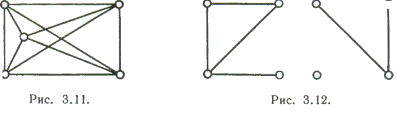
Очевидно, что всякий несвязный граф G можно представить в виде объединения конечного числа связных
графов - каждый из таких связных графов называется компонентой (связности)
графа G. (На Рис. 12 изображен граф с тремя
компонентами.) Доказательство некоторых утверждений для произвольных графов
часто бывает удобно сначала провести для связных графов, а затем применить их к
каждой компоненте в отдельности.
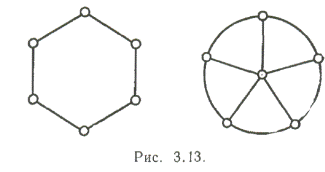
Циклические графы и колеса. Связный регулярный граф степени 2
называется циклическим графом (или циклом); циклический граф, с n вершинами обозначается через Сn. Соединение графов N1 и Сn-1 (n ≥ 3) называется колесом с n вершинами и обозначается Wn. На Рис. 13 изображены С6
и W6; граф W4 уже появлялся на Рис. 2.
Дополнение простого графа. Пусть G - простой граф
с множеством вершин V(G). Дополнением G графа G называется простой граф с множеством вершин V(G), в котором две вершины смежны тогда и только тогда, когда
они не смежны в G. Отсюда следует,
что если граф G содержит n вершин, то граф G можно построить, удалив из графа Кn все ребра, принадлежащие G (здесь G
считается подграфом Kn).
Заметим, что дополнение полного графа является вполне несвязным графом и
наоборот; дополнение регулярного графа регулярно.
§3. Связность графов
Одна из топологических характеристик графа. Граф
называется связным, если для любых его вершин u и v существует цепь,
соединяющая эти вершины. Числом вершинной связности графа G [обозначение à(G)] наз. наименьшее число вершин,
удаление к-рых (вместе с инцидентными им ребрами) приводит к несвязному графу
или к графу, состоящему из одной изолированной вершины. Числом реберной
связности [обозначение λ(G)] наз. наименьшее число ребер графа G, удаление к-рых
приводит к несвязному графу. Граф G наз. k-связным, если à(G) ≥ k, и k-реберно связным, если
λ(G) ≥ k. Максимальный по включению
k-связный подграф графа G наз. его k-связной компонентой; 1-связная компонента
наз. компонентой связности. При исследовании коммуникационных и логических
сетей числа связности соответствующих графов можно интерпретировать как степень
надежности этих сетей.
В теории графов изучаются способы установления Г. с,
условия, при к-рых граф является k-связным или k-реберно связным, соотношения
между различными видами связности, зависимость чисел связности от других
параметров графа и т. п. Так, если δ(G) - минимальная степень вершин графа
G, то справедливы следующие неравенства: à(G) ≤ λ(G) ≤ δ(G).
Для любых целых а, b, с (0 < а ≤ b ≤ с)
существует граф G, у к-рого à(G) = a, λ(G) = b, δ(G) = c. Если граф G имеет n вершин и δ(G) ≥ [n/2], то λ(G) = δ(G). Говорят, что множество S вершин,
ребер или вершин и ребер разделяет вершины u и v, если u и v принадлежат разным
компонентам связности графа G-S, полученного из G удалением элементов множества
S. Справедливы следующие утверждения.
Наименьшее число вершин, разделяющих две несмежные
вершины u и v, равно наибольшему числу простых цепей, не имеющих общих вершин,
соединяющих u и v. Граф G является k-связным тогда и только тогда, когда любая
пара его вершин соединена по крайней мере к вершинно непересекающимися цепями.
Аналогичные теоремы справедливы и для реберной связности. Граф k-реберно связен
тогда и только тогда, когда любая пара его вершин соединена по крайней мере к
реберно непересекающимися цепями. Множество ребер, удаление к-рых приводит к
несвязному графу, наз. разрезом. В каждом графе наибольшее число реберно
непересекающихся разрезов, разделяющих вершины u и v, равно наименьшему числу
ребер простой цепи, соединяющей u и v, т. е. расстоянию d(u, v) между u и v.
Теорема несвязности графов
Граф является несвязным тогда и только тогда, когда
множество его вершин V можно разбить на два непустых подмножества V1 и V2 так,
чтобы любое ребро графа соединяло вершины из одного подмножества.
Доказательство
Пусть G(V,E) - несвязный граф. Зафиксируем некоторую
вершину v графа и обозначим через V1 множество, состоящее из вершины v и всех
тех вершин из V, которые соединены цепями с вершиной v. Множество V1 не пусто
(оно содержит, но крайней мере, вершину v) и не совпадает с множеством V (при
V1=V граф G(V,E)- связный, т.к. между его любыми двумя различными вершинами
существует цепь, проходящая через v). Рассмотрим дополнение V2=V \ V1.
Множество V2- не пусто, и никакое ребро графа G(V,E)
не соединяет ни одну вершину из V1 ни с одной вершиной из V2. Поэтому
построенные множества V1 и V2 образуют искомое разбиение множества V.
Обратно, пусть существует разбиение V1 ∪ V2, множества V, удовлетворяющее
условию теоремы.
Докажем, что тогда граф G(V,E) несвязный. Возьмем
произвольную пару вершин v ∈ V1 и w ∈ V2 , из разных подмножеств и
предположим, что существует цепь, соединяющая эти вершины. Такая цепь включает
ребро, концы которого принадлежат разным подмножествам, что противоречит
условию. Теорема доказана.
Вершина w графа называется достижимой из вершины v,
если либо w=v, либо существует цепь с началом v и концом w.
Следствие из теоремы
Для того чтобы граф G был связным необходимо и
достаточно, чтобы в нем из любой фиксированной вершины были достижимы все
остальные вершины этого графа.
Свойства графов
Свойства графов:
°. Каждая вершина графа входит в одну и только в одну
компоненту связности.
°. Любой конечный граф имеет конечное число компонент
связности.
°. Граф, состоящий из единственной компоненты
связности, является связным.
°. Каждая компонента связности графа является его
подграфом.
°. Для любого графа либо он сам, либо его дополнение
является связным.
Доказательства свойств
Докажем свойства 4° и 5°.
°. Пусть G1(V1,E1) - некоторая компонента связности
графа G(V,E) . Рассмотрим множество вершин V2=V \V1 графа G, не входящих в
компоненту G1(V1,E1) . Если удалить каждую вершину из V2 вместе со всеми
инцидентными ей ребрами, получим подграф графа G(V,E) совпадающий с компонентой
связности G1(V1,E1).
°. Пусть G(V,E) некоторый граф порядка n, а G=(V,E) -
его дополнение до графа Кn. Когда граф G связен, утверждение очевидно. Пусть G
несвязный граф G1(V1,E1) - одна из его компонент связности и V2=V \V1. Тогда
для любых вершин v ∈ V1 , w ∈ V2 -, в дополнении G существует ребро vw ∈ E . Значит, любая вершина из V2
соединена с любой вершиной из V1ребром, принадлежащим E , а любые две вершины
из V1 соединены цепью длины 2, оба звена которой также лежат в E . Поэтому граф
G связен.
граф непустой вершина связь
Глава 2. Цепи и циклы
§4. Новые определения
Маршрутом в данном графе G
называется конечная последовательность ребер вида
{v0,v1},{v1,v2}, …, {vm-1,vm}
(обозначаемая также через (v0→ v1→ v2→ …→ vm) Очевидно следующее свойство
маршрута: любые два последовательных ребра либо смежны, либо одинаковы. Но не
всякая последовательность ребер, обладающая этим свойством, является маршрутом
(в качестве примера рассмотрим звездный граф и возьмем его ребра в произвольном
порядке). Каждому маршруту соответствует последовательность вершин vо, v1, ..., vm; v0 называется начальной вершиной, а vm - конечной вершиной маршрута. Таким
образом, мы будем говорить о маршруте из v0 в vm. Заметим, что для любой вершины V^ тривиальным маршрутом, вообще не
содержащим ребер, является маршрут из v0 в v0. Длиной маршрута называется число ребер в нем;
например, на Рис. 1 маршрут v→w→x→y→z→z→y→w из v в w
имеет длину, равную семи.
Маршрут называется цепью, если все его ребра различны, и простой цепью,
если все вершины v0, v1 ..., vm различны (кроме, может быть, v0= vm).
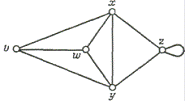
Рис 4.1
Цепь или простая цепь замкнуты, если v0= vm. Замкнутая простая цепь, содержащая
по крайней мере одно ребро, называется циклом; в частности, любая петля или
любая пара кратных ребер образует цикл.
Замечание. Маршрут, также называют путем, реберной последовательностью.
Цепь называют путем, полупростым путем; простую цепь - цепью, путем, дугой,
простым путем, элементарной цепью; замкнутую цепь - циклической цепью,
контуром; цикл - контуром, контурной цепью, простым циклом, элементарным
циклом.
Чтобы разобраться в приведенных выше определениях, рассмотрим еще раз
Рис. 1. Мы видим, что v→w→x→y→z→z→x -
цепь, v→w→x→y→z- простая цепь, v→w→x→y→z→x→v -
замкнутая цепь и v→w→x→y→v- цикл. Цикл длины три (например, v→w→x→v) называется треугольником.
Дадим теперь другое, быть может, более удобное определение связных
графов. Граф G называется связным, если для любых
двух его вершин v и w существует
простая цепь из v в w. Любой граф
можно разбить на непересекающиеся связные подграфы, называемые компонентами
(связности), задав следующее отношение эквивалентности на множестве его вершин:
две вершины эквивалентны (или связаны), если существует простая цепь из одной в
другую. Оставим читателю доказательство того, что связанность вершин
действительно является отношением эквивалентности и что вершины, принадлежащие
одному классу эквивалентности, вместе с инцидентными им ребрами образуют
компоненты (связности) графа. Очевидно, что связный граф состоит из одной
компоненты. Граф называется несвязным, если число его компонент больше единицы.
Докажем теперь, что данные здесь определения не противоречат определениям из §
3.
Теорема 5А. Граф является связным в смысле данного выше определения
тогда и только тогда, когда он связен в смысле определения из §3.
Доказательство. => Пусть граф G связен в смысле определения из данного параграфа. Допустим,
что G представляет собой объединение двух
(непересекающихся) подграфов, а v и w - вершины, принадлежащие разным
подграфам. Любая простая цепь из v в w должна содержать ребро, инцидентное некоторым двум вершинам из разных
подграфов; так как такого ребра не существует, получили противоречие.
<= Теперь предположим, что граф G связен в смысле определения из § 3 и не существует никакой
простой цепи, связывающей заданную пару вершин v и w. Тогда, по данному выше определению компонент связности,
вершины v и w будут принадлежать разным
компонентам. Исходя из этого, можно представить G в виде объединения двух графов, одним из которых является
компонента, содержащая v, а другим - объединение оставшихся компонент. Отсюда и
получаем нужное противоречие. //
Теперь, когда мы представляем себе, что такое связность, естественно
попытаться найти какие-нибудь свойства связных графов. Одно направление
исследования - поиск оценок для числа ребер простого графа с n вершинами и заданным числом
компонент. Если такой граф связен, то естественно ожидать, что число ребер в
нем минимально тогда, когда он не имеет циклов (такой граф называется деревом),
и максимально, когда он является полным графом. Отсюда следовало бы, что число
ребер в связном графе заключено между n- 1 и n(n - 1)/2. Этот результат является частным случаем более
сильного утверждения, которое сейчас докажем.
Теорема 5В. Пусть G -
простой граф с n вершинами и k компонентами. Тогда число m его ребер удовлетворяет неравенствам
n - k < m < (n - k)(n - k +
1)/2.
Доказательство. Неравенство m ≥
n - k докажем индукцией по числу ребер в G. Если О - вполне несвязный граф, то утверждение очевидно.
Если в графе G число ребер минимально (скажем m0), то удаление любого ребра должно привести к
увеличению числа компонент на единицу. Таким образом, в получившемся графе
будет n вершин, k + 1 компонент и m0 - 1 ребер.
Следовательно, в силу индуктивного предположения m0 - 1 > n - (k+1), откуда сразу же получается m0 > n - k, что и утверждалось.
Для доказательства оценки сверху можно считать каждую компоненту графа G полным графом. Предположим, что Сi и Сj - две компоненты соответственно с ni и nj; вершинами и ni ≥ nj≥
1. Если мы заменим Сi и Сj; на полные графы с ni + 1 и nj - 1 вершинами, то общее число вершин
не изменится, а число ребер увеличится на положительную величину
/2{(ni+1) ni - ni (ni -1)}-1/2{ nj (nj -1)-( nj -1)( nj -2)} = ni- nj +1.
Следовательно, для того чтобы число ребер в графе G было максимально возможным (при
заданных n и k), G
должен состоять из k- 1 изолированных
вершин и полного графа с n - k + 1 вершинами. Отсюда сразу вытекает
нужное неравенство. //
Следствие 5С. Любой простой граф с т вершинами и более чем (n- 1)(n - 2)/2 ребрами связен. //
Другое направление исследования связных графов задается следующим
вопросом: насколько сильно связен связный граф? Этот вопрос можно
сформулировать и так: сколько ребер нужно удалить из графа, чтобы он перестал
быть связным?
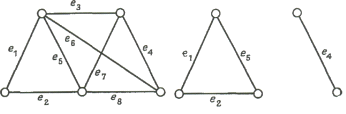
Рис. 2 Рис. 3
Для обсуждения данного вопроса удобно ввести еще два определения.
Разделяющим множеством связного графа G называется такое множество его ребер, удаление которого приводит к
несвязному графу. Например, в графе, изображенном на Рис. 2, каждое из множеств
{е1 ,е2, е5} и {е3, е6,
е7, е8) является разделяющим; несвязный граф, оставшийся
после удаления второго из этих множеств, показан на Рис. 3. Далее, назовем разрезом
такое разделяющее множество, никакое собственное подмножество которого не
является разделяющим. В рассмотренном выше примере разрезом будет только второе
разделяющее множество. Легко видеть, что после удаления ребер, принадлежащих
разрезу, остается граф, имеющий ровно две компоненты. Если разрез состоит из
единственного ребра e, то е называется
мостом, или перешейком (Рис. 4).
Все эти определения легко переносятся на несвязные графы. В произвольном
графе G разделяющим множеством называется такое множество ребер,
удаление которого увеличивает число компонент вG. Разрезом в G называется разделяющее множество, никакое собственное подмножество
которого не является разделяющим. Заметим, что в результате удаления ребер,
принадлежащих разрезу, число компонент в G увеличивается ровно на единицу.
§5. Эйлеровы графы
Связный граф G называется эйлеровым,
если существует замкнутая цепь, проходящая через каждое его ребро; такая цепь
называется эйлеровой цепью. Отметим, что в этом определении требуется,
чтобы каждое ребро проходилось 1 только один раз.
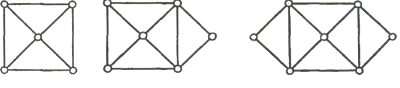
2 3
Если снять ограничение на замкнутость цепи, то граф называется полуэйлеровым;
при этом каждый эйлеров граф будет полуэйлеровым. На Рис. 1, 2 и 3 изображены
соответственно не эйлеров, полуэйлеров и эйлеров графы. Заметим, что
предположение о связности графа G
введено только ради удобства, так как оно позволяет не рассматривать
тривиальный случай графа, содержащего несколько изолированных вершин.
Название «эйлеров» возникло в связи с тем, что Эйлер первым решил
знаменитую задачу о кёнигсбергских мостах, в которой нужно было узнать, имеет
ли граф, изображенный на Рис. 4, эйлерову цепь (не имеет!).Сразу же возникает
вопрос: можно ли найти необходимые и достаточные условия для того, чтобы граф
был эйлеровым?
Лемма 6А. Если степень каждой вершины графа G не меньше двух, то G содержит цикл.
Доказательство. Если в графе G имеются петли или кратные ребра, то утверждение очевидно; поэтому
предположим, что G является простым
графом. Пусть v - произвольная вершина графа G; построим по индукции маршрут v→ v1→ v2→…, выбирая вершину v1 смежной вершине v, а
для i ≥ 1 - выбирая vi+1 смежной vi и отличной от vi-1(существование такой вершины vi+1 гарантировано условием леммы). Так
как G имеет конечное число вершин, то в
конце концов придем к вершине, которая уже была выбрана раньше. Предположим,
что ад - первая такая вершина; тогда часть маршрута, лежащая между двумя
вхождениями vk, и является требуемым циклом.
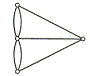
Рис 4
Теорема 6В. Связный граф G
является эйлеровым тогда и только тогда, когда каждая вершина в G имеет четную степень.
Доказательство. => Предположим, что Р является эйлеровой цепью в графе
G. Тогда при всяком прохождении цепи Р
через любую из вершин графа степень этой вершины увеличивается на два. А так
как каждое ребро встречается в Р ровно один раз, то каждая вершина должна иметь
четную степень.
Рис 5
Следствие 6С. Связный граф является эйлеровым тогда и только тогда, когда
семейство его ребер можно разбить на непересекающиеся циклы. //
Следствие 6В. Связный граф является полуэйлеровым тогда и только тогда,
когда в нем не более двух вершин имеют нечетные степени. //
Заметим, что если полуэйлеров граф содержит ровно две вершины с нечетными
степенями, то в любой полуэйлеровой цепи (смысл этого понятия очевиден) одна из
этих вершин обязательно будет начальной, а другая - конечной. По лемме о
рукопожатиях граф не может иметь только одну вершину нечетной степени.
Завершая рассмотрение эйлеровых графов, дадим алгоритм построения
эйлеровой цепи в данном эйлеровом графе. Этот метод известен под названием
алгоритма Флёри.
Теорема 6Е. Пусть G -
эйлеров граф; тогда следующая процедура всегда возможна и приводит к эйлеровой
цепи графа G. Выходя из произвольной вершины и,
идем по ребрам графа произвольным образом, соблюдая лишь следующие правила: (i) стираем ребра по мере их
прохождения и стираем также изолированные вершины, которые при этом образуются;
(ii) на каждом этапе идем по мосту
только тогда, когда нет других возможностей.
Доказательство. Предположим, что достигли некоторой вершины v; тогда если v ≠ u, то оставшийся подграф Н связен и
содержит ровно две вершины нечетной степени, а именно u и v. Согласно следствию 6D, граф H
содержит полуэйлерову цепь Р из v и u. Поскольку удаление первого ребра цепи Р не нарушает связности графа H, отсюда следует, что описанное в
теореме построение возможно на каждом этапе. Если же v = u, то доказательство остается тем же
самым до тех пор, пока есть еще ребра, инцидентные вершине u.
Осталось только показать, что данная процедура всегда приводит к полной
эйлеровой цепи. Но это очевидно, так как в G не может быть ребер, оставшихся непройденными после
использования последнего ребра, инцидентного и (в противном случае удаление
некоторого ребра, смежного одному из оставшихся, привело бы к несвязному графу,
что противоречит (ii)).
§6. Гамильтоновы графы
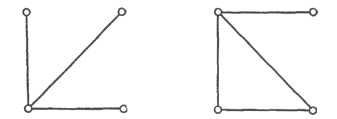
Рис 1 Рис. 2
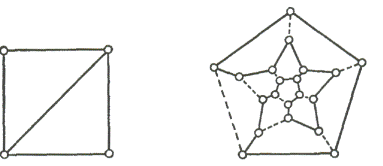
Рис. 3 Рис. 4
граф связанность цепь дерево
В предыдущем параграфе мы обсудили проблему существования замкнутой цепи,
проходящей через каждое ребро заданного связного графа G. Можно рассмотреть аналогичную проблему существования
замкнутой цепи, проходящей ровно один раз через каждую вершину графа G. Ясно, что такая цепь должна быть
циклом (исключая тривиальный случай, когда G является графом N1); если такой цикл существует,
то он называется гамильтоновым циклом, а G называется гамильтоновым графом. Граф, который содержит
простую цепь, проходящую через каждую его вершину, называется
полугамильтоновым; заметим, что всякий гамильтонов граф является
полугамильтоновым. На Рис. 1, 2 и 3 изображены соответственно не гамильтонов,
полугамильтонов и гамильтонов графы.
Название «гамильтонов цикл» возникло в связи с тем, что сэр Уильям
Гамильтон занимался исследованием существования таких циклов в графе,
соответствующем додекаэдру; на Рис. 4 показан такой цикл (его ребра изображены
сплошными линиями).
В теореме 6В получили необходимое и достаточное условие для того, чтобы
связный граф был эйлеровым. Естественно было бы надеяться, что и для
гамильтоновых графов удастся получить аналогичный критерий. Однако поиск такого
критерия стал одной из главных нерешенных задач теории графов! О гамильтоновых
графах в общем-то известно очень мало. Большинство известных теорем имеет вид:
«если G имеет достаточное число ребер, то G является гамильтоновым графом»;
вероятно, самой знаменитой из них является следующая теорема, принадлежащая Г.
Э. Дираку и потому известная как теорема Дирака.
Теорема 7А (Дирак 1952). Если в простом графе с n (≥ 3) вершинами р(v) ≥ n/2 для любой вершины v, то граф G является гамильтоновым.
Замечание. Существует несколько доказательств этой широко известной
теоремы; здесь приведем доказательство, принадлежащее Д. Дж. Ньюману.
Доказательство. Добавим к графу k новых вершин, соединяя каждую из них с каждой вершиной из G. Будем предполагать, что k - наименьшее число вершин, нужных
для того, чтобы полученный граф G'
стал гамильтоновым. Затем, считая, что k > 0, придем к противоречию.
Пусть v→p→w→…→v- гамильтонов цикл в G', где v и w - вершины из G, а р
- одна из новых вершин. Тогда w не
является смежной с v, так как в противном случае могли бы не использовать
вершину р, что противоречит минимальности k. Более того, вершина (скажем w'), смежная вершине w, не может непосредственно следовать за вершиной v’, смежной вершине v, потому что тогда могли бы заменить v→p→w→…→v’→w’→…→v на v→v’→…→w→w’→…→ v, перевернув часть
цикла, заключенную между w и v'. Отсюда следует, что число вершин
графа G', не являющихся смежными с v, не меньше числа вершин, смежных с v
(т. е. равно по меньшей мере n/2 + k); с другой стороны, очевидно, что
число вершин графа G', смежных с w, тоже равно по меньшей мере n/2 + k. А так как ни одна вершина графа G' не может быть одновременно смежной и не смежной вершине w, то общее число вершин графа G', равное n +k, не меньше, чем n + 2k. Это и есть искомое противоречие. //
§7. Бесконечные графы
В этом параграфе покажу, как можно обобщить некоторые определения, данные
в предыдущих параграфах, на случай бесконечных графов. Напомним читателю, что
бесконечным графом называется пара (V(G), Е(G))> где V(G)- бесконечное множество элементов, называемых вершинами, а
Е(G) - бесконечное семейство
неупорядоченных пар элементов из V(G) у называемых ребрами. Если
оба множества V(G) и Е(G)
счетны, то G называется счетным графом. Заметим,
что наши определения исключают те случаи, когда V(G) бесконечно, а
Е(G) конечно (такие объекты являются
всего лишь конечными графами с бесконечным множеством изолированных вершин),
или когда Е(G) бесконечно, а V(G) конечно (такие объекты являются конечными графами с
бесконечным числом петель или кратных ребер).

Рис. 1
Некоторые определения, данные в гл. 2 (таких понятий, как «смежный»,
«инцидентный», «изоморфный», «подграф», «объединение», «связный»,
«компонента»), сразу переносятся на бесконечные графы. Степенью вершины
v бесконечного графа называется мощность множества ребер, инцидентных v степень
вершины может быть конечной или бесконечной. Бесконечный граф, все вершины
которого имеют конечные степени, называется локально конечным; хорошо
известным примером такого графа является бесконечная квадратная решетка, часть
которой изображена на Рис. 1. Аналогичным образом можно определить локально
счетный бесконечный граф - как граф, все вершины которого имеют счетную
степень). Пользуясь этими определениями, докажем сейчас простой, но важный
результат.
Теорема 8А. Каждый связный локально счетный бесконечный граф является
счетным.
Доказательство. Пусть v - произвольная вершина такого бесконечного графа,
и пусть А1 - множество вершин, смежных v, A2 - множество всех вершин, смежных вершинам
из А1 и т. д. По условию теоремы А1 - счетно и,
следовательно, множества A2, A3, ... тоже счетны (здесь используем тот факт, что объединение
не более чем счетного множества счетных множеств счетно); следовательно, {v}, А1,
А2,…- последовательность множеств, объединение которых счетно. Кроме
того, эта последовательность содержит каждую вершину бесконечного графа в силу
его связности. Отсюда и следует нужный результат. //
Следствие 8В. Каждый связный локально конечный бесконечный граф является
счетным. //
Помимо этого, на бесконечный граф G можно перенести понятие маршрута, причем тремя различными
способами:
(i) конечный маршрут в G определяется так же, как и в §5;
(ii) бесконечным в одну сторону
маршрутом в G (с начальной вершиной v0,) называется бесконечная последовательность ребер
вида {v0, v1}, {v1, v2}, ... ;
(iii) бесконечным в обе стороны маршрутом
в G называется бесконечная
последовательность ребер вида ..., {v-2, v-1 }, { v-2, v0}, { v0, v1},{ v1, v2} ,... .
Бесконечные в одну сторону и в обе стороны цепи и простые цепи
определяются очевидным образом, так же как и понятия длины цепи и расстояния
между вершинами. Следующий результат, известный как лемма Кёнига,
говорит о том, что бесконечные простые цепи не так уж трудно обнаружить.
Теорема 8С (Кёниг 1936). Пусть G - связный локально конечный бесконечный граф; тогда для
любой его вершины v существует бесконечная в одну сторону простая цепь с
начальной вершиной v.
Доказательство. Если z -
произвольная вершина графа G,
отличная от v, то существует нетривиальная простая
цепь от v до z; отсюда следует, что в G имеется бесконечно много простых
цепей с начальной вершиной v. Поскольку степень v конечна, то бесконечное
множество таких простых цепей должно начинаться с одного и того же ребра. Если
таким ребром является {v, v1}, то, повторяя эту процедуру для
вершины v1, получим новую вершину v2 и соответствующее ей
ребро {v1, v2}. Продолжая таким образом, получим
бесконечную в одну сторону простую цепь v→v1→v2… .
Важное значение леммы Кёнига состоит в том, что она позволяет получать
результаты о бесконечных графах из соответствующих результатов для конечных
графов. Типичным примером этого является следующая теорема.
Теорема 8D. Пусть G - счетный граф, каждый конечный
подграф которого планарен; тогда и G планарен.
Доказательство. Так как G-
счетный граф, то его вершины можно занумеровать в последовательность v1,
v2, v3,.... Исходя из нее, построим строго
возрастающую последовательность G1 G2 G3 ... подграфов графа G, выбирая в качестве Gk подграф с вершинами v1, ..., vk и ребрами графа G,
соединяющими только эти вершины между собой. Далее, примем на веру тот факт,
что графы Gi могут быть уложены на плоскости
конечным числом (скажем m(i)) топологически различных способов,
и построим еще один бесконечный граф H. Его вершины wij (i≥1, 1 ≤ j ≤ m(i)) пусть соответствуют различным
укладкам графов {Gi}, а
его ребра соединяют те из вершин wij и wkl, для которых k = i + 1 и плоская укладка,
соответствующая wkl
«расширяется» (очевидным образом) до укладки, соответствующей wij. Легко видеть, что граф H связен и локально конечен, поэтому,
как следует из леммы Кёнига, он содержит бесконечную в одну сторону простую
цепь. А так как граф G
является счетным, то эта бесконечная простая цепь и дает требуемую плоскую
укладку графа G. //
Стоит подчеркнуть, что если принять дальнейшие аксиомы теории множеств (в
частности, аксиому выбора для несчетных множеств), то многие результаты
(подобные только что доказанному) можно перенести и на такие бесконечные графы,
которые не обязательно являются счетными.
В заключение этого небольшого отступления в область бесконечных графов
дадим краткий обзор свойств бесконечных эйлеровых графов. Естественно назвать
связный бесконечный граф (эйлеровым, если в нем существует бесконечная в обе
стороны цепь, содержащая каждое ребро графа G; такая бесконечная цепь называется (двусторонней) эйлеровой
цепью. Далее, назовем граф G
полуэйлеровым, если в нем существует бесконечная (в одну или в обе стороны)
цепь, содержащая каждое ребро графа G. Заметим, что эти определения требуют счетности графа G. В следующих теоремах даны условия,
необходимые для того, чтобы бесконечный граф был эйлеровым или полуэйлеровым.
Теорема 8Е. Пусть G -
связный счетный граф, являющийся эйлеровым. Тогда (i) в графе G нет
вершин нечетной степени; (ii)
для каждого конечного подграфа Н графа G бесконечный граф Н (полученный удалением из G ребер графа Н) имеет не более двух
бесконечных, связных компонент; (iii)
если, кроме того, степень любой вершины из Н четна, то Н имеет ровно одну
бесконечную связную компоненту.
Доказательство. (i)
Предположим, что Р - эйлерова цепь; тогда, рассуждая так же, как и в
доказательстве теоремы 6В, получим, что степень любой вершины из G должна быть либо четной, либо
бесконечной.
(ii) Разобьем цепь Р на три подцепи Р_,
Р0 и Р+ так, что Р0 - конечная цепь,
содержащая все ребра графа Н (и, быть может, другие ребра), а Р- и Р+
- две бесконечные в одну сторону цепи. Тогда бесконечный граф /С, образованный
ребрами цепей Р_ и Р+(а также инцидентными им вершинами) имеет не более
двух бесконечных компонент. Так как H получается из K
присоединением лишь конечного множества ребер, то отсюда и следует нужный
результат.
(iii) Пусть v и w - начальная и конечная вершины цепи Р0; v и w связаны в Н. Если v = w, то это очевидно; если v ≠w, то,
применяя следствие 6D к графу,
полученному из Р0 удалением ребер графа Н (по предположению в этом
графе ровно две вершины, а именно v и w, имеют нечетные степени), получим требуемый результат. //
Можно получить соответствующие необходимые условия для полуэйлеровых
бесконечных графов.
Теорема 8F.
Пусть G - связный счетный граф, являющийся полуэйлеровым, но не эйлеровым;
тогда (i) G содержит либо не более одной вершины нечетной степени, либо
не менее одной вершины бесконечной степени; (ii) для каждого конечного подграфа Н графа G бесконечный граф Н (описанный ранее)
содержит ровно одну бесконечную компоненту. //
Теорема 8G.
Пусть G- связный счетный граф; G является эйлеровым графом тогда и
только тогда, когда выполнены условия (i), (ii) и
(iii) теоремы 8Е. Более того, G является полуэйлеровым тогда и
только тогда, когда выполнены либо эти условия, либо условия (i) и (ii) теоремы 8F.
Глава 3. Деревья
§8. Элементарные свойства деревьев
Лесом называется граф, не содержащий циклов; связный лес называется
деревом. Например, на Рис. 1 изображен лес, состоящий из четырех компонент,
каждая из которых является деревом. Заметим, что по определению деревья и леса
являются простыми графами.
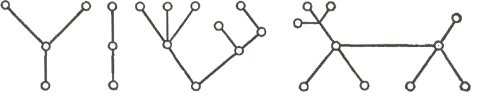
Рис.1
По многим показателям дерево представляет собой простейший нетривиальный
тип графа. Как будет показано в теореме 9А, оно обладает некоторыми «приятными»
свойствами; например, любые две его вершины соединены единственной простой
цепью. Пытаясь доказать какой-нибудь общий результат или проверить гипотезу для
графов, удобно бывает начать с деревьев, хотя и существует несколько гипотез,
которые еще не доказаны для произвольных графов, несмотря на то, что они верны
для деревьев.
В следующей теореме перечислены некоторые простые свойства деревьев.
Теорема 9А. Пусть граф Т имеет n вершин. Тогда следующие утверждения эквивалентны: (i) Т является деревом, (ii) Т не содержит циклов и имеет n - 1 ребер; (iii) Т связен и имеет n - 1 ребер; (iv) Т связен и каждое его ребро является мостом;
(v) любые две вершины графа Т соединены ровно одной простой цепъю; (vi) Т не
содержит циклов, но, добавляя к нему любое новое ребро, получим ровно один
цикл.
Доказательство. Если n = 1,
утверждение очевидно. Предположим поэтому, что n≥ 2.
(i) => (ii). По определению Т не содержит циклов,удаление любого ребра
разбивает Т на два графа, каждый из которых является деревом. По индуктивному
предположению число ребер в каждом из этих деревьев на единицу меньше числа
вершин. Отсюда выводим, что полное число ребер графа Т равно n - 1.
(ii) => (iii). Если граф Т несвязен, то каждая его компонента
представляет собой связный граф без циклов. Из предыдущей части доказательства
следует, что число вершин в каждой из компонент больше числа ее ребер на
единицу. Значит, полное число вершин графа Т больше полного числа его ребер по
крайней мере на 2, а это противоречит тому, что Т имеет n - 1 ребер.
(iii)=> (iv). Удаление любого ребра
приводит к графу с n вершинами и n - 2 ребрами, который не может быть
связным по теореме 5В.
(iv)=>(v). Так как Т
связен, то каждая пара его вершин соединена по крайней мере одной простой
цепью. Если же данная пара вершин соединена двумя простыми цепями, то они
замыкаются в цикл, а это противоречит тому, что каждое ребро в Т является
мостом.
(v)=> (vi). Если Т содержит цикл, то
любые две вершины этого цикла соединены по крайней мере двумя простыми цепями.
Добавим теперь к графу Т какое-то ребро е; тогда получим цикл, поскольку
инцидентные ребру е вершины уже соединены в Т простой цепью. То, что при этом мы
получим только один цикл.
(vi)=> (i). Предположим, что Т несвязен; тогда добавление любого
ребра, соединяющего вершину одной компоненты с вершиной другой компоненты, не
приводит к образованию цикла.
Следствие 9В. Пусть G -
лес с n вершинами и k компонентами, тогда G имеет n - k ребер.
Доказательство. Применим к каждой компоненте графа G предложение (ii) теоремы 9А. //
Заметим, что по лемме о рукопожатиях сумма степеней всех n вершин дерева равна удвоенному числу
его ребер (2n - 2); отсюда следует, что при n ≥ 2 дерево, имеющее n вершин, всегда содержит не менее двух висячих вершин.
Известно, что в связном графе G удаление одного ребра, принадлежащего некоторому выбранному циклу, не
нарушает связности оставшегося графа. Применим эту процедуру к одному из оставшихся
циклов, и так до тех пор, пока не останется ни одного цикла. В результате
получим дерево, связывающее все вершины графа G; оно называется остовным деревом графа G. Пример графа и одного из его
остовных деревьев дан на Рис. 2 и 8.3.
В общем случае обозначим через G произвольный граф с n
вершинами, m ребрами и k компонентами. Применяя описанную выше процедуру к каждой
компоненте G, получим в результате граф,
называемый остовным лесом. Число удаленных в этой процедуре ребер называется
циклическим рангом (или дипломатическим числом) графа G и обозначается через γ(G). Легко видеть, что γ(G)= m - n + k и является неотрицательным целым
числом (по теореме 5В). Таким образом, циклический ранг дает меру связности
графа: циклический ранг дерева равен нулю, а циклический ранг циклического
графа равен единице. Удобно также определить коциклический ранг (или ранг
разреза) графа G как число ребер
в его остовном лесе; коциклический ранг обозначается через х(G) и равен n - k.

Докажем два простых результата, касающихся остовных лесов. В этой теореме
дополнением остовного леса Т некоторого (необязательно простого) графа G
является граф, полученный из G
удалением ребер Т.
Теорема 9С. Если Т - остовный лес графа П, то (i) всякий разрез в G имеет общее ребро с Т; (ii) каждый цикл в G имеет общее ребро с дополнением Т.
Доказательство. (i)
Пусть С* - разрез графа G,
удаление которого разбивает одну из компонент G на два подграфа H и K. Поскольку Т - остовный лес, в нем
должно содержаться ребро, соединяющее вершину из H с вершиной из K; это
и есть требуемое ребро.
(ii) Пусть С - цикл в графе G, не имеющий ни одного общего ребра с
дополнением Т; тогда С содержится в Т, что невозможно.
С понятием остовного леса Т графа G тесно связано понятие фундаментальной системы циклов,
ассоциированной с Т. Оно определяется следующим образом: если добавить к Т
любое не содержащееся в нем ребро графа G , то по предложению (vi) теоремы 9А получим единственный
цикл; множество всех циклов, получаемых таким способом (т. е. путем добавления
по отдельности каждого ребра из G, не
содержащегося в Т), называется фундаментальной системой циклов, ассоциированной
с T. В том случае, когда нас не
интересует, какой остовный лес рассматривается, фундаментальная система циклов
графа G. Ясно, что циклы данной
фундаментальной системы должны быть различными и что их число должно равняться
циклическому рангу графа G. На
Рис. 4 показана фундаментальная система циклов графа, изображенного на Рис. 2,
ассоциированная с остовным деревом, изображенным на Рис. 3.
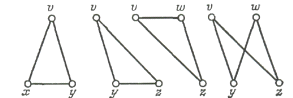
Рис. 4
Надеяться, что удастся определить фундаментальную систему разрезов графа
С, ассоциированную с данным остовным лесом Т. Покажу, что это действительно
можно сделать. По предложению (iv) теоремы 9А удаление любого ребра из Т
разбивает множество вершин дерева Т на два непересекающихся подмножества V1
и V2. Множество всех, ребер графа G, каждое из которых соединяет вершину из V1 с вершиной из V2 является разрезом графа G. Множество всех разрезов, полученных таким способом (т. е.
удалением по отдельности каждого ребра из Т), называется фундаментальной
системой разрезов, ассоциированной с Т. Ясно, что разрезы данной
фундаментальной системы должны быть различными и что их число должно равняться
коциклическому рангу графа С. Фундаментальной системой разрезов графа,
изображенного на Рис. 2, ассоциированной с остовным деревом, изображенным на
Рис. 3, является такая система: {е1, е5}, {е2,
е5, е7, е8}, {е3, е6, е7,
е8} и {е4, е6, е8}.
ПРАКТИЧЕСКАЯ ЧАСТЬ
1)
Можно ли ходом шахматного коня обойти шахматную доску размером
Х8 так, чтобы каждый ход встречался ровно один раз (при этом мы считаем,
что ход «встречался», если конь переместился с одной клетки на другую любым из
двух возможных способов)? Тот же вопрос для короля и ладьи. Как изменятся
ответы для шахматной доски размером 7X7? Изложите свои ответы в терминах теории
графов.
Ответ: Для доски 8х8:Что бы каждый ход встречался ровно один раз,должно
выполняться условие: конь должен зайти на клетку и сойти с неё т.е перейдя к
терминам теории графов ,получим :клетка-вершина графа ,каждая вершина имеет
степень равную 2 (есть 2 ребра вход и выход).Значит степень каждой вершины
будет чётной => согласно теореме этот граф будет гамильтоновым, а значит
существует гамильтонова цепь-путь обхода шахматной доски. Данное утверждение
справедливо не только для коня, но для ладьи и короля. Эти соображения не
изменяются и для шахматной доски размером 7х7.
2)
В графе Петерсена найдите (i)
маршрут длины 4; (ii) циклы длины 5,
6, 8 и 9; (iii) разрезы, содержащие 3, 4 и 5 ребер
Ответ:
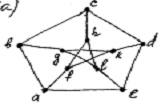
) a>b>c>h>l(маршрут длины 4)
) а)f>h>l>g>k>f
(цикл длины 5)
В) a>b>c>d>k>f>a (6))
h>l>g>k>f>a>b>c>h (8))
d>e>l>g>b>c>h>f>k>d (9)
3) a) {1,2,3}
-(разрез,содержащий 3 ребра)
b) {1,2,3,7} (4)
c) {4,5,6,7,8} (5)
3) Докажите, что ребро связного графа является мостом и
в том и только в том случае, когда оно не содержится ни в одном из циклов
Ответ: Ребро {a,b}
является мостом в том и только в том случае ,если оно не принадлежит ни одному
циклу.
Прямая теорема: Если ребро{a,b} не
принадлежит ни одному циклу ,при его удалении не остаётся пути, связывающего а
и в то есть {a,b} является мостом.
Обратная теорема: Если ребро
{a,b} -мост, то {a,b} не
принадлежит ни одному циклу. Если бы ребро {a,b}
принадлежало циклу, то пути удалении ребра {a,b}
остался бы второй путь, связывающий а и в , то есть ребро {a,b} не
было бы мостом следовательно {a,b} не принадлежит циклу.
4) В обеденный перерыв члены строительной бригады
разговорились о том, кто сколько газет читает. Выяснилось, что каждый
выписывает и читает две и только две газеты, каждую газету читает пять человек,
и любая комбинация читается одним человеком. Сколько различных газет выписывают
члены бригады? Сколько человек в бригаде?
Ответ:
Решение этой задачи
достигается построением графа, где каждая вершина обозначает соответствующую
газету и соответственно 5 подписчиков, а каждое ребро будет соответствовать одному
подписчику.
Иными словами, суть метода
решения этой и подобных ей задач состоит в установлении связей между множеством
вершин и множеством ребер графа.
Любая географическая карта
является многоугольным графом, в котором страны будут гранями, границы - ребрами,
а окружающий страны Мировой океан - бесконечной гранью.Для лучшего зрительного
восприятия необходимо, чтобы страны с общей границей были раскрашены в разные
цвета. Такую карту называют "правильно" раскрашенной.
Широко известное
предположение состоит в том, что каждая карта может быть раскрашена с
соблюдением требуемых условий при помощи четырех красок. Этому вопросу
уделяется большое внимание в популярной литературе, и здесь мы не будем
останавливаться на его рассмотрении.
Задачи на проведение эйлеровых
линий без повторений и без отрыва карандаша от бумаги являются одним из
математических развлечений. При решении подобных задач необходимо помнить
следующее положение.
Для того, чтобы на графе
имелась цепь, соединяющая АА и ВВ, содержащая все его ребра в точности по
одному разу, необходимо и достаточно, чтобы АА и ВВ были единственными
нечетными вершинами, т. е. вершинами с нечетной степенью.
5) Из трех человек, стоящих рядом, один всегда говорит
правду (правдолюб), другой всегда лжет (лжец), а третий, смотря по
обстоятельствам, говорит либо правду, либо ложь (дипломат). У стоящего слева
спросили: "Кто стоит рядом с тобой?". Он ответил:
"Правдолюб". Стоящему в центре задали вопрос: "Кто ты?", и
он ответил: "Я дипломат". Когда у стоящего справа спросили: "Кто
стоит рядом с тобой?", он сказал: "Лжец". Кто где стоял?
Ответ: Если в данной задаче
ребро графа будет соответствовать месту, занимаемому тем или иным человеком, то
нам могут представиться следующие возможности .
Рассмотрим первую
возможность. Если "правдолюб" стоит слева, то рядом с ним, судя по
его ответу, также стоит "правдолюб". У нас же стоит "лжец".
Следовательно, эта расстановка не удовлетворяет условию задачи. Рассмотрев
таким образом все остальные возможности, мы придем к выводу, что позиция "дипломат",
"лжец", "правдолюб" удовлетворяет задаче. Действительно,
если "правдолюб" стоит справа, то, по его ответу, рядом с ним стоит
"лжец", что выполняется. Стоящий в центре заявляет, что он "дипломат",
и, следовательно, лжет (что возможно из условия), а стоящий справа также лжет.
Таким образом, все условия задачи выполнены.
Заключение
Графы и информация
Двоичные деревья играют весьма важную роль в теории информации.
Предположим, что определенное число сообщений требуется закодировать в виде
конечных последовательностей различной длины, состоящих из нулей и единиц. Если
вероятности кодовых слов заданы, то наилучшим считается код, в котором средняя
длина слов минимальна по сравнению с прочими распределениями вероятности.
Задачу о построении такого оптимального кода позволяет решить алгоритм
Хаффмана.
Двоичные кодовые деревья допускают интерпретацию в рамках теории поиска.
Каждой вершине при этом сопоставляется вопрос, ответить на который можно либо
"да", либо "нет". Утвердительному и отрицательному ответу
соответствуют два ребра, выходящие из вершины. "Опрос" завершается,
когда удается установить то, что требовалось.
Таким образом, если кому-то понадобится взять интервью у различных людей,
и ответ на очередной вопрос будет зависеть от заранее неизвестного ответа на
предыдущий вопрос, то план такого интервью можно представить в виде двоичного
дерева.
Графы и химия
Еще А. Кэли рассмотрел задачу о возможных структурах насыщенных (или
предельных) углеводородов, молекулы которых задаются формулой:
CnH2n+2
Все атомы углеводорода четырехвалентны, все атомы водорода одновалентны.
Структурные формулы простейших углеводородов показаны на рисунке 6.1 (а - метан
CH4, б - этан C2H6).
Молекула каждого предельного углеводорода представляет собой дерево. Если
удалить все атомы водорода, то оставшиеся атомы углеводорода также будут
образовывать дерево, каждая вершина которого имеет степень не выше 4.
Следовательно, число возможных структур предельных углеводородов, т. е. число
гомологов данного вещества, равно числу деревьев с вершинами степени не больше
четырех.
Таким образом, подсчет числа гомологов предельных углеводородов также
приводит к задаче о перечислении деревьев определенного типа. Эту задачу и ее
обобщения рассмотрел Д. Пойа.
Графы и биология
Деревья играют большую роль в биологической теории ветвящихся процессов.
Для простоты мы рассмотрим только одну разновидность ветвящихся процессов -
размножение бактерий. Предположим, что через определенный промежуток времени
каждая бактерия либо делится на две новые, либо погибает. Тогда для потомства
одной бактерии мы получим двоичное дерево.
Нас будет интересовать лишь один вопрос: в скольких случаях n-е поколение одной бактерии
насчитывает ровно k потомков?
Рекуррентное соотношение, обозначающее число необходимых случаев, известно в
биологии под названием процесса Гальтона-Ватсона. Его можно рассматривать как
частный случай многих общих формул.
Графы и физика
Еще недавно одной из наиболее сложных и утомительных задач для
радиолюбителей было конструирование печатных схем.
Печатной схемой называют пластинку из какого-либо диэлектрика
(изолирующего материала), на которой в виде металлических полосок вытравлены
дорожки. Пересекаться дорожки могут только в определенных точках, куда
устанавливаются необходимые элементы (диоды, триоды, резисторы и другие), их
пересечение в других местах вызовет замыкание электрической цепи.
В ходе решения этой задачи необходимо вычертить плоский граф, с вершинами
в указанных точках.
Итак, из всего вышесказанного неопровержимо следует практическая ценность
теории графов, доказательство которой и являлось целью данной работы.
Список используемой литературы:
1. Уилсон Р.
Введение в теорию графов.- М.:Мир,1977
2. Белов
В.В., Воробьев Е.М., Шаталов В.Е. Теория графов. - М.: ВШ, 1976
. Березина
Л.Ю. Графы и их применения. - М., 1979
. Новиков
Ф.А. Дискретная математика для программистов. - Спб.: Питер, 2003.-304с
. Кузнецов
О.П., Адельсон-Вельский Г.М. Дискретная математика для инженера.- 2-е изд.,
перераб. и доп. - М.: Энергоатомиздат,1988.-480с
6. Новиков,
Ф.А. Дискретная математика для программистов [Текст]/Ф.А. Новиков. - СПб.:
Питер, 2003. - 304 с.
7. Овчинников,
В.А. Алгоритмизация комбинаторно-оптимизационных задач при проектировании ЭВМ и
систем: учебник для вузов [Текст]/В.А. Овчинников. - М.: Изд-во МГТУ им.
Н.Э.Баумана, 2001. - 228 с.
8. Подготовка к ЕГЭ. Информатика и ИКТ.[Текст]:учебное пособие / Под ред.
Н. В. Макаровой. - СПб.: Питер, 2007.-160c.